Shear Wave Dispersion as a Potential Biomarker for Cervical Remodeling During Pregnancy: Evidence From a Non-Human Primate Model

1 Introduction

Preterm birth is the main cause of death in newborn children and its incidence rate is increasing [1, 2]. A factor contributing to this problem is the lack of objective methods to describe the structural and functional changes that gestational tissues go through during pregnancy and labor [3].

One of the gestational tissues that suffers the most dramatic transformation is the cervix. The cervix is a cylindrical-shaped structure at the lower uterus that, during pregnancy, serves as a protective barrier between the developing fetus and the exterior. As pregnancy advances, the cervix softens and, close to delivery, shortens, ripens, and dilates to allow for vaginal parturition. In both term and preterm births, this transformation is achieved through a dramatic biochemical and structural transformation of the cellular and extracellular components of the cervical stroma [4].

The extracellular matrix of the cervix is composed of layers of semi-aligned collagen fibers immersed in a viscous matrix of long-chain molecules such as proteo- and glycosaminoglycans [5]. As pregnancy progresses, mature crosslinks holding together collagen fibrils are replaced by immature crosslinks. As a result, collagen organization is gradually lost and the cervix softens [4]. During the ripening stage, the concentration of sulfated glycosaminoglycans increases, particularly that of hyaluronic acid (HA) [6]. Due to the hydrophilic nature of HA, cervical hydration augments, further separating collagen fibrils [7–14]. All these changes alter drastically the mechanical properties of the cervix, such as its stiffness and viscosity [15].

During the last decade, various groups have investigated the use of Shear Wave Elasticity Imaging (SWEI) to objectively quantify changes in cervical stiffness during pregnancy and to assess the risk of preterm birth [16–21]. SWEI is an ultrasound-based method that generates shear waves in the tissue of interest using an acoustic radiation force impulse (ARFI) produced with a clinical transducer. The ARFI-induced shear wave motion is tracked with pulse-echo imaging techniques, allowing analysis of the propagation of the shear wave. If the medium is assumed to be linear, purely elastic, isotropic, and homogeneous, a simple relationship between the shear wave group speed $V_g$ and the tissue stiffness described by its shear modulus μ can be established: $\mu =\rho V_g^2$, where ρ is the medium mass density [22]. Various studies have demonstrated a significant reduction of $V_g$ during pregnancy in ex vivo and in vivo studies in humans and animal models [17, 20, 23–25]. However, these studies are limited by the aforementioned assumptions behind the link between the group velocity and the shear modulus, which ignore the effects that the complex extracellular matrix has on shear wave propagation.

The layered collagenous microstructure of the cervix and the presence of the highly viscous ground substance cause shear wave dispersion, i.e., the phase speed (the speed at which different frequency components of the shear wave move) varies with frequency. Shear wave dispersion has been demonstrated in other structurally complex tissues such as tendon and muscle [26, 27]. Using a multi-scale simulation strategy with different viscoelastic models Peralta et al. [28] demonstrated significant shear wave dispersion in the cervix. More recently, our group observed that the slope of the phase velocity vs. frequency in ex vivo cervix samples from a non-human primate (NHP) model was 5.5 m/s-kHz (interquartile range: 1.5–12.0 m/s-kHz) [20]. In the same study, we also demonstrated that shear wave dispersion could be indirectly assessed by comparing the group speeds determined with particle velocity and particle displacement. The time derivative relationship between the particle velocity and the particle displacement makes the former more sensitive to higher frequencies, thus resulting in higher group speed values than those obtained with the particle displacement [29]. Interestingly, no differences in dispersion were observed between normal cervix samples and those in which ripening was induced with the prostaglandin Misoprostol. This was attributed to the large variance of shear wave displacements, probably related to the larger stiffness of the rhesus macaque cervix compared to the human one [20, 30]. The quantification of descriptors of shear wave dispersion could provide quantitative imaging biomarkers that could be more sensitive than the group speed to changes in mechanical properties of the cervix.

Thus, in this study, we present evidence from a NHP model of the pregnant cervix that shear wave dispersion quantified with SWEI can be used as a quantitative imaging biomarker for cervical remodeling. We chose to work with the NHP model, in particular the Rhesus macaque, because of its similar maternal-fetal physiology to humans. Furthermore, because Rhesus macaques are non-obligated quadripeds, the mechanical loading on the cervix is more similar to the human case [31–35]. Previous studies from our group have shown similar rates of shear wave reduction during pregnancy in humans and Rhesus macaques, thus showing the suitability of this model [21, 24]. To overcome the limitations of high displacement variance in the Rhesus macaque cervix, we performed a pre-selection of two possible descriptors of dispersion, the ratio of group speeds from particle velocity/particle displacement and the slope of the phase velocity vs. frequency, combined with two noise reduction strategies. After the pre-selection stage, the descriptor with larger changes due to dispersion was applied to SWEI data from the mid-pregnancy and late-pregnancy NHP cervix.

2 Materials and Methods

2.1 SWEI-Based Descriptors of Dispersion

We investigated two possible SWEI-based descriptors of dispersion, one defined in the time domain, and another in the Fourier domain. The time-domain descriptor is the ratio R of group speeds computed with particle velocity $v_p$ over particle displacement $u_p$:

$R=\frac{V_g\left(v_p\right)}{V_g\left(u_p\right)},(1)$

where $v_p$ can be determined from $u_p$ by:

$v_p=d{u}_p/dt.(2)$

$V_g$ is usually estimated by tracking the time of flight of the maximum particle displacement or particle velocity away from the ARFI excitation [36]. In an approximately purely elastic material, both estimates of $V_g$ agree. However, this is not the case in viscoelastic media because the time-derivative in Eq. 2 acts as a high-pass filter in the frequency domain [29]. Thus, the more dispersive the medium is, the larger $V_g\left(v_p\right)$ is over $V_g\left(u_p\right)$ [20, 37]. In other words, for a purely elastic material, $R=1$, and for a viscoelastic one, $R>1$. This descriptor takes advantage of the various robust methods that have been proposed to quantify the group speed, such as the random sample consensus, or RANSAC, algorithm [38] or the Radon sum method [36, 37]

The Fourier-domain descriptor directly quantifies dispersion as the slope S of the phase velocity vs. frequency over the shear wave bandwidth [20]. To quantify S, we computed the particle velocity power spectrum $V\left(k,\omega \right)$, i.e., the square magnitude of the 2D-Fourier transform for the particle velocity $v_p\left(x,t\right)$, where k is the wave number and ω is the angular frequency [39]. To parameterize the frequency dependence of the phase speed $V_p\left(\omega \right)$ we used a linear model defined by an intercept $V_{p,0}$ and a slope $d{V}_p/d\omega$. To find the values of the parameters of the linear fit, a Radon-sum strategy proposed by [40] was used. Briefly, curved trajectories are defined on the velocity power spectrum as function of the linear fit parameters. The values of the parameters are selected from the trajectory along which the sum of the spectrum values is maximized. The sum was done over the -6 dB spatial and temporal frequency bandwidth. Finally, we used $S=d{V}_p/d\omega$ as the Fourier-domain descriptor of dispersion.

2.2 Pre-selection Stage

The pre-selection stage consisted of selecting the descriptor with the largest changes in dispersion in viscoelastic media over the estimation variance. To have control over the degree of dispersion, we used computational phantoms based on finite-element models of Zener viscoelastic solids implemented on LS-Dyna (Version 3.2 β, Livermore, Software Technology Corp., Livermore, CA) following the method described by [41]. Dispersion was controlled by varying the viscous component of the Zener model (one spring in parallel with a series of a spring and a dashpot). Shear waves were created through fields of axial stresses with spatial Gaussian symmetry that simulated acoustic radiation force impulse stimuli produced by clinical ultrasound transducers [29]. The width of the Gaussian profile was 0.1 mm, based on a previously reported computational optimization [42]. The stress fields were applied during 0.1 ms. The center of the stress field was at a depth of 30 mm, corresponding the axial center of the simulated computational phantom [41].

The stress relaxation response of the Zener model has three parameters, the instantaneous shear modulus $G_0$, the equilibrium shear modulus $G_{\infty }$, and the time constant b. The values of $G_0$ and $G_{\infty }$ were fixed at 20 kPa and 2 kPa, respectively, and the value of b was varied from 3,000 s to 30,000 s, corresponding to changes in the viscous component from 0.6 to 6.0 Pa s. The temporal and spatial sampling rates of the simulated mechanical response (shear wave displacements) were 0.1 $\mu s$ and 0.25 mm, respectively, for a total simulated time of 10 ms. For the shear wave frequencies that were simulated (peak temporal frequencies between 100 and 200 Hz as shown in Figure 1), there were at least 10 nodes per wavelength. To mimic the pulse repetitions frequencies used in commercial scanners such as the one used in the animal model study, the displacements were down sampled to 0.1 ms. The axial and lateral length was 60 mm and 20 mm respectively; additionally a 5-element thick perfect matching layer was added to all outward faces of the mesh to suppress reflections back into the analysis ROI. The analysis of shear wave propagation was done over a 5 mm axial extent centered at the ARF focus (30 mm deep), similarly to the analysis done in the animal model. Zero-mean Gaussian noise was added to particle displacements to analyze the compromise between changes of the descriptors due to dispersion and estimation variance [43]. The level of noise was controlled by a factor k that defined the standard deviation as a factor of the maximum displacement induced by the stress field in each simulation. The value of k was varied from 0 to 0.1.

FIGURE 1

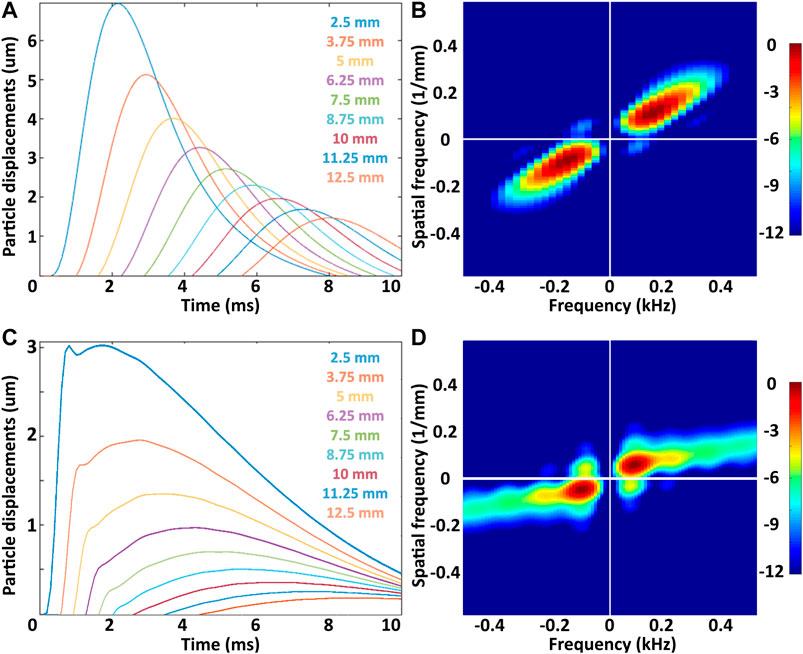
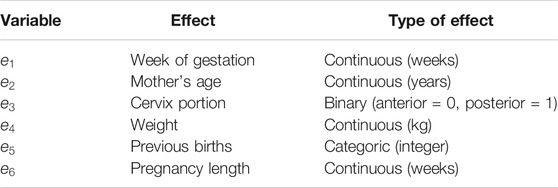
FIGURE 1. (A) and (C) Particle displacements as a function of time induced in the simulated viscoelastic media with 0.6 and 6 Pa s viscosity, respectively. Labels indicate the distance from the center of the ARF stimulus. (B) y (D) Fourier spectra for the same media. The spectrum peak occurs within a frequency range from 100 to 200 Hz.

The compromise between changes of each parameter and the estimation variance was quantified in terms of the contrast-to-noise ratio of each descriptor with respect to its value for the least dispersive medium. The CNR was mathematically defined as:

$\text{CNR}=\frac{\left|P_{{\eta }_i}-P_{{\eta }_{\min }}\right|}{\sqrt{{\sigma }_{P_{{\eta }_i}}^2+{\sigma }_{P_{{\eta }_{\min }}}^2}},(3)$

where $P_{{\eta }_i}$ is the value of either S or R for the material width the ith value of viscosity η, and $P_{{\eta }_{\min }}$ is the value of the same parameter for the least viscous medium. ${\sigma }_{P_{{\eta }_i}}$ and ${\sigma }_{P_{{\eta }_{\min }}}$ are the standard deviations of these parameters. The value of the CNR for each parameter was computed for different combinations of viscosity and noise. Twenty independent realizations of the noise were added to the simulated shear wave fields to estimate the mean and standard deviation of the CNR.

2.3 Noise Reduction Strategies

Preliminary estimates of shear wave dispersion in the ex vivo NHP cervix [20] showed large variance possibly related to the high stiffness of cervical tissue compared to other soft tissues such as liver. To overcome this limitation and increase the sensitivity of dispersion descriptors, we implemented two noise reduction strategies.

2.3.1 Automated Low-Pass Filter

Because random noise dominates at high temporal frequencies [44], low-pass filters have been commonly used in previous applications of shear wave elasticity imaging on cervical tissue [24]. We implemented this strategy and designed an automated criterion to select the cutoff frequency. This allowed us to automatically adapt the filter to the noise level in each simulated condition. To this end, we first obtained the maximum projection of the 2D spectrum of the particle velocity to obtain the velocity power spectrum vs. temporal frequency. Then, the cut-off frequency was defined by the intersection of two lines fitted to the velocity power spectrum vs. temporal frequency within a bandwidth that contains the shear wave signal (100–500 Hz) and a high-frequency bandwidth that contains noise (1–5 kHz). This is graphically represented in Figure 2.

FIGURE 2

FIGURE 2. Projected particle velocity spectrum of a viscoelastic solid with 6.0 Pa s viscosity and a $k=0.1$ noise level (orange curve). The green and yellow lines are linear fits to the noisy spectrum at low (0.1kHz–0.5 kHz) and high frequencies (1 kHz–5 kHz), respectively. The intersection of both fits allows determination of the cutoff frequency $f_c$. The blue curve shows the noise-free case to demonstrate the agreement of the fit over noisy data to the noiseless case.

2.3.2 Singular Value Decomposition Filter

The second strategy consisted of a filter based on the singular value decomposition (SVD) of shear wave displacements. This technique has been used to reduce clutter in other ultrasound techniques such as Doppler imaging and functional ultrasound [45]. The SVD filtering strategy is based on the fact that noise components of the displacement field have low spatial and frequency correlation compared to the components caused by shear wave propagation. Thus, unlike the low-pass filter strategy defined above, the SVD filter considers both temporal and spatial information. Also, in contrast to previous uses of the SVD, we aim at maintaining highly correlated components of the displacement field. To apply this filter, the 2D displacements are sorted into a Casorati Matrix $\mathbf{S}$ with the spatial information in the columns and the temporal information in the rows [45]. The Casorati matrix is decomposed into the product of three matrices, $\mathbf{S}=\mathbf{U}\mathbf{\Delta }{\mathbf{V}}^{\ast }$, where matrices $\mathbf{U}$ and $\mathbf{V}$ contain the eigenvectors of the covariance matrices $\mathbf{S}{\mathbf{S}}^{\ast }$ and ${\mathbf{S}}^{\ast }\mathbf{S}$, respectively, and $\mathbf{\Delta }$ is a diagonal matrix containing the singular values (square root of the eigenvalues of the covariance matrices) in decreasing order [46]. The first diagonal elements represent the contribution of the shear wave to the covariance (high contributions), while the last ones represent the contribution of random noise (low contributions). To filter noise, a displacement matrix $\mathbf{S}\prime$ is reconstructed removing the eigenvalues smaller than the cutoff eigenvalue, corresponding to the seventh eigenvector. The cutoff index value was defined by minimizing the tradeoff between bias and variance in the estimation of dispersion based on simulations. This tradeoff was quantified in terms of the Contrast-to-Total-Error-Ratio (CTER), defined as the ratio of the contrast of parameter P with respect to its value in the least dispersive medium over the combined root mean squared error RMSE:

$\text{CTER}=\frac{P_{\eta }-P_{{\eta }_{\min }}}{\sqrt{\text{RMSE}{\left(\eta \right)}^2+\text{RMSE}{\left({\eta }_{\min }\right)}^2}},(4)$

where RMSE was computed as:

$\text{RMSE}\left(\eta \right)=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^N{\left(P_{\eta ,e}-P_{{\eta }_i}\right)}^2}}{N}},(5)$

where $P_{\eta ,e}$ is the expected value of the parameter for each degree of viscosity.

The CNR of R and S for media with different dispersion (from different degrees of viscosity) and different noise levels where compared with and without each of the noise reduction strategies to identify the combination that maximized the CNR.

2.4 In vivo Application to Pregnant Rhesus Macaques

After identifying the combination of the dispersion descriptor and noise reduction strategy that maximized CNR, the combination was used to evaluate changes in the dispersion properties of the NHP cervix during pregnancy. To this end we used data from a longitudinal SWEI study on 18 pregnant Rhesus macaques acquired at weeks 10 and 23 of gestation, corresponding to mid and late pregnancy [21]. The study was performed at the Wisconsin National Primate Research Center and the protocol was approved by the Institutional Animal Care and Use Committee of the University of Wisconsin-Madison. Characteristics of the subjects are described in Table 1.

TABLE 1

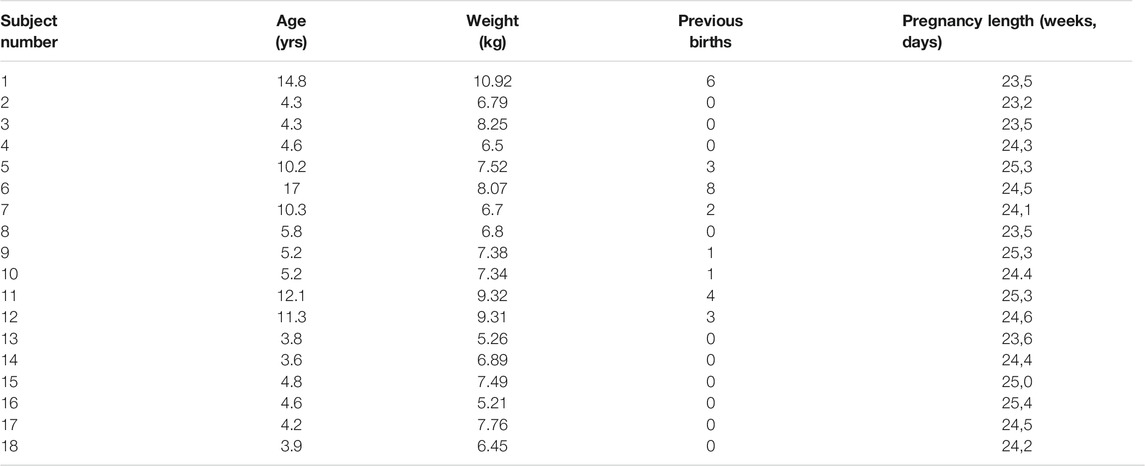
TABLE 1. Characteristics of the macaques. For each macaque, tissue measurements were taken in the anterior and posterior region with respect to the cervical canal during gestation weeks 10 and 23.

SWEI data was acquired from the NHP cervix using a transrectal scanning approach on a longitudinal view of the cervix. Data was acquired with a prototype catheter transducer on a Siemens Acuson S2000 ultrasound scanner (Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA, USA). Technical details about SWEI implementation can be found in [21]. Shear waves were induced in two propagation directions (from the uterine end to the vaginal end of the cervix, and vice versa) and were tracked over a $6\times 5$ ${mm}^2$ region of interest centered first on the posterior and then on the anterior portions of the cervix.

Shear-wave induced displacements were estimated from raw IQ data obtained from the system’s Axius Direct Ultrasound Research Interface [47] with Loupas’ correlation method [48]. Displacement estimates were rejected based on values of the correlation coefficient ($<$0.98) and filtered to eliminate low frequency biological motion using a second-order polynomial motion filter [40]. The first lateral millimeter of the displacement field was discarded due to ARF stimulus effects. In vivo data quality was assessed through three criteria (Figure 3):

1. Evidence of a planar wavefront: Maps of the laterally-integrated particle displacement vs axial position and time must show no variation over the axial position (planar wavefront), and should gradually decrease over time mainly due to attenuation (Figure 3A). Data not showing these characteristics were rejected (Figure 3D).

2. Statistically significant particle displacements. Following a criterion proposed by [20], particle displacements were compared to those estimated from reference tracking frames acquired before the application of the ARF stimulus (Figure 3B). Data was rejected if time-averaged displacements (pink curve in Figures 3B,E) were not larger than a threshold (red dashed line) defined as three times the standard deviation of the reference particle displacements (black dashed line) over more than half of the axial span of the ROI. For the rest of the data, we only processed displacements that were continuously above the threshold (right side of vertical green line in Figure 3E).

3. Data with high noise after filtering: Finally, we rejected all the filtered data with noise levels at high temporal frequencies above -6 dB of the maximum signal (Figures 3C,F).

FIGURE 3

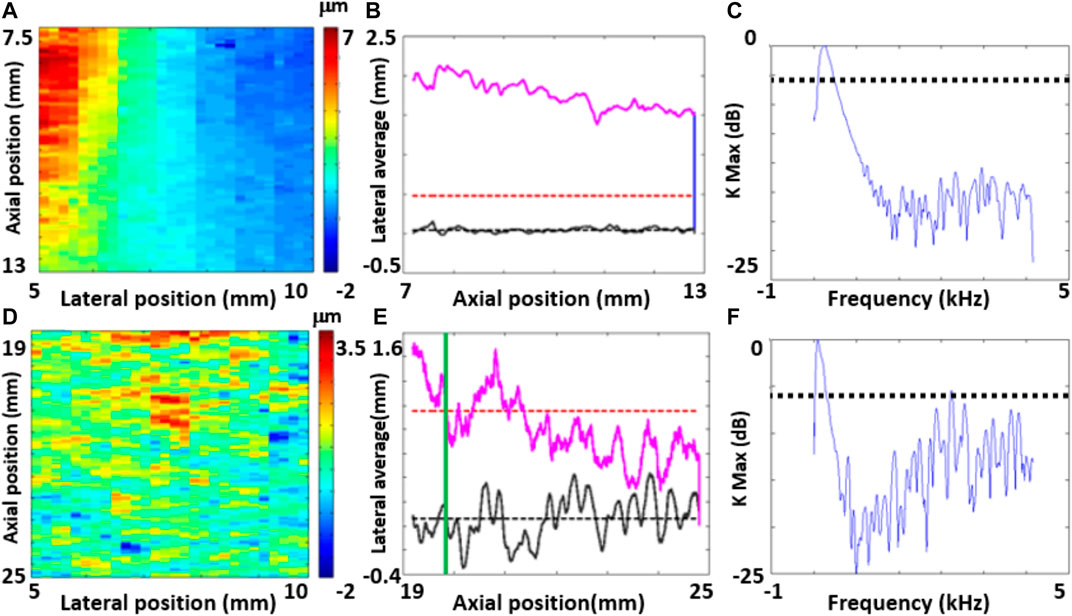
FIGURE 3. Examples of data that was included (A and B,C) and rejected (D and E,F) based on the quality criteria defined for the longitudinal study in Rhesus macaques.

2.4.1 Statistical Analysis

We used a linear mixed effects model to evaluate the significance of the relationship between the optimized dispersion parameter, gestational age, and other experimental variables [49]. According to this model, the optimized parameter P can be written as a linear combination of each variable $e_i$ and of their interactions $e_i\ast e_j$:

$P=P_0+{\displaystyle \sum _i\left(C_i{e}_i+{\displaystyle \sum _{j\ne i}{C}_{i,j}{e}_i\ast e_j}\right)},(6)$

where $P_0$ is the intercept of the model, $C_i$ is the contribution of each variable to the model, and $C_{i,j}$ is the contribution of the interaction of each pair of variables. Table 2 defines the variables $e_i$. We used a maximum likelihood strategy to fit the model using the Matlab’s function fitlme. The model was applied in a sequential manner, discarding non-significant variables in each iteration. We report the final model that included significant variables only. A Shapiro-Wilk test was applied to the values of the optimized parameter grouped by gestation week and cervix portion in order to verify the assumption of normality.

TABLE 2

TABLE 2. Variables of the mixed effects model applied to the optimized dispersion parameter.

3 Results

3.1 Simulations

The CNR of both dispersion descriptors R and S increased with viscosity. In addition, we computed the values of the dispersion descriptors R and S (see description below) for a purely elastic medium (no viscosity), obtaining R = 0.998 and S = 0.01 (close to the values expected under no dispersion, i.e., R = 1 and S = 0). This demonstrates the absence of surface effects in shear wave propagation. Also, when no noise-reduction strategies were applied, R was found to be more robust to high levels of noise than parameter S. Figures 4A,B show the CNR of R and S, respectively, as a function of viscosity. Each curve corresponds to a different noise level. For low noise levels ($k\le 0.02$), the CNR of S was higher than the CNR of R by a factor of six for the low viscosity material and a factor of 5.5 for the high viscosity material. However, beyond $k=0.05$ the CNR of S was negligible compared to the CNR of R.

FIGURE 4

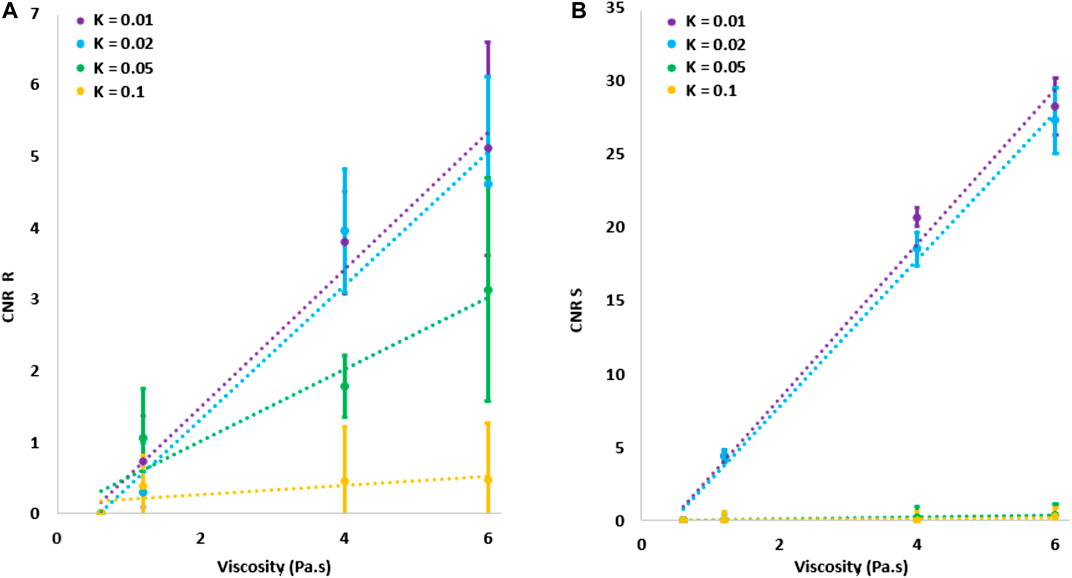
FIGURE 4. Contrast-to-noise ratio for either R and S parameters in function of the viscosity for different levels of noise. Error bars represent standard deviations over twenty repetitions.

For the low-pass noise filtering method, the automatically-selected cut-off frequency increased as a function of viscosity and decreased as a function of the noise level. This is shown in Figure 5, where the cutoff frequency is plotted as a function of the noise factor k. Each curve corresponds to a different degree of viscosity.

FIGURE 5

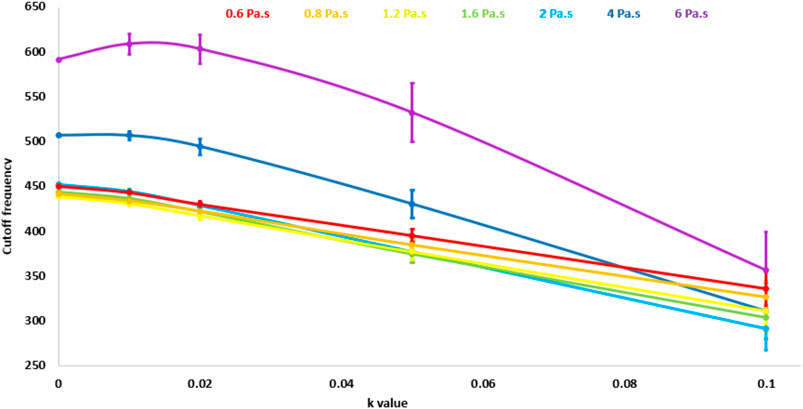
FIGURE 5. Cutoff frequency values obtained through the automatic method as a function of the noise parameter k. Each curve corresponds to a different viscosity degree.

For the SVD noise filtering method, the optimum singular value cutoff was chosen based on the maximum value of the CTER. Figure 6 shows the CTER as a function of the singular value cutoff index for the material with 0.8 Pa s viscosity and the material with 6 Pa s viscosity. The CTER had a maximum value around the index seven for both materials. Thus, we selected a value of seven for the cutoff index.

FIGURE 6

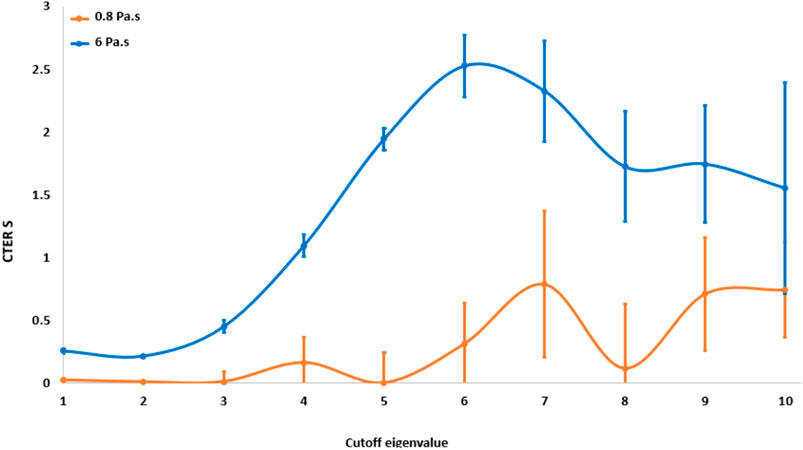
FIGURE 6. CTER values of the S parameter as a function of the cutoff eigenvalue for the most viscous medium (6 Pa s) and the less viscous (0.8 Pa s).

Figure 7 shows parameter S obtained after applying the low-pass filter (a) and the SVD filter (b), as a function of the noise parameter k and for various degrees of viscosity. With the low pass filter, changes in S as viscosity increases were not significant as indicated by the overlapping error bars. Furthermore, the highest value of S does not occur with the higher values of viscosity, suggesting ambiguity in the values of S that result from the use of this filtering strategy. This did not occur with the SVD filter, for which S increased monotonically with viscosity and changes with viscosity did not overlap. Because of this, the low pass filter was rejected.

FIGURE 7

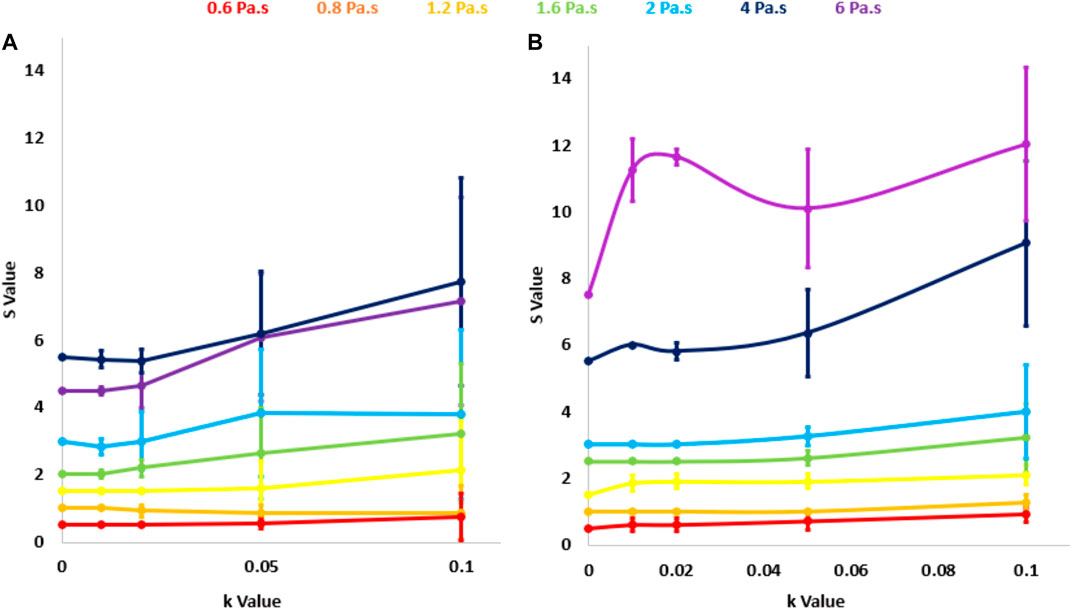
FIGURE 7. S parameter calculated with the automated low-pass filter (A) and the singular value decomposition filter (B) as a function of the noise level k. Each curve corresponds to a different degree of viscosity η.

After applying the SVD filter, the S parameter showed the highest CNR for each degree of noise and viscosity. Figure 8 shows the CNR of both R and S as a function of the noise factor without any filter and with the SVD filter. The combination of descriptor S and the SVD filtering for the highest level of noise resulted in 11.6 times higher CNR than R descriptor with the same filtering strategy. We applied the SVD filter to the estimation of descriptor S to data from the in vivo NHP study, zeroing singular values at and beyond index 7.

FIGURE 8

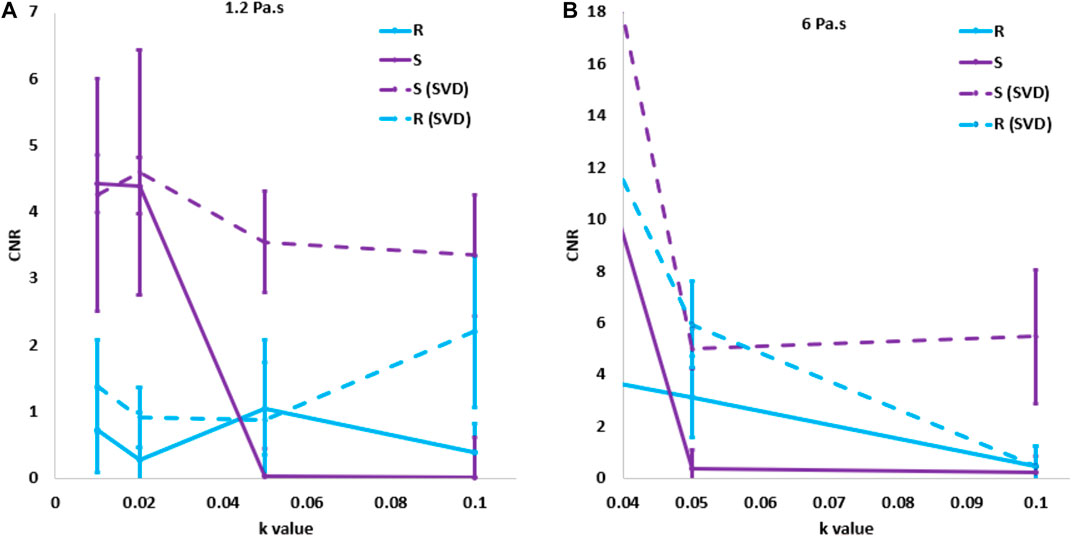
FIGURE 8. Comparison of the contrast-to-noise ratio as a function of the noise level for the highest and lowest degrees of viscosity before and after apply the singular value decomposition filter.

3.2 In vivo NHP Application

Table 3 summarizes the mean and standard deviations of the S parameter at weeks 10 and 23 for the anterior and posterior regions of the 18 macaques. Empty cells correspond to cases in which no measurements passed the quality criteria described above. No standard deviations (ND) are reported for those cases in which only one measurement passed the quality criteria. Mean cervical thickens for each animal is also reported in Table 3. Figure 9 shows an example of the particle displacements (a,d), particle velocities (b,e) and dispersion curves (c and f) for data from different subjects at week 10 (top row) and week 23 (bottom row). In this example, the maximum values of the particle velocity propagate at a faster rate at early pregnancy than at late pregnancy, which indicates overall stiffer tissue in the former case. Dispersion curves show higher phase velocities vs. frequency at mid pregnancy than at late pregnancy.

TABLE 3

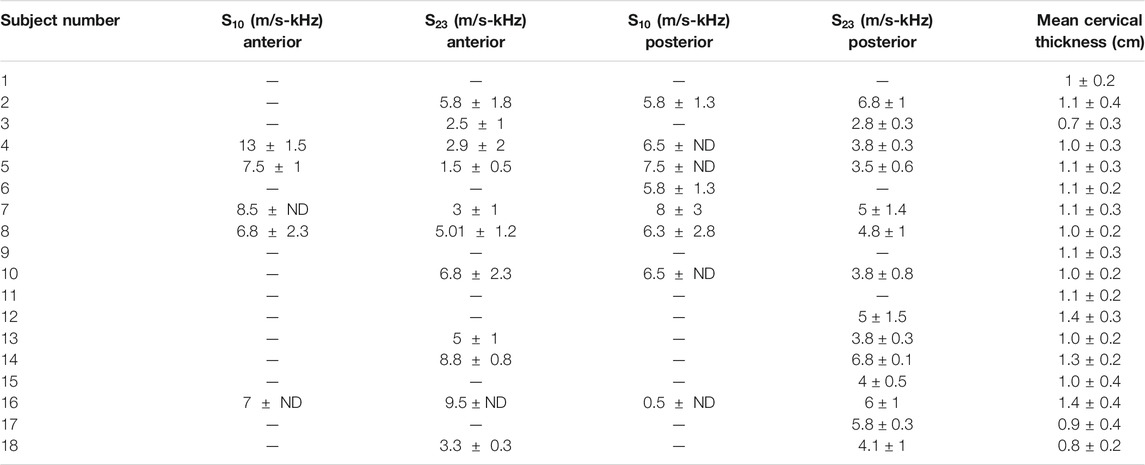
TABLE 3. S values of each macaque calculated in the anterior and posterior region with respect to the cervical canal during gestation weeks 10 and 23. Cervical mean thickens is also showed for each macaque.

FIGURE 9

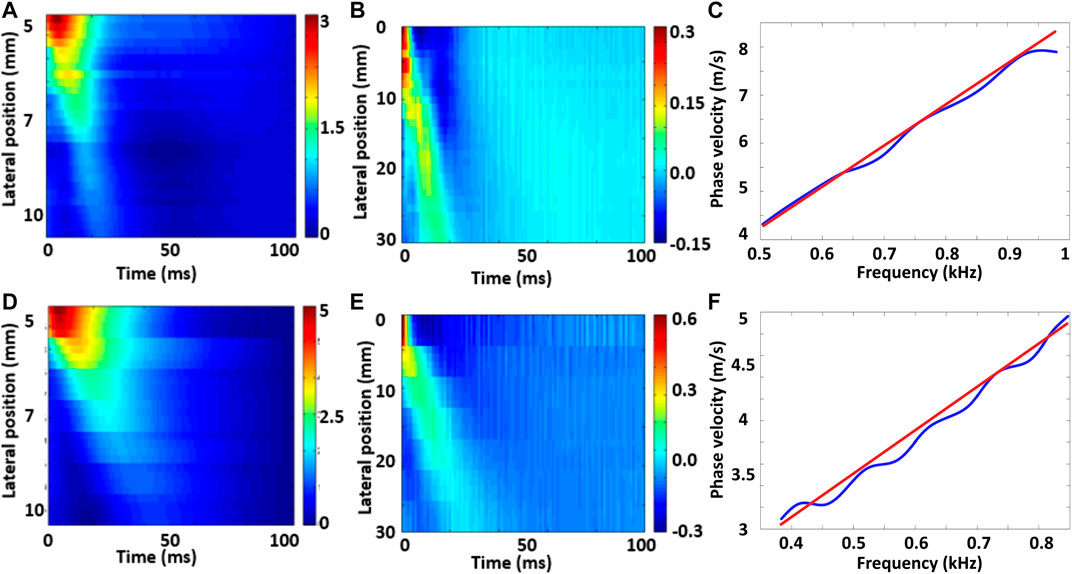
FIGURE 9. Particle displacements (A and D), particle velocities (B and E) and dispersion curves (C and F) for the filtered data in the early (A–C) and late (D–F) week of gestation in the longitudinal study. In the dispersion curves, the blue line is the value of the phase velocity measured at the maximum power at each temporal frequency, and the red line is the linear fit.

In general, S decreased between weeks 10 and 23 in the anterior cervix portion (Wilcoxon p = 0.03). Shear wave dispersion also decreased in the posterior portion, but the difference was not statistically significant (Wilcoxon p = 0.051). Figure 10 shows box plots that group estimates of S for all the subjects that passed the quality criteria at weeks 10 and 23 for (a) the anterior and (b) the posterior portions of the cervix.

FIGURE 10

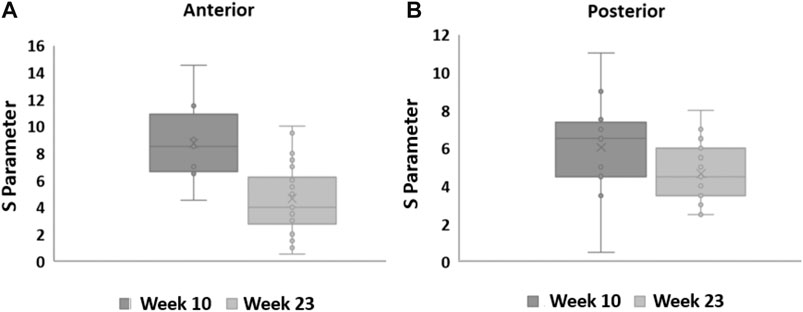
FIGURE 10. Box plots for the S parameter estimated from in vivo NHP SWEI data at weeks 10 and 23 of pregnancy. The central line and cross indicate the median and mean, the top and bottom limits of the box represent the interquarrtile range, the wiskers indicate the range defined as 1.95 times the interquartile range above and below the 25 and 75 percentiles, and the circles indicate values for each subject.

With exception of S values in the posterior side at week 23 ($p=0.065$), all data complied with the assumption of normality. Table 4 summarizes the results of the final LME model after sequentially rejecting non-significant effects. The most significant effect was that of the week of gestation $\left(p<0.00001\right)$, which resulted in a reduction of $0.37\pm 0.07$ m/s-kHz per week from the initial value of $15.5\pm 1.9$ m/s-KHz. Also, dispersion decreased with the mother’s age ($p=0.008$) and was higher in the anterior portion ($p=0.0009$). Furthermore, significant correlations were found between the week of gestation and the cervical portion, and the maternal age and the cervical portion.

TABLE 4

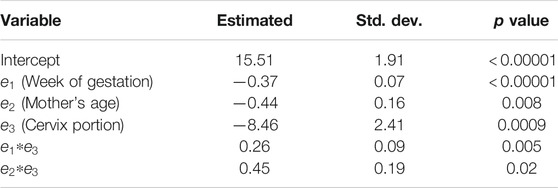
TABLE 4. Estimated coefficients, standard deviations, and p values for statistical significance of the linear mixed effects model for S in the in vivo NHP pregnant cervix.

4 Discussion

The goal of this study was to evaluate the changes in shear wave dispersion quantified through SWEI in an in vivo NHP model of the cervix between mid and late gestation. To this end, we performed a pre-selection of two SWEI-based descriptors of shear wave dispersion, R and S and noise reduction strategies using finite-element simulations of viscoelastic media. The most important findings of this study are:

• The S parameter with the SVD noise reduction strategy showed the highest dispersion-based CNR compared to other combinations of parameter and noise reduction strategies.

• The combination of the S parameter and the SVD filter led to observe a significant reduction of shear wave dispersion in NHP cervix between mid and late pregnancy.

• As result of the application of the LME model, we found other significant effects that influence the value of the S parameter and included the mother’s age and the cervix portion (anterior vs. posterior).

Based on a finite-element model, we observed that the frequency-domain parameter S in combination with the SVD filtering strategy produced the largest CNR among materials with different degrees of dispersion. The advantage of the SVD method over the automated low pass filter is based on its capacity to reduce both spatial and temporal contributions to noise. A disadvantage of this technique is the need to define an optimum cutoff value. A particularly complicated situation is how to treat frequency content due to bulk motion. In order to reduce the effects of such motion in the implementation of the optimized SVD strategy, we applied a second-order motion filter, as done by [40]. In the future, we will investigate the optimization of the selection of the singular value cutoff index to also reduce the contribution of bulk motion.

Other studies have applied SVD filtering in ultrasound studies like blood flow imaging [50]. However, the optimization of the cutoff value of SVD filtering for SWEI has not been widely studied. A particular case of SVD filtering in shear wave analysis can be found in geophysics applications. Chevrot and Girardin [51] used SVD filtering to reduce the noise in shear waves from seismic signals. In that study, a cutoff value was selected when a regular decrease of the singular spectrum was observed, which led to a cutoff index of 6. Here, we proposed a quantitative selection criterion considering the bias and variance in the estimation of the dispersion slope based on simulations with a large range of viscosity. The selected cutoff value of 7 was similar to that of [51].

In the animal study, we observed that the slope of the phase velocity vs. frequency decreased between mid and late pregnancy. Shear wave dispersion in the cervix can be attributed to the layered structure of collagen bundles, and to the presence of the viscous components of the extracellular matrix such as glycosaminoglycans. The collagen bundles are arranged in approximately three bands: an inner band with bundles aligned radially from the canal, a middle one with circumferential bundles, and an outer one with longitudinal bundles parallel to the canal [3]. Each band, with thickness of a few millimeters, can guide the propagation of the shear waves, as observed in tendon [26]. As pregnancy progresses, the layered collagen structure is lost and, therefore, shear wave dispersion caused by guided wave phenomena should decrease.

In addition to the bands of collagen, the thickness of the anterior and posterior portion of the cervix can lead to shear wave dispersion to the presence of Lamb waves. The average half-thickness (thickness of either the anterior or posterior portions) were 2.3 $\pm$ 0.3 and 1.1 $\pm$ 0.2 cm, respectively. We measured the half thickness instead of the full thickness because each half portion (anterior and posterior) is bounded by the cervical canal and the surrounding fascia. Because of this, we restricted the analysis of shear wave propagation to either the anterior or the posterior portions. To study the correlation between shear wave dispersion and the cervical thickness, we added a plot of the parameter S and cervical thickness (Figure 11). Even if the wavelength is similar to the cervix half thickness, we did not find any correlation between the values of the S parameter and the cervical thickness and length (as indicated by the Pearson’s correlation coefficient ρ = 0.07 (p = 0.71)). Also, the concentration of viscous components such as hyaluronan, decorin, and versican varies during pregnancy [52]. Thus, changes in shear wave dispersion during pregnancy result from competing phenomena. Taken together, our results suggest that the structural component of dispersion may have a larger influence on the observed changes between weeks 10 and 23 in the pregnant NHP cervix. To deepen our understanding of the influence of the different structural and molecular components of the cervix on dispersion measurements through SWEI, our laboratory is developing simulation tools based on the finite element methods.

FIGURE 11

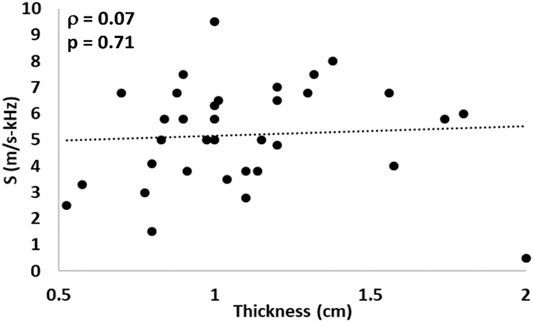
FIGURE 11. Shear wave dispersion parameter S vs. cervical thickness in the NHP model. Pearson’s correlation values was ρ = 0.07 (p = 0.71).

After applying the criteria for reliability of dispersion measurements, eight of the 18 subjects showed reliable estimates in week 10, and 15 in week 23. The larger rejection of data in week 10 can be attributed to the fact that the NHP cervix is stiffer than the human cervix and other organs in which SWEI has been successfully applied, like the liver. The larger stiffness leads to noisier shear wave displacement values. Furthermore, the rejection of a large number of data is common in the initial steps of the development of quantitative imaging. For example, Castañeda-Martinez et al. [53] rejected data from 11 out of 16 subjects while implementing Ultrasound Backscatter Spectroscopy in the neonatal brain. Also, Wang et al. [54] rejected 50% of measurements when using shear wave elasticity imaging in the liver. Because the human cervix is softer than the NHP, we are confident that we will achieve more reliable dispersion estimates in the clinical application of the technique developed in this work.

Various works have reported the use of the shear wave group speed $V_g$ as a surrogate for cervical softness in primates and humans [20, 23, 24, 30, 55–58]. For example [59], reported a decrease in the group speed of shear waves between ripened and unripened ex vivo human cervical samples, $39\text{\%}$ for the anterior region and $25\text{\%}$ for the posterior region with a p value $<0.05$. Also, in a study in patients with a term pregnancy, $V_g$ decreased $39\text{\%}$ between pre and post-ripening in the context of labor induction, with a p value $<0.001$ [18]. Here we observed a reduction in dispersion of $53\text{\%}$ with a p value much smaller than the reported changes for the group speed. This indicates that the shear wave dispersion can be more sensitive to cervical remodeling than the group speed. This could be attributed to the more direct relationship between shear wave dispersion and structural properties of the cervix, as well as the optimization of noise reduction strategies.

Using the linear mixed-effects model on the values of S, we found that age and cervix portion (anterior vs. posterior) had a significant influence on shear wave dispersion. Rosado-Mendez et al. [21] observed significant differences in the group speed between the anterior and posterior NHP cervix. Carlson et al. [60] reported similar differences in humans. These differences can be attributed to spatial variations in the microstructural properties of the cervix, a weight gradient created by the fetus, and/or the rotated orientation of the cervix with respect to propagation direction of the shear wave. Another factor could be a pre-compresion of the posterior cervix due to the presence of the transducer. Also, these differences could be attributed to variations in the shear wave frequency content due the attenuation and focusing of the pushing beam. The significance of the mother’s age could be attributed to the changes in the production and reception of glycosaminoglycans as the mother age increases [61]. Despite the influence of these factors, the most important effect on shear wave dispersion was the week of gestation, thus indicating the potential of this technique to track cervical remodeling during pregnancy.

This study had various limitations. The noise model that we used in the simulation part was Gaussian and modulated by the maximum shear wave displacement of each displacement field [38]. Although simplistic, this model allowed us to performed a comparative selection of the descriptor of dispersion that maximized the detection of different levels of dispersion. The second limitation is the large fraction of rejected data at week 10. This can be attributed to the stiffer state of the cervix at mid pregnancy compared to late pregnancy, which results in lower signal/noise of displacements estimates. This might be a limitation when performing future comparisons of the early vs. late pregnancy cervix. Since the human cervix is slightly softer than the NHP cervix, we expect that the rejection rate will not be as high in clinical applications of the proposed technique. Finally, the S parameter does not provide a quantitative assessment of the changes in the structural components that determine the dispersive response of the cervix. We are currently exploring the quantification of shear wave attenuation and the fit of rheological models to shear wave dispersion and attenuation to obtain a more detailed characterization of the cervix structural components. Although this strategy has been proposed by other groups, they used simplistic viscoelastic models such as Voigt’s [28]. Other models such as the Prony series may provide a more accurate assessment of the structural components.

5 Conclusion

In this study we used shear wave dispersion as a surrogate of cervical remodeling during pregnancy in a non-human primate model. We compared the sensitivity of two dispersion descriptors extracted from either a time-domain or a frequency-domain analysis of shear wave propagation in finite element simulations of viscoelastic media. We observed that the frequency-domain parameter S, defined as the phase velocity slope vs. frequency, in combination with noise-filtering based on singular value decomposition provided better differentiation of viscoelastic materials with different levels of dispersion than other combinations of parameters and filtering strategies. When applied to the NHP model, we observed a significant reduction of shear wave dispersion between mid and late pregnancy in the NHP model, likely due to the disorganization of cervical collagen during pregnancy. Our results suggest the potential of shear wave dispersion as a quantitative imaging biomarker of cervical remodeling. Future studies will apply this analysis to data from longitudinal human studies of normal and preterm pregnancy.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The animal study was reviewed and approved by the Institutional Animal Care and Use Committee of the University of Wisconsin-Madison.

Author Contributions

AT contributed with data processing, analysis and discussion of results, and manuscript drafting. MP contributed with generation of simulations and discussion of results. HF contributed with data acquisition, analysis and discussion of results, and manuscript drafting. TH contributed to the discussion of results and manuscript drafting. IR-M contributed with data acquisition, supervising data processing, manuscript drafting, and discussion of results.

Funding

This work was supported by UNAM-PAPIIT IA104518, IN103219, and IA102320, and by the graduate studies scholarship from the Consejo Nacional de Ciencia y Tecnología to AT. (CVU 863045). This work was also supported by the National Institutes of Health grants T32CA009206 from the National Cancer Institute, and F31HD082911, R21HD061896, R21HD063031, and R01HD072077 from the Eunice Kennedy Shriver National Institute of Child Health and Human Development.

Conflict of Interest

This research was performed with support (equipment loan and technical assistance) from Siemens Healthcare.

Acknowledgments

The authors thank Lindsey Carlson, Quinton Guerrero, Andrew Santoso, Bin Huang, Sarah Kohn, and Michele Shotzko for helping with data acquisition.

References

1. Vogel JP, Chawanpaiboon S, Watananirun K, Lumbiganon P, Petzold M, Moller AB, et al. Global, regional and national levels and trends of preterm birth rates for 1990 to 2014: protocol for development of world health organization estimates. Reprod Health (2016) 13:76. doi:10.1186/s12978-016-0193-1

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Feltovich H. Cervical evaluation: from ancient medicine to precision medicine. Obstet Gynecol (2017) 130:51. doi:10.1097/AOG.0000000000002106

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Feltovich H, Hall TJ, Berghella V. Beyond cervical length: emerging technologies for assessing the pregnant cervix. Am J Obstet Gynecol (2012) 207:345–54. doi:10.1016/j.ajog.2012.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Yellon SM. Immunobiology of cervix ripening. Front Immunol (2019) 10:3156. doi:10.3389/fimmu.2019.03156

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Akgul Y, Holt R, Mummert M, Word A, Mahendroo M. Dynamic changes in cervical glycosaminoglycan composition during normal pregnancy and preterm birth. Endocrinology (2012) 153:3493–503. doi:10.1210/en.2011-1950

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Myers K, Socrate S, Tzeranis D, House M. Changes in the biochemical constituents and morphologic appearance of the human cervical stroma during pregnancy. Eur J Obstet Gynecol Reprod Biol (2009) 144(Suppl 1):S82. doi:10.1016/j.ejogrb.2009.02.008–S89

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Nallasamy S, Mahendroo M. Distinct roles of cervical epithelia and stroma in pregnancy and parturition. Semin Reprod Med (2017) 35:190–200. doi:10.1055/s-0037-1599091

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Danforth DN, Veis A, Breen M, Weinstein HG, Buckingham JC, Manalo P. The effect of pregnancy and labor on the human cervix: changes in collagen, glycoproteins, and glycosaminoglycans. Am J Obstet Gynecol (1974) 120:641–51. doi:10.1016/0002-9378(74)90608-5

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Rechberger T, Uldbjerg N, Oxlund H. Connective tissue changes in the cervix during normal pregnancy and pregnancy complicated by cervical incompetence. Obstet Gynecol (1988) 71:563–7.

PubMed Abstract | Google Scholar

10. Von Maillot KV, Zimmermann BK. The solubility of collagen of the uterine cervix during pregnancy and labour. Arch Gynakol (1976) 220:275–80. doi:10.1007/bf00673411

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Kleissl HP, Van Der Rest M, Naftolin F, Glorieux FH, De Leon A. Collagen changes in the human uterine cervix at parturition. Am J Obstet Gynecol (1978) 130:748–53. doi:10.1016/0002-9378(78)90003-0

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Ito A, Kitamura K, Mori Y, Hirakawa S. The change in solubility of type i collagen in human uterine cervix in pregnancy at term. Biochem Med (1979) 21:262–70. doi:10.1016/0006-2944(79)90081-4

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Granström L, Ekman G, Malmström A. Insufficient remodelling of the uterine connective tissue in women with protracted labour. Br J Obstet Gynaecol (1991) 98:1212–6. doi:10.1111/j.1471-0528.1991.tb15391.x

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Mahendroo M. Cervical hyaluronan biology in pregnancy, parturition and preterm birth. Matrix Biol (2019) 78-79:24–31. doi:10.1016/j.matbio.2018.03.002

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Akins ML, Luby-Phelps K, Mahendroo M. Second harmonic generation imaging as a potential tool for staging pregnancy and predicting preterm birth. J Biomed Optic (2010) 15:026020. doi:10.1117/1.3381184

CrossRef Full Text | Google Scholar

16. Carlson LC, Hall TJ, Rosado-Mendez IM, Palmeri ML, Feltovich H. Detection of changes in cervical softness using shear wave speed in early versus late pregnancy: an in vivo cross-sectional study. Ultrasound Med Biol (2018) 44:515–21. doi:10.1016/j.ultrasmedbio.2017.10.017

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Muller M, Aït-Belkacem D, Hessabi M, Gennisson JL, Grangé G, Goffinet F, et al. Assessment of the cervix in pregnant women using shear wave elastography: a feasibility study. Ultrasound Med Biol (2015) 41:2789–97. doi:10.1016/j.ultrasmedbio.2015.06.020

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Carlson LC, Romero ST, Palmeri ML, Muñoz Del Rio A, Esplin SM, Rotemberg VM, et al. Changes in shear wave speed pre- and post-induction of labor: a feasibility study. Ultrasound Obstet Gynecol (2015) 46:93–8. doi:10.1002/uog.14663

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Hernandez-Andrade E, Aurioles-Garibay A, Garcia M, Korzeniewski SJ, Schwartz AG, Ahn H, et al. Effect of depth on shear-wave elastography estimated in the internal and external cervical os during pregnancy. J Perinat Med (2014) 42:549–57. doi:10.1515/jpm-2014-0073

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Rosado-Mendez IM, Palmeri ML, Drehfal LC, Guerrero QW, Simmons H, Feltovich H, et al. Assessment of structural heterogeneity and viscosity in the cervix using shear wave elasticity imaging: initial results from a Rhesus macaque model. Ultrasound Med Biol (2017) 43:790–803. doi:10.1016/j.ultrasmedbio.2016.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rosado-Mendez IM, Carlson LC, Woo KM, Santoso AP, Guerrero QW, Palmeri ML, et al. Quantitative assessment of cervical softening during pregnancy in the rhesus macaque with shear wave elasticity imaging. Phys Med Biol (2018) 63:085016. doi:10.1088/1361-6560/aab532

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Sarvazyan A, Hall TJ, Urban MW, Fatemi M, Aglyamov SR, Garra BS. AN overview OF elastography - an emerging branch OF medical imaging. Curr Med Imag Rev (2011) 7:255–82. doi:10.2174/157340511798038684TM

CrossRef Full Text | Google Scholar

23. Rosado-Mendez IM, Guerrero QW, Drehfal LC, Santoso AP, Subramanian S, Kohn S, et al. Changes in cervical stiffness during pregnancy: preliminary assessment with shear wave elasticity imaging in the Rhesus macaque. In: AIP conference proceedings, 1747. Melville, NY: AIP Publishing (2016). p. 50–2.

Google Scholar

24. Carlson LC, Hall TJ, Rosado-Mendez IM, Mao L, Feltovich H. Quantitative assessment of cervical softening during pregnancy with shear wave elasticity imaging: an in vivo longitudinal study. Interface focus (2019) 9:20190030. doi:10.1098/rsfs.2019.0030

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Hernandez-Andrade E, Hassan SS, Ahn H, Korzeniewski SJ, Yeo L, Chaiworapongsa T, et al. Evaluation of cervical stiffness during pregnancy using semiquantitative ultrasound elastography. Ultrasound Obstet Gynecol (2013) 41:152–61. doi:10.1002/uog.12344

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Brum J, Bernal M, Gennisson JL, Tanter M. In vivo evaluation of the elastic anisotropy of the human achilles tendon using shear wave dispersion analysis. Phys Med Biol (2014) 59:505. doi:10.1088/0031-9155/59/3/505

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Gennisson JL, Deffieux T, Macé E, Montaldo G, Fink M, Tanter M. Viscoelastic and anisotropic mechanical properties of in vivo muscle tissue assessed by supersonic shear imaging. Ultrasound Med Biol (2010) 36:789–801. doi:10.1016/j.ultrasmedbio.2010.02.013

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Peralta L, Rus G, Bochud N, Molina FS. Assessing viscoelasticity of shear wave propagation in cervical tissue by multiscale computational simulation. J Biomech (2015) 48:1549–56. doi:10.1016/j.jbiomech.2015.01.044

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Rouze NC, Palmeri ML, Nightingale KR. An analytic, fourier domain description of shear wave propagation in a viscoelastic medium using asymmetric Gaussian sources. J Acoust Soc Am (2015) 138:1012–22. doi:10.1121/1.4927492

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Huang B, Drehfal LC, Rosado-Mendez IM, Guerrero QW, Palmeri ML, Simmons HA, et al. Estimation of shear wave speed in the rhesus macaques' uterine cervix. IEEE Trans Ultrason Ferroelectrics Freq Contr (2016) 63:1243–52. doi:10.1109/TUFFC.2016.2524259

CrossRef Full Text | Google Scholar

31. Haluska GJ, West NB, Novy MJ, Brenner RM. Uterine estrogen receptors are increased by ru486 in late pregnant rhesus macaques but not after spontaneous labor. J Clin Endocrinol Metab (1990) 70:181–6. doi:10.1210/jcem-70-1-181

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Hafez ESE, Jaszczak S. Comparative anatomy and histology of the cervix uteri in non-human primates. Primates (1972) 13:297–314. doi:10.1007/bf01730575

CrossRef Full Text | Google Scholar

33. Owiti GE, Tarantal AF, Lasley BL, Hendrickx AG. The effect of the anti-progestin ru 486 on early pregnancy in the long-tailed macaque (macaca fascicularis). Contraception (1989) 40:201–11. doi:10.1016/0010-7824(89)90007-3

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Wolfgang MJ, Eisele SG, Knowles L, Browne MA, Schotzko ML, Golos TG. Pregnancy and live birth from nonsurgical transfer of in vivo- and in vitro-produced blastocysts in the rhesus monkey. J Med Primatol (2001) 30:148–55. doi:10.1111/j.1600-0684.2001.tb00003.x

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Adams Waldorf KM, Singh N, Mohan AR, Young RC, Ngo L, Das A, et al. Uterine overdistention induces preterm labor mediated by inflammation: observations in pregnant women and nonhuman primates. Am J Obstet Gynecol (2015) 213:830–e19. doi:10.1016/j.ajog.2015.08.028

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Palmeri ML, Feltovich H, Homyk AD, Carlson LC, Hall TJ. Evaluating the feasibility of acoustic radiation force impulse shear wave elasticity imaging of the uterine cervix with an intracavity array: a simulation study. IEEE Trans Ultrason Ferroelectrics Freq Contr (2013) 60:2053–64. doi:10.1109/TUFFC.2013.2796

CrossRef Full Text | Google Scholar

37. Rouze NC, Deng Y, Trutna CA, Palmeri ML, Nightingale KR. Characterization of viscoelastic materials using group shear wave speeds. IEEE Trans Ultrason Ferroelectrics Freq Contr (2018) 65:780–94. doi:10.1109/TUFFC.2018.2815505

CrossRef Full Text | Google Scholar

38. Wang M, Byram B, Palmeri M, Rouze N, Nightingale K. On the precision of time-of-flight shear wave speed estimation in homogeneous soft solids: initial results using a matrix array transducer. IEEE Trans Ultrason Ferroelectrics Freq Contr (2013) 60:758–70. doi:10.1109/TUFFC.2013.2624

CrossRef Full Text | Google Scholar

39. Deffieux T, Montaldo G, Tanter M, Fink M. Shear wave spectroscopy for in vivo quantification of human soft tissues visco-elasticity. IEEE Trans Med Imag (2008) 28:313–22. doi:10.1109/TMI.2008.925077

CrossRef Full Text | Google Scholar

40. Nightingale KR, Rouze NC, Rosenzweig SJ, Wang MH, Abdelmalek MF, Guy CD, et al. Derivation and analysis of viscoelastic properties in human liver: impact of frequency on fibrosis and steatosis staging. IEEE Trans Ultrason Ferroelectrics Freq Contr (2015) 62:165–75. doi:10.1109/TUFFC.2014.006653

CrossRef Full Text | Google Scholar

41. Palmeri ML, Sharma AC, Bouchard RR, Nightingale RW, Nightingale KR. A finite-element method model of soft tissue response to impulsive acoustic radiation force. IEEE Trans Ultrason Ferroelectrics Freq Contr (2005) 52:1699–712. doi:10.1109/tuffc.2005.1561624

CrossRef Full Text | Google Scholar

42. Torres A, Palmeri ML, Feltovich H, Hall TJ, Rosado-Mendez IM. Evaluation of sensitivity of ultrasound imaging biomarkers of cervical viscosity based on shear wave elasticity imaging: a simulation study. In: AIP conference proceedings, 2090. Melville, NY: AIP Publishing LLC (2019). p. 040011.

Google Scholar

43. Dumont D, Palmeri M, Eyerly S, Wolf P, Byram B. Feasibility of using a generalized-Gaussian Markov random field prior for bayesian speckle tracking of small displacements. In Proceedings of the IEEE International Ultrasonics Symposium; 2014 September 3–6; Chicago, IL; New York, NY: IEEE (2014). p. 1845–8.

Google Scholar

44. Achim A, Bezerianos A, Tsakalides P. Novel bayesian multiscale method for speckle removal in medical ultrasound images. IEEE Trans Med Imag (2001) 20:772–83. doi:10.1109/42.938245

CrossRef Full Text | Google Scholar

45. Demené C, Deffieux T, Pernot M, Osmanski BF, Biran V, Gennisson JL, et al. Spatiotemporal clutter filtering of ultrafast ultrasound data highly increases Doppler and fultrasound sensitivity. IEEE Trans Med Imag (2015) 34:2271–85. doi:10.1109/TMI.2015.2428634

CrossRef Full Text | Google Scholar

46. Van Loan CF. Generalizing the singular value decomposition. SIAM J Numer Anal (1976) 13:76–83. doi:10.1137/0713009

CrossRef Full Text | Google Scholar

47. Brunke SS, Insana MF, Dahl JJ, Hansen C, Ashfaq M, Ermert H. An ultrasound research interface for a clinical system. IEEE Trans Ultrason Ferroelectrics Freq Contr (2007) 54:198–210. doi:10.1109/tuffc.2007.226

CrossRef Full Text | Google Scholar

48. Loupas T, Powers JT, Gill RW. An axial velocity estimator for ultrasound blood flow imaging, based on a full evaluation of the Doppler equation by means of a two-dimensional autocorrelation approach. IEEE Trans Ultrason Ferroelectrics Freq Contr (1995) 42:672–88. doi:10.1109/58.393110

CrossRef Full Text | Google Scholar

49. Gałecki A, Burzykowski T. Linear mixed-effects models using R. Berlin, Germany: Springer (2013). p. 245–73.

Google Scholar

50. Ikeda H, Yoshizawa S, Maeda M, Umemura S-i., Saijo Y. Blood flow imaging using singular value decomposition filter during high-intensity focused ultrasound exposure. Jpn J Appl Phys (2019) 58:SGGE15. doi:10.7567/1347-4065/ab1a2e

CrossRef Full Text | Google Scholar

51. Chevrot S, Girardin N. On the detection and identification of converted and reflected phases from receiver functions. Geophys J Int (2000) 141:801–8. doi:10.1046/j.1365-246x.2000.00139.x

CrossRef Full Text | Google Scholar

52. Myers KM, Paskaleva AP, House M, Socrate S. Mechanical and biochemical properties of human cervical tissue. Acta Biomater (2008) 4:104–16. doi:10.1016/j.actbio.2007.04.009

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Castañeda-Martinez L, Noguchi KK, Ikonomidou C, Zagzebski JA, Hall TJ, Rosado-Mendez IM. Ultrasound in medicine & biology (2020). Optimization of ultrasound backscatter spectroscopy to assess neurotoxic effects of anesthesia in the newborn non-human primate brain.

Google Scholar

54. Wang MH, Palmeri ML, Rotemberg VM, Rouze NC, Nightingale KR. Improving the robustness of time-of-flight based shear wave speed reconstruction methods using ransac in human liver in vivo. Ultrasound Med Biol (2010) 36:802–13. doi:10.1016/j.ultrasmedbio.2010.02.007

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Carlson LC, Feltovich H, Palmeri ML, Dahl JJ, Munoz del Rio A, Hall TJ. Estimation of shear wave speed in the human uterine cervix. Ultrasound Obstet Gynecol (2014a) 43:452–8. doi:10.1002/uog.12555

PubMed Abstract | CrossRef Full Text | Google Scholar

56. O’Hara S, Zelesco M, Sun Z. Shear wave elastography on the uterine cervix: technical development for the transvaginal approach. J Ultrasound Med (2019a) 38:1049–60.

Google Scholar

57. O’Hara S, Zelesco M, Sun Z. Shear wave elastography of the maternal cervix: a transabdominal technique. Australasian Journal of Ultrasound in Medicine (2019b) 22:96–103.

Google Scholar

58. Wang B, Zhang Y, Chen S, Xiang X, Wen J, Yi M, et al. Diagnostic accuracy of cervical elastography in predicting preterm delivery: a systematic review and meta-analysis. Medicine (Baltim) (2019) 98:e16449. doi:10.1097/MD.0000000000016449

CrossRef Full Text | Google Scholar

59. Carlson LC, Feltovich H, Palmeri ML, del Rio AM, Hall TJ. Statistical analysis of shear wave speed in the uterine cervix. IEEE Trans Ultrason Ferroelectrics Freq Contr (2014b) 61:1651–60. doi:10.1109/tuffc.2014.006360

CrossRef Full Text | Google Scholar

60. Carlson LC, Feltovich H, Palmeri ML, Dahl JJ, Munoz del Rio A, Hall TJ. Estimation of shear wave speed in the human uterine cervix. Ultrasound Obstet Gynecol (2014c) 43:452. doi:10.1002/uog.12555

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Vo NV, Hartman RA, Patil PR, Risbud MV, Kletsas D, Iatridis JC, et al. Molecular mechanisms of biological aging in intervertebral discs. J Orthop Res (2016) 34:1289–306. doi:10.1002/jor.23195

PubMed Abstract | CrossRef Full Text | Google Scholar