The Concept of Cooperative Dynamics in Simulations of Soft Matter

Introduction

Molecular transport in crowded environments plays a key role in a variety of areas [1–4] while dynamic behavior in such systems is not fully recognized and even its origin is debatable [5–10]. Major experimental techniques used for studies of transport in disordered systems are mainly fluorescence correlation spectroscopy [11] and single particle tracking [12, 13]. The main parameter describing the diffusive behavior is the mean square displacement of objects, defined as

$\langle \Delta r^2\left(t\right)\rangle =\frac{1}{n}{{\displaystyle \sum _{i=1}^n\left[{\mathbf{r}}_i\left(t\right)-{\mathbf{r}}_i\left(0\right)\right]}}^2(1)$

where r_i(t) are the coordinates of the ith object while n stands for the number of mobile objects. The diffusion is considered normal when $\langle \Delta r^2\rangle$ is depends linearly on time. An anomalous diffusion is considered when scaling of $\langle \Delta r^2\rangle$ is different:

$\langle \Delta r^2\rangle \sim t^{\alpha }(2)$

In the case α < 1 a subdiffusive motion is present [5, 9]. Real experiments showed exponent α between 0.2 and 0.9 [5, 14] while computer simulations for matrices of obstacles revealed that at the percolation threshold the exponent α approached the value 0.697 [10, 14–19] An anomalous diffusion was found in several models but we are interested in the case of obstructive motion where it is caused by the presence of other objects [5, 15, 16]. When the concentration of obstacles was below the percolation point an anomalous diffusion appeared transient while above the threshold it remains anomalous all the time [5, 17, 18]. Simple obstructive model was extended by changing and differentiating size of obstructing objects, their distribution [14, 19–21], mobility [22–24] or interactions [23–27]. Most of the simulations of such systems were performed by means of molecular dynamics employing coarse-grained and atomistic representation [14, 17, 19, 20, 22–25, 28–32] as well as dynamic Monte Carlo [33, 34], discontinuous molecular dynamics [21], and model based on the Lorentz gas [35, 36]. The high densities and large time scales caused significant computational problems. Most of Monte Carlo simulation algorithms are not able to work at these conditions. The only algorithms that can deal with this problem have to include a cooperative motion where the motion of molecules is correlated with the movement of its neighbors.

This work reviews the problem of dynamics in a soft matter model employing the Dynamic lattice liquid (DLL) [37, 38] where the correlations in motion between mobile objects were introduced into the system. The most striking effects of dynamics in disordered systems modeled as systems with obstacles were compared to the results of a very popular SAM where correlations in motion and hydrodynamic effects were totally ignored [5].

Cooperative Motion in Soft Matter

Crowded environments have a very complex structure spanning many scales of size and are characterized by very complex dynamics that lead to relaxation processes spanning many time scales. Due to the high density of their physical state (solution, mixture, glass or crystal), the transport of particles is confined and connected with the motion of particles in the vicinity. Despite this rather complicated picture, it is usually possible to distinguish individual time scales [39–41]. The shortest timescale τ_v corresponds to the time the molecules vibrate around a position, which is the result of being temporarily trapped by other molecules. It is obvious that translational movements of molecules from their momentary position require a more extended time scale τ_α, which is related to the participation of molecules in cooperative processes. Thus, paths of particles in a crowded environment can be considered as a combination of two types of motion: oscillations around a momentary position resulting from entrapment by other molecules and not very frequent changes of momentary position (translation). Thus, the flow of the fluid on the macroscopic level corresponds to the time scale τ_α, for which the alignment of the particles is no longer stable because each of the molecules in this time scale can participate in the movement. The above image of the movement of particles in a liquid is generally accepted and well documented by molecular dynamics simulation for dense systems of discs in which Lennard-Jones potential interactions were used [42, 43] but it is not obvious what exact conditions are required for a single diffusion step. The known theories of the fluid transport phenomena do not also closely examine this problem. The Brownian motion theories [44, 45] treat the trajectories of particles as random walks, and thus the time scale in which the movements of particles are observed is much longer than the time scale corresponding to the elementary diffusion step. The “mode coupling” theory [40] considers several time scales, but so far there is no precise picture of the memory function that would allow considering the motion of molecules at the microscopic level. In contrast, phenomenological models such as the free-volume model [46] or the Adam-Gibbs model [47] lack a microscopic picture of dynamics.

Cooperativity is considered to be one of the main factors responsible for the relaxation mechanism in molecular fluids. It has remained a poorly defined phenomenon for a long time. It was especially difficult to associate cooperativity with a well-defined microscopic image. The solution to this problem is proposed by the DLL model [17, 19, 48].

The Most Important Results Featuring Dynamic Lattice Liquid

The DLL model is a simple model of fluid dynamics [49] which takes into account the cooperative movement of molecules based on the lattice structure. The position of the molecule in this model corresponds to a lattice node. We assume that objects occupy all places in the lattice, but the system has some additional volume, which allows the objects to oscillate around the position determined by the lattice site. We also assume that the oscillations have a frequency ofν_v=1/τ_v, which correspond to a short time scale, i.e., the vibrations of particles around the average location are associated with the place of temporary entrapment by neighboring molecules. Each shift of a molecule from an average position defined by a lattice node to another lattice node (new average position) corresponds to a translation and hence to a time scale τ_α; most attempts of this translational movement fail. It results from the assumption that the system remains quasi-continuous all the time, i.e., that:

(1) in the system, no free spaces can be created, the sizes of which would be comparable to the sizes of the molecules under consideration,

(2) the excluded volume condition is fulfilled, i.e., a lattice node cannot be occupied by more than one molecule at the same time.

As a consequence of the assumptions presented above, most attempts of a move are unsuccessful and after a time τ_ν the molecule returns to its original position. The attempts that coincide with other attempts of motion of two or more adjacent molecules in combination with the formation of a closed loop in which the total shift of the elements is approximately 0 will be successful. In order to determine the probability of such an event one has to calculate the probability of the formation of a closed loop (for a given type of lattice) with self-avoidance, i.e., a loop that does not intersect with itself. Intensive research on this problem has led to a generally accepted result that the probability of the formation of such a loop can be described by the expression [50]:

$P\left(n\right)=B{n}^{-h}{\mu }^n(3)$

where n is the length of the loop, B is a constant depending on the lattice type, μ is the effective coordination number of the lattice (also called the connective constant) and the exponent h is a positive quantity which weakly depends on the lattice type, i.e., its coordination number and the dimension of space [17, 51]. If one knows the probability, then one can determine the mean position relaxation time corresponding to the time needed for the molecule to change its position as:

$\tau ={\left(B{\displaystyle \sum _3^{\infty }{n}^{-h+1}}{\mu }^n\right)}^{-1}(4)$

The DLL algorithm is ergodic and the proof of micro-reversibility can be easily obtained using the properties of the permutation group [38]. It should be emphasized that all the above considerations were carried out with the assumption that the lattice is isotropic and the effective coordination number takes the maximum value for a given lattice and that the system is densely packed. In this case, the exclusion of the molecule from motion is due to the continuity condition, but all attempts to move should be considered as potentially possible. The situation presented above corresponds to the so-called an athermal case, i.e., when the system does not take into account other interactions apart from the interactions related to the existence of the excluded volume. The introduction of interactions and temperature will lead to limitations of movement, and thus to a change in the effective value of the coordination number, which determines the mobility of the elements. Molecular Dynamics simulations revealed similar to assumed in the DLL model vibrations and collective jumps of group of atoms in densely packed disordered systems like glasses and undercooled liquids [48]. This situation is illustrated in Figure 1, where schemes of molecular dynamics and DLL model are shown together with trajectories obtained in simulations.

FIGURE 1

FIGURE 1. The scheme of molecular dynamics simulations of hard disks (left), trajectories of simulated hard disks (middle), and a scheme of cooperative loops in the dynamic lattice liquid model (right): green–a cooperative motion is possible, yellow, red and pink–no cooperative loop of motion.

The DLL model became a starting point for the development of other models based on the concept of cooperative dynamics. After introducing constraints (stiff bonds) into this model the structure and dynamics of macromolecular systems were studied [51–55]. Two models of soft-material membrane were developed directly from the DLL model which appeared to be appropriate for studies of subdiffusive behavior [56, 57].

As mentioned earlier, the main feature of crowded environments is the fact that the movement of an object is closely correlated with the movement of neighboring objects. The strong correlation in the motion between objects leads to a significantly greater impact of obstacles (or other types of restrictions) on the motion of individual elements as a result of the transfer of hydrodynamic forces. It results in dramatic changes in the objects trajectories, and thus in the dynamics in the system. Hence, it is of interest to compare two extremely different situations that correspond to a strong correlation in movement (the DLL model) and a single agent model (SAM) case where there are no such correlations at all. The diffusion coefficient D is defined by the Einstein relation and for system in two dimensions it can be calculated from the following formula [58].

$\langle \Delta r^2\rangle =4Dt(5)$

The assumption that the dependence of $\langle \Delta r^2\rangle$ on time is linear is not always valid and an anomalous diffusion appears in random media. Impenetrable obstacles having the same size as mobile objects were placed randomly and the concentration of obstacles is defined as the ratio of the number of obstacles to the total number of sites in the system. The percolation threshold due to the presence of these obstacles is important here, as above this threshold the motion is limited. The percolation threshold was determined using the scaling analysis of the diffusion coefficient [16]. The differences in the dynamic properties in both models near the percolation threshold can be studied by monitoring the behavior of $\langle \Delta r^2\rangle$ what is presented in Figure 2A.The lowest values of the exponent α found at the percolation threshold were also marked: 0.697 from other simulations and theoretical considerations [2, 17] and 0.37 found recently within the frame of the DLL model. In the SAM model the mobility of molecules is greater than that of the DLL model in spite of higher concentration of obstacles. The main reason is the lack of any correlations in motion of moving objects in the SAM model. When correlations in motion are included into the model like in the DLL case, many moving objects begin to play a role similar to the obstacles (as a result of the proximity of obstacles) what drastically affects the dynamics of the system. Subdiffusive regions are better defined in the DLL model, thus the caging effect is stronger here than in SAM. In the latter model such regions appear very quickly and an initial region of a normal diffusion is very short. The non-Gaussian parameter can give additional insight into the dynamics in disordered system. This parameter is defined as Ref. [9]:

${\alpha }_2\left(t\right)=\frac{\langle \Delta r^4\left(t\right)\rangle }{2{\langle \Delta r^2\left(t\right)\rangle }^2}-1(6)$

The α₂ parameter measures the deviation of the distribution of object’s displacements from the Gaussian distribution. Therefore, it can be treated as a measure of the dynamic heterogeneity of a given system and α₂ remains near zero in the case of a normal diffusion and its value increases when dealing with a non-Fickian diffusion. Inset to Figure 2A shows the variation of α₂ with time for both models in the vicinity of the percolation threshold. The presence of a distinct peak on the DLL curve confirms stronger heterogeneity of motion, i.e., caging effects in the DLL model [36]. It was already confirmed that this heterogeneity was correlated with structural heterogenicity [17]. One can distinguish three regimes on Δr² curves: normal, subdiffusive and normal again. As the first one is also well defined we were able to calculate a diffusion coefficient and called it a short-time diffusion coefficient. The diffusion coefficient was determined according to Eq 5 for short time and long time and presented in Figures 2B as a function of the obstacles concentration. Short time diffusion coefficients decrease exponentially with the obstacle concentration while those determined long time decrease considerably stronger. For both models a rapid decrease of long time diffusion coefficient is visible near the percolation threshold. A universal scaling formula relates the long time diffusion coefficient in the vicinity of the percolation threshold c_p: D ∼ ɛ^μ where ɛ=|c–c_p|/c_p and µ is a critical exponent. In the case of SAM µ = 1.31 as predicted by the theory [58] but in the case of the DLL model µ = 4.34 [17] what in turn leads to different values of the exponents:α ≈ 0.37 and 0.37 for SAM and DLL models respectively. Changes of the dynamic of the system when approaching the percolation threshold resembles the glass transition although both of these are completely different phenomena. Moreover, we can actually observe a breakdown of the Stokes-Einstein relation. According to the Stokes-Einstein relation the product $D\eta /T$ (and hence Dτ/T) should remain constant (η is the dynamic viscosity, τ is the structural relaxation time and T is the temperature) as a function of T. In our work we did not use the temperature explicitly but it can be assumed that the concentration of the obstacles c plays a role of the temperature (however, one has to remember that the regarded phenomena are of a quite different nature). In Ref. [48] we concluded that the product βc (β is a constant and c is a concentration of obstacles) can be interpreted as a factor (−E/kT) (here β corresponds to E/k and c corresponds to 1/T). Thus, the equation $D\eta /T$ can be written in the form Dτc as the relaxation time was obtained by averaging the waiting time for a move in the DLL model for a given concentration of obstacles (the discussion on the waiting time was also give in Ref. [48]). Figure 2C presents the dependency of Dτc on the obstacle concentration c. One can observe that for low obstacle concentrations which corresponds to high temperatures the product Dτc remains approximately constant but for the concentrations c ≈ 0.26 a rapid decrease of Dτc is observed what suggests the breakdown of Stokes-Einstein relation similarly as near the glass transition.

FIGURE 2

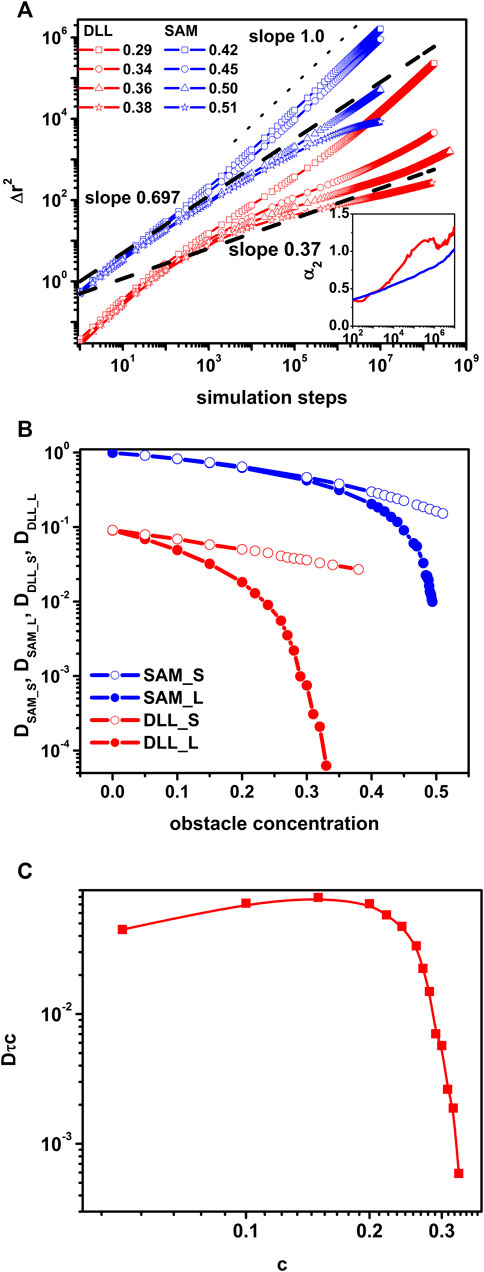
FIGURE 2. The comparison of dynamic lattice liquid and single agent model models near the percolation point. <∆r²> vs. time for concentrations of obstacles indicated in top left corner (the inset shows the non-Gaussian parameter vs. time near the percolation threshold) (A); short-time (S) and long-time (L) diffusion coefficient D as functions of the obstacles concentration (B); the product Dτc as a function of the obstacles concentration (C).

Conclusions

The example of DLL showed that the introduction of a cooperative model of transport led to the dramatic changes in the motion of objects in disordered systems. The deviations from a normal diffusion are definitely more pronounced in the DLL model cooperative motion assumed here generates additional caging effect. The percolation threshold and critical exponents were found to be dependent on the model of transport. Although the DLL model had been designed and initially developed for studies of liquids it found application in soft matter systems like membranes, porous materials, polymers and gels [51–55, 59–62]. The mechanism of molecular transport introduced in DLL was also found to be applicable in soft matter reproducing the dynamic behavior in many systems including biological materials. The case of macromolecular systems containing long chains is much more difficult for studies under the DLL model because relaxation of such systems via cooperative loops is very long but it possible to study the entire process of polymerization [37, 38]. It has also be noted that it is possible to introduce the temperature into this model via free-volume or directly in potentials of interaction.

Author Contributions

Both authors planned the review, collected the bibliography and made a direct contribution to the work. They prepared the final manuscript for the publication.

Funding

This work was supported by the Polish National Science Center grant UMO-2017/25/B/ST5/01970. Simulations were partially performed on the dedicated parallel machine ARUZ, BioNanoPark in Łódź, Poland.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Almeida PFF, Vaz WLC. Handbook of biological physics. In: Lipovsky, R, and Sackman, E, editors. Structure and dynamics of membranes: from cells to vesicles. Vol. 1. Amsterdam, NL: Elsevier/North Holland (1995) p. 1–1020.

CrossRef Full Text | Google Scholar

2. Küntz M, Lavallée P. Experimental evidence and theoretical analysis of anomalous diffusion during water infiltration in porous building materials. J Phys D Appl Phys (2001) 34:2547–5410. doi:1088/0022-3727/34/16/322.

CrossRef Full Text | Google Scholar

3. Berthier L, Biroli G. Theoretical perspective on the glass transition and amorphous materials. Rev Mod Phys (2011) 83:587–645. doi:10.1103/RevModPhys.83.587.

CrossRef Full Text CrossRef Full Text | Google Scholar

4. Biroli DC, Morgenstern K, Verheij LH, Rosenfeld G, Besenbacher F, Cosma G. Kinetics of island diffusion on Cu(111) and Ag(111) studied with variable-temperature STM. Surf Sci (2000) 465:19–39. doi:10.1016/S0039-6028(00)00682-8

CrossRef Full Text | Google Scholar

5. Bouchaud J-P, Georges A. Anomalous diffusion in disordered media: statistical mechanisms, models and physical applications. Phys Rep (1990) 195:127–293. doi:10.1016/0370-1573(90)90099-n.

CrossRef Full Text | Google Scholar

6. Dix JA, Verkman AS. Crowding effects on diffusion in solutions and cells. Annu Rev Biophys (2008) 37:247–63. doi:10.1146/annurev.biophys.37.032807.125824. |

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Zhou H-X, Rivas G, Minton AP. Macromolecular crowding and confinement: biochemical, biophysical, and potential physiological consequences. Annu Rev Biophys (2008) 37:375–97. doi:10.1146/annurev.biophys.032807.125817. |

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Sokolov IM. Models of anomalous diffusion in crowded environments. Soft Matter (2012) 8:9043–52. doi:10.1039/C2SM25701G.

CrossRef Full Text | Google Scholar

9. Höfling F, Franosch T. Anomalous transport in the crowded world of biological cells. Rep Prog Phys (2013) 76:046602. doi:10.1088/0034-4885/76/4/046602.

CrossRef Full Text | Google Scholar

10. Javanainen M, Hammaren H, Monticelli L, Jeon J-H, Miettinen MS, Martinez-Seara H, et al. Anomalous and normal diffusion of proteins and lipids in crowded lipid membranes. Faraday Discuss (2013) 161:397–417. doi:10.1039/C2FD20085F. |

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Rivas G, Minton AP. Macromolecular crowding in vitro , in vivo , and in between, Trends Biochem Sci (2016) 41:970–81. doi:10.1016/j.tibs.2016.08.013. |

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Selle C, Rückerl F, Martin DS, Forstner MB, Käs JA. Measurement of diffusion in Langmuir monolayers by single-particle tracking. Phys Chem Chem Phys (2004) 6:5535–42. doi:10.1039/B412680G.

CrossRef Full Text | Google Scholar

13. Metzler R, Jeon J-H, Cherstvy AG, Barkai E. Anomalous diffusion models and their properties: non-stationarity, non-ergodicity, and ageing at the centenary of single particle tracking. Phys Chem Chem Phys (2014) 16:24128–64. doi:10.1039/C4CP03465A. |

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Sung BJ, Yethiraj A. The effect of matrix structure on the diffusion of fluids in porous media. J Chem Phys (2008) 128:054702. doi:10.1063/1.2823735. |

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Saxton MJ. A biological interpretation of transient anomalous subdiffusion. I. Qualitative model. Biophys J (2007) 92:1178–91. doi:10.1529/biophysj.106.092619. |

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ben-Avraham D, Havlin S. Diffusion and reactions in fractals and disordered systems. Cambridge, UK: Cambridge University Press (2000) p. 316.

Google Scholar

17. Polanowski P, Sikorski A. Simulation of diffusion in a crowded environment. Soft Matter (2014) 10:3597–607. doi:10.1039/C3SM52861H. |

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Kammerer A, Höfling F, Franosch T. Cluster-resolved dynamic scaling theory and universal corrections for transport on percolating systems. Europhys Lett (2008) 84:66002. doi:10.1209/0295-5075/84/66002.

CrossRef Full Text | Google Scholar

19. Polanowski P, Sikorski A. Diffusion of small particles in polymer films. J Chem Phys (2017) 147:014902. doi:10.1063/1.4990414. |

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Polanowski P, Sikorski A. Motion in a crowded environment: the influence of obstacle’s size and shape and model of transport. J Mol Model (2019) 25:84. doi:10.1007/s00894-019-3968-9. |

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Cho HW, Kwon G, Sung BJ, Yethiraj A. Effect of polydispersity on diffusion in random obstacle matrices. Phys Rev Lett (2012) 109:155901. doi:10.1103/physrevlett.109.155901.

CrossRef Full Text | Google Scholar

22. Polanowski P, Sikorski A. Simulation of molecular transport in systems containing mobile obstacles. J Phys Chem B (2016) 120:7529–37. doi:10.1021/acs.jpcb.6b02682. |

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Vilaseca E, Isvoran A, Madurga S, Pastor I, Garcés JL, Mas F. New insights into diffusion in 3D crowded media by Monte Carlo simulations: effect of size, mobility and spatial distribution of obstacles. Phys Chem Chem Phys (2011) 13:7396–407. doi:10.1039/C0CP01218A. |

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Berry H, Chaté H. Anomalous diffusion due to hindering by mobile obstacles undergoing Brownian motion or Orstein-Ulhenbeck processes. Phys Rev E (2014) 89:022708. doi:10.1103/PhysRevE.89.022708.

CrossRef Full Text CrossRef Full Text | Google Scholar

25. Polanowski P, Sikorski A. Molecular transport in systems containing binding obstacles. Soft Matter (2019) 15:10045–54. doi:10.1039/C9SM01876J. |

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Ghosh SK, Cherstvy AG, Metzler R. Non-universal tracer diffusion in crowded media of non-inert obstacles. Phys Chem Chem Phys (2015) 17:1847–58. doi:10.1039/C4CP03599B. |

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Stefferson MW, Norris SL, Vernerey FJ, Betterton MD, Hough LE. Effects of soft interactions and bound mobility on diffusion in crowded environments: a model of sticky and slippery obstacles. Phys Biol (2017) 14:045008. doi:10.1088/1478-3975/aa7869. |

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Brown FLH. Continuum simulations of biomembrane dynamics and the importance of hydrodynamic effects. Q Rev Biophys (2011) 44:391–432. doi:10.1017/S0033583511000047. |

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Voigtmann T, Horbach J. Double Transition scenario for anomalous diffusion in glass-forming mixtures. Phys Rev Lett (2009) 103:205901. doi:10.1103/PhysRevLett.103.205901. |

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kim K, Miyazaki K, Saito S. Slow dynamics in random media: crossover from glass to localization transition. Europhys Lett (2009) 88:36002. doi:10.1209/0295-5075/88/36002.

CrossRef Full Text | Google Scholar

31. Kurzidim J, Coslovich D, Kahl G. Single-particle and collective slow dynamics of colloids in porous confinement. Phys Rev Lett (2009) 103:138303. doi:10.1103/PhysRevLett.103.138303. |

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Skinner TOE, Schnyder SK, Aarts DGAL, Horbach J, Dullens RPA. Localization dynamics of fluids in random confinement, Phys Rev Lett (2013) 111:128301. doi:10.1103/PhysRevLett.111.128301. |

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Cho HW, Yethiraj A, Sung BJ. Non-universality of the dynamic exponent in two-dimensional random media. Sci Rep (2019) 9:251. doi:10.1038/s41598-018-36236-z.

CrossRef Full Text | Google Scholar

34. Sung BJ, Yethiraj A. Lateral diffusion of proteins in the plasma membrane: spatial tessellation and percolation theory. J Phys Chem B (2008) 112:143–9. doi:10.1021/jp0772068.

CrossRef Full Text | Google Scholar

35. Bauer T, Höfling F, Munk T, Frey E, Franosch T. The localization transition of the two-dimensional Lorentz model. Eur Phys J Spec Top (2010) 189:103–18. doi:10.1140/epjst/e2010-01313-1.

CrossRef Full Text | Google Scholar

36. Höfling F, Franosch T, Frey E. Localization transition of the three-dimensional Lorentz model and continuum percolation. Phys Rev Lett (2006) 96:165901. doi:10.1103/PhysRevLett.96.165901.

CrossRef Full Text | Google Scholar

37. Polanowski P, Pakula T. Studies of polymer conformation and dynamics in two dimensions using simulations based on the dynamic lattice liquid (DLL) model. J Chem Phys (2002) 117:4022–9. doi:10.1063/1.1495836.

CrossRef Full Text | Google Scholar

38. Pakula T. Simulation on the completely occupied lattices. In: Kotelyanskii, M, and Theodorou, DN, editors. Simulation methods for polymers. New York, Basel: Marcel Dekker (2004) p. 990.

Google Scholar

39. Brower S. Relaxation in viscous liquids and glasses. Columbus, OH: The Am. Ceramic Soc. (1985) p. 220.

Google Scholar

40. Götze W. Liquids, freezing and glass transition. Hansen, JP, Levesque, D, and Zinn-Justin, J, editors. Amsterdam, NL: North-Holland (1991) p. 931.

Google Scholar

41. Donth W. Relaxation and thermodynamics in polymers. Berlin, Germany: Akademie Verlag (1992) p. 335.

Google Scholar

42. Alder BJ, Wainwright TE. Studies in molecular dynamics. I. General method. J Chem Phys (1959) 31:459–66. doi:10.1063/1.1730376.

CrossRef Full Text | Google Scholar

43. Barker JA, Henderson D. What is “liquid”? understanding the states of matter. Rev Mod Phys (1976) 48:587–671. doi:10.1103/RevModPhys.48.587.

CrossRef Full Text CrossRef Full Text | Google Scholar

44. Widom A. Velocity fluctuations of a hard-core Brownian particle. Phys. Rev. A (1971) 3:1394–6. doi:10.1103/PhysRevA.3.1394.

CrossRef Full Text CrossRef Full Text | Google Scholar

45. Kubo R. The fluctuation-dissipation theorem. Rep Prog Phys (1966) 29:255–84. doi:10.1088/0034-4885/29/1/306.

CrossRef Full Text | Google Scholar

46. Cohen MH, Grest GS. Liquid-glass transition, a free-volume approach. Phys Rev B (1979) 20:1077–98. doi:10.1103/PhysRevB.20.1077.

CrossRef Full Text | Google Scholar

47. Adam G, Gibbs JH. On the temperature dependence of cooperative relaxation properties in glass‐forming liquids. J Chem Phys (1965) 43:139–46. doi:10.1063/1.1696442.

CrossRef Full Text | Google Scholar

48. Polanowski P, Sikorski A. Comparison of different models of motion in a crowded environment: a Monte Carlo study. Soft Matter (2017) 13:1693–701. doi:10.1039/C6SM02308H. |

PubMed Abstract | CrossRef Full Text | Google Scholar

49. Pakula T, Teichmann J. A model for relaxation in supercooled liquids and polymer melts. MRS Proc (1996) 455:211–22. doi:10.1557/PROC-455-211.

CrossRef Full Text | Google Scholar

50. Hughes BD. Random walk and random environments. Oxford, NY: Clarendon Press (1995) p. 550.

Google Scholar

51. P Polanowski, T Pakula. Studies of polymer conformation and dynamics in two dimensions using simulations based on the dynamic lattice liquid (DLL) model. J Chem Phys (2002) 117:4022–9. doi:10.1063/1.1495836.

CrossRef Full Text | Google Scholar

52. P Polanowski, T Pakula. Simulation of polymer-polymer interdiffusion using the dynamic lattice liquid model. J Chem Phys (2004) 120:6306–11. doi:10.1063/1.1649313. |

PubMed Abstract | CrossRef Full Text | Google Scholar

53. P Polanowski, JK Jeszka, A Sikorski. Dynamic properties of linear and cyclic chains in two dimensions. Computer simulation studies. Macromolecules (2014) 47:4830–9. doi:10.1021/ma5004460b10.1021/ma500460b.

CrossRef Full Text | Google Scholar

54. M Kozanecki, K Halagan, J Saramak, K Matyjaszewski. Diffusive properties of solvent molecules in the neighborhood of a polymer chain as seen by Monte-Carlo simulations, Soft Matter (2016) 12:5519–28. doi:10.1039/C6SM00569A. |

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Blim A, Kowalczyk T. Dynamic lattice liquid (DLL) model in computer simulation of the structure and dynamics of polymer condensed systems. E-Polymers (2012) 12:1–11. doi:10.1515/epoly.2012.12.1.922.

CrossRef Full Text CrossRef Full Text | Google Scholar

56. Ishimoto Y, Murashima T, Taniguchi T, Yamamoto R. Two-dimensional lattice liquid models. Phys Rev E (2012) 86:031124. doi:10.1103/PhysRevE.86.031124.

CrossRef Full Text CrossRef Full Text | Google Scholar

57. Schober HR. Collectivity of motion in undercooled liquids and amorphous solids. J Non-Cryst Solids (2002) 307–310:40–9. doi:10.106/S0022-3093(02)01438-2.

CrossRef Full Text CrossRef Full Text | Google Scholar

58. Ben-Avraham D, Havlin S. Diffusion and reactions in fractals and disordered systems. chap. 6. Cambridge, UK: Cambridge University Press (2000) p. 74–97.

Google Scholar

59. P Polanowski, T Pakula. Studies of mobility, interdiffusion, and self-diffusion in two-component mixtures using the dynamic lattice liquid model. J Chem Phys (2003) 118:11139–46. doi:10.1063/1.1576214.

CrossRef Full Text CrossRef Full Text | Google Scholar

60. P Polanowski, Z Koza. Reaction-diffusion fronts in systems with concentration-dependent diffusivities. Phys Rev E (2006) 74:36103. doi:10.1103/PhysRevE.74.036103.

CrossRef Full Text CrossRef Full Text | Google Scholar

61. H Gao, P Polanowski, K Matyjaszewski. Gelation in living copolymerization of monomer and divinyl cross-linker: comparison of ATRP experiments with Monte Carlo simulations. Macromolecules (2009) 42:5925–32. doi:10.1021/ma901005d.

CrossRef Full Text CrossRef Full Text | Google Scholar

62. P Polanowski, JK Jeszka, K Matyjaszewski. Polymer brushes in pores by ATRP: Monte Carlo simulations. Polymer (2020) 211:123124–196. doi:10.1016/j.polymer.2020.12312410.1016/j.polymer.2019.04.023.

CrossRef Full Text CrossRef Full Text | Google Scholar