- Department of Theoretical Physics, Research School of Physics, The Australian National University, Canberra, NSW, Australia
The nonlinear Schrödinger equation has wide range of applications in physics with spatial scales that vary from microns to kilometres. Consequently, its solutions are also universal and can be applied to water waves, optics, plasma and Bose-Einstein condensate. The most remarkable solution presently known as the Peregrine solution describes waves that appear from nowhere. This solution describes unique events localized both in time and in space. Following the language of mariners they are called “rogue waves”. As thorough mathematical analysis shows, these waves have properties that differ them from any other nonlinear waves known before. Peregrine waves can serve as ‘elementary particles’ in more complex structures that are also exact solutions of the nonlinear Schrödinger equation. These structures lead to specific patterns with various degrees of symmetry. Some of them resemble “atomic like structures”. The number of particles in these structures is not arbitrary but satisfies strict rules. Similar structures may be observed in systems described by other equations of mathematical physics: Hirota equation, Davey-Stewartson equations, Sasa-Satsuma equation, generalized Landau-Lifshitz equation, complex KdV equation and even the coupled Higgs field equations describing nucleons interacting with neutral scalar mesons. This means that the ideas of rogue waves enter nearly all areas of physics including the field of elementary particles.
1 Introduction
The nonlinear Schrödinger equation (NLSE) has wide range of applications in physics with spatial scales that vary from microns to kilometres and even light years. It describes nonlinear wave phenomena in optics [1, 2], oceanography [3, 4], plasmas [5, 6], atmosphere [7], Bose-Einstein condensate [8, 9] and cosmology [10]. Taking into account the lowest order nonlinearity and dispersion, this equation describes nonlinear wave phenomena at the fundamental level. NLSE serves as a basic tool for understanding modulation instability [11, 12], solitons [13], periodic waves [14] and extreme waves [15, 16]. The ideas born in the studies of NLSE solutions can be transferred to many other systems. Despite being studied for nearly 50 years, the NLSE solutions have a rich structure and provide surprises for researchers even today [17].
Being a practical introduction to a special issue, this article provides a basic review of mathematical results on NLSE that are important for understanding the nonlinear phenomena in general. It leaves aside the complexities of inverse scattering technique [13], Darboux transformation [18], theta functions [19] and other sophistications of modern mathematics [20]. Instead, it provides solutions in explicit form so that everyone can appreciate their clarity, simplicity of making useful plots and most importantly, the possibility of using them in applications.
The NLSE describes systems with an infinite number of degrees of freedom. Being integrable, it has an infinite number of solutions that can be presented in analytic form. Among them, there are fundamental ones such as soliton solutions [13], Akhmediev breathers [21–24], the Peregrine solution [26–28] and the general doubly-periodic solutions [17, 22]. These can be considered as fundamental modes of the nonlinear system each with a specific single eigenvalue of the inverse scattering transform [13]. More complicated solutions are nonlinear superpositions of these fundamental ones. Although mathematically, these superpositions may look highly complicated, conceptually, they can be understood as a combination of fundamental solutions. The corresponding spectrum of eigenvalues for complex solutions is a combined set of individual eigenvalues.
Presently, the most studied combinations are multi-soliton solutions [13, 29]. Next in complexity are multi-Akhmediev breathers [25, 31]. Rogue waves can also be superimposed resulting in multi-rogue wave solutions. In contrast to multi-solitons and multi-ABs, multi-rogue waves are degenerate solutions. The eigenvalues corresponding to the individual contributions are located at the same point of the complex plane. Despite this complication, multi-rogue waves are also well studied [32–34] but, perhaps, their physics is less understood [35–37] than the physics of any other solutions of the NLSE. The main reason is the unusual set of rules that control their superposition [35]. On the other hand, the superpositions of elementary doubly-periodic solutions studied in [17, 22] still need to be constructed. This task is mathematically challenging and has not been addressed so far. Existence of “explicit” solutions in terms of theta functions [19] does not provide any clue for solving this highly involved task.
Building higher-order superpositions consisting of the same type of fundamental solutions, say, multi-soliton solutions is relatively simple task [38]. This may be done using techniques such as Darboux transformation [30]. Mixing different types of fundamental solutions is more difficult. However, this has also been done in a few recent works. Mixing them is the way to address problems such as rogue waves on top of a periodic background [39, 40]. The number of possibilities is literally infinite.
After what is said above, it may seem strange that the NLSE model is the simplest one among the existing nonlinear evolution equations. However, this is indeed the case. The NLSE provides the conceptual background for further developments in the science of rogue waves. We should keep in mind that the first known integrable equation which is the real KdV equation [41] does not have rogue wave solutions. It cannot be used as a mathematical platform for rogue wave research. On the contrary, the ideas developed in the studies of NLSE solutions can be further extended to many other systems. These include Hirota equation [42], Sasa-Satsuma equation [43], Davey-Stewartson equations [44–46], Sine-Gordon equation [47], Landau-Lifschitz equation [48] and many others. The basic concepts are valid not only for integrable equations but can be expanded to non-integrable cases [49, 50] and, to some extent, to dissipative systems [51, 52].
The generality of the concept of rogue waves can be further expanded to extreme events in nature. Clearly, the equations that describe natural phenomena are more complex than the NLSE [53]. Nevertheless, these are also evolution equations that can be solved if not analytically, then numerically [54]. Rogue waves must be part of complex evolution of the system with either regular or chaotic initial conditions. These rogue waves may take more complicated forms than a simple Peregrine wave. They can take the form of tornadoes or hurricanes. These are also formations that “appear from nowhere”. Thus, they do belong to the class of rogue waves or “extreme events”.
Our task here is well defined by the subject of the special issue. Therefore, we will concentrate on the Peregrine wave, its analogs and its higher-order combinations. This is a very small subset of the whole set of multi-parameter families of solutions of the NLSE. Nevertheless, this subset plays an important role in explaining extreme events in many physical situations. Understanding variety of complex phenomena starts with the studies of simple examples. These simple examples are listed in the present rendition.
2 NLSE
The relative simplicity of the nonlinear Schrödinger equation, its integrability [13] and its applicability to many weakly nonlinear dispersive systems made it a universal model for wave propagation. The most common applications include deep ocean water waves [3, 4] and waves in an optical fiber [1, 2]. Universality means that this equation can be written in a standard form that is applicable to all major physical settings. Variables in this form are dimensionless and there are no free parameters. Namely,
Here, we consider x as the propagation distance and t as the retarded time in a reference frame moving with the group velocity. The function ψ means the envelope of the wave packet. Being a complex function, it defines both, the amplitude of the envelope and the phase shift of the carrier wave.
For a given central frequency of narrow banded waves, the group velocity of the waves is well defined by the dispersion relation. In this case, the propagation distance and time in the moving frame are linearly related. This means that the time and the distance can be easily exchanged in Eq. 1 [4]. This replacement creates an alternative form of the equation that has been used in the earlier descriptions of water wave propagation [4]. Evolution in time is also convenient in problems related to Bose-Einstein condensate. For experiments in water tanks and in optical fibers, it is more convenient to stick to the notations taken in Eq. 1. Then waves are evolving along the tank or along the fiber and the shape of the wave envelope can be observed moving along with the wave packet.
All solutions below will be given in dimensionless form that directly satisfy Eq. 1. For practical applications, solutions must be rescaled to dimensional variables, i.e. they must be expressed in meters (kilometres) along the tank or along the fiber, in seconds for the transverse variable and in the amplitude units for ψ. In the case of an optical fiber, this rescaling is given by:
where
In the case of waves in deep water the rescaling takes the form:
where X is dimensional distance along the tank, T is dimensional time in the frame moving with the group velocity
Further adjustment of solutions can be done with the use of scaling transformation
Namely, if
3 Peregrine Wave
One of the simplest non-singular rational solutions of the NLSE 1) is given by [15, 16, 26]:
It is known as the Peregrine solution or Peregrine soliton [27] or Peregrine breather [28]. The modulus of this complex solution is shown in Figure 1. The main feature of this solution is the localization of its central peak both in time and in space. The constant background represents a plane wave with an infinite source of energy. This solution has all features of rogue waves in the ocean [15, 16]. It represents an unexpected wave event on an otherwise flat background.
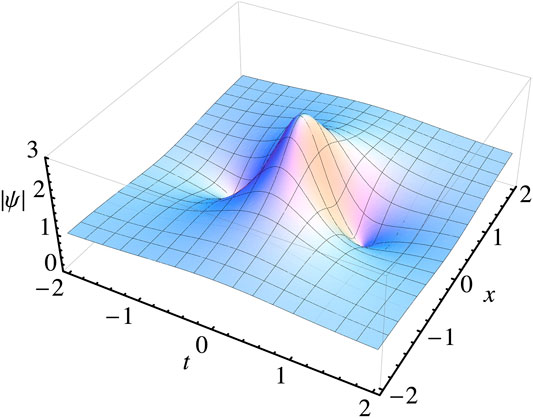
FIGURE 1. A single Peregrine wave of the NLSE [15]. The maximum amplitude at the origin is three while the background amplitude is 1. The solution has two zeros along the t axis at each side of the maximum. This simple wave structure appears in more complicated rogue wave patterns.
Peregrine solution has been observed in various experiments. The most notable ones are in water waves [55] and in optical fibers [27]. This solution appears in field evolution dynamics with variety of initial conditions [56]. Moreover, the Peregrine solution can be considered as a universal structure emerging in any type of intensity localization of high power pulses [57]. We can consider it as an “elementary particle” of more complicated patterns that can appear on a plane wave background. As the NLSE is the envelope equation, the Peregrine solution may describe both the wave of elevation or a depression. The latter is known as the rogue wave hole [58]. Solutions similar to the Peregrine one can also be found in other physical systems [5960–62]. Thus, the phenomenon of rogue wave is even more universal than we can imagine.
4 HIGHER-ORDER Rogue Wave Solutions
There are higher-order rational solutions of the NLSE that we can call rogue waves. The second order solution has been first presented in [14]. Several methods are known for constructing higher-order solutions of integrable equations [18, 32–34]. A hierarchy of rogue wave solutions with progressively increasing central amplitudes are presently known as Akhmediev-Peregrine (AP) breathers [636465–66]. Their general form can be written as:
where G, H and D are polynomials, and N is the order of the solution. In the case of the Peregrine solution (5),
For the second order solution, the polynomials are given by [14, 67]:
This solutions is shown in Figure 2A. While for the first order solution shown in Figure 1 the amplitude is 3 times the background, the maximum amplitude of the second order solution shown in Figure 2A is 5 times the background.
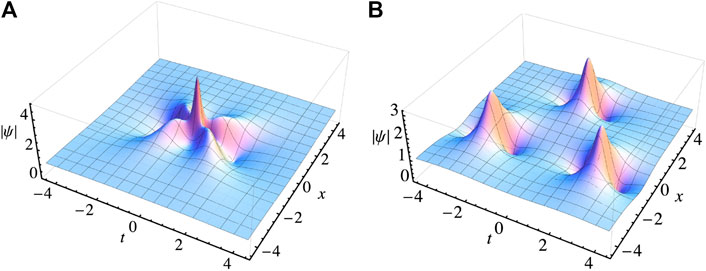
FIGURE 2. (A) AP solution of the second order [15]. (B) Rogue wave triplet with parameters
The second-order solution with free parameters has been given earlier in [32, 73]. The solution intensity
where β and γ are free real parameters of the solution. This solution is shown in Figure 2B. When
The general form of the third-order rogue wave solution is cumbersome. It has several free parameters. Various forms of the third-order solution have been presented in [71, 73–75] and [76]. Instead of giving the general form, we restrict ourselves with a simpler one-parameter case. As the solution intensity
where the polynomials
The third-order solutions are shown in Figure 3 for the cases
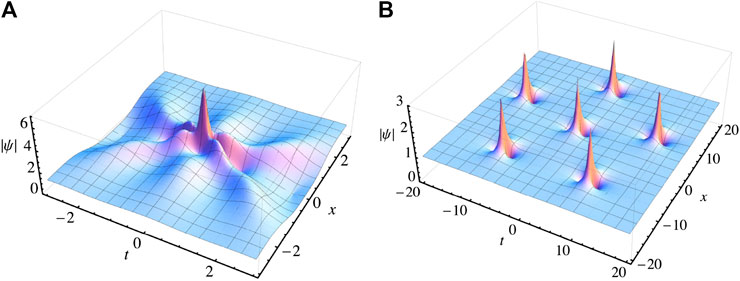
FIGURE 3. (A) Third order rogue wave solution given by Eq. (7) with
5 Complex Rogue Wave Patterns
The
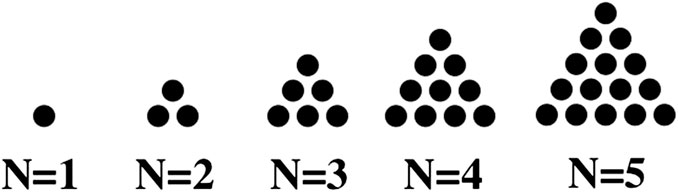
FIGURE 4. The first five triangular numbers. They are represented by the number of solid dots within each triangle.
Rogue wave patterns are defined by the order of the solution, N, and may depend on additional free parameters. Two examples are given above. These free parameters split the solution into individual Peregrine waves. These parameters specify separations and relative positions of the individual components on the
The maximal amplitude of a rogue wave is one of its main characteristics. The maximal amplitude of the higher-order AP solutions when all Peregrine waves are located at the origin is
A detailed classification of the rogue wave patterns has been given in [72]. The main results of this classification are shown in Figure 5. It shows the calculated rogue wave patterns that increase in order from top to bottom of table. A single Peregrine wave that is the solution of the first order is located in the top left cell. Higher-order AP solutions are located in the left column. The figure shows only solutions of up to 6-th order, although the list can be continued indefinitely. The second column represents regular triangular structures. The third column represents pentagram patterns. The fourth column provides examples of heptagram structures, i.e., patterns with seven Peregrine waves on one or several circles of different radii. Further columns have 9, 11, … Peregrine waves in the outer and inner shells of the structure.
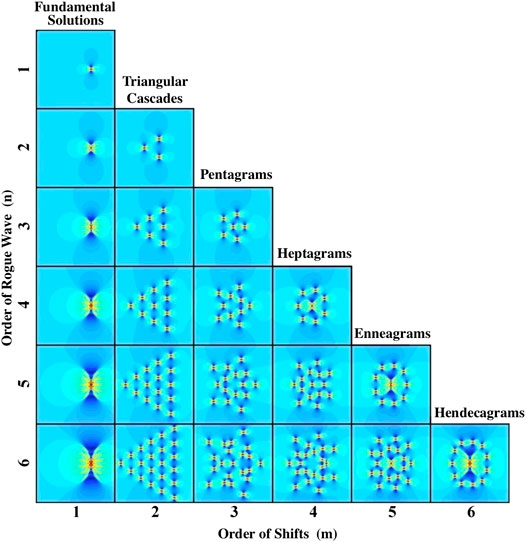
FIGURE 5. Patterns of higher-order rogue wave solutions [72]. Only solutions of up to order six are shown. The Peregrine soliton is on the first row. Second-order solutions are of two types: the AP solution and the triplet. They are located in the second row. Variety of patterns increases with the order. For example, the third order solutions do exist in the AP, triangular and pentagram forms. This happens because of the larger number of free parameters in the solution. Patterns located along the diagonal line are circular. They have a ring of
“Atomic-like” circular structures are located along the diagonal line. Starting from order 3, they consist of a central nucleus containing
There is no doubt that these patterns can be observed experimentally. Indeed, a single Peregrine wave has been observed in optics [27], in water waves [55] and in a multicomponent plasma [77]. It may soon be observed in Bose-Einstein condensate [78, 79]. The rogue wave triplet has been observed in a water wave tank [80]. AP solutions up to fifth-order have also been observed in water waves [81]. As the NLSE has a wide range of applications, these solutions may appear in situations that we cannot even predict right now.
Can this approach be used for a description of elementary particles and atomic structures? Obviously, this will need more sophisticated equation than the NLSE. As mentioned, the phenomena described in this review are not unique to the NLSE although, perhaps, the NLSE case is the most studied of all. Rogue waves have been found in systems described by the Hirota and Maxwell-Bloch equations [42, 82], Sasa-Satsuma equation [83], Fokas-Lenells equation [84], in systems with self-steepening effect [85, 86] and even in the case of the complex KdV equation [87, 88]. Patterns of multi-rogue wave solutions similar to those in Figure 5 have been found for the complex modified KdV equation [89], Kundu–Eckhaus equation [90], coupled nonlinear Schrödinger–Boussinesq equations [91], generalized derivative nonlinear Schrödinger equations [92, 93], generalized Landau-Lifshitz equation [48], Manakov equations [94], the three–wave resonant interaction equations [95, 96], discrete Ablowitz-Ladik equations [97] and even in the case of breather collisions [98, 99]. Most recent work [100] shows that the ideas of rogue waves now enter the field of elementary particles. Namely, patterns similar to those in Figure 5 may appear in the case of coupled Higgs field equations describing nucleons interacting with neutral scalar mesons [100]. Further developments of the rogue wave theory along these lines may boost our vision of the complex world and how it is build out of simple fundamental particles.
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Hasegawa A, Tappert F. Transmission of stationary nonlinear optical pulses in dispersive dielectric fibers. I. Anomalous dispersion. Appl Phys Lett (1973) 23:142–4. doi:10.1063/1.1654836
3. Zakharov VE. Stability of periodic waves of finite amplitude on a surface of deep fluid. J Appl Mech Tech Phys (1968) 9:190–4. doi:10.1007/BF00913182
5. Moslem WM, Shukla PK, Eliasson B. Surface plasma rogue waves. Europhys Lett (2011) 96:25002. doi:10.1209/0295-5075/96/25002
6. El-Tantawy SA. Rogue waves in electronegative space plasmas: the link between the family of the KdV equations and the nonlinear Schrödinger equation. Astrophys Space Sci (2016) 361:164. doi:10.1007/s10509-016-2754-8
7. Stenflo L, Marklund M. Rogue waves in the atmosphere. J Plasma Phys (2010) 76:293. doi:10.1017/S0022377809990481
8. Gross EP. Structure of a quantized vortex in boson systems. Nuovo Cimento (1961) 20:454. doi:10.1007/BF02731494
10. Lidsey JE. Scalar field cosmologies hidden within the nonlinear Schrödinger equation (2013). Available at: https://arxiv.org/abs/1309.7181 (Accessed September 27 2013).
11. Bespalov VI, Talanov VI. Filamentary structure of light beams in nonlinear liquids. Sov Phys JETP Lett (1966) 3:307.
12. Benjamin TB, Feir J. The disintegration of wave trains on deep water: Part 1. Theory J Fluid Mech (1967) 27:417. doi:10.1017/S002211206700045X
13. Zakharov VE, Shabat AB. Exact theory of two-dimensional self-focusing and one-dimensional self-modulation of waves in nonlinear media. J Exp Theor Phys (1972) 34:62–9.
14. Akhmediev N, Eleonskii VM, Kulagin NE. Generation of periodic trains of picosecond pulses in an optical fiber: exact solutions. Sov Phys JETP (1985) 62(5):894–9.
15. Akhmediev N, Ankiewicz A, Taki M. Waves that appear from nowhere and disappear without a trace. Phys Lett (2009) 373:675–8. doi:10.1016/j.physleta.2008.12.036
16. Shrira VI, Geogjaev VV. What makes the Peregrine soliton so special as a prototype of freak waves? J Eng Math (2009) 67:11–22. doi:10.1007/s10665-009-9347-2
17. Conforti M, Mussot A, Kudlinski A, Trillo S, Akhmediev N. Doubly periodic solutions of the focusing nonlinear Schrödinger equation: recurrence, period doubling, and amplification outside the conventional modulation-instability band. Phys Rev (2020) 101:023843. doi:10.1103/PhysRevA.101.023843
19. Its OR, Kotlyarov V. Explicit formulas for solutions of the Schrödinger nonlinear equation. Doklady Akad. Nauk Ukrainian SSR (1976) 10:965–8.
20. Its AR, Rybin AV, Sall MA. Exact integration of nonlinear Schrodinger equation[original in Russian: teor. Theor Math Phys (1988) 69:29–32.
21. Akhmediev N, Korneev VI. Modulation instability and periodic solutions of nonlinear Schrödinger equation. Theor Math Phys (1986) 69:189–94.
22. Akhmediev N, Eleonskii VM, Kulagin NE. Exact first-order solutions of the nonlinear Schrödinger equation. Theor Math Phys (1987) 72:809.
23. Yang G, Wu FO, Lopez Aviles HE, Christodoulides D. Optical amplification and transmission of attenuated multi-soliton based on spectral characteristics of Akhmediev breather. Optic Commun (2020) 473:125899.
24. Andral U, Kibler B, Dudley JM, Finot C. Akhmediev breather signatures from dispersive propagation of a periodically phase-modulated continuous. wave Motion (2020) 95:102545.
25. Akhmediev N, Korneev VI, Mitskevich NV. N-modulation signals in a single-mode optical waveguide under nonlinear conditions. Zh Exp Teor Fiz (1988) 94:159–70.
26. Peregrine DH. Water waves, nonlinear Schrödinger equations and their solutions. J Australian Math Soc Ser B (1983) 25:16.
27. Kibler B, Fatome J, Finot C, Millot G, Dias F, Genty G, et al. The Peregrine soliton in nonlinear fibre optics. Nat Phys (2010) 6:790–5.
28. Gaillard P, Gastineau M. The Peregrine breather of order nine and its deformations with sixteen parameters solutions to the NLS equation. Phys Lett (2015) 379:1309–13.
29. Ablowitz MJ, Segur H. Solitons and the inverse scattering transform Philadelphia, Pa, USA: SIAM (1981).
30. Akhmediev N, Mitskevich NV. Extremely high degree of N-soliton pulse compression in an optical fiber. IEEE J Quantum Electron QE (1991) 27:849–57.
31. Akhmediev N, Soto-Crespo JM, Ankiewicz A. Extreme waves that appear from nowhere: on the nature of rogue waves. Phys Lett (2009) 373:2137–45. doi:10.1016/j.physleta.2009.04.023
32. Dubard P, Gaillard P, Klein C, Matveev VB. On multi-rogue wave solutions of the NLS equation and positon solutions of the KdV equation. Eur Phys J Spec Top (2010) 185:247–58. doi:10.1140/epjst/e2010-01252-9
33. Ohta Y, Yang J. General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. Proc R Soc A (2012) 468:1716–40.
34. Gaillard P. Degenerate determinant representation of solutions of the nonlinear Schrödinger equation, higher order Peregrine breathers and multi-rogue waves. J Math Phys (2013) 54:013504. doi:10.1063/1.4773096
36. Kedziora DJ, Ankiewicz A, Akhmediev N. Triangular rogue wave cascades. Phys Rev E Stat Nonlinear Soft Matter Phys (2012) 86:056602. doi:10.1103/PhysRevE.86.056602
37. Kedziora DJ, Ankiewicz A, Akhmediev N. Circular rogue wave clusters. Phys Rev E Stat Nonlinear Soft Matter Phys (2011) 84:056611. doi:10.1103/PhysRevE.84.056611
38. Satsuma J, Yajima N. Initial value problems of one-dimensional self-modulation of nonlinear waves in dispersive media. Prog Theor Phys Suppl (1974) 55:284.
39. Kedziora DJ, Ankiewicz A, Akhmediev N. Rogue waves and solitons on a cnoidal background. Eur Phys J Spec Top (2014) 223:43–62. 10.1140/epjst/e2014-02083-4.
40. Chen J, Pelinovsky DE, White RE. Rogue waves on the double-periodic background in the focusing nonlinear Schrödinger equation. Phys Rev E (2019) 100:052219. doi:10.1103/PhysRevE.100.052219
41. Zabusky NJ, Kruskal MD. Interaction of “solitons” in a collisionless plasma and the recurrence of initial states. Phys Rev Lett (1965) 15:240–3.
42. Ankiewicz A, Soto-Crespo JM, Akhmediev N. Rogue waves and rational solutions of the Hirota equation. Phys Rev E Stat Nonlinear Soft Matter Phys (2010) 81:046602. doi:10.1103/PhysRevE.81.046602
43. Bandelow U, Akhmediev N. Persistence of rogue waves in extended nonlinear Schrödinger equations: integrable Sasa-Satsuma case. Phys Lett (2012) 376:1558–61. doi:10.1016/J.PHYSLETA.2012.03.032
44. Ohta Y, Yang J. Rogue waves in the Davey-Stewartson I equation. Phys Rev E Stat Nonlinear Soft Matter Phys (2012) 86:036604. doi:10.1103/PhysRevE.86.036604
45. Ohta Y, Yang JK. Dynamics of rogue waves in the Davey – stewartson II equation. J Phys Math Theor (2013) 46:105202. doi:10.1088/1751-8113/46/10/105202
46. Rao J, Cheng Y, He J. Rational and semirational solutions of the nonlocal Davey–Stewartson equations. Stud Appl Math (2017) 139:568–98. doi:10.1111/sapm.12178
47. Li R, Geng X. Rogue periodic waves of the sine—Gordon equation. Appl Math Lett (2020) 102:106147. doi:10.1016/j.aml.2019.106147
48. Li R, Geng X, Xue B. A generalization of the Landau-Lifschitz equation: breathers and rogue waves. J Nonlinear Math Phys (2020) 27:279–94. doi:10.1080/14029251.2020.1700636
49. Ankiewicz A, Devine N, Akhmediev N. Are rogue waves robust against perturbations? Phys Lett (2009) 373:3997–4000. doi:10.1016/j.physleta.2009.08.053
50. Ankiewicz A, Soto-Crespo JM, Chowdhury MA, Akhmediev N. Rogue waves in optical fibers in presence of third-order dispersion, self-steepening, and self-frequency shift. J Opt Soc Am B (2013) 30:87–94. doi:10.1364/JOSAB.30.000087
51. Zaviyalov A, Egorov O, Iliew R, Lederer F. Rogue waves in mode-locked fibre lasers. Phys Rev (2012) 85:013828. doi:10.1103/PhysRevA.85.013828
52. Soto-Crespo JM, Grelu P, Akhmediev N. Dissipative rogue waves: extreme pulses generated by passively mode-locked lasers. Phys Rev E Stat Nonlinear Soft Matter Phys (2011) 84:016604. doi:10.1103/PhysRevE.84.016604
53. Lynch P. The origins of computer weather prediction and climate modelling. J Comput Phys (2008) 227:3431–44. doi:10.1016/j.jcp.2007.02.034
54. Krishnamurti TN. Numerical weather prediction. Annu Rev Fluid Mech (1995) 27:195–225. doi:10.1146/annurev.fl.27.010195.001211
55. Chabchoub A, Hoffmann NP, Akhmediev N. Rogue wave observation in a water wave tank. Phys Rev Lett (2011) 106:204502. doi:10.1103/PhysRevLett.106.204502
56. Bertola M, Tovbis A. Universality for the focusing nonlinear Schrödinger equation at the gradient catastrophe point: rational breathers and poles of the tritronqué solution to Painlevé I, Commun. Pure Appl Math (2012) 66:678. doi:10.1002/cpa.21445
57. Tikan A, Billet C, El G, Tovbis A, Bertola M, Sylvestre T, et al. Universal Peregrine soliton structure in nonlinear pulse compression in optical fiber. Phys Rev Lett (2017) 119:033901. doi:10.1103/PhysRevLett.119.033901
58. Chabchoub A, Hoffmann NP, Akhmediev N. Observation of rogue wave holes in a water wave tank. J Geophys Res (2012) 117:C00J02. doi:10.1029/2011JC007636
59. Chen S, Grelu P, Soto-Crespo JM. Dark- and bright-rogue-wave solutions for media with long-wave-short-wave resonance. Phys Rev E Stat Nonlinear Soft Matter Phys (2014) 89:011201. doi:10.1103/PhysRevE.89.011201
60. Baronio F, Degasperis A, Conforti M, Wabnitz S. Solutions of the vector nonlinear Schrödinger equations: evidence for deterministic rogue waves. Phys Rev Lett (2012) 109:044102. doi:10.1103/PhysRevLett.109.044102
61. Baronio F. Akhmediev breathers and Peregrine solitary waves in a quadratic medium. Opt Lett (2017) 42:1756. doi:10.1364/OL.42.001756
62. Baronio F, Conforti M, Degasperis A, Lombardo S. Rogue waves emerging from the resonant interaction of three waves. Phys Rev Lett (2013) 111:114101. doi:10.1103/PhysRevLett.111.114101
63. Gaillard P. Other 2N-2 parameters solutions of the NLS equation and 2N+1 highest amplitude of the modulus of the N-th order Akhmediev-Peregrine breather. J Phys Math Theor (2015) 48:145203. doi:10.1088/1751-8113/48/14/145203
64. Dontsop PYG, Essama BGO, Doing JM, Dedzo MM, Atangana J, Yemele D, et al. Akhmediev-Peregrine rogue waves generation in a composite right/left-handed transmission line. Opt Quant Electron (2016) 48:59. doi:10.1007/s11082-015-0333-9
65. Chabchoub A, Fink M. Time-reversal generation of rogue waves. Phys Rev Lett (2014) 112:124101. doi:10.1103/PhysRevLett.112.124101
66. Vitanov NK, Chabchoub A, Hoffmann N. Deep-water waves: on the nonlinear Schrödinger equation and its solutions. J Theor Appl Mech Sofia (2013) 43:43–54. doi:10.2478/jtam-2013-0013
68. Ankiewicz A, Clarkson P, Akhmediev N. Rogue waves, rational solutions, the patterns of their zeros and integral relations. J Phys Math Theor (2010) 43:122002.
69. Wang L, Yang C, Wang J, He J. The height of an n-th order fundamental rogue wave for the nonlinear Schrödinger equation. Phys Lett (2017) 381:1714–8. doi:10.1016/j.physleta.2017.03.023
70. Chin SA, Ashour OA, Nikolić SN, Belić MR. Maximal intensity higher-order Akhmediev breathers of the nonlinear Schrödinger equation and their systematic generation. Phys Lett (2016) 380:3625–9. doi:10.1016/j.physleta.2016.08.038
71. Ling L, Zhao LC. Simple determinant representation for rogue waves of the nonlinear Schrödinger equation. Phys Rev E Stat Nonlinear Soft Matter Phys (2013) 88:043201. doi:10.1103/PhysRevE.88.043201
72. Kedziora DJ, Ankiewicz A, Akhmediev N. Classifying the hierarchy of nonlinear-Schrödinger-equation rogue-wave solutions. Phys Rev E - Stat Nonlinear Soft Matter Phys (2013) 88:013207. doi:10.1103/PhysRevE.88.013207
73. Ankiewicz A, Kedziora DJ, Akhmediev N. Rogue wave triplets. Phys Lett (2011) 375:2782–5. doi:10.1016/j.physleta.2011.05.047
74. Gaillard P. Deformations of third-order Peregrine breather solutions of the nonlinear Schrödinger equation with four parameters. Phys Rev E Stat Nonlinear Soft Matter Phys (2013) 88:042903. doi:10.1103/PhysRevE.88.042903
75. Gaillard P. Degenerate determinant representation of solutions of the nonlinear Schrödinger equation, higher order Peregrine breathers and multi-rogue waves. J Math Phys (2013) 54:013504. doi:10.1063/1.4773096
76. Akhmediev N, Ankiewicz A, Soto-Crespo JM. Rogue waves and rational solutions of the nonlinear Schrödinger equation. Phys Rev E - Stat Nonlinear Soft Matter Phys (2009) 80:026601. doi:10.1103/PhysRevE.80.026601
77. Bailung H, Sharma SK, Nakamura Y. Observation of Peregrine solitons in a multicomponent plasma with negative ions. Phys Rev Lett (2011) 107:255005. doi:10.1103/PhysRevLett.107.255005
78. Bludov YV, Konotop VV, Akhmediev N. Matter rogue waves. Phys Rev (2009) 80:033610. doi:10.1103/PhysRevA.80.033610
79. Nguyen JHV, Luo D, Hulet RG. Formation of matter-wave soliton trains by modulational instability. Science (2017) 356:422–6. doi:10.1126/science.aal3220
80. Chabchoub A, Akhmediev N. Observation of rogue wave triplets in water waves. Phys Lett (2013) 377:2590–3. doi:10.1016/j.physleta.2013.07.027
81. Chabchoub A, Hoffmann N, Onorato M, Slunyaev A, Sergeeva A, Pelinovsky E, et al. Observation of a hierarchy of up to fifth-order rogue waves in a water tank. Phys Rev E Stat Nonlinear Soft Matter Phys (2012) 86:056601. doi:10.1103/PhysRevE.86.056601
82. Li C, He J, Porsezian K, Porseizan K. Rogue waves of the Hirota and the Maxwell-Bloch equations. Phys Rev E Stat Nonlinear Soft Matter Phys (2013) 87:012913. doi:10.1103/PhysRevE.87.012913
83. Gui M, Qin Z, Grimshaw R, Akhmediev N. Intricate dynamics of rogue waves governed by the Sasa-Satsuma equation. Physica D (2020) 402:132252. doi:10.1016/j.physd.2019.132252
84. He J, Xu S, Porsezian K. Rogue waves of the Fokas-Lenells equation. J. Phys. Soc. Japan (2012) 81:124007. doi:10.1143/JPSJ.81.124007
85. Liu C, Akhmediev N. Super-regular breathers in nonlinear systems with self-steepening effect. Phys Rev E (2019) 100:062201. doi:10.1103/PhysRevE.100.062201
86. Chen S, Pan C, Grelu P, Baronio F, Akhmediev N. Fundamental Peregrine solitons of ultrastrong amplitude enhancement through self-steepening in vector nonlinear systems. Phys Rev Lett (2020) 124:113901. doi:10.1103/PhysRevLett.124.113901
87. Ankiewicz A, Bokaeeyan M, Akhmediev N. Shallow-water rogue waves: an approach based on complex solutions of the Korteweg–de Vries equation. Phys Rev E (2019) 99:050201. doi:10.1103/PhysRevE.99.050201
88. Crabb M, Akhmediev N. Rogue wave multiplets in the complex KdV equation. Rom Rep Phys (2020) 72:118.
89. He J, Wang L, Li L, Porsezian K, Erdélyi R. Few-cycle optical rogue waves: complex modified Korteweg-de Vries equation. Phys Rev E Stat Nonlinear Soft Matter Phys (2014) 89:062917. doi:10.1103/PhysRevE.89.062917
90. Qiu D, He J, Zhang Y, Porsezian K. The Darboux transformation of the Kundu-Eckhaus equation. Proc Royal Soc A Math Phys Eng Sci (2015) 471:20150236. doi:10.1098/rspa.2015.0236
91. Zhang , Chen Y. General high-order rogue waves to nonlinear Schrödinger–Boussinesq equation with the dynamical analysis. Nonlinear Dynam (2018) 93:2169–84. doi:10.1007/s11071-018-4317-8
92. Yang B, Chen J, Yang J. Rogue waves in the generalised derivative nonlinear Schrödinger equations. J. Nonlin. Science (2020) 30:3027–56.
93. Yang B, Yang J. Universal patterns of rogue waves Available at: https://arxiv.org/abs/2009.06060 (Accessed September 13 2020).
94. Chen S, Mihalache D. Vector rogue waves in the Manakov system: diversity and compossibility. J Phys Math Theor (2015) 48:215202. doi:10.1088/1751-8113/48/21/215202
95. Chen S, Soto-Crespo JM, Grelu P. Watch-hand-like optical rogue waves in three-wave interactions. Optic Express (2015) 23:349–59. doi:10.1364/OE.23.000349
96. Wang X, Cao J, Chen Y. Higher-order rogue wave solutions of the three–wave resonant interaction equation via the generalized Darboux transformation. Phys Scripta (2015) 90:105201. doi:10.1088/0031-8949/90/10/105201
97. Ohta Y, Yang J. General rogue waves in the focusing and defocusing Ablowitz—Ladik equations. J Phys Math Theor (2014) 47:255201. doi:10.1088/1751-8113/47/25/255201
98. Kedziora DJ, Ankiewicz A, Akhmediev N. Second-order nonlinear Schrödinger equation breather solutions in the degenerate and rogue wave limits. Phys Rev E Stat Nonlinear Soft Matter Phys (2012) 85:066601. doi:10.1103/PhysRevE.85.066601
99. Wang L, He J, Xu H, Wang J, Porsezian K. Generation of higher-order rogue waves from multibreathers by double degeneracy in an optical fiber. Phys Rev E (2017) 95:042217. doi:10.1103/PhysRevE.95.042217
Keywords: nonlinear schrodinger equation, rogue waves, peregrine wave, water waves, optical fibers
Citation: Akhmediev N (2021) Waves that Appear From Nowhere: Complex Rogue Wave Structures and Their Elementary Particles. Front. Phys. 8:612318. doi: 10.3389/fphy.2020.612318
Received: 30 September 2020; Accepted: 01 December 2020;
Published: 15 January 2021.
Edited by:
Amin Chabchoub, The University of Sydney, AustraliaReviewed by:
Fabio Baronio, University of Brescia, ItalyNorbert Hoffmann, Hamburg University of Technology, Germany
Copyright © 2021 Akhmediev. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nail Akhmediev, bm5hMTI0QHJzcGh5c3NlLmFudS5lZHUuYXU=
 Nail Akhmediev
Nail Akhmediev