- 1Department of Physics, Faculty of Science, Ege University, Izmir, Turkey
- 2Centro Brasileiro de Pesquisas Fisicas and National Institute of Science and Technology for Complex Systems, Rio de Janeiro, Brazil
- 3Santa Fe Institute, Santa Fe, NM, United States
- 4Complexity Science Hub Vienna, Vienna, Austria
We generalize the phenomenological, law of mass action-like, SIR and SEIR epidemiological models to situations with anomalous kinetics. Specifically, the contagion and removal terms, normally linear in the fraction I of infected people, are taken to depend on
1 Introduction
The classic and still widely used SIR and SEIR epidemiological models [1] represent contagion and removal in analogy with the law of mass action in chemistry, corresponding to a mean-field approach based on the assumption of homogeneous mixing. The latter hypothesis constitutes an oversimplification, particularly for the COVID-19 pandemic, due to strong government intervention (social distancing; lockdown) and underreporting as the number of cases grows beyond testing capacity. Diverse aspects are discussed, assuming homogeneous or nonhomogeneous mixing, in epidemiological models in general [2–4], as well as in the current pandemic [5–15].
Epidemic models can be formulated on varying levels of detail, from individual agents in geographically realistic settings to models of large populations without spatial structure. Each level has its own benefits and costs; the study of an ensemble of models is expected to yield a more reliable description than any single approach in isolation. In chemical kinetics of processes involving anomalous diffusion and/or complex conformational pathways, effective descriptions typically employ noninteger power-law terms where the mean-field or mass-action analysis involves integer powers of concentrations, as in the analysis of reassociation of folded proteins [16, 17]. With this motivation, we consider SIR- and SEIR-like models in which the contagion and removal terms depend on
Let us now follow along lines close to [16], which provided a satisfactory description of reassociation in folded proteins [17]. Consider the equation
Its solution is given by
with
2 Generalized Models
2.1 q-SIR Model
The SIR set of equations is (see [1] for instance) as follows:
with
with
The particular limit
and hence,
where
Before the peak,
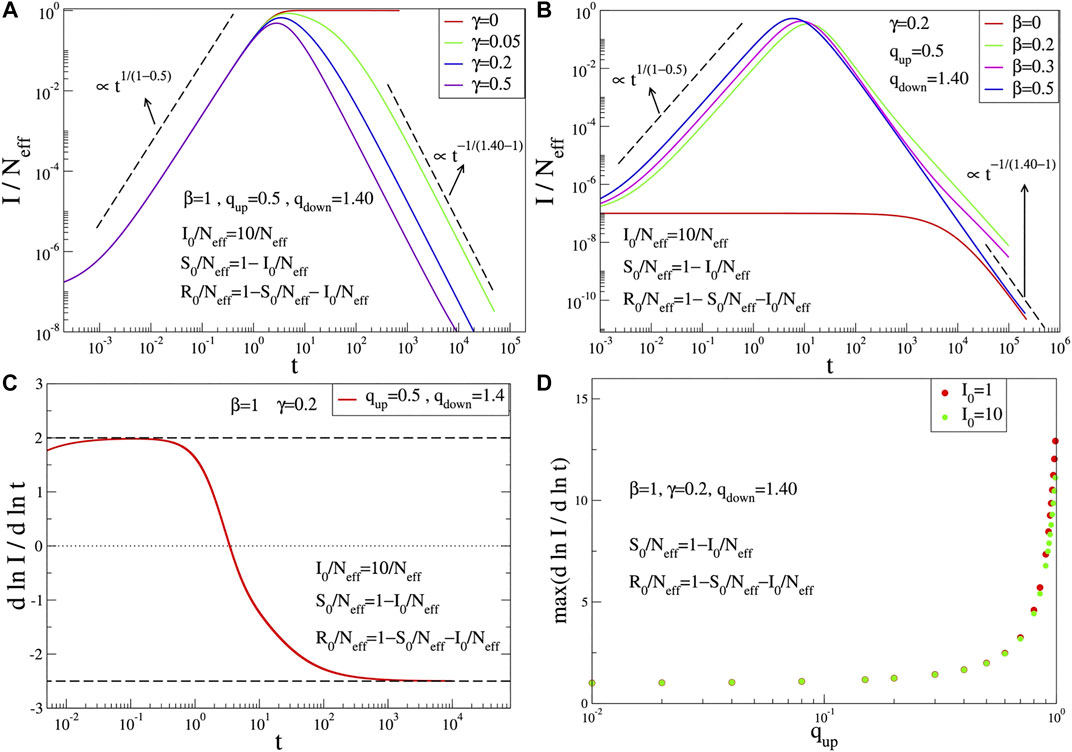
FIGURE 1. Time evolution of
We have checked that the q-SIR model provides functions
2.2 q-SEIR Model
The q-SIR model is not capable (for any choice of its parameters) of correctly fitting the epidemiologically crucial function
with
where once again we have generalized the bilinear couplings between subpopulations into nonbilinear ones and the linear
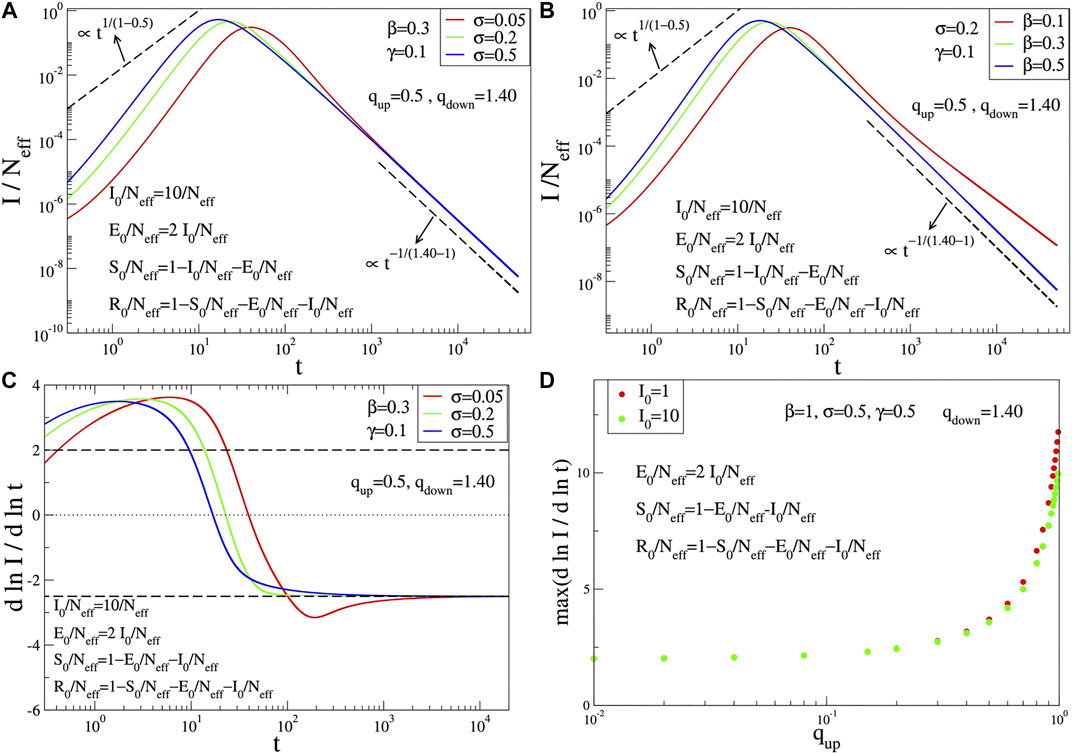
FIGURE 2. Time evolution of
3 Application of q-SEIR Model to COVID-19 Pandemic
In Figures 3 and 4, we have illustrations of this model for realistic COVID-19 cases. We identify the present variable I with the number of active cases,1 as regularly updated online [27]. We verify that the description provided by the q-SEIR model for nonhomogeneous epidemiological mixing is indeed quite satisfactory for the early stages of the pandemic (before an unpredictable but possible second wave). Let us also mention that we have not followed here a road looking for the minimal number of free parameters, but rather a road where various realistic elements are taken into account, even if at the fitting-parameter level some of them might be redundant. Any further model yielding a deeper, or even first-principle, expression of exponents such as
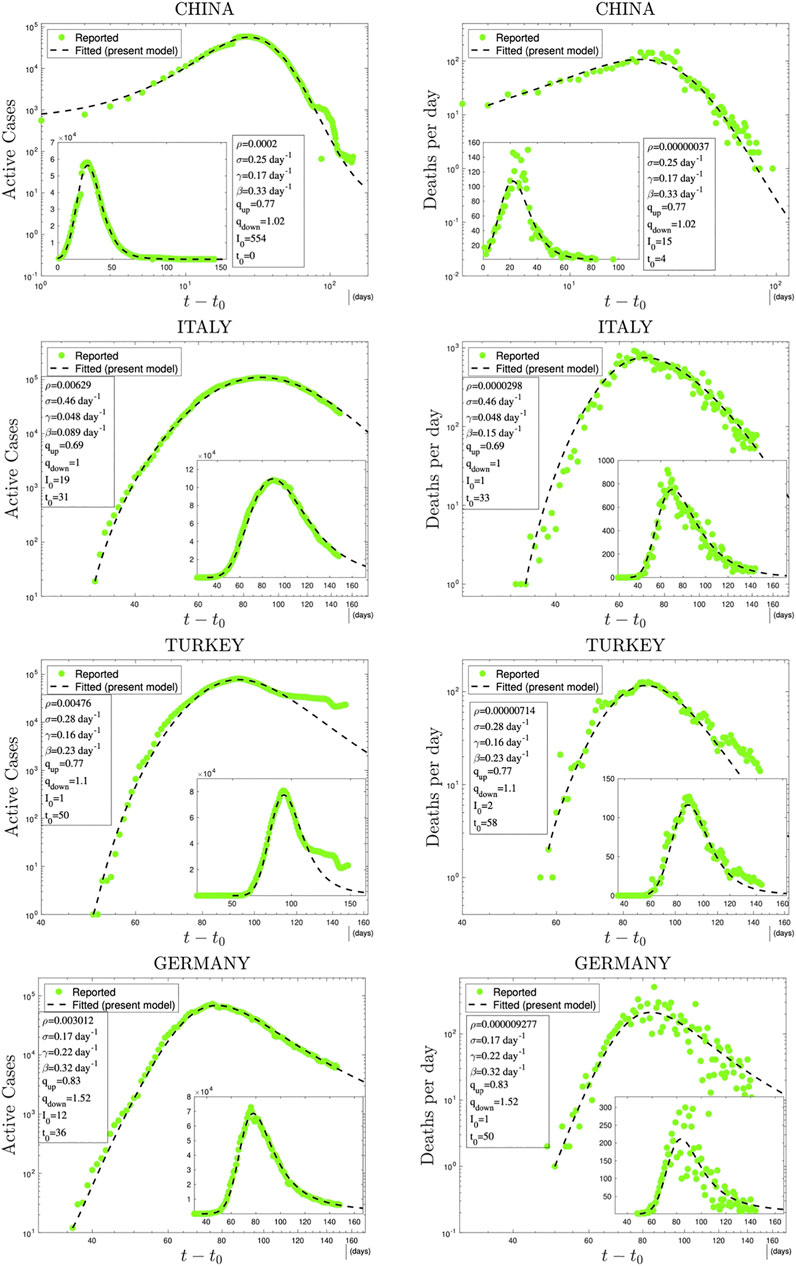
FIGURE 3. Time evolution of available data for COVID-19 numbers of active cases (probably under-reported in most cases) and deaths per day [27] and their (linear scale) Least Squares Method fittings with
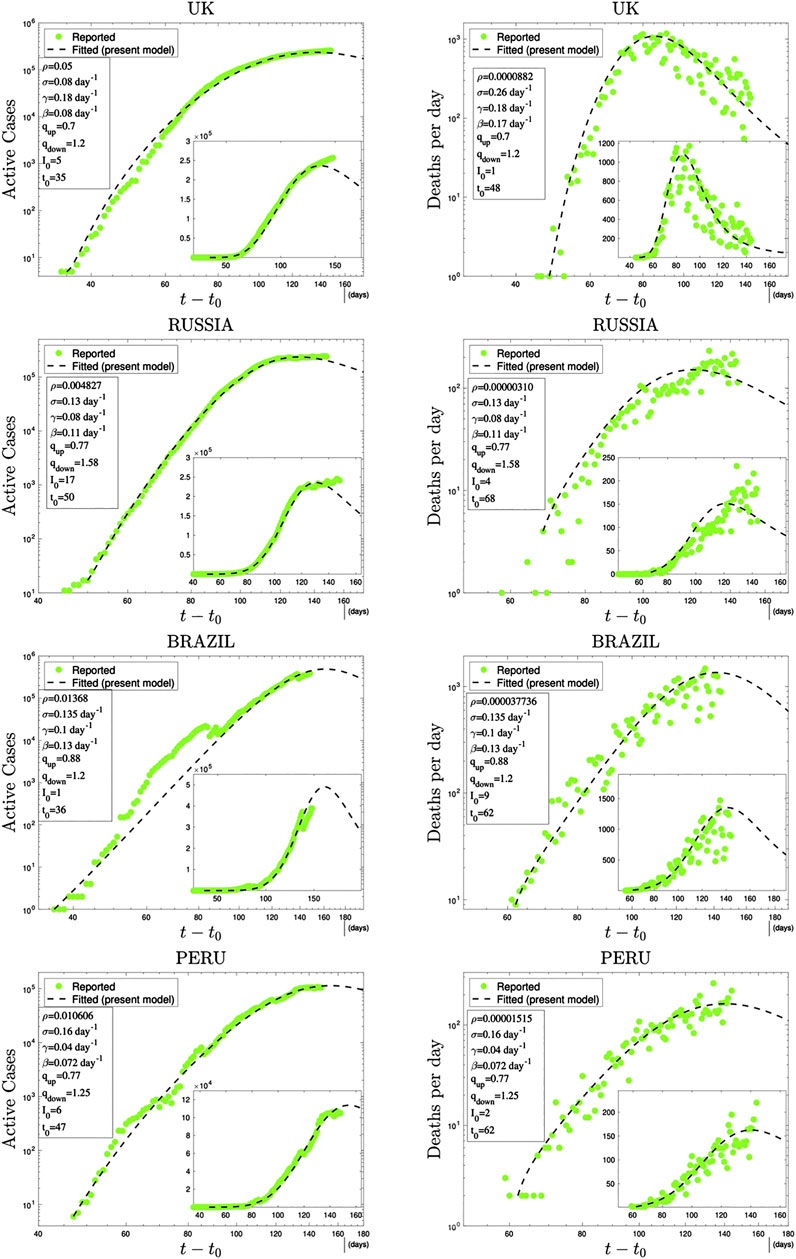
FIGURE 4. Continuation of Figure 3.
From a general perspective, let us stress that the law of mass action, the Arrhenius relaxation law, and the Kramers mechanism [38] of escape over a barrier through normal diffusion constitute pillars of contemporary chemistry. They are consistent with Boltzmann-Gibbs (BG) statistical mechanics and constitute some of its important successes. However, they need to be modified when the system exhibits complexity due to hierarchical space and/or time structures. It is along this line that a generalization has been proposed based on nonadditive entropies [20], characterized by the index q (
At the level of the numerical performance of the present q-SEIR model for the COVID-19 pandemic, it advantageously compares with models including time-dependent coefficients [44–47]. For instance, the SEIQRDP model [44, 45, 47] includes seven equations with several coefficients, two of them phenomenologically being time-dependent. It does fit rather well the COVID-19 reported data until a given date. However, the q-SEIR, which includes four (instead of seven) equations with several coefficients, all of them being fixed in time, fits definitively better the same data for all the countries that we have checked: see illustrations in Figure 5.
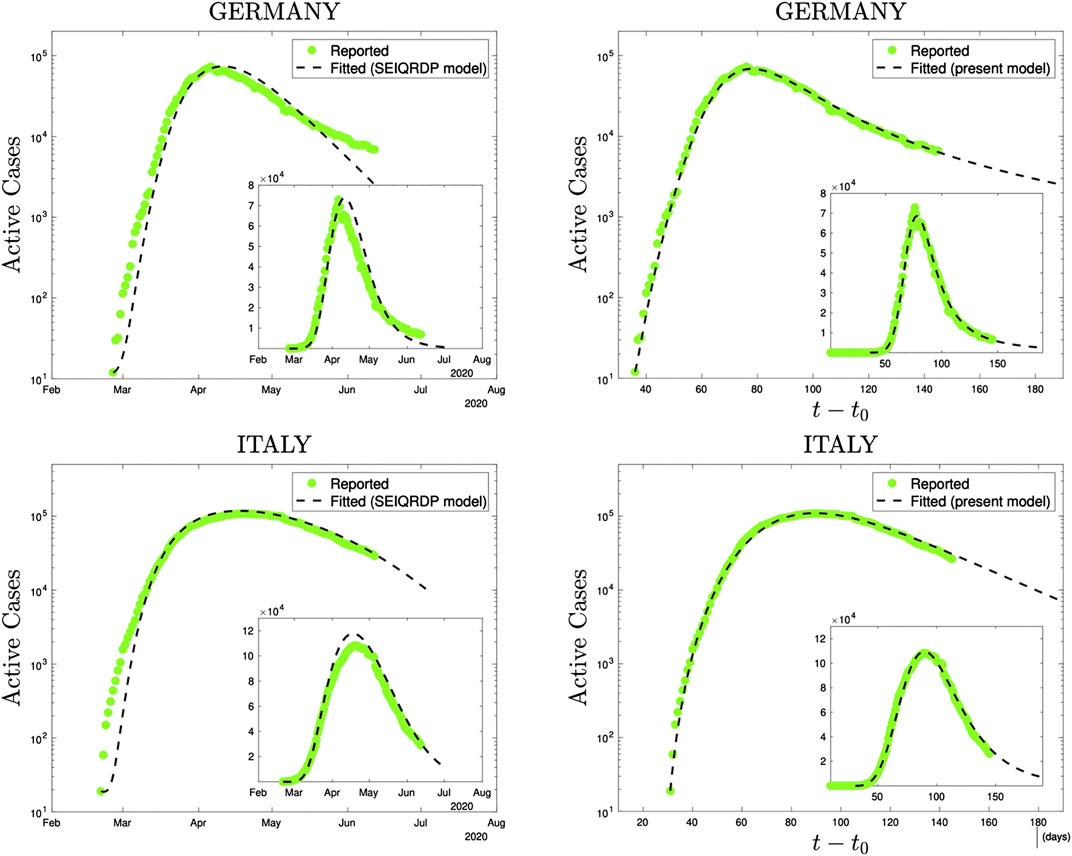
FIGURE 5. Comparison, using precisely the same reported data (green dots), of the SEIQRDP model (left plots) and the q-SEIR model (right plots) for the time series of Germany (from February 26th to June 13th 2020) and of Italy (from February 21st to June 13th 2020). To obtain the SEIQRDP fittings (seven linear/bilinear equations satisfying
At this stage, let us emphasize a rather interesting fact. Neither the SIR nor the SEIR models distinguish the dead from the recovered, within the removed (R) subpopulation. However, the same values for
4 Conclusion
To conclude, let us remind that the q-SEIR model recovers, as particular instances, the q-SIR model introduced here, as well as the traditional SEIR and SIR ones. It has, however, an important mathematical difference with the usual epidemiological models. Virtually all these models (SIR, SEIR, SAIR, SEAIR, SIRASD, SEAUCR, and SEIQRDP) are defined through equations that are multilinear in their variables; i.e., that are linear in each one of its variables. This multilinearity disappears in models such as the present q-SIR and q-SEIR ones if either
Data Availability Statement
The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases
Author Contributions
All authors contributed equally to the article.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We have greatly benefitted from very fruitful discussions with R. Dickman, T. Pereira and D. Eroglu, as well as from partial financial support by CNPq and Faperj (Brazilian agencies).
Footnotes
1At this point, it should be noted that the variable I in the model represents both detected plus undetected active cases although, of course, the database includes only detected ones as active cases. However, since these cases are roughly proportional to each other (with a proportionality coefficient which might change from country to country), we use the model variable I to fit the active cases reflecting the incorporation of this proportionality into
References
1. Daley DJ, Gani JM. Epidemic modelling: an introduction. Cambridge: Cambridge University Press (1999).
2. Bansal S, Grenfell BT, Meyers LA. When individual behaviour matters: homogeneous and network models in epidemiology. J R Soc Interface (2007) 4:879. doi:10.1098/rsif.2007.1100
3. Burr TL, Chowell G. Signatures of non-homogeneous mixing in disease outbreaks, Math Comput Model (2008) 48:122. doi:10.1016/j.mcm.2007.09.009
4. Milwid RM, O’Sullivan TL, Poljak Z, Laskowski M, Greer AL. Comparing the effects of non- homogenous mixing patterns on epidemiological outcomes in equine populations: a mathematical modelling study, Sci Rep (2019) 9:3227. doi:10.1038/s41598-019-40151-2
5. Tsallis C, Tirnakli U. Predicting COVID-19 peaks around the world. Front Phys (2020) 8, 217. doi:10.3389/fphy.2020.00217
6. Sebastiani G, Massa M, Riboli E. COVID-19 epidemic in Italy: evolution, projections and impact of government measures. Eur J Epidemiol (2020) 35:341. doi:10.1007/s10654-020-00631-6
7. Chowdhury R, Heng K, Shawon MSR, Goh G, Okonofua D, Ochoa-Rosales C, et al. Dynamic interventions to control COVID-19 pandemic: a multivariate prediction modelling study comparing 16 worldwide countries, Eur J Epidemiol (2020) 35:389. doi:10.1007/s10654-020-00649-w
8. Wang L, Chen H, Qiu S, Song H, Evaluation of control measures for COVID-19 in Wuhan, China. J Infect (2020) 81:318. doi:10.1016/j.jinf.2020.03.043
9. Manchein C, Brugnago EL, da Silva RM, Mendes CFO, Beims MW. Strong correlations between power-law growth of COVID-19 in four continents and the inefficiency of soft quarantine strategies, Chaos (2020) 30:041102. doi:10.1063/5.0009454
10. Ashurov R, Umarov S. Determination of the order of fractional derivative for subdiffusion equation. arxiv 13468 (2020).
11. Ziff AL, Ziff RM, et al. Fractal kinetics of COVID-19 pandemic (with update 3/1/20) medRxiv preprint (2020). doi:10.1101/2020.02.16.20023820
12. Vasconcelos GL, Macedo AMS, Ospina R, Almeida FAG, Duarte-Filho GC, Brum AA, et al. Modelling fatality curves of COVID-19 and the effectiveness of intervention strategies. PeerJ (2020) 8:e9421. doi:10.7717/peerj.9421
13. Curado EMF, Curado MR. A discrete-time-evolution model to forecast progress of COVID-19 outbreak. PLoS ONE (2020) 15:e0241472. doi:10.1371/journal.pone.0241472
14. Costa GS, Cota W, Ferreira SC, Metapopulation modeling of COVID-19 advancing into the countryside: an analysis of mitigation strategies for Brazil. medRxiv preprint (2020). doi:10.1101/2020.05.06.20093492
15. Pires MA, Crokidakis N, Cajueiro DO, de Menezes MA, Queiros SMD. What is the potential for a second peak in the evolution of SARS-CoV-2 in Brazil? Insights from a SIRASD model considering the informal economy. Preprint (2020) 2005:09019. doi:10.1016/j.meegid.2020.104502
16. Tsallis C, Bemski G, Mendes RS. Is re-association in folded proteins a case of nonextensivity?, Phys Lett (1999) 257:93. doi:10.1016/s0375-9601(99)00270-4
17. Austin RH, Beeson K, Eisenstein L, Frauenfelder H, Gunsalus IC, Marshall VP. Activation energy spectrum of a biomolecule: photodissociation of carbonmonoxy myoglobin at low temperatures. Phys Rev Lett (1974) 32:403. doi:10.1103/physrevlett.32.403
18. Brockmann D, Hufnagel L, Geisel T. The scaling laws of human travel. Nature (2006) 439:26. doi:10.1038/nature04292
19. Brockmann D, David V, Morales Gallardo A. Human mobility and spatial disease dynamics. In: C, Chmelik, N, Kanellopoulos, J, Kärger, and D, Theodorou, editors Diffusion fundamentals III. Leipzig: Leipziger Universitatsverlag (2009).
20. Tsallis C. Possible generalization of Boltzmann–Gibbs statistics. J Stat Phys (1988) 52:479. doi:10.1007/bf01016429
21. Prem K, Liu Y, Russell TW, Kucharski AJ, Eggo RM, Davies N, et al. The effect of control strategies to reduce social mixing on outcomes of the COVID-19 epidemic in Wuhan, China: a modelling study. Lancet Public Health (2020) 5:e261–270. doi:10.1016/s2468-2667(20)30073-6
22. Li Q, Guan X, Wu P, Wang X, Zhou L, Tong Y, et al. Early transmission dynamics in Wuhan, China, of novel Coronavirus-infected pneumonia. N Engl J Med (2020) 382:1199. doi:10.1056/NEJMoa2001316
23. Boldog P, Tekeli T, Vizi Z, Dénes A, Bartha FA, Röst G. Risk assessment of novel Coronavirus COVID-19 outbreaks outside China. JCM (2020) 9:571. doi:10.3390/jcm9020571
24. Yuan G, Li M, Lv G, Lu ZK. Monitoring transmissibility and mortality of COVID-19 in Europe. Int J Infect Dis (2020) 95:311–5. doi:10.1016/j.ijid.2020.03.050
25. Wang G, Wang Z, Dong Y, Chang R, Xu C, Yu X, et al. Phase-adjusted estimation of the number of Coronavirus disease 2019 cases in Wuhan, China. Cell Discov (2020) 6:10. doi:10.1038/s41421-020-0148-0
26. Liu W-m, Levin SA, Iwasa Y. Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models. J Math Biol (1986) 23:187. doi:10.1007/bf00276956
27.https://www.worldometers.info/coronavirus/#countries; https://data.humdata.org/dataset/novel-coronavirus-2019-ncov-cases
29. Plastino AR, Plastino A. Non-extensive statistical mechanics and generalized Fokker-Planck equation, Phys Stat Mech Appl (1995) 222:347. doi:10.1016/0378-4371(95)00211-1
30. Tsallis C, Bukman DJ. Anomalous diffusion in the presence of external forces: exact time-dependent solutions and their thermostatistical basis. Phys Rev E (1996) 54:R2197. doi:10.1103/physreve.54.r2197
31. Combe G, Richefeu V, Stasiak M, Atman APF. Experimental validation of nonextensive scaling law in confined granular media, Phys Rev Lett (2015) 115:238301. doi:10.1103/physrevlett.115.238301
32. Andrade JS, da Silva JFT, Moreira AA, Nobre FD, Curado EMF. Thermostatistics of overdamped motion of interacting particles, Phys Rev Lett (2010) 105:260601. doi:10.1103/physrevlett.105.260601
33. Moreira AA, Vieira CM, Carmona HA, Andrade JS, Tsallis C. Overdamped dynamics of particles with repulsive power-law interactions. Phys Rev E (2018) 98:032138. doi:10.1103/physreve.98.032138
34. Curado EMF, Souza AMC, Nobre FD, Andrade RFS. Carnot cycle for interacting particles in the absence of thermal noise. Phys Rev E (2014) 89:022117. doi:10.1103/physreve.89.022117
35. Andrade RFS, Souza AMC, Curado EMF, Nobre FD. A thermodynamical formalism describing mechanical interactions, Europhys Lett (2014) 108:20001. doi:10.1209/0295-5075/108/20001
36. Nobre FD, Curado EMF, Souza AMC, Andrade RFS. Consistent thermodynamic framework for interacting particles by neglecting thermal noise, Phys Rev E (2015) 91:022135. doi:10.1103/physreve.91.022135
37. Souza AMC, Andrade RFS, Nobre FD, Curado EMF. Thermodynamic framework for compact q-Gaussian distributions. Phys Stat Mech Appl (2018) 491:153. doi:10.1016/j.physa.2017.09.013
38. Kramers HA. Brownian motion in a field of force and the diffusion model of chemical reactions. Physica (1940) 7(4):284. doi:10.1016/s0031-8914(40)90098-2
39. Lenzi EK, Anteneodo C, Borland L. Escape time in anomalous diffusive media. Phys Rev E (2001) 63:051109. doi:10.1103/physreve.63.051109
40. Aquilanti V, Borges EP, Coutinho ND, Mundim KC, Carvalho-Silva VH. From statistical thermodynamics to molecular kinetics: the change, the chance and the choice. Rendiconti Lincei: Scienze Fisiche e Naturali (2018).
41. Mundim KC, Baraldi S, Machado HG, Vieira FMC. Temperature coefficient (Q10) and its applications in biological systems: beyond the Arrhenius theory. Ecol Model (2020) 431:109127. doi:10.1016/j.ecolmodel.2020.109127
42. Tsallis C, Gell-Mann M, Sato Y. Asymptotically scale-invariant occupancy of phase space makes the entropy Sq extensive. Proc Natl Acad Sci Unit States Am (2005) 102:15377–82. doi:10.1073/pnas.0503807102
43. Gazeau JP, Tsallis C. Möbius transforms, cycles and q-triplets in statistical mechanics. Entropy (2019) 21:1155. doi:10.3390/e21121155
44. Peng L, Yang W, Zhang D, Zhuge C, Hong L. Epidemic analysis of COVID-19 in China by dynamical modeling. medRxiv (2020). doi:10.1101/2020.02.16.20023465
45. Godio A, Pace F, Vergnano A. SEIR modeling of the Italian epidemic of SARS-CoV-2 using computational swarm intelligence. IJERPH (2020) 17:3535. doi:10.3390/ijerph17103535
46. Lopez L, Rodo X. A modified SEIR model to predict the COVID-19 outbreak in Spain and Italy: simulating control scenarios and multi-scale epidemics. medRxiv (2020). doi:10.1101/2020.03.27.20045005
48. Piccolomini EL, Zama F. Monitoring Italian COVID-19 spread by a forced SEIRD model. PLoS ONE (2020) 15:e0237417. doi:10.1371/journal.pone.0237417
Keywords: COVID-19, pandemics, complex systems, nonextensive statistical mechanics, epidemiological models
Citation: Tirnakli U and Tsallis C (2020) Epidemiological Model With Anomalous Kinetics: Early Stages of the COVID-19 Pandemic. Front. Phys. 8:613168. doi: 10.3389/fphy.2020.613168
Received: 01 October 2020; Accepted: 02 November 2020;
Published: 05 December 2020.
Edited by:
Matjaž Perc, University of Maribor, SloveniaReviewed by:
Tassos Bountis, University of Patras, GreeceOscar Sotolongo, University of Havana, Cuba
Airton Deppman, University of São Paulo, Brazil
Copyright © 2020 Tirnakli and Tsallis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Ugur Tirnakli, dWd1ci50aXJuYWtsaUBlZ2UuZWR1LnRy
 Ugur Tirnakli
Ugur Tirnakli Constantino Tsallis
Constantino Tsallis