Electronic Transport Through Double Quantum Dot Coupled to Majorana Bound States and Ferromagnetic Leads

1 Introduction

Electronic transport through structures composing of quantum dots (QDs) hybridized with a topological superconductor nanowire (TSNW) hosting Majorana bound states (MBSs) [1–3] has aroused much interest in recent years. The zero-energy MBSs are exotic self-conjugate quasiparticles that have been successfully realized in encouraging experiments [4–6] during the last decade. One of the most attractive platforms [7, 8] to host and detect MBSs is a superconductor proximitized semiconductor nanowire having the spin–orbit interaction and strong Zeeman splitting. Previous theoretical work predicted that the combined effects of the spin–orbit interaction and the large enough Zeeman splitting will convert an ordinary $s$-wave superconductor into a $p$-wave one so as to realize the MBSs. Recently, quantized electrical conductance peak at zero-bias voltage [9, 10] in a TSNW device was observed, which is a significant breakthrough for the demonstration of MBSs. Unfortunately, this zero-bias abnormal conductance peak cannot solely be attributed to the existence of MBSs and then some other means, such as the fractional Josephson effect [11–13] and thermoelectric effect [14–18] in systems composing of QDs with side-coupled MBSs were proposed to detect the existence of MBSs.

Some previous theoretical and experimental work has shown that the MBSs will affect the electronic transport processes through QD-based devices in a significant way [19, 20]. For example, Baranger and his co-author proved that the value of the conductance in a single QD, which is coupled to the left and right leads, will remain at half of its quantum value $e^2/2h$, regardless of the positions of the dot’s energy levels [21]. If both the spin directions of electrons on the QD are coupled to the MBSs [20, 22–24] with different hybridization amplitudes, which depend on the spin–orbit interaction length in the TSNW, they will interfere with each other through the MBSs and then will change the current significantly. For electron–hole symmetry, the zero-bias conductance is $3e^2/2h$ which is the sum of $e^2/2h$ for one spin direction and $e^2/h$ for the opposite spin direction. In addition to the single-QD structure, impacts of MBSs in the double quantum dot (DQD) have also been investigated in recent years [25–27]. As compared to the single QD, there are richer physical contents in the DQD with more tunable system parameters, such as the interaction between the two dots, arrangement of the dots’ energy levels, separate coupling between the dots and the leads, and so on.

It is known that the zero-energy MBSs exert remarkable effects on the electrical conductance and current around the zero-bias regimes. But under such a condition, the amplitude and changes of the above quantities are usually small and hard to be detected. In fact, the quantity of tunnel magnetoresistance (TMR) [28–30], which measures the relative change of the currents’ amplitude, is frequently used as detection means in electronic transport. It is also a key quantity in spintronic devices. The TMR is defined as $\text{TMR}=\left(J_P-J_{AP}\right)/J_{AP}$, where $J_{P\left(AP\right)}$ is the electrical current when the ferromagnetic leads’ magnetic moments are arranged in parallel (antiparallel) configuration. Usually, the value of TMR is positive because $J_P$ is contributed from transport processes when electrons tunnel between the majority–majority and minority–minority spin bands, whereas $J_{AP}$ is from electronic transport between major–minority spin bands. The tunneling in parallel configuration is easier than in the antiparallel one, inducing a positive TMR [28–30]. In the presence of coupling between the QDs and MBSs, however, the electrical current when the leads’ magnetic moments are in antiparallel can be enhanced to be larger than that of the parallel configuration. Such a change in the currents will induce a negative TMR which is promising in detection of the MBSs, as was proved in our previous work [31], in which we found two criteria that can be used for detecting the existence of MBSs. One is the peak to valley evolution of TMR when the dot’s level is fixed at zero, and the other is the sign change of TMR for the nonzero QD’s energy level. Moreover, we have found that the negative TMR can be significantly enhanced by the left–right asymmetry of the line-width functions. In the present DQD system, however, we study other mechanisms to reverse the sign of TMR, that is, the spin polarization of the DQD–MBS coupling strength. The most interesting result we find is that the magnitude of TMR can be either enhanced or suppressed by changing the sign of the spin polarization of the dot–MBS coupling strength. The negative TMR is unchanged by various system parameters, such as the direct overlapping between the MBSs, the difference between the dots’ level, and the tunnel coupling between the two dots. Single QD has been successfully inserted in between the ferromagnetic leads [32], and abnormal sign change of the TMR may be realized in experiments. There are also investigations on the Kondo effect in a single QD coupled to ferromagnetic leads [24] and showed that the impacts of the ferromagnetism on the leads will induce more interesting result due to the presence of the MBSs [33]. As a natural extension, we study properties of the electrical current and TMR in a DQD coupled to ferromagnetic leads and MBSs (see Figure 1). Different from some previous work [31, 33], we consider that the case that spin-up and spin-down electrons on the QD are coupled to the MBSs with different hybridization amplitudes [20, 22–24]. Our results show that the sign and the amplitude of the TMR can be adjusted in a large regime by variation of several system parameters, especially the spin polarization of the DQD–MBS hybridization, which is useful in detection of the MBSs, as well as in the design of spintronic devices or information processes. It should be noted that except the topological superconductor nanowires, the MBSs have also be prepared in some other systems, such as electrostatic defects in topological superconductors [34], the semiconductor [7], or ferromagnetic [35] nanowires with native strong spin–orbit interaction proximitization to a conventional s-wave superconductors, and theJosephson junctions [11].

FIGURE 1

FIGURE 1. Schematic plot of the DQD coupled to ferromagnetic leads with coupling strength ${\Gamma }_{\sigma }^{L/R}$ and to each other by $t_c$. The left and right dots interact individually with one mode of the MBSs at the end of topological superconductor nanowire with spin-dependent hybridization amplitude is given by ${\lambda }_{1\left(2\right)\sigma }=\lambda \left(1+\sigma \Delta \lambda \right)$, in which $\Delta \lambda$ is the spin polarization of the dot–MBS coupling strength. The two modes of the MBSs overlap with each other with amplitude of ${\delta }_M$.

2 Model and Methods

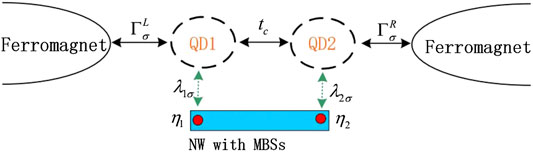
The Hamiltonian of the studied system shown in Figure 1, which is composed of the DQD each of which connected to the left and right ferromagnetic leads and to one mode of the MBSs, can be written as the following form [21, 24],

$\begin{array}{l}H={\displaystyle \sum _{k\alpha \sigma }{\epsilon }_{k\alpha \sigma }{\epsilon }_{k\alpha \sigma }^{+}{\epsilon }_{k\alpha \sigma }}+{\displaystyle \sum _{i=\mathrm{1,2};\sigma }{\epsilon }_i{d}_{i\sigma }^{+}{d}_{i\sigma }}+t_c{\displaystyle \sum _{\sigma }\left(d_{1\sigma }^{+}{d}_{2\sigma }+d_{2\sigma }^{+}{d}_{1\sigma }\right)}\\ +{\displaystyle \sum _{ki\sigma }\left(V_{kL\sigma }{d}_{1\sigma }^{+}{c}_{kL\sigma }+V_{kR\sigma }{d}_{2\sigma }^{+}{c}_{kR\sigma }+H.c.\right)}+H_{MBSs},\end{array}(1)$

where the creation (annihilation) operator $c_{k\alpha \sigma }^{†}\left(c_{k\alpha \sigma }\right)$ is for electrons having wave vector $k$, energy ${\epsilon }_{k\alpha \sigma }$, and spin $\sigma =\uparrow ,\downarrow$ in the $\alpha$-th $\left(\alpha =L/R\right)$ ferromagnetic lead. The second term in the right side of Eq. 1 is for electrons on the DQD with energy level ${\epsilon }_i$. The creation (annihilation) operator of the electrons on the QD-$i$ is $d_{i\sigma }^{†}\left(d_{i\sigma }\right)$. The third term in the right side of Eq. 1 denotes hopping between the two dots via a tunnel barrier with strength $t_c$. The forth term in the right side of Eq. 1 describes tunneling between the dots and ferromagnetic leads with amplitude $V_{k\alpha \sigma }$. In the present structure, QDs 1 and 2 are connected to the left and right ferromagnetic leads, respectively. The last term in Eq. 1 is for the MBSs realized at opposite ends of the TSNW and their couplings to the DQD [21, 24],

$H_{MBSs}={\displaystyle \sum _{\sigma }\frac{{\lambda }_{1\sigma }}{\sqrt{2}}\left(d_{1\sigma }-d_{1\sigma }^{+}\right){\gamma }_2+i{\displaystyle \sum _{\sigma }\frac{{\lambda }_{2\sigma }}{\sqrt{2}}\left(d_{2\sigma }+d_{2\sigma }^{+}\right){\gamma }_2}}+i{\delta }_M{\gamma }_1{\gamma }_2,(2)$

in which ${\lambda }_{i\sigma }={\lambda }_i\left(1+\sigma \Delta \lambda \right)$ is the spin-dependent coupling strength between the QD-$i$ and the mode-$i$ of the MBSs, in which ${\lambda }_i$ is the QD–MBS coupling strength independent of the electron spin and $\Delta \lambda$ is the spin polarization of the coupling strength. The operators of the MBSs have the properties of ${\gamma }_{1\left(2\right)}={\gamma }_{1\left(2\right)}^{†}$ and $\left\{{\gamma }_i,{\gamma }_j\right\}=2{\delta }_{ij}$. For the convenience of calculations [21], we replace the Majorana fermion operators ${\gamma }_{1\left(2\right)}$ with the regular fermion operators $f$ and $f^{†}$ by the transformation of ${\gamma }_1=\frac{1}{\sqrt{2}}\left(f^{+}+f\right),{\gamma }_2=\frac{i}{\sqrt{2}}\left(f^{+}-f\right)$, and then Eq. 2 is rewritten as

$H_{MBSs}={\delta }_M\left(f^{+}f-\frac{1}{2}\right)+{\displaystyle \sum _{\sigma }\left[\frac{{\lambda }_{1\sigma }}{\sqrt{2}}\left(d_{1\sigma }-d_{1\sigma }^{+}\right)\left(f+f^{+}\right)+\frac{{\lambda }_{2\sigma }}{\sqrt{2}}\left(d_{2\sigma }+d_{2\sigma }^{+}\right)\left(f-f^{+}\right)\right]},(3)$

In terms of the Hamiltonians given by Eqs 1 and 3, spin-dependent electrical currents $J_{\sigma }$ can be calculated by the nonequilibrium Green’s function technique as [23, 24]

$J_{\sigma }={\displaystyle \int d\epsilon }{T}_{\sigma }\left(\epsilon \right)\left[f_L\left(\epsilon \right)-f_R\left(\epsilon \right)\right](4)$

in which the Fermi distribution function for the left and right leads are given by $f_{L/R}\left(\epsilon \right)={\left[\exp \left[\left(\epsilon -{\mu }_{L/R}\right)/k_B{T}_e\right]+1\right]}^{-1}$, with ${\mu }_{L/R}$ being the chemical potential in the left/right lead held at temperature $T_e$. The transmission coefficient $T_{\sigma }\left(\epsilon \right)$ in Eq. 4 is calculated with the help of Green’s function as [34] $T_{\sigma }\left(\epsilon \right)={\Gamma }_{\sigma }^L{\Gamma }_{\sigma }^R{\left|G_{12,\sigma }^r\left(\epsilon \right)\right|}^2$, where $G_{12,\sigma }^r\left(\epsilon \right)$ is the electron retarded Green’s function and ${\Gamma }_{\sigma }^{\alpha }=2\pi {\left|V_{k\alpha \sigma }\right|}^2{\rho }_{\alpha \sigma }$ is the line-width function with ${\rho }_{\alpha \sigma }$ being the local density of states in the lead $\alpha$ [28–30]. As an equivalent choice, the ferromagnetism on the leads is considered by the spin-dependent tunneling amplitude between the leads and the dot $V_{k\alpha \sigma }$. Introducing the spin polarization of the leads $p_{L\left(R\right)}=\left({\Gamma }_{\uparrow }^{L\left(R\right)}-{\Gamma }_{\downarrow }^{L\left(R\right)}\right)/\left({\Gamma }_{\uparrow }^{L\left(R\right)}+{\Gamma }_{\downarrow }^{L\left(R\right)}\right)$, we obtain ${\Gamma }_{\uparrow }^{L/R}=\Gamma \left(1+p_{L\left(R\right)}\right)$ and ${\Gamma }_{\downarrow }^{L/R}=\Gamma \left(1-p_{L\left(R\right)}\right)$, where $\Gamma =\left({\Gamma }_{\uparrow }^{L/R}+{\Gamma }_{\downarrow }^{L/R}\right)/2$. In the present article, we consider that the cases of the magnetic moments are arranged in parallel $\left(p_L=p_R=p\right)$ and antiparallel ($\left(p_L=-p_R=p\right)$) configurations. We calculate Green’s function in terms of the Dyson equation technique [24], that is, first, we calculate the free dots’ Green’s function by the equation of motion method and then the interactions between the dots and the leads, as well as with the MBSs are taken into consideration in the form of self-energies. In the absence of the Coulomb interaction between electrons, the present Dyson equation will give essentially the same Green’s function as that derived by the equation of motion method [23, 36, 37]. Choosing the basis as $\Psi =\left(\begin{array}{cccccccccc}{d}_{1\uparrow }& d_{1\uparrow }^{+}& d_{1\downarrow }& d_{1\downarrow }^{+}& d_{2\uparrow }& d_{2\uparrow }^{+}& d_{2\downarrow }& d_{2\downarrow }^{+}& f& f^{+}\end{array}\right)$, the Dyson equation is written in a matrix form as ${\widehat{G}}^r={\left({\widehat{g}}^{r-1}-{\widehat{\Sigma }}^r\right)}^{-1}$, in which ${\widehat{g}}^r$ is the dot’s retarded Green’s function in the absence of all interactions and ${\widehat{\Sigma }}^r$ is the self-energy. The matrix form of ${\widehat{g}}^r$ is

${\widehat{g}}^r=\left(\begin{array}{ccc}{\left[{\widehat{g}}_{11}^r\left(\epsilon \right)\right]}_{4\times 4}& 0& 0\\ 0& {\left[{\widehat{g}}_{22}^r\left(\epsilon \right)\right]}_{4\times 4}& 0\\ 0& 0& {\left[{\widehat{g}}_{MM}^r\left(\epsilon \right)\right]}_{2\times 2}\end{array}\right)(5)$

in which the diagonal matrix is

${\widehat{g}}_{11\left(22\right)}^r\left(\epsilon \right)=\left(\begin{array}{cccc}{g}_{11\left(22\right),\uparrow }^r\left(\epsilon \right)& 0& 0& 0\\ 0& {\tilde{g}}_{11\left(22\right),\uparrow }^r\left(\epsilon \right)& 0& 0\\ 0& 0& g_{11\left(22\right),\downarrow }^r\left(\epsilon \right)& 0\\ 0& 0& 0& {\tilde{g}}_{11\left(22\right),\downarrow }^r\left(\epsilon \right)\end{array}\right)(6)$

with $g_{ii,\sigma }^r\left(\epsilon \right)=1/\left(\epsilon -{\epsilon }_i\right),$${\tilde{g}}_{ii,\sigma }^r\left(\epsilon \right)=1/\left(\epsilon +{\epsilon }_i\right),$$g_{MM}^r\left(\epsilon \right)=1/\left(\epsilon -{\delta }_M\right),$ and ${\tilde{g}}_{MM}^r\left(\epsilon \right)=1/\left(\epsilon +{\delta }_M\right).$ The matrix self-energy ${\widehat{\Sigma }}^r$ is composed by the line-width function (for interaction between the dots and the leads) ${\Gamma }_{\sigma }^{\alpha }$ and the dot–MBS coupling strength ${\lambda }_{1\left(2\right)\sigma }$; its expression is

${\Sigma }^r=\left(\begin{array}{ccc}{\left[{\widehat{\Sigma }}^{L,r}\right]}_{4\times 4}& {\left[{\widehat{T}}_c\right]}_{4\times 4}& {\left[{\widehat{K}}_1\right]}_{4\times 2}\\ {\left[{\widehat{T}}_c^{\ast }\right]}_{4\times 4}& {\left[{\widehat{\Sigma }}^{R,r}\left(\epsilon \right)\right]}_{4\times 4}& {\left[{\widehat{K}}_2\right]}_{4\times 2}\\ {\left[{\widehat{K}}_1^{\ast }\right]}_{2\times 4}& {\left[{\widehat{K}}_1^{\ast }\right]}_{2\times 4}& {\left[0\right]}_{2\times 2}\end{array}\right)(7)$

in which

${\widehat{\Sigma }}^{L/R,r}=\left(\begin{array}{cccc}-i{\Gamma }_{\uparrow }^{L/R}/2& 0& 0& 0\\ 0& -i{\Gamma }_{\uparrow }^{L/R}/2& 0& 0\\ 0& 0& -i{\Gamma }_{\downarrow }^{L/R}/2& 0\\ 0& 0& 0& -i{\Gamma }_{\downarrow }^{L/R}/2\end{array}\right)(\mathrm{8a})$

${\widehat{T}}_c=\left(\begin{array}{cccc}{t}_c& 0& 0& 0\\ 0& -t_c& 0& 0\\ 0& 0& t_c& 0\\ 0& 0& 0& -t_c\end{array}\right)(\mathrm{8b})$

${\widehat{K}}_{1\left(2\right)}=\left(\begin{array}{cc}{\lambda }_{1\left(2\right)\uparrow }/\sqrt{2}& {\lambda }_{1\left(2\right)\uparrow }/\sqrt{2}\\ -{\lambda }_{1\left(2\right)\uparrow }/\sqrt{2}& -{\lambda }_{1\left(2\right)\uparrow }/\sqrt{2}\\ {\lambda }_{1\left(2\right)\downarrow }/\sqrt{2}& {\lambda }_{1\left(2\right)\downarrow }/\sqrt{2}\\ -{\lambda }_{1\left(2\right)\downarrow }/\sqrt{2}& -{\lambda }_{1\left(2\right)\downarrow }/\sqrt{2}\end{array}\right)(\mathrm{8c})$

The spin-dependent transmission is then calculated by [24] $T_{\uparrow (\downarrow )}\left(\epsilon \right)={\Gamma }_{\uparrow (\downarrow )}^L{\Gamma }_{\uparrow (\downarrow )}^R{\left|{\left[{\widehat{G}}^r\right]}_{15\left(37\right)}\right|}^2$.

3 Results and Discussion

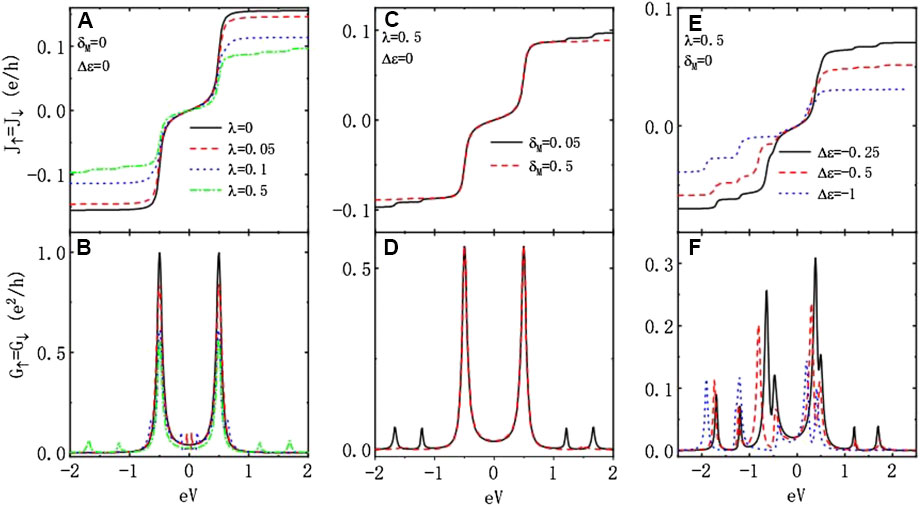
In this section, we present our numerical results for the spin-dependent currents and TMR. We choose the leads’ bandwidth $D\equiv 40$ as the energy unit with fixed ${\mu }_L=eV$, ${\mu }_R=0$, $\Gamma =0.1$, and $T_e=0.001$ throughout the article. Figure 2 shows the impacts of dot–MBS coupling strength ${\lambda }_1={\lambda }_2=\lambda$, overlap amplitude between the MBSs ${\delta }_M$, and difference between the dots’ levels $\Delta \epsilon ={\epsilon }_1-{\epsilon }_2$ on the currents $J_{\uparrow }=J_{\downarrow }$ and differential conductance $G_{\sigma }=d{J}_{\sigma }/dV$ without ferromagnetism on the leads $\left(p=0\right)$ and spin polarization of the dot–MBS coupling strength $\left(\Delta \lambda =0\right)$. In the absence of interaction between the DQD and MBSs, the molecular states of the system are positioned at $\epsilon =\left({\epsilon }_1+{\epsilon }_2\right)/2\pm \sqrt{{\left({\epsilon }_1-{\epsilon }_2\right)}^2/4+t_c^2}$, around which the current develops a step as shown in Figure 2A [38]. For the chosen parameters, the molecular states in Figure 2A are at $\epsilon =\pm t_c$, where the conductance arises a peak as seen from the solid black line. The reason is that when the bias voltage $eV$ (Fermi level of the left lead ${\mu }_L$) equals to each of the molecular states, electrons will tunnel into the dots from one lead and out to the other one, resulting in an increase of the current [34, 35]. Note that the current is attributed from electrons whose energy is close to the Fermi level of the leads. Therefore, the current reaches a plateau when the bias voltage is shift away from the molecular state as all the electrons have taken part in transportation (see also the conductance in Figure 2B which is almost zero when the bias voltage is larger or smaller than the resonant energies). In the presence of coupling between the MBSs and DQD $\left(\lambda \ne 0\right)$, the states on the dots are split. For the case of $\lambda <t_c$, the states are roughly at [24, 27] $\pm \sqrt{2}\lambda$ and $\pm t_c$ and then are shifted to $\pm t_c$ and $\pm \left(\sqrt{2}\lambda \pm t_c\right)$ for $\lambda \ge t_c$, at which the conductance in Figure 2B develops peaks. It should be emphasized that the steps (peaks) in the current (conductance) at the molecular states $eV=\pm t_c$ are robust against the dot–MBS coupling. The peaks at $eV=\pm t_c$ are lowered by increasing $\lambda$ but remain at the same positions. The stabilization of the states at $\pm t_c$ can also be seen from Figures 2C, D, in which the steps of the current and peaks of the conductance at $\pm t_c$ are almost unchanged by the variation of ${\delta }_M$. The two molecular states (peaks in the conductance) at large bias voltage regimes disappear due to the presence of direct coupling between the MBSs ${\delta }_M$, which is consistent with the previous results that the overlapping between the two modes of the MBSs will reduce their impacts on the electronic transport processes [19, 20]. One of the attractive advantages in the DQD as compared to the simple single QD is the tunable difference between dots’ levels that can adjust tunneling through the system. Figures 2E, F present the current and conductance under different values of $\Delta \epsilon$, respectively. As was indicated above, the difference between the dots’ levels shifts the positions of the molecular states and then the positions of the steps (peaks) in the current (conductance). Moreover, the magnitudes of the currents and the conductance are weakened by increasing $\Delta \epsilon$, as shown by the dashed and dotted lines in Figures 2E, F. This is because that the direct tunneling under the condition of identical dots’ levels is blockaded in the presence of $\Delta \epsilon$, and then, electronic transport can only take place through the levels mediated by the MBSs [24, 27, 34]. From Figure 2, one can see that the influences of the MBSs on the transport properties through the present DQD are quite different from those in the single QD system. For example, the zero-bias peaks in electrical conductance formed in the single dot structure by the presence of MBSs disappear in this DQD due to the direct tunneling between the two dots. Moreover, the value of the conductance in the single dot keeps at its half of quantum value $e^2/2h$ at sufficiently low temperatures, regardless of the dot’ level [21], but in the DQD, there is no certain value in the presence of coupling between the DQD and MBSs.

FIGURE 2

FIGURE 2. Electronic current $J_{\sigma }$ in A,C, and E and the associated differential conductance in B,D, and F varying with respect to the bias voltage $eV$ for the case of the DQD coupled to nonmagnetic leads ($p=0$). In addition to the parameters given in the figure, other ones are $\Gamma =0.1$, $T_e=0.001$, ${\epsilon }_1={\epsilon }_2=0$, $t_c=0.5$, and $\Delta \lambda =0$. In such a system, the spin-up and spin-down currents are identical.

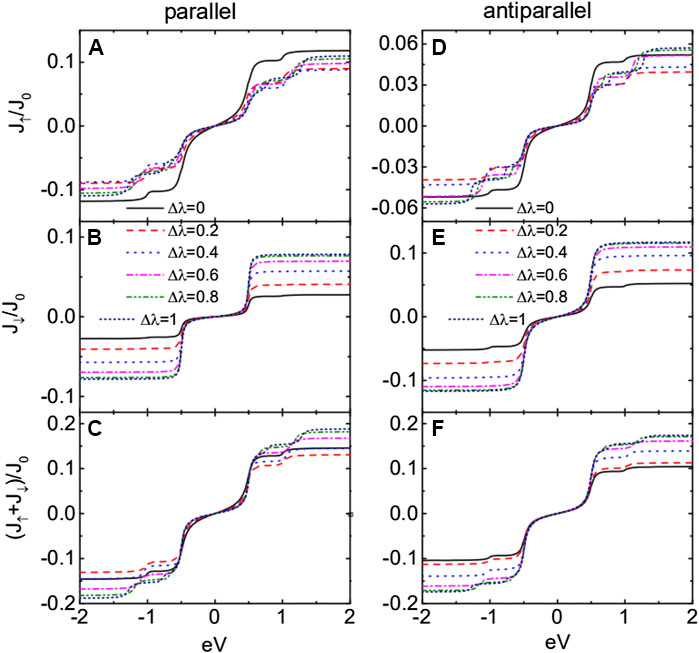
With the results in Figure 2, we now study the currents in Figure 3 for different values of $\Delta \lambda$ when the dots are coupled to ferromagnetic leads whose magnetic moments are arranged in either parallel or antiparallel configurations. The spin-up current $J_{\uparrow }$ in Figure 3A is suppressed with increasing $\Delta \lambda$ in a non-monotonous way due to the complex molecular states induced by dot–MBS coupling. Since both spin-up and spin-down electrons interact with the MBSs, they will interfere with each other during tunneling through the structure [20, 24]. Therefore, the transport processes in the present DQD are more interesting and complex than those in the absence of MBSs. The absolute value of $J_{\uparrow }$ in Figure 3B is monotonously enhanced with increasing $\Delta \lambda$ due to the weaker coupling strength between spin-down electrons and the MBS. The absolute value of the total current $J_P$ in Figure 3C is mainly suppressed (enhanced) in the bias voltages $\left|eV\right|\le t_c\left(\left|eV\right|>t_c\right)$. When the magnetic moments of the two leads are arranged in antiparallel configuration, the properties of the currents essentially resemble those in the parallel configuration. By comparing Figure 3C with Figure 3F, one can see that the total current in antiparallel $J_{AP}$ changes more obviously than $J_P$. The reason can be explained as follows [30, 31, 38]: when the magnetic moments of the leads are in parallel configuration, spin-up and spin-down electrons transport through the DQD from the major–major and minor–minor bands, respectively. Now the incoming and outgoing tunneling rates (line-width function) are the same for both spin directions. But when the leads’ magnetic moments are in antiparallel configuration, both of the spin-up and spin-down electrons are transporting between major and minor bands, which means that the incoming and outgoing tunneling rates are different from each other, and then, the current’s amplitude is weaker than that in the parallel configuration. In the presence of coupling between the dots and MBSs, the currents in the parallel configuration are changed more obviously than those in the antiparallel one [20, 31]. This may cause the total current in the parallel configuration to be larger than that in the antiparallel one and induce a negative TMR as will be shown later.

FIGURE 3

FIGURE 3. Spin-dependent and total currents for parallel configuration in A–C, and antiparallel one in D–F with $\lambda =0.25$, $p=0.5$, and different values of $\Delta \lambda$. Other parameters are as in Figure 2.

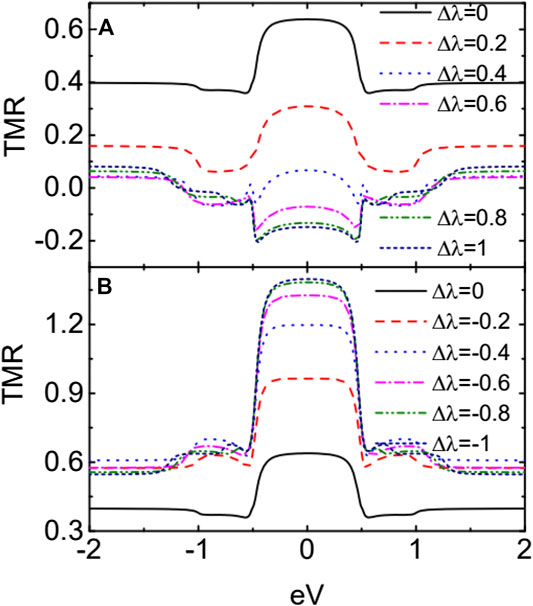
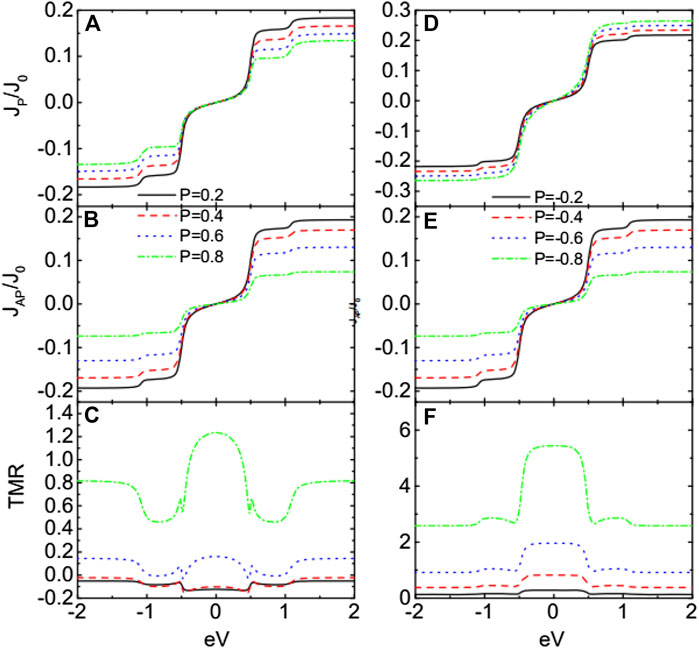
As is seen from Figures 2, 3, the variation of the currents around the zero bias, where the MBSs play an important role, is quite nonobvious. We then present the TMR in Figure 4 varying with respect to the bias voltage for both positive and negative $\Delta \lambda$. For $\Delta \lambda >0$, the coupling strength ${\lambda }_{1\left(2\right)\uparrow }$ is larger than ${\lambda }_{1\left(2\right)\downarrow }$ and then the current contributed from spin-up electrons, which tunnel between major–major spin bands in the parallel configuration and are the main contribution to the total current, is suppressed [24, 34, 35]. Even the spin-down electrons in the parallel configuration is slightly enhanced; the total current near zero bias is suppressed which can be seen from Figure 3. When the magnetic moments are arranged in the antiparallel configuration, the change of the total current is relatively small as the electrons tunnel between major–minor spin bands. Due to the above change of the current in different configurations, the TMR is negative for sufficiently large $\Delta \lambda$ in Figure 4A. When the spin polarization of the dot–MBS coupling strength is negative $\Delta \lambda <0$, the coupling between spin-up electrons becomes weaker with increasing $\Delta \lambda$, and then, the magnitude of the spin-up current is enhanced, accordingly. Since the spin-up electrons are the main contribution to the current in the parallel configuration, the total current will also increase with increasing $\Delta \lambda$. Just for the same reason, the total current in the antiparallel configuration changes much less obviously than that in the parallel configuration. These result in an enhanced positive TMR as shown in Figure 4B. In the bias regimes of $\left|eV\right|\le t_c$, both negative and positive TMR develop a plateau at large $\Delta \lambda$. This change from the positive peak to negative dip in the TMR is quite interesting as it is useful in either detection of the MBSs or design of spintronic devices.

FIGURE 4

FIGURE 4. TMR for positive $\Delta \lambda$ in A and negative $\Delta \lambda$ in B. Other parameters are as in Figures 2, 3.

Figure 5 shows the influences of the ferromagnetism of the leads on the currents and the TMR for $\Delta \lambda =0.8$, which gives the dot–MBS coupling strength as ${\lambda }_{1\left(2\right)\uparrow }=0.45$ and ${\lambda }_{1\left(2\right)\downarrow }=0.05$. For the case of $p>0$, $\left|J_{\uparrow }\right|$ in the parallel configuration decreases with increasing $p$ in that more electrons are influenced by the MBSs. As for the spin-down electrons that are less influenced by the MBSs because their coupling between the leads are weakened with increasing $p$, the absolute current contributed from them is suppressed. The properties of the current in the antiparallel configuration can be explained in the same way. The TMR for $p>0$ changes from the negative value to the positive one with increasing $p$ as shown in Figure 4C. This is because that the negative TMR arises from the coupling between the QDs and MBSs. With increasing spin polarization of the leads, the coupling between spin-up electron and the leads is enhanced due to the increased spin-up line-width function. Therefore, the impacts of the dot–MBS coupling on the current then become relatively weak with increasing $p$, and then, the value of TMR is enhanced to positive. When $p<0$, the absolute value of current in the parallel (antiparallel) configuration is enhanced (suppressed) with increasing $p$, which results in larger TMR shown in Figure 5F. The value of the TMR for $p=-0.8$ is about ten times larger than that of $p=-0.2$, a phenomenon useful in spintronics.

FIGURE 5

FIGURE 5. Total currents in parallel configuration $J_P$ and antiparallel configuration $J_{AP}$ and TMR for positive $p$ in A–C and negative $p$ in D–F. Here, we set $\Delta \lambda =0.8$, and other parameters are as in Figures 2,3.

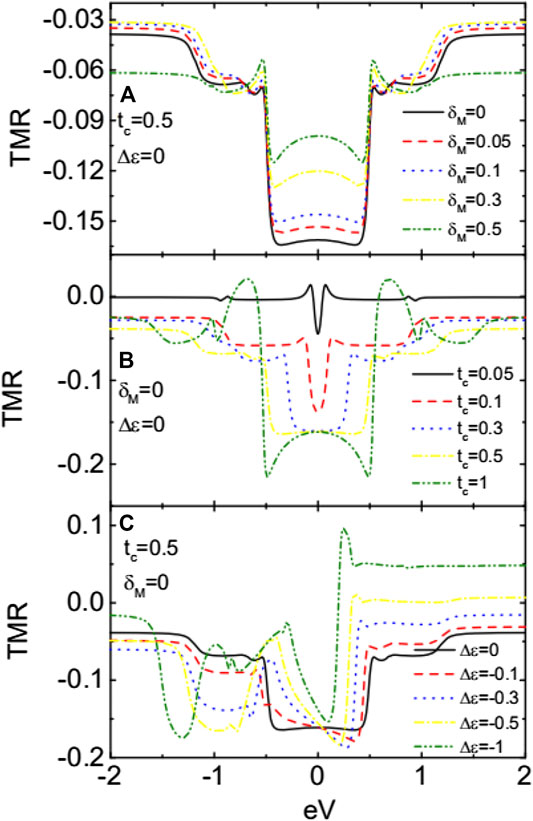
Figure 6 presents the impacts of ${\delta }_M$, $t_c$, and $\Delta \epsilon$ on the TMR. As is known, the direct overlapping between the two modes of the MBSs will weaken the influences of MBSs on electronic transport around zero-bias regime. This can be seen from Figure 6A that the negative plateau of the TMR in the bias regimes of $\left|eV\right|\le t_c$ is raised with increasing ${\delta }_M$. But even for ${\delta }_M=0.5$, the TMR remains negative with a relatively large value. Figure 6B indicates that the negative plateau becomes wider and lower with increasing $t_c$, which is consistent with the above discussions. For sufficiently large $t_c\ge 0.3$, the zero-bias TMR keeps at a minimum value. Figure 6C shows that the plateau of negative TMR is split into two dips by the presence of $\Delta \epsilon$ due to the shift of the molecular states as indicated in Figure 2. Interestingly, the magnitude of the negative TMR remains almost unchanged even if the dots’ levels are different from each other. The above three figures indicate that the phenomenon of negative TMR are rather stable in this DQD structure and may provide a reliable means to detect the existence of the MBSs. It is known that the Coulomb interaction between electrons plays an important role in transport processes. At temperatures higher than Kondo one [24], the Coulomb interaction mainly induces the so-called Coulomb blockade effect [23] in mesoscopic systems, that is, the current–voltage curve will display steps corresponding to the peaks in the electrical conductance, which arises from the blockade of additional electron transport processes when the scattering regions (such as QD) are occupied by electrons. In the present article, however, we neglect the impacts of the Coulomb blockade effect in that the MBSs affect transport processes when the dots’ level is aligned to the Fermi levels in the leads. The Coulomb interaction will only induce another step in the current in higher energy levels, where the impacts of MBSs are weak.

FIGURE 6

FIGURE 6. TMR for different values of ${\delta }_M$ in A, different $t_c$ in B, and different $\Delta \epsilon$ in C. In addition to the parameters given in each figure, other ones are as in Figures 2,3.

4 Summary

In summary, we have studied the spin-polarized currents and TMR in a DQD coupled to both ferromagnetic leads and MBSs formed at the ends of a topological superconductor nanowire. Our calculation results show that the currents through the system can be effectively adjusted in terms of the spin polarization of either ferromagnetic leads or coupling strength between the dots and the MBSs. When the two spin polarizations are the same in sign, the currents’ amplitude in the antiparallel configuration can be larger than that in the parallel one, which results in an obvious negative TMR that can be used for detecting the existence of the MBSs. If the two spin polarizations are different in sign, however, then the TMR is positive and can be further enhanced by adjusting system’s parameters. Such a result is useful in designing high-efficiency spintronic devices. The negative or positive TMR is robust against variations of the overlapping between the MBSs, the tunnel coupling between the two dots, or even the difference between the dots’ energy levels.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

W-GM and L-WT contributed the ideas equally and performed the numerical calculations. L-WT derived the formulae in the paper and wrote the original manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11772287 and 11572277).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Kitaev AY. Unpaired Majorana fermions in quantum wires. Phys Usp (2001) 44:131–6. doi:10.1070/1063-7869/44/10S/S29

CrossRef Full Text | Google Scholar

2. Fu L, Kane CL. Superconducting proximity effect and Majorana fermions at the surface of a topological insulator. Phys Rev Lett (2008) 100:096407. doi:10.1103/PhysRevLett.100.096407

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Nayak C, Simon SH, Stern A, Freedman M, Sarma SD. Non-Abelian anyons and topological quantum computation. Rev Mod Phys (2008) 80:1083–159. doi:10.1103/RevModPhys.80.1083

CrossRef Full Text | Google Scholar

4. Mourik V, Zuo K, Frolov SM, Plissard SR, Bakkers EPAM, Kouwenhoven LP. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science (2012) 336:1003–7. doi:10.1126/science.1222360

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Finck ADK, Van Harlingen DJ, Mohseni PK, Jung K, Li X. Anomalous modulation of a zero-bias peak in a hybrid nanowire-superconductor device. Phys Rev Lett (2013) 110:12–22. doi:10.1103/PhysRevLett.110.126406

CrossRef Full Text | Google Scholar

6. Albrecht SM, Higginbotham AP, Madsen M, Kuemmeth F, Jespersen TS, Nygård J, et al. Exponential protection of zero modes in Majorana islands. Nature (2016) 531:206–9. doi:10.1038/nature17162

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sau JD, Lutchyn RM, Tewari S, Sarma SD. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys Rev Lett (2010) 104:4–29. doi:10.1103/PhysRevLett.104.040502

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Oreg Y, Refael G, Oppen F. Helical liquids and Majorana bound states in quantum wires. Phys Rev Lett (2010) 105:17–22. doi:10.1103/PhysRevLett.105.177002

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Zhang H, Liu CX, Gazibegovic S, Xu D, Logan JA, Wang G, et al. Quantized Majorana conductance. Nature (2018) 556:74–9. doi:10.1038/nature26142

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Gül Ö, Zhang H, Bommer JDS, Moor MWA, Car D, Plissard SR, et al. Ballistic Majorana nanowire devices. Nat Nanotechnol (2018) 13:192–7. doi:10.1038/s41565-017-0032-8

PubMed Abstract | CrossRef Full Text | Google Scholar

11. San-Jose P, Prada E, Aguado R. AC Josephson effect in finite-length nanowire junctions with Majorana modes. Phys Rev Lett (2012) 108:257001. doi:10.1103/PhysRevLett.108.257001

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Xu L, Li XQ, Sun QF. Majorana dc Josephson current mediated by a quantum dot. J Phys Condens Matter (2017) 29:195301. doi:10.1088/1361-648X/aa6661

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Chiu CK, Das Sarma S. Fractional Josephson effect with and without Majorana zero modes. Phys Rev B (2019) 99:035312. doi:10.1103/PhysRevB.99.035312

CrossRef Full Text | Google Scholar

14. Leijinse M. Thermoelectric signatures of a Majorana bound state coupled to a quantum dot. New J Phys (2014) 16:89–97. doi:10.1088/1367-2630/16/1/015029

CrossRef Full Text | Google Scholar

15. López R, Lee M, Serra L, Lim JS. Thermoelectrical detection of Majorana states. Phys Rev B (2014) 89:205418. doi:10.1103/physrevb.89.205418

CrossRef Full Text | Google Scholar

16. Hong L, Chi F, Fu ZG, Hou YF, Wang ZG, Li KM, et al. Large enhancement of thermoelectric effect by Majorana bound states coupled to a quantum dot. J Appl Phys (2020) 127:124302. doi:10.1063/1.5125971

CrossRef Full Text | Google Scholar

17. Chi F, Fu ZG, Liu J, Li KM, Wang ZG, Zhang P. Thermoelectric effect in a quantum dot side-coupled to Majorana bound states. Nanoscale Res Lett (2020) 15:79. doi:10.1186/s11671-020-03307-y

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Niu PB, Liu LX, Su XQ, Dong LJ, Shi YL, Luo HG. Spin Seebeck effect induced by a Majorana zero mode in a nanomagnet. Phys E (2020) 124:114313. doi:10.1016/j.physe.2020.114313

CrossRef Full Text | Google Scholar

19. Lee EJH, Jiang XC, Aguado R, Katsaros G, Lieber CM, Franceschi SD. Zero-Bias anomaly in a nanowire quantum dot coupled to superconductors. Phys Rev Lett (2012) 109:186802. doi:10.1103/PhysRevLett.109.186802

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Deng MT, Vaitiekėnas S, Hansen EB, Danon J, Leijnse M, Flensberg K, et al. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science (2016) 354:1557–62. doi:10.1126/science.aaf3961

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Liu DE, Baranger HU. Detecting a Majorana-fermion zero mode using a quantum dot. Phys Rev B (2011) 84:1–4. doi:10.1103/PhysRevB.84.201308

CrossRef Full Text | Google Scholar

22. Hoffman S, Chevallier D, Loss D, Klinovaja J. Spin-dependent coupling between quantum dots and topological quantum wirs. Phys Rev B (2017) 96:1–18. doi:10.1103/PhysRevB.96.045440

CrossRef Full Text | Google Scholar

23. Elsa P, Ramon A, Pablo S. Measuring Majorana non-locality and spin structure with a quantum dot. Phys Rev B (2017) 96:1–11. doi:10.1103/PhysRevB.96.085418

CrossRef Full Text | Google Scholar

24. Górski G, Kucab K. The spin-dependent coupling in the hybrid quantum dot–Majorana wire system. Phys Status Solidi B (2019) 256:1800492. doi:10.1002/pssb.201800492

CrossRef Full Text | Google Scholar

25. Leijnse M, Flensberg K. Parity qubits and poor man’s Majorana bound states in double quantum dots. Phys Rev B (2012) 86:134528. doi:10.1103/PhysRevB.86.134528

CrossRef Full Text | Google Scholar

26. Sherman D, Yodh JS, Albrecht SM, Nygård J, Krogstrup P, Marcus CM. Normal, superconducting and topological regimes of hybrid double quantum dots. Nat Nanotechnol (2017) 12:212–7. doi:10.1038/nnano.2016.227

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Ivanov TI. Coherent tunneling through a double quantum dot coupled to Majorana bound states. Phys Rev B (2017) 96:035417. doi:10.1103/PhysRevB.96.035417

CrossRef Full Text | Google Scholar

28. Barnaś J, Martinek J, Michałek G, Bułka BR, Fert A. Spin effects in ferromagnetic single electron transistors. Phys Rev B (2000) 62:12363–73. doi:10.1103/PhysRevB.62.12363

CrossRef Full Text | Google Scholar

29. Chi F, Zeng H, Yuan X. Flux-dependent tunnel magnetoresistance in parallel-coupled double quantum dots. Superlattice Microst (2009) 46:523–32. doi:10.1016/j.spmi.2009.04.002

CrossRef Full Text | Google Scholar

30. Stefanski P. Tunneling magnetoresistance anomalies in a Coulomb blockaded quantum dot. Phys Rev B (2009) 79:085312. doi:10.1103/PhysRevB.79.085312

CrossRef Full Text | Google Scholar

31. Tang LW, Wei GM. Detection of Majorana bound states by sign change of the tunnel magnetoresistance in a quantum dot coupled to ferromagnetic electrodes. Front Phys (2020) 8:147. doi:10.3389/fphy.2020.00147

CrossRef Full Text | Google Scholar

32. Hamaya K, Kitabatake M, Shibata K, Jung M, Kawamura M, Ishida S, et al. Oscillatory changes in the tunneling magnetoresistance effect in semiconductor quantum-dot spin valves. Phys Rev B (2008) 77:081302. doi:10.1103/PhysRevB.77.081302

CrossRef Full Text | Google Scholar

33. Yang FB. Spin-polarized transport through a hybrid Majorana quantum dot system coupled ferromagnetic leads. Phys E (2019) 109:164–8. doi:10.1016/j.physe.2019.01.020

CrossRef Full Text | Google Scholar

34. Wimmer M, Akhmerov AR, Medvedyeva MV. Majorana bound states without vortices in topological superconductors with electrostatic defects. Phys Rev Lett (2010) 105:046803. doi:10.1103/PhysRevLett.105.046803

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Choy TP, Edge JM, Akhmerov AR. Majorana fermions emerging from magnetic nanoparticles on a superconductor without spin-orbit coupling. Phys Rev B (2011) 84:195442. doi:10.1103/PhysRevB.84.195442

CrossRef Full Text | Google Scholar

36. Deng MT, Vaitiekenas S, Prada E, San-Jose P, Nygard J, Krogstrup P, et al. Nonlocality of Majorana modes in hybrid nanowires. Phys Rev B (2018) 98:085125. doi:10.1103/PhysRevB.98.085125

CrossRef Full Text | Google Scholar

37. Ricco LS, de Souza M, Figueira MS. Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: distinguishing isolated Majorana fermions from Andreev bound states. Phys Rev B (2019) 99:155159. doi:10.1103/PhysRevB.99.155159

CrossRef Full Text | Google Scholar

38. Weymann I, Barns J. Transport through two-level quantum dots weakly coupled to ferromagnetic leads. J Phys Condens Matter (2007) 19:1–21. doi:10.1088/0953-8984/19/9/ 096208

CrossRef Full Text | Google Scholar