Transmission Structured Illumination Microscopy for Quantitative Phase and Scattering Imaging

In this paper, we demonstrate a digital micromirror device (DMD) based optical microscopic apparatus for quantitative differential phase contrast (qDIC) imaging, coherent structured illumination microscopy (SIM), and dual-modality (scattering/fluorescent) imaging. For both the qDIC imaging and the coherent SIM, two sets of fringe patterns with orthogonal orientations and five phase-shifts for each orientation, are generated by a DMD and projected on a sample. A CCD camera records the generated images in a defocusing manner for qDIC and an in-focus manner for coherent SIM. Both quantitative phase images and super-resolved scattering/fluorescence images can be reconstructed from the recorded intensity images. Moreover, fluorescent imaging modality is integrated, providing specific biochemical structures of the sample once using fluorescent labeling.

Introduction

Quantitative phase microscopy (QPM) utilizing the phase information of the object wave can provide not only phase-contrast images but also quantitative information about the three-dimensional morphology and refractive index distribution of the samples [1–8]. Recently, a more compact module, nominated as quadriwave lateral shearing interferometry (QWLSI), was proved for quantitative phase imaging with one-shot. The QWLSI splits an object wave into four copies, two of which are sheared along the -x and -y directions respectively [9–11].

Most of the phase imaging techniques, or the coherent imaging techniques in more general cases, utilize monochromatic plane-wave illumination and consequently, the resolution of imaging systems is limited by wavelength (λ) and numerical aperture (NA) of the system [12]. A higher spatial resolution is favorable to resolve the finer details of the sample for everyone. However, when designing a microscopic objective, a higher spatial resolution often needs to be traded with a smaller field of view (FOV). People appeal an approach that can enhance spatial resolution and at the same time, maintain a large field of view. To meet this demand, synthetic aperture approaches in QPM have been reported, for instance, oblique illumination [13–15], structured illumination [16–19], and speckle illumination [20–22] (just to cite a few) have been proposed to improve the spatial resolution (or the space-bandwidth product) in QPM. Of note, structured illumination microscopy (SIM) [23–25], is a wide-field, minimally-invasive, super-resolution imaging technique, which utilizes moiré patterns created by illuminating the sample with periodic stripes. The structured illumination can downshift unresolvable high-frequency information into low-frequency falling in the supporting area of the system, as illustrated in Figure 1C, [26]. Furthermore, SIM was demonstrated having an optical sectioning capability comparable with confocal microscopy [27]. Hence, SIM has found widespread applications in biomedical imaging [28, 29], and notably long-term observing dynamics in living cells [25, 30]. Recently, SIM was applied to phase imaging of transparent samples when being combined with digital holographic microscopy [31] or reference-less phase retrieval approaches [18, 32]. Till yet, QPM with structured illumination has been implemented using gratings or spatial light modulator (SLM), and the phase imaging modality is often isolated from other imaging modalities such as fluorescence imaging. Therefore, the value of QPM is limited due to the lack of multi-dimensional information for the same sample.

FIGURE 1

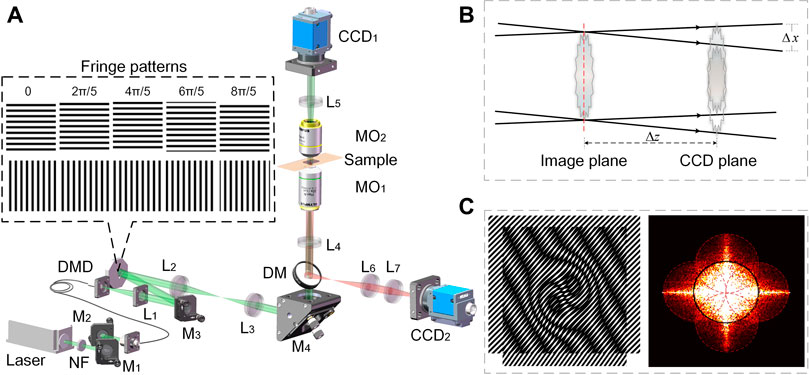
FIGURE 1. The schematic diagram of DMD-based SIM apparatus for multi-modality imaging. (A) Experimental setup. Insets: structured illumination patterns (B) lateral shearing of the ±1 orders in qDIC modality; (C) resolution enhancement upon structured illumination. DM, dichroic mirrors; L₁-L₇, achromatic lens; MO₁-MO₂, microscopic objectives; M₁-M₄, mirrors; NF, neutral density filter.

In this paper, we propose a DMD based optical microscope that integrate multiple imaging modalities. At first, structured illumination based QPM enables to providing quantitative phase image of a sample without fluorescent labeling. Second, coherent SIM provides absorption/scattering images of unlabeled samples with resolution-enhancement. Third, this system is integrated with a fluorescence imaging modality, providing additional (functional/biochemical) information on the same sample.

Methods

The schematic diagram of the system is shown in Figure 1A, of which a diode laser with a wavelength of 561 nm (MLL-U-561, Changchun New Industries Optoelectronics Technology Co., Ltd., China) is used as the illumination source. After being reflected by the mirrors M₁ and M₂ sequentially, the laser beam is coupled into a fiber and sent to the setup. In the output end, the light from the fiber is collimated by the lens L₁ and guided by the mirror M₃ to a DMD (1920 × 1080 pixels, pixel size 7.56 μm, DLP F6500, UPOLabs, China) at an incidence angle of 24°. On DMD, two groups of fringe patterns with orthogonal orientations and five-phase shifts (δ_m = 2 (m-1)π/5, m = 1, … , 5.) for each orientation are loaded to the DMD in sequence (as shown in the inset of Figure 1A). The fringe patterns displayed on the DMD are further relayed by the telescope systems L₂-L₃ and L₄-MO₁, and eventually projected onto the sample placed on the common focal plane of MO₁ and MO₂. Preferably, the illumination beam is filtered before entering the sample plane: the illumination light is Fourier transformed by the lens L₂ and its spectrum appears in the focal plane of L₂. A mask is located in the Fourier plane and blocks the unwanted diffraction orders except the ±1st orders. As a consequence, the fringe patterns on the sample plane are of ideal cosine distribution. Upon the fringe illumination, the sample is then imaged by the telescope system MO₂-L₅ to the image plane with a distance Δz apart from the CCD plane (CCD₁, 4000 × 3000 pixels, pixel size 1.85 μm, DMK 33UX226, The Imaging Source Asia Co., Ltd., China). The camera CCD₁ records diffraction images for different imaging modes, defocused images in qDIC and focused images in coherent SIM. Meanwhile, the emission light (fluorescence) from the sample will propagate along the opposite direction of the illumination light, and is then collected by the camera CCD₂. It is worth mentioning that the camera CCD₁ and CCD₂ are synchronized with the DMD, yielding an acquisition speed of 15 frames per second, providing a sub-second imaging speed for every channel.

Quantitative Differential Phase-Contrast (qDIC) Microscopy With Structured Illumination

The structured illumination for qDIC microscopy (Figure 1B) can be expressed as $A_m^{\xi }$ = 2cos (2r/Λ+δ_m) with m = 1, 2, … , 5, and ξ indicates the orientation indices of x and y, respectively. r is the spatial position vector, Λ is the stripe’s period, and δ_m is the phase shift. Passing through the sample, the object wave under $A_m^{\xi }$ is diffracted and relayed by the telescope system MO₂-L₅ to the image plane. After diffraction of a distance of Δz, the diffraction patterns are recorded by the CCD₁ camera. The waves along the ±1st orders of $A_m^{\xi }$ at the camera plane are $U_1^{\xi }$ and $U_{+1}^{\xi }$. These two waves interfere with each other at the camera plane and the intensity distribution of the interferogram captured by the camera can be written as:

$\begin{array}{c}{I}_m^{\xi }\left(r\right)={\left|U_{+1}^{\xi }\left(r\right)\right|}^2+{\left|U_{-1}^{\xi }\left(r\right)\right|}^2+U_{+1}^{\xi }\left(r\right)U_{-1}^{\xi \ast }\left(r\right)+U_{-1}^{\xi }\left(r\right)U_{+1}^{\xi \ast }\left(r\right)\\ ={\alpha }_0^{\xi }+{\alpha }_1^{\xi }\exp \left(i2{\delta }_m\right)+{\alpha }_2^{\xi }\exp \left(-i2{\delta }_m\right)\end{array}(1)$

where, ${\alpha }_0^{\xi }$ equals to $|U_{+1}^{\xi }\left(r\right){|}^2+|U_{-1}^{\xi }\left(r\right){|}^2$, ${\alpha }_1^{\xi }$ equals to ${\left[I_{+1}^{\xi }\left(r\right)I_{-1}^{\xi }\left(r\right)\right]}^{1/2}exp\left[i({\phi }_{diff}^{\xi }+2\pi r/\Lambda )\right]$, and ${\alpha }_2^{\xi }$ equals to ${\left[I_{+1}^{\xi }\left(r\right)I_{-1}^{\xi }\left(r\right)\right]}^{1/2}exp[-i({\phi }_{diff}^{\xi }+2\pi r/\Lambda )]$. Here, ${\phi }_{diff}^{\xi }$ denotes the phase difference between $U_1^{\xi }$ and $U_{-1}^{\xi }$ which is generated by the lateral shearing. And δ_m = 2 (m-1)π/5 (m = 1, 2, … , 5.) is the phase shift induced by laterally translating the fringe on DMD. Despite three-step phase-shifting is enough to solve these three terms ${\alpha }_0^{\xi }$, ${\alpha }_1^{\xi }$, and ${\alpha }_2^{\xi }$, we use the five-step phase shifting to achieve a better reconstruction immune to phase shift error and environmental instability [33]. Accordingly, Eq. 1 can be rewritten as:

$\left(\begin{array}{ccc}1& \exp \left(i2{\delta }_1\right)& \exp \left(-i2{\delta }_1\right)\\ 1& \exp \left(i2{\delta }_2\right)& \exp \left(-i2{\delta }_2\right)\\ 1& \exp \left(i2{\delta }_3\right)& \exp \left(-i2{\delta }_3\right)\\ 1& \exp \left(i2{\delta }_4\right)& \exp \left(-i2{\delta }_4\right)\\ 1& \exp \left(i2{\delta }_5\right)& \exp \left(-i2{\delta }_5\right)\end{array}\right)\cdot \left(\begin{array}{c}{\alpha }_0^{\xi }\\ {\alpha }_1^{\xi }\\ {\alpha }_2^{\xi }\end{array}\right)=\left(\begin{array}{c}{I}_1^{\xi }\left(r\right)\\ I_2^{\xi }\left(r\right)\\ I_3^{\xi }\left(r\right)\\ I_4^{\xi }\left(r\right)\\ I_5^{\xi }\left(r\right)\end{array}\right)(2)$

Here ${\alpha }_0^{\xi }$, ${\alpha }_1^{\xi }$, and ${\alpha }_2^{\xi }$ can be solved in a least-square manner via multiplying both sides of Eq. 2 with the transpose of the coefficient matrix. Therefore, ${\alpha }_0^{\xi }$, ${\alpha }_1^{\xi }$, and ${\alpha }_2^{\xi }$ along the ξ-direction can be achieved, respectively. In order to compensate for the linear phase terms in ${\alpha }_1^{\xi }$ and ${\alpha }_2^{\xi }$ induced by the oblique illumination of the ±1st orders of the structured illuminations, an accurate calibration was performed. Actually, the calibration was performed with the same procedure but in the absence of any samples, and we can get new terms ${\alpha }_{b0}^{\xi }$, ${\alpha }_{b1}^{\xi }$, and ${\alpha }_{b2}^{\xi }$. Eventually, the pure phase difference of the sample can be obtained by ${\phi }_{diff}^{\xi }=\mathrm{A}\mathrm{n}\mathrm{g}\{{\alpha }_1^{\xi }/{\alpha }_{b1}^{\xi }\}$, where Ang{·} denotes the argument retrieval operator. Similarly, the phase difference ${\phi }_{diff}^{\xi }$ along the x- and y-axes can be obtained by rotating the fringe 90^o with the same calculation procedure. Ultimately, the phase distribution φ(r) can be obtained by integrating ${\phi }_{diff}^x$ and ${\phi }_{diff}^y$ [34]:

$\phi \left(r\right)=IFT\left\{\frac{-i[v^{x}FT\left\{{\phi }_{\text{diff}}^x\right\}+v^{y}FT\left\{{\phi }_{\text{diff}}^y\right\}]}{2\pi {\left(v^x\right)}^2+{\left(v^y\right)}^2}\right\}(3)$

where v^x and v^y are the coordinates in the Frequency domain, respectively. FT{·} and IFT{·} represent the Fourier transform and inverse Fourier transform, respectively.

Super-Resolution Scattering Imaging With Coherent Structured Illumination

Using the same stripes projection method as in phase imaging, a resolution enhancement in non-fluorescent imaging can be realized by using coherent structured illumination. The key to enhancing the spatial resolution in non-fluorescent/scattering imaging is the synthetic-aperture effect, as shown in Figure 1C, which can bring unobservable high-frequency information into the low-frequency supporting area through oblique illumination. Different from the phase imaging, the scattering imaging here records the diffraction patterns in an in-focus manner. Mathematically, the intensity images in the CCD₁ plane can be written as $I_m^{\xi }\left(r\right)=|h_c\left(r\right)\otimes [O\left(r\right)\cdot A_m^{\xi }]{|}^2$, where h_c(r) is the coherent point spread function of the system, $\otimes$ is the convolution operator, O(r) is the object transmittance function, and $A_m^{\xi }$ is the structured illumination filed in the sample plane. After a Fourier transform, we can obtain the spectrum distribution of $I_m^{\xi }\left(r\right)$:

${\tilde{I}}_m^{\xi }\left(v\right)=\left[G_0^{\xi }\left(v\right)+\exp \left(i2{\delta }_m\right)\cdot G_{+1}^{\xi }\left(v-v_0^{\xi }\right)+\exp \left(-i2{\delta }_m\right)\cdot G_{-1}\left(v+v_0^{\xi }\right)\right](4)$

where ${\tilde{I}}_m^{\xi }\left(v\right)$ is the Fourier transform of $I_m^{\xi }\left(r\right)$, v is the spatial frequency vector, and $G_m^{\xi }$ (m = 0, ±1) represent the spectral components along x- and y-directions. Notably, $G_{+1}^{\xi }\left(v-v_0^{\xi }\right)$ and $G_{-1}\left(v+v_0^{\xi }\right)$ have the high-frequency spectrum surpassing the supporting pupil of the imaging system, which was downshifted by the oblique illumination and therefore passing through the imaging system. To acquire these three spectral components, five-step phase-shifting was performed with the phase shifts δ_m = 2 (m-1)π/5. After similar mathematical operations as described in Quantitative Differential Phase-Contrast (qDIC) Microscopy With Structured Illumination different spectra along with the 0th, and ±1st orders of the structured illuminations can be solved, and an extended-spectrum can be synthesized with:

$G_{SI}\left(v\right)=\frac{1}{2}\cdot [G_0^x\left(v\right)+G_0^y\left(v\right)]+G_1^x(v-v_0^x)+G_{-1}^x(v+v_0^x)+G_1^y(v-v_0^y)+G_{-1}^y(v+v_0^y)(5)$

Afterward, the resolution-enhanced image can be achieved using an inverse Fourier transform on Eq. 5 and multiplying weight factor. It is worth noting that in such a coherent imaging system the phase distribution of different $G_m^{\xi }$ (m = 0, ±1) should be compensated e.g., with the experiment without any samples, making sure that there are no additional phase shifts between different terms in Eq. 5.

Experiments and Results

qDIC Microscopy Imaging of Living Cells

In the first experiment, a confirmatory experiment is carried out to demonstrate qDIC for live samples imaging without fluorescent labeling. For this purpose, live mouse adipose stem cells were used as phase samples. The magnification and numerical aperture of the imaging system MO₂-L₅ are 10× and 0.32, respectively. Two groups of binary patterns with the orientation along the x- and y-directions were loaded on the DMD, of which the period was set as ten pixels and the modulation depth is 1. The x- and y- orientated patterns were shifted by five times and each time had a phase shift δ_m = 2 (m-1)π/5 (m = 1, 2, … , 5.). The generated diffraction patterns were recorded by the CCD₁ camera, and shown in Figures 2A,B respectively. Using the reconstruction method described with Eqs. 1, 2, both the amplitude and phase derivatives of the sample are obtained. Figures 2C,D show the phase gradients along the x- and y- orientations, respectively. Despite the contours of the cells become visible in Figures 2C,D, the result is a mixture of amplitude and phase-gradient in a nonlinear manner. The final phase distribution of the sample is then obtained by integrating the phase derivatives along the x- and y- orientations, as shown in Figure 2F. Compared to the amplitude image of the sample shown in Figure 2E, where the structures of the cells are nearly invisible, the phase image (Figure 2F) visualizes clearly the structures of the cells, and notably in a quantitative manner. The comparison reveals that qDIC can not only visualize the transparent samples with high contrast but also provide us the quantitative information on the optical path difference (OPD) of the sample.

FIGURE 2

FIGURE 2. qDIC imaging of mouse adipose stem cells. (A,B) The diffraction patterns along the x- and y-directions; (C,D) reconstructed phase derivatives of the cells along the x- and y- orientations, respectively; (E,F) reconstructed amplitude and phase distribution of the mouse adipose stem cells, respectively. The scale bar in (E), 40 μm.

Coherent SIM Imaging of SiO₂ Particles

In the second experiment, resolution-enhanced nonfluorescent/scattering imaging using coherent structured illumination was proved by imaging SiO₂ beads (diameter: 500-nm). Binary fringe patterns were loaded on DMD to generate sinusoidal fringe stripes at the sample plane after being filtered in the Fourier plane. The period of the binary patterns was set as five pixels, and after the de-magnification, the period of the sinusoidal fringe stripes was 0.95 μm at the sample plane. As explained in Super-Resolution Scattering Imaging With Coherent Structured Illumination, the binary fringe patterns were shifted by five times (yielding the phase shifts δ_m = 2 (m-1)π/5, m = 1, 2, … , 5) along the x- and y-direction, and the generated diffraction patterns are recorded in sequence by CCD₁ located at the image plane. The super-resolution reconstruction is then realized with the method elaborated in Super-Resolution Scattering Imaging With Coherent Structured Illumination. The reconstructed image of SiO₂ beads is shown in Figures 3A,B shows the conventional wide-field image obtained using a perpendicular plane-wave illumination. It is clear that the coherent structured illumination provides a high-resolution image on the SiO₂ beads.

FIGURE 3

FIGURE 3. Coherent SIM imaging of 500 nm SiO₂ beads. The images obtained using the convention al optical microscope under plane-wave illumination (A) and coherent SIM (B). (C) The intensity profiles along the blue/red solid lines in (A) and (B). The scale bar in (A), 30 μm.

The numerical aperture (NA_detect = 0.32) of the detection objective MO₂ limits the lateral resolution to δ_plan = 1.44 μm for the conventional imaging using a perpendicular plane wave illumination. When the structured illumination is used, the illumination angle of the ±1st diffraction orders of the fringe stripes is θ_illum = 0.30 rad, and thus the theoretical lateral resolution can be estimated with δ_str = 0.82λ/(sin (θ_illum)+NA_detect) = 0.75 μm [35]. For a quantitative evaluation of the lateral resolution, ten random SiO₂ beads were randomly chosen, and the intensity distributions along the line crossing the center of each bead are analyzed, as shown in Figure 3C. The statistics on the ten beads tells that the averaged full widths at half maximum (FWHM) under these two illuminations are 1.86 ± 0.20 μm for perpendicular uniform illumination while 1.10 ± 0.10 μm for coherent structured illumination. When considering the non-negligible size (the diameter d = 500 nm) of the SiO₂ beads, the final resolution can be calculated by ${\delta }_{res}={[{\left({\delta }_{plan/str}\right)}^2-d^2]}^{1/2}$, yielding the lateral resolution ${\delta }_{res}$ = 1.80 ± 0.20 μm and 0.98 ± 0.10 μm for the conventional wide-field imaging mode and coherent structured illumination mode, respectively. It should be noted that there is a mismatch between the measured and theoretical resolutions due to the system’s aberration and other uncertain factors.

Dual-Modality (Scattering/Fluorescence) Imaging of Lily Anther

In the third experiment, the dual-modality (non-fluorescent scattering/fluorescent) imaging capability of the proposed SIM apparatus was demonstrated with lily anther as the sample. The coherent SIM image was shown in Figure 4B, and the fluorescence image was captured by the camera CCD₂ after being filtered by a color filter (600/50 nm, central wavelength/full-width at half maximum) and is shown in Figure 4C. Compared with the wide-field image in Figure 4A obtained by using a uniform illumination, the SIM image in Figure 4B shows more detailed structures and clearer background. Moreover, the fluorescent image in Figure 4C shows clear pollen structures (having autofluorescence) in the context of a clean background. It is also distinct that the SIM image (transmission) and the fluorescent image (reflection) have the opposite contrast for the same sample.

FIGURE 4

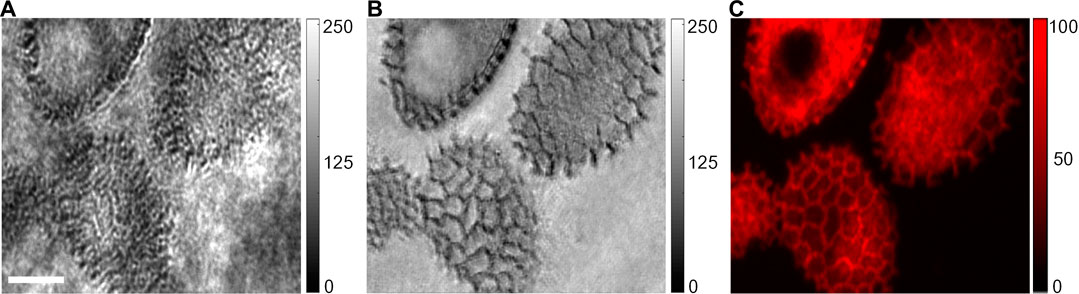
FIGURE 4. Dual-modality imaging of lily anther. The image obtained using the conventional optical microscope under plane-wave illumination (A) and coherent SIM (B). (C) Fluorescence image (spectrum band: 600/50 nm) of the same pollens. The scale bar in (A), 30 μm.

Discussion

In this paper, we have proposed a DMD based transmission SIM apparatus, which can be exploited for multi-modality imaging, including quantitative differential phase-contrast (qDIC) imaging, coherent SIM with resolution enhancement, fluorescence imaging. Structured illumination based qDIC is immune to environmental disturbances, compared with interferometric approaches. Coherent SIM provides super-resolved, scattering images of non-fluorescent samples. Fluorescent imaging furnishes specific, biochemical structures of samples once using fluorescent labeling. For both qDIC and coherent SIM, a DMD is used to generate structured illumination, and therefore, it has the features of high speed and high flexibility. It is worth noting that the qDIC is only applicable to continuous samples since the integration of phase derivatives are used. Moreover, both qDIC and coherent SIM cannot be realized in a real-time manner since both need to record multiple raw images once a sample is illuminated with structured patterns of different orientations and phase shifts. We believe such a simple and versatile apparatus will be widely applied for biomedical fields and life science.

In the proposed approach periodic patterns were projected to obtain the resolution enhancement and/or the phase information. As future prospective non periodic patterns (e.g., Walsh functions) can be projected and by that practically obtain the decomposing of the spatial information of the inspected sample. Projecting such functions can also be connected to compressed sensing and it may allow high resolution extraction of the spatial information in the inspected sample with smaller number of projected patterns (i.e., having faster process of information extraction).

Funding

This work is supported by National Natural Science Foundation of China (NSFC 62075177); Natural Science Foundation of Shaanxi Province (2020JM-193, 2020JQ-324); the Fund of State Key Laboratory of Transient Optics and Photonics (SKLST201804) and Key Laboratory of Image Processing and Pattern Recognition, Jiangxi Province.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JZ conceived and supervised the project. KW and YM performed experiments and data analysis. ML, JL, and ZZ contributed to data analysis. KW, YM, and JZ wrote the draft of the manuscript; All the authors edited the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Micó V, Zheng J, Garcia J, Zalevsky Z, Gao P. Resolution enhancement in quantitative phase microscopy. Adv Optic Photon (2019) 11:135–214. doi:10.1364/AOP.11.000135

CrossRef Full Text | Google Scholar

2. Zhang M, Ma Y, Wang Y, Wen K, Zheng J, Liu L, et al. Polarization grating based on diffraction phase microscopy for quantitative phase imaging of paramecia. Optic Express (2020) 28:29775–87. doi:10.1364/OE.404289

CrossRef Full Text | Google Scholar

3. Zernike F. Phase contrast, a new method for the microscopic observation of transparent objects. Physica (1942) 9:974–86. doi:10.1016/S0031-8914(42)80035-X

CrossRef Full Text | Google Scholar

4. Ma Y, Guo S, Pan Y, Fan R, Smith Z, Lane SM, et al. Quantitative phase microscopy with enhanced contrast and improved resolution through ultra‐oblique illumination (UO‐QPM). J Biophot (2019) 12:e201900011. doi:10.1002/jbio.201900011

CrossRef Full Text | Google Scholar

5. Shribak M, Larkin K, Biggs D. Mapping of optical path length and image enhancement using orientation-independent differential interference contrast microscopy. J Biomed Optic (2017) 22:016006. doi:10.1117/1.JBO.22.1.016006

CrossRef Full Text | Google Scholar

6. Ding C, Li C, Deng F, Simpson GJ. Axially-offset differential interference contrast microscopy via polarization wavefront shaping. Optic Express (2019) 27:3837–50. doi:10.1364/OE.27.003837

CrossRef Full Text | Google Scholar

7. Vishnyakov G, Levin G, Minaev V, Latushko M, Nekrasov N, Pickalov V. Differential interference contrast tomography. Opt Lett (2016) 41:3037–40. doi:10.1364/OL.41.003037

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Arnison MR, Larkin KG, Sheppard CJ, Smith NI, Cogswell CJ. Linear phase imaging using differential interference contrast microscopy. J Microsc (2004) 214:7–12. doi:10.1111/j.0022-2720.2004.01293.x

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Primot J. Theoretical description of Shack–Hartmann wave-front sensor. Optic Commun (2003) 222:81–92. doi:10.1016/S0030-4018(03)01565-7

CrossRef Full Text | Google Scholar

10. Aknoun S, Bon P, Savatier J, Wattellier B, Monneret S. Quantitative retardance imaging of biological samples using quadriwave lateral shearing interferometry. Optic Express (2015) 23:16383–406. doi:10.1364/OE.23.016383

CrossRef Full Text | Google Scholar

11. Bon P, Maucort G, Wattellier B, Monneret S. Quadriwave lateral shearing interferometry for quantitative phase microscopy of living cells. Optic Express (2009) 17:13080–94. doi:10.1364/OE.17.013080

CrossRef Full Text | Google Scholar

12. Heintzmann R, Cremer C. Laterally modulated excitation microscopy: improvement of resolution by using a diffraction grating. Proc SPIE (1999) 3568:185–96. doi:10.1117/12.336833

CrossRef Full Text | Google Scholar

13. Alexandrov SA, Hillman TR, Gutzler T, Sampson DD. Synthetic aperture Fourier holographic optical microscopy. Phys Rev Lett (2006) 97:168102. doi:10.1103/physrevlett.97.168102

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ou X, Horstmeyer R, Zheng G, Yang C. High numerical aperture Fourier ptychography: principle, implementation and characterization. Optic Express (2015) 23:3472–91. doi:10.1364/OE.23.003472

CrossRef Full Text | Google Scholar

15. Lee K, Kim H-D, Kim K, Kim Y, Hillman TR, Min B, et al. Synthetic Fourier transform light scattering. Optic Express (2013) 21:22453–63. doi:10.1364/OE.21.022453

CrossRef Full Text | Google Scholar

16. Littleton B, Lai K, Longstaff D, Sarafis V, Munroe P, Heckenberg N, et al. Coherent super-resolution microscopy via laterally structured illumination. Micron (2007) 38:150–7. doi:10.1016/j.micron.2006.07.010

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Chowdhury S, Izatt J. Structured illumination diffraction phase microscopy for broadband, subdiffraction resolution, quantitative phase imaging. Opt Lett (2014) 39:1015–8. doi:10.1364/OL.39.001015

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Gao P, Pedrini G, Osten W. Phase retrieval with resolution enhancement by using structured illumination. Opt Lett (2013) 38:5204–7. doi:10.1364/OL.38.005204

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Mudassar AA, Hussain A. Super-resolution of active spatial frequency heterodyning using holographic approach. Appl Optic (2010) 49:3434–41. doi:10.1364/AO.49.003434

CrossRef Full Text | Google Scholar

20. Park Y, Choi W, Yaqoob Z, Dasari R, Badizadegan K, Feld MS. Speckle-field digital holographic microscopy. Optic Express (2009) 17:12285–92. doi:10.1364/OE.17.012285

CrossRef Full Text | Google Scholar

21. Zhang H, Jiang S, Liao J, Deng J, Liu J, Zhang Y, et al. Near-field Fourier ptychography: super-resolution phase retrieval via speckle illumination. Optic Express (2019) 27:7498–512. doi:10.1364/OE.27.007498

CrossRef Full Text | Google Scholar

22. Zheng J, Pedrini G, Gao P, Yao B, Osten W. Autofocusing and resolution enhancement in digital holographic microscopy by using speckle-illumination. J Optic (2015) 17:085301. doi:10.1088/2040-8978/17/8/085301

CrossRef Full Text | Google Scholar

23. Gustafsson MG. Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy. J. Microsc. (2000) 198:82–7. doi:10.1046/j.1365-2818.2000.00710.x

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Kim Y-D, Ahn M, Kim T, Yoo H, Gweon D. Design and analysis of a cross-type structured-illumination confocal microscope for high speed and high resolution. Meas Sci Technol (2012) 23:105403. doi:10.1088/0957-0233/23/10/105403

CrossRef Full Text | Google Scholar

25. Shao L, Kner P, Rego EH, Gustafsson MG. Super-resolution 3D microscopy of live whole cells using structured illumination. Nat Methods (2011) 8:1044–6. doi:10.1038/nmeth.1734

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Gustafsson MG. Nonlinear structured-illumination microscopy: wide-field fluorescence imaging with theoretically unlimited resolution. Proc Natl Acad Sci U.S.A. (2005) 102:13081–6. doi:10.1073/pnas.0406877102

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Neil MA, Juškaitis R, Wilson T. Method of obtaining optical sectioning by using structured light in a conventional microscope. Opt Lett (1997) 22:1905–7. doi:10.1364/OL.22.001905

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Schermelleh L, Carlton PM, Haase S, Shao L, Winoto L, Kner P, et al. Subdiffraction multicolor imaging of the nuclear periphery with 3D structured illumination microscopy. Science (2008) 320:1332–6. doi:10.1126/science.1156947

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Fitzgibbon J, Bell K, King E, Oparka K. Super-resolution imaging of plasmodesmata using three-dimensional structured illumination microscopy. Plant Physiol (2010) 153:1453–63. doi:10.1104/pp.110.157941

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Keller PJ, Schmidt AD, Santella A, Khairy K, Bao Z, Wittbrodt J, et al. Fast, high-contrast imaging of animal development with scanned light sheet–based structured-illumination microscopy. Nat Methods (2010) 7:637–42. doi:10.1038/nmeth.1476

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Gao P, Pedrini G, Osten W. Structured illumination for resolution enhancement and autofocusing in digital holographic microscopy. Opt Lett (2013) 38:1328–30. doi:10.1364/OL.38.001328

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Gao P, Wen K, Liu L, Zheng J. Computational phase microscopy with modulated illumination. Proc SPIE (2020) 11438:1143813. doi:10.1117/12.2551362

CrossRef Full Text | Google Scholar

33. Abdelsalam DG, Kim D. Two-wavelength in-line phase-shifting interferometry based on polarizing separation for accurate surface profiling. Appl Optic (2011) 50:6153–61. doi:10.1364/AO.50.006153

CrossRef Full Text | Google Scholar

34. Frankot RT, Chellappa R. A method for enforcing integrability in shape from shading algorithms. IEEE T. Pattern Anal (1988) 10:439–51. doi:10.1109/34.3909

CrossRef Full Text | Google Scholar

35. Born M, Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light. New York: Cambridge University Press (2013). 417 p.

Google Scholar