Time-Dependent Fractional Diffusion and Friction Functions for Anomalous Diffusion

The precise determination of diffusive properties is presented for a system described by the generalized Langevin equation. The time-dependent fractional diffusion function and the Green-Kubo relation as well as the generalized Stokes-Einstein formula, in the spirit of ensemble averages, are reconfigured. The effective friction function is introduced as a measure of the influence of frequency-dependent friction on the evolution of the system. This is applied to the generalized Debye model, from which self-oscillation emerges as indicative of ergodicity that breaks due to high finite-frequency cutoff. Moreover, several inconsistent conclusions that have appeared in the literature are revised.

1 Introduction

In the early 20th century, Brownian motion became the subject of a theoretical investigation by Einstein, Langevin, Smoluchowski, and others [1–3]. The well-known conclusion was that the mean squared displacement of a force-free particle grows linearly in time. Because the Brownian trajectories were relatively short, Jean Perrin in 1908 used an ensemble average over many particle traces to obtain meaningful statistics. A few years later, Ivar Nordlune conceived a method for recording much longer time series. This let him determine time average individual trajectories and thus avoid average ensembles of particles that were probably not identical [3]. The average can be understood either as an ensemble average over a large number of trajectories or as a temporal moving average over a very long time trajectory. Nevertheless, the time average diffusion coefficient might be a random variable different from that of the ensemble, albeit the measurement time is long [4–6]. Since the ergodicity is broken in this sense, the diffusion coefficient can only be calculated by using the ensemble average. In theory, one mostly considers ensemble average; in the experiment, however, it is sometimes the former that taken the place of time averages because only one realization of a process is recorded. For an ergodic system, the time average is the same as the ensemble average [7]. The ensemble averaging result can be regarded as a comparable criterion.

Superseding Einstein’s theory of Brownian movement, anomalous diffusion is characterized by the variance of the position of a diffusing particle increasing with time in a power-law form [8–11]. From an analysis of experimental data, the variance of the position for a force-free particle may be written in scalar form,

$\langle \Delta x^2\left(t\right)\rangle =2D_{\alpha }{L}_1\left(t\right)t^{\alpha }+L_2\left(t\right),(1)$

where $\langle \cdots \rangle$ denotes the ensemble average and $0<\alpha \le 2$. This setup allows for various sorts of different physical realizations. The expectation for the particular behaviors of $L_1\left(t\right)$ and $L_2\left(t\right)$ is: $L_1\left(t\right)>0$, $L_1\left(t\to \infty \right)=1$, $L_2\left(0\right)=0$, and ${\lim }_{t\to \infty }{t}^{-\alpha }{L}_2\left(t\right)=0$. There have been a number of attempts to calculate the coefficients of transport for apparently dissipative systems, the Fourier transform of the velocity autocorrelation function (VACF) being widely used in semi-phenomenological spectral studies of fluids, magnets, and other systems [12]. Furthermore, the diffusion constant $D_{\alpha }$ and exponent α deduced from data analyses need to be addressed accurately. In the anomalous diffusion sense, the generalization of the two basic statistical-dynamics laws—the Green-Kubo and the Stokes-Einstein relations—regarding measurable approaches for arbitrary frequency-dependent friction also has importance. This aids our understanding of the characteristic behaviors of anomalous, diffusive, and nonergodic systems [7, 13].

There are many formalisms that describe anomalous diffusion, and growing interest has gathered around using the generalized Langevin equation (GLE) [14–16] as a viable alternative for investigating anomalous diffusion. One of the key features of the GLE is that it contains an after-effect function, termed a memory function [17, 18], which can be obtained from experiments or molecular dynamics simulations [19, 20]. Previous works on anomalous diffusion using the non-Ohmic friction model without high-frequency decay modulation showed that the VACF varies with time governed by the Mittag-Leffler function [21–25]. Indeed, a little transitive friction information can be extracted, although one knows that the diffusion coefficient determined by standard approaches vanishes for subdiffusion and diverges for superdiffusion. Furthermore, the issue of long-term memory [26] is always of central importance in nonequilibrium statistical mechanics, but there are several grounds for doubt [27], e.g., the dynamical effect related to the sharp cutoff in the spectrum being widely used, that require clarification.

The purpose of this paper is to set the diffusion coefficient and scaling exponent for anomalous diffusion processes; in particular, we will introduce another quantity, the effective friction function related to non-Stokesian relaxation, to account for the after-effect of anomalous diffusion. A measurement of this function does not present major difficulties for experiments yet provides a novel characterization of the underlying evolutionary process. The following questions also arise: What forms do the generalized Green-Kubo and Stokes-Einstein relations take in regard to anomalous diffusion? Can the coefficient of diffusion and the exponent be measured accurately? How strong is the effect of the high finite-frequency cutoff on the dynamics? The answers will become clear in the present study.

2 Relations Between Various Temporal Functions

2.1 Time-Dependent Fractional Diffusion Function

To extract the pre-time coefficient $D_{\alpha }$ in Eq. 1 when the exponent α is known, we have to generalize the definition of the coefficient of diffusion [28] using L’Hôpital’s rule. The “fractional diffusion function” is assumed to be time-dependent, i.e.,

${\tilde{D}}_{\alpha }\left(t\right)=\frac{1}{2}{ }_0{\partial }_t^{\alpha }\langle \Delta x^2\left(t\right)\rangle ,(2)$

where $0{\partial }_t^{\alpha }$ denotes a fractional Riemann-Liouville derivative of order α [23–25]. Here, ${\tilde{D}}_{\alpha }\left(t\right)$ is related to $D_{\alpha }{L}_1\left(t\right)$ in Eq. 1, which converges asymptotically to the constant $D_{\alpha }$. For normal diffusion with $\alpha =1$, Eq. 2 reduces to the standard diffusion function defined as $D\left(t\right)=\frac{1}{2}\frac{d}{dt}\langle \Delta x^2\left(t\right)\rangle$ [28, 29]. The latter has a clear physical meaning representing the temporal expansion rate of the spatial distribution. We establish a relation between the above two diffusion functions:

${\tilde{D}}_{\alpha }\left(t\right)=\frac{d^n}{d{t}^n}{\displaystyle {\int }_0^t\frac{{\left(t-t^{\prime }\right)}^{\beta -1}}{\Gamma \left(\beta \right)}}D\left(t^{\prime }\right)d{t}^{\prime },(3)$

where $\Gamma \left(\beta \right)$ is the gamma function, and setting $\alpha =n-\beta +1$, where $n=\mathrm{0,1,2},\dots$ is a non-negative integer and $\beta \ge 0$ a real number. In calculations concerning subdiffusion and normal diffusion $\left(0<\alpha \le 1\right)$, we choose $n=1$ and then; for superdiffusion and ballistic diffusion [30, 31] $\left(1<\alpha \le 2\right)$, we choose $n=2$ and then $\beta =3-\alpha$. To date, no systematic numerical results regarding the fractional diffusion function for any contexts have been provided. However, they are required to understand the experimental observations.

2.2 Generalization of Two Famous Statistical-Dynamics Relations

The motion of a particle driven by a Gaussian distributed noise $\epsilon \left(t\right)$ is described by the following GLE:

$m\dot{v}+m{\displaystyle {\int }_0^t{M}_1\left(t-t^{\prime }\right)v\left(t^{\prime }\right)d{t}^{\prime }+U^{\prime }\left(x\right)=\epsilon \left(t\right)},(4)$

where $M_1\left(t\right)$ is the memory function and $U\left(x\right)$ the potential. In general, colored noise $\epsilon \left(t\right)$ has a vanishing mean and is not correlated with the initial velocity. The noise correlation and memory function satisfy the fluctuation-dissipation theorem, expressed as $\langle \epsilon \left(t\right)\epsilon \left(t^{\prime }\right)\rangle =m{k}_{B}T{M}_1\left(\left|t-t^{\prime }\right|\right)$, where $k_B$ denotes Boltzmann constant and T the temperature. We emphasize that, under the physical requirements of noisy dynamics [28, 32, 33], a rather free choice of the memory kernel or of the noise autocorrelation function is possible [34].

When the external potential is absent, i.e., when dealing with free diffusive motion, the formal solution of Eq. 4 is obtained by means of the Laplace-transform technique [35–38], which yields $v\left(t\right)=v\left(0\right)h\left(t\right)+\frac{1}{m}{\displaystyle {\int }_0^{t}h\left(t-t^{\prime }\right)\epsilon \left(t^{\prime }\right)d{t}^{\prime }}$ and $x\left(t\right)=x\left(0\right)+v\left(0\right)H\left(t\right)+\frac{1}{m}{\displaystyle {\int }_0^{t}H\left(t-t^{\prime }\right)\epsilon \left(t^{\prime }\right)d{t}^{\prime }}$. The Laplace transform of the velocity relaxation function $h\left(t\right)$ yields $\widehat{h}\left(s\right)={\left[s+{\widehat{M}}_1\left(s\right)\right]}^{-1}$, where ${\widehat{M}}_1\left(s\right)$ is the Laplace transform of the memory function given by ${\widehat{M}}_1\left(s\right)={\displaystyle {\int }_0^{\infty }{M}_1\left(t\right)\exp \left(-st\right)dt}$ and $H\left(t\right)={\displaystyle {\int }_0^{t}h\left(t^{\prime }\right)d{t}^{\prime }}$. The average position of the particle is $\left\{\langle x\left(t\right)\rangle \right\}=\left\{x\left(0\right)\right\}+\left\{v\left(0\right)\right\}H\left(t\right)$. Herein we indicate by $\{\cdots \}$ the average with respect to the initial values of the state variables and by $\langle \cdots \rangle$ the average over the noise $\epsilon \left(t\right)$. The mean squared displacement (MSD) is expressed in the general form,

$\left\{\langle x^2\left(t\right)\rangle \right\}=\left\{{\langle x\left(t\right)\rangle }^2\right\}+\left\{\langle \Delta x^2\left(t\right)\rangle \right\}=\left\{x^2\left(0\right)\right\}+2\left\{x\left(0\right)v\left(0\right)\right\}H\left(t\right)+\left\{v^2\left(0\right)\right\}{H}^2\left(t\right)-\frac{k_{B}T}{m}{H}^2\left(t\right)+\frac{2k_{B}T}{m}{\displaystyle {\int }_0^{t}H\left(t^{\prime }\right)d{t}^{\prime }}.(5)$

The sum of the first three terms represents the square of the average position, and the sum of the latter two terms is the position variance. Note that the position variance is independent of the initial preparation of the particle.

We have found that the time-dependent diffusion functions, calculated by taking the time-derivative of the position variance and the MSD, are different. If the particle is confined initially at the origin $x\left(0\right)=0$ and its velocity obeys the Maxwell equilibrium distribution with $\left\{v^2\left(0\right)\right\}=k_{B}T/m$ rather than rest, using Eq. 5 and $H\left(t\right)={\displaystyle {\int }_0^{t}h\left(t^{\prime }\right)d{t}^{\prime }}=\frac{k_{B}T}{m}{\displaystyle {\int }_0^t{\tilde{C}}_v\left(t^{\prime }\right)d{t}^{\prime }}$, the MSD is expressed as

$\left\{\langle x^2\left(t\right)\rangle \right\}=\frac{2k_{B}T}{m}{\displaystyle {\int }_0^{t}d{t}^{\prime }}{\displaystyle {\int }_0^{t^{\prime }}d\tau {\tilde{C}}_v\left(\tau \right)}.(6)$

Therefore, the diffusion function obtained by differentiating Eq. 6 yields $D\left(t\right)={\displaystyle {\int }_0^t{C}_v\left(\tau \right)d\tau }$ with $C_v\left(t\right)=\frac{k_{B}T}{m}{\tilde{C}}_v\left(t\right)$. This is specifically an expression of the time-dependent Kubo relation encountered in the literature [11]. From the time derivative of the variance of position, i.e., Eq. 5, we obtain a rigorous exact relation between the standard diffusion function and the two relaxation functions, i.e., $D\left(t\right)=\frac{1}{2}\frac{d}{dt}\langle \Delta x^2\left(t\right)\rangle =k_{B}T{m}^{-1}\left[1-h\left(t\right)\right]H\left(t\right)$ [38]. Indeed, $h\left(t\right)$ may be expressed as a normalized VACF, i.e., $h\left(t\right)=\langle v\left(t\right)v\left(0\right)\rangle /\left\{v^2\left(0\right)\right\}={\tilde{C}}_v\left(t\right)$. The VACF is calculated numerically from a homogeneous integro-differential equation, ${\dot{\tilde{C}}}_v\left(t\right)=-{\displaystyle {\int }_0^t{M}_1\left(t-t^{\prime }\right){\tilde{C}}_v\left(t^{\prime }\right)d{t}^{\prime }}$ with ${\tilde{C}}_v\left(0\right)=1$. Here, we report a generalized time-dependent Green-Kubo relation,

$D\left(t\right)=\frac{k_{B}T}{m}\left[1-{\tilde{C}}_v\left(t\right)\right]{\displaystyle {\int }_0^t{\tilde{C}}_v\left(t^{\prime }\right)d{t}^{\prime }}.(7)$

This expression is valid for anomalous diffusion and nonergodic processes as well as for arbitrary initial preparations. Equation 7 is referred to as the generalized time-dependent Kubo relation. In particular, under the condition $C_v\left(t\to \infty \right)=0$, $D\left(t\right)$ approaches a constant when the upper limit of the integral is set to infinity, and, under $\left\{v^2\left(0\right)\right\}=\frac{k_{B}T}{m}$, Eq. 7 reduces to the standard Kubo relation [28].

The standard Stokes-Einstein expression that has just been reviewed applies to steady motion only and should be regarded as a zero-frequency theory. It is not consistent with using a coefficient of friction derived assuming steady motion describing changes in velocity. For this reason, the generalization of the Stokes-Einstein formula for an arbitrary frequency is of interest. For a broad class of systems, relaxation into the stationary state is exponentially fast; however, this is not true for all physical systems. Some systems may possess a stationary process, but the relaxation toward this state may be slow, and the well-known Stokes-Einstein formula thus needs to be generalized more. For anomalous diffusion, with a stationary VACF, the limiting result of the ratio of the time-dependent diffusion function to the velocity relaxation time, we report a generalized Stokes-Einstein relation:

$\underset{t\to \infty }{\lim }\frac{D\left(t\right)}{{\tau }_v\left(t\right)}=\frac{k_{B}T}{m}\left(1-b\right).(8)$

Here ${\tau }_v\left(t\right)={\displaystyle {\int }_0^t{\tilde{C}}_v\left(t^{\prime }\right)d{t}^{\prime }}$ is called the non-Stokesian relaxation time, which may become zero or infinity, and $b={\tilde{C}}_v\left(t\to \infty \right)={\left(1+{\widehat{M}}_1^{\prime }\left(0\right)\right)}^{-1}$ represents the nonergodic strength of the first type [39, 40]; however, $b=0$ for ergodic processes.

In fact, Eq. 8 involves a spectral result [19], ${\lim }_{t\to \infty }\left[D\left(t\right){\displaystyle {\int }_0^t{M}_1\left(t^{\prime }\right)d{t}^{\prime }}\right]=\frac{k_{B}T}{m}$, which also differs from recent work on the generalized asymptotic Einstein relation [20]. The latter reported a scale-dependent asymptotical Einstein relation for anomalous diffusion, i.e., ${\lim }_{t\to \infty }\left[D\left(t\right){{{\displaystyle \int }}^{\text{}}}_0^t{M}_1\left(t^{\prime }\right)d{t}^{\prime }\right]=2C\left(0\right)/m^2\Gamma \left(\alpha \right)\Gamma \left(2-\alpha \right)$, where $C\left(0\right)$ is the noise correlation strength [20]. Fortunately, the present result [Eq. 8] seems universal as long as the integral over the VACF is used to replace that over the memory function.

2.3 Typical Long-Range Memory

We now consider a generic noise spectral density (NSD) generated by a model for non-Ohmic friction [21, 22], for which the memory function takes the form

$M_1\left(t\right)={\gamma }_{\delta }\frac{2}{\pi }{\displaystyle {\int }_0^{\infty }{\left(\frac{\omega }{\tilde{\omega }}\right)}^{\delta -1}f\left(\omega \right)\cos \left(\omega t\right)d\omega },(9)$

where $\tilde{\omega }$ denotes the reference frequency for friction ${\gamma }_{\delta }$ having the dimensions of viscosity for any δ and $f\left(\omega \right)$ the modulation function of the frequency. In addition, the constant ${\gamma }_{\delta }$ allows for GLE (4) to have the correct dimension as well as $f\left(\omega \right)$ is a frequency modulate function. When $0<\delta <2$, the diffusive exponent $\alpha =\delta$ in Eq. 1, one can safely set $f\left(\omega \right)=1$ [21]; nevertheless $\delta >2$, $\alpha =2$, a decay form for $f\left(\omega \right)$, must be addressed.

In Figure 1, we plot the time-dependent fractional diffusion function calculated numerically using Eq. 3 combined with Eqs 7,9. All values of quantities used here on in are stated in dimensionless form, (i.e. $k_{B}T=1$, $m=1$, ${\gamma }_{\delta }=1$, and $\tilde{\omega }=1$). The scale-dependent fractional derivative is sufficient to produce finite fractional coefficients of diffusion in the long-time limit as expected. Notably, an overshooting peak arises during intermediate time periods, implying a strongly temporal “diffusion rate”. For sub-diffusive situations, because of thermal fluctuations, the diffusion function starts from zero, increases with time, and finally decays to zero at late times. Hence, it remarkably ensures the existence of a temporal diffusive maximum.

FIGURE 1

FIGURE 1. Time-dependent fractional diffusion function calculated using Eq. 3 for various known values of the exponents δ. Here, $f\left(\omega \right)=\exp \left(-\omega /{\omega }_c\right)$ and ${\omega }_c=2.0$ are used.

3 Effective Friction Function

3.1 Self-Consistent Extraction

More importantly, we want to introduce the temporal effective friction function, which is extracted consistently from Eq. 7 by assuming

$D\left(t\right)=\frac{k_{B}T}{m{\gamma }_{eff}\left(t\right)}.(10)$

Starting from experimental sampling of the velocities of tagged particles with injection velocity $v\left(0\right)$, we express the two functions $h\left(t\right)$ and $H\left(t\right)$ in alternative forms,

$h\left(t\right)=\frac{\langle v\left(t\right)\rangle }{v\left(0\right)},H\left(t\right)=t\frac{1}{t}{\displaystyle {\int }_0^t\frac{\langle v\left(t^{\prime }\right)\rangle }{v\left(0\right)}d{t}^{\prime }=\frac{\overline{\langle v\left(t\right)\rangle }}{v\left(0\right)}t}.(11)$

An effective friction function that depends on both the physical features and the underling process is then defined,

${\gamma }_{\text{eff}}\left(t\right)=\left[\left(1-\frac{\langle v\left(t\right)\rangle }{v\left(0\right)}\right)\frac{\overline{\langle v\left(t\right)\rangle }}{v\left(0\right)}\right]t^{-1}.(12)$

The advantage of this approach is that the entire configurational details are reduced to the particle’s velocity, which is easily measured. Theoretically, it is easier to discuss a double average, one over time and the other over the ensemble of different trajectories.

For example, for the Ohmic friction $\left(\delta =1\right)$ with $f\left(\omega \right)={\omega }^2/\left({\omega }^2+{\omega }_c^2\right)$, the Ornstein-Uhlenbeck (OU) colored noise is reached as $M_1\left(t\right)={\gamma }_1{\omega }_c\exp \left(-{\omega }_{c}t\right)$ (the noise correlation time is ${\tau }_c={\omega }_c^{-1}$). Then the effective friction function can be obtained analytically,

${\gamma }_{eff}\left(t\right)={\left[1-A\exp \left(z_{1}t\right)-B\exp \left(z_{2}t\right)\right]}^{-1}\cdot {\left(\frac{A}{z_1}\left[\exp \left(z_{1}t\right)-1\right]+\frac{B}{z_2}\left[\exp \left(z_{2}t\right)-1\right]\right)}^{-1},(13)$

where $A=\left({\omega }_c+z_1\right)/\left({\omega }_c+2z_1\right)$, $B=\left({\omega }_c+z_2\right)/\left({\omega }_c+2z_2\right)$, $z_1=-\frac{1}{2}{\omega }_c+\frac{1}{2}{\omega }_c\sqrt{1-4{\gamma }_1/{\omega }_c}$, and $z_2=-\frac{1}{2}{\omega }_c+\frac{1}{2}{\omega }_c\sqrt{1-4{\gamma }_1/{\omega }_c}$. Hence, ${\gamma }_{\text{eff}}\left(t\to \infty \right)={\gamma }_1$. When ${\omega }_c\to \infty$, which results in Markovian Brownian motion, we have ${\gamma }_{\text{eff}}\left(t\right)={\gamma }_1{\left[1-\exp \left(-{\gamma }_{1}t\right)\right]}^{-2}$. In addition, ${\displaystyle {\int }_0^t{M}_1\left(t^{\prime }\right)d{t}^{\prime }}={\gamma }_1\left[1-\text{exp}\left(-{\omega }_{c}t\right)\right]$.

Figure 2 shows the time-dependent effective friction function for various δ. It starts from infinity because the system does not yet receive any dissipative energy from its environment at the initial time. This function approaches a constant value for normal diffusion, i.e., the low-frequency Markovian friction strength ${\widehat{M}}_1\left(0\right)$. With observations, a decrease/increase in the effective friction function corresponds to superdiffusion/subdiffusion. In contrast to the usual understanding, the effective friction function emphasizes the process dependence rather than the static result. From Eq. 13, the steady value of ${\gamma }_{\text{eff}}\left(t\right)$ increases with decreasing ${\omega }_c$. Indeed, friction does vanish, but there is still no thermal excitation when ${\omega }_c\to 0$. This implies that the effective friction function reflects its diffusive nature in that two effects are combined, the memory damping force and the random force, in generalized Brownian motion.

FIGURE 2

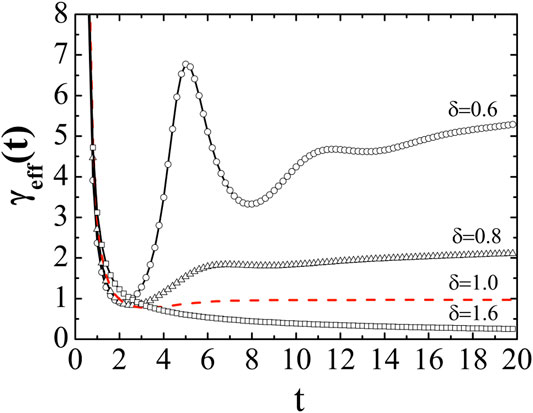
FIGURE 2. Effective friction function calculated from the non-Ohmic friction model for various δ. Here $f\left(\omega \right)=\exp \left(-\omega /{\omega }_c\right)$ with ${\omega }_c=2.0$.

4 SELF-OSCILLATION Diffusion

4.1 Determination of Diffusive Exponent

Lastly, the thorny problem is the measurement of the power-law exponent α from observed data. Of note is the fact that if $L_2\left(t\right)$ in Eq. 1 is a non-stationary function of time, the local differential method should be invalid for this situation. Although the leading term in the variance of the position may exceed the $L_2\left(t\right)$ oscillation term, as long as the time derivative of this variance is performed, the oscillating behavior is revealed. Previously, the approach $\alpha ={\lim }_{t\to \infty }\left(t\frac{d\ln \langle \Delta x^2\left(t\right)\rangle }{dt}\right)$ was used to evaluate the power exponent [41]. However, what is not valid for the situation of diffusion accompanied by oscillation when the spectral density of driving noise is the cut at finite or infinite frequency. Here, we propose a whole approach using the slope of the logarithm of the coordinate at large times,

$\alpha =\frac{\ln \langle \Delta x^2\left(t_2\right)\rangle -\ln \langle \Delta x^2\left(t_1\right)\rangle }{\ln t_2-\ln t_1},(14)$

where $t_1$ and $t_2$ are two observation times at which the system has evolved into the asymptotic state.

4.2 The Effect of High-Frequency Cutoff

In contrast to usual understanding, the notion of the effective friction function proposed here is dependent on underlying processes rather than the static result. It is concluded from Figure 2, (e.g., the comparison between solid and dashed lines when $\delta =1$) and Eq. 13 that the steady value of ${\gamma }_{\text{eff}}\left(t\right)$ increases with a decrease of ${\omega }_c$. In fact, the friction does vanish, but there is yet no thermal excitation when ${\omega }_c\to 0$. This implies that the effective friction function reflects a diffusive feature, which combines two effects of the memory damping force and random force in generalized Brownian motion.

Nevertheless, the first choice in Eq. 9 cannot be adopted when $\delta >2$, which results in that the noise correlation function corresponding to the memory function does not approach vanishing at long times. This violates Kubo’s requirements of noisy dynamics [28]. However, the cutoff function $f\left(\omega \right)$ in Eq. 9 should be applied safely. It is known that the treatment of high-frequency cutoff has been applied widely as well as $\alpha =\delta$ when $0<\delta <2$ and $\alpha =2$ when $\delta >2$ [21]. However, little attention was given to the influence of this cutoff on dynamics.

The Laplace transform of the memory function for the non-Ohmic friction model combining with $f\left(\omega \right)=\Theta \left({\omega }_c-\omega \right)$, where $\Theta \left({\omega }_c-\omega \right)$ is the Heaviside function, equaling unity when $\omega \le {\omega }_c$ and vanishing when $\omega >{\omega }_c$, is given by

${\widehat{M}}_1\left(s\right)=\frac{{\gamma }_{\delta }{\omega }_c^{\delta }}{\pi \text{Γ}\left(1+\delta /2\right)}{}_2{F}_1\left(1,\frac{\delta }{2},1+\frac{\delta }{2};-\frac{{\omega }_c^2}{s^2}\right)s^{-1},(15)$

where $2F_1$ denotes the hypergometric function. In particular, when $\delta =1$, $2_{F}1\left(1,1/2,3/2,-x^2\right)=\sqrt{\pi }\arctan \left(x\right)/x$. Assuming that $s=s_1+i{s}_2$,

$\arctan \left(\frac{{\omega }_c}{s}\right)=\frac{1}{2i}\left[\ln \frac{\sqrt{{\left(s_1^2+s_2^2-{\omega }_c^2\right)}^2+4{\left(s_1{\omega }_c\right)}^2}}{s_1^2+{\left(s_2-{\omega }_c\right)}^2}+i\left(\theta +2\pi n\right)\right]\left(n=0,\pm 1,\pm 2,\dots \right),(16)$

where $\theta =\arctan \left[\left(2s_1{\omega }_c\right)/\left(s_1^2+s_2^2-{\omega }_c^2\right)\right]$. Although ${\widehat{M}}_1\left(s\right)$ is a multi-value function on the complex plane, where exists at least a fair of pure complex roots (i.e., $s=\pm i{s}_2$) for the characteristic equation: $s+A\arctan \left({\omega }_c/s\right)=0$, which is given by $s_2=\frac{A}{2}\ln \left[\left(s_2+{\omega }_c\right)/\left(s_2-{\omega }_c\right)\right]$ with $s_2>{\omega }_c$. This results in a time-oscillation part appear in the VACF and thus the ergodicity is broken.

According to the Khinchin theorem, if ${\text{lim}}_{t\to \infty }{C}_v\left(t\right)\ne 0$, ergodicity is broken [42, 43]. Two situations arise depending on whether $C_v\left(t\to \infty \right)={\text{lim}}_{s\to 0}\left[s\widehat{h}\left(s\right)\right]=b\left\{v^2\left(0\right)\right\}\ne 0$ or whether it does not exist. We establish here a universal condition for ergodicity breaking that there exists a zero root or at least a pair of real complex roots for the characteristic equation: $s+{\widehat{M}}_1\left(s\right)=0$, namely,

$s+\frac{2}{\pi }{\displaystyle {\int }_0^{\infty }\frac{\rho \left(\omega \right)s}{s^2+{\omega }^2}d\omega =0},(17)$

and the residues do not equal zero at these poles. The second term on the l.h.s of Eq. 17 is the Laplace transform of the memory function. We report also an alternative NSD, which can induce nonergodicity of three types, i.e.,

$\rho \left(\omega \right)={\rho }_0\left(\omega \right)\Theta \left(\omega -{\omega }_L\right)\Theta \left({\omega }_1-\omega \right)\Theta \left(\omega -{\omega }_2\right)\Theta \left({\omega }_H-\omega \right),(18)$

where ${\rho }_0\left(\omega \right)$ is a function of the frequency, $0\le {\omega }_L<{\omega }_1<{\omega }_2<{\omega }_H<\infty$. Eq. 18 can be used to physically describe the generalized Debye model [16], the long-wavelength limit of acoustic phonon [44], the Bethe lattice [45], and the localized mode [46].

Applying the residue theorem [47, 48], we obtain a general result for the velocity relaxation function,

$h\left(t\right)=b+A_1\cos \left({\lambda }_{1}t\right)+A_2\cos \left({\lambda }_{2}t\right)+\frac{1}{2\pi i}{\displaystyle {\int }_0^{\infty }\left(\frac{\exp \left(-rt\right)}{-r+{\widehat{M}}_1\left(r{e}^{-\pi i}\right)}-\frac{\exp \left(-rt\right)}{-r+{\widehat{M}}_1\left(r{e}^{\pi i}\right)}\right)dr}+{\displaystyle \sum _{n=1}^{2N}res\left[{\widehat{M}}_1\left(s_n\right)\right]\exp \left(s_{n}t\right)},(19)$

where

$b={\left(1+\frac{2}{\pi }{\displaystyle {\int }_{{\omega }_L}^{\infty }\frac{{\rho }_0\left(\omega \right)}{{\omega }^2}d\omega }\right)}^{-1}.(20)$

The quantity is equal to a constant less than unity as long as ${\rho }_0\left(\omega \right)\sim {\omega }^{\delta }$$\left(\delta >1\right)$ at low frequencies when ${\omega }_L=0$ and ${\rho }_0\left(\omega \right)\sim {\omega }^{\delta }$$\left(\delta <1\right)$ at high frequencies if ${\omega }_L\ne 0$. The existence of time oscillations in the VACF is because $s=\pm i{\lambda }_1$ and $s=\pm i{\lambda }_2$ may be numerical solutions of Eq. 17, which requires ${\omega }_1<{\lambda }_1<{\omega }_2$ and ${\omega }_H<{\lambda }_2$; also, $A_1$ and $A_2$ are each twice the residue at its respective pole. The last two terms in Eq. 19 vanish in the long-time limit because Re $s_n<0$ for any n.

Clearly, the upper-limit of the summation in Eq. 19 may be infinity because ${\widehat{M}}_1\left(s\right)$ calculated using Eq. 18 is a multi-valued function on the complex plane. Let us perform an integration via parts in Eq. 17 to render explicit the dependence of ${\widehat{M}}_1\left(s\right)$ on s,

${\widehat{M}}_1\left(s\right)=\frac{2}{\pi }\left[{\rho }_0\left({\omega }_H\right)\arctan \left({\omega }_H/s\right)-{\displaystyle {\int }_0^{{\omega }_H}\arctan \left(\omega /s\right){{\rho }^{\prime }}_0\left(\omega \right)d\omega }\right].(21)$

For a complex variable s, we have $\arctan \left(\omega /s\right)={\left(2i\right)}^{-1}\ln \left|\left(s+i\omega \right)/\left(s-i\omega \right)\right|+\frac{1}{2}\left(\theta +2n\pi \right)$ with $n=0,\pm 1,\pm 2,\dots$, where θ is the angle of the complex variable $\left(s+i\omega \right)/\left(s-i\omega \right)$ obtained by expressing it as an exponential function. Further, it is noticed that both the well-known Mittag-Leffler function [22] and the series solution [43, 44] cannot be used to demonstrate the self-oscillating result at large times but Eq. 19 is reasonable.

Figure 3 shows the resulting VACF for various δ and two different modulation functions of the frequency. Evidently, there exist three types of nonergodicity where the VACF 1) approaches a positive constant, 2) oscillates with time around a plateau value, or 3) oscillates with time around zero; the simple conditions satisfied by the NSD are low-hindering, band-passing, and high-hindering or band-hindering. This forces the ensemble to become unstable, although the GLE used is initially stationary. The oscillation implies that the particle tends to reverse its direction of motion frequently relative to its former step. This classification of the nonergodic behavior may be regarded as a probe of a more precise estimation of the low and high frequencies distribution for thermal colored noise. In addition, from the microscopic Hamiltonian viewpoint, ergodicity breakage is caused by a localized mode with an isolated frequency from the continued phonon spectrum [46, 49].

FIGURE 3

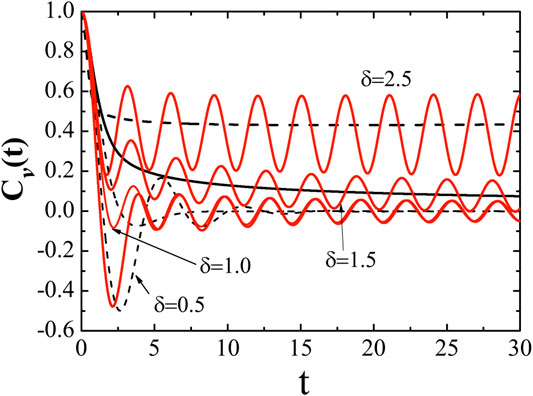
FIGURE 3. VACF for various exponents δ using the non-Ohmic friction model with $f\left(\omega \right)=\exp \left(-\omega /{\omega }_c\right)$ (dashed lines) and $f\left(\omega \right)=\Theta \left({\omega }_c-\omega \right)$ (solid lines). The parameter settings used are ${\gamma }_{\delta }=1.0$ and ${\omega }_c=2.0$.

In Figure 4, we plot the time-dependent diffusion function for various situations and show the diffusion function oscillating with time. Because the diffusion function produced carries out a time derivative over the MSD, the whole approach [Eq. 14] rather than a local differential method must be used to determine the power-law exponent of diffusion. Many models may induce such a phenomenon, and several famous examples have been mentioned before. A somewhat surprising result for us is that the system associated with the Debye frequency-cutoff does not yield ergodic behavior.

FIGURE 4

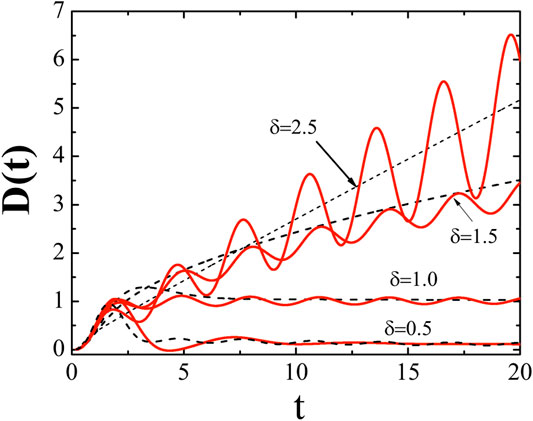
FIGURE 4. Diffusion function for various exponents δ using the non-Ohmic friction model. The corresponding situations and parameter settings used are the same as in Figure 3.

5 Summary

This work aims at furnishing a connection between velocity autocorrelation function (VACF) and frictional kernel in the generalized Langevin equation (GLE) framework for the diffusion dynamics. On the one hand, the VACF is a quantity that can be obtained from experimental or numerical data; on the other hand, the friction kernel incorporates the noise correlation properties. However, this relation is hard to achieve by analytical means, and we thus introduce an effective friction function that depends solely on the VACF and is supposed to inform on the retarded memory effects on the dynamics. The notion of effective friction function has been observed as an echo of the non-Markovian Brownian motion, which is associated with the diffusion function and is measured through a tagged particle’s average velocity. This provides interesting information regarding the evolution of kinetics. We have obtained alternative time-dependent Green-Kubo and generalized Stokes-Einstein relations to universal situations connected with anomalous diffusion and nonergodic processes. The effect of finite or high-frequency cutoff as a facile method on the dynamics is numerically investigated. A self-oscillation phenomenon emerges as a manifestation of ergodicity breakdown. In particular, several inconsistent conclusions in the literature, e.g., the analysis requirement of susceptibility, the friction feature extracted by the generalized Fokker-Planck equation, and the power-law exponent obtained from data, have been clarified. We are also confident that the present results will serviceably impact complex dissipative systems.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China under Grant No. 11735005.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Appendix

The Friction Function in GFPE

An important application concerns non-Markovian Brownian motion within fluctuating hydrodynamics with a non-Stokesian drag having a power-law VACF, i.e., $C_v\left(t\right)\sim t^{-3/2}$ at late times [50], which emerges as subdiffusion. The asymptotical behavior of the diffusion function is $D\left(t\right)\sim t^{-1/2}$ and then ${\lim }_{t\to \infty }\left[D\left(t\right)/{\tau }_v\left(t\right)\right]=k_{B}T/m$. Moreover, the effective friction function proposed here varies with time ${\gamma }_{\text{eff}}\left(t\right)\sim t^{1/2}$. Hence our result demonstrates reliably the characteristic feature of generalized Stokesian dissipation. Unfortunately, the friction function defined in the generalized Fokker-Planck equation (GFPE) description [51] exhibits an identical form of decay in the inverse ratio of time if the VACF has a power-law form at late times. Starting from the exact velocity probability density function of a force-free driven by a Gaussian but non-Markovian noise, Adelman [51], Fox [50], Volkov and Pokrovsky [52] obtained the GFPE as

$\frac{\partial }{\partial t}P\left(v,v_0;t\right)=\tilde{\gamma }\left(t\right)\frac{\partial }{\partial v}\left[vP\left(v,v_0;t\right)\right]+\frac{k_{B}T}{m}\tilde{\gamma }\left(t\right)\frac{{\partial }^2}{\partial v^2}P\left(v,v_0;t\right),$(A.1)

where the friction function was defined by $\tilde{\gamma }\left(t\right)=-{\dot{C}}_v\left(t\right)/C_v\left(t\right)$.

It is found to be valid only when the memory kernel is a delta function. Moreover, if $C_v\left(t\right)\sim t^{\alpha -2}$, the GFPE gives $\tilde{\gamma }\left(t\right)\sim t^{-1}$ at large times. This contradicts the subdiffusion criterion for $0<\alpha <1$. Within the framework of GLE associated with the FDT, however, we observe from Figure 2 that, at large times, the friction function increases with the increase of time for the subdiffusion situation. Hence, we deem that the friction function $\tilde{\gamma }\left(t\right)$ appearing in the GFPE [A.1] might not provide a self-consistent physical feature.

In addition, Adelman [51] ignored the inertia and then defined the diffusion function as $D\left(t\right)=\left(k_{B}T/m\right)L^{-1}{\left[s{\widehat{M}}_1\left(s\right)\right]}^{-1}$ where $L^{-1}$ denotes the inverse-Laplace-transform operation. Correspondingly, our result [Eq. 7] can be rewritten as $D\left(t\right)=\left(k_{B}T/m\right)\left[1-L^{-1}{\left(s+{\widehat{M}}_1\left(s\right)\right)}^{-1}\right]L^{-1}{\left(s^2+s{\widehat{M}}_1\left(s\right)\right)}^{-1}$. It is concluded that the former is expressed as a static result and the latter is dependent of an underlying dissipative process.

References

1. Einstein A. Investigations on the theory of the brownian movement New York, NY, United States: Dover (1956).

2. Hänggi P., Marchesoni F. Introduction: 100 years of brownian motion. Chaos (2005) 15:26101. doi:10.1063/1.1895505

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Barkai E., Garini Y., Metzler R. Strange kinetics of single molecules in living cells. Phys Today (2012) 65(8):29. doi:10.1063/pt.3.1677

CrossRef Full Text | Google Scholar

4. He Y., Burov S., Metzler R., Barkai E. Random time-scale invariant diffusion and transport coefficients. Phys Rev Lett (2008) 101:058101. doi:10.1103/PhysRevLett.101.058101

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Lubelski A., Sokolov I. M., Klafter J. Nonergodicity mimics inhomogeneity in single particle tracking. Phys Rev Lett (2008) 100:250602. doi:10.1103/PhysRevLett.100.250602

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Burov S., Metzler R., Barkai E. Aging and nonergodicity beyond the Khinchin theorem. Proc Natl Acad Sci United States (2010) 107:13228. doi:10.1073/pnas.1003693107

CrossRef Full Text | Google Scholar

7. Meyer P., Barkai E., Kantz H. Scale-invariant Green-Kubo relation for time-averaged diffusivity. Phys. Rev. E. E (2017) 96:062122. doi:10.1103/PhysRevE.96.062122

CrossRef Full Text | Google Scholar

8. Metzler R., Klafter J. The random walk's guide to anomalous diffusion: a fractional dynamics approach. Phys. Rep (2000) 339:1–17. doi:10.1016/s0370-1573(00)00070-3

CrossRef Full Text | Google Scholar

9. Thiel F., Flegel F., Sokolov I. M. Disentangling sources of anomalous diffusion. Phys. Rev. Lett (2013) 111:010601. doi:10.1103/PhysRevLett.111.010601

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Flekkøy E. G. Minimal model for anomalous diffusion. Phys. Rev. E. E (2017) 95:012139. doi:10.1103/PhysRevE.95.012139

CrossRef Full Text | Google Scholar

11. Sokolov I. M. Models of anomalous diffusion in crowded environments. Soft Matter (2012) 8:9043. doi:10.1039/c2sm25701g

CrossRef Full Text | Google Scholar

12. Boon J. P., Yip S., Hansen J. P. Moclecular hydrodynamics 1986 In: McDonald IR. Theory of simple liquids New York, NY, United States: McGraw-HillAcademic (1980)

13. Dechant A., Lutz E., Kessler D. A., Barkai E. Scaling Green-Kubo relation and application to three aging systems. Phys. Rev. E. X (2014) 4:011022. doi:10.1103/physrevx.4.011022

CrossRef Full Text | Google Scholar

14. Mori H. A quantum-statistical theory of transport processes. J. Phys. Soc. Jpn (1956) 11:1029. doi:10.1143/jpsj.11.1029

CrossRef Full Text | Google Scholar

15. Mori H. Transport, collective motion, and Brownian motionA continued-fraction representation of the time-correlation function. Prog. Theor. Phys (1965) 34:399–416. doi:10.1143/ptp.34.399

CrossRef Full Text | Google Scholar

16. Zwanzig R. Nonlinear generalized Langevin equations. J. Stat. Phys (1973) 9:215. doi:10.1007/bf01008729

CrossRef Full Text | Google Scholar

17. Sagnlla D. E., Straub J. E., Thirumalai D. Time scales and pathways for kinetic energy relaxation in solvated proteins: application to carbonmonoxy myoglobin. J. Chem. Phys (2000) 113:7702. doi:10.1063/1.1313554

CrossRef Full Text | Google Scholar

18. Mokshin A. V., Yulmetyev R. M., Hänggi P. Simple measure of memory for dynamical processes described by a generalized Langevin equation. Phys. Rev. Lett (2005) 95:200601. doi:10.1103/PhysRevLett.95.200601

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sanghi T., Bhadauria R., Aluru N. R. Memory effects in nanoparticle dynamics and transport. J. Chem. Phys (2016) 145:134108. doi:10.1063/1.4964287

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Shin H. K., Choi B., Talkner P., Lee E. K. Normal versus anomalous self-diffusion in two-dimensional fluids: memory function approach and generalized asymptotic Einstein relation. J. Chem. Phys (2014) 141:214112. doi:10.1063/1.4902409

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Weiss U. Quantum dissipative systems 3rd ed. Singapore: World Scientific (2008)

22. Pottier N. Aging properties of an anomalously diffusion particule. Physica. A (2004) 291:371–82. doi:10.1016/S0378-4371(02)01361-4

CrossRef Full Text | Google Scholar

23. Barkai E., Silbey R. J. Fractional kramers equation†. J. Phys. Chem. B (2000) 104:3866. doi:10.1021/jp993491m

CrossRef Full Text | Google Scholar

24. Kneller G. R. Communication: a scaling approach to anomalous diffusion. J. Chem. Phys (2014) 141:041105. doi:10.1063/1.4891357

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Stachura S., Kneller G. R. Communication: probing anomalous diffusion in frequency space. J. Chem. Phys (2015) 143:191103. doi:10.1063/1.4936129

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Hänggi P., Grabert H., Ingold G. L., Weiss U. Quantum theory of activated events in presence of long-time memory. Phys. Rev. Lett (1985) 55:761. doi:10.1103/PhysRevLett.55.761

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Srokowski S. Nonstationarity induced by long-time noise correlations in the Langevin equation. Phys. Rev. Lett (2000) 85:2232. doi:10.1103/PhysRevLett.85.2232

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Kubo R., Toda M., Hashitsume N. Statistical Physics II, nonequilibrium statistical mechanics 2nd ed. Berlin, Germany: Springer-Verlag (1991)

29. Marchesoni F., Taloni A. Subdiffusion and long-time anticorrelations in a stochastic single file. Phys. Rev. Lett (2006) 97:106101. doi:10.1103/PhysRevLett.97.106101

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Bao J. D., Zhuo Y. Z. Ballistic diffusion induced by a thermal broadband noise. Phys. Rev. Lett (2003) 91:138104. doi:10.1103/PhysRevLett.91.138104

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Pereira A. P. P., Fernandes J. P., Atman A. P. F., Acebal J. L. Parameter calibration between models and simulations: connecting linear and non-linear descriptions of anomalous diffusion. Phys Stat Mech Appl (2018) 509:369. doi:10.1016/j.physa.2018.06.025

CrossRef Full Text | Google Scholar

32. Ford G. W., Lewis J. T., O’Connell R. F. Quantum Langevin equation. Phys. Rev. A. Gen. Phys (1988) 37:4419. doi:10.1103/physreva.37.4419

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Bao J. D. Generalization of the Kubo relation for confined motion and ergodicity breakdown. Phys. Rev. E. E (2020) 101:062131. doi:10.1103/PhysRevE.101.062131

CrossRef Full Text | Google Scholar

34. Ferrari L. Test particles in a gas: Markovian and non-Markovian Langevin dynamics. Chem. Phys (2019) 523:42. doi:10.1016/j.chemphys.2019.03.011

CrossRef Full Text | Google Scholar

35. Mazo R. M. In: L. Garrido, P. Seglar, and P. J. Shepherd, editors. Stochastic processes in nonequilibrium systems New York, NY, United States: Springrt-Verlag (1965)

36. Porr J. M., Wang K. G., Masoliver J. Generalized Langevin equations: anomalous diffusion and probability distributions. Phys Rev E: Stat Phys, Plasmas, Fluids, Relat Interdiscip Top (1996) 53:5872. doi:10.1103/physreve.53.5872

CrossRef Full Text | Google Scholar

37. Taloni A., Lomholt M. A. Langevin formulation for single-file diffusion. Phys. Rev. E. Stat. Nonlin Soft Matter Phys (2008) 78:051116. doi:10.1103/PhysRevE.78.051116

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Bao J.-D. Non-Markovian two-time correlation dynamics and nonergodicity. J. Stat. Phys (2017) 168:561. doi:10.1007/s10955-017-1815-x

CrossRef Full Text | Google Scholar

39. Bao J. D., Hänggi P., Zhuo Y. Z. Non-Markovian Brownian dynamics and nonergodicity. Phys. Rev. E. Stat. Nonlin Soft Matter Phys (2005) 72:061107. doi:10.1103/PhysRevE.72.061107

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bao J. D., Zhuo Y. Z., Oliveira F. A., Hänggi P. Intermediate dynamics between Newton and Langevin. Phys. Rev. E. Stat. Nonlin Soft Matter Phys (2006) 74:061111. doi:10.1103/PhysRevE.74.061111

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Spiechowicz J., Hänggi P., Łuczka J. Coexistence of absolute negative mobility and anomalous diffusion. New J. Phys (2019) 21:083029. doi:10.1088/1367-2630/ab3764

CrossRef Full Text | Google Scholar

42. Lee M. H. Why irreversibility is not a sufficient condition for ergodicity. Phys. Rev. Lett (2007) 98:190601. doi:10.1103/PhysRevLett.98.190601

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Lapas L. C., Morgado R., Vainstein M. H., Rubí J. M., Oliveira F. A. Khinchin theorem and anomalous diffusion. Phys. Rev. Lett (2008) 101:230602. doi:10.1103/PhysRevLett.101.230602

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Oliveira F. A., Ferreira R. M. S., Lapas L. C., Vainstein M. H. Anomalous diffusion: a basic mechanism for the evolution of inhomogeneous systems. Front. Physiol (2019) 7:18. doi:10.3389/fphy.2019.00018

CrossRef Full Text | Google Scholar

45. Kim J., Sawada I. Dynamics of a harmonic oscillator on the Bethe lattice. Phys. Rev. E. E (2000) 61:R2172. doi:10.1103/physreve.61.r2172

CrossRef Full Text | Google Scholar

46. Ishikawa F., Todo S. Localized mode and nonergodicity of a harmonic oscillator chain. Phys. Rev. E. E (2018) 98:062140. doi:10.1103/physreve.98.062140

CrossRef Full Text | Google Scholar

47. Muralidhar R., Jacobs D. J., Ramkrishna D., Nakanishi H. Diffusion on two-dimensional percolation clusters: influence of cluster anisotropy. Phys. Rev. A (1991) 43:6503. doi:10.1103/physreva.43.6503

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Bao J. D. Generalized Einstein relations and conditions for anomalous relaxation. Phys. Rev. E. E (2019) 100:052149. doi:10.1103/PhysRevE.100.052149

CrossRef Full Text | Google Scholar

49. Qiu Q., Shi X. Y., Bao J. D. Mixed nonergodicity of a forced system and its non-stationary strength. Europhys. Lett (2019) 128:2005. doi:10.1209/0295-5075/128/20005

CrossRef Full Text | Google Scholar

50. Fox R. F. The generalized Langevin equation with Gaussian fluctuations. J. Math Phys (1977) 18:2331. doi:10.1063/1.523242

CrossRef Full Text | Google Scholar

51. Adelman S. A. Fokker-Planck equations for simple non‐Markovian systems. J. Chem. Phys (1976) 64:124. doi:10.1063/1.431961

CrossRef Full Text | Google Scholar

52. Volkov V. S., Pokrovsky V. N. Generalized Fokker-Planck equation for non‐Markovian processes. J. Math Phys (1983) 24:267. doi:10.1063/1.525701

CrossRef Full Text | Google Scholar