Monte Carlo Comparison of Proton and Helium-ion Minibeam Generation Techniques

Proton minibeam radiation therapy (pMBRT) is a novel therapeutic strategy that combines the normal tissue sparing of submillimetric, spatially fractionated beams with the improved dose deposition of protons. In contrast to conventional approaches which work with comparatively large beam diameters (5 mm to several centimetres) producing laterally homogeneous fields, pMBRT uses submillimetric minibeams to create a distinct spatial modulation of the dose featuring alternating regions of high dose (peaks) and low dose (valleys). This spatial fractionation can increase the tolerance of normal tissue and may allow a safe dose escalation in the tumour. Important quantities in this context are the valley dose as well as the peak-to-valley dose ratio (PVDR). Creating submillimetric proton beams for clinical applications is a challenging task that until now has been realized with mechanical collimators (metal blocks with thin slits or holes). However, this method is inherently inefficient, inflexible and creates undesirable secondary neutrons. We therefore recently proposed a method for obtaining clinical minibeams using only magnetic focusing. In this study, we performed Monte Carlo simulations in order to compare minibeams generated using the new method of magnetic focusing with two techniques involving mechanical collimators (collimator and broad beam irradiation, collimator and pencil beam scanning). The dose deposition in water was simulated and dosimetric aspects [beam broadening, depth-dose profiles, PVDR and Bragg-peak-to-entrance dose ratio (BEDR)] as well as irradiation efficiencies were evaluated. Apart from protons, we also considered helium ions which, due to their reduced lateral scattering and sharper Bragg peak, may present a promising alternative for minibeam radiation therapy. Magnetically focused minibeams exhibited a 20–60 times higher PVDR than mechanically collimated minibeams and yielded an increase in irradiation efficiency of up to two orders of magnitude. Compared to proton minibeams, helium ion minibeams were found to broaden at a slower rate and yield an even higher PVDR (at the same minibeam spacing) as well as a more favourable BEDR. Moreover, the simulations showed that methods developed for proton minibeams are suitable for the generation of helium ion minibeams.

1 Introduction

Technological advances in radiation therapy have led to a notable improvement of dose conformity in the tumour as well as a reduction of the dose given to organs-at-risk [1]. Nonetheless, the tolerance dose of normal tissue continues to be an important limitation for the treatment of some radioresistant tumours, such as brain tumours, or certain paediatric cancers.

Spatial modification of the dose distribution, as in spatially fractionated radiation therapy (SFRT), has shown great potential in this context [2–7]. In SFRT, the dose profiles are a succession of areas of high dose (peaks) and areas of low dose (valleys). The ratio between the peak and valley doses (peak-to-valley dose ratio, PVDR) is believed to be a biologically relevant parameter: high PVDR with low valleys favours normal tissue sparing [8]. While the exact radiobiological effects underlying SFRT are not yet completely known, possible actors promoting normal tissue sparing might include dose-volume effects [9, 10], cell signalling effects [11] and the so called microscopic prompt tissue-repair effect [7].

While SFRT has been mainly explored with X-rays [12], the use of protons can offer several advantages [13, 14]. Proton beams can stop in the patient and exhibit a depth-dose distribution characterized by a localized maximum (Bragg peak) beyond which only a negligible dose is deposited. This helps to improve the dose conformity and increase tissue sparing in particular in healthy tissue behind the tumour which can further reduce secondary effects. In addition, the gradual beam broadening caused by multiple Coulomb scattering of protons allows to obtain a homogeneous dose distribution in the tumour with only one array of proton minibeams [13, 14]. In contrast to this, SFRT with X-rays requires a superposition of several arrays to yield a (quasi-)homogeneous dose distribution in the target which leads to a more complex and error-prone irradiation geometry. Along these lines, proton minibeam radiation therapy (pMBRT) has already shown a remarkable reduction of neurotoxicity [15] as well as an important widening of the therapeutic window for the treatment of high-grade gliomas in small animal experiments [16, 17].

Next to protons, helium ions might also present a good candidate for MBRT [18]. Compared to protons, they experience reduced multiple Coulomb scattering which could lead to further improvements of the dose distributions and a higher PVDR. Moreover, the cross-section for nuclear fragmentation of helium ions is lower than that of heavier ions such that issues related to fragmentation tails beyond the Bragg peak can be avoided [19–22].

Recently, pMBRT was implemented at the Orsay Proton Therapy Centre (ICPO) using a multislit collimator attached at the end of the nozzle. This method has been evaluated both in passive scattering [23, 24] and pencil beam scanning mode [25]. While such a mechanical collimation presents a straightforward way to implement pMBRT at an existing facility, it may come at the cost of a reduced dose rate and overall efficiency. Furthermore, the collimator becomes an additional source of secondary neutrons which, although contributing less than 1% to the patient dose [24], are generally undesirable. Lastly, this technique is rather inflexible as it may be necessary to fabricate a new collimator for different patients or patient groups.

As an approach to overcome these limitations, we have recently considered pMBRT with magnetically focused and scanned minibeams [26]. While this method is conceptually very similar to established pencil beam scanning (PBS) techniques, a crucial difference lies in the beam sizes used in the two cases: Beams used for PBS typically have a diameter of 1–2 cm (full width at half maximum at the isocentre) [27, 28] whereas minibeams are preferably no wider than about 1 mm to optimally exploit tissue sparing effects. We recently proposed a new nozzle design capable of generating such minibeams through magnetic focusing only [26].

The goal of this study was to perform a thorough comparison of the three minibeam generation techniques (collimator and broad beam, collimator and PBS, magnetic focusing) and to assess the possible advantages and shortcomings of each method in terms of dose distributions, PVDR and efficiency. The study was realized as Monte Carlo simulations using the toolkit TOPAS and proton as well as helium ion minibeams were considered.

2 Materials and Methods

Monte Carlo simulations were conducted to evaluate three different techniques for generating planar minibeams:

• Collimator and broad beam (C+BB),

• Collimator and magnetically scanned pencil beam (C+PBS),

• Magnetically focused and scanned minibeam (MF).

The three techniques were compared with respect to the dose distribution in a water phantom and the irradiation efficiency (average dose deposited per primary particle). Each technique was evaluated both with protons and ⁴He ions and for different, clinically relevant ranges. The considered ranges were approximately 7.7 cm (protons 100 MeV, helium ions 400 MeV), 11.1 cm (protons 123 MeV, helium ions 492 MeV) and 15.8 cm (protons 150 MeV, helium ions 600 MeV).

2.1 Monte Carlo Simulation Details

The simulations were performed with the Geant4-based toolkit TOPAS¹ version 3.2. p2 [29]. The physics list was built using the Geant4_Modular option with the recommended modules for proton therapy (g4em-standard_opt3, g4h-phy_QGSP_BIC_HP, g4decay, g4ion-binarycascade, g4h-elastic_HP, g4stopping and g4radioactivedecay) [30–33] and the range cut was 10 µm in all volumes and for all particles. While the simulated beam-shaping components were different for each minibeam generation technique (see below), the irradiation target was always a 4 × 4 × 20 cm³ water phantom.

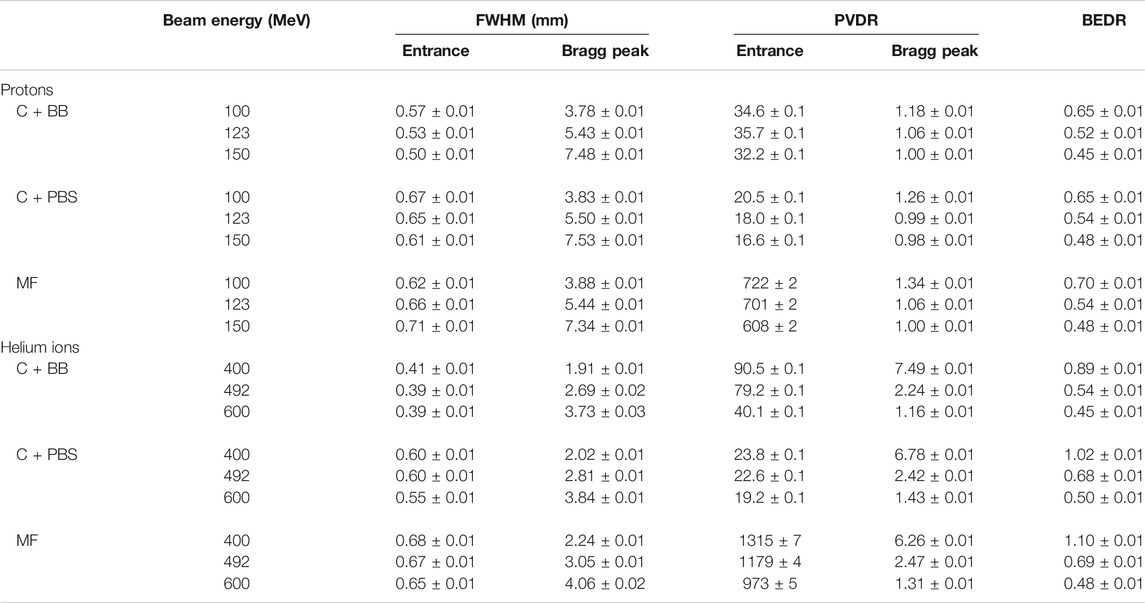
An identical minibeam pattern was simulated in all cases, consisting of five vertical planar minibeams spaced out horizontally at a centre-to-centre distance of 4 mm. This corresponds to an irradiation configuration that was frequently used in our previous preclinical experiments [15, 16, 25, 34]. Figure 1 shows an example of a dose distribution produced with this pattern. The horizontal full width at half maximum (FWHM) of the minibeams at the phantom entrance was between 0.39 and 0.71 mm (see Table 1) and the total area covered by the minibeams was roughly 2 × 2 cm². The minibeam geometry and pattern were therefore similar to those used in previous pMBRT studies [13, 15, 16, 18, 25, 34].

FIGURE 1

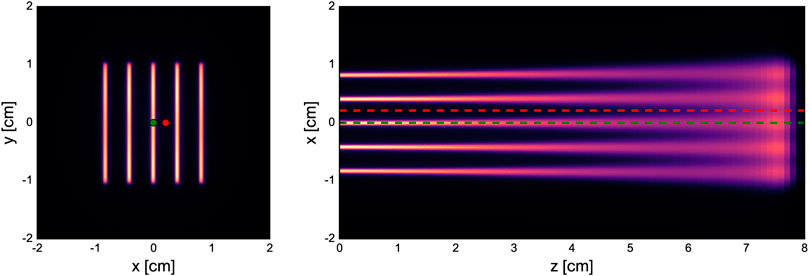
FIGURE 1. Dose distribution in the water phantom for 100-MeV minibeams obtained with collimator and PBS (C+PBS). Left: lateral cross section at the phantom entrance. Right: longitudinal cross section at y = 0 cm. The green and red dots/dashed lines indicate considered peak and valley regions, respectively.

TABLE 1

TABLE 1. FWHM and PVDR at phantom entrance and Bragg peak depth and BEDR of all considered cases.

Details of the different minibeam generation techniques are given in the following subsections. Schematics of the simulated geometries are shown in Figure 2 and the beam source parameters are compiled in Table 2.

FIGURE 2

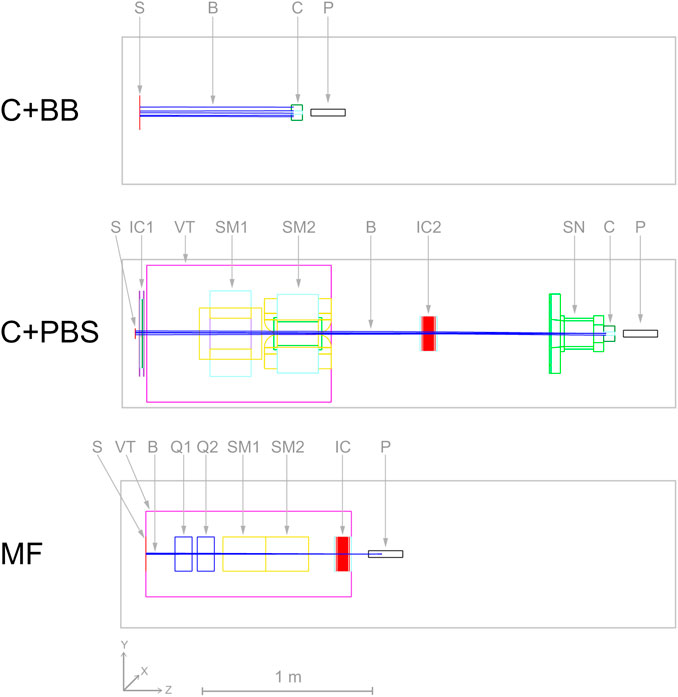
FIGURE 2. Simulated geometries of the three different minibeam generation techniques. Abbreviations stand for: S - source, B - beam, C - collimator, P - phantom, IC - ionization chamber, VT - vacuum tank, SM - scanning dipole magnet, SN - snout, Q - focusing quadrupole magnet.

TABLE 2

TABLE 2. Beam source parameters used for protons and helium ions. The energy of the helium ion beams (values in parantheses) was four times that of the proton beams.

2.1.1 Collimator and Broad Beam

The first evaluated technique represents the most straightforward approach of minibeam generation where a collimator is uniformly irradiated with a broad beam. A cylindrical brass collimator (radius 4.5 cm, thickness 6.5 cm) with five parallel slits (400 µm × 2 cm) was used. The centre-to-centre distance between the slits was 4 mm and there was a 5 cm air gap between the collimator exit and the phantom entrance.

A theoretical beam source was considered with parameters corresponding to a best case scenario, i.e. the beam particles propagate parallel to each other and the collimator is covered uniformly. For this, an instance of TOPAS’ beam type source was used with a flat spatial distribution and a Gaussian angular distribution with a very small standard deviation of 0.5 mrad. The field size was 10 × 10 cm² and covered the entire collimator (diameter of 9 cm). The beam source was placed 100 cm upstream of the phantom entrance (88.5 cm upstream of the collimator) and an energy spread of 1% was assumed.

2.1.2 Collimator and Pencil Beam Scanning

The second minibeam generation technique was based on the method of De Marzi et al. [25], where a pencil beam is magnetically scanned across the collimator. Compared to the broad beam approach, this is expected to reduce the proportion of the beam getting blocked by the collimator which in turn should improve the delivery efficiency, increase the dose rate and decrease the neutron production.

For this case, the complete universal nozzle of the Orsay Proton Therapy Centre in PBS mode was simulated. The individual nozzle components and the collimator had the same geometry as in the work of De Marzi et al. [25, 28] and the air gap between collimator exit and phantom entrance was again 5 cm. The beam source was placed at the nozzle entrance (vacuum window) and the source parameters are listed in Table 2.

The pencil beam was laterally moved across the entrance face of the collimator by simulating magnetic dipole fields in the scanning magnets SM1 and SM2 (see Figure 2) using TOPAS’ DipoleMagnet feature. It should be emphasized that, in contrast to the parallel slits of the collimator irradiated with broad beams, the collimator used in this case had slightly divergent slits (angle of 0.125 degrees between adjacent slits) to account for the inclination angle of the scanned pencil beams. The scanning pattern for the uncollimated beam consisted of five columns corresponding to the five slits in the collimator: the beam was scanned vertically along each slit such that the centres of the slit and beam spot coincided. It should be noted that a beam spot always covered multiple slits due to the comparatively large size of the pencil beams. Therefore, the relative weights of the columns had to be adjusted to yield a laterally more homogenous dose distribution in the phantom.

2.1.3 Magnetic Focusing

We have previously proposed a new nozzle design suitable for the delivery of magnetically focused and scanned minibeams which forms the basis of the third technique considered in this study. This new design features a more compact nozzle comprised of a pair of focusing quadrupole magnets, a pair of scanning dipole magnets and an ionization chamber for beam monitoring, all contained in an evacuated environment (see Schneider et al., 2020 [26] for more details). The configuration considered in this study assumed an air gap of 10 cm between the nozzle exit and phantom entrance.

The beam source was placed at the nozzle entrance and parametrized according to the aforementioned article. Table 2 summarizes the used beam source parameters. The setting of the focusing quadrupole magnets was adjusted such that the beam size at the phantom entrance was approximately constant (0.6–0.7 mm FWHM) for all considered beam energies. Note that the magnetic focusing produced symmetric pencil-shaped minibeams, i.e. the horizontal and vertical beam sizes were equal. Thus, in order to obtain the same planar minibeams generated with the collimators, the pencil-shaped minibeams were magnetically scanned across the phantom to create five vertical columns with a height of 2 cm and a centre-to-centre distance of 4 mm. A number of 50 and 100 spot positions per column were used for proton and helium ion beams, respectively, in order to obtain a homogeneous vertical profile. The scanning was again simulated by attaching dipole fields to the according volumes (SM1 and SM2), using TOPAS’ DipoleMagnet feature.

2.2 Dosimetric Evaluation

The dose distributions in the phantom were recorded using TOPAS’ DoseToWater scorer. The voxel size was 0.1 × 0.1 × 1 mm³. For each voxel, the dose uncertainty was calculated by considering the standard deviation of multiple repetitions of the simulations (between 20 and 120, depending on the number of primary particles arriving at the phantom in each case). Subsequently, the global relative uncertainty was then computed as the root mean square of the voxel uncertainties over all voxels with at least half the maximum dose. It was ≤1.28% in all cases.

The analysis of the dose distributions included the consideration of depth-dose profiles along the central peak and an adjacent valley region and the calculation of the Bragg-peak-to-entrance dose ratio (BEDR) for the central minibeam. Moreover, the peak-to-valley dose ratio (PVDR) and the size of the central minibeam were assessed as functions of the depth. For the latter, additional simulations were performed considering only the central minibeam (using a special single-slit collimator in the cases C+BB and C+PBS). The beam size of this central beam is stated as the FWHM of the lateral dose profile in the phantom and was determined via a Gaussian fit.

The uncertainties of the PVDR and BEDR values were calculated by propagating the uncertainties of the corresponding dose voxels while the beam size uncertainties were provided by the fitting algorithm.

2.3 Irradiation Efficiency

The efficiency was determined as the laterally integrated dose at the Bragg peak depth divided by the number of primary particles. In the case C+BB, the number of primaries included a correction factor to account for the fact that the beam was larger than the collimator: As the size of the beam was 10 × 10 cm² = 100 cm² whereas the cross-sectional area of the collimator was only π × 4.5² cm² ≈ 63.6 cm², the number of primaries was first reduced by a factor of 0.636 to obtain the effective number of primaries incident on the collimator.

As before, stated uncertainties correspond to the standard deviation of multiple repetitions of the simulations.

3 Results

3.1 Dosimetric Evaluation

The dosimetric evaluation was separated into multiple parts. The evolution of the beam size as a function of the depth is shown in Figure 3 while lateral dose profiles at the phantom entrance are displayed in Figure 4. Figure 5 presents the peak and valley depth-dose profiles as well as the associated PVDR as a function of the depth. Finally, Table 1 compiles the beam sizes (FWHM) and PVDR at the phantom entrance and Bragg peak depth and lists the BEDR for all cases.

FIGURE 3

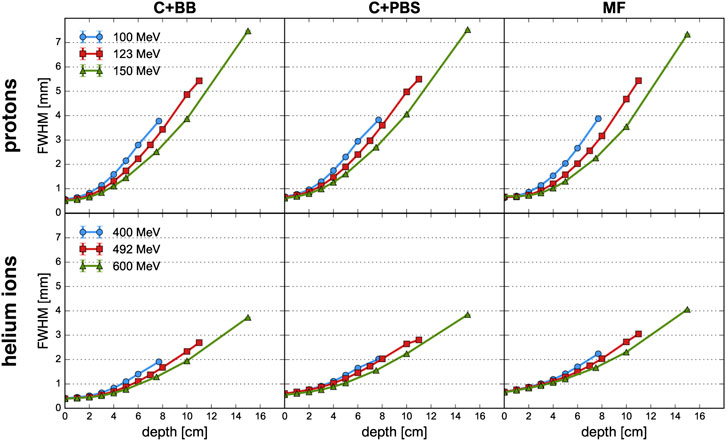
FIGURE 3. Evolution of the FWHM as a function of depth for proton beams (top row) and helium ion beams (bottom row) and for the different minibeam techniques (columns). The uncertainty bars are smaller than the markers.

FIGURE 4

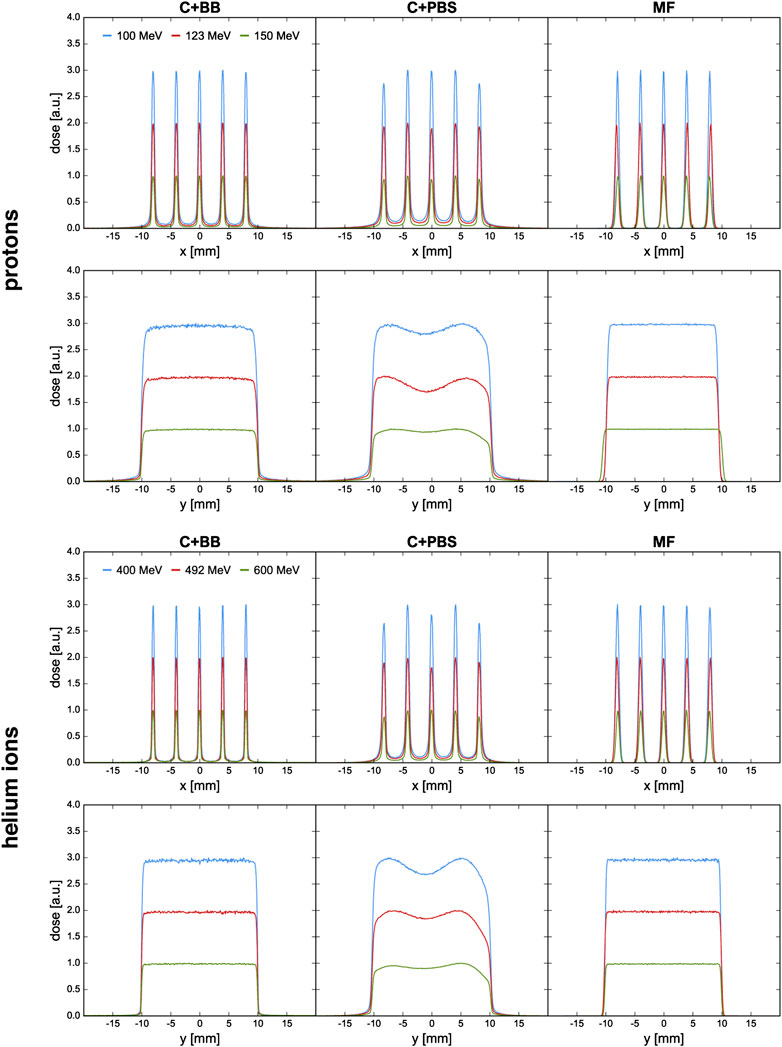
FIGURE 4. Lateral dose profiles at the phantom entrance for proton and helium ion beams and for the different minibeam techniques (columns). The blue and red curves are artificially scaled by a factor of 3 and 2, respectively, to provide better visual distinction. The first and third row show the horizontal profiles at y = 0 cm; the second and fourth row show the vertical profiles at x = 0 cm.

FIGURE 5

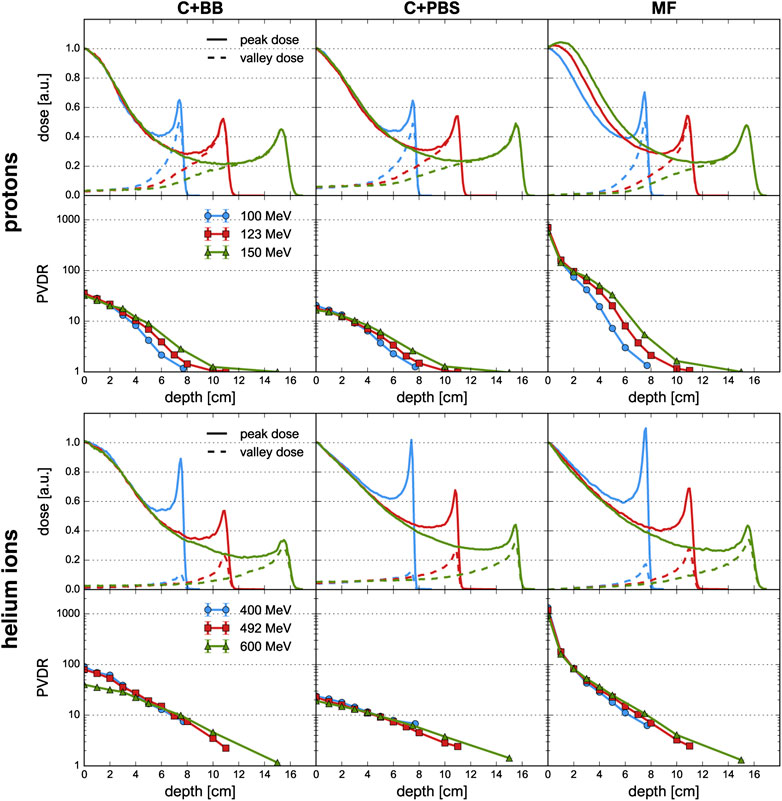
FIGURE 5. Depth-dose profiles and PVDR evolution for proton and helium ion beams and for the different minibeam techniques (columns). First and third row: depth-dose profiles along peak (solid lines) and valley (dashed lines) regions. Second and fourth row: Evolution of PVDR as a function of depth, the uncertainty bars are smaller than the markers.

3.1.1 Beam size

The beam broadening is virtually identical for the three minibeam techniques and only depends on the beam energy. Beams with a higher energy grow at a slower rate because they have a greater forward momentum and are therefore less affected by lateral deflections due to multiple Coulomb scattering [35, 36]. The same principle explains why the size of the mechanically collimated beams at the phantom entrance decreases slightly with increasing beam energy (see Table 1). For the case of magnetic focusing, it should be noted that the quadrupole settings and beam source parameters were manually adapted as to always yield a beam size between 0.6 and 0.7 mm FWHM at the phantom entrance. Therefore, the effect of a decreasing beam size with increasing beam energy is not observed for this technique.

Compared to protons, helium ions experience much less lateral scattering which results in a much slower growth of the beam width. At Bragg peak depth, the FWHM is only about half as large as for the corresponding proton minibeams.

Lastly, small differences in beam broadening are observed between the collimator techniques: For PBS, the minibeams were observed to broaden slightly quicker than for the case of broad beam irradiation. This can be seen in particular for the higher energies where the FWHM at the phantom entrance and at the Bragg peak is consistently at least 0.1 mm larger for C+PBS than for C+BB. The reason for this lies in the different divergences that were used for the beam sources (2–3 mrad for the pencil beams vs. 0.5 mrad for the broad beam). It should be reiterated that the small divergence of the broad beam was chosen deliberately to represent a best case scenario.

3.1.2 Lateral Dose Profiles

Figure 4 shows the horizontal and vertical dose profiles at the phantom entrance. As explained in the work by De Marzi et al. [25], the orientation of the collimator slits must be tailored to the irradiation setup in order to account for the internal divergence of the uncollimated beam. For the case of C+PBS, variations are observed between the intensities of the five minibeams and the vertical dose profiles exhibit inhomogeneities. It was attempted to mitigate these effects by adjusting the weights of the individual pencil beam spots and a continued optimization of the spot weights may be expected to further improve the profiles.

At any rate, the need for these adjustments shows that the use of collimators for minibeam generation complicates treatment planning and underlines the inflexibility of collimated minibeams. In comparison to this, much smoother dose profiles could be obtained with the magnetically focused minibeams.

3.1.3 Depth-Dose Profiles and Peak-to-Valley Dose Ratio

Figure 5 shows the peak and valley depth-dose profiles as well as the PVDR as a function of depth. The sampling locations of the depth-dose profiles are indicated in Figure 1. The depth-dose profiles obtained with the different minibeam techniques are generally very similar except for one important difference: compared to magnetic focusing, mechanical collimation yields higher valley doses at low depths which can be attributed to intra-slit leakage and scattered primary particles as well as an increased number of secondaries produced in the collimator.

For the case of magnetic focusing, the peak profiles exhibit a small shoulder at a depth of 1–2 cm, in particular for proton beams of 123 and 150 MeV. This can be interpreted as a consequence of the focal point of the beam being located inside the phantom so that the beam broadening due to lateral scattering is compensated by a converging motion of the focused beam particles. Indeed, considering again the beam broadening (Figure 3), one observes that in these two cases the width of the minibeams stays almost constant over the first 2 cm whereas the curve corresponding to the 100 MeV beam exhibits notable broadening.

Helium ions yield a much sharper and higher Bragg peak than protons. As a result, the BEDR is about 30–40% higher for the lowest energies (100 MeV proton beams, 400 MeV He beams), however this difference becomes less pronounced as the beam energy increases. Moreover, the Bragg peak becomes more smeared out and the BEDR decreases for higher energies. This is because range straggling becomes more important as the range increases and more primary particles are lost in nuclear interactions, leading to a reduction of the Bragg peak height [37]. In almost all cases, the BEDR of the peak dose profiles is <1 which represents an important difference compared to the standard Bragg curve observed for conventional hadron therapy with supermillimetric beams. A BEDR smaller than one implies an increased dose deposition in shallow tissue or at the skin level and must be considered disadvantageous for healthy tissue sparing. However, the high entrance dose is restricted to the peak regions and may be compensated for by the tissue sparing effects of the spatial fractionation.

A high PVDR >10 is observed in all cases, at least at shallow depths. By far the highest PVDR is observed for magnetic focusing (about 20–60 times higher than those for C+BB and C+PBS, respectively). This is a direct consequence of the much lower valley doses. Analogously, the helium ion beams yield a higher PVDR than the proton beams.

The PVDR decreases more slowly when the beam energy is higher. This can be understood as a consequence of the reduced multiple Coulomb scattering at higher energies: higher-energetic beams broaden more slowly which means that the valleys fill up more slowly. At the phantom entrance, however, beams with a higher energy were observed to yield a lower PVDR (Table 1).

Lastly, it should be noted that lateral homogenization of the dose (i.e. PVDR ≈ 1) at the Bragg peak depth is only observed for the proton beams at an energy of 123 and 150 MeV. This is because the spacing of the collimator slits was optimized for these cases but the same minibeam pattern with identical centre-to-centre distances was also considered for all other cases. More details on this are given in Section 4.

3.2 Efficiency

Figure 6 shows the dose efficiencies (mean dose deposited at Bragg peak depth per primary particle). Magnetic focusing is found to be the most efficient minibeam delivery method, both for protons and helium ions, yielding an increase in efficiency of one to two orders of magnitude compared to the collimator techniques. Moreover, the efficiency of helium ions is 3–4 times higher than that of protons. This is in agreement with the fact that helium ions yield sharper and higher Bragg peaks, as mentioned before.

FIGURE 6

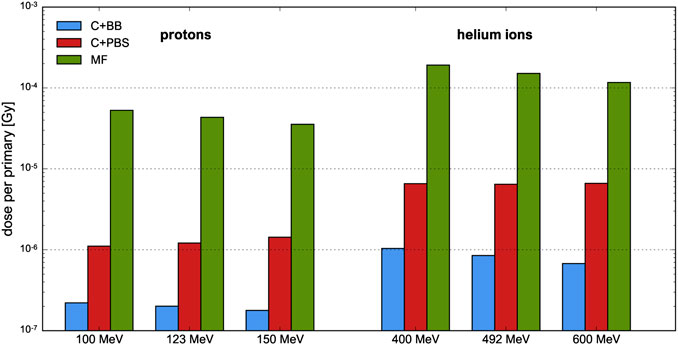
FIGURE 6. Efficiency of proton and helium ion beams at different beam energies and for different minibeam techniques. The uncertainty bars are very small and barely visible.

For the cases C+BB and MF, the efficiency tends to decrease slightly as the beam energy increases. This is a consequence to the Bragg peak becoming flatter and more smeared out due to enhanced range straggling, as argued in Section 3.1.3. An opposite effect is observed for the case C+PBS with proton beams (and to a much smaller degree also with helium ion beams) which may be explained with the widths of the uncollimated pencil beams. The widths become smaller as the energy increases, so a larger proportion of the initial beam passes the collimator.

Between the two methods involving a collimator, irradiation with a scanned pencil beam was found to be about 5–10 times more efficient than broad beam irradiation. It should be noted, however, that the efficiency of the C+BB case strongly depends on the ratio between the sizes of the initial uncollimated beam and the collimator but also on the size and number of the collimator slits. This point is further discussed in the next section.

4 Discussion

Proton minibeam radiation therapy is a novel therapeutic approach which, in preclinical experiments, has shown significant increases in the preservation of normal tissue [38, 39] while providing equivalent or superior tumour control [16, 17]. The generation of very narrow proton beams, intense enough to deliver the required dose in a reasonable amount of time (a few minutes) at existing clinical facilities, is a challenging task. The current implementation at clinical centres uses mechanical collimation which, despite representing a straightforward and readily applicable method, is suboptimal due to flux reduction, limited flexibility and neutron production (although evaluations have shown only a modest increase of <1% for the biological neutron dose in the patient [24]). In a previous work, we have thus proposed a new nozzle design capable of generating magnetically focused proton minibeams at a clinical centre [26].

In this study, we evaluated the differences between minibeam techniques using mechanical collimation and magnetic focusing. The aim of this comparison was twofold, considering gains in terms of efficiency but also whether there exists any advantage concerning the dose distributions. The simulations were performed with protons as well as helium ions which experience less multiple Coulomb scattering and which could therefore further improve the dose distributions.

As expected, magnetic focusing was shown to be much more efficient than mechanical collimation due to the fact that the entire beam can be used for dose deposition in the target. Compared to the collimator techniques, the mean dose per primary particle deposited at Bragg peak depth was at least 20 times higher with magnetic focusing in all cases. Such a gain is interesting in particular regarding a potential combination of pMBRT and FLASH therapy [40, 41] which requires very high dose rates. Moreover, helium ions were observed to be more efficient than protons which, in the context of the used metric, can be explained by the sharper Bragg peaks.

Between the two collimator techniques, irradiation with scanned pencil beams (C+PBS) has shown an improved efficiency compared to broad beam irradiation (C+BB). As stated above, the efficiency in the latter case depends strongly on the field size and the collimator geometry. The considered collimator was already used in previous studies [25, 42] (with the exception that parallel slits were used for the case C+BB) and a uniform irradiation of the entire cross-section of the collimator was assumed, approximating the conditions of a passively scattering beamline. It should be noted, however, that a reduction of the size of the uncollimated beam could drastically improve the efficiency. For instance, a four-fold increase of the efficiency would be expected from geometrical considerations for a field size of 5 × 5 cm².

Concerning the dosimetric evaluation, a substantially enhanced PVDR at shallow depths was observed for magnetically focused minibeams compared to mechanically collimated ones. Similarly, helium ions were found to yield a higher PVDR than protons. This is desirable as it has been shown that a high PVDR favours normal tissue sparing [8]. In terms of BEDR, magnetic focusing does not offer any improvements over mechanical collimation. Instead, protons could be replaced by helium ions to obtain a more favourable ratio between the entrance and Bragg peak doses.

It should be emphasized again that the PVDR is very dependent on the spacing between the minibeams and that the value considered in this study was optimized for proton beams of 123–150 MeV (cf. De Marzi et al. [25]). The idea here was to use the model of an existing collimator for proton beams and to evaluate whether it could also be used with helium ions. Our results show that collimators designed for proton beams could also be used to produce helium ion minibeams.

In order to attain lateral homogenization at the Bragg peak depth with helium ions, a narrower centre-to-centre distance would be required, in particular at lower beam energies. This would result in a significantly lower PVDR which generally implies a reduction of tissue sparing effects. However, recent experiments indicate that homogenous dose coverage of the target may not be needed to achieve tumour control [16, 17]. A more detailed discussion of these aspects can be found in one of our previous works [18].

While the focus of this study lay on the comparison of the dose distributions and neutron production, another important factor is the linear energy transfer (LET) as it can influence the biological effectiveness of the irradiation. Previous works on pMBRT by our group found a slightly higher LET in the valley regions than in the peak regions [18, 42]. From these studies, it appears that collimator-generated minibeams [42] yield a less favourable ratio (i.e. higher valley LET) than magnetically focused minibeams [18]. In this light, future studies should therefore also evaluate the peak-to-valley LET ratio (see e.g. González and Prezado [43]).

Following previous works [25, 42], this study evaluated beam energies between 100 and 150 MeV/u which would be adequate e.g. for the treatment of brain tumours [15, 16, 42]. Nonetheless, proton minibeams of ≥200 MeV have also been considered, using both collimation techniques [28] and magnetic focusing [26]. Due to the reduced importance of lateral scattering, the generation of magnetically focused minibeams becomes easier at higher energies whereas the production of unwanted secondary particles in the collimator increases. The advantages of magnetic focusing over mechanical collimation demonstrated in this study can therefore be expected to apply also at higher energies. It should be noted, however, that the results presented here are based on Monte Carlo simulations. We are currently working toward a physical implementation of magnetically focused minibeams and hope to soon be able to perform experimental validations.

Lastly, it should be mentioned that, at least for now, mechanical collimation represents the technically easier approach for minibeam generation. Indeed, all existing implementations of pMBRT at clinically relevant energies use collimators [17, 23, 25] and this technique can in principle be readily applied at any proton therapy centre [26, 44]. In contrast to this, the generation of magnetically focused minibeams will likely not be achievable with current clinical nozzles [26]. However, our simulations indicate the compatibility of the new nozzle design considered in this study with existing proton therapy technology such as synchrotron-based facilities (see Schneider et al. [26] for more details).

The new minibeam nozzle design uses standard components (electromagnets, ionization chambers) so that no additional costs are expected compared to conventional PBS nozzles. On the contrary, the improved flexibility and efficiency of magnetic focusing would likely allow a much more economic implementation of pMBRT than mechanical collimators. Moreover, also standard PBS techniques could benefit from the new nozzle design and its ability to deliver smaller beams with sharper penumbrae.

5 Conclusion

The results of our study show that magnetic focusing represents a better approach for minibeam generation than mechanical collimation, exhibiting substantial improvements in terms of irradiation efficiency and PVDR. Moreover, they indicate that helium ion minibeams can be generated using the same techniques that were developed for pMBRT. Despite the technical challenges related to a practical implementation of magnetically focused minibeams, our results support and further motivate the work toward the physical realization of such a system at a clinical centre.

Data Availability Statement

The datasets generated for this study are available on request to the corresponding author.

Author Contributions

TS designed and carried out the studies (Monte Carlo simulations and data analysis) and wrote the manuscript. YP conceived the project. YP and AP supervised the studies. LD provided data and template files for the Monte Carlo simulations of the C+PBS case. All authors participated in scientific discussions, read and approved the manuscript.

Funding

This project has received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No 817908) and this project has also been partially funded by SIRIC 2018–2022: INCa-DGOS-Inserm_12,554. Calculation time was granted at the supercomputer Joliot Curie SKL Très grand centre de calcul (TGCC) of Commisariat Energie Atomique (CEA), from the Partnership for Advanced Computing in Europe (PRACE Project Access Call 19th, proposal number 2019204903).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

TS thanks Consuelo Guardiola for her help in initial discussions regarding the simulations of the C+BB case.

Footnotes

¹http://www.topasmc.org

References

1. Garibaldi C, Jereczek-Fossa BA, Marvaso G, Dicuonzo S, Rojas DP, Cattani F, et al. Recent advances in radiation oncology. Ecancermedicalscience (2017) 11:785. doi:10.3332/ecancer.2017.785

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Köhler A. Theorie einer methode, bisher unmöglich unanwendbar hohe dosen röntgenstrahlen in der tiefe des gewebes zur therapeutischen wirksamkeit zu bringen ohne schwere schäden des patienten, zugleich eine methode des schutzes gegen röntgenverbrennungen überhaupt. Fortschr Geb Roentgenstr (1909) 14:27–9.

Google Scholar

3. Mohiuddin M, Fujita M, Regine WF, Megooni AS, Ibbott GS, Ahmed MM. High-dose spatially-fractionated radiation (grid): a new paradigm in the management of advanced cancers. Int J Radiat Oncol Biol Phys (1999) 45:721–7. doi:10.1016/s0360-3016(99)00170-4

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Slatkin DN, Spanne P, Dilmanian FA, Gebbers JO, Laissue JA. Subacute neuropathological effects of microplanar beams of x-rays from a synchrotron wiggler. Proc Natl Acad Sci USA (1995) 92:8783–7. doi:10.1073/pnas.92.19.8783

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Dilmanian FA, Zhong Z, Bacarian T, Benveniste H, Romanelli P, Wang R, et al. Interlaced x-ray microplanar beams: a radiosurgery approach with clinical potential. Proc Natl Acad Sci USA (2006) 103:9709–14. doi:10.1073/pnas.0603567103

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Prezado Y, Deman P, Varlet P, Jouvion G, Gil S, Le Clec'H C, et al. Tolerance to dose escalation in minibeam radiation therapy applied to normal rat brain: long-term clinical, radiological and histopathological analysis. Radiat Res (2015) 184:314–21. doi:10.1667/RR14018.1

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bouchet , Serduc R, Laissue JA, Djonov V. Effects of microbeam radiation therapy on normal and tumoral blood vessels. Phys Med (2015) 31:634–41. doi:10.1016/j.ejmp.2015.04.014

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Dilmanian FA, Button TM, Le Duc G, Zhong N, Peña LA, Smith JAL, et al. Response of rat intracranial 9L gliosarcoma to microbeam radiation therapy. Neuro Oncol (2002) 4:26–38. doi:10.1093/neuonc/4.1.2610.1215/15228517-4-1-26

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Curtis HJ. The use of deuteron microbeam for simulating the biological effects of heavy cosmic-ray particles. Radiat Res Suppl (1967) 7:250–7. doi:10.2307/3583718

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hopewell JW, Trott KR. Volume effects in radiobiology as applied to radiotherapy. Radiother Oncol (2000) 56:283–8. doi:10.1016/s0167-8140(00)00236-x

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Crosbie JC, Anderson RL, Rothkamm K, Restall CM, Cann L, Ruwanpura SS, et al. Tumor cell response to synchrotron microbeam radiation therapy differs markedly from cells in normal tissues. Int J Radiat Oncol Biol Phys (2010) 77:886–94. doi:10.1016/j.ijrobp.2010.01.035

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Yan W, Khan MK, Wu X, Simone CB, Fan J, Gressen E, et al. Spatially fractionated radiation therapy: history, present and the future. Clin Transl Radiat Oncol (2020) 20:30–8. doi:10.1016/j.ctro.2019.10.004

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Prezado Y, Fois GR. Proton-minibeam radiation therapy: a proof of concept. Med Phys (2013) 40:031712. doi:10.1118/1.4791648

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zlobinskaya O, Girst S, Greubel C, Hable V, Siebenwirth C, Walsh DWM, et al. Reduced side effects by proton microchannel radiotherapy: study in a human skin model. Radiat Environ Biophys (2013) 52:123–33. doi:10.1007/s00411-012-0450-9

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Prezado Y, Jouvion G, Hardy D, Patriarca A, Nauraye C, Bergs JJ, et al. Proton minibeam radiation therapy spares normal rat brain: long-term clinical, radiological and histopathological analysis. Sci Rep (2017) 7:14403. doi:10.1038/s41598-017-14786-y

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Prezado Y, Jouvion G, Patriarca A, Nauraye C, Guardiola C, Juchaux M, et al. Proton minibeam radiation therapy widens the therapeutic index for high-grade gliomas. Sci Rep (2018) 8:16479. doi:10.1038/s41598-018-34796-8

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Prezado Y, Jouvion G, Guardiola C, Gonzalez W, Juchaux M, Bergs J, et al. Tumor control in RG2 glioma-bearing rats: a comparison between proton minibeam therapy and standard proton therapy. Int J Radiat Oncol Biol Phys (2019) 104:266–71. doi:10.1016/j.ijrobp.2019.01.080

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Schneider T, Patriarca A, Prezado Y. Improving the dose distributions in minibeam radiation therapy: helium ions vs protons. Med Phys (2019) 46:3640–8. doi:10.1002/mp.13646

PubMed Abstract | CrossRef Full Text | Google Scholar

19. González W, Peucelle C, Prezado Y. Theoretical dosimetric evaluation of carbon and oxygen minibeam radiation therapy. Med Phys (2017) 44:1921–9. doi:10.1002/mp.12175

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Ströbele J, Schreiner T, Fuchs H, Georg D. Comparison of basic features of proton and helium ion pencil beams in water using gate. Z Med Phys (2012) 22:170–8. doi:10.1016/j.zemedi.2011.12.001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Grün R, Friedrich T, Krämer M, Zink K, Durante M, Engenhart-Cabillic R, et al. Assessment of potential advantages of relevant ions for particle therapy: a model based study. Med Phys (2015) 42:1037–47. doi:10.1118/1.4905374

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Tessonnier T, Mairani A, Chen W, Sala P, Cerutti F, Ferrari A, et al. Proton and helium ion radiotherapy for meningioma tumors: a Monte Carlo-based treatment planning comparison. Radiat Oncol (2018) 13:2. doi:10.1186/s13014-017-0944-3

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Peucelle C, Nauraye C, Patriarca A, Hierso E, Fournier-Bidoz N, Martínez-Rovira I, et al. Proton minibeam radiation therapy: experimental dosimetry evaluation. Med Phys (2015) 42:7108–13. doi:10.1118/1.4935868

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Guardiola C, Peucelle C, Prezado Y. Optimization of the mechanical collimation for minibeam generation in proton minibeam radiation therapy. Med Phys (2017) 44:1470–8. doi:10.1002/mp.12131

PubMed Abstract | CrossRef Full Text | Google Scholar

25. De Marzi L, Patriarca A, Nauraye C, Hierso E, Dendale R, Guardiola C, et al. Implementation of planar proton minibeam radiation therapy using a pencil beam scanning system: a proof of concept study. Med Phys (2018) 45:5305–16. doi:10.1002/mp.13209

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Schneider T, De Marzi L, Patriarca A, Prezado Y. Advancing proton minibeam radiation therapy: magnetically focussed proton minibeams at a clinical centre. Sci Rep (2020) 10:1384. doi:10.1038/s41598-020-58052-0

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Pedroni E, Meer D, Bula C, Safai S, Zenklusen S. Pencil beam characteristics of the next-generation proton scanning gantry of psi: design issues and initial commissioning results. Eur Phys J Plus (2011) 126:66. doi:10.1140/epjp/i2011-11066-0

CrossRef Full Text | Google Scholar

28. De Marzi L, Da Fonseca A, Moignier C, Patriarca A, Goudjil F, Mazal A, et al. Experimental characterisation of a proton kernel model for pencil beam scanning techniques. Phys Med (2019) 64:195–203. doi:10.1016/j.ejmp.2019.07.013

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Perl J, Shin J, Schumann J, Faddegon B, Paganetti H. Topas: an innovative proton Monte Carlo platform for research and clinical applications. Med Phys (2012) 39:6818–37. doi:10.1118/1.4758060

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Arce P, Bolst D, Bordage MC, Brown JMC, Cirrone P, Cortés-Giraldo MA, et al. Report on G4-med, a geant4 benchmarking system for medical physics applications developed by the geant4 medical simulation benchmarking group. Med Phys (2020) 48:19–56. doi:10.1002/mp.14226

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Testa M, Schümann J, Lu HM, Shin J, Faddegon B, Perl J, et al. Experimental validation of the topas Monte Carlo system for passive scattering proton therapy. Med Phys (2013) 40:121719. doi:10.1118/1.4828781

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Zacharatou Jarlskog C, Paganetti H. Physics settings for using the geant4 physics settings for using the geant4 toolkit in proton therapy. IEEE Trans Nucl Sci (2008) 55:1018–25. doi:10.1109/tns.2008.922816

CrossRef Full Text | Google Scholar

33. Grevillot L, Frisson T, Zahra N, Bertrand D, Stichelbaut F, Freud N, et al. Optimization of geant4 settings for proton pencil beam scanning simulations using gate. Nucl Instr Methods Phys Res Sec B: Beam Interaction Mater Atoms (2010) 268:3295–305. doi:10.1016/j.nimb.2010.07.011

CrossRef Full Text | Google Scholar

34. Peucelle C, Martínez-Rovira I, Prezado Y. Spatial fractionation of the dose using neon and heavier ions: a Monte Carlo study. Med Phys (2015) 42:5928–36. doi:10.1118/1.4930960

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Gottschalk B. Chapter 2 ‐ Physics of Proton Interactions in Matter. In: Paganetti H, editor. Proton Therapy Physics. 2nd ed. Taylor & Francis (2018).

Google Scholar

36. Highland VL. Some practical remarks on multiple scattering. Nucl Instr Methods (1975) 129:497–9. doi:10.1016/0029-554X(75)90743-0

CrossRef Full Text | Google Scholar

37. Newhauser WD, Zhang R. The physics of proton therapy. Phys Med Biol (2015) 60:R155–209. doi:10.1088/0031-9155/60/8/R155

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Prezado Y, Dos Santos M, Gonzalez W, Jouvion G, Guardiola C, Heinrich S, et al. Transfer of minibeam radiation therapy into a cost-effective equipment for radiobiological studies: a proof of concept. Sci Rep (2017) 7:17295. doi:10.1038/s41598-017-17543-3

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Girst S, Greubel C, Reindl J, Siebenwirth C, Zlobinskaya O, Walsh DWM, et al. Proton minibeam radiation therapy reduces side effects in an in vivo mouse ear model. Int J Radiat Oncol Biol Phys (2016) 95:234–41. doi:10.1016/j.ijrobp.2015.10.020

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Favaudon V, Caplier L, Monceau V, Pouzoulet F, Sayarath M, Fouillade C, et al. Ultrahigh dose-rate flash irradiation increases the differential response between normal and tumor tissue in mice. Sci Transl Med (2014) 6:245ra93. doi:10.1126/scitranslmed.3008973

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Reindl J, Girst S. Pmb flash-status and perspectives of combining proton minibeam with flash radiotherapy. J Cancer Immunol (2019) 1:14–23. doi:10.33696/cancerimmunol.1.003

CrossRef Full Text | Google Scholar

42. Lansonneur P, Mammar H, Nauraye C, Patriarca A, Hierso E, Dendale R, et al. First proton minibeam radiation therapy treatment plan evaluation. Sci Rep (2020) 10:7025. doi:10.1038/s41598-020-63975-9

PubMed Abstract | CrossRef Full Text | Google Scholar

43. González W, Prezado Y. Spatial fractionation of the dose in heavy ions therapy: an optimization study. Med Phys (2018) 45:2620–7. doi:10.1002/mp.12902

PubMed Abstract | CrossRef Full Text | Google Scholar

44. McAuley GA, Teran AV, McGee PQ, Nguyen TT, Slater JM, Slater JD, et al. Experimental validation of magnetically focused proton beams for radiosurgery. Phys Med Biol (2019) 64:115024. doi:10.1088/1361-6560/ab0db1

PubMed Abstract | CrossRef Full Text | Google Scholar