- Department of Mathematics, McMaster University, Hamilton, ON, Canada
It is shown how to compute the instability rates for the double-periodic solutions to the cubic NLS (nonlinear Schrödinger) equation by using the Lax linear equations. The wave function modulus of the double-periodic solutions is periodic both in space and time coordinates; such solutions generalize the standing waves which have the time-independent and space-periodic wave function modulus. Similar to other waves in the NLS equation, the double-periodic solutions are spectrally unstable and this instability is related to the bands of the Lax spectrum outside the imaginary axis. A simple numerical method is used to compute the unstable spectrum and to compare the instability rates of the double-periodic solutions with those of the standing periodic waves.
1 Introduction
Peregrine breather is a rogue wave arising on the background of the constant-amplitude wave due to its modulational instability [1, 2]. The focusing cubic NLS (nonlinear Schrödinger) equation is the canonical model which describes both the modulational instability and the formation of rogue waves. Formation of rogue waves on the constant-amplitude background have been modeled from different initial data such as local condensates [3], multi-soliton gases [4–6], and periodic perturbations [7, 8]. Rogue waves have been experimentally observed both in hydrodynamical and optical laboratories [9] (see recent reviews in [10, 11]).
Mathematical theory of rogue waves on the constant-amplitude background has seen many recent developments. universal behavior of the modulationally unstable constant-amplitude background was studied asymptotically in [12, 13]. The finite-gap method was employed to relate the unstable modes on the constant-amplitude background with the occurrence of rogue waves [14, 15]. Rogue waves of infinite order were constructed in [16] based on recent developments in the inverse scattering method [17]. Rogue waves of the soliton superposition were studied asymptotically in the limit of many solitons [18, 19].
At the same time, rogue waves were also investigated on the background of standing periodic waves expressed by the Jacobian elliptic functions. Such exact solutions to the NLS equation were constructed first in [20] (see also early numerical work in [21] and the recent generalization in [22]). It was confirmed in [23] that these rogue waves arise due to the modulational instability of the standing periodic waves [24] (see also [25, 26]). Instability of the periodic standing waves can be characterized by the separation of variables in the Lax system of linear equations [27] (see also [28, 29]), compatibility of which gives the NLS equation. Instability and rogue waves on the background of standing periodic waves have been experimentally observed in [30].
The main goal of this paper is to compute the instability rates for the double-periodic solutions to the NLS equation, for which the wave function modulus is periodic with respect to both space and time coordinates. In particular, we consider two families of double-periodic solutions expressed as rational functions of the Jacobian elliptic functions which were constructed in the pioneering work [31]. These solutions represent perturbations of the Akhmediev breathers and describe generation of either phase-repeated or phase-alternating wave patterns [32, 33]. Rogue waves on the background of the double-periodic solutions were studied in [34] (see also numerical work in [35, 36]). Experimental observation of the double-periodic solutions in optical fibers was reported in [37].
The double-periodic solutions constructed in [31] are particular cases of the quasi-periodic solutions of the NLS equation given by the Riemann Theta functions of genus two [38–40]. Rogue waves for general quasi-periodic solutions of any genus were considered in [41–43].
Instability of the double-periodic solutions is studied using the Floquet theory for the Lax system of linear equations both in space and time coordinates. We compute the instability rates of the double-periodic solutions and compare them with those for the standing periodic waves. In order to provide a fair comparison, we normalize the amplitude of all solutions to unity. As a main outcome of this work, we show that the instability rates are larger for the constant-amplitude waves and smaller for the double-periodic waves.
The article is organized as follows. The explicit solutions to the NLS equation are reviewed in Section 2. Instability rates for the standing periodic waves and the double-periodic solutions are computed in Sections 3 and 4 respectively. Further directions are discussed in Section 5.
2 Explicit Solutions to the NLS Equation
The nonlinear Schrödinger (NLS) equation is a fundamental model for nonlinear wave dynamics [44, 45]. We take the NLS equation in the standard form:
This model has several physical symmetries which are checked directly:
translation:
scaling:
Lorentz transformation:
In what follows, we use the scaling symmetry Eq. 2.3 to normalize the amplitude of periodic and double-periodic solutions to unity and the Lorentz symmetry Eq. 2.4 to set the wave speed to zero. We also neglect the translational parameters
A solution
and
where
The algebraic method developed in [34] allows us to construct the stationary (Lax–Novikov) equations which admit a large class of bounded periodic and quasi-periodic solutions to the NLS Eq. 2.1 The simplest first-order Lax–Novikov equation is given by
where c is arbitrary real parameter. A general solution of this equation is given by
where
The second-order Lax–Novikov equation is given by
where
Without loss of generality, we set
and
where the parameter
Due to the well-known expansion formulas
both the periodic waves Eqs. 2.11, 2.12 approaches the NLS soliton
The third-order Lax–Novikov equation is given by
where
where
and
where
The double-periodic solutions Eqs. 2.15, 2.16 can be written in the form:
where
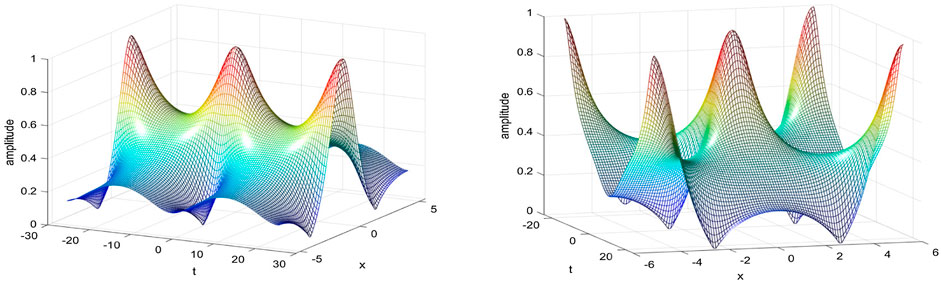
Figure 1 shows surface plots of
As
As
whereas the solution Eq. 2.16 approaches the scaled cnoidal wave
These limits are useful to control accuracy of numerical computations of the modulational instability rate for the double-periodic solutions in comparison with the similar numerical computations for the standing waves.
3 Instability of Standing Waves
Here we review how to use the linear Eq. 2.5, 2.6 in order to compute the instability rates for the standing periodic waves (Eq. 2.10) (see [23, 27]). Due to the separation of variables in Eq. 2.10, one can write
where
and
We say that λ belongs to the Lax spectrum of the spectral problem Eq. 3.2 if
where
Since the spectral problem Eq. (3.3) is a linear algebraic system, it admits a nonzero solution if and only if the determinant of the coefficient matrix is zero. The latter condition yields the x-independent relation between
with parameters a and d being the conserved quantities of the second-order Eq. 2.9:
and
Polynomial
where the turning points
Roots of
so that the polynomial
By adding a perturbation v to the standing wave u in the form
and dropping the quadratic terms in v, we obtain the linearized system of equations which describe linear stability of the standing waves (Eq. 2.10):
The variables can be separated in the form:
where
where
We say that
Validity of Eq. 3.16 can be checked directly from Eqs. 3.2, 3.3, 3.14, and 3.15. If
The importance of distinguishing between spectral and modulational instability of the periodic standing waves appears in the existence of rogue waves on their background. It was shown in [46] that if the periodic standing waves are spectrally unstable but modulationally stable, the rogue waves are not fully localized and degenerate into propagating algebraic solitons. Similarly, it was shown in [23] that if the unstable spectrum with
Next, we compute the instability rates for the standing periodic waves (2.10) of the trivial phase with
For the
Since the
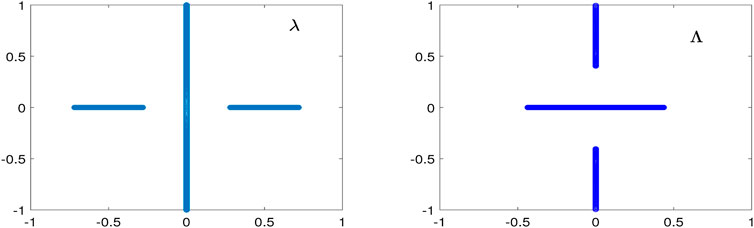
FIGURE 2. Lax spectrum on the λ-plane (left) and stability spectrum on the
For the

FIGURE 3. The same as Figure 2 but for the amplitude-normalized
Figure 4 compares the instability rates for different standing waves of the same unit amplitude.
Due to the scaling transformation Eq. 2.3 and the expansion Eq. 3.17, the maximal growth rate in the limit
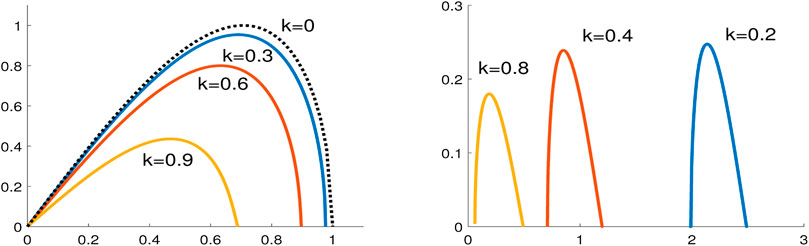
FIGURE 4. Instability rate
4 Instability of Double-Periodic Waves
Here we describe the main result on how to compute the instability rates for the double-periodic waves by using the linear Eqs. 2.5, 2.6. We write the solutions Eqs. 2.15, 2.16 in the form Eq. 2.17. We represent solution φ to the linear Eqs. 2.5, 2.6 in the form:
where
and
Parameters
By Floquet theorem, spectral parameters
The Lax spectrum is defined by the condition that λ belongs to an admissible set for which the solution Eq. 4.1 is bounded in x. Hence
With λ defined in the Lax spectrum, the spectral problem Eq. 4.3 can be solved for the spectral parameter
If
For the amplitude-normalized double-periodic wave Eq. 2.15 with
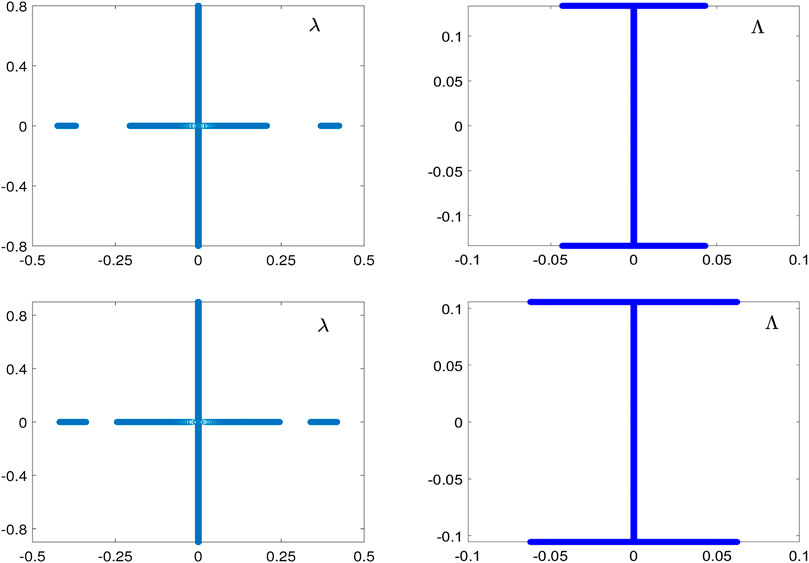
FIGURE 5. Lax spectrum on the λ-plane (left) and stability spectrum on the
Figure 6 shows the same as Figure 5 but for the amplitude-normalized double-periodic wave Eq. 2.16 with
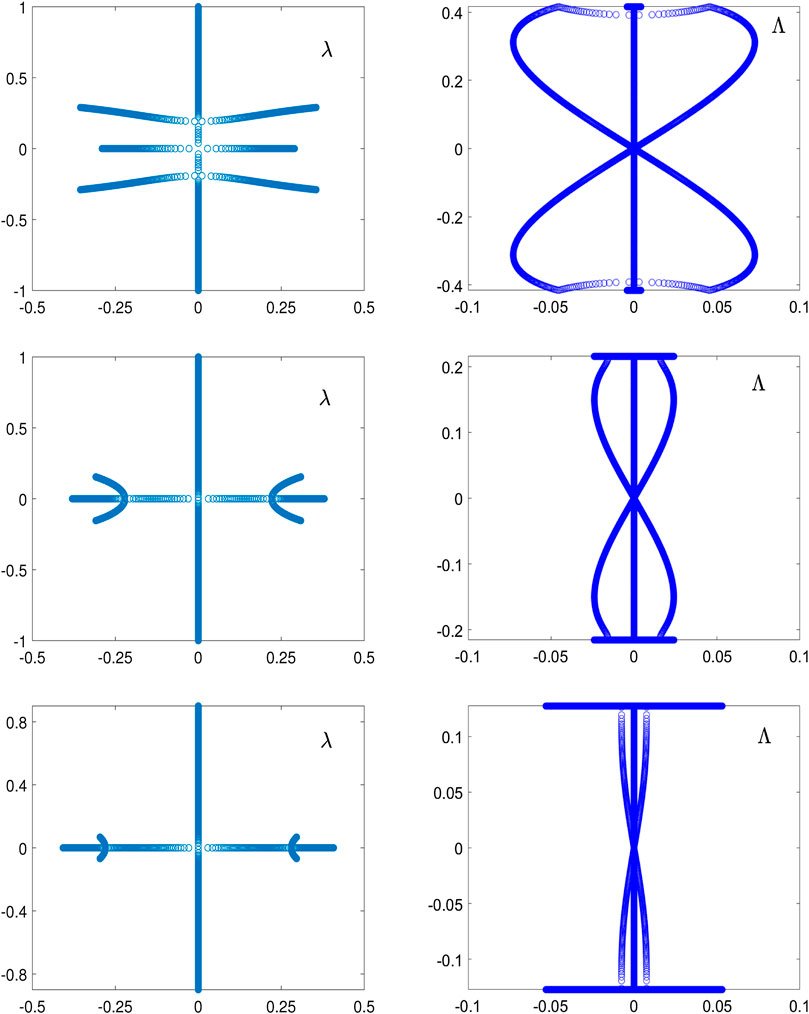
FIGURE 6. The same as Figure 5 but for the amplitude-normalized double-periodic wave (2.16) with
Figure 7 compares the instability rates for different double-periodic waves of the same unit amplitude.
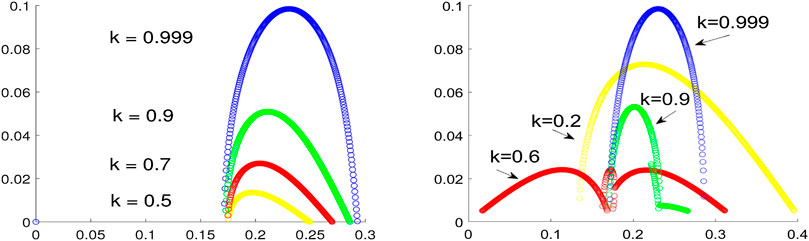
FIGURE 7. Instability rate
For the amplitude-normalized double-periodic wave Eq. 2.15 (left), the instability rate is maximal as
For the amplitude-normalized double-periodic wave Eq. 2.16 (right), the instability rate is large in the limit
5 Conclusion
We have computed the instability rates for the double-periodic waves of the NLS equation. By using the Lax pair of linear equations, we obtain the Lax spectrum with the Floquet theory in the spatial coordinate at fixed t and the stability spectrum with the Floquet theory in the temporal coordinate at fixed x. This separation of variables is computationally simpler than solving the full two-dimensional system of linearized NLS equations on the double-periodic solutions.
As the main outcome of the method, we have shown instability of the double-periodic solutions and have computed their instability rates, which are generally smaller compared to those for the standing periodic waves.
The concept can be extended to other double-periodic solutions of the NLS equation which satisfy the higher-order Lax–Novikov equations. Unfortunately, the other double-periodic solutions are only available in Riemann theta functions of genus
Author Contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Conflict of Interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China (No. 11971103).
References
1. Peregrine DH. Water waves, nonlinear Schrödinger equations and their solutions. J Aust Math Soc Series B Appl Math (1983) 25:16–43. doi:10.1017/s0334270000003891
2. Akhmediev NN, Eleonsky VM, Kulagin NE. Generation of periodic trains of picosecond pulses in an optical fiber: exact solutions. Sov Phys JETP (1985) 62:894–899.
3. Gelash AA, “Formation of rogue waves from a locally perturbed condensate”, Phys Rev E (2018) 97:022208. doi:10.1103/PhysRevE.97.022208
4. Zakharov VE, Gelash AA, “Nonlinear stage of modulation instability”, Phys Rev Lett (2013) 111:054101. doi:10.1103/PhysRevLett.111.054101
5. Gelash AA, Agafontsev DS, “Strongly interacting soliton gas and formation of rogue waves”, Phys Rev E (2018) 98:042210. doi:10.1103/physreve.98.042210
6. Gelash AA, Agafontsev D, Zakharov V, El G, Randoux S, Suret P, “Bound state soliton gas dynamics underling the spontaneous modulational instability”, Phys Rev Lett (2019) 123:234102. doi:10.1103/physrevlett.123.234102
7. Agafontsev DS, Zakharov VE. Integrable turbulence and formation of rogue waves. Nonlinearity (2015) 28:2791–2821. doi:10.1088/0951-7715/28/8/2791
8. Agafontsev DS, Zakharov VE. Integrable turbulence generated from modulational instability of conoidal waves. Nonlinearity (2016) 29:3551–3578. doi:10.1088/0951-7715/29/11/3551
9. Randoux S, Suret P, Chabchoub A, Kibler B, El G, “Nonlinear spectral analysis of Peregrine solitons observed in optics and in hydrodynamic experiments”, Phys Rev E (2018) 98:022219. doi:10.1103/PhysRevE.98.022219
10. Dudley JM, Genty G, Mussot A, Chabchoub A, Dias F. Rogue waves and analogies in optics and oceanography. Nat Rev Phys (2019) 1:675. doi:10.1038/s42254-019-0100-0
11. Copie F, Randoux S, Suret P, “The Physics of the one-dimensional nonlinear Schrödinger equation in fiber optics: rogue waves, modulation instability and self-focusing phenomena”, Reviews in Physics (2020) 5:100037. doi:10.1016/j.revip.2019.100037
12. Biondini G, Mantzavinos D, “Universal nature of the nonlinear stage of modulational instability”, Phys Rev Lett (2016) 116:043902. doi:10.1103/PhysRevLett.116.043902
13. Biondini G, Li S, Mantzavinos D, Trillo S. Universal behavior of modulationally unstable media. SIAM Rev (2018) 60:888–908. doi:10.1137/17m1112765
14. Grinevich PG, Santini PM. The finite gap method and the analytic description of the exact rogue wave recurrence in the periodic NLS Cauchy problem. 1. Nonlinearity (2018) 31:5258–5308. doi:10.1088/1361-6544/aaddcf
15. Grinevich PG, Santini PM. The finite-gap method and the periodic NLS Cauchy problem of anomalous waves for a finite number of unstable modes. Russ Math Surv (2019) 74:211–263. doi:10.1070/rm9863
16. Bilman D, Ling L, Miller PD. Extreme superposition: rogue waves of infinite order and the Painlevé-III hierarchy. Duke Math J (2020) 169:671–760. doi:10.1215/00127094-2019-0066
17. Bilman D, Miller PD. A robust inverse scattering transform for the focusing nonlinear schrödinger equation. Commun Pure Appl Math (2019) 72:1722–1805. doi:10.1002/cpa.21819
18. Slunyaev AV, Pelinovsky EN, “Role of multiple soliton Interactions in the generation of rogue waves: the modified Korteweg-de Vries framework”, Phys Rev Lett (2016) 117:214501. doi:10.1103/PhysRevLett.117.214501
19. Bilman D, Buckingham R. Large-order asymptotics for multiple-Pole solitons of the focusing nonlinear schrödinger equation. J Nonlinear Sci (2019) 29:2185–2229. doi:10.1007/s00332-019-09542-7
20. Chen J, Pelinovsky DE, “Rogue periodic waves of the focusing nonlinear Schrödinger equation”, Proc R Soc A (2018) 474:20170814. doi:10.1098/rspa.2017.0814
21. Kedziora DJ, Ankiewicz A, Akhmediev N. Rogue waves and solitons on a conoidal background. Eur Phys J Spec Top (2014) 223:43–62. doi:10.1140/epjst/e2014-02083-4
22. Feng BF, Ling L, Takahashi DA. Multi‐breather and high‐order rogue waves for the nonlinear Schrödinger equation on the elliptic function background. Stud Appl Math (2020) 144:46–101. doi:10.1111/sapm.12287
23. Chen J, Pelinovsky DE, White RE, “Periodic standing waves in the focusing nonlinear Schrödinger equation: rogue waves and modulation instability”, Physica D (2020) 405:132378. doi:10.1016/j.physd.2020.132378
24. Bronski JC, Hur VM, Johnson MA. “Instability in equations of KdV type”, In: New approaches to nonlinear waves, lecture notes in phys. Cham: Springer (2016) 908:83–133.
25. Kamchatnov AM. On improving the effectiveness of periodic solutions of the NLS and DNLS equations. J Phys Math Gen (1990) 23:2945–2960. doi:10.1088/0305-4470/23/13/031
26. Kamchatnov A. New approach to periodic solutions of integrable equations and nonlinear theory of modulational instability. Phys Rep (1997) 286:199–270. doi:10.1016/s0370-1573(96)00049-x
27. Deconinck B, Segal BL. The stability spectrum for elliptic solutions to the focusing NLS equation. Physica D (2017) 346:1–19. doi:10.1016/j.physd.2017.01.004
28. Deconinck B, Upsal J. The orbital stability of elliptic solutions of the focusing nonlinear schrödinger equation. SIAM J Math Anal (2020) 52:1–41. doi:10.1137/19m1240757
29. Upsal J, Deconinck B. Real Lax spectrum implies spectral stability. Stud Appl Math (2020) 145:765–790. doi:10.1111/sapm.12335
30. Xu G, Chabchoub A, Pelinovsky DE, Kibler B, “Observation of modulation instability and rogue breathers on stationary periodic waves”, Phys Rev Res (2020) 2:033528. doi:10.1103/physrevresearch.2.033528
31. Akhmediev NN, Eleonskii VM, Kulagin NE. Exact first-order solutions of the nonlinear Schrödinger equation. Theor Math Phys (1987) 72:809–818. doi:10.1007/bf01017105
32. Akhmediev N, Ankiewicz A, Soto-Crespo JM, “Rogue waves and rational solutions of the nonlinear Schrödinger equation”, Phys Rev E Stat Nonlinear Soft Matter Phys (2009) 80:026601. doi:10.1103/PhysRevE.80.026601
33. Kimmoun O, Hsu HC, Branger H, Li MS, Chen YY, Kharif C, et al. Modulation instability and phase-shifted Fermi-pasta-ulam recurrence, Sci Rep (2016) 6:28516. doi:10.1038/srep28516
34. Chen J, Pelinovsky DE, White RE, “Rogue waves on the double-periodic background in the focusing nonlinear Schrödinger equation”, Phys Rev E (2019) 100:052219. doi:10.1103/PhysRevE.100.052219
35. Calini A, Schober CM. Characterizing JONSWAP rogue waves and their statistics via inverse spectral data. Wave Motion (2017) 71:5–17. doi:10.1016/j.wavemoti.2016.06.007
36. Conforti M, Mussot A, Kudlinski A, Trillo S, Akhmediev N, “Doubly periodic solutions of the focusing nonlinear Schrödinger equation: recurrence, period doubling, and amplification outside the conventional modulation-instability band”, Phys Rev A (2020) 101:023843. doi:10.1103/physreva.101.023843
37. Vanderhaegen G, Szriftgiser P, Naveau C, Kudlinski A, Conforti M, Trillo S, et al. Observation of doubly periodic solutions of the nonlinear Schrödinger equation in optical fibers. Opt Lett (2020) 45:3757–3760. doi:10.1364/OL.394604
38. Smirnov AO. Solution of a nonlinear Schrödinger equation in the form of two-phase freak waves. Theor Math Phys (2012) 173:1403–1416. doi:10.1007/s11232-012-0122-6
39. Smirnov AO. Periodic two-phase “Rogue waves”. Math Notes (2013) 94:897–907. doi:10.1134/s0001434613110266
40. Wright OC. Effective integration of ultra-elliptic solutions of the focusing nonlinear Schrödinger equation. Phys Nonlinear Phenom (2016) 321-322:16–38. doi:10.1016/j.physd.2016.03.002
41. Bertola M, El GA, Tovbis A, “Rogue waves in multiphase solutions of the focusing nonlinear Schrödinger equation”, Proc R Soc A (2016) 472:20160340. doi:10.1098/rspa.2016.0340
42. Bertola M, Tovbis A. Maximal amplitudes of finite-gap solutions for the focusing Nonlinear Schrödinger equation. Commun Math Phys (2017) 354:525–47. doi:10.1007/s00220-017-2895-9
43. Wright OC. Sharp upper bound for amplitudes of hyperelliptic solutions of the focusing nonlinear Schrödinger equation. Nonlinearity (2019) 32:1929–1966. doi:10.1088/1361-6544/aafbd2
44. Sulem C, Sulem PL, The nonlinear Schrödinger equation: self-focusing and wave collapse. In: Applied mathematical sciences. New York: Springer-Verlag (1999) 139.
45. Fibich G, The nonlinear Schrödinger equation: singular solutions and optical collapse. In: Applied mathematical sciences. New York: Springer-Verlag (2015) 192.
Keywords: modulational instability, double-periodic solutions, Floquet spectrum, nonlinear Schrödinger equation, standing waves
Citation: Pelinovsky DE (2021) Instability of Double-Periodic Waves in the Nonlinear Schrödinger Equation. Front. Phys. 9:599146. doi: 10.3389/fphy.2021.599146
Received: 26 August 2020; Accepted: 04 January 2021;
Published: 22 February 2021.
Edited by:
Heremba Bailung, Ministry of Science and Technology, IndiaReviewed by:
Maximo Aguero, Universidad Autónoma del Estado de México, MexicoConstance Schober, University of Central Florida, United States
Copyright © 2021 Pelinovsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dmitry E. Pelinovsky, ZG1wZWxpQG1hdGgubWNtYXN0ZXIuY2E=
 Dmitry E. Pelinovsky
Dmitry E. Pelinovsky