Machine Learning in Model-free Mechanical Property Imaging: Novel Integration of Physics With the Constrained Optimization Process

1 Introduction

Soft tissues are complex structures that exhibit non-linear, time-dependent elastic properties. Variations in mechanical properties can provide information pertaining to tissue health, including detecting and diagnosing lesions of the breast [6, 34], liver [26, 47, 56], and thyroid [9, 10, 54], monitoring thermal lesions during ablation therapy [41, 53], and characterizing atherosclerotic plaques [2, 3, 11]. Conventional medical imaging modalities are insensitive to this mechanical contrast. Elasticity imaging methods have been developed to fill this niche and directly evaluate the mechanical properties of soft tissue.

Elasticity imaging can be largely grouped into quasi-static or dynamic methods based on the type of mechanical stimulus applied to induce tissue motion. Comprehensive reviews of the various techniques can be found in several articles [33, 35, 38, 39, 46, 52]. We focus our discussion on quasi-static ultrasound elastography (QUSE), wherein local tissue displacements are estimated from RF echo frames acquired as an ultrasound probe is slowly pressed into the tissue surface. Quasi-static loading allows time for the force stimulus to propagate through the entire tissue section. The resulting force-displacement measurements at points provide an enormous amount of information pertaining to tissue material properties throughout the contiguous volume and at boundaries.

Estimating material properties from force-displacement measurements constitutes the inverse problem in QUSE. The majority of quantitative QUSE approaches are built upon model-based optimization methods. While effective, model-based methods are prone to modeling errors that can lead to artifacts in reconstructed images of pre-selected material property distributions. More importantly, mathematically defined constitutive models are inherently limited in their ability to capture material behavior. This limitation could preclude discovery of clinically relevant soft tissue material properties.

Data-driven inverse methods circumvent modeling errors by removing the constitutive model assumption and building a soft-computational model of material behavior from measurement data. The Autoprogressive Method (AutoP) is one such method. Unlike other data-driven approaches, AutoP combines physical modeling through finite element analysis (FEA) with artificial neural networks (ANNs) to extract the stress-strain relationship embedded within force-displacement measurements. In the context of elasticity imaging, ANNs characterizing the stress-strain behavior of soft tissues can be interrogated to infer material parameters that best summarize the learned mechanical properties.

Many of the research articles that employed AutoP have described the training process, but none have directly compared and contrasted its operation with the more typical model-based approaches. In this review, we aim to more thoroughly examine the operating principles behind AutoP to better highlight the fundamental differences when compared to model-based inverse methods. Of particular importance is the manner in which physical principles are directly exploited in AutoP to generate increasingly accurate estimates of stress and strain distributions from force-displacement measurements under arbitrary geometry and loading. We believe the working principles of AutoP can be applied as a data-driven, physics-guided alternative to other difficult boundary value inverse problems.

Section 2 reviews model-based inverse methods in QUSE to establish a basis for comparison. We focus on iterative methods utilizing FEA as the forward solver to keep the discussion concise and comparable to AutoP. Section 3 reviews AutoP and builds intuition of its operation by drawing parallels to typical optimization methods. We also cover a novel neural network architecture developed for QUSE and a regularization term uniquely suited for AutoP. Challenges with non-linear viscoelasticity imaging and potential approaches with alternative ANN structures are briefly discussed in Section 4. Data acquisition and displacement estimation details are omitted from our discussions, but are available in [24, 25]. Even though such details are important in practice and will affect the efficacy of QUSE methods, we wish to compare the operation of AutoP and model-based methods at a more conceptual level.

2 Model-Based Inverse Methods

Reconstructing a map of material properties from force-displacement measurements is an ill-posed inverse problem.¹ By combining a prior assumption of the underlying mechanical behavior with a system model incorporating physical principles, model-based inverse methods reduce the solution space and estimate parameter values of a pre-selected constitutive model. The goal of QUSE methods is to find the set of spatially distributed material parameters $\theta \left(x\right)$ that minimize the difference between displacements $U\left(x\right)$ computed in a forward problem and measured displacements $\tilde{U}\left(x\right)$,

$\widehat{\theta }=\underset{\theta \in \mathrm{ℝ}}{\text{argmin}}{\displaystyle {\int }_{\text{Ω}}\mathcal{C}\left(U,\tilde{U}\right)}d\Omega ,(1)$

where $\text{Ω}$ denotes domain of the scan plane(s). The dependence of variables on position $x$ is assumed and not explicitly stated to simplify notation. The cost function $\mathcal{C}$ in Eq. 1 is often defined as the $L_2$-norm of the difference between computed and measured displacements, augmented by a regularization term $\mathrm{ℛ}\left(\theta \right)$ acting on the set of parameters,

$\mathcal{C}\left(U,\tilde{U}\right)=\frac{1}{2}{\left(U-\tilde{U}\right)}^2+\alpha \mathrm{ℛ}\left(\theta \right),(2)$

where α is a hyperparameter that controls how strongly the regularization term affects the solution.

2.1 Finite Element Analysis

In modern methods, the forward problem is usually solved through finite element analysis (FEA). A brief description of the FEA formulation for solid mechanics follows; more thorough treatments can be found in [12, 18]. The strong form of the governing equations for a solid continuum under quasi-static loading is

$\nabla \cdot \mathit{\sigma }=0\text{in}\text{Ω},(3)$

$u=\tilde{u}\mathrm{on}{\Gamma }_D,(4)$

$\sigma \cdot n=\tilde{p}\mathrm{on}{\Gamma }_N,(5)$

where $\sigma$ denotes the stress tensor and $u$ are displacements throughout the continuum $\text{Ω}$. Displacement boundary conditions (BCs) are represented by $\tilde{u}$ whereas surface traction BCs are denoted by $\tilde{p}$. In the latter two equations, ${\text{Γ}}_D$ represents the set of boundary points over which displacements are measured, ${\text{Γ}}_N$ is the set of boundary points corresponding to measurements of surface tractions with surface normal $n$, and ${\text{Γ}}_D\cap {\text{Γ}}_N=\varnothing$.

The finite element formulation expresses the boundary-value problem as a system of equations,

$\left[K\left(\theta \right)\right]U=P,(6)$

$K\left(\theta \right)={\displaystyle \sum }^{N_e}{\displaystyle {\int }_{{\Omega }_e}{B}_e^T{D}_e\left(\theta \right)B_{e}d{\Omega }_e,}(7)$

$P={\displaystyle \sum }^{N_e}{\displaystyle {\int }_{{\Omega }_e}{B}_e^T{\sigma }_{e}d{\Omega }_e.}(8)$

where $N_e$ is the number of elements in the mesh, $B_e$ is the strain-displacement matrix for a given element, and the summation symbols represent the assembly operation. The matrix $K\left(\theta \right)$ is determined directly from the material property matrix $D\left(\theta \right)$. Any displacement BCs are imposed in global displacement vector $U$. Likewise, force BCs are included in the global force vector $P$.² We chose to express $P$ in Eq. 8 as a function of stress, instead of as a function of the surface traction BCs, to emphasize the relationship between stress and force. Generally, the solution for a mechanical system is found through FEA by discretizing the domain (i.e., “meshing”), applying load BCs in the global node force and displacement vectors, and solving for the remaining “free” nodal displacements and reaction forces.

FEA solutions of a mechanical system must satisfy both equilibrium and compatibility requirements. The former is specified by Eq. 8 and relates stresses to forces. Compatibility, on the other hand, relates displacements to strains and, in simple terms, precludes elements in the mesh from overlapping or separating during deformation. These physical principles combined with object geometry and a valid constitutive model determine the set of admissible deformations under loading (Figure 1A). The importance of these principles in solving the inverse problem will be made clear in the following sections.

FIGURE 1

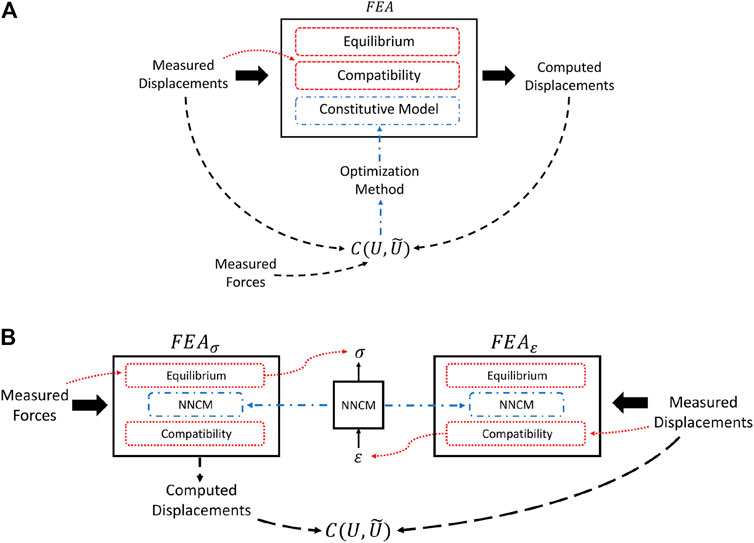
FIGURE 1. (A) Summary of model-based inverse methods. Deformations computed in the forward problem are dependent on the estimated material properties and physical principles. Existing model-based QUSE methods that utilize force measurements use the data as input directly to the cost function or to calibrate the magnitude of the modulus estimates after the optimization procedure. (B) Illustration of AutoP training process. Applying force and displacement measurements in separate FEAs exploits equilibrium and compatibility requirements to generate physically consistent stresses and strains.

2.2 QUSE as an Optimization Problem

Gradient or Hessian-based optimization techniques are typically applied to solve Eq. 1, wherein the parameter estimates are iteratively updated through the gradient of the error computed in Eq. 2. The solution process for QUSE can be generalized to five steps:

The diagram in Figure 1A provides a simplified illustration of the role of FEA within an optimization-based solution method while simultaneously highlighting the fact that the cost function directly affects estimated parameter values. Optimization methods often have intuitive geometric interpretations that aid in understanding the solution procedure. For example, consider the method proposed by Kallel and Bertrand [29]. Define the operator $\mathcal{T}\left(E\right)=U$ as the solution of a FEA where the material is assumed to be linear-elastic with spatial distribution of Young’s modulus $E\left(x\right)$. The goal is to find $E\left(x\right)$ that minimizes the cost function

$\mathcal{C}\left(E\right)=\frac{1}{2}{\Vert \tilde{U}-\mathcal{T}\left(E\right)\Vert }_2^2(9)$

$\widehat{E}=\underset{E\in {ℝ}^{+}}{\arg \min }\left[\mathcal{C}\left(E\right)\right],(10)$

where $\left|\right|\cdot \left|\right|{}_2$ is the $L_2$-norm and ${\mathrm{ℝ}}^{+}$ represents the set of positive-valued real numbers.

Adopting an iterative, Hessian-based solution procedure with k indicating the current iteration, the Young’s modulus values can be found,

$E_{k+1}=E_k+\Delta E_k(11)$

$\Delta E_k=\stackrel{H}{\overbrace{{\left(J_k^T{J}_k\right)}^{-1}}}{J}_k^T\Delta U_k(12)$

$\Delta U_k=\tilde{U}-\mathcal{T}\left(E_k\right)(13)$

$J_k=\frac{\partial \mathcal{T}\left(E\right)}{\partial E}(14)$

Geometrically, the curvature of the forward operator (the Hessian $H$), guides the Young’s modulus update in Eq. 12. A perhaps more intuitive geometric interpretation is achieved by setting the Hessian equal to the negative identity matrix $H=-I$, changing the update Eq. 11 to

${\mathit{E}}_{k+1}={\mathit{E}}_k-{\mathit{J}}_k^{\text{T}}\text{Δ}{\mathit{U}}_k.(15)$

In this form, the operator gradient forming the sensitivity matrix $J_k$ coupled with the displacement error directs the iterative parameter updates. Iterative QUSE methods typically follow a Hessian or gradient-based optimization procedure. A review of relevant methods can be found in [13, 36] Algorithm 1. We will show in Section 3 how displacement errors also influence the material properties learned by ANNs trained in AutoP, albeit indirectly.

Algorithm 1 Optimization-based QUSE Inverse Method.

[1] Apply displacement BCs at the mesh boundary

[2] Compute the displacements over the whole scan plane through FEA

[3] Compare the computed displacements to the measured values (i.e., evaluate Eq. 2)

[4] Update the parameter estimates based on the error

[5] If solution converges, exit, otherwise return to [1].

QUSE methods utilizing only displacement measurements can provide quantitative parameter estimates up to a multiplicative constant, unless the parameter value(s) is known for some portion of the boundary or interior [4, 5]. That is, through compatibility requirements embedded within FEA, at best the distribution of relative parameter values can be inferred from displacement BCs. Incorporating measurements of surface force or boundary stresses can provide the additional information necessary to estimate parameter values exactly [51]. This can be seen directly from Eqs. 5,8: if no values of reaction forces corresponding to displacement BCs are known, there exists no means to calibrate the magnitude of forces in $P$. In short, both equilibrium and compatibility requirements affect the solution in model-based QUSE but are not directly exploited.

Force and displacement measurements coupled with FEA are insufficient for overcoming the ill-posed nature of the inverse problem, hence the inclusion of a regularization term in Eq. 2. The choice of regularization depends on some presumed property of the solution; e.g., Tikhonov regularization is founded in energy arguments, $L_1$-norm to promote sparse solutions, or total variation to encourage smooth solutions [43]. Although effective and often necessary, the form of regularization will significantly alter the solution in model-based methods and requires skill in choosing appropriately. We will introduce a regularization term in Section 3.1 that is unique to AutoP and arises from physical principles, removing operator judgment from its use.

Model-based QUSE methods are effective when the applied load and true tissue material properties match the selected constitutive model and loading geometry. Choosing the wrong constitutive model can cause artifacts in the resulting elasticity images that corrupts or discards clinically relevant diagnostic information not described by the selected model parameters. The limited flexibility of model-based methods makes them ineffective at discovering material properties. Overcoming limitations of model-based methods and inferring mechanical behavior from measurement data without constraints imposed by constitutive model assumptions may allow investigators to find new clinically relevant material properties.

3 The Autoprogressive Method

Contrary to model-based inverse methods, the goal of AutoP is to describe the mechanical behavior of a material non-parametrically. By replacing the classic mathematically defined constitutive model with an artificial neural network, any arbitrary stress-strain relationship can be captured. This formulation replaces parameters in Eq. 1 with the connection weights of one or more ANNs³. The resulting, trained ANN describing the stress-strain behavior is referred to as a neural network constitutive model (NNCM). One example of a NNCM architecture is shown in Figure 2A (left). The NNCM displayed is a feed-forward, fully connected ANN that accepts a strain vector as input and returns a stress vector at the output. Alternative network architectures have been proposed by other investigators, but this form is the basis for most AutoP applications thus far. Even considering the various NNCM architectures utilized within AutoP, to the best of our knowledge all have comprised at most two hidden layers with up to a few dozen nodes each. Compared to deep-learning methods, NNCMs are very small ANNs.

FIGURE 2

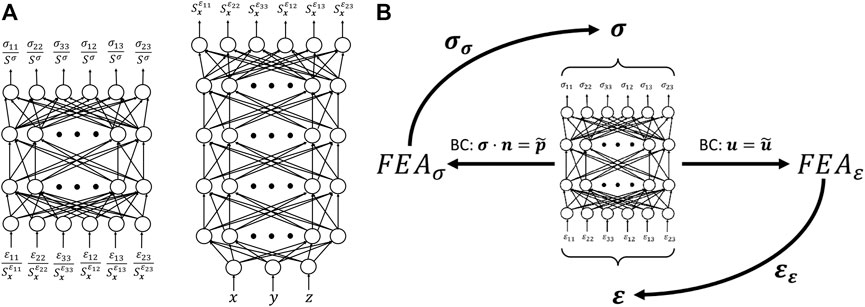
FIGURE 2. (A) A material property network (left) is the basis for many NNCM architectures previously used in AutoP. The combination of a spatial network (right) operating in tandem with a MPN is referred to as a CaNNCM. (B) Illustration of the self-learning property of AutoP.

Existing efforts to build model-free descriptions of material behavior typically rely on experimental test data acquired from a sample in a well-defined loading scenario, such as strip extensiometry, to obtain stress-strain data from force-displacement measurements. Recent investigations in data-driven mechanics use this type of measurement data directly (i.e., no NNCM) to solve computational mechanics problems [31, 32, 37, 50]. Alternatively, stress-strain measurement data can be used to train NNCMs for later use in computational problems (see reviews [14, 15, 44, 55]). More recently, researchers have developed physics-informed deep neural networks (PINNs) that embed physical laws into the cost function used in backpropagation-based training [40].

Some measure of success has been achieved with each of these methods; however, the resulting soft-computational constitutive model, in whichever applicable form, is fully defined by the measurement data acquired from a homogeneous sample. That is, the models are trained once and deployed. When used for inference against input data not within the domain of the training set, the solution becomes unreliable, analogous to modeling errors in model-based inverse methods. Furthermore, these methods rely on the existence of stress-strain training data. Unfortunately, the complexity of soft tissues precludes excision of geometrically precise, homogeneous samples for measurement in well-defined loading scenarios. Nor do ex vivo load tests provide a good measure of soft tissue properties in vivo. In short, current data-driven methods fail to extract relevant information from the available force-displacement measurements acquired in a normal clinical setting.

The Autoprogressive Method [17] circumvents limitations with model-based and other data-driven methods through a tight coupling of NNCMs with FEA and knowledge of both internal and external object geometry. It has been successfully used to build soft-computational mechanical models of many different materials in a multitude of loading scenarios, including soils [19, 20], concrete [27, 28], steel [30, 57], red blood cells [48, 49], and the cornea [16]. AutoP has even been applied to thermal constitutive models [1]. More recently, we have been developing an adaptation of AutoP for QUSE using both boundary and interior displacement measurements [22]. The caveat that internal geometry must be known precludes most clinical imaging applications and is addressed by introducing a new type of NNCM, discussed in Section 3.1.

AutoP is a method for generating information from measurements. When applied to inverse problems in continuum mechanics, the goal is to recover the stress and strain fields induced by measured forces and displacements in a model-free way. Replacing the mathematical constitutive model with an ANN is paramount to provide the flexibility inherent to said networks, but alone is not a sufficient strategy. The two key components that make AutoP work are 1) the application of force and displacement BCs in separate FEAs—FEA_σ and FEA_ε—to obtain physically consistent estimates of stresses and strains through known physical principles and 2) NNCMs participate in the generation of their own training data by acting as the material model in the assembly of the system of equations in Eq. 6. The former point is analogous to model-based inverse methods wherein the parameter estimates in the current iteration affect the displacements computed in the forward problem. For clarity, the FEA equations can be rewritten as

${\sigma }^{NN}=\text{NN}\left(\mathit{\epsilon }\right),(16)$

$D^{NN}=\frac{\partial {\sigma }^{NN}}{\partial \mathit{\epsilon }},(17)$

$K\left(\theta \right)={\displaystyle \sum }^{N_e}{\displaystyle {\int }_{{\Omega }_e}{B}_e^T{D}_e^{NN}\left(\theta \right)B_{e}d{\Omega }_e},(18)$

$P={\displaystyle \sum }^{N_e}{\displaystyle {\int }_{{\Omega }_e}{B}_e^T{\sigma }_e^{NN}d{\Omega }_e}.(19)$

We introduce the operator $\text{NN}(\cdot )$ to represent inference by the NNCM. The analytical expression for $D^{NN}$ is derived in [21].

Imposing measured forces and displacements in separate FEAs exploits stress equilibrium and compatibility requirements. In FEA_σ, measured forces are applied as force BCs $\left(\sigma \cdot n=\tilde{p}\right)$⁴. Stress equilibrium, defined in Eq. 3, relates forces to stresses and we therefore claim the stresses ${\sigma }_{\sigma }$ computed in FEA_σ are physically consistent approximations of the true stress field. In a separate FEA_ε, corresponding displacement measurements are applied as displacement BCs $\left(u=\tilde{u}\right)$. Because compatibility requirements relate displacements to strain, we claim the strains ${\epsilon }_{\epsilon }$ computed in FEA_ε are physically consistent approximations of the true strain field. The AutoP training process is summarized in Figure 1B and can be broken into the five steps listed in Algorithm 2.

Algorithm 2 AutoP Training of NNCMs.

[0] Linear-elastic NNCM pretraining

[1] Apply force BCs in FEA_σ, compute ${\sigma }_{\sigma }$

[2] Apply displacement BCs in FEA_ε, compute ${\epsilon }_{\epsilon }$

[3] Train NNCM(s)

[4]If displacement error converged, exit, otherwise return to [1].

Linear-elastic pretraining is used only to provide NNCMs with a physically consistent starting state. Unlike model-based reconstruction methods that can be sensitive to parameter initialization [4], investigations with AutoP have demonstrated that linear-elastic pretraining does not constrain the mechanical properties learned by the NNCMs.

Convergence in AutoP is determined by comparing the values of a cost function to predefined limits. In most AutoP applications thus far, the cost function has assumed the form [17].

$\Phi \left(\theta \right)={\Vert U-\tilde{U}\Vert }_1.(20)$

Aside from the use of the $L_1$-norm to diminish the effects of outliers, it is important to note that the magnitude of the cost function has no direct effect on the backpropagation-based training of the NNCMs. Even so, training the NNCMs with the stresses and strains computed in FEA_σ and FEA_ε, respectively, adjust the connection weights so that the material properties described by the NNCMs more accurately resemble the true material properties. We also note that the because the cost function does not directly influence NNCM training, adjustments to $\Phi \left(\theta \right)$ do not significantly affect AutoP whereas altering the cost function in model-based inverse methods can significantly change the resulting parameter estimates.

It is not immediately clear why the combination of the stresses and strains from FEAs solved under separate, but conjugate, boundary conditions should lead the ANNs to the correct material properties. We will demonstrate that it is in fact an implicit displacement error that guides the learning process. Define $u_{\sigma }$ to be the full set of displacements computed in the solution of FEA_σ, including any imposed BCs. Likewise, $u_{\epsilon }$ represents the displacements computed in the solution of FEA_ε. By definition of a NNCM, ${\sigma }^{NN}=NN\left(\epsilon \right)=NN\left[f_u\left(u\right)\right]$, where ${\text{f}}_u(\cdot )$ is a function that receives a displacement vector as input and returns the corresponding strain vector. Let $\Delta u=u_{\sigma }-u_{\epsilon }$. Thus, $u_{\sigma }=u_{\epsilon }+\Delta u$ and therefore ${\sigma }_{\sigma }=NN\left[f_u\left(u_{\epsilon }+\Delta u\right)\right]$. What does this mean? Inference by the NNCM using physically consistent strains ${\epsilon }_{\epsilon }$ as input results in physically consistent stresses ${\sigma }_{\sigma }$ only when the input is augmented by the displacement error.

To better understand this interaction, assume the NNCM describes a linear-elastic material so that ${\sigma }^{NN}\approx D^{NN}\cdot \epsilon$ and deformation is infinitesimal, leading to ${\text{f}}_u\left(u+\text{Δ}u\right)={\text{f}}_u\left(u\right)+{\text{f}}_u\left(\text{Δ}u\right)$. We also denote the strains computed in FEA_σ as ${\mathit{\epsilon }}_{\sigma }$ while ${\sigma }_{\epsilon }=NN\left({\epsilon }_{\epsilon }\right)$ are the stresses output by the NNCM when strains computed in FEA_ε are supplied as input to the network. Training a NNCM with a backpropagation-based method consists of minimizing a cost function, in this case

${\widehat{R}}_{{\theta }_m}=\underset{R_{{\mathit{\theta }}_m}\in \mathrm{ℝ}}{\text{argmin}}\frac{1}{2}{\Vert \overline{{\sigma }_{\sigma }}-{\sigma }_{\epsilon }\left({\epsilon }_{\epsilon };R_{{\theta }_m}\right)\Vert }^2(21)$

$=\underset{R_{{\mathit{\theta }}_m}\in \mathrm{ℝ}}{\text{argmin}}\frac{1}{2}\Vert {\overline{NN}\left({\mathit{\epsilon }}_{\sigma }\right)-NN\left({\epsilon }_{\epsilon };R_{{\theta }_m}\right)\Vert }^2,(22)$

where $R_{{\theta }_m}$ denotes the NNCM connection weights and the overline is used to indicate a constant term. $\overline{NN}$ is the same NNCM used to solve FEA_σ and FEA_ε whereas $NN\left({\epsilon }_{\epsilon };\theta \right)$ changes each training iteration as the NNCM weights are updated. Applying the aforementioned linear approximations, Eq. 22 can be expressed as

${\widehat{R}}_{{\theta }_m}=\underset{R_{{\mathit{\theta }}_m}\in \mathrm{ℝ}}{\text{argmin}}\frac{1}{2}{\Vert \overline{NN}\left[{\text{f}}_u\left(u_{\epsilon }+\Delta u\right)\right]-NN\left[{\text{f}}_u\left(u_{\epsilon };R_{{\theta }_m}\right)\right]\Vert }^2(23)$

$\approx \underset{R_{{\theta }_m}\in \mathrm{ℝ}}{\text{argmin}}\frac{1}{2}{\Vert \overline{D^{NN}}\cdot \left[{\text{f}}_u\left(u_{\epsilon }+\Delta u\right)\right]-D^{NN}\left(R_{{\theta }_m}\right)\cdot \left[{\text{f}}_u\left(u_{\epsilon }\right)\right]\Vert }^2(24)$

If we consider the first iteration of training when $\overline{D^{NN}}=D^{NN}\left(R_{{\theta }_m}\right)$, the cost function further reduces to

$\approx \underset{R_{{\theta }_m}\in \mathrm{ℝ}}{\text{argmin}}\frac{1}{2}{\Vert D^{NN}\cdot {\text{f}}_u\left(\Delta u\right)\Vert }^2,(25)$

and reverts back to Eq. 24 after the first training iteration and the NNCM weights $R_{{\mathit{\theta }}_m}$ change.

The preceding argument does not imply NNCMs trained in AutoP are limited to learning linear-elastic material properties. Rather, the case of linear materials was chosen as an example to best highlight the effect of displacement error in NNCM training. We emphasize that, similar to model-based methods, the displacement error is a driving force in the solution of the inverse problem as approached through AutoP. However, in the case of AutoP, the effect of displacement error emerges from the inconsistency between stresses and strains computed in FEA_σ and FEA_ε. It is a characteristic that arises out of the equilibrium and compatibility requirements rather than an explicitly defined error measure to direct the parameter search.

Much like optimization-based methods, the parameter estimates in the current iteration—the weights of the ANNs—affect the solution of the forward problem. Moreover, the error when comparing the forward problem solution to experimental measurements affects the parameter updates. What sets AutoP apart from typical model-based and machine learning techniques is its self-learning paradigm guided by physical principles. When applied to QUSE, the result is a patient-specific soft-computational material model. Figure 2B aims to illustrate the self-learning property of AutoP. Imposing measurement data as BCs in separate FEAs forces the material properties learned by the ANNs to satisfy physical principles and be self-consistent.

3.1 Cartesian NNCMs

The discussion of AutoP thus far has assumed that the finite element mesh conformed to both internal and external object geometry with a different NNCM assigned for each unique material. Eq. 18 implies this fact in that $D_e^{NN}\left(\theta \right)$ is constant over the entire domain of an element. The FEA solution procedure requires the appropriate NNCM to be selected for the element when evaluating the integral. This formulation of AutoP is not suitable for biomedical imaging applications because the internal tissue structure is normally not known a priori nor segmented into discrete regions with homogeneous material properties. As a consequence, the goal of AutoP must be adjusted to infer both material properties and geometry from the set of force-displacement measurements.

Two significant changes were made toward this goal. First, the structure of the NNCM was changed by adding a second network that interacted with the existing NNCM and was responsible for learning spatial information. We deemed these networks Cartesian neural network constitutive models (CaNNCMs) [23–25]. The CaNNCM architecture is illustrated in Figure 2A. To identify the individual subnetworks, we refer to the one which learns the “average” stress-strain relationship of the entire object as the material property network (MPN, Figure 2A left) and the network that maps a Cartesian coordinate input to a spatially varying value as the spatial network (SN, Figure 2A right). A thorough description of CaNNCM theory of operation can be found in [23, 24]. Unlike NNCMs previously utilized with AutoP, a single CaNNCM is capable of characterizing the heterogeneous material properties of an entire object. The FEA equations are adjusted slightly to accommodate this change:

$K\left(\theta \right)={\displaystyle \sum }^{N_e}{\displaystyle {\int }_{{\Omega }_e}{B}_e^T{D}^{NN}\left(x,\theta \right)B_{e}d{\Omega }_e},(26)$

$P={\displaystyle \sum }^{N_e}{\displaystyle {\int }_{{\Omega }_e}{B}_e^T{\sigma }^{NN}\left(x\right)d{\Omega }_e}.(27)$

Spatial information is encoded within a set of spatial scaling values $S_x^{\epsilon }$ . The SN is responsible for learning the mapping $\mathrm{SN}:x\to S_x^{\epsilon }$. Given a spatial location and strain vector, the SN provides the corresponding $S_x^{\epsilon }$ and the stress vector is then calculated as ${\sigma }^{NN}\left(\epsilon ,x\right)=NN\left(\epsilon /S_x^{\epsilon }\right)$, where the division is element-wize and the operator $NN(\cdot )$ refers to the MPN. Determining the spatial values is not trivial, although they can be readily computed from the stresses and strains already available in AutoP in conjunction with the MPN, as detailed in [23]. AutoP training must also be adjusted to accommodate CaNNCMs as described in Algorithm 3.

Algorithm 3 AutoP Training of CaNNCMs.

[0] Pretrain CaNNCM as homogeneous, linear-elastic material

[1] Apply force BCs in FEA_σ, compute ${\sigma }_{\sigma }$

[2] Apply displacement BCs in FEA_ε, compute ${\epsilon }_{\epsilon }$

[3] Train MPN

[4a] Update $S_x^{\epsilon }$

[4b] Train SN

[5]If displacement error converged, exit, otherwise back to [1].

CaNNCMs work well in QUSE because information pertaining to the interior geometry can be gleaned from internal displacement measurements available through US imaging. In unpublished work, we found that CaNNCMs trained in AutoP using only boundary information were unable to recover internal structure away from the surface. Part of the shortcoming is due to the lack of surface force distribution measurements. Rather, the force measured experimentally is the sum of forces over the face of the US transducer that provides information about the mean stress distribution over the surface. Coupling these boundary data with prior knowledge of internal geometry is sufficient for a set of NNCMs to learn the heterogeneous material properties of an object. Therefore, in order for CaNNCMs to learn both material properties and geometry, some measurement data containing spatial information must be provided.

Interestingly, we found that incorporating internal displacements in FEA_ε was insufficient for accurately estimating material property distributions, particularly when measurements were acquired by loading from a single direction [25]. The reason can be seen from Eq. 27. By making the stress term explicitly dependent on spatial position, additional force measurements populating $P$ are required to ensure the internal resisting forces computed within the integral are correctly calibrated. Acquiring measurements from multiple sides and loading angles provides an immense amount of information for CaNNCMs at the cost of significantly increased FE modeling complexity and computational load.

An alternative strategy is to add a regularization term to augment the available information. Our solution was to add additional physical constraints during the calculation of $S_x^{\epsilon }$ in Step 4a of AutoP. To understand the functionality of the regularization term, we first summarize the detailed methods in [23]. The spatial values are computed by minimizing a cost function very similar to Eq. 21, with the primary difference being the parameters over which the function is minimized changes from the MPN connection weights to the spatial values,

$\widehat{S_x^{\epsilon }}=\underset{S_x^{\epsilon }\in ℝ}{\text{argmin}}\frac{1}{2}{\Vert \overline{{\sigma }_{\sigma }}-{\sigma }_{\epsilon }\left({\epsilon }_{\epsilon }/S_x^{\epsilon };R_{{\theta }_m}\right)\Vert }^2(28)$

The purpose of the spatial values is to further reduce the error in Eq. 21 by storing the information not captured by the spatially independent MPN weights.

Implementing Eq. 28 in AutoP as defined will lead to erroneous material property distribution estimates. Perhaps the most intuitive explanation starts by noting the CaNNCM is pretrained as a homogeneous, linear-elastic material. Then, when computing spatial values in Step 4a, the $S_x^{\epsilon }$ found as the solution of Eq. 28 map a heterogeneous strain field to a homogeneous stress field because the surface force BCs applied in FEA_σ contain no spatial information.

We introduced σ-matching regularization to inject spatial information into Eq. 28 by imposing the physical constraint that conjugate force-displacement BCs imposed in separate FEAs should produce the same stress fields,

${\mathrm{ℛ}}_{\sigma }=\left|\overline{{\sigma }_{\sigma }}-\overline{{\sigma }_{\epsilon }}\right|\cdot \text{sign}\left(\overline{{\sigma }_{\sigma }}\right).(29)$

Note that the stress terms are constant, hence the multiplication by $\text{sign}\left(\overline{{\sigma }_{\sigma }}\right)$ to account for the lack of gradient information. We again chose the $L_1$-norm to reduce the effects of outliers. If the same linear approximations from Eq. 21 are applied to the σ-matching term, we can show that the displacement error is influencing the result:

${\mathrm{ℛ}}_{\sigma }=\left|\overline{NN}\left({\epsilon }_{\sigma }\right)-\overline{NN}\left({\epsilon }_{\epsilon }\right)\right|\cdot \text{sign}\left(\overline{{\sigma }_{\sigma }}\right),(30)$

$\approx \left|\overline{D^{NN}}\cdot {\text{f}}_u\left(u_{\epsilon }+\Delta u\right)-\overline{D^{NN}}\cdot {\text{f}}_u\left(u_{\epsilon }\right)\right|\cdot \text{sign}\left(\overline{{\sigma }_{\sigma }}\right),(31)$

$\approx |\overline{D^{NN}}\cdot {\text{f}}_u\left(\Delta u\right)|\cdot \text{sign}\left(\overline{{\sigma }_{\sigma }}\right).(32)$

Adding the regularization term to the cost function for computing ${\mathit{S}}_{\mathit{x}}^{\epsilon }$ with free parameter ${\beta }_{\sigma }$ to control its influence on the solution, Eq. 28 becomes

$\widehat{S_x^{\epsilon }}=\underset{S_x^{\epsilon }\in ℝ}{\text{argmin}}\frac{1}{2}{\Vert \overline{{\sigma }_{\sigma }}-{\sigma }_{\epsilon }\left({\epsilon }_{\epsilon }/S_x^{\epsilon };R_{{\theta }_m}\right)+{\beta }_{\sigma }{\mathrm{ℛ}}_{\sigma }\Vert }^2.(33)$

A significant difference between regularization terms typically used in model-based inverse methods and 33) is the appearance of σ-matching within the $L_2$-norm. Because it is constant, simply adding the σ-matching term to the existing cost function would have no effect on the computed spatial values. Adding σ-matching as we have in Eq. 33 can be interpreted as adjusting the (constant) stresses ${\overline{\sigma }}_{\sigma }$ computed in FEA_σ with spatial information encoded within displacement measurements through the displacement error.

We demonstrated in [25] the significant improvement in material property estimates when σ-matching was incorporated into AutoP training, even with a relatively sparse set of force-displacement measurements. Contrary to typical forms of regularization, σ-matching is based on a physical principle that will always be true, not a prior assumption about the property the solution should exhibit. Furthermore, it is uniquely suited to AutoP because of the way equilibrium and compatibility requirements are exploited by FEA_σ and FEA_ε. Other constraints on physical properties will likely be incorporated into AutoP as CaNNCMs are further developed for imaging the non-linear and time-dependent properties of soft tissues.

4 Non-linear Elasticity Imaging with AutoP

The preceding discussion of NNCMS and AutoP was limited to objects under loads inducing small deformation. Mathematically, the strain tensor in the limit of infinitesimal deformation is expressed as $\mathit{\epsilon }=\frac{1}{2}\left(\nabla u+\nabla u^T\right)$. Under this linear kinematic assumption, appropriate when induced strains are less than 5%, elastic solids can be adequately described by a linear-elastic constitutive model.

Probing the non-linear mechanical properties of deep structures in QUSE requires application of large loads to sufficiently deform distal tissues. In these scenarios, a large deformation framework must be invoked wherein the strain tensor includes geometrically non-linear terms. As an example, one potential definition of geometrically non-linear strain is $\mathit{\epsilon }=\frac{1}{2}\left(\nabla u+\nabla u^T+\nabla u^T\nabla u\right)$. Application of large compressive loads coupled with the non-linear and time-dependent mechanical behavior of soft tissues implies that one or two linear-elastic parameters are ineffective for clinical QUSE. More importantly, the complex non-linear and viscoelastic properties of soft tissues may provide a significant amount of diagnostic information [42], reinforcing the value of reconstructing elasticity images beyond shear modulus.

The problem then arises of selecting an appropriate non-linear and/or viscoelastic constitutive model that describes tissue behavior and maximizes the diagnostic information in QUSE images. Complexity is further increased when considering the likelihood that different tissues or tissue states (i.e., healthy tissue, benign lesions, and malignant tumors) are best described by different material models. Current model-based approaches assume homogeneity of the underlying constitutive model for the entire imaged tissue section and estimate the spatial variation of the corresponding model parameters. There exists no model-based QUSE inverse method capable of discovering the set of constitutive models—and estimating values of the corresponding parameters—that adequately describes a heterogeneous group of tissues. The combination of AutoP with CaNNCMs can fill this void.

AutoP has been applied to build soft-computational models of complex materials undergoing small and large deformation when the total geometry was known (e.g. [19, 27, 28, 30, 45, 58]). To achieve non-linear, time-dependent material property imaging with AutoP, CaNNCMs must be modified to 1) accommodate geometrically non-linear deformation to facilitate non-linear elasticity imaging and 2) incorporate additional stress-strain state information as network input to properly capture a heterogeneous distribution of complex mechanical behaviors. Prior successes with AutoP lead us to believe there exists an adaptation to the CaNNCM architecture and/or AutoP that will accomplish both tasks.

The difficulty of this problem can be understood by comparing the information required for a NNCM to compute a stress vector for materials of varying complexity. For linear-elastic materials, the NNCM output is defined as ${\sigma }^{NN}=NN\left(\epsilon \right)$. Non-linear, viscoelastic materials require time information to fully define the stress-strain response, ${\sigma }^{NN}=NN\left(\epsilon ,t\right)$. It is further complicated for objects under large deformation because of the need to account for differences in Lagrangian and Eulerian descriptions of stress and strain. It is clear the NNCM inputs must be changed. Our current work is toward the goal of identifying a NNCM architecture capable of learning the stress-strain response of hyperelastic materials.

Projecting further, adjustments to the CaNNCM architecture will also be necessary to characterize a heterogeneous distribution of non-linear, viscoelastic materials. If the operating principle of linear-elastic CaNNCMs is retained, the stress-strain response would take the form ${\sigma }^{NN}=NN\left(\epsilon /S_x^{\epsilon },t\right)$, where spatial information is again encoded within the spatial scaling values $S_x^{\epsilon }$ . Less obvious from this relationship is the necessity of stress-strain state information at the spatial network input to account for the non-linear and time-dependent stress responses. This requirement can be understood by expanding on the explanation provided in [24] for the operation of spatial scaling values. When all materials are linear-elastic, the stiffness matrix $D^{NN}$ (recall its use in Eq. 18) computed from the weights of the MPN is constant. The role of $S_x^{\epsilon }$ is to vary the effective “stiffness” described by $D^{NN}$ based on position. Because the materials considered were linear-elastic, the modified stiffness matrix is independent of time and state of deformation, meaning $S_x^{\epsilon }$ is constant at $x$. Conversely, $D^{NN}$ computed from a non-linear MPN will not be constant, nor will the rate at which it changes be the same at all points. Therefore, values of $S_x^{\epsilon }$ will need to change based not only on position, but also the current (or previous) stress-strain states.

5 Discussion

Quantitative elasticity imaging is a challenging problem. Much of the difficulty arises from the limited measurement data that can be acquired during a clinical US imaging exam. Model-based inverse methods address the ill-posed inverse problem by constraining the solutions through geometric and constitutive model assumptions, well-defined force loads, and application of regularization to the solution. While effective, deviation of measurement data from the model assumptions can introduce large artifacts in the reconstructed material property images, potentially corrupting diagnostic information, and the regularization method is almost never grounded in physical laws. Furthermore, parameters associated with the pre-selected constitutive model may only capture a portion of the tissue mechanical properties, missing information that could be important to clinical decision making.

AutoP and NNCMs are a fundamentally different approach to the inverse problem in elasticity imaging. Rather than constraining the solution through model assumptions, AutoP extracts material property information from force-displacement measurements through a combination of physical modeling and machine learning. In this review, we presented AutoP in a new way to highlight similarities of the procedure with well-known optimization methods. Specifically, we demonstrated how the principles of stress equilibrium and strain compatibility are exploited through application of measurement data as BCs in separate FEAs, from which naturally arises an implicit displacement error that drives NNCM training.

The primary benefit of AutoP over model-based inverse methods is the potential to discover 3-D mechanical properties of soft tissues in vivo. Full computational modeling of applied force loads means measurements need not be acquired in a constrained manner; e.g., uniaxial compression by a large platen. Nor is 3-D displacement data necessary to reconstruct material properties throughout a volume, as we demonstrated in [25]. However, the use of arbitrary force-displacement measurements as input to AutoP significantly increases the computational load. Furthermore, we expect intelligent sampling strategies will need to be developed in order to maximize the information content of measurement data and reduce the computational burden of AutoP. Good sampling strategies will likely be essential for effectively imaging non-linear, time-dependent material properties.

One particularly exciting prospect of CaNNCMs and AutoP is the ability to identify mechanical properties from a heterogeneous distribution of material types. Classic model-based inverse methods must first assume the form of the constitutive model for the entire tissue section. The solution is the spatial variation of corresponding parameters that best fits the measurement data. AutoP reverses this order to first build a non-parametric, soft-computational model that describes the spatially varying material properties encoded in force-displacement data. Parameter estimation occurs after relevant information has been extracted from measurements. Successfully developing this capability would represent a paradigm shift in not only QUSE, but inverse identification of material properties in general.

AutoP is at its core a method to solve boundary value inverse problems. It is naturally suited for elasticity imaging because the physical principles of stress equilibrium and strain compatibility are built into the forward model. These principles relate the available force-displacement measurement data to the desired stress and strain distributions. By combining the physical principles through forward modeling with the flexibility of ANNs, virtually any type of continuum material can be described non-parametrically. AutoP could be applicable to other inverse problems with well-defined physical laws relating measurement data to the desired quantities. Nevertheless, AutoP is just one example of integrating physical modeling with machine learning to build powerful methods of solving inverse problems.

Author Contributions

The manuscript was written by CH with substantial intellectual input from each author.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

Research reported in this publication was supported by NCI and NIBIB of the National Institutes of Health under Award Numbers R01 CA168575 and R21 EB023402. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Footnotes

¹Inverse problems and image science are expansive fields of study. Some foundational textbooks with comprehensive coverage of these topics are [7, 8].

²Only the linear form of the FEA is expressed in Eq. 6 for clarity. When the system includes non-linear materials or deformation, a Taylor expansion of Eq. 6 reformulates the problem in an iterative, incremental form.

³Node biases would also comprise the set of parameters if included in the network architecture.

⁴There exist certain geometric displacement BCs that are applied in all FEAs. For our examples, such BCs are the bottom surface of the scanned object being “pinned” and having zero displacement

References

1. Aquino W, Brigham JC. Self-learning Finite Elements for Inverse Estimation of thermal Constitutive Models. Int J Heat Mass Transfer (2006) 49:2466–78. doi:10.1016/j.ijheatmasstransfer.2006.01.031

CrossRef Full Text | Google Scholar

2. Baldewsing RA, Danilouchkine MG, Mastik F, Schaar JA, Serruys PW, van der Steen AFW. An Inverse Method for Imaging the Local Elasticity of Atherosclerotic Coronary Plaques. IEEE Trans Inform Technol Biomed (2008) 12:277–89. doi:10.1109/titb.2007.907980

CrossRef Full Text | Google Scholar

3. Baldewsing RA, Schaar JA, Mastik F, van der Steen AFW. Local Elasticity Imaging of Vulnerable Atherosclerotic Coronary Plaques. In Atherosclerosis, Large Arteries and Cardiovascular Risk. Karger Publishers (2007). p. 35–61. doi:10.1159/000096719

CrossRef Full Text | Google Scholar

4. Barbone PE, Bamber JC. Quantitative Elasticity Imaging: what Can and Cannot Be Inferred from Strain Images. Phys Med Biol (2002) 47:2147–64. doi:10.1088/0031-9155/47/12/310

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Barbone PE, Gokhale NH. Elastic Modulus Imaging: on the Uniqueness and Nonuniqueness of the Elastography Inverse Problem in Two Dimensions. Inverse Probl (2004) 20:283–96. doi:10.1088/0266-5611/20/1/017

CrossRef Full Text | Google Scholar

6. Barr RG, Destounis S, Lackey LB, Svensson WE, Balleyguier C, Smith C. Evaluation of Breast Lesions Using Sonographic Elasticity Imaging. J Ultrasound Med (2012) 31:281–7. doi:10.7863/jum.2012.31.2.281

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Barrett HH, Myers KJ. Foundations of Image Science. John Wiley & Sons (2013).

8. Bertero M, Boccacci P. Introduction to Inverse Problems in Imaging. CRC Press (2020).

9. Bhatia KSS, Tong CSL, Cho CCM, Yuen EHY, Lee YYP, Ahuja AT. Shear Wave Elastography of Thyroid Nodules in Routine Clinical Practice: Preliminary Observations and Utility for Detecting Malignancy. Eur Radiol (2012) 22:2397–406. doi:10.1007/s00330-012-2495-1

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Bojunga J, Herrmann E, Meyer G, Weber S, Zeuzem S, Friedrich-Rust M. Real-time Elastography for the Differentiation of Benign and Malignant Thyroid Nodules: a Meta-Analysis. Thyroid (2010) 20:1145–50. doi:10.1089/thy.2010.0079

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Dahl JJ, Dumont DM, Allen JD, Miller EM, Trahey GE. Acoustic Radiation Force Impulse Imaging for Noninvasive Characterization of Carotid Artery Atherosclerotic Plaques: a Feasibility Study. Ultrasound Med Biol (2009) 35:707–16. doi:10.1016/j.ultrasmedbio.2008.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

12. De Borst R, Crisfield MA, Remmers JJ, Verhoosel CV. Nonlinear Finite Element Analysis of Solids and Structures. John Wiley & Sons (2012).

13. Doyley MM. Model-based Elastography: a Survey of Approaches to the Inverse Elasticity Problem. Phys Med Biol (2012) 57:R35–R73. doi:10.1088/0031-9155/57/3/r35

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Ghaboussi J. Advances in Neural Networks in Computational Mechanics and Engineering. In Advances of soft computing in engineering. Springer (2010). p. 191–236. doi:10.1007/978-3-211-99768-0_4

CrossRef Full Text | Google Scholar

15. Ghaboussi J. Soft Computing in Engineering. CRC Press (2018).

16. Ghaboussi J, Pecknold D, Hashash Y, Kwon T. Accurate Determination of Intraocular Pressure and Characterization of Mechanical Properties of the Cornea. US Patent (2011) 8(070):679.

Google Scholar

17. Ghaboussi J, Pecknold DA, Zhang M, Haj-ali RM. Autoprogressive Training of Neural Network Constitutive Models. Int J Numer Meth Engng (1998) 42:105–26. doi:10.1002/(sici)1097-0207(19980515)42:1<105::aid-nme356>3.0.co;2-v

CrossRef Full Text | Google Scholar

18. Ghaboussi J, Wu XS, Pecknold DA. Nonlinear Computational Solid Mechanics. CRC Press (2017).

19. Hashash YMA, Marulanda C, Ghaboussi J, Jung S. Systematic Update of a Deep Excavation Model Using Field Performance Data. Comput Geotechnics (2003) 30:477–88. doi:10.1016/s0266-352x(03)00056-9

CrossRef Full Text | Google Scholar

20. Hashash YM, Ghaboussi J, Fu Q, Marulanda C (2006). Constitutive Soil Behavior Representation via Artificial Neural Networks: a Shift from Soil Models to Soil Behavior Data. In GeoCongress 2006: Geotechnical Engineering in the Information Technology Age. 1–6.

CrossRef Full Text | Google Scholar

21. Hashash YMA, Jung S, Ghaboussi J. Numerical Implementation of a Neural Network Based Material Model in Finite Element Analysis. Int J Numer Meth Engng (2004) 59:989–1005. doi:10.1002/nme.905

CrossRef Full Text | Google Scholar

22. Hoerig C, Ghaboussi J, Insana MF. An Information-Based Machine Learning Approach to Elasticity Imaging. Biomech Model Mechanobiol (2017) 16:805–22. doi:10.1007/s10237-016-0854-6

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Hoerig C, Ghaboussi J, Insana MF. Cartesian Neural Network Constitutive Models for Data-Driven Elasticity Imaging (2018). arXiv preprint arXiv:1809.04121.

24. Hoerig C, Ghaboussi J, Insana MF. Data-driven Elasticity Imaging Using Cartesian Neural Network Constitutive Models and the Autoprogressive Method. IEEE Trans Med Imaging (2019) 38:1150–60. doi:10.1109/tmi.2018.2879495

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Hoerig C, Ghaboussi J, Insana MF. Physics-guided Machine Learning for 3-D Quantitative Quasi-Static Elasticity Imaging. Phys Med Biol (2020) 65:065011. doi:10.1088/1361-6560/ab7505

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Huwart L, Peeters F, Sinkus R, Annet L, Salameh N, ter Beek LC, et al. Liver Fibrosis: Non-invasive Assessment with Mr Elastography. NMR Biomed (2006) 19:173–9. doi:10.1002/nbm.1030

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Jung S, Ghaboussi J. Characterizing Rate-dependent Material Behaviors in Self-Learning Simulation. Comp Methods Appl Mech Eng (2006) 196:608–19. doi:10.1016/j.cma.2006.06.006

CrossRef Full Text | Google Scholar

28. Jung S, Ghaboussi J. Inverse Identification of Creep of concrete from In Situ Load-Displacement Monitoring. Eng Structures (2010) 32:1437–45. doi:10.1016/j.engstruct.2010.01.022

CrossRef Full Text | Google Scholar

29. Kallel F, Bertrand M. Tissue Elasticity Reconstruction Using Linear Perturbation Method. IEEE Trans Med Imaging (1996) 15:299–313. doi:10.1109/42.500139

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Kim J, Ghaboussi J, Elnashai AS. Hysteretic Mechanical-Informational Modeling of Bolted Steel Frame Connections. Eng Structures (2012) 45:1–11. doi:10.1016/j.engstruct.2012.06.014

CrossRef Full Text | Google Scholar

31. Kirchdoerfer T, Ortiz M. Data Driven Computing with Noisy Material Data Sets. Comp Methods Appl Mech Eng (2017) 326:622–41. doi:10.1016/j.cma.2017.07.039

CrossRef Full Text | Google Scholar

32. Ladevèze P, Néron D, Gerbaud P-W. Data-driven Computation for History-dependent Materials. Comptes Rendus Mécanique (2019) 347:831–44. doi:10.1016/j.crme.2019.11.008

CrossRef Full Text | Google Scholar

33. Larin KV, Sampson DD. Optical Coherence Elastography - OCT at Work in Tissue Biomechanics [Invited]. Biomed Opt Express (2017) 8:1172–202. doi:10.1364/boe.8.001172

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Liu B, Zheng Y, Huang G, Lin M, Shan Q, Lu Y, et al. Breast Lesions: Quantitative Diagnosis Using Ultrasound Shear Wave Elastography-A Systematic Review and Meta-Analysis. Ultrasound Med Biol (2016) 42:835–47. doi:10.1016/j.ultrasmedbio.2015.10.024

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Mariappan YK, Glaser KJ, Ehman RL. Magnetic Resonance Elastography: a Review. Clin Anat (2010) 23:497–511. doi:10.1002/ca.21006

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Nenadic IZ, Urban MW, Greenleaf JF, Gennisson J-L, Bernal M, Tanter M. Ultrasound Elastography for Biomedical Applications and Medicine. John Wiley & Sons (2019).

37. Nguyen LTK, Rambausek M, Keip M-A. Variational Framework for Distance-Minimizing Method in Data-Driven Computational Mechanics. Comp Methods Appl Mech Eng (2020) 365:112898. doi:10.1016/j.cma.2020.112898

CrossRef Full Text | Google Scholar

38. Nightingale K. Acoustic Radiation Force Impulse (ARFI) Imaging: a Review. Cmir (2011) 7:328–39. doi:10.2174/157340511798038657

CrossRef Full Text | Google Scholar

39. Parker KJ, Doyley MM, Rubens DJ. Imaging the Elastic Properties of Tissue: the 20 Year Perspective. Phys Med Biol (2010) 56:R1–R29. doi:10.1088/0031-9155/56/1/r01

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Raissi M, Perdikaris P, Karniadakis GE. Physics-informed Neural Networks: A Deep Learning Framework for Solving Forward and Inverse Problems Involving Nonlinear Partial Differential Equations. J Comput Phys (2019) 378:686–707. doi:10.1016/j.jcp.2018.10.045

CrossRef Full Text | Google Scholar

41. Righetti R, Kallel F, Stafford RJ, Price RE, Krouskop TA, Hazle JD, et al. Elastographic Characterization of HIFU-Induced Lesions in Canine Livers. Ultrasound Med Biol (1999) 25:1099–113. doi:10.1016/s0301-5629(99)00044-7

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Rus Carlborg G, Faris I, Torres J, Callejas A, Melchor J, et al. Why Are Viscosity and Nonlinearity Bound to Make an Impact in Clinical Elastographic Diagnosis? Sensors (2020) 20. doi:10.3390/s20082379

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Scherzer O, Grasmair M, Grossauer H, Haltmeier M, Lenzen F. Variational Methods in Imaging. Springer (2009).

44. Shahin MA, Jaksa MB, Maier HR. State of the Art of Artificial Neural Networks in Geotechnical Engineering. Electron J Geotechnical Eng (2008) 8:1–26.

Google Scholar

45. Sidarta DE. Neural Network-Based Constitutive Modeling of Granular Material. Ph.D. thesis. University of Illinois at Urbana-Champaign (2001).

46. Singh MS, Thomas A. Photoacoustic Elastography Imaging: a Review. J Biomed Opt (2019) 24:1–15. doi:10.1117/1.jbo.24.4.040902

CrossRef Full Text | Google Scholar

47. Sinkus R, Daire J-L, Vilgrain V, E. Van Beers B. Elasticity Imaging via MRI: Basics, Overcoming the Waveguide Limit, and Clinical Liver Results. Cmir (2012) 8:56–63. doi:10.2174/157340512799220544

CrossRef Full Text | Google Scholar

48. Song H, Hashash YMA. Characterization of Stress-Strain Behaviour of Red Blood Cells (RBCs), Part I: Methodology Development and Application to Healthy RBCs. Inverse Probl Sci Eng (2015) 23:913–31. doi:10.1080/17415977.2014.954111

CrossRef Full Text | Google Scholar

49. Song H., Hashash Y. M. A. Characterization of stress-strain behaviour of red blood cells (RBCs), part II: response of malaria-infected RBCs. Inverse Problems in Science and Engineering (2015b) 23:413–424. doi:10.1080/17415977.2014.922072

CrossRef Full Text | Google Scholar

50. Stainier L, Leygue A, Ortiz M. Model-free Data-Driven Methods in Mechanics: Material Data Identification and Solvers. Comput Mech (2019) 64:381–93. doi:10.1007/s00466-019-01731-1

CrossRef Full Text | Google Scholar

51. Tyagi M, Goenezen S, Barbone PE, Oberai AA. Algorithms for Quantitative Quasi-Static Elasticity Imaging Using Force Data. Int J Numer Meth Biomed Engng (2014) 30:1421–36. doi:10.1002/cnm.2665

CrossRef Full Text | Google Scholar

52. Vappou J. Magnetic Resonance− and Ultrasound Imaging−Based Elasticity Imaging Methods: A Review. Crit Rev Biomed Eng (2012) 40:121–34. doi:10.1615/critrevbiomedeng.v40.i2.30

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Varghese T, Shi H. Elastographic Imaging of thermal Lesions in Liver In-Vivo Using Diaphragmatic Stimuli. Ultrason Imaging (2004) 26:18–28. doi:10.1177/016173460402600102

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Xu J-M, Xu X-H, Xu H-X, Zhang Y-F, Zhang J, Guo L-H, et al. Conventional US, US Elasticity Imaging, and Acoustic Radiation Force Impulse Imaging for Prediction of Malignancy in Thyroid Nodules. Radiology (2014) 272:577–86. doi:10.1148/radiol.14132438

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Yagawa G, Okuda H. Neural Networks in Computational Mechanics. Arco (1996) 3:435–512. doi:10.1007/bf02818935

CrossRef Full Text | Google Scholar

56. Yeh W-C, Li P-C, Jeng Y-M, Hsu H-C, Kuo P-L, Li M-L, et al. Elastic Modulus Measurements of Human Liver and Correlation with Pathology. Ultrasound Med Biol (2002) 28:467–74. doi:10.1016/s0301-5629(02)00489-1

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Yun GJ, Ghaboussi J, Elnashai AS. Development of Neural Network Based Hysteretic Models for Steel Beam-Column Connections through Self-Learning Simulation. J Earthquake Eng (2007) 11:453–67. doi:10.1080/13632460601123180

CrossRef Full Text | Google Scholar

58. Yun GJ, Ghaboussi J, Elnashai AS. Self-learning Simulation Method for Inverse Nonlinear Modeling of Cyclic Behavior of Connections. Comp Methods Appl Mech Eng (2008) 197:2836–57. doi:10.1016/j.cma.2008.01.021

CrossRef Full Text | Google Scholar