- 1School of Mathematical Sciences, Queen Mary University of London, London, United Kingdom
- 2Centre for Advanced Spatial Analysis, University College London, London, United Kingdom
- 3Centre de Physique Théorique, CNRS, Aix Marseille Université, Université de Toulon, Marseille, France
- 4The Alan Turing Institute, The British Library, London, United Kingdom
- 5Dipartimento di Fisica ed Astronomia, Università di Catania and INFN, Catania, Italy
- 6Complexity Science Hub Vienna, Vienna, Austria
Adoption processes in socio-technological systems have been widely studied both empirically and theoretically. The way in which social norms, behaviors, and even items such as books, music, or other commercial or technological products spread in a population is usually modeled as a process of social contagion, in which the agents of a social system can infect their neighbors on the underlying network of social contacts. More recently, various models have also been proposed to reproduce the typical dynamics of a process of discovery, in which an agent explores a space of relations between ideas or items in search for novelties. In both types of processes, the structure of the underlying networks, respectively, the network of social contacts in the first case, and the network of relations among items in the second one, plays a fundamental role. However, the two processes have been traditionally seen and studied independently. Here, we provide a brief overview of the existing models of social spreading and exploration and of the latest advancements in both directions. We propose to look at them as two complementary aspects of the same adoption process: on the one hand, there are items spreading over a social network of individuals influencing each other, and on the other hand, individuals explore a network of similarities among items to adopt. The two-fold nature of the approach proposed opens up new stimulating challenges for the scientific community of network and data scientists. We conclude by outlining some possible directions that we believe may be relevant to be explored in the coming years.
1 Introduction
Networks constitute the backbone of complex systems, from the human brain to computer communications, and from metabolic and protein systems to online and offline social systems. Characterizing their structure improves our ability to understand the physical, biological, and social phenomena that shape our world [1–4]. The structure of the network plays in fact a major role in the dynamics of a complex system and characterizes both the emergence and the properties of its collective behaviors [5, 6]. In particular, over the last twenty years, networks have been extensively used to model human behavior, and such studies have attracted the attention of sociologists, economists, physicists, and computer scientists. The network approach, eventually integrated with the opportunities offered by the newly available data sources [7, 8], has largely contributed to the growth of new interdisciplinary fields such as those of sociophysics [9–11] and computational social science [12–15].
In this study, we focus on network approaches that aim at capturing and modeling the fundamental mechanisms behind the social dynamics of adoption [16, 17]. The processes through which humans discover and adopt novel items—where by items we indicate not only artifacts or new technological or commercial products but also concepts, ideas, social norms, and behaviors—can be described in two radically different ways, both involving the presence of a complex network, whose nature is different in the two cases.
Indeed, on the one hand, item adoption can be seen as a contagion dynamics over a social network of individuals influencing each other through their social connections. On the other hand, it can be described as an exploration dynamics over a network of similarities among the different possible items that an individual can adopt. In the first case, a single item (a single product, idea, or behavior) is considered at once, and the transmission from one individual to another over a social system is modeled as an epidemic-like spreading process [18, 19] across the links of a social network [20–22]. Hence, the focus here is on the complex structure of the underlying social network. In the second case, the main focus is instead on the network of existing relations between different items [23]. Hence, the modeling attention is shifted toward the cognitive processes through which single individuals explore the space of different possibilities and produce sequences of explored items in search of novelties [24–26]. In this latter way of interpreting adoption dynamics, different exploration (and innovation) models have been proposed to replicate the process of exploration, according to which one idea, concept, or item leads to another, and a discovery can trigger further ones [27, 28]. Here, we present a brief overview of two different types of mechanisms that can contribute to a process of adoption in socio-technological systems, namely, social contagion on the one hand and item exploration on the other. More specifically, in Section 2 and Section 3, we will discuss the two different aspects of adoption dynamics, briefly describing the various modeling approaches that have been proposed and the latest advancements in both directions. In Section 4, we will elaborate more on this duality, illustrating the potential of constructing more elaborate models that consider at the same time the two types of processes. Finally, in Section 5, we will highlight various directions in which models could be expanded by implementing more elaborated mechanisms both at the level of the discovery dynamics and at that of the social contagion process.
2 Modeling Social Contagion
Quantitative studies of contagion phenomena have helped shading light on the similar dynamics at which information, viruses, knowledge, rumors, and innovations spread in a population [18, 29–31]. Contagion processes are usually mediated by interactions that should therefore be taken into account into the modeling framework [32–35]. As a consequence, as for other landmark dynamical processes widely studied within the complex system community, the interplay between the social structure and the contagion dynamics that unfolds upon it has been the focus of many studies [34, 36, 37]. The mechanisms of a basic contagion dynamics are illustrated in Figure 1. Given a single behavior, like smoking [38], the diffusion of the habit can be thought as a spreading process over a network of social relationships, in which individuals influence each other toward the adoption of the behavior, thus going from Figure 1A to Figure 1B. In this basic representation, the spreading dynamics through a population of interacting individuals is similar to the one of pathogens [18], and the typical modeling approach, akin to the one of disease spreading, relies on compartments into which individuals are classified according to their status: adopters/infected (I) and non-adopters/susceptible (S). Susceptible–Infected (SI) is thus the simplest model in this setting, where an individual can move—after a contact with an I—from compartment S to I with a given probability of infection. In the Susceptible–Infected–Susceptible (SIS) variation, the infection process is reversible, and infected individuals can recover. This transition involves a second parameter, the recovery rate. These models can be very informative, but their simple mechanisms work only at a first approximation. In fact, when dealing with human systems, there is a variety of behavioral aspects influencing the social dynamics that cannot be overlooked [39]. In many cases, the dynamics cannot be simply explained in terms of basic disease epidemic models, which would result too reductive. Instead, the social nature of the contacts mediating these processes deserves special attention, calling for ad hoc modeling adjustments and tailored experimental techniques to measure social effects [40, 41].
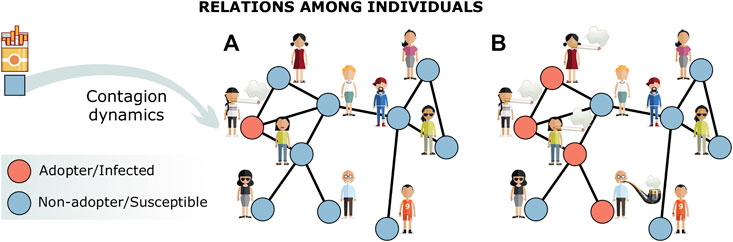
FIGURE 1. Illustration of a contagion process. The adoption of norms, behaviors, ideas, technological items, etc. is typically modeled as a spreading process over a network of social contacts. Red and blue nodes of the social network denote, respectively, the adopters (or infected individuals) and the non-adopters (or susceptible) of the item that is spreading. For example, in (A), a smoker transmits the—bad—habit to its neighboring agents, which in turn can transmit it again through their social links (B).
Along this line, recent investigations have empirically shown that simple contagion rules (SI→2I) are not appropriate to describe the more complex mechanisms of social influence that are at work when humans interact [22, 38, 42, 43]. This evidence, mostly provided by digital traces, relates to different contexts, ranging from the adoption of applications [42, 44] and technologies [45, 46] to the spreading of obesity [47] and happiness [48]. These considerations gave rise to new streams of research focused on translating theories coming from the social sciences into mechanistic models. Among these, complex contagion is a particularly popular theory according to which—differently from simple contagion—multiple stimuli are necessary to trigger a behavioral change in a population of interacting individuals [22, 49]. Current efforts in this direction have been summarized by Guilbeault et al. in Ref. 50. Although supported by a mounting body of empirical studies [22, 43, 44, 51, 52], complex contagion is not the only theory out there, and alternative mechanisms have been theorized. For example, [51] proposed structural diversity, a local measure of the neighborhood of a node, quantified in terms of the number of connected components having at least one adopter. When empirically tested on data of adoption of online platforms upon invitation, this measure turned out to be a better predictor of the probability of adoption with respect to more conventional measures like the number of adopters among the peers. Complex contagion and structural diversity have also been tested against embeddedness and tie strength theories, in which friendship overlap and intensity are the key drivers of social contagion instead [53, 54].
While most of the works mentioned so far focused on the adoption mechanism from the single-sided transition that leads to the adoption, some attention has been also given to the opposite process, in which adopters abandon the new product or technology and become “susceptible” again (I→S). Recently, it has been shown that differences between the recovery rates of the nodes, that is, considering heterogeneous distributions of parameters instead of constant, can also dramatically change the epidemiological dynamics [55–57]. In addition, models of complex recovery, in which the social influence mechanism acts on the recovery rule rather than on the infection one, showed that this change of perspective might lead to explosive adoption dynamics [58]. This behavior is especially pronounced in spatial systems, whose effects on the contagion dynamics have also been the focus of several studies [59–62]. Yet, among humans, communication interactions can occur in groups of three or more agents, and often cannot be simply factored into a collection of dyadic contacts. Expanding the pairwise representation given by graphs in favor of a non-pairwise one, like simplicial complexes or hypergraphs, is a recent research direction that finds in social systems a particularly suitable playground [4]. A paradigmatic example is the model of simplicial contagion that shows how the inclusion of these higher-order group interactions can dramatically alter the spreading dynamics and lead to the emergence of novel phenomena, such as discontinuous transitions and bistability [63]. Similar results can be also found when hypergraphs are used to encode social patterns underneath the spreading process instead [64, 65].
3 Modeling Discovery Processes
Novelties are part of our daily life. The discovery dynamics at which an individual consumes goods or listens to songs can be described, using the words by Thomas Kuhn [66], in terms of the essential tension between exploitation and exploration. This eternal trade-off recurs in a variety of different systems. For example, people move between different locations, mostly switching between already known places, but also visiting new ones from time to time [67–70]. The individual propensity toward “uncharted seas” enters in each discovery processes and enables classifications, such as the returners vs. explorer dichotomy for human mobility [67]. If we think of each visit of a place, listening of a song, or, more in general, collection of an item as the addition of a symbol to a symbolic sequence, the series of actions of an individual (agent) can be represented as a sequence that grows in time, over an alphabet that represents a space of possibilities. Symbolic sequences have a long history in text analysis, but recently, sequences of item adoptions have been used to study human behavior, leveraging sequences of purchases as tracked by credit card data [71] or supermarket fidelity cards [72, 73]. Any process involving individuals and objects that can be encoded into a sequence of actions can be framed in this way. People explore a space, adopt new items, and often return on their steps. Every time a new item enters the sequence, it can thus be seen as a novelty.
This precise mechanism of exploration and exploitation becomes particularly relevant at the collective level, where novelties can be interpreted as innovations [74]. In fact, the first discovery by any individual of a population represents a novelty for everybody. In this scenario, the essential tension between tradition and innovation has been the focus of many studies that analyzed the collective action of researchers determining scientific progress [75–79]. On the same line, patent data have been largely used to explore the dynamics of technological ecosystems [80, 81] with the aim of predicting the innovation dynamics and eventually detecting the best strategies that could influence the rate of innovation [80, 82, 83]. Researchers have been tackling the problem of the emergence of innovation from different angles. For example, some studies have been focusing on the dynamics of substitutive systems, in which the new always replaces the old [84]. Here instead, we keep the focus on the dynamics leading to the emergence of the new; we frame the problem in a cumulative way such that the new, intentionally very broadly defined always comes as an addition to the existing. More precisely, the existing environment is actually a necessary condition that paves the way to the emergence of the new. In fact, from Parmenides to modern evolutionary biology, “nothing comes from nothing” is a dictum at the essence of each process involving real-world systems. Thus, even if we neglect that new items might arise from the recombination of existing ones [85, 86], there is still an essential ingredient that models should take into account, that is, the structure underneath these items which determines the way in which individuals can navigate it [87, 88] moving from one item to the next. For example, knowing the bestseller of a book writer is often a condition that puts us in the position of deepening our research toward minor novels of the same author. Similarly, in scientific production, early research on the properties of random walks enabled further studies on biased random walks. In this setting, one can think of knowledge as an unexplored space of relationships between concepts and objects to be discovered by—more or less “innovative”—investigations and experiments [89, 90]. These could be interpreted either as an exploration process of an abstract space of concepts, ideas, and items [91], or as a knowledge acquisition process [92–94], like people acquiring information through online searches [95, 96]. Research experiments in this direction aim at understanding how humans explore and build mental representations of these spaces through the experience of sequential items. Ref. 97 is a review of the recent efforts, framed under the graph learning paradigm. An important aspect in this scenario is that the structure of this space does matter, since some portions of the space are only visible from certain positions. This concept resonates with the evolutionary theory of the adjacent possible developed by Stuart Kauffman [98]. According to this framework, we can split the knowledge space into what has already been discovered (the actual) and what is left to explore (the possible). Notice, however, that only one tiny fraction of the possible is achievable from the actual, and this is precisely the adjacent possible, that is situated one step away from what is already known.
Many models have been put forward. At their essence, there is often a reinforcement mechanism, akin to the rich-get-richer paradigm [99], that accounts for self-reinforcing properties. This is an essential ingredient that allows to recover the scaling laws emerging from discovery processes in real-world systems [27, 100], like the well-known Heaps’, Zipf’s, and Taylor’s laws [101–103], for example, via sample space–reducing mechanisms [104]. The Yule process [105] is one of the first mechanisms employed to generate the empirically observed power laws. From there, many processes with reinforcement have been developed [106]. At their root, there are the famous standard urn processes [107], like the ones of Pólya and Hoppe [108, 109]. However, these basic processes have been slowly modified and tuned with empirical data in order to better capture the observed patterns. An example is the generalization of the Yule–Simon process developed to mimic the dynamics of collaborative tagging, where online users associate tags (descriptive keywords) to items, generating fat-tailed frequency distributions of tags [110]. Later, the urn framework has been further enriched in order to account for the dynamics of correlated novelties. In fact, empirical traces of human activities show that discoveries come in clusters, and the symbolic sequences generated by discovery processes are thus correlated [27, 100]. Models can mimic this behavior by letting the space grow together with the process, such that novelties increase the number of possible discoveries via triggering mechanisms. A review of these models of expanding spaces can be found in Ref. 111. Leveraging the concept of the adjacent possible, triggering mechanisms showed good agreement with empirical data in reproducing both the scaling laws associated to the discovery processes and the correlated nature of the sequences they produce. This is the case of the urn model with triggering mechanism [27] that incorporates the adjacent possible within the urn process, or the edge-reinforced random walk model [28] that encodes it into the topology of a network of concepts and ideas. It is easy to see how the network representation of the space of items naturally accounts for the adjacent possible, since paths are restricted to existing connections, and the discovery (visit) of a given node can provide access to a different set of nodes not directly accessible before. This is illustrated in Figure 2. The use of networks as an underlying structure for search strategies and navigation is strictly linked to the literature in random walks and optimal foraging [112], but lately, it has been applied to various contexts. For example, in cognitive sciences, networks have been used at length to encode the patterns behind mental representations [113–116]. There, as for contagions, understanding the influence of these structures on the process of discovery that unfolds on top remains a fascinating problem.
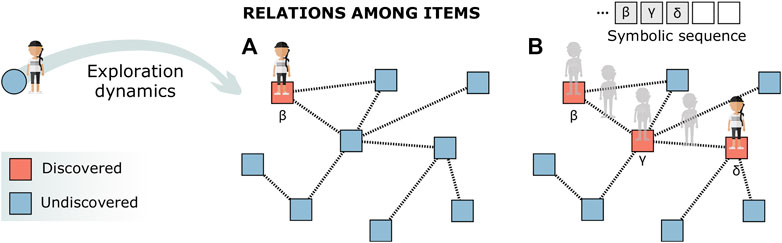
FIGURE 2. Illustration of an exploration process. The cognitive process through which an individual agent explores the space of possibilities in search of novel items (novel ideas and technological discoveries) is usually modeled as a walk over a network of relations (similarities or proximity) among items. For example, in (A), the agent discovers item β and then continues the exploration over the links of the network by sequentially moving to node γ and then to node δ. In (B), three items have been discovered, and the exploratory walk can be seen as a sequence of symbols representing the visited nodes.
4 Coupling the Dynamics of Discovery and Contagion
The two previous sections have shown that adoption processes can be approached from two different angles. However, this has turned into a sort of dual nature of adoption processes, as most of the studies have proposed either to model how an individual explores a network of items or how one item spreads over a social network. Focusing either on one item or on one individual at a time means neglecting a fundamental aspect of socio-technological systems, that is, their multi-agent nature. In a scenario with non-substitutive items, the interactions between multiple items (or behaviors) simultaneously spreading on a social network can ultimately affect the process, eventually favoring or inhibiting the adoption, as it happens for the spreading of multiple infectious diseases over a population [117]. This mechanism would be less pronounced in competitive environments, when at each time, nodes can take only one of many possible states [118], and different states would correspond, for example, to the items agents are presently trying to share. However, even in this case, the state of the neighboring nodes could influence the adoption process as well. In fact, people do not live and work in isolation, and social ties can shape their behaviors [119]. As such, discovery processes of different individuals are surely not independent from one another. For example, a higher similarity has been found in the mobility patterns (extracted from the sequences of visited cell phone towers) of individuals who share a social tie—when compared to the case of strangers [23]. In music listening habits, it has been found that going to a concert increases the amount of post-event plays of that artist for both attendees and attendees’ friends who did not even attended the concert [120]. Thus, these purely social effects would also have an impact on the dynamics of novelties, as it has been recently shown with a model of interacting discovery processes [121]. When urn processes (representing individual explorers) are coupled through the links of a social network, so that explorers can exploit opportunities (possible discoveries) coming from their social contacts, the position in the network affects the ability to discover novelties; individuals with large values of centrality over the social network have a higher discovery pace, in general.
Despite some preliminary and promising results in this direction, a comprehensive framework that bridges together the dual nature of adoption processes, namely, discovery and contagion, is still missing. Ideally, a general model should consider and couple together two different networks, namely, the network of social relations among the agents of a social system and the network of relations among items. As discussed in Section 2, contagion occurs through social interactions, and thus the process of contagion would use a social network as a substrate. In parallel, there could be an exploration process with reinforcement—akin to those introduced in Section 3—that takes place over a different network of relations/similarities between items. Individuals could perform independent searches over the space of items, [90, 111] modeled, for example, as random walks with reinforcement. In this case, the strength of the links could vary across different explorers according to their personal history. By using edge-reinforced random walks [28], walkers would share the same structure of the network of items, while the strengths of the connections would coevolve with the dynamics of the walkers, highlighting the fact that different walkers can prefer to move toward different items (i.e., can prefer certain cognitive associations more than others) also according to their memory. The reinforcement mechanism, which quantifies the tendency of each explorer to go back on her/his steps, reflects the fact that some individuals might be more inclined to the exploration, while others might be less keen to adventure and would rather prefer to exploit the already known [67]. Thus, while the results in Ref. 121 stress the impact of the social network, as given by the node centrality, in determining the speed at which identical individual discover new items, the impact of having heterogeneous individual “memory” remains a fascinating aspect to be explored. In addition, due to the reinforcement, discovering new ideas would become more and more difficult, and walkers will often return on their steps. This implies that the last novelty found will remain unchanged for some time. As for processes of individual and collective attention in social and substitutive systems [84], individuals will focus on a single novelty at the time. A simple way to couple discovery and contagion is illustrated in Figure 3, where each individual tries to spread this last novelty to her/his neighbors through the links of the social network by means of a simple SI contagion process. If such a novelty will spread enough, it will eventually become popular. This could be linked to recent works that have shown how simple mathematical models can accurately describe processes of topics and memes that compete for collective attention, displaying bursts and decays [122–125]. In a novelty-driven scenario, every time that a walker finds a novelty, she would consequently try to spread it to a neighbor in the social network. If the neighbor will adopt such a novelty (this might depend on an individual “susceptibility”), then she would immediately move to the correspondent node on the network of items, ultimately adding long jumps to the random walk process. Without these jumps, the exploration probability of the individuals would decrease over time due to the reinforcement. However, this would be in contrast with the long-term evolution of the strains of activities that has been empirically observed on human mobility traces [70]. Thus, while standard mechanisms to overcome this issue involve the use of finite memory and recency [126], the social benefits induced by the coupling could represent an alternative mechanism, where individuals “stuck” with a certain set of established items may evolve their preferences due to social influence.
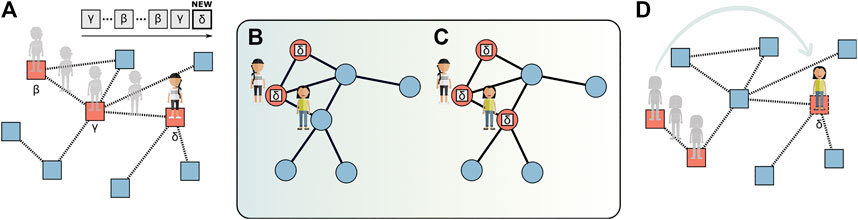
FIGURE 3. Coupling the dynamics of discovery and contagion. (A) A walker explores the space of items. Every time a node is visited, the corresponding item is added to the sequence associated to the agent. Walking on δ represents the discovery of a novelty, since it never appeared in the sequence of before. (B) At this point, the new item δ can spread from the walker to his neighbors through the link of a social network following a process of social contagion. In particular, in (C), a neighbor discovers δ through the social contagion dynamics. As a consequence, her position on the network of items is updated by means of a flight (D).
5 Perspective and Future Directions
Discovery and contagion are two important processes in social systems, whose basic mechanisms and dynamical behaviors have been extensively studied both empirically and theoretically. However, with very few exceptions, these two processes have always been seen and studied separately.
In this perspective, we have shown that the two processes can be considered as two different aspects of a single process of adoption in a social system. The dynamics of adoption of items, which can either be concrete objects or behaviors and social norms, can indeed be seen from two different angles as: 1) a contagion process occurring over a network of individuals influencing one another or 2) as an exploration dynamics over a network of items that an individual can adopt. This means considering either the point of view of a single item spreading over a social network of individuals or the point of view a single individual sequentially moving from adopting one item to adopting a similar one. In this work, we have discussed such a duality, the latest modeling advancements, and we have proposed an example of how to couple these two complementary processes of discovery and contagion in a single social adoption model. Merging together discovery and contagion models would enable to explore the effects of social influence on the mechanisms behind the exploration of new items [121]. However, while the coupled dynamics of discovery and contagion proposed here relies on simple contagion mechanisms, future research could make use of more sophisticated contagion mechanisms, such as threshold models. It would also be interesting to investigate whether the jumps induced by the social contagion can disrupt the composition of the set of exploited items, as it happens in social networks [127]. We hope that the ideas introduced here can represent only the first step of what can be a long journey. In fact, different important aspects need to be further explored on both sides, and many existing models of discovery and contagion could be coupled. Regarding discovery processes, an essential mechanism that should be included in future works is the dynamics of item recombinations. In processes of semantic associations, the combination of remote ideas can lead to Eureka moments [128]. Similarly, in real-world systems, new items can be generated and thus discovered by combining existing ones. An example is the model of Schumpeterian economic dynamics proposed by Ref. 85 that relies on creation and destruction tables. More interestingly, the action of creating compounds of items could be influenced by complementary skills that become available once exploiting the social network. Some early works in this direction involve the combination of medicinal plants to generate novel drugs in an innovation model of hunter-gatherers [129] and the creation of scientific knowledge from the combination of different expertise to generate high-impact science [130]. In addition, some recent advances in the foundation of complex systems have started to consider the higher-order nature of interactions in real-world systems [4]. While the role of these higher-order structures with respect to the dynamics of spreading and diffusion has started to be explored [63], most of the literature on discovery processes is still limited to pairwise representations. Instead, the fundamental units of scientific productivity are research groups and teams [131, 132], and thus higher-order approaches could naturally be used when studying processes of collective scientific discoveries and teamwork [133–135]. In fact, scientific collaborations are the perfect examples of higher-order system whose representation demands for non-pairwise building blocks [136, 137]. Finally, more sophisticated discovery mechanisms could be included in the models. For example, explorers could interact in different ways with each other and with different items [138, 139]. Alternatively, the exploration mechanism could rely on an intrinsic fitness for possible discoveries [140, 141], and one could add a parameter controlling for the strength of the coupling to further investigate the relation between the coupling of the two networks and the distribution of item popularity [142].
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author Contributions
Conceived and designed the paper: II and VL. Performed the analysis and produced the figures: II. Wrote the paper: II and VL.
Funding
II acknowledges support from the UK RDRF-Urban Dynamics Lab under the EPSRC (Grant No. EP/M023583/1) and from the Agence Nationale de la Recherche (ANR) project DATAREDUX (ANR-19-CE46-0008). VL acknowledges support from the Leverhulme Trust Research Fellowship 278 “CREATE: the network components of creativity and success.”
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
Figure icons made by Tana from www.flaticon.com.
References
3. Latora V, Nicosia V, Russo G. Complex networks: principles, methods and applications. Cambridge, UK: Cambridge University Press (2017).
4. Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A. Networks beyond pairwise interactions: structure and dynamics. Phys Rep (2020) 874:1–92. doi:10.1016/j.physrep.2020.05.004
5. Barrat A, Barthelemy M, Vespignani A. Dynamical processes on complex networks. Cambridge, UK: Cambridge University Press (2008).
6. Vespignani A. Modelling dynamical processes in complex socio-technical systems. Nat Phys (2012) 8:32–39. doi:10.1038/nphys2160
7. Salganik M. Bit by bit: social research in the digital age. Princeton, NJ: Princeton University Press (2019).
8. Ledford H. How facebook, twitter and other data troves are revolutionizing social science. Nature (2020) 582:328–30. doi:10.1038/d41586-020-01747-1
9. Castellano C, Fortunato S, Loreto V. Statistical physics of social dynamics. Rev Mod Phys (2009) 81:591. doi:10.1103/revmodphys.81.591
10. Sen P, Chakrabarti BK. Sociophysics: an introduction. Oxford, UK: Oxford University Press (2014).
11. Baronchelli A. The emergence of consensus: a primer. R Soc Open Sci (2018) 5:172189. doi:10.1098/rsos.172189
12. Lazer D, Pentland A, Adamic L, Aral S, Barabási AL, Brewer D. Computational social science. Science (2009) 323:721–3. doi:10.1126/science.1167742
13. Conte R, Gilbert N, Bonelli G, Cioffi-Revilla C, Deffuant G, Kertesz J. Manifesto of computational social science. Eur Phys J-spec Top (2012) 214:325–46. doi:10.1140/epjst/e2012-01697-8
14. Golder SA, Macy MW. Digital footprints: opportunities and challenges for online social research. Annu Rev Sociol (2014) 40:129–52. doi:10.1146/annurev-soc-071913-043145
15. Lazer DM, Pentland A, Watts DJ, Aral S, Athey S, Contractor N. Computational social science: obstacles and opportunities. Science (2020) 369:1060–2. doi:10.1126/science.aaz8170
16. Granovetter MS. The strength of weak ties. In: Social Networks. Amsterdam, Netherlands: Elsevier (1977). p. 347–67.
17. Valente TW. Network models of the diffusion of innovations. 303.484 V3. New York, NY: Hampton Press (1995).
18. Goffman W, Newill VA. Generalization of epidemic theory: an application to the transmission of ideas. Nature (1964) 204:225–8. doi:10.1038/204225a0
19. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev Mod Phys (2015) 87:925. doi:10.1103/revmodphys.87.925
20. Bass FM. A new product growth for model consumer durables. Manage Sci (1969) 15:215–27. doi:10.1287/mnsc.15.5.215
21. Centola D, Macy M. Complex contagions and the weakness of long ties. Am J Sociol (2007) 113:702–34. doi:10.1086/521848
22. Centola D. The spread of behavior in an online social network experiment. Science (2010) 329:1194–7. doi:10.1126/science.1185231
23. Toole JL, Herrera-Yaqüe C, Schneider CM, González MC. Coupling human mobility and social ties. J R Soc Interface (2015) 12:20141128. doi:10.1098/rsif.2014.1128
24. Bendetowicz D, Urbanski M, Garcin B, Foulon C, Levy R, Bréchemier M-L. Two critical brain networks for generation and combination of remote associations. Brain (2018) 141:217–33. doi:10.1093/brain/awx294
25. Siew CS, Wulff DU, Beckage NM, Kenett YN. Cognitive network science: a review of research on cognition through the lens of network representations, processes, and dynamics. Complexity (2019) 2019:1–24. doi:10.1155/2019/2108423
26. Zhou D, Lydon-Staley DM, Zurn P, Bassett DS. The growth and form of knowledge networks by kinesthetic curiosity. Curr Opin Behav Sci (2020) 35: 125–134. doi:10.1016/j.cobeha.2020.09.007
27. Tria F, Loreto V, Servedio VDP, Strogatz SH. The dynamics of correlated novelties. Sci Rep (2014) 4:5890. doi:10.1038/srep05890
28. Iacopini I, Milojević S, Latora V. Network dynamics of innovation processes. Phys Rev Lett (2018) 120:048301. doi:10.1103/physrevlett.120.048301
30. Lloyd AL, May RM. Epidemiology: how viruses spread among computers and people. Science (2001) 292:1316–7. doi:10.1126/science.1061076
31. Young HP. Innovation diffusion in heterogeneous populations: contagion, social influence, and social learning. Am Econ Rev (2009) 99:1899–924. doi:10.1257/aer.99.5.1899
32. Watts DJ. A simple model of global cascades on random networks. Proc Natl Aca Sci U S A (2002) 99:5766–71. doi:10.1073/pnas.082090499
33. de Arruda GF, Rodrigues FA, Moreno Y. Fundamentals of spreading processes in single and multilayer complex networks. Phys Rep (2018) 756:1–59. doi:10.1016/j.physrep.2018.06.007
34. Christakis NA, Fowler JH. Social contagion theory: examining dynamic social networks and human behavior. Statist Med (2013) 32:556–77. doi:10.1002/sim.5408
35. Gleeson JP. Binary-state dynamics on complex networks: pair approximation and beyond. Phys Rev X (2013) 3:021004. doi:10.1103/physrevx.3.021004
36. Gleeson JP, O’Sullivan KP, Baños RA, Moreno Y. Effects of network structure, competition and memory time on social spreading phenomena. Phys Rev X (2016) 6:021019. doi:10.1103/physrevx.6.021019
37. Pond T, Magsarjav S, South T, Mitchell L, Bagrow JP. Complex contagion features without social reinforcement in a model of social information flow. Entropy (2020) 22:265. doi:10.3390/e22030265
38. Christakis NA, Fowler JH. The collective dynamics of smoking in a large social network. N Engl J Med (2008) 358:2249–58. doi:10.1056/nejmsa0706154
39. Hodas NO, Lerman K. The simple rules of social contagion. Sci Rep (2014) 4:4343. doi:10.1038/srep04343
40. Aral S, Muchnik L, Sundararajan A. Distinguishing influence-based contagion from homophily-driven diffusion in dynamic networks. Proc Natl Acad Sci U S A (2009) 106:21544–9. doi:10.1073/pnas.0908800106
41. Aral S, Walker D. Creating social contagion through viral product design: a randomized trial of peer influence in networks. Manage Sci (2011) 57:1623–39. doi:10.1287/mnsc.1110.1421
42. Onnela J-P, Reed-Tsochas F. Spontaneous emergence of social influence in online systems. Proc Natl Acad Sci U S A (2010) 107:18375–80. doi:10.1073/pnas.0914572107
43. Mønsted B, Sapieżyński P, Ferrara E, Lehmann S. Evidence of complex contagion of information in social media: an experiment using twitter bots. PLoS One (2017) 12:e0184148. doi:10.1371/journal.pone.0184148
44. Karsai M, Iñiguez G, Kaski K, Kertész J. Complex contagion process in spreading of online innovation. J R Soc Interface (2014) 11:20140694. doi:10.1098/rsif.2014.0694
45. Bandiera O, Rasul I. Social networks and technology adoption in northern Mozambique. Econ J (2006) 116:869–902. doi:10.1111/j.1468-0297.2006.01115.x
46. Oster E, Thornton R. Determinants of technology adoption: peer effects in menstrual cup take-up. J Eur Econ Assoc (2012) 10:1263–93. doi:10.1111/j.1542-4774.2012.01090.x
47. Christakis NA, Fowler JH. The spread of obesity in a large social network over 32 years. N Engl J Med (2007) 357:370–9. doi:10.1056/nejmsa066082
48. Fowler JH, Christakis NA. Dynamic spread of happiness in a large social network: longitudinal analysis over 20 years in the framingham heart study. BMJ (2008) 337:a2338. doi:10.1136/bmj.a2338
49. Centola D. How behavior spreads: the science of complex contagions. Princeton, NJ: Princeton University Press (2018), Vol. 3.
50. Guilbeault D, Becker J, Centola D. Complex contagions: a decade in review. Complex spreading phenomena in social systems. Berlin, Germany: Springer (2018). p. 3–25.
51. Ugander J, Backstrom L, Marlow C, Kleinberg J. Structural diversity in social contagion. Proc Natl Acad Sci U S A (2012) 109:5962. doi:10.1073/pnas.1116502109
52. Lehmann S, Ahn YY. Complex spreading phenomena in social systems. Berlin, Germany: Springer (2018).
53. Aral S, Walker D. Tie strength, embeddedness, and social influence: a large-scale networked experiment. Manage Sci (2014) 60:1352–70. doi:10.1287/mnsc.2014.1936
54. Aral S, Nicolaides C. Exercise contagion in a global social network. Nat Commun (2017) 8:1–8. doi:10.1038/ncomms14753
55. de Arruda GF, Petri G, Rodrigues FA, Moreno Y. Impact of the distribution of recovery rates on disease spreading in complex networks. Phys Rev Res (2020a) 2:013046. doi:10.1103/physrevresearch.2.013046
56. Darbon A, Colombi D, Valdano E, Savini L, Giovannini A, Colizza V. Disease persistence on temporal contact networks accounting for heterogeneous infectious periods. R Soc Open Sci (2019) 6:181404. doi:10.1098/rsos.181404
57. Brett T, Loukas G, Moreno Y, Perra N. Spreading of computer viruses on time-varying networks. Phys Rev E (2019) 99:050303. doi:10.1103/physreve.99.050303
58. Iacopini I, Schäfer B, Arcaute E, Beck C, Latora V. Multilayer modeling of adoption dynamics in energy demand management. Chaos (2020a) 30:013153. doi:10.1063/1.5122313
59. Strang D, Tuma NB. Spatial and temporal heterogeneity in diffusion. Am J Sociol (1993) 99:614–39. doi:10.1086/230318
60. Toole JL, Cha M, González MC. Modeling the adoption of innovations in the presence of geographic and media influences. PLoS One (2012) 7:e29528. doi:10.1371/journal.pone.0029528
61. Lengyel B, Bokányi E, Di Clemente R, Kertész J, González MC. The role of geography in the complex diffusion of innovations. Sci Rep (2020) 10:1–11. doi:10.1038/s41598-020-72137-w
62. Davis JT, Perra N, Zhang Q, Moreno Y, Vespignani A. Phase transitions in information spreading on structured populations. Nat Phys (2020) 16:590–6. doi:10.1038/s41567-020-0810-3
63. Iacopini I, Petri G, Barrat A, Latora V. Simplicial models of social contagion. Nat Commun (2019) 10:2485. doi:10.1038/s41467-019-10431-6
64. de Arruda GF, Petri G, Moreno Y. Social contagion models on hypergraphs. Phys Rev Res (2020b) 2:023032. doi:10.1103/physrevresearch.2.023032
65. Landry NW, Restrepo JG. The effect of heterogeneity on hypergraph contagion models. Chaos (2020) 30:103117. doi:10.1063/5.0020034
67. Pappalardo L, Simini F, Rinzivillo S, Pedreschi D, Giannotti F, Barabási AL. Returners and explorers dichotomy in human mobility. Nat Commun (2015) 6:8166. doi:10.1038/ncomms9166
68. Yan XY, Wang WX, Gao ZY, Lai YC. Universal model of individual and population mobility on diverse spatial scales. Nat Commun (2017) 8:1639. doi:10.1038/s41467-017-01892-8
69. Alessandretti L, Lehmann S, Baronchelli A. Understanding the interplay between social and spatial behaviour. EPJ Data Sci (2018a) 7:36. doi:10.1140/epjds/s13688-018-0164-6
70. Alessandretti L, Sapiezynski P, Sekara V, Lehmann S, Baronchelli A. Evidence for a conserved quantity in human mobility. Nat Hum Behav (2018b) 2:485–91. doi:10.1038/s41562-018-0364-x
71. Di Clemente R, Luengo-Oroz M, Travizano M, Xu S, Vaitla B, González MC. Sequences of purchases in credit card data reveal lifestyles in urban populations. Nat Commun (2018) 9:3330. doi:10.1038/s41467-018-05690-8
72. Aiello LM, Schifanella R, Quercia D, Del Prete L. Large-scale and high-resolution analysis of food purchases and health outcomes. EPJ Data Sci (2019) 8:14. doi:10.1140/epjds/s13688-019-0191-y
73. Aiello LM, Quercia D, Schifanella R, Del Prete L. Tesco grocery 1.0, a large-scale dataset of grocery purchases in london. Sci Data (2020) 7:57. doi:10.1038/s41597-020-0397-7
74. Johnson S. Where good ideas come from: the natural history of innovation. London, UK: Penguin Books (2010).
75. Foster JG, Rzhetsky A, Evans JA. Tradition and innovation in scientists’ research strategies. Am Sociol Rev (2015) 80:875–908. doi:10.1177/0003122415601618
76. Clauset A, Larremore DB, Sinatra R. Data-driven predictions in the science of science. Science (2017) 355:477–80. doi:10.1126/science.aal4217
77. Murdock J, Allen C, DeDeo S. Exploration and exploitation of Victorian science in Darwin’s reading notebooks. Cognition (2017) 159:117–26. doi:10.1016/j.cognition.2016.11.012
78. Aleta A, Meloni S, Perra N, Moreno Y. Explore with caution: mapping the evolution of scientific interest in physics. EPJ Data Sci (2019) 8:27. doi:10.1140/epjds/s13688-019-0205-9
79. Hofstra B, Kulkarni VV, Galvez SMN, He B, Jurafsky D, McFarland DA. The diversity–innovation paradox in science. Proc Natl Acad Sci U S A (2020) 117:9284–91. doi:10.1073/pnas.1915378117
80. Coccia M. Driving forces of technological change: the relation between population growth and technological innovation: analysis of the optimal interaction across countries. Technol Forecast Soc Change (2014) 82:52–65. doi:10.1016/j.techfore.2013.06.001
81. Pichler A, Lafond F, Farmer JD. Technological interdependencies predict innovation dynamics. arXiv:2003.00580 (2020).
82. Fink T, Reeves M, Palma R, Farr R. Serendipity and strategy in rapid innovation. Nat Commun (2017) 8:2002. doi:10.1038/s41467-017-02042-w
83. Fink TMA, Reeves M. How much can we influence the rate of innovation?. Sci Adv (2019) 5:eaat6107. doi:10.1126/sciadv.aat6107
84. Jin C, Song C, Bjelland J, Canright G, Wang D. Emergence of scaling in complex substitutive systems. Nat Hum Behav (2019) 3:837–46. doi:10.1038/s41562-019-0638-y
85. Thurner S, Klimek P, Hanel R. Schumpeterian economic dynamics as a quantifiable model of evolution. New J Phys (2010) 12:075029. doi:10.1088/1367-2630/12/7/075029
86. Youn H, Strumsky D, Bettencourt LMA, Lobo J. Invention as a combinatorial process: evidence from us patents. J R Soc Interface (2015) 12:20150272. doi:10.1098/rsif.2015.0272
87. Corrêa EA, Marinho VQ, Amancio DR. Semantic flow in language networks. arXiv preprint arXiv:1905.07595 (2019).
88. Lynn CW, Papadopoulos L, Kahn AE, Bassett DS. Human information processing in complex networks. Nat Phys (2020) 16:965–73. doi:10.1038/s41567-020-0924-7
89. Rzhetsky A, Foster JG, Foster IT, Evans JA. Choosing experiments to accelerate collective discovery. Proc Natl Acad Sci U S A (2015) 112:14569–74. doi:10.1073/pnas.1509757112
90. Zurn P, Bassett DS. Network architectures supporting learnability. Phil Trans R Soc B (2020) 375:20190323. doi:10.1098/rstb.2019.0323
91. Cattuto C, Barrat A, Baldassarri A, Schehr G, Loreto V. Collective dynamics of social annotation. Proc Nat Acad Sci (2009) 106:10511–5. doi:10.1073/pnas.0901136106
92. Rodi G, Loreto V, Servedio V, Tria F. Optimal learning paths in information networks. Sci Rep (2015) 5:10286. doi:10.1038/srep10286
93. de Arruda HF, Silva FN, Costa Ld. F, Amancio DR. Knowledge acquisition: a complex networks approach. Inf Sci (2017) 421:154–66. doi:10.1016/j.ins.2017.08.091
94. Lima TS, de Arruda HF, Silva FN, Comin CH, Amancio DR, Costa LdF. The dynamics of knowledge acquisition via self-learning in complex networks. Chaos (2018) 28:083106. doi:10.1063/1.5027007
95. Rodi GC, Loreto V, Tria F. Search strategies of wikipedia readers. PLoS One (2017) 12:e0170746. doi:10.1371/journal.pone.0170746
96. Lydon-Staley DM, Zhou D, Blevins AS, Zurn P, Bassett DS. Hunters, busybodies and the knowledge network building associated with deprivation curiosity. Nat Hum Behav (2020) 5:327–36. doi:10.1038/s41562-020-00985-7
97. Lynn CW, Bassett DS. How humans learn and represent networks. Proc Natl Acad Sci USA (2020) 117:29407–15. doi:10.1073/pnas.1912328117
98. Kauffman SA. Investigations: the nature of autonomous agents and the worlds they mutually create SFI working papers. Santa Fe, NM: Santa Fe Institute (1996).
99. Perc M. The matthew effect in empirical data. J R Soc Interface (2014) 11:20140378. doi:10.1098/rsif.2014.0378
100. Monechi B, Ruiz-Serrano à , Tria F, Loreto V. Waves of novelties in the expansion into the adjacent possible. PLoS One (2017) 12:e0179303. doi:10.1371/journal.pone.0179303
101. Heaps HS. Information retrieval: computational and theoretical aspects. Cambridge, MA: Academic Press (1978).
102. Zipf GK. Human Behavior and the Principle of Least Effort: An Introduction to Human Ecology. Cambridge, England Ravenio (2016).
103. Tria F, Loreto V, Servedio V. Zipf’s, Heaps’ and Taylor’s laws are determined by the expansion into the adjacent possible. Entropy (2018) 20:752. doi:10.3390/e20100752
104. Mazzolini A, Colliva A, Caselle M, Osella M. Heaps’ law, statistics of shared components, and temporal patterns from a sample-space-reducing process. Phys Rev E (2018) 98:052139. doi:10.1103/physreve.98.052139
105. Yule GU. Ii.–a mathematical theory of evolution, based on the conclusions of dr. jc willis, fr s. Phil Trans R Soc Lond B (1925) 213:21–87.
106. Pemantle R. A survey of random processes with reinforcement. Probab Surv (2007) 4:1–79. doi:10.1214/07-ps094
107. Johnson NL, Kotz S. Urn models and their application; an approach to modern discrete probability theory. London, UK: Royal Statistical Society (1977).
108. Pólya G. Sur quelques points de la théorie des probabilités. Annales de l’institut Henri Poincaré (1930). p. 117–61.
109. Hoppe FM. Pólya-like urns and the ewens’ sampling formula. J Math Biol (1984) 20:91–4. doi:10.1007/bf00275863
110. Cattuto C, Loreto V, Pietronero L. Semiotic dynamics and collaborative tagging. Proc Natl Acad Sci U S A (2007) 104:1461–4. doi:10.1073/pnas.0610487104
111. Loreto V, Servedio VD, Strogatz SH, Tria F. Dynamics on expanding spaces: modeling the emergence of novelties. Creativity and universality in language. Berlin, Germany: Springer (2016). p. 59–83.
112. Masuda N, Porter MA, Lambiotte R. Random walks and diffusion on networks. Phys Rep (2017) 716–717:1–58. doi:10.1016/j.physrep.2017.07.007
114. Borge-Holthoefer J, Arenas A. Semantic networks: structure and dynamics. Entropy (2010) 12:1264–1302. doi:10.3390/e12051264
115. Baronchelli A, Ferrer-i-Cancho R, Pastor-Satorras R, Chater N, Christiansen MH. Networks in cognitive science. Trends Cogn Sci (2013) 17:348–60. doi:10.1016/j.tics.2013.04.010
116. Castro N, Siew CSQ. Contributions of modern network science to the cognitive sciences: revisiting research spirals of representation and process. Proc R Soc A (2020) 476:20190825. doi:10.1098/rspa.2019.0825
117. Wang W, Liu Q-H, Liang J, Hu Y, Zhou T. Coevolution spreading in complex networks. Phys Rep (2019) 820:1–51. doi:10.1016/j.physrep.2019.07.001
118. Fennell PG, Gleeson JP. Multistate dynamical processes on networks: analysis through degree-based approximation frameworks. SIAM Rev (2019) 61:92–118. doi:10.1137/16m1109345
119. McPherson M, Smith-Lovin L, Cook JM. Birds of a feather: homophily in social networks. Annu Rev Sociol (2001) 27:415–44. doi:10.1146/annurev.soc.27.1.415
120. Ternovski J, Yasseri T. Social complex contagion in music listenership: a natural experiment with 1.3 million participants. Social Networks (2020) 61:144–52. doi:10.1016/j.socnet.2019.10.005
121. Iacopini I, Di Bona G, Ubaldi E, Loreto V, Latora V. Interacting discovery processes on complex networks. Phys Rev Lett (2020b) 125:248301. doi:10.1103/physrevlett.125.248301
122. Weng L, Flammini A, Vespignani A, Menczer F. Competition among memes in a world with limited attention. Sci Rep (2012) 2:335. doi:10.1038/srep00335
123. Gleeson JP, Ward JA, O’sullivan KP, Lee WT. Competition-induced criticality in a model of meme popularity. Phys Rev Lett (2014a) 112:048701. doi:10.1103/physrevlett.112.048701
124. Lorenz-Spreen P, Mønsted BM, Hövel P, Lehmann S. Accelerating dynamics of collective attention. Nat Commun (2019) 10:1759. doi:10.1038/s41467-019-09311-w
125. Candia C, Jara-Figueroa C, Rodriguez-Sickert C, Barabási A-L, Hidalgo CA. The universal decay of collective memory and attention. Nat Hum Behav (2019) 3:82–91. doi:10.1038/s41562-018-0474-5
126. Barbosa H, de Lima-Neto FB, Evsukoff A, Menezes R. The effect of recency to human mobility. EPJ Data Sci (2015) 4:21. doi:10.1140/epjds/s13688-015-0059-8
127. Saramäki J, Leicht EA, López E, Roberts SGB, Reed-Tsochas F, Dunbar RIM. Persistence of social signatures in human communication. Proc Nat Acad Sci U S A (2014) 111:942–7. doi:10.1073/pnas.1308540110
128. Bendetowicz D, Urbanski M, Aichelburg C, Levy R, Volle E. Brain morphometry predicts individual creative potential and the ability to combine remote ideas. Cortex (2017) 86:216–29. doi:10.1016/j.cortex.2016.10.021
129. Migliano AB, Battiston F, Viguier S, Page AE, Dyble M, Schlaepfer R. Hunter-gatherer multilevel sociality accelerates cumulative cultural evolution. Sci Adv (2020) 6:eaax5913. doi:10.1126/sciadv.aax5913
130. Uzzi B, Mukherjee S, Stringer M, Jones B. Atypical combinations and scientific impact. Science (2013) 342:468–72. doi:10.1126/science.1240474
131. Guimera R, Uzzi B, Spiro J, Amaral LAN. Team assembly mechanisms determine collaboration network structure and team performance. Science (2005) 308:697–702. doi:10.1126/science.1106340
132. Bonaventura M, Ciotti V, Panzarasa P, Liverani S, Lacasa L, Latora V. Predicting success in the worldwide start-up network. Sci Rep (2020) 10:345. doi:10.1038/s41598-019-57209-w
133. Torrisi S, Manfredi S, Iacopini I, Latora V. Creative connectivity project-a network based approach to understand correlations between interdisciplinary group dynamics and creative performance. In: 21st International Conference on Engineering and Product Design Education (E&PDE 2019); September 11–13, 2019; Scotland, UK (2019). p. 530–5.
134. Monechi B, Pullano G, Loreto V. Efficient team structures in an open-ended cooperative creativity experiment. Proc Natl Acad Sci U S A (2019) 116:22088–93. doi:10.1073/pnas.1909827116
135. Almaatouq A, Rahimian MA, Alhajri A. When social influence promotes the wisdom of crowds. arXiv preprint arXiv:2006 12471 (2020).
136. Yang G-Y, Hu Z-L, Liu J-G. Knowledge diffusion in the collaboration hypernetwork. Phys A: Stat Mech Appl (2015) 419:429–36. doi:10.1016/j.physa.2014.10.012
137. Patania A, Petri G, Vaccarino F. The shape of collaborations. EPJ Data Sci (2017) 6:18. doi:10.1140/epjds/s13688-017-0114-8
138. Cencetti G, Battiston F, Fanelli D, Latora V. Reactive random walkers on complex networks. Phys Rev E (2018) 98:052302. doi:10.1103/physreve.98.052302
139. Skardal PS, Adhikari S. Dynamics of nonlinear random walks on complex networks. J Nonlinear Sci (2019) 29:1419–44. doi:10.1007/s00332-018-9521-7
140. Caldarelli G, Capocci A, De Los Rios P, Munoz MA. Scale-free networks from varying vertex intrinsic fitness. Phys Rev Lett (2002) 89:258702. doi:10.1103/physrevlett.89.258702
141. Wang D, Song C, Barabási A-L. Quantifying long-term scientific impact. Science (2013) 342:127–32. doi:10.1126/science.1237825
Keywords: social contagion, spreading process, complex network, discovery process, dynamical process, random walk
Citation: Iacopini I and Latora V (2021) On the Dual Nature of Adoption Processes in Complex Networks. Front. Phys. 9:604102. doi: 10.3389/fphy.2021.604102
Received: 08 September 2020; Accepted: 12 February 2021;
Published: 19 April 2021.
Edited by:
Andrea Pizzoferrato, University of Bath, United KingdomReviewed by:
Gerardo Iñiguez, Central European University, HungaryLaura Alessandretti, Technical University of Denmark, Denmark
Copyright © 2021 Iacopini and Latora. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Iacopo Iacopini, aWFjb3BpbmlpYWNvcG9AZ21haWwuY29t
 Iacopo Iacopini
Iacopo Iacopini Vito Latora1,4,5,6
Vito Latora1,4,5,6