Self-Organization Toward Criticality by Synaptic Plasticity

Self-organized criticality has been proposed to be a universal mechanism for the emergence of scale-free dynamics in many complex systems, and possibly in the brain. While such scale-free patterns were identified experimentally in many different types of neural recordings, the biological principles behind their emergence remained unknown. Utilizing different network models and motivated by experimental observations, synaptic plasticity was proposed as a possible mechanism to self-organize brain dynamics toward a critical point. In this review, we discuss how various biologically plausible plasticity rules operating across multiple timescales are implemented in the models and how they alter the network’s dynamical state through modification of number and strength of the connections between the neurons. Some of these rules help to stabilize criticality, some need additional mechanisms to prevent divergence from the critical state. We propose that rules that are capable of bringing the network to criticality can be classified by how long the near-critical dynamics persists after their disabling. Finally, we discuss the role of self-organization and criticality in computation. Overall, the concept of criticality helps to shed light on brain function and self-organization, yet the overall dynamics of living neural networks seem to harnesses not only criticality for computation, but also deviations thereof.

Introduction

More than 30 years ago, Per Bak, Chao Tang, and Kurt Wiesenfeld [1] discovered a strikingly simple way to generate scale-free relaxation dynamics and pattern statistic, that had been observed in systems as different as earthquakes [2, 3], snow avalanches [4], forest fires [5], or river networks [6, 7]. Thereafter, hopes were expressed that this self-organization mechanism for scale-free emergent phenomena would explain how any complex system in nature worked, and hence it did not take long until the hypothesis sparked that brains should be self-organized critical as well [8].

The idea that potentially the most complex object we know, the human brain, self-organizes to a critical state was explored early on by theoretical studies [9–12], but it took more than 15 years until the first scale-free “neuronal avalanches” were discovered [8]. Since then, we have seen a continuous, and very active interaction between experiment and theory. The initial, simple and optimistic idea that the brain is self-organized critical similar to a sandpile has been refined and diversified. Now we have a multitude of neuroscience-inspired models, some showing classical self-organized critical dynamics, but many employing a set of crucial parameters to switch between critical and non-critical states [12–16]. Likewise the views on neural activity have been extended: We now have the means to quantify the distance to criticality even from the very few neurons we can record in parallel [17]. Overall, we have observed in experiments, how developing networks self-organize to a critical state [18–20], how states may change from wakefulness to deep sleep [21–25], under drugs [26] or in a disease like epilepsy [27–30]. Criticality was mainly investigated in in vivo neural activity during the resting state dynamics [31–34], but there are also some studies during task-induced changes and in presence of external stimuli [35–39]. These results show how criticality and the deviations thereof can be harnessed for computation, but can also reflect cases where self-organization fails.

Parallel to the rapid accumulation of experimental data, models describing the complex brain dynamics were developed to draw a richer picture. It is worthwhile noting that the seminal sandpile model [40] already bears a striking similarity with the brain: The distribution of heights at each site of the system beautifully corresponds to the membrane potential of neurons, and in both systems, small perturbations can lead to scale-free distributed avalanches. However, whereas in the sandpile the number of grains naturally obeys a conservation law, the number of spikes or the summed potential in a neural network does not.

This points to a significant difference between classical SOC models and the brain: While in the SOC model, the conservation law fixes the interaction between sites [40–44], in neuroscience, connections strengths are ever-changing. Incorporating biologically plausible interactions is one of the largest challenges, but also the greatest opportunity for building the neuronal equivalent of a SOC model. Synaptic plasticity rules governing changes in the connections strengths often couple the interactions to the activity on different timescales. Thus, they can serve as the perfect mechanism for the self-organization and tuning the network’s activity to the desired regime.

Here we systematically review biologically plausible models of avalanche-related criticality with plastic connections. We discuss the degree to which they can be considered SOC proper, quasi-critical, or hovering around a critical state. We examine how they can be tuned toward and away from the classical critical state, and in particular, what are the biological control mechanisms that determine self-organization. Our main focus is on models that exhibit scale-free dynamics as measured by avalanche size distributions. Such models are usually referred to as critical, although the presence of power laws in avalanches properties is not a sufficient condition for the dynamics to be critical [45–48].

Modeling Neural Networks With Plastic Synapses

Let us briefly introduce the very basics of neural networks, modeling neural circuits and synaptic plasticity. Most of these knowledge can be found in larger details in neuroscience text-books [49–51]. The human brain contains about 80 billion neurons. Each neuron is connected to thousands of other neurons. The connections between the neurons are located on fine and long trees of “cables”. Each neuron has one such tree to collect signals from other neurons (dendritic tree), and a different tree to send out signals to another set of neurons (axonal tree). Biophysically, the connections between two neurons are realized by synapses. These synapses are special: Only if a synapse is present between a dendrite and an axon can one neuron activate the other (but not necessarily conversely). The strength or weight $w_{ij}$ of a synapse determines how strongly neuron j contributes to activating neuron i. If the summed input to a neuron exceeds a certain threshold within a short time window, the receiving neuron gets activated and fires a spike (a binary signal). If a synapse $w_{ij}$ allows neuron j to send signals to neuron i, it does not mean that the reverse synapse, $w_{ji}$ is also present. Thus, unlike classical physics systems, interactions between units are not symmetric but determined by a sparse, non-symmetric weight matrix W. Moreover, interactions are not continuous but pulse-like (spike), and they are time-delayed by a few milliseconds: It takes a few milliseconds for a spike to travel along an axon, cross the synapse, and reach the cell body of the receiving neuron. Most interestingly, the synaptic weights $w_{ji}$ change over time. This is termed synaptic plasticity and is the core mechanism behind learning.

Before we turn to studying synaptic plasticity in a model, the complexity of a living brain has to be reduced into a simplified model. Typically, neural networks are modeled with a few hundred or thousand of neurons. These neurons are either spiking, or approximated by “rate neurons” which represent the joint activity of an ensemble of neurons. Such rate neurons also exist in vivo, e.g., in small animals, releasing graded potentials instead of spikes. Of all neurons in the human cortex, 80% are often modeled as excitatory neurons; when active, excitatory neurons contribute to activating their post-synaptic neurons (i.e., the neurons to whom they send their signal). The other 20% of neurons are inhibitory, bringing their post-synaptic neurons further away from their firing threshold. Effectively, an inhibitory neuron is modeled as having negative outgoing synaptic weights $w_{ij}$, whereas excitatory neurons have positive outgoing weights. In many simplified models, only one excitatory population is considered, and inhibition is implicitly assumed to be contributing to activity propagation probability that is already included in the excitatory connections. The connectivity matrix W between the neurons is typically sparse, since most of the possible synapses are not realized. In models, the connectivity and initial strength of synapses are often drawn from some random distribution. In some studies, however, the impact of specific choices for connectivity and topology is explicitly explored, as outlined in this review (Network Rewiring and Growth). Finally, the model neurons often receive some external activation or input in addition to the input generated from the network connections to keep the network going and avoid an absorbing (quiescent) state.

Numerous types of plasticity mechanisms shape the activity propagation in neuronal systems. One type of plasticity acts at the synapses regulating their creation and deletion, and determining changes in their weights $w_{ij}$. Thereby, regulating postsynaptic potentials, which govern the ability of the sending neuron to contribute to the activation of the receiving neuron and thus to activity propagation in the network. The other types of plasticity mechanisms regulate the overall excitability of the neuron, for example, by changing the spiking (activation) threshold or by adaptation currents.

The reasons and mechanisms of changing synaptic strength and neural excitability differ broadly. Changes of the synaptic strengths and excitability in the brain occur at different timescales that might be particularly important for maintaining the critical dynamics. Some are very rapid acting within tens of milliseconds, or associated with every spike; others only make changes on the order of hours or even slower. For this review we simplified the classification in three temporally and functionally distinct classes, Figure 1.

FIGURE 1

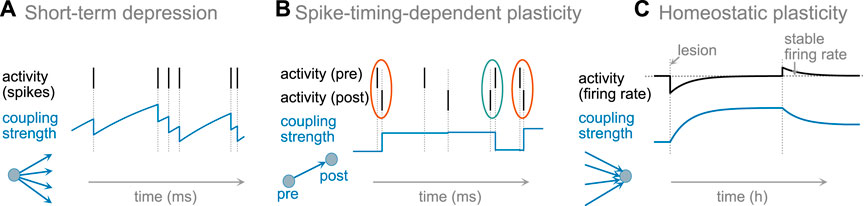
FIGURE 1. Schematic examples of synaptic plasticity. (A) short-term synaptic depression acts on the timescale of spiking activity, and does not generate long-lasting changes. (B) For spike-timing dependent plasticity (STDP), a synapse is potentiated upon causal pairing of pre- and postsynaptic activity (framed orange) and depressed upon anti-causal pairing (framed green), forming long-lasting changes after multiple repetitions of pairing. (C) Homeostatic plasticity adjusts presynaptic weights (or excitability) to maintain a stable firing rate. After reduction of a neuron’s firing rate (e.g., after a lesion and reduction of input), the strengths of incoming excitatory synapses are increased to re-establish the neuron’s target firing rate. In contrast, if the actual firing rate is higher than the target rate, then synapses are weakened, and the neuron returns to its firing rate–on the timescales of hours or days.

The timescale of a plasticity rule influences how it contributes to the state and collective dynamics of brain networks. At the first level, we separate short-term plasticity acting on the timescale of dozens milliseconds, from the long-term plasticity acting with a time constant of minutes to days. As an illustration for short-term plasticity, we present prominent examples of short-term depression (see Short-Term Synaptic Plasticity). Among the long-term plasticity rules, we separate two distinct classes. First, plasticity rules that are explicitly associated with learning structures for specific activity propagation such as Hebbian and spike-timing-dependent plasticity (STDP, Figure 1, middle). Second, homeostatic plasticity that maintains stable firing rate by up or down regulating neuronal excitability or synaptic strength to achieve a stable target firing rate over long time. This plasticity rule is particularly active after sudden or gradual changes in input to a neuron or neural network, and aims at re-establishing the neuron’s firing rate (Figure 1, right).

Criticality in Network Models

Studying the distributions of avalanches is a common way to characterize critical dynamics in network models. Depending on the model, avalanches can be defined in different ways. When it is meaningful to impose the separation of timescales (STS), an avalanche is measured as the entire cascade of events following a small perturbation (e.g., activation of a single neuron) - until the activity dies out. However, the STS cannot be completely mapped to living neural systems due to the presence of spontaneous activity or external input. The external input and spontaneous activation impedes the pauses between avalanches and makes an unambigous separation difficult [52]. In models, such external input can be explicitly incorporated to make them more realistic. To extract avalanches from living networks or from models with input, a pragmatic approach is often chosen. If the recorded signal can be approximated by a point process (e.g., spikes recorded from neurons), the data is summed over all signal sources (e.g., electrodes or neurons) and then binned in small time bins. This way, we obtain a single discrete time-series representing a number of events in all time-bins. An avalanche is then defined as a sequence of active bins between two silent bins. If the recorded signal is continuous (like EEG, fMRI, and LFP), it is first thresholded at a certain level and then binned in time [8]. For each signal source (e.g., each electrode or channel), an individual binary sequence is obtained: one if the signal in the bin is larger than the threshold and zero otherwise. After that, the binary data is summed up across all the signal sources, and the same definition as above is applied. Another option to define avalanches in continuous signals is to first sum over the signals across different sources (e.g., electrodes) and then threshold the compound continuous signal. In this method, the beginning of an avalanche is defined as a crossing of the threshold level by the compound activity process from below, and the end is defined as the threshold crossing from above [53, 54]. In this case the proper measure of the avalanche sizes would be the integral between two crossings of the threshold-subtracted compound process [55].

While both binning and thresholding methods are widely used, concerns were raised that depending on the bin size [8, 21, 52, 56], the value of the threshold [55], or the intensity of input [57] distribution of observed avalanches and estimated power-law exponents might be altered. Therefore, to characterize critical dynamics using avalanches it is important to investigate the fundamental scaling relations between the exponents of avalanche size, duration and shapes to avoid misleading results [58, 59], or instead use approaches to assess criticality that do not require the definition of avalanches [17, 60]. We elaborate on these challenges and bias-free solutions in a review book chapter [61]; for the remainder of this review, we assume that avalanches can be assessed unambiguously.

The timescale of a plasticity rule might play a deciding role for the plasticity’s ability of reaching and maintaining closeness to criticality. While short-term plasticity acts very quickly, it does not generate long-lasting, stable modifications of the network; and it can clearly serve as a feedback between activity and connection strength. Long-term plasticity, on the other side, takes longer to act, but can result in a stable convergence to critical dynamics, Figure 2. To summarize their properties:

• Long-term plasticity is timescale-separated from activity propagation, whereas short-term plasticity evolves at similar timescales.

• Long-term plasticity can self-organize a network to a critical state.

• Short-term plasticity constitutes an inseparable part of the network dynamics. It generates critical statistics in the data, working as a negative feedback.

The core difference: long-term plasticity, after convergence, can be switched off and the system will remain at criticality. Switching off short-term plasticity will almost surely destroy apparent critical dynamics.

• There is a continuum of mechanisms on different timescales between these two extremes. Rules from this continuum can generate critical states that persist for varying time after rule-disabling, potentially even infinitely.

FIGURE 2

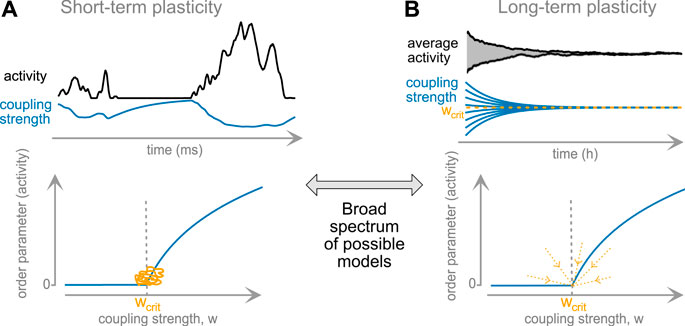
FIGURE 2. Classical plasticity rules and set-points of network activity. (A) Short-term plasticity serves as immediate feedback (top). The resulting long-term behavior of the network hovers near the critical point (orange trace, bottom panel). (B) Long-term plasticity results in slow (timescale of hours or longer) convergence to the fixpoint of global coupling strength. In some settings, this fixpoint may correspond to the second-order phase-transition point (bottom), rendering the critical point a global attractor of dynamics.

Short-Term Synaptic Plasticity

The short-term plasticity (STP) describes activity-related changes in connection strength at a timescale close to the timescale of activity propagation, typically on the order of hundreds to thousands of milliseconds. There are two dominant contributors to the short-term synaptic plasticity: the depletion of synaptic resources used for synaptic transmission, and the transient accumulation of the $\mathrm{C}{\mathrm{a}}^{2+}$ ions that are entering the cell after each spike [62].

At every spike, a synapse needs resources. In more detail, at the presynaptic side, vesicles from the readily-releasable pool are fused with the membrane; once fused, the vesicle is not available until it is replaced by a new one. This fast fusion, and slow filling of the readily releasable pool leads to synaptic depression, i.e., decreasing coupling strength after one or more spikes (Figure 1A). Synapses whose dynamics is dominated by depletion are called depressing synapses [63]. At the same time, for some types of synapses, recent firing increases the probability of release for the vesicles in a readily-releasable pool. This mechanism leads to the increase of the coupling strength for a range of firing frequencies. Synapses with measurable contributions from it are called facilitating synapses [64]. Hence, depending on their past activity, some synapses lower their release (i.e., activation) probability, others increase it, leading effectively to a weakening or strengthening of the synaptic strength.

Short-term plasticity (STP) appears to be an inevitable consequence of synaptic physiology. Nonetheless, numerous studies found that it can play an essential role in multiple brain functions. The most straightforward role is in the temporal filtering of inputs, i.e., short-term depression will result in low-pass filtering [65] that can be employed to reduce redundancy in the incoming signals [66]. Additionally, it was shown to explain aspects of working memory [67].

We consider a network of neurons (in the simplest case, non-leaky threshold integrators) that interact by exchanging spikes. The state $V_i\ge 0$ of neuron $i=1,\dots ,N$ represents the membrane potential and obeys the following equation:

${\dot{V}}_i={\delta }_{i,{\zeta }_{\tau }\left(t\right)}I+C_N{\displaystyle \sum _{j=1}^N{w}_{ij}\left(t_{\text{sp}}^j\right)\delta \left(t-t_{\text{sp}}^j-{\tau }_d\right)},(1)$

where $t_{\text{sp}}^j$ is the time of the spike of presynaptic neuron j, $w_{ij}\left(t_{\text{sp}}^j\right)$ is the strength of synapse between neuron j and i at time $t_{\text{sp}}^j$. Each neuron integrates inputs until it reaches a threshold θ. As soon as $V_i\left(t\right)>\theta$, the neuron emits a spike and delivers excitatory postsynaptic potentials to every connected neuron in the network after a fixed delay ${\tau }_d$. The neurons receive external input defined by a random process ${\zeta }_{\tau }\left(t\right)\in \left\{1,\dots ,N\right\}$ that acts on a very slow timescale $\tau \gg {\tau }_d$ (timescale separation) by selecting a random neuron and increasing its membrane potential by an amount I. The timescale τ defines a time-step in the discrete simulation between the avalanches.

To model the changes in the connection strength associated with short-term synaptic plasticity, it is sufficient to introduce two additional dynamic variables: $J_i$ indicates the number of synaptic resources (i.e., vesicles) available in neuron i, and $u_i$ the fraction of these resources that is used for one spike. Coupling strength is captured by $w_i\left(t\right)=J_i\left(t\right)u_i\left(t\right)$. Each time when neuron i emits a spike at time $t_{\text{sp}}^i$, $J_i$ is reduced by $J_i\left(t_{\text{sp}}^i\right)u_i\left(t_{\text{sp}}^i\right)$. This reflects the use of one or more vesicles to transmit the spike. After a spikes, the resources recover (i.e., the readily-releasable vesicle pool is filled again), and $J_i$ approaches its resting value $J_{\text{rest}}$ at a time scale ${\tau }_J$.

${\dot{J}}_i=\frac{1}{{\tau }_J}\left(J_{\text{rest}}-J_i\right)-u_i{J}_i\delta \left(t-t_{\text{sp}}^i\right),(2)$

with δ denoting Dirac delta function. To add synaptic facilitation, we equip $u_i$ with temporal dynamics, increasing it at each spike and decreasing between the spikes:

${\dot{u}}_i=\frac{1}{{\tau }_u}\left(u_{\text{rest}}-u_i\right)+\left(1-u_i\right)u_{\text{rest}}\delta \left(t-t_{\text{sp}}^j\right).(3)$

Including depressing synapses (Eq. 2) in the integrate-and-fire neuronal network was shown to increase the range of coupling parameters leading to the power-law scaling of avalanche size distribution [68] as compared to the network without synaptic dynamics (Figure 3). If facilitation (Eq. 3) is included in the model, an additional first-order transition arises [69] (Figure 3). Both models have an analytical mean-field solution. In the limit of the infinite network size, the critical dynamics is obtained for any large enough coupling parameter. It was later suggested that the state reached by the system equipped with depressing synapses is not SOC, but self-organized quasi-criticality [70], as it is not locally energy preserving.

FIGURE 3

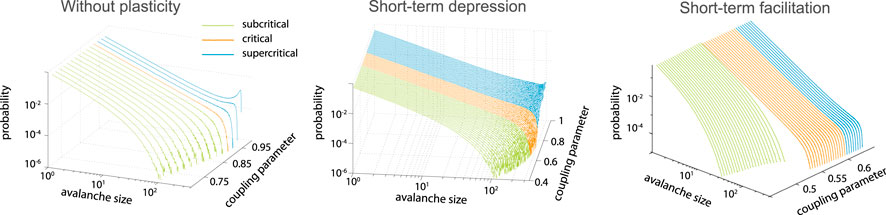
FIGURE 3. Short-term plasticity increases the range of the near critical regime. Left: model without plasticity reaches critical point only for single coupling parameter, $w_i\left(t\right)=w$. Middle: short-term depression extends the range of parameters resulting in the critical dynamics. Fraction $u_i$ of synaptic resources for each spike: $u_i=u=0.2$, coupling parameter represents resting synaptic strength $w_{\text{rest}}=u{J}_{\text{rest}}=0.2J_{\text{rest}}$. An actual connection strength at time t is $w_i\left(t\right)=u{J}_i\left(t\right)$, where $J_i\left(t\right)$ is described by Eq. 2. Different lines correspond to different values of $J_{\text{rest}}\in \left[\mathrm{2,5}\right]$. Right: short-term facilitation and depression together generate a discontinuous (first order - like) phase transition. Resting state fraction of synaptic resources $u_{\text{rest}}=0.1$, coupling parameter is resting state synaptic strength $w_{\text{rest}}=u_{\text{rest}}{J}_{\text{rest}}$, connection strength $w_i\left(t\right)=u_i\left(t\right)J_i\left(t\right)$ is given by Eqs 2,3. Different lines correspond to different values of $J_{\text{rest}}\in \left[4.5,6.5\right]$. For all simulations, network size $N=300$, ${\tau }_u={\tau }_J=10N\tau$, where τ is a timescale of external drive.

The mechanism of the near-critical region extension with depressing synapses is rather intuitive. If there is a large event propagating through the network, the massive usage of synaptic resources effectively decouples the network. This in turn prevents the next large event for a while, until the resources are recovered. At the same time, series of small events allow to build up connection strength increasing the probability of large avalanche. Thus, for the coupling parameters above the critical values, the negative feedback generated by the synaptic depression allows to bring the system closer to the critical state. Complimentary, short-term facilitation can help to shift slightly subcritical systems to a critical state.

A network with STD is essentially a two-dimensional dynamical system (with one variable corresponding to activity, and other to momentary coupling strength). Critical behavior is observed in the activity-dimension, over a long period of time while the coupling is hovering around the mean value as response to the changing activity. If the plasticity is “switched off”, the system may be close to–or relatively far from the critical point of the networks. The probability that the system happens to be precisely at its critical state when plasticity is switched off goes to zero, because 1) criticality only presents one point in this one-dimensional phase transition, and 2) for the large system size, already the smallest parameter deviation results in a big difference in the observed avalanche distribution, rendering the probability to switch off plasticity at the moment of critical coupling strength effectively 0.

In critical systems, not only the avalanche size distribution, but also the absence or presence of correlation between the avalanches are of interest. Already in the classical Bak-Tang-Wiesenfeld model [40], subsequent avalanche sizes are not statistically independent, whereas in the branching process they are. Hence, the correlation structure of subsequent avalanche sizes allows inference about the underlying model and self-organization mechanisms. In the presence of such correlations, fitting the avalanche distributions and investigating power-law statistics should also be applied properly [71]. For models with short-term plasticity, both the avalanche sizes and inter-avalanche intervals are correlated, and similar correlations were observed in the neuronal data in vitro [72].

After the first publication [73], short-term depression was employed in multiple models discussing other mechanisms or different model for individual neurons. To name just a few: in binary probabilistic networks [74], in networks with long-term plasticity [75, 76], in spatially pre-structured networks [77, 78]. In one of the few studies using leaky integrate-and-fire neurons, short term depression was also found to result in critical dynamics if neuronal avalanches are defined by following the causal activation chains between the neurons [79]. However, it was shown later that the causal definition of avalanches will lead to power-law statistics even in clearly non-critical systems [80]. In all cases, the short-term plasticity contributes to the generation of a stable critical regime for a broad parameter range.

Long-Term Synaptic Plasticity and Network Reorganization

Long-term modifications in neuronal networks are created by two mechanisms: long-term synaptic plasticity and structural plasticity (i.e., changes of the topology). With long-term synaptic plasticity, synaptic weights change over a timescale of hours or slower, but the adjacency matrix of the network remains unchanged. However, with structural plasticity, new synapses are created or removed. Both these mechanisms can contribute to self-organizing the network dynamics toward or away from criticality.

Three types of long-term synaptic plasticity have been proposed as possible mechanisms for SOC: Hebbian plasticity, Spike-timing-dependent plasticity (STDP) and homeostatic plasticity. In Hebbian plasticity connections between near-synchronously active neurons are strengthened. In STDP, a temporally asymmetric rule is applied, where weights are strengthened or weakened depending on the order of pre- and post-synaptic spike-times. Last, homeostatic plasticity adapts the synaptic strength as a negative feedback, decreasing excitatory synapses if the firing rate is too high, and increasing it otherwise. Thereby, it stabilizes the network’s firing rate. In the following, we will discuss how each of these mechanisms can contribute to creating self-organized critical dynamics and deviations thereof.

Hebbian-Like Plasticity

Hebbian plasticity is typically formulated in a slogan-like form: Neurons that fire together, wire together. This means that connections between neurons with similar spike-timing will be strengthened. This rule can imprint stable attractors into the network’s dynamics, constituting the best candidate mechanism for memory formation. Hebbian plasticity in its standard form does not reduce coupling strength, thus without additional stabilization mechanisms Hebbian plasticity leads to runaway excitation. Additionally, presence of stable attractors makes it hard to maintain the scale-free distribution of avalanche sizes.

The first papers uniting Hebbian-like plasticity and criticality came from Lucilla de Arcangelis’ and Hans J. Herrmann’s labs [81–83]. In a series of publications, they demonstrated that a network of non-leaky integrators, equipped with plasticity and stabilizing synaptic scaling develops both power-law scaling of avalanches (with exponent 1.2 or 1.5 depending on the external drive) and power-law scaling of spectral density [81, 82]. In the follow up paper, they realized multiple logical gates using additional supervised learning paradigm [83].

Using Hebbian-like plasticity to imprint patterns in the network and simultaneously maintain critical dynamics is a very non-trivial task. Uhlig et al. [84] achieved it by alternating Hebbian learning epochs with the epochs of normalizing synaptic strength to return to a critical state. The memory capacity of the trained network was close to the maximal possible capacity and remain close to criticality. However, the network without homeostatic regulation toward a critical state achieved better retrieval. This might point to the possibility that classical criticality is not an optimal substrate for storing simple memories as attractors. However, in the so-far unstudied setting of storing memories as dynamic attractors, the critical system’s sensitivity might make it the best solution.

Spike-timing-dependent Plasticity

Spike-timing-dependent plasticity (STDP) is a form of activity-dependent plasticity in which synaptic strength is adjusted as a function of timing of spikes in pre- and post-synaptic neurons. It can appear both in the form of long-term potentiation (LTP) or long-term depression (LTD) [85]. Suppose the post-synaptic neuron fires shortly after the pre-synaptic neuron. In that case, the connection from pre-to the post-synaptic neuron is strengthened (LTP), but if the post-synaptic neuron fires after the pre-synaptic neuron, the connection is weakened (LTP), Figure 1B. Millisecond temporal resolution measurements of pre- and postsynaptic spikes experimentally by Markram et al. [86–88] together with theoretical model proposed by Gerstner et al. [89] put forward STDP as a mechanism for sequence learning. Shortly after that other theoretical studies [90–94] incorporated STDP in their models as a local learning rule.

Different functional forms of STDP are observed in different brain areas and across various species (for a review see [95]). For example, STDP in hippocampal excitatory synapses appear to have equal temporal windows for LTD and LTP [86, 96, 97], while in neocortical synapses it exhibits longer LTD temporal windows [98, 99]. Interestingly, an even broader variety of different STDP kernels were observed for inhibitory connections [100].

The classical STDP is often modeled by modifying the synaptic weight $w_{ij}$ from pre-synptic neuron j to post-synaptic neuron i as

$\text{Δ}{w}_{ij}=\{\begin{array}{cc}{A}_{+}\left(w_{ij}\right)\text{exp}\left(\frac{t_j-t_i}{{\tau }_{+}}\right)& t_j<t_i\\ -A_{-}\left(w_{ij}\right)\text{exp}\left(\frac{t_j-t_i}{{\tau }_{-}}\right)& t_j\ge t_i\end{array}(4)$

where $t_i$ and $t_j$ are latest spikes of neurons i and j and ${\tau }_{+}$ and ${\tau }_{-}$ are LTP and LTD time constants. Weight dependence functions $A_{+}\left(w_{ij}\right)$ and $A_{-}\left(w_{ij}\right)$ control the synaptic weights to stay between 0 and $w_{max}$, which is required from the biological point of view. Two families of weight dependence functions have been introduced: 1) soft weight bounds (multiplicative weights) [103], 2) hard weight bounds (additive weights) [89]. Soft weight bounds are implemented as

$A_{+}\left(w_{ij}\right)=\left(w_{max}-w_{ij}\right){\eta }_{+},A_{-}\left(w_{ij}\right)=w_{ij}{\eta }_{-},(5)$

where ${\eta }_{+}<1$ and ${\eta }_{-}<1$ are positive constants. Weight dependence functions with hard bounds are defined using a Heaviside step function $H\left(x\right)$ as

$A_{+}\left(w_{ij}\right)=H\left(w_{max}-w_{ij}\right){\eta }_{+},A_{-}\left(w_{ij}\right)=H\left(-w_{ij}\right){\eta }_{-}.(6)$

There are two types of critical points that can be attained by networks with STDP. The first transition type is characterized by statistics of weights in the converged network. For instance, at this point synaptic coupling strengths [104] or the fluctuations in coupling strengths [105] follow a power-law distribution. The second transition type is related to network’s dynamics, it is characterized by presence of scale-free avalanches [101, 102, 106]. In these models STDP is usually accompanied by fine-tuning of some parameters or properties of the network to create critical dynamics. This suggests that STDP alone might not be sufficient for SOC.

Rubinov et al. [101] developed a leaky integrate-and-fire (LIF) network model with modular connectivity (Figures 4A,B). In their model, STDP only gives rise to power-law distributions of avalanches when the ratio of connection between and within modules is tuned to a particular value. Their results were unchanged for STDP rules with both soft and hard bounds. However, they reported that switching off the STDP dynamics leads to the deterioration of the critical state, which disappears completely after a while. This property places the model in-between truly long-term and short-term mechanisms. Additionally, avalanches were defined based on the activity of modules (simultaneous activation of a large number of neurons within a module). In this modular definition of activity, SOC is achieved by potentiating within-module synaptic weights during module activation and depression of weights in-between module activations. While the module-based definition of avalanches could be relevant to the dynamics of cell-assemblies in the brain or more coarse-grained activity such as local field potentials (LFP), further investigation of avalanches statistics based on individual neurons activity is required.

FIGURE 4

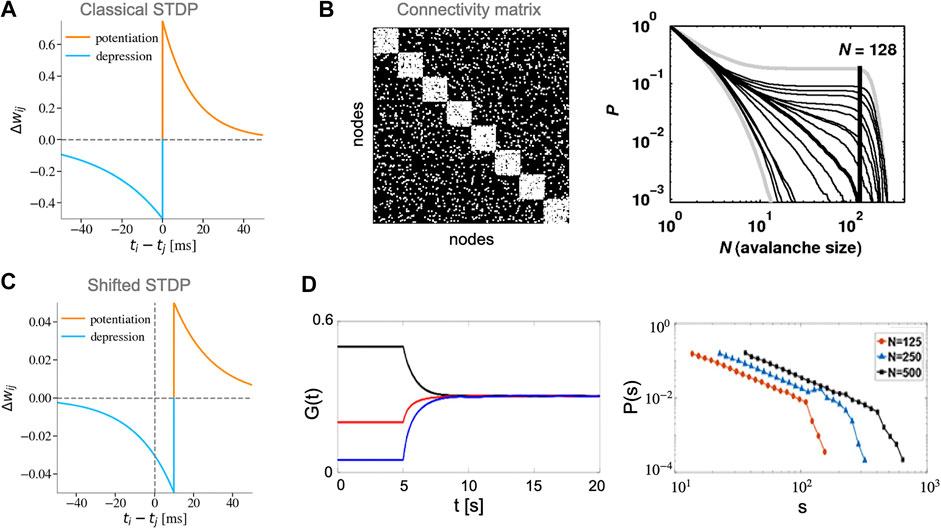
FIGURE 4. Different STDP rules and their role in creating SOC. (A) Classical STDP rule with asymmetric temporal windows (STDP parameters: ${\tau }_{+}=15\mathrm{ms}$, ${\tau }_{-}=30\mathrm{ms}$, $w_{max}=1$, ${\eta }_{+}=0.75$, ${\eta }_{-}=0.5$). (B) A modular network that is rewired to create particular inter- and intra-modules connections (left) combined with classical STDP gives rise to dynamics characterized by power-law avalanche-size distribution (right, thick line). Non-power-law avalanche-size distributions correspond to other rewiring probabilities with the gray lines showing the two extremes of ordered and random networks (reproduced from [101] under CC BY license). (C) Shifted STDP rule (STDP parameters: ${\tau }_{+}={\tau }_{-}=20\mathrm{ms}$, $w_{max}=0.6$, ${\eta }_{+}={\eta }_{-}=0.05$, time-shift = 10 ms). (D)(left) Average coupling strength G(t) in a network with shifted STDP will converge to a steady state value. (right) Setting the STDP time-shift to $\tau =10\mathrm{ms}$ (equal to axonal delay time-constant) leads to emergence of power-law avalanche-size distributions that scale with the system size (reproduced from [102] under CC BY license). N indicates the network size.

Observation of power-law avalanche distributions was later extended to a network of Izhikevich neurons with a temporally shifted soft-bound STDP rule [102] (Figures 4C,D). The shift in the boundary between potentiation and depression reduces the immediate synchronization between pre- and post-synaptic neurons that eventually stabilizes the synaptic weights and the post-synaptic firing rate similar to a homeostasis regulation [107]. In the model, the STDP time-shift is set to be equal to the axonal delay time constant that also acts as a control parameter for the state of dynamics in the network. The authors showed that for a physiologically plausible time constant $\left(\tau =10\mathrm{ms}\right)$ network dynamics self-organizes to the edge of synchronization transition point. At this transition point, distribution of size and duration of avalanches follow a power-law-like distribution. They showed that the power-law exponents can be approximately fitted in the standard scaling relation required for a critical system [59]. However, since they defined avalanches based on thresholding of the global network firing, estimated avalanche distributions and fitted exponents might be generated by the thresholding [55].

Homeostatic Regulations

Homeostatic plasticity is a mechanism that regulates neural activity on a long timescale [108–113]. In a nutshell, one assumes that every neuron has some intrinsic target activity rate. Homeostatic plasticity then presents a negative feedback loop that maintains that target rate and thereby stabilize network dynamics. In general, it reduces (increases) excitatory synaptic strength or neural excitability if the spike rate is above (below) a target rate, Figure 1C. This mechanism can stabilize a potentially unconstrained positive feedback loop through Hebbian-type plasticity [114–121]. The physiological mechanisms of homeostatic plasticity are not fully disentangled yet. It can be implemented by a number of physiological candidate mechanisms, such as redistribution of synaptic efficacy [63, 122], synaptic scaling [108–110, 123], adaptation of membrane excitability [112, 124], or through interactions with glial cells [125, 126]. Recent results highlight the involvement of homeostatic plasticity in generating robust yet complex dynamics in recurrent networks [127–129].

In models, homeostatic plasticity was identified as one of the primary candidates to tune networks to criticality. The mechanism of it is straightforward: taking the analogy of the branching process, where one neuron (or unit) on average activates m neurons in the subsequent time step, the stable sustained activity that is the goal function of the homeostatic regulation requires $m=m_c=1$ which is precisely the critical value [130]. In 2007, Levina and colleagues made use of this principle. They devised a homeostasis-like rule, where all outgoing weights were normalized such that each neuron in the fully connected network activated on average $m=1$ neurons in the next time step [131, 132]. Thereby, the network tuned itself to a critical state.

Similar ideas have been proposed and implemented first in simple models [133] and later also in more detailed models. In the latter, homeostatic regulation tunes the ratio between excitatory and inhibitory synaptic strength [53, 129, 134–136]. It then turned out that due to the diverging temporal correlations, which emerge at criticality, the time-scale of homeostasis would also have to diverge [135]. If the time-scale of the homeostasis is faster than the timescale of the dynamics, then the network does not converge to a critical point, but hovers around it, potentially resembling supercritical dynamics [14, 135]. It is now clear that a self-organization to a critical state (instead of hovering around a critical state) requires that the timescale of homeostasis is slower than that of the network dynamics [14, 135].

Whether a system self-organizes to a critical state, or to a sub- or supercritical one is determined by a further parameter, which has been overlooked for a while: The rate of external input. This rate should be close to zero in critical systems to foster a separation of time scales [52, 137]. Hence, basically all models that studied criticality were implemented with a vanishing external input rate. In neural systems, however, sensory input, spontaneous activation, and other brain areas provide continuous drive, and hence a separation of timescales is typically not realized [52]. As a consequence, avalanches merge, coalesce, and separate [51, 56, 137]. It turns out that under homeostatic plasticity, the external input strength can become a control parameter for the dynamics [14]: If the input strength is high, the system self-organizes to a subcritical state (Figure 5, right). With weaker input, the network approaches a critical state (Figure 5, middle). However when the input is too weak, pauses between bursts get so long that the timescale of the homeostasis again plays a role - and the network does not converge to a single state but hovers between sub- and supercritical dynamics (Figure 5, left). This study shows that under homeostasis the external input strength determines the collective dynamics of the network.

FIGURE 5

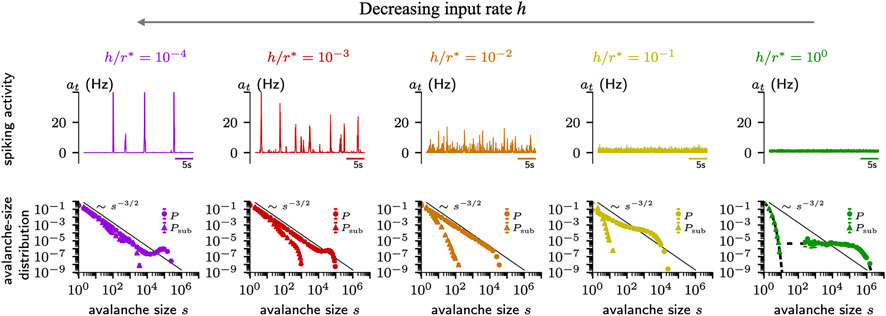
FIGURE 5. Homeostatic plasticity regulation can create different types of dynamics in the network depending on input strength h, target firing rate $r^{\text{*}}$ and recurrent interactions. (top) example spiking activity traces. (bottom) full-sampled (circles) and subsampled (triangles) avalanche size distributions averaged over 12 independent simulations. From left to right: network generates supercritical bursting ($m>1$, $h/r^{\text{*}}\le {10}^{-3}$, purple-red), fluctuating ($m\approx 0.99$, $h/r^{\text{*}}\approx {10}^{-2}$ and $m\approx 0.9$, $h/r^{\text{*}}\approx {10}^{-1}$, orange-yellow) and irregular ($m\approx 0$, $h/r^{\text{*}}=1$, green) activity. Solid lines show the critical branching process avalanche-size distribution $P\left(s\right)\propto s^{-3/2}$ [130] and dashed line is the analytical avalanche-size distribution of a Poisson process [47] (reproduced from [14] by permission).

Assuming that in vivo, cortical activity is subject to some level of non-zero input, one expects a sightly subcritical state - which is indeed found consistently across different animals [14, 17, 30, 139, 140]. In vitro systems, however, which lack external input, are expected to show bursty avalanche dynamics, potentially hovering around a critical point with excursions to supercriticality [14, 136]. Such burst behavior is indeed characteristic for in vitro systems [8, 14, 19, 59].

Recently, Ma and colleagues characterized in experiments how homeostatic scaling might re-establish close-to-critical dynamics in vivo after perturbing sensory input [139] (Figure 6). The past theoretical results would predict that after blocking sensory input in a living animal, the spike rate should diminish, and with the time-scale of homeostatic plasticity, a state close to critical or even super-critical would be obtained [14, 136]. In a recent experiment, however, the behavior is more intricate. Soon after blocking visual input, the network became subcritical (branching ratio m smaller than one [17, 130]) and not supercritical. It then recovered to a close-to-critical state again within two days, potentially compensating the lack of input by coupling stronger to other brain areas. The avalanche size distributions agree with the transient deviation to subcritical dynamics. This deviation to subcriticality is the opposite of what one might have expected under reduced input, and apparently cannot be attributed to concurrent rate changes (which otherwise can challenge the identification of avalanche distributions [47]): The firing rate only started to decrease one day after blocking visual input. The authors attribute this delay in rate decay to excitation and inhibition reacting with different time constants to the blocking of visual input [139].

FIGURE 6

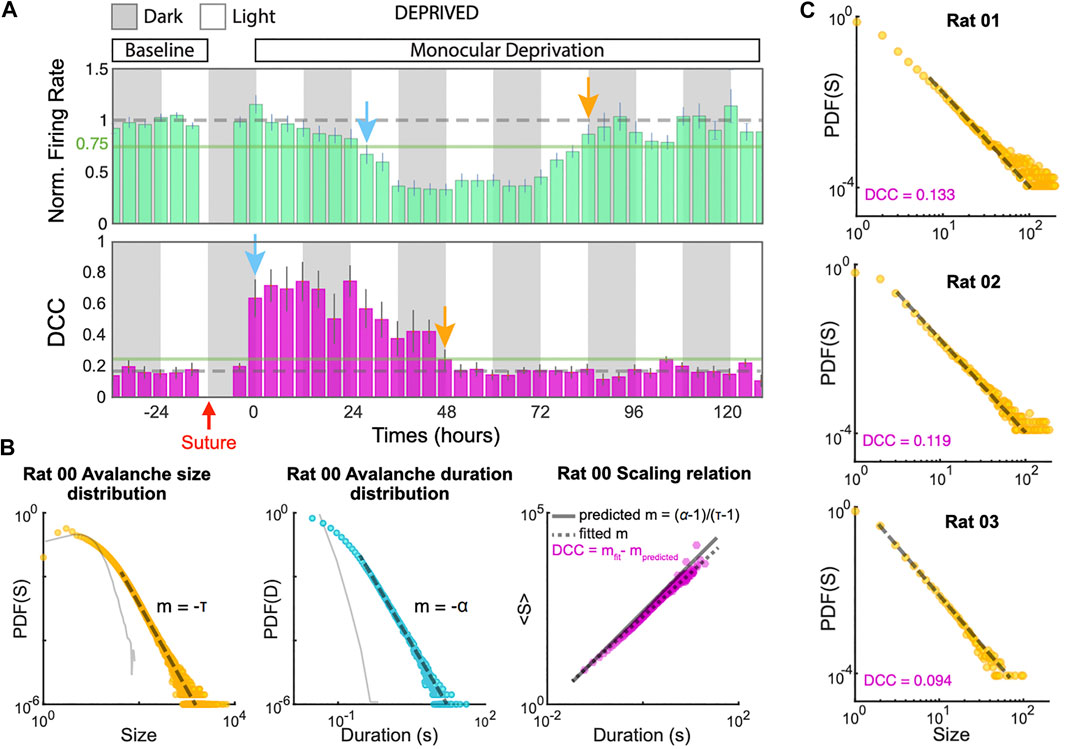
FIGURE 6. Homeostatic regulations in visual cortex of rats tune the network dynamics to near criticality. (A)(top) Firing rate of excitatory neurons during 7 days of recording exhibit a biphasic response to monocular deprivation (MD). After 37 h following MD firing rates were maximally suppressed (blue arrow) but came back to baseline by 84 h (orange arrow). Rates are normalized to 24 h of baseline recordings before MD. (bottom) Measuring the distance to criticality coefficient (DCC) in the same recordings. The mean DCC was significantly increased (blue arrow) upon MD, but was restored to baseline levels (near-critical regime) at 48 h (orange arrow). (B) An example of estimation of DDC (right) using the power-law exponents from the avalanche-size distribution (left) and the avalanche-duration distribution (middle). Solid gray traces show avalanche distributions in shuffled data. DCC is defined as the difference between the empirical scaling (dashed gray line) and the theoretical value (solid gray line) predicted from the exponents for a critical system as the displayed formula [59]. (C) Avalanche-size distributions and DCCs computed from 4 h of single-unit data in three example animals show the diversity of experimental observations (reproduced from the bioRxiv version of [139] under CC-BY-NC-ND 4.0 international license).

Overall, although the exact implementation of the homeostatic plasticity on the pre- and postsynaptic sides of excitatory and inhibitory neurons remains a topic of current research, the general mechanism allows for the long-term convergence of the system to the critical point, Figure 1B. Homeostasis importantly contributes to many models including different learning mechanisms, stabilizing them.

Network Rewiring and Growth

Specific network structures such as small-world [68, 81, 141, 142] or scale-free [75, 83, 143–146] networks were found to be beneficial for the emergence of critical dynamics. These network structures are in particular interesting since they have been also observed in both anatomical and functional brain networks [147–150]. To create such topologies in neural networks long-term plasticity mechanisms have been used. For instance, scale-free and small-world structures emerge as a consequence of STDP between the neurons [105]. In addition, Hebbian plasticity can generate small-world networks [151].

Another prominent form of network structures are hierarchical modular networks (HMN) that can sustain critical regime for a broader range of control parameters [77, 101, 152]. Unlike a conventional critical point where control parameter at a single value leads to scale-free avalanches, in HMNs power-law scaling emerges for a wide range of parameters. This extended critical-like region can correspond to a Griffits phase in statistical mechanics [152]. Different rewiring algorithms have been proposed to generate HMN from an initially randomly connected [77] or a fully connected modular network [101, 152].

Experimental observations in developing neural cultures suggest that connections between neurons grow in a way such that the dynamics of the network eventually self-organizes to a critical point (i.e., observation of scale-free avalanches) [18, 19]. Motivated by this observation, different models have been developed to explain how neural networks can grow connections to achieve and maintain such critical dynamics using homeostatic structural plasticity [19, 153–158] (for a review see [159]). In addition to homeostatic plasticity, other rewiring rules inspired by Hebbian learning were also proposed to bring the network dynamics toward criticality [160–162]. However, implementation of such network reorganizations seems to be less biologically plausible.

In most of the models with homeostatic structural plasticity, the growth of neuronal axons and dendrites is modeled as an expanding (or shrinking) circular neurite field. The growth of the neurite field for each neuron is defined based on the neuron’s firing rate (or internal $\mathrm{C}{\mathrm{a}}^{2+}$ concentration). A firing rate below the homeostatic target rate $\left(f_{target}\right)$ expands the neurite field, and a firing rate above the homeostatic target rate shrinks it. In addition, when neurite fields of two neurons overlap a connection between them will be created with a strength proportional to the overlapped area. Kalle Kossio et al. [156] showed analytically that if the homeostatic target rate is significantly larger than the spontaneous firing rate of the network, such growth mechanism would bring the network dynamics to a critical point with scale-free avalanches (Figure 7). However, for a small target rate subcritical dynamics will arise.

FIGURE 7

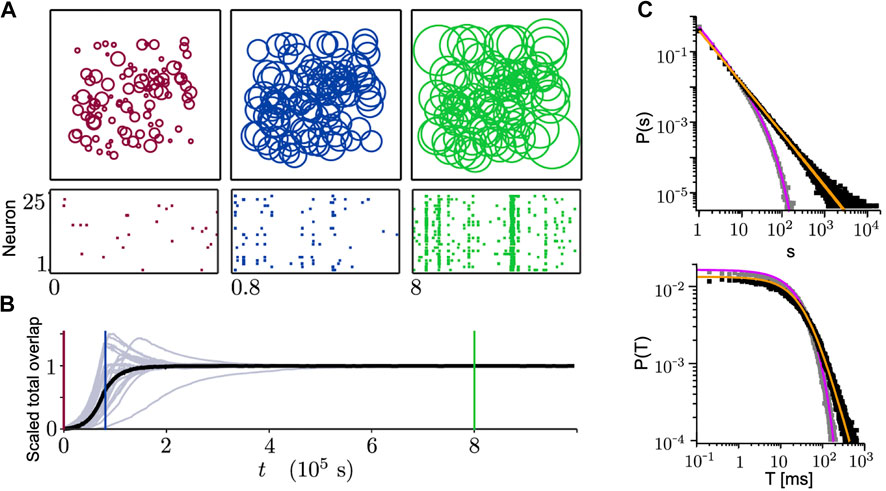
FIGURE 7. Growing connections based on the homeostatic structural plasticity in a network model leads to SOC. (A) Size of neurite fields (top) and spiking activity (bottom) change during the network growth process (from 25 sample neurons). From left to right: initial state (red), state with average growth (blue), stationary state reaching the homeostatic target rate (green). (B) Corresponding scaled total overlaps of 25 sample neurons (gray) and the population average (black) to the three different time points in (A). (C) Avalanche-size (top) and avalanche-duration (bottom) distributions. If the homeostatic target rate $\left(f_{target}=2\mathrm{HZ}\right)$ is significantly larger than the spontaneous rate $\left(f_0=0.01\mathrm{HZ}\right)$ both distributions follow a power-law (black: simulation, orange: analytic). Small homeostatic target rate $\left(f_{target}=0.04\mathrm{HZ}\right)$ leads to subcritical dynamics (gray: simulation, pink: analytic) (reproduced from [156] with permission).

Tetzlaff et al. [19] proposed a slightly different mechanism where two neurites fields are assigned separately for axonal growth and dendritic growth to each neuron. While changes in the size of dendritic neurite fields follows the same rule as explained above, neurite fields of axons follow an exact opposite rule. The model simulations start with all excitatoryry neurons, but in the middle phase 20% of the neurons are changed into inhibitory ones. This switch is motivated by the transformation of GABA neurotransmitters from excitatory to inhibitory during development [163]. They showed that when the network dynamics converge to a steady-state regime, avalanche-size distributions follow a power-law.

Hybrid Mechanisms of Learning and Task Performance

In living neural networks, multiple plasticity mechanisms occur simultaneously. The joint contribution of diverse mechanisms has been studied in the context of criticality in a set of models [75, 164, 165]. A combination with homeostatic-like regulation is typically necessary to stabilize Hebbian or spike-timing-dependent plasticity (STDP), e.g., learning binary tasks such as an XOR rule with Hebbian plasticity [75] or sequence learning with STDP [166–170]. These classic plasticity rules have been paired with regulatory normalization of synaptic weights to avoid a self-amplified destabilization [119–121]. Additionally, short-term synaptic depression stabilizes the critical regime, and if it is augmented with meta-plasticity [164] the stability interval is increased even further, possibly allowing for stable learning.

In a series of studies, Scarpetta and colleagues investigated how sequences can be memorized by STDP, while criticality is maintained [166–168]. By controlling the excitability of the neurons, they achieved a balance between partial replays and noise resulting in power-law distributed avalanche sizes and durations [166]. They later reformulated the model and used the average connection strength as a control parameter, obtaining similar results [167, 168]. Whereas STDP fosters the formation of sequence memory, Hebbian plasticity is known to form assemblies (associations), and in the Hopfield network enables memory completion and recall [171]. A number of studies showed that the formation of such Hebbian ensembles is also possible while maintaining critical dynamics [84, 168, 172]. These studies show that critical dynamics can be maintained in networks, which are learning classical tasks.

The critical network can support not only memory but also real computations such as performing logical operations (OR, AND or even XOR) [75, 83]. To achieve this, the authors build upon the model with Hebbian-like plasticity that previously shown to bring the network to a critical point [81]. They added the central learning signal [173], resembling dopaminergic neuromodulation. Authors demonstrated both with [75] and without [83] short-term plasticity that the network can be trained to solve XOR-gate task.

These examples lead to the natural question of whether criticality is always optimal for learning. The criticality hypothesis attracted much attention, precisely because models at criticality show properties supporting optimal task performance. A core properties of criticality is a maximization of the dynamic range [174, 175], the sensitivity to input, and diverging spatial and temporal correlation lengths [176, 177]. In recurrent network models and experiments, such boost of input sensitivity and memory have been demonstrated by tuning networks systematically toward and away from criticality [174, 178–182].

When not explicitly incorporating a mechanism that drives the network to criticality, learning networks can be pushed away from criticality to a subcritical regime [15, 16, 170, 183, 184]. This is in line with the results above that networks with homeostatic mechanisms become subcritical under increasing network input (Figure 5). Subcritical dynamics might indeed be favorable when reliable task performance is required, as the inherent variability of critical systems may corroborate performance variability [52, 185–190].

Recently, the optimal working points of recurrent neural networks on a neuromorphic chip were demonstrated to depend on task complexity [15, 16]. The neuromorphic chip implements spiking integrate-and-fire neurons with STDP-like depressive plasticity and slow homeostatic recovery of synaptic strength. It was found that complex tasks, which require integration of information over long time-windows, indeed profit from critical dynamics, whereas for simple tasks the optimal working point of the recurrent network was in the subcritical regime [15, 16]. Criticality thus seems to be optimal particularly when a task makes use of this large variability, or explicitly requires the long-range correlation in time or space, e.g., for active memory storage.

Discussion

We summarized how different types of plasticity contribute to the convergence and maintenance of the critical state in neuronal models. The short-term plasticity rules were generally leading to hovering around the critical point, which extended the critical-like dynamics for an extensive range of parameters. The long-term homeostatic network growth and homeostatic plasticity, for some settings, could create a global attractor at the critical state. Long-term plasticity associated with learning sequences, patterns or tasks required additional mechanisms (i.e., homeostasis) to maintain criticality.

The first problem with finding the best recipe for criticality in the brain is our inability to identify the brain’s state from the observations we can make. We are slowly learning how to deal with strong subsampling (under-observation) of the brain network [17, 20, 56, 191–193]. However, even if we obtained a perfectly resolved observation of all activity in the brain, we would face the problem of constant input and spontaneous activation that renders it impossible to find natural pauses between avalanches, and hence makes avalanche-based analyses ambiguous [52]. Hence, multiple avalanche-independent options were proposed as alternative assessments of criticality in the brain: 1) detrended fluctuation analysis [60] allows to capture the scale-free behavior in long-range temporal correlations of EEG/MEG data, 2) critical slowing down [194] suggests a closeness to a bifurcation point, 3) divergence of susceptibility in the maximal entropy model fitted to the neural data [195], divergence of Fisher information [196], or the renormalization group approach [197] indicates a closeness to criticality in the sense of thermodynamic phase-transitions, and 4) estimating the branching parameter directly became feasible even from a small set of neurons; this estimate returns a quantification of the distance to criticality [17, 39]. It was recently pointed out that the results from fitting the maximal entropy models [198, 199] and coarse-graining [200, 201] based on empirical correlations should be interpreted with caution. Finding the best way to unite these definitions, and select the most suitable ones for a given experiment remains largely an open problem.

Investigating the criticality hypothesis for brain dynamics has strongly evolved in the past decades, but is far from being concluded. On the experimental side, sampling limits our access to collective neural dynamics [20, 202], and hence it is not perfectly clear yet how close to a critical point different brain areas operate. For cortex in awake animals, evidence points to a close-to-critical, but slightly subcritical state [30, 139, 140]. The precise working point might well depend on the specific brain area, cognitive state and task requirement [15, 16, 32, 35, 36, 179, 188, 190, 203–206]. Thus instead of self-organizing precisely to criticality, the brain could make use of the divergence of processing capabilities around the critical point. Thereby, each brain area might optimize its computational properties by tuning itself toward and away from criticality in a flexible, adaptive manner [188]. In the past decades, the community has revealed the local plasticity rules that would enable such a tuning and adaption of the working point. Unlike classical physics systems, which are constrained by conservation laws, the brain and the propagation of neural activity is more flexible and hence can adhere in principle a large repertoire of working points - depending on task requirements.

Criticality has been very inspiring to understand brain dynamics and function. We assume that being perfectly critical is not an optimal solution for many brain areas, during different task epochs. However, studying and modeling brain dynamics from a criticality point of view allows to make sense of the high-dimensional neural data, its large variability, and to formulate meaningful hypothesis about dynamics and computation, many of which still wait to be tested.

Author Contributions

RZ, VP, and AL designed the research. RZ and AL prepared the figures. All authors contributed to writing and reviewing the manuscript.

Funding

This work was supported by a Sofja Kovalevskaja Award from the Alexander von Humboldt Foundation, endowed by the Federal Ministry of Education and Research (RZ, AL), Max Planck Society (VP), SMARTSTART 2 program provided by Bernstein Center for Computational Neuroscience and Volkswagen Foundation (RZ). We acknowledge the support from the BMBF through the Tübingen AI Center (FKZ: 01IS18039B).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We are very thankful to SK, MG, and SA for reading the initial version of the manuscript and their constructive comments. The authors thank the International Max Planck Research School for the Mechanisms of Mental Function and Dysfunction (IMPRS-MMFD) for supporting RZ. We acknowledge support by Open Access Publishing Fund of University of Tübingen.

References

1. Bak P, Tang C, Wiesenfeld K. Self-organized criticality. Phys Rev A (1988) 38:364–74. doi:10.1103/PhysRevA.38.364

CrossRef Full Text | Google Scholar

2. Gutenberg B, Richter C. Seismicity of the earth. New York: Geological Society of America (1941), p. 1–126.

3. Gutenberg B, Richter CF. Earthquake magnitude, intensity, energy, and acceleration(Second paper). Bull Seismol Soc Am (1956) 46:105–45.

Google Scholar

4. Birkeland KW, Landry CC. Power-laws and snow avalanches. Geophys Res Lett (2002) 29:49 1–49 3. doi:10.1029/2001GL014623

CrossRef Full Text | Google Scholar

5. Malamud BD, Morein G, Turcotte DL. Forest fires: an example of self-organized critical behavior. Science (1998) 281:1840–2. doi:10.1126/science.281.5384.1840

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Scheidegger A. A complete thermodynamic analogy for landscape evolution. Bull Int Assoc Sci Hydrol (1967) 12:57–62. doi:10.1080/02626666709493550

CrossRef Full Text | Google Scholar

7. Takayasu H, Inaoka H. New type of self-organized criticality in a model of erosion. Phys Rev Lett (1992) 68:966–9. doi:10.1103/PhysRevLett.68.966

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Beggs J, Plenz D. Neuronal avalanches in neocortical circuits. J Neurosci (2003) 23:11167–77. doi:10.1523/JNEUROSCI.23-35-11167.2003

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Chen DM, Wu S, Guo A, Yang ZR. Self-organized criticality in a cellular automaton model of pulse-coupled integrate-and-fire neurons. J Phys A: Math Gen (1995) 28:5177–82. doi:10.1088/0305-4470/28/18/009

CrossRef Full Text | Google Scholar

10. Corral Á, Pérez CJ, Diaz-Guilera A, Arenas A. Self-organized criticality and synchronization in a lattice model of integrate-and-fire oscillators. Phys Rev Lett (1995) 74:118–21. doi:10.1103/PhysRevLett.74.118

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Herz AVM, Hopfield JJ. Earthquake cycles and neural reverberations: collective oscillations in systems with pulse-coupled threshold elements. Phys Rev Lett (1995) 75:1222–5. doi:10.1103/PhysRevLett.75.1222

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Eurich CW, Herrmann JM, Ernst UA. Finite-size effects of avalanche dynamics. Phys Rev E (2002) 66:066137. doi:10.1103/PhysRevE.66.066137

CrossRef Full Text | Google Scholar

13. Haldeman C, Beggs J. Critical branching captures activity in living neural networks and maximizes the number of metastable states. Phys Rev Lett (2005) 94:058101. doi:10.1103/PhysRevLett.94.058101

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Zierenberg J, Wilting J, Priesemann V. Homeostatic plasticity and external input shape neural network dynamics. Phys Rev X (2018) 8:031018. doi:10.1103/PhysRevX.8.031018

CrossRef Full Text | Google Scholar

15. Cramer B, Stöckel D, Kreft M, Wibral M, Schemmel J, Meier K, et al. Control of criticality and computation in spiking neuromorphic networks with plasticity. Nat Commun (2020) 11:2853. doi:10.1038/s41467-020-16548-3

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Prosi J, Khajehabdollahi S, Giannakakis E, Martius G, Levina A. The dynamical regime and its importance for evolvability, task performance and generalization. arXiv [preprint arXiv:2103.12184] (2021).

17. Wilting J, Priesemann V. Inferring collective dynamical states from widely unobserved systems. Nat Commun (2018) 9:2325. doi:10.1038/s41467-018-04725-4

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yada Y, Mita T, Sanada A, Yano R, Kanzaki R, Bakkum DJ, et al. Development of neural population activity toward self-organized criticality. Neuroscience (2017) 343:55–65. doi:10.1016/j.neuroscience.2016.11.031

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Tetzlaff C, Okujeni S, Egert U, Wörgötter F, Butz M. Self-organized criticality in developing neuronal networks. PLoS Comput Biol (2010) 6:e1001013. doi:10.1371/journal.pcbi.1001013

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Levina A, Priesemann V. Subsampling scaling. Nat Commun (2017) 8:15140. doi:10.1038/ncomms15140

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Priesemann V, Valderrama M, Wibral M, Le Van Quyen M. Neuronal avalanches differ from wakefulness to deep sleep–evidence from intracranial depth recordings in humans. PLoS Comput Biol (2013) 9:e1002985. doi:10.1371/journal.pcbi.1002985

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Lo CC, Chou T, Penzel T, Scammell TE, Strecker RE, Stanley HE, et al. Common scale-invariant patterns of sleep–wake transitions across mammalian species. Proc Natl Acad Sci (2004) 101:17545–8. doi:10.1073/pnas.0408242101

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Allegrini P, Paradisi P, Menicucci D, Laurino M, Piarulli A, Gemignani A. Self-organized dynamical complexity in human wakefulness and sleep: different critical brain-activity feedback for conscious and unconscious states. Phys Rev E (2015) 92:032808. doi:10.1103/PhysRevE.92.032808

CrossRef Full Text | Google Scholar

24. Bocaccio H, Pallavicini C, Castro MN, Sánchez SM, De Pino G, Laufs H, et al. The avalanche-like behaviour of large-scale haemodynamic activity from wakefulness to deep sleep. J R Soc Interf (2019) 16:20190262. doi:10.1098/rsif.2019.0262

CrossRef Full Text | Google Scholar

25. Lombardi F, Gómez-Extremera M, Bernaola-Galván P, Vetrivelan R, Saper CB, Scammell TE, et al. Critical dynamics and coupling in bursts of cortical rhythms indicate non-homeostatic mechanism for sleep-stage transitions and dual role of VLPO neurons in both sleep and wake. J Neurosci (2020) 40:171–90. doi:10.1523/JNEUROSCI.1278-19.2019

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Meisel C., 117. Antiepileptic drugs induce subcritical dynamics in human cortical networks. Proc Natl Acad Sci (2020). p. 11118–25. ISBN: 9781911461111. doi:10.1073/pnas.1911461117

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Scheffer M, Bascompte J, Brock WA, Brovkin V, Carpenter SR, Dakos V, et al. Early-warning signals for critical transitions. Nature (2009) 461:53–9. doi:10.1038/nature08227

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Meisel C, Storch A, Hallmeyer-Elgner S, Bullmore E, Gross T. Failure of adaptive self-organized criticality during epileptic seizure attacks. PLoS Comput Biol (2012) 8:e1002312. doi:10.1371/journal.pcbi.1002312

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Arviv O, Medvedovsky M, Sheintuch L, Goldstein A, Shriki O. Deviations from critical dynamics in interictal epileptiform activity. J Neurosci (2016) 36:12276–92. doi:10.1523/JNEUROSCI.0809-16.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Hagemann A, Wilting J, Samimizad B, Mormann F, Priesemann V. No evidence that epilepsy impacts criticality in pre-seizure single-neuron activity of human cortex. arXiv: 2004.10642 [physics, q-bio] (2020).

Google Scholar

31. Deco G, Jirsa VK. Ongoing cortical activity at rest: criticality, multistability, and ghost attractors. J Neurosci (2012) 32:3366–75. doi:10.1523/JNEUROSCI.2523-11.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Tagliazucchi E, von Wegner F, Morzelewski A, Brodbeck V, Jahnke K, Laufs H. Breakdown of long-range temporal dependence in default mode and attention networks during deep sleep. Proc Natl Acad Sci (2013) 110(38):15419–24. doi:10.1073/pnas.1312848110

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Hahn G, Ponce-Alvarez A, Monier C, Benvenuti G, Kumar A, Chavane F, et al. Spontaneous cortical activity is transiently poised close to criticality. PLoS Comput Biol (2017) 13:e1005543. doi:10.1371/journal.pcbi.1005543

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Petermann T, Thiagarajan TC, Lebedev MA, Nicolelis MA, Chialvo DR, Plenz D. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc Natl Acad Sci USA (2009) 106:15921–6. doi:10.1073/pnas.0904089106

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Yu S, Ribeiro TL, Meisel C, Chou S, Mitz A, Saunders R, et al. Maintained avalanche dynamics during task-induced changes of neuronal activity in nonhuman primates. eLife Sci (2017) 6:e27119. doi:10.7554/eLife.27119

CrossRef Full Text | Google Scholar

36. Shew WL, Clawson WP, Pobst J, Karimipanah Y, Wright NC, Wessel R. Adaptation to sensory input tunes visual cortex to criticality. Nat Phys (2015) 11:659–63. doi:10.1038/nphys3370

CrossRef Full Text | Google Scholar

37. Gautam SH, Hoang TT, McClanahan K, Grady SK, Shew WL. Maximizing sensory dynamic range by tuning the cortical state to criticality. PLoS Comput Biol (2015) 11:e1004576. doi:10.1371/journal.pcbi.1004576

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Stephani T, Waterstraat G, Haufe S, Curio G, Villringer A, Nikulin VV. Temporal signatures of criticality in human cortical excitability as probed by early somatosensory responses. J Neurosci (2020) 40:6572–83. doi:10.1523/JNEUROSCI.0241-20.2020

PubMed Abstract | CrossRef Full Text | Google Scholar

39. de Heuvel J, Wilting J, Becker M, Priesemann V, Zierenberg J. Characterizing spreading dynamics of subsampled systems with nonstationary external input. Phys Rev E (2020) 102:040301. doi:10.1103/PhysRevE.102.040301

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Bak P, Tang C, Wiesenfeld K. Self-organized criticality: an explanation of noise. Phys Rev Lett (1987) 59:381–4. doi:10.1103/PhysRevLett.59.381

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Dhar D, Ramaswamy R. Exactly solved model of self-organized critical phenomena. Phys Rev Lett (1989) 63:1659–62. doi:10.1103/PhysRevLett.63.1659

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Manna S. Two-state model of self-organized criticality. J Phys A: Math Gen Phy (1991) 24:L363. doi:10.1088/0305-4470/24/7/009

CrossRef Full Text | Google Scholar

43. Drossel B, Schwabl F. Self-organized criticality in a forest-fire model. Physica A: Stat Mech its Appl (1992) 191:47–50. doi:10.1016/0378-4371(92)90504-J

CrossRef Full Text | Google Scholar

44. Munoz MA. Colloquium: criticality and dynamical scaling in living systems. Rev Mod Phys (2018) 90:031001. doi:10.1103/RevModPhys.90.031001

CrossRef Full Text | Google Scholar

45. Touboul J, Destexhe A. Power-law statistics and universal scaling in the absence of criticality. Phys Rev E (2017) 95:012413. doi:10.1103/PhysRevE.95.012413

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Faqeeh A, Osat S, Radicchi F, Gleeson JP. Emergence of power laws in noncritical neuronal systems. Phys Rev E (2019) 100:010401. doi:10.1103/PhysRevE.100.010401

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Priesemann V, Shriki O. Can a time varying external drive give rise to apparent criticality in neural systems? PLOS Comput Biol (2018) 14:e1006081. doi:10.1371/journal.pcbi.1006081

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Newman MEJ. Power laws, pareto distributions and zipf’s law. Contemp Phys (2005) 46:323. doi:10.1080/00107510500052444

CrossRef Full Text | Google Scholar

49. Kandel ER, Schwartz JH, Jessell TM. Principles of neural science. 3 edn. New York: Elsevier Science Publishing Co Inc (1991).

50. Dayan P, Abbott L. Theoretical neuroscience. Cambridge: MIT Press (2001).

51. Gerstner W, Kistler WM. Spiking neuron models. Single neurons, populations, plasticity. Cambridge: Cambridge University Press (2002).

52. Priesemann V, Wibral M, Valderrama M, Pröpper R, Le Van Quyen M, Geisel T, et al. Spike avalanches in vivo suggest a driven, slightly subcritical brain state. Front Syst Neurosci (2014) 8:108. doi:10.3389/fnsys.2014.00108

PubMed Abstract | CrossRef Full Text | Google Scholar

53. Poil SS, Hardstone R, Mansvelder HD, Linkenkaer-Hansen K. Critical-state dynamics of avalanches and oscillations jointly emerge from balanced excitation/inhibition in neuronal networks. J Neurosci (2012) 32:9817–23. doi:10.1523/JNEUROSCI.5990-11.2012

PubMed Abstract | CrossRef Full Text | Google Scholar

54. Larremore DB, Shew WL, Ott E, Sorrentino F, Restrepo JG. Inhibition causes ceaseless dynamics in networks of excitable nodes. Phys Rev Lett (2014) 112:138103. doi:10.1103/PhysRevLett.112.138103

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Villegas P, di Santo S, Burioni R, Muñoz MA. Time-series thresholding and the definition of avalanche size. Phys Rev E (2019) 100:012133. doi:10.1103/PhysRevE.100.012133

PubMed Abstract | CrossRef Full Text | Google Scholar

56. Priesemann V, Munk M, Wibral M. Subsampling effects in neuronal avalanche distributions recorded in vivo. BMC Neurosci (2009) 10:40. doi:10.1186/1471-2202-10-40

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Das A, Levina A. Critical neuronal models with relaxed timescale separation. Phys Rev X (2019) 9:021062. doi:10.1103/PhysRevX.9.021062

CrossRef Full Text | Google Scholar

58. Muñoz MA, Dickman R, Vespignani A, Zapperi S. Avalanche and spreading exponents in systems with absorbing states. Phys Rev E (1999) 59:6175–9. doi:10.1103/physreve.59.6175

CrossRef Full Text | Google Scholar

59. Friedman N, Ito S, Brinkman BAW, Shimono M, DeVille REL, Dahmen KA, et al. Universal critical dynamics in high resolution neuronal avalanche data. Phys Rev Lett (2012) 108:208102. doi:10.1103/PhysRevLett.108.208102

PubMed Abstract | CrossRef Full Text | Google Scholar

60. Linkenkaer-Hansen K, Nikouline VV, Palva JM, Ilmoniemi RJ. Long-range temporal correlations and scaling behavior in human brain oscillations. J Neurosci (2001) 21:1370–7. doi:10.1002/anie.201106423

PubMed Abstract | CrossRef Full Text | Google Scholar

61. Priesemann V, Levina A, Wilting J. Assessing criticality in experiments. In: N Tomen, JM Herrmann, and U Ernst., editors. The functional role of critical dynamics in neural systems. Springer Series on Bio- and Neurosystems. Cham: Springer International Publishing (2019). p. 199–232. doi:10.1007/978-3-030-20965-0˙11

CrossRef Full Text | Google Scholar

62. Zucker RS, Regehr WG. Short-term synaptic plasticity. Annu Rew Physiol (2002) 64:355–405. doi:10.1146/annurev.physiol.64.092501.114547

CrossRef Full Text | Google Scholar

63. Markram H, Tsodyks M. Redistribution of synaptic efficacy between pyramidal neurons. Nature (1996) 382:807–10. doi:10.1038/382807a0

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Tsodyks M, Pawelzik K, Markram H. Neural networks with dynamic synapses. Neural Comput (1998) 10:821–35. doi:10.1162/089976698300017502

PubMed Abstract | CrossRef Full Text | Google Scholar

65. Abbott LF, Varela JA, Sen K, Nelson SB. Synaptic depression and cortical gain control. Science (1997) 275:220–4. doi:10.1126/science.275.5297.221

PubMed Abstract | CrossRef Full Text | Google Scholar

66. Goldman MS, Maldonado P, Abbott L. Redundancy reduction and sustained firing with stochastic depressing synapses. J Neurosci (2002) 22:584–91. doi:10.1523/JNEUROSCI.22-02-00584.2002

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Mongillo G, Barak O, Tsodyks M. Synaptic theory of working memory. Science (2008) 319:1543–6. doi:10.1126/science.1150769

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Levina A, Herrmann JM, Geisel T. Dynamical synapses causing self-organized criticality in neural networks. Nat Phys (2007a) 3:857–60. doi:10.1038/nphys758

CrossRef Full Text | Google Scholar

69. Levina A, Herrmann JM, Geisel T. Phase transitions towards criticality in a neural system with adaptive interactions. Phys Rev Lett (2009) 102:118110. doi:10.1103/PhysRevLett.102.118110

PubMed Abstract | CrossRef Full Text | Google Scholar

70. Bonachela JA, De Franciscis S, Torres JJ, Munoz MA. Self-organization without conservation: are neuronal avalanches generically critical? J Stat Mech Theor Exp (2010) 2010:P02015. doi:10.1088/1742-5468/2010/02/P02015

CrossRef Full Text | Google Scholar

71. Gerlach M, Altmann EG. Testing statistical laws in complex systems. Phys Rev Lett (2019) 122:168301. doi:10.1103/PhysRevLett.122.168301

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Lombardi F, Herrmann HJ, Plenz D, de Arcangelis L. Temporal correlations in neuronal avalanche occurrence. Scientific Rep (2016) 6:1–12. doi:10.1038/srep24690

CrossRef Full Text | Google Scholar

73. Levina A, Herrmann JM, Geisel T. Dynamical synapses give rise to a power-law distribution of neuronal avalanches. In: Y Weiss, B Schölkopf, and J Platt., editors. Advances in neural information processing systems. Cambridge, MA: MIT Press (2006), 18. p. 771–8.

Google Scholar

74. Kinouchi O, Brochini L, Costa AA, Campos JGF, Copelli M. Stochastic oscillations and dragon king avalanches in self-organized quasi-critical systems. Sci Rep (2019) 9:1–12. doi:10.1038/s41598-019-40473-1

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Michiels van Kessenich L, Luković M, de Arcangelis L, Herrmann HJ. Critical neural networks with short- and long-term plasticity. Phys Rev E (2018) 97:032312. doi:10.1103/PhysRevE.97.032312

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Zeng G, Huang X, Jiang T, Yu S. Short-term synaptic plasticity expands the operational range of long-term synaptic changes in neural networks. Neural Networks (2019) 118:140–7. doi:10.1016/j.neunet.2019.06.002

PubMed Abstract | CrossRef Full Text | Google Scholar

77. Wang SJ, Zhou C. Hierarchical modular structure enhances the robustness of self-organized criticality in neural networks. New J Phys (2012) 14:22. doi:10.1088/1367-2630/14/2/023005

CrossRef Full Text | Google Scholar

78. Jung N, Le QA, Lee KE, Lee JW. Avalanche size distribution of an integrate-and-fire neural model on complex networks. Chaos: Interdiscip J Nonlinear Sci (2020) 30:063118. doi:10.1063/5.0008767

CrossRef Full Text | Google Scholar

79. Millman D, Mihalas S, Kirkwood A, Niebur E. Self-organized criticality occurs in non-conservative neuronal networks during ’up’ states. Nat Phys (2010) 6:801–5. doi:10.1038/nphys1757

PubMed Abstract | CrossRef Full Text | Google Scholar

80. Martinello M, Hidalgo J, Maritan A, Di Santo S, Plenz D, Muñoz MA. Neutral theory and scale-free neural dynamics. Phys Rev X (2017) 7:041071. doi:10.1103/PhysRevX.7.041071

CrossRef Full Text | Google Scholar

81. de Arcangelis L, Perrone-Capano C, Herrmann HJ. Self-organized criticality model for brain plasticity. Phys Rev Lett (2006) 96(2):028107. doi:10.1103/PhysRevLett.96.028107

PubMed Abstract | CrossRef Full Text | Google Scholar

82. Pellegrini GL, de Arcangelis L, Herrmann HJ, Perrone-Capano C. Activity-dependent neural network model on scale-free networks. Phys Rev E (2007) 76:016107. doi:10.1103/PhysRevE.76.016107

CrossRef Full Text | Google Scholar

83. de Arcangelis L, Herrmann HJ. Learning as a phenomenon occurring in a critical state. Proc Natl Acad Sci (2010) 107(9):3977–81. doi:10.1073/pnas.0912289107

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Uhlig M, Levina A, Geisel T, Herrmann JM. Critical dynamics in associative memory networks. Front Comput Neurosci (2013) 7:87. doi:10.3389/fncom.2013.00087

PubMed Abstract | CrossRef Full Text | Google Scholar

85. Sjöström J, Gerstner W. Spike-timing dependent plasticity. Scholarpedia (2010) 5:1362. doi:10.4249/scholarpedia.1362

CrossRef Full Text | Google Scholar

86. Bi G, Poo M. Synaptic modifications in cultured hippocampal neurons: dependence on spike timing, synaptic strength, and postsynaptic cell type. J Neurosci (1998) 18:10464–72. doi:10.1523/JNEUROSCI.18-24-10464.1998

PubMed Abstract | CrossRef Full Text | Google Scholar

87. Markram H, Helm PJ, Sakmann B. Dendritic calcium transients evoked by single back-propagating action potentials in rat neocortical pyramidal neurons. J Physiol (1995) 485:1–20. doi:10.1113/jphysiol.1995.sp020708

PubMed Abstract | CrossRef Full Text | Google Scholar

88. Markram H. Regulation of synaptic efficacy by coincidence of postsynaptic APs and EPSPs. Science (1997) 275:213–5. doi:10.1126/science.275.5297.213

PubMed Abstract | CrossRef Full Text | Google Scholar

89. Gerstner W, Kempter R, van Hemmen JL, Wagner H. A neuronal learning rule for sub-millisecond temporal coding. Nature (1996) 383:76–8. doi:10.1038/383076a0

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Kempter R, Gerstner W, van Hemmen JL. Hebbian learning and spiking neurons. Phys Rev E (1999) 59:4498–514. doi:10.1103/PhysRevE.59.4498

CrossRef Full Text | Google Scholar

91. Roberts PD, Bell CC. Computational consequences of temporally asymmetric learning rules: II. Sensory image cancellation. J Comput Neurosci (2000) 9:67–83. doi:10.1023/A:1008938428112

PubMed Abstract | CrossRef Full Text | Google Scholar

92. Guyonneau R, VanRullen R, Thorpe SJ. Neurons tune to the earliest spikes through STDP. Neural Comput (2005) 17:859–79. doi:10.1162/0899766053429390

PubMed Abstract | CrossRef Full Text | Google Scholar

93. Farries MA, Fairhall AL. Reinforcement learning with modulated spike timing–dependent synaptic plasticity. J Neurophysiol (2007) 98:3648–65. doi:10.1152/jn.00364.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

94. Costa RP, Froemke RC, Sjöström PJ, van Rossum MC. Unified pre- and postsynaptic long-term plasticity enables reliable and flexible learning. eLife (2015) 4:e09457. doi:10.7554/eLife.09457

PubMed Abstract | CrossRef Full Text | Google Scholar

95. Sjöström PJ, Rancz EA, Roth A, Häusser M. Dendritic excitability and synaptic plasticity. Physiol Rev (2008) 88:769–840. doi:10.1152/physrev.00016.2007

PubMed Abstract | CrossRef Full Text | Google Scholar

96. Nishiyama M, Hong K, Mikoshiba K, Poo M, Kato K. Calcium stores regulate the polarity and input specificity of synaptic modification. Nature (2000) 408:584–8. doi:10.1038/35046067

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Zhang YC. Scaling theory of self-organized criticality. Phys Rev Lett (1989) 63:470–3. doi:10.1103/PhysRevLett.63.470

PubMed Abstract | CrossRef Full Text | Google Scholar

98. Feldman DE. Timing-based LTP and LTD at vertical inputs to layer II/III pyramidal cells in rat barrel cortex. Neuron (2000) 27:45–56. doi:10.1016/S0896-6273(00)00008-8

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Sjöström PJ, Turrigiano GG, Nelson SB. Rate, timing, and cooperativity jointly determine cortical synaptic plasticity. Neuron (2001) 32:1149–64. doi:10.1016/S0896-6273(01)00542-6

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Hennequin G, Agnes EJ, Vogels TP. Inhibitory plasticity: balance, control, and codependence. Annu Rev Neurosci (2017) 40:557–79. doi:10.1146/annurev-neuro-072116-031005

PubMed Abstract | CrossRef Full Text | Google Scholar

101. Rubinov M, Sporns O, Thivierge JP, Breakspear M. Neurobiologically realistic determinants of self-organized criticality in networks of spiking neurons. PLoS Comput Biol (2011) 7:e1002038. doi:10.1371/journal.pcbi.1002038

PubMed Abstract | CrossRef Full Text | Google Scholar

102. Khoshkhou M, Montakhab A. Spike-timing-dependent plasticity with axonal delay tunes networks of Izhikevich neurons to the edge of synchronization transition with scale-free avalanches. Front Syst Neurosci (2019) 13:73. doi:10.3389/fnsys.2019.00073

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Van Rossum MC, Bi GQ, Turrigiano GG. Stable hebbian learning from spike timing-dependent plasticity. J Neurosci (2000) 20(23):8812–21. doi:10.1523/JNEUROSCI.20-23-08812.2000

PubMed Abstract | CrossRef Full Text | Google Scholar

104. Meisel C, Gross T. Adaptive self-organization in a realistic neural network model. Phys Rev E (2009) 80:061917. doi:10.1103/PhysRevE.80.061917

CrossRef Full Text | Google Scholar

105. Shin CW, Kim S. Self-organized criticality and scale-free properties in emergent functional neural networks. Phys Rev E (2006) 74:045101. doi:10.1103/PhysRevE.74.045101

CrossRef Full Text | Google Scholar

106. Hernandez-Urbina V, Herrmann JM. Self-organized criticality via retro-synaptic signals. Front Phys (2017) 4. doi:10.3389/fphy.2016.00054

CrossRef Full Text | Google Scholar

107. Babadi B, Abbott LF. Intrinsic stability of temporally shifted spike-timing dependent plasticity. PLoS Comput Biol (2010) 6:e1000961. doi:10.1371/journal.pcbi.1000961

PubMed Abstract | CrossRef Full Text | Google Scholar

108. Turrigiano GG, Leslie KR, Desai NS, Rutherford LC, Nelson SB. Activity-dependent scaling of quantal amplitude in neocortical pyramidal neurons. Nature (1998) 391:892–6. doi:10.1038/36103

PubMed Abstract | CrossRef Full Text | Google Scholar

109. Lissin DV, Gomperts SN, Carroll RC, Christine CW, Kalman D, Kitamura M, et al. Activity differentially regulates the surface expression of synaptic AMPA and NMDA glutamate receptors. Proc Natl Acad Sci (1998) 95:7097–102. doi:10.1073/pnas.95.12.7097

PubMed Abstract | CrossRef Full Text | Google Scholar

110. O’Brien RJ, Kamboj S, Ehlers MD, Rosen KR, Fischbach GD, Huganir RL. Activity-dependent modulation of synaptic AMPA receptor accumulation. Neuron (1998) 21:1067–78. doi:10.1016/S0896-6273(00)80624-8

PubMed Abstract | CrossRef Full Text | Google Scholar

111. Turrigiano GG, Nelson SB. Homeostatic plasticity in the developing nervous system. Nat Rev Neurosci (2004) 5:97–107. doi:10.1038/nrn1327

PubMed Abstract | CrossRef Full Text | Google Scholar

112. Davis GW. Homeostatic control OF neural activity: from phenomenology to molecular design. Annu Rev Neurosci (2006) 29:307–23. doi:10.1146/annurev.neuro.28.061604.135751

PubMed Abstract | CrossRef Full Text | Google Scholar

113. Williams AH, O’Leary T, Marder E. Homeostatic regulation of neuronal excitability. Scholarpedia (2013) 8:1656. doi:10.4249/scholarpedia.1656

CrossRef Full Text | Google Scholar

114. Bienenstock EL, Cooper LN, Munro PW. Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex. J Neurosci (1982) 2:32–48. doi:10.1523/JNEUROSCI.02-01-00032.1982

PubMed Abstract | CrossRef Full Text | Google Scholar

115. Miller KD, MacKay DJC. The role of constraints in hebbian learning. Neural Comput (1994) 6:100–26. doi:10.1162/neco.1994.6.1.100

CrossRef Full Text | Google Scholar

116. Abbott LF, Nelson SB. Synaptic plasticity: taming the beast. Nat Neurosci (2000) 3:1178–83. doi:10.1038/81453

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Turrigiano GG, Nelson SB. Hebb and homeostasis in neuronal plasticity. Curr Opin Neurobiol (2000) 10:358–64. doi:10.1016/S0959-4388(00)00091-X

PubMed Abstract | CrossRef Full Text | Google Scholar

118. Tetzlaff C, Kolodziejski C, Timme M, Wörgötter F. Synaptic scaling in combination with many generic plasticity mechanisms stabilizes circuit connectivity. Front Comput Neurosci (2011) 5:47.

PubMed Abstract | CrossRef Full Text | Google Scholar

119. Zenke F, Hennequin G, Gerstner W. Synaptic plasticity in neural networks needs homeostasis with a fast rate detector. PLOS Comput Biol (2013) 9:e1003330. doi:10.1371/journal.pcbi.1003330

PubMed Abstract | CrossRef Full Text | Google Scholar

120. Keck T, Toyoizumi T, Chen L, Doiron B, Feldman DE, Fox K, et al. Integrating Hebbian and homeostatic plasticity: the current state of the field and future research directions. Philos Trans R Soc B: Biol Sci (2017) 372:20160158. doi:10.1098/rstb.2016.0158

PubMed Abstract | CrossRef Full Text | Google Scholar

121. Zenke F, Gerstner W. Hebbian plasticity requires compensatory processes on multiple timescales. Philos Trans R Soc B: Biol Sci (2017) 372:20160259. doi:10.1098/rstb.2016.0259

PubMed Abstract | CrossRef Full Text | Google Scholar

122. Tsodyks MV, Markram H. The neural code between neocortical pyramidal neurons depends on neurotransmitter release probability. Proc Natl Acad Sci USA (1997) 94:719–23. doi:10.1073/pnas.94.2.719

PubMed Abstract | CrossRef Full Text | Google Scholar

123. Fong M, Newman JP, Potter SM, Wenner P. Upward synaptic scaling is dependent on neurotransmission rather than spiking. Nat Commun (2015) 6:6339. doi:10.1038/ncomms7339

PubMed Abstract | CrossRef Full Text | Google Scholar

124. Pozo K, Goda Y. Unraveling mechanisms of homeostatic synaptic plasticity. Neuron (2010) 66:337–51. doi:10.1016/j.neuron.2010.04.028

PubMed Abstract | CrossRef Full Text | Google Scholar

125. De Pittà M, Brunel N, Volterra A. Astrocytes: orchestrating synaptic plasticity? Neuroscience (2016) 323:43–61. doi:10.1016/j.neuroscience.2015.04.001

PubMed Abstract | CrossRef Full Text | Google Scholar

126. Virkar YS, Shew WL, Restrepo JG, Ott E. Feedback control stabilization of critical dynamics via resource transport on multilayer networks: how glia enable learning dynamics in the brain. Phys Rev E (2016) 94:042310. doi:10.1103/PhysRevE.94.042310

PubMed Abstract | CrossRef Full Text | Google Scholar

127. Naudé J, Cessac B, Berry H, Delord B. Effects of cellular homeostatic intrinsic plasticity on dynamical and computational properties of biological recurrent neural networks. J Neurosci (2013) 33:15032–43. doi:10.1523/JNEUROSCI.0870-13.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

128. Gjorgjieva J, Evers JF, Eglen SJ. Homeostatic activity-dependent tuning of recurrent networks for robust propagation of activity. J Neurosci (2016) 36:3722–34. doi:10.1523/JNEUROSCI.2511-15.2016

PubMed Abstract | CrossRef Full Text | Google Scholar

129. Hellyer PJ, Jachs B, Clopath C, Leech R. Local inhibitory plasticity tunes macroscopic brain dynamics and allows the emergence of functional brain networks. NeuroImage (2016) 124:85–95. doi:10.1016/j.neuroimage.2015.08.069

PubMed Abstract | CrossRef Full Text | Google Scholar

130. Harris TE. The Theory of Branching Processes. Grundlehren der mathematischen Wissenschaften. Berlin Heidelberg: Springer-Verlag (1963).

131. Levina A, Ernst U, Herrmann JM. Criticality of avalanche dynamics in adaptive recurrent networks. Neurocomputing (2007b) 70:1877–81. doi:10.1016/j.neucom.2006.10.056

CrossRef Full Text | Google Scholar

132. Levina A, Herrmann JM, Denker M. Critical branching processes in neural networks. PAMM (2007c) 7:1030701–2. doi:10.1002/pamm.200700029

CrossRef Full Text | Google Scholar

133. Rocha RP, Koçillari L, Suweis S, Corbetta M, Maritan A. Homeostatic plasticity and emergence of functional networks in a whole-brain model at criticality. Sci Rep (2018) 8:15682. doi:10.1038/s41598-018-33923-9

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Girardi-Schappo M, Brochini L, Costa AA, Carvalho TTA, Kinouchi O. Synaptic balance due to homeostatically self-organized quasicritical dynamics. Phys Rev Res (2020) 2:012042. doi:10.1103/PhysRevResearch.2.012042

CrossRef Full Text | Google Scholar

135. Brochini L, de Andrade Costa A, Abadi M, Roque AC, Stolfi J, Kinouchi O. Phase transitions and self-organized criticality in networks of stochastic spiking neurons. Scientific Rep (2016) 6:35831. doi:10.1038/srep35831

CrossRef Full Text | Google Scholar

136. Costa AA, Brochini L, Kinouchi O. Self-organized supercriticality and oscillations in networks of stochastic spiking neurons. Entropy (2017) 19:399. doi:10.3390/e19080399

CrossRef Full Text | Google Scholar

137. Dickman R, Muñoz MA, Vespignani A, Zapperi S. Paths to self-organized criticality. Braz J Phys (2000) 30:27–41. doi:10.1590/S0103-97332000000100004

CrossRef Full Text | Google Scholar

138. Zierenberg J, Wilting J, Priesemann V, Levina A. Description of spreading dynamics by microscopic network models and macroscopic branching processes can differ due to coalescence. Phys Rev E (2020a) 101:022301. doi:10.1103/PhysRevE.101.022301

PubMed Abstract | CrossRef Full Text | Google Scholar

139. Ma Z, Turrigiano GG, Wessel R, Hengen KB. Cortical circuit dynamics are homeostatically tuned to criticality In vivo. Neuron (2019) 104:655–64.e4. doi:10.1016/j.neuron.2019.08.031

PubMed Abstract | CrossRef Full Text | Google Scholar

140. Wilting J, Priesemann V. Between perfectly critical and fully irregular: a reverberating model captures and predicts cortical spike propagation. Cereb Cortex (2019a) 29:2759–70. doi:10.1093/cercor/bhz049

PubMed Abstract | CrossRef Full Text | Google Scholar

141. Lin M, Chen T. Self-organized criticality in a simple model of neurons based on small-world networks. Phys Rev E (2005) 71:016133. doi:10.1103/PhysRevE.71.016133

CrossRef Full Text | Google Scholar

142. de Arcangelis L, Herrmann HJ. Self-organized criticality on small world networks. Physica A: Stat Mech its Appl (2002) 308:545–9. doi:10.1016/S0378-4371(02)00549-6

CrossRef Full Text | Google Scholar

143. Fronczak P, Fronczak A, Hołyst JA. Self-organized criticality and coevolution of network structure and dynamics. Phys Rev E (2006) 73:046117. doi:10.1103/PhysRevE.73.046117

CrossRef Full Text | Google Scholar

144. Bianconi G, Marsili M. Clogging and self-organized criticality in complex networks. Phys Rev E (2004) 70:035105. doi:10.1103/PhysRevE.70.035105

CrossRef Full Text | Google Scholar

145. Hughes D, Paczuski M, Dendy RO, Helander P, McClements KG. Solar flares as cascades of reconnecting magnetic loops. Phys Rev Lett (2003) 90:131101. doi:10.1103/PhysRevLett.90.131101

PubMed Abstract | CrossRef Full Text | Google Scholar

146. Paczuski M, Hughes D. A heavenly example of scale-free networks and self-organized criticality. Physica A: Stat Mech its Appl (2004) 342:158–63. doi:10.1016/j.physa.2004.04.073

CrossRef Full Text | Google Scholar

147. Bassett DS, Bullmore E. Small-world brain networks. The Neuroscientist (2006) 12:512–23. doi:10.1177/1073858406293182

PubMed Abstract | CrossRef Full Text | Google Scholar

148. Bullmore E, Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat Rev Neurosci (2009) 10:186–98. doi:10.1038/nrn2575

PubMed Abstract | CrossRef Full Text | Google Scholar

149. He BJ. Scale-free brain activity: past, present, and future. Trends Cogn Sci (2014) 18:480–7. doi:10.1016/j.tics.2014.04.003

PubMed Abstract | CrossRef Full Text | Google Scholar

150. Eguíluz VM, Chialvo DR, Cecchi GA, Baliki M, Apkarian AV. Scale-free brain functional networks. Phys Rev Lett (2005) 94:018102. doi:10.1103/PhysRevLett.94.018102

PubMed Abstract | CrossRef Full Text | Google Scholar

151. Siri B, Quoy M, Delord B, Cessac B, Berry H. Effects of Hebbian learning on the dynamics and structure of random networks with inhibitory and excitatory neurons. J Physiol-Paris (2007) 101:136–48. doi:10.1016/j.jphysparis.2007.10.003

PubMed Abstract | CrossRef Full Text | Google Scholar

152. Moretti P, Muñoz MA. Griffiths phases and the stretching of criticality in brain networks. Nat Commun (2013) 4:2521. doi:10.1038/ncomms3521

PubMed Abstract | CrossRef Full Text | Google Scholar

153. van Ooyen A, van Pelt J. Activity-dependent outgrowth of neurons and overshoot phenomena in developing neural networks. J Theor Biol (1994) 167:27–43. doi:10.1006/jtbi.1994.1047

CrossRef Full Text | Google Scholar

154. van Ooyen A, van Pelt J. Complex periodic behaviour in a neural network model with activity-dependent neurite outgrowth. J Theor Biol (1996) 179:229–42. doi:10.1006/jtbi.1996.0063

PubMed Abstract | CrossRef Full Text | Google Scholar

155. Abbott LF, Rohrkemper R. A simple growth model constructs critical avalanche networks. Prog Brain Res (2007) 165:13–9. doi:10.1016/S0079-6123(06)65002-4

PubMed Abstract | CrossRef Full Text | Google Scholar

156. Kalle Kossio FY, Goedeke S, van den Akker B, Ibarz B, Memmesheimer RM. Growing critical: self-organized criticality in a developing neural system. Phys Rev Lett (2018) 121(5):058301. doi:10.1103/PhysRevLett.121.058301

PubMed Abstract | CrossRef Full Text | Google Scholar

157. Droste F, Do AL, Gross T. Analytical investigation of self-organized criticality in neural networks. J R Soc Interf (2013) 10:20120558. doi:10.1098/rsif.2012.0558

CrossRef Full Text | Google Scholar

158. Landmann S, Baumgarten L, Bornholdt S. Self-organized criticality in neural networks from activity-based rewiring. arXiv:2009.11781 [cond-mat, physics:nlin, q-bio] (2020).

Google Scholar

159. van Ooyen A, Butz-Ostendorf M. Homeostatic structural plasticity can build critical networks. In: N Tomen, JM Herrmann, and U Ernst., editors. The functional role of critical dynamics in neural systems. Springer series on bio- and neurosystems. Cham: Springer International Publishing (2019). p. 117–37. doi:10.1007/978-3-030-20965-0˙7

CrossRef Full Text | Google Scholar

160. Bornholdt S, Rohlf T. Topological evolution of dynamical networks: global criticality from local dynamics. Phys Rev Lett (2000) 84:6114–7. doi:10.1103/PhysRevLett.84.6114

PubMed Abstract | CrossRef Full Text | Google Scholar

161. Bornholdt S, Röhl T. Self-organized critical neural networks. Phys Rev E (2003) 67:066118. doi:10.1103/PhysRevE.67.066118

CrossRef Full Text | Google Scholar

162. Rybarsch M, Bornholdt S. Avalanches in self-organized critical neural networks: a minimal model for the neural soc universality class. PLoS one (2014) 9:e93090. doi:10.1371/journal.pone.0093090

PubMed Abstract | CrossRef Full Text | Google Scholar

163. Ben-Ari Y, Khalilov I, Kahle KT, Cherubini E. The GABA excitatory/inhibitory shift in brain maturation and neurological disorders. The Neurosci (2012) 18:467–86. doi:10.1177/1073858412438697

CrossRef Full Text | Google Scholar

164. Peng J, Beggs JM. Attaining and maintaining criticality in a neuronal network model. Physica A: Stat Mech its Appl (2013) 392:1611–20. doi:10.1016/j.physa.2012.11.013

CrossRef Full Text | Google Scholar

165. Stepp N, Plenz D, Srinivasa N. Synaptic plasticity enables adaptive self-tuning critical networks. PLoS Comput Biol (2015) 11:e1004043. doi:10.1371/journal.pcbi.1004043

PubMed Abstract | CrossRef Full Text | Google Scholar

166. Scarpetta S, Giacco F, Lombardi F, de Candia A. Effects of Poisson noise in a IF model with STDP and spontaneous replay of periodic spatiotemporal patterns, in absence of cue stimulation. Biosystems (2013) 112:258–64. doi:10.1016/j.biosystems.2013.03.017

PubMed Abstract | CrossRef Full Text | Google Scholar

167. Scarpetta S, de Candia A. Alternation of up and down states at a dynamical phase-transition of a neural network with spatiotemporal attractors. Front Syst Neurosci (2014) 8:88. doi:10.3389/fnsys.2014.00088

PubMed Abstract | CrossRef Full Text | Google Scholar

168. Scarpetta S, Apicella I, Minati L, de Candia A. Hysteresis, neural avalanches, and critical behavior near a first-order transition of a spiking neural network. Phys Rev E (2018) 97:062305. doi:10.1103/PhysRevE.97.062305

PubMed Abstract | CrossRef Full Text | Google Scholar

169. Loidolt M, Rudelt L, Priesemann V. Sequence memory in recurrent neuronal network can develop without structured input. bioRxiv (2020). doi:10.1101/2020.09.15.297580

CrossRef Full Text | Google Scholar

170. Papa BD, Priesemann V, Triesch J. Criticality meets learning: criticality signatures in a self-organizing recurrent neural network. PLoS One (2017) 12:e0178683. doi:10.1371/journal.pone.0178683

PubMed Abstract | CrossRef Full Text | Google Scholar

171. Hopfield JJ. Neural networks and physical systems with emergent collective computational abilities. Proc Natl Acad Sci USA (1982) 79:2554–8. doi:10.1073/pnas.79.8.2554

PubMed Abstract | CrossRef Full Text | Google Scholar

172. Scarpetta S, Candia A. Neural avalanches at the critical point between replay and non-replay of spatiotemporal patterns. PLOS ONE (2013) 8:e64162. doi:10.1371/journal.pone.0064162

PubMed Abstract | CrossRef Full Text | Google Scholar

173. Bak P, Chialvo DR. Adaptive learning by extremal dynamics and negative feedback. Phys Rev E (2001) 63:031912. doi:10.1103/PhysRevE.63.031912

CrossRef Full Text | Google Scholar

174. Kinouchi O, Copelli M. Optimal dynamical range of excitable networks at criticality. Nat Phys (2006) 2:348–51. doi:10.1038/nphys289

CrossRef Full Text | Google Scholar

175. Zierenberg J, Wilting J, Priesemann V, Levina A. Tailored ensembles of neural networks optimize sensitivity to stimulus statistics. Phys Rev Res (2020b) 2:013115. doi:10.1103/PhysRevResearch.2.013115

CrossRef Full Text | Google Scholar

176. Stanley HE. Introduction to phase transitions and critical phenomena. Am J Phys (1972) 40:927–8. doi:10.1119/1.1986710

CrossRef Full Text | Google Scholar

177. Sethna J. Statistical mechanics: entropy, order parameters, and complexity. Oxford, United Kingdom: Oxford University Press (2021).

178. Shew WL, Yang H, Petermann T, Roy R, Plenz D. Neuronal avalanches imply maximum dynamic range in cortical networks at criticality. J Neurosci (2009) 29:15595–600. doi:10.1523/JNEUROSCI.3864-09.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

179. Shew WL, Plenz D. The functional benefits of criticality in the cortex. Neuroscientist (2013) 19:88–100. doi:10.1177/1073858412445487

PubMed Abstract | CrossRef Full Text | Google Scholar

180. Boedecker J, Obst O, Lizier JT, Mayer NM, Asada M. Information processing in echo state networks at the edge of chaos. Theor Biosci (2012) 131:205–13. doi:10.1007/s12064-011-0146-8

CrossRef Full Text | Google Scholar

181. Boedecker J, Lampe T, Riedmiller M. Modeling effects of intrinsic and extrinsic rewards on the competition between striatal learning systems. Front Psychol (2013) 4:739. doi:10.3389/fpsyg.2013.00739

PubMed Abstract | CrossRef Full Text | Google Scholar

182. Bertschinger N, Natschläger T. Real-time computation at the edge of chaos in recurrent neural networks. Neural Comput (2004) 16:1413–36. doi:10.1162/089976604323057443

PubMed Abstract | CrossRef Full Text | Google Scholar

183. Lazar A, Pipa G, Triesch J. SORN: a self-organizing recurrent neural network. Front Comput Neurosci (2009) 3:23. doi:10.3389/neuro.10.023.2009

PubMed Abstract | CrossRef Full Text | Google Scholar

184. Del Papa B, Priesemann V, Triesch J. Fading memory, plasticity, and criticality in recurrent networks. In: N Tomen, JM Herrmann, and U Ernst., editors. The functional role of critical dynamics in neural systems. Springer series on bio- and neurosystems. Cham: Springer International Publishing (2019). p. 95–115. doi:10.1007/978-3-030-20965-0_6

CrossRef Full Text | Google Scholar

185. Cocchi L, Gollo LL, Zalesky A, Breakspear M. Criticality in the brain: a synthesis of neurobiology, models and cognition. Prog Neurobiol (2017) 158:132–52. doi:10.1016/j.pneurobio.2017.07.002

PubMed Abstract | CrossRef Full Text | Google Scholar

186. Nolte M, Reimann MW, King JG, Markram H, Muller EB. Cortical reliability amid noise and chaos. Nat Commun (2019) 10:3792. doi:10.1038/s41467-019-11633-8

PubMed Abstract | CrossRef Full Text | Google Scholar

187. Gollo LL. Coexistence of critical sensitivity and subcritical specificity can yield optimal population coding. J R Soc Interf (2017) 14:20170207. doi:10.1098/rsif.2017.0207

CrossRef Full Text | Google Scholar

188. Wilting J, Dehning J, Pinheiro Neto J, Rudelt L, Wibral M, Zierenberg J, et al. Operating in a reverberating regime enables rapid tuning of network states to task requirements. Front Syst Neurosci (2018) 12. doi:10.3389/fnsys.2018.00055

PubMed Abstract | CrossRef Full Text | Google Scholar

189. Wilting J, Priesemann V. 25 years of criticality in neuroscience — established results, open controversies, novel concepts. Curr Opin Neurobiol (2019b) 58:105–11. doi:10.1016/j.conb.2019.08.002

PubMed Abstract | CrossRef Full Text | Google Scholar

190. Tomen N, Rotermund D, Ernst U. Marginally subcritical dynamics explain enhanced stimulus discriminability under attention. Front Syst Neurosci (2014) 8:1–15. doi:10.3389/fnsys.2014.00151

PubMed Abstract | CrossRef Full Text | Google Scholar

191. Ribeiro TL, Copelli M, Caixeta F, Belchior H, Chialvo DR, Nicolelis MA, et al. Spike avalanches exhibit universal dynamics across the sleep-wake cycle. PLoS One (2010) 5:e14129. doi:10.1371/journal.pone.0014129

PubMed Abstract | CrossRef Full Text | Google Scholar

192. Spitzner FP, Dehning J, Wilting J, Hagemann A, Neto JP, Zierenberg J, et al. MR. Estimator, a toolbox to determine intrinsic timescales from subsampled spiking activity. arXiv:2007.03367 [physics, q-bio] (2020).

Google Scholar

193. Zeraati R, Engel TA, Levina A. Estimation of autocorrelation timescales with approximate bayesian computations. bioRxiv (2020). doi:10.1101/2020.08.11.245944

CrossRef Full Text | Google Scholar

194. Meisel C, Klaus A, Kuehn C, Plenz D. Critical slowing down governs the transition to neuron spiking. PLoS Comput Biol (2015) 11:e1004097. doi:10.1371/journal.pcbi.1004097

PubMed Abstract | CrossRef Full Text | Google Scholar

195. Tkacik G, Mora T, Marre O, Amodei D, Palmer SE, Bialek W. Thermodynamics and signatures of criticality in a network of neurons. PNAS (2015) 112:11508–13. doi:10.1073/pnas.1514188112

PubMed Abstract | CrossRef Full Text | Google Scholar

196. Hidalgo J, Grilli J, Suweis S, Munoz MA, Banavar JR, Maritan A. Information-based fitness and the emergence of criticality in living systems. Proc Natl Acad Sci (2014) 111:10095–100. doi:10.1073/pnas.1319166111

PubMed Abstract | CrossRef Full Text | Google Scholar

197. Meshulam L, Gauthier JL, Brody CD, Tank DW, Bialek W. Coarse graining, fixed points, and scaling in a large population of neurons. Phys Rev Lett (2019) 123:178103. doi:10.1103/PhysRevLett.123.178103

PubMed Abstract | CrossRef Full Text | Google Scholar

198. Nonnenmacher M, Behrens C, Berens P, Bethge M, Macke JH. Signatures of criticality arise from random subsampling in simple population models. PLoS Comput Biol (2017) 13:e1005718. doi:10.1371/journal.pcbi.1005718

PubMed Abstract | CrossRef Full Text | Google Scholar

199. Mastromatteo I, Marsili M. On the criticality of inferred models. J Stat Mech Theor Exp (2011) 2011:P10012. doi:10.1088/1742-5468/2011/10/P10012

CrossRef Full Text | Google Scholar

200. Nicoletti G, Suweis S, Maritan A. Scaling and criticality in a phenomenological renormalization group. Phys Rev Res (2020) 2:023144. doi:10.1103/PhysRevResearch.2.023144

CrossRef Full Text | Google Scholar

201. Morrell MC, Sederberg AJ, Nemenman I. Latent dynamical variables produce signatures of spatiotemporal criticality in large biological systems. arXiv preprint arXiv:2008.04435 (2020).

Google Scholar

202. Neto JP, Spitzner FP, Priesemann V. A unified picture of neuronal avalanches arises from the understanding of sampling effects. arXiv:1910.09984 [cond-mat, physics:nlin, physics:physics, q-bio] (2020).

Google Scholar

203. Shriki O, Alstott J, Carver F, Holroyd T, Henson RN, Smith ML, et al. Neuronal avalanches in the resting meg of the human brain. J Neurosci (2013) 33:7079–90. doi:10.1523/JNEUROSCI.4286-12.2013

PubMed Abstract | CrossRef Full Text | Google Scholar

204. Clawson WP, Wright NC, Wessel R, Shew WL. Adaptation towards scale-free dynamics improves cortical stimulus discrimination at the cost of reduced detection. PLoS Comput Biol (2017) 13:e1005574. doi:10.1371/journal.pcbi.1005574

PubMed Abstract | CrossRef Full Text | Google Scholar

205. Carhart-Harris RL, Muthukumaraswamy S, Roseman L, Kaelen M, Droog W, Murphy K, et al. Neural correlates of the LSD experience revealed by multimodal neuroimaging. Proc Natl Acad Sci (2016) 113:4853–8. doi:10.1073/pnas.1518377113

PubMed Abstract | CrossRef Full Text | Google Scholar

206. Simola J, Zhigalov A, Morales-Muñoz I, Palva JM, Palva S. Critical dynamics of endogenous fluctuations predict cognitive flexibility in the Go/NoGo task. Sci Rep (2017) 7:2909. doi:10.1038/s41598-017-02750-9

PubMed Abstract | CrossRef Full Text | Google Scholar