- 1Department of Electrical and Computer Engineering, COMSATS University Islamabad, Attock, Pakistan
- 2Department of Mathematics, COMSATS University Islamabad, Attock, Pakistan
- 3Future Technology Research Center, National Yunlin University of Science and Technology, Douliou, Taiwan
- 4Mechanical Engineering Department, King Fahd University of Petroleum and Minerals, Dhahran, Saudi Arabia
- 5School of Electrical Engineering and Automation, Wuhan University, Wuhan, China
The presented communication provides the analysis of entropy generation and heat transport rate in peristalsis of hybrid nanofluid induced by metachronal ciliary beating under magnetic environment for sufficiently large magnetic Reynolds number. Nanoparticles of Cu and Al2O3 are suspended in water. Features of their structures are determined by using long-wavelength approximation with zero Reynolds number. Adams Bashforth method has been applied to compute the results of the flow variables as well as entropy generation number from the formulated differential system which are then interpreted graphically to establish physical significance for different values of physical interest. This investigation reveals that thermal performance of fluid can be boosted by utilizing hybrid nanomaterial about the strength of a wall for stability. Irreversibility analysis ensures that entropy reduced for strong magnetic field while thermal heat generation results in an increase in temperature causing an enhancement in entropy of the system. Error analysis has been performed with reasonably accurate tolerance level. The comparative outcomes of both numerical approaches are presented with plentiful graphical as well as numerical demonstrations which demonstrate the importance in terms of robustness, accuracy and stability.
Introduction
Peristalsis is a spontaneous process of a progressive symmetrical wave’s extension and contraction along elastic walls of a fluid-filled tube. Physiologically, a tubular smooth muscle structure has an intrinsic neuromuscular characteristic which interprets the peristaltic phenomenon. Novel application of peristalsis is to stabilize the blood flow which reduces the risk of stroke and heart attack. It has become a field of curiosity for researchers and engineers due to its pertinent applications in human physiological systems such as in the food bolus transport from digestive tract, in cilia movement and blood transport in small blood vessels, and in fluids motion through lymphatic vessels, peristaltic pumping in biomedical appliances, like blood pump machine, finger pumps, heart-lung machine as well as for the noxious fluid flow in nuclear industries. Initially, the topic has been studied by Engelman [1] in the human physiological system. Later on, Zhang et al [2] examined fluid motion in peristaltic pump. Peristaltic flow of viscous fluid with variable viscosity bounded by convective walls has been inspected by Awais et al. [3]. It was observed that heat and mass Biot numbers increases heat transfer rate and concentration of fluid. Influences of chemical reaction and Lorentz force on peristaltic flow of Jeffrey fluid through a permeable channel by considering wall suction/injection are studied by Abbas et al. [4]. Streamline analysis was performed in the existence of convective mass and heat transfer conditions. Awais et al. [5] theoretically inspected the peristaltic rheology of copper-water nanofluid for slip and Hall effects with non-uniform viscosity through generalized compliant walls. It was concluded that first and second order velocity slip parameters have an effect of increasing velocity of fluid while heat transfer rate is maximum near channel walls. Over and above that, peristaltic flow induced by ciliary action appears significantly in various physiological transportation processes. Cilia are microscopic, contractile structures that transpire throughout the surface of a cell and biological vessels. They tend to beat in a coordinated rhythm called metachronic rhythm and resulting waves are metachronal waves. Important functions subjected with cilia comprise heat control, surface energy amendment and actuation. In the human body, cilia exist in the renal system, in photoreceptors of the retina, digestive tract and embryological organs. Abrar et al. [6] investigated ciliary induced nanofluid dynamics under magnetic effects for second law analysis. It was found that angle of inclination and Hartmann number both have an increasing impact on pressure gradient. Moreover, flow variables and entropy generation were observed to be symmetric about the radial axis. Awais et al. [7] inspected magnetic induction effects on peristaltic flow coatings with power-law hybrid nanofluid induced by ciliary activity. It was noticed that nanoparticles’ coating perks up characteristics of pumping and heat transfer which made them useful in endoscopy and cancer treatment. Mathematical models of cilia-induced biofluid dynamics are consequently of enormous significance in further illuminating the multifaceted characteristics built-in many biological structures and have been investigated [8–10].
Heat transfer in peristalsis of physiological fluids is of great significance as examined in hemodialysis, blood oxygenation, convection of heat from pores of tissues during blood flow, tissue conduction, and heat transfer through dilation of blood vessels. In the ancient times, heat transfer characteristics have been revealed through classical Fourier’s law of conduction which imitates the parabolic nature of energy equation. Physically, it indicates that any disturbance is transferred promptly through considered substance. Researchers attempted different heat flux models along with number of physical factors regarding applications of heat transfer processes. Muhammad et al. [11] examined ferrohydrodynamic boundary layer flow by employing hybrid isothermal model for the homogeneous-heterogeneous reactions. Fourier’s law of heat flux was considered for analysis of magnetic dipole and Newtonian heating. Dynamics of micropolar fluid and heat transfer rate for the influence of variable transport properties and heat generation are discussed by Khan et al. [12]. Fourier's heat flux model is implemented in the analysis of heat transfer. Variation in transport characteristics leads to an increment in thermal exchange rate and reduction in skin friction. Several attempts are provided in literature [13–18]. Recently, there has been an explosion of emerging conductive and highly thermal resistive nano-particles, initially introduced by Choi [19], to enhance thermal characteristics of such fluids. Nanofluids, a colloidal suspension prepared by mixing nanometer-sized particles with base fluid (e.g., water and oil, etc), are stable, introduces very little pressure drop, and can pass through nanochannels. Muhammad and Nadeem [20] investigated convective heat transfer performance in the dynamics of ferromagnetic nanofluid for ferrite nanoparticles Ni-ZnFe2O4, Mn-ZnFe2O4 and Fe2O4. It was noticed that the characteristics of magneto-thermo mechanical interaction slows down the fluid particles motion, thereby lessen the heat transfer rate at the surface. Further, solid volume fraction has escalating effect on thermal exchange rate. Awais et al. [21] demonstrated nanoparticles and nonlinear thermal radiation characteristics in the dynamics of polymeric fluid dispersed by nanoparticles considering Oldroyd-B model. They concluded that Nusselt number and Sherwood number show conflicting behavior toward Deborah numbers while increase against Pr. Muhammad et al. [22] analyzed ferrite nanoparticles in the course of six different ferromagnetic nanofluids dispersed in the mixture of water and ethylene glycol. In its perspective, it was evident that Newtonian heating has an enhancing effect on heat transfer rate. Ahmed et al. [23] deliberated double stratification effect on radiative SWCNT and MWCNT nanofluid transport of Falkner-Skan problem. Muhammad et al. [24] analyzed mixed convection effects in Ag/ethylene glycol nanofluid flow through a cavity with thin central heater by implementing finite volume method. Investigators have performed remarkable theoretical as well as experimental attempts and some are cited as [25–32]. Despite the significant consequences of researchers’ attempts, genuine applications demanded transaction in different properties of nanofluids and consequently hybrid nanofluids were synthesized by dispersing nanoparticles of dissimilar materials in base fluid. For instance, an investigation of MHD peristaltic flow of Jeffrey material dispersed by (TiO2–Cu/H2O) hybrid nanofluid with slip conditions was done by Ali et al. [33]. Mumraiz et al. [34] demonstrated entropy rate in the flow of electrical MHD (Al2O3–Cu/H2O) hybrid nanofluid by considering variable heat flux. Lund et al. [35] established multiple solutions for MHD (Cu–Fe3O4/H2O) hybrid nanofluid dynamics occurred due to nonlinear stretching/shrinking surface. By implementing stability analysis, it was concluded that first solution is stable. Parveen et al. [36] predicted heat transfer rate and pressure rise for Au-Al2O3/Blood Ree-Eyring hybrid nanofluid under induced magnetic field effects through endoscope. It was revealed that computational results for pressure rise against M and α correspond to strengthen pumping whereas more pumping required for rising χ. Moreover, heat transfer coefficient was seen to enhance toward Br and χ. Neural network algorithm was implemented for validation of experimental data and very accurate results were found. Research community has exploited hybrid nanomaterials in diverse applications with an aim to use a small-volume fraction of nanoparticles at lower production cost and some efforts are listed as [37–40]. Moreover, metallic nanoparticles possess unique optoelectrical properties and high thermal conductivities while metal oxides such as Al2O3 show excellent chemical inertness as well as stability [41]. Hence these are useful in physiological applications of nanofluids including drug delivery, chemical and biological sensing, data storage magnetic resonance imaging and biomedicine. In the drug delivery, these particles act like heat source where drug is injected near tumor and absorbed by tumor through high gradient magnetic field. At low scale of particles’ size, the magnetic properties of nanoparticles perk up efficiently which make these particles priceless. In this regard, composition of Cu, having thermal conductivity 700 times higher than water, and Al2O3 is preferred in present theoretical assessment to put on the maximum composite thermal conductivity, stability and chemical inertness. Moreover, mass-based single-phase hybrid nanofluid model is adopted which possesses both Cu and Al2O3 nanoparticles along with base fluid act as a single substance to obtain required thermal features. While two phase model consists of such substances which possess dissimilar chemical properties like a mixture of air and water [42].
Furthermore, Saqib et al. [43] presented an overview of different models of thermophysical properties of nanofluids and hybrid nanofluids regarding theoretical and experimental studies including Aminossadati and Ghasemi model for density, Bourantas and Loukopoulos model for heat capacitance and thermal expansion coefficient, Brinkmann model for dynamic viscosity and Hamilton-Crosser model for thermal conductivity of nanofluids and hybrid nanofluids. Therefore, the model adopted in present theoretical work is an appropriate one.
In thermo dynamical investigations of flow and heat transfer processes in the intricate physiological structures, one issue of essential interest is to reduce heat losses in the system, a quantitative evaluation of which is called entropy generation. Entropy generation analysis in MHD peristaltic flow of copper–water nanofluid along with slip conditions for velocity and temperature was explored by Ali et al. [44]. Khan et al. [45] analyzed entropy minimization, activation energy and heat transfer in squeezing second grade nanofluid between infinite plates. It was revealed that entropy generation number increases for squeezing fluid parameter. Entropy optimized Darcy-Forchheimer nanofluid consisting Silicon dioxide and Molybdenum disulfide associated with variable viscosity was investigated by Abbas et al. [46]. It was significant that entropy generation rate is higher in SiO2/H2O. Entropy generation in fully developed Darcy-Forchheimer flow over a curved surface with mixed convection and activation energy was studied by Muhammad et al. [47]. Muhammad and Khan [48] studied influence of second order slip on MHD radiated nanofluid flow by a curved surface with entropy generation. They found that both Bejan number and entropy generation rose against heterogeneous reaction parameter. Nayak et al. [49] probed entropy optimization in MHD non-Newtonian nanofluid in order to characterize a high-quality solar energy absorber as well as intensification of heat transfer. Abbas et al. [50] scrutinized entropy generation rate in fully developed MHD nanofluid flow with second order velocity slip and activation energy. They depicted that entropy rate raised vs. second order velocity slip parameter.
Primary motivation behind this effort is to extend ciliary induced peristaltic transport with magnetic induction phenomenon into new directions by carrying entropy optimization and heat transfer analysis in addition of hybrid nanofluid. Salient features of the under study problem are briefly narrated as follows:
• A novel investigation has been presented for the peristaltic analysis of hybrid nanoparticles, a combination of Cu and Al2O3, caused by 2 waves of cilia through an axisymmetric tube under induced magnetic field effects.
• Entropy generation and heat transport analysis are presented to study the internal heat generation and viscous dissipation effects.
• Numerical analysis has been employed to compute the formulated differential order system along with error analysis to establish the validity of the derived solutions.
• Graphical and numerical illustrations for flow profiles and entropy generation toward different emerging parameters are used to interpret the behavior of flow variables and analyze their physical significance.
Problem Formulation
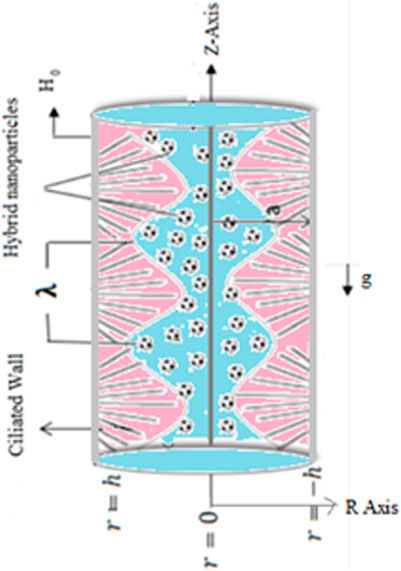
Consider the peristaltic flow of (Cu-Al2O3/H2O) hybrid nanofluid in an axisymmetric tube having radius a caused by metachronal waves having speed c with ciliary length b, and wavelength
Considering motion of cilia in elliptical path, horizontal position of cilia tips are written as:
In view of Eqs 1, Eq. 3 becomes:
Let (R, Z, U, W) and (r, z, u, w) respectively represent the coordinates and velocities in the fixed and wave frame. The following transformations switched from fixed frame to wave frame for steady flow are as:
Moreover, a uniform magnetic field of strength H0 is applied in a radial direction which produces an induced magnetic field
The mass conservation equation is:
Radial and azimuthal components of momentum conservation equation for hybrid nanofluid flow in an axisymmetric tube along with the effects of buoyancy force and magnetic induction are:
Energy conservation equation including the influences of internal heat generation and viscous dissipation is:
where
Radial and azimuthal components of conservation of magnetic induction equation using Maxwell’s equations are expressed as:
In the above expressions, u, w, H1, and H3 respectively denote r- and z-components of velocity and induced magnetic field profiles. Moreover, T0 and p stands for temperature and pressure at the center of the tube, respectively. Mathematical relations for thermophysical properties of hybrid nanofluid are given as [36]:
Now, introduce the following dimensionless quantities with wall temperature
In the sight of the above quantities along with long wavelength and creeping Stokesian flow approach, we get:
Emerging parameters in the dimensionless model are expressed as:
Where,
Corresponding dimensionless boundary conditions are:
The volumetric entropy generation rate in the co-occurrence of the induced magnetic field can be articulated as:
Characteristic entropy generation rate is:
The dimensionless form of the entropy generation number is:
It is clear from the above relation that three major sources are dominant in generating irreversibility, i.e., thermal diffusion, viscous forces, and magnetic effects, respectively.
Numerical Procedure
We have employed Adam’s predictor-corrector method along with the finite difference method [52–56] to solve the system model of the peristaltic flow of a hybrid nanofluid in an axisymmetric tube under induced magnetic effects as shown in Figure 2. Grid independent testor grid convergence to describe the improvement of outcomes with smaller mesh size is performed for both Adam’s predictor-corrector method and Finite Difference method to access their accuracy, convergence and stability. The smaller mesh size on the other hand increases the computations considerably, therefore, an appropriate size of meshes are used on the basis of tradeoff between the accuracy and complexity for both numerical procedures.
Adams Method
In Adam’s method, we first predict the solution and after that the corrector is used for an accurate solution. For this purpose, a generic representation of temperature, axial velocity, and axial induced magnetic field variables are as follows [57, 58]:
For the above mentioned profiles, two step Adams-Moulton predictor relations are presented as:
while, the two-step Adams-Moulton corrector formulas for temperature, axial velocity, and axial induced magnetic field profiles are:
Similarly, Adam-Moulton four-step predictor-corrector relations for the aforementioned profiles can be found.
Finite Difference Method
The system model is executed by manipulating the spirit of the finite-difference concept [59–61] through standard derivative definition. The formula for the discretization of backward difference method for axial induced magnetic field profile based on 5 point stencils are:
Accordingly, the discretization formulas for w and
Analysis of Results
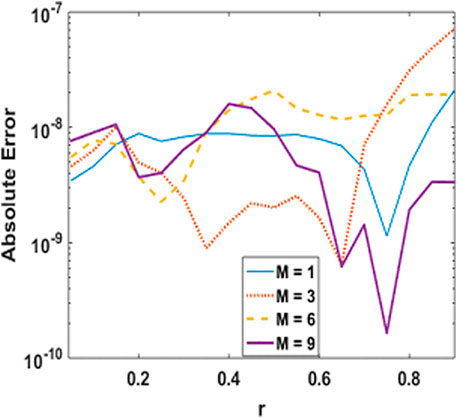
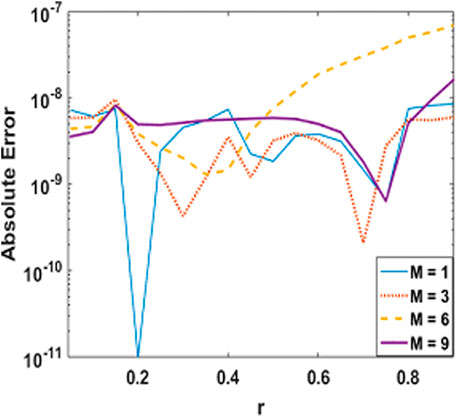
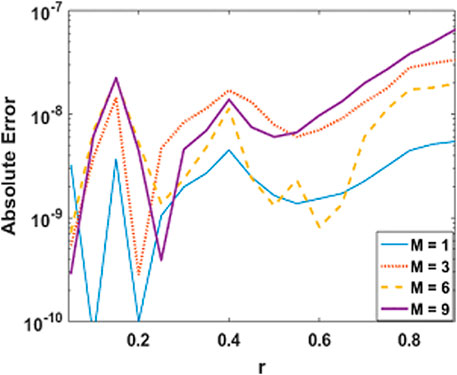
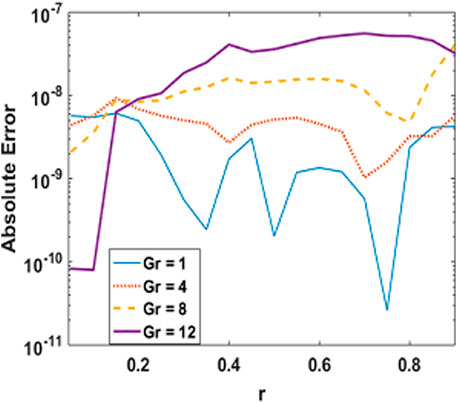
In order to test the stability and convergence of the solutions, we have prepared error graphs for axial velocity, axial induced magnetic field profile and temperature profile with prominent parameters which are presented in Figures 3–6. These plots show that obtained solutions are convergent and satisfying the tolerance level i.e., 10–8. Figures 3, 4 are showing the absolute error for axial velocity and axial induce magnetic field with M while Figures 5, 6 illustrate the behavior of absolute error by using Adam’s method and finite difference method for temperature with M and Gr parameters, respectively. From Figures 3–6, it is observed that absolute error is found within the limits of 10–10 → 10–08 which is quite negligible.
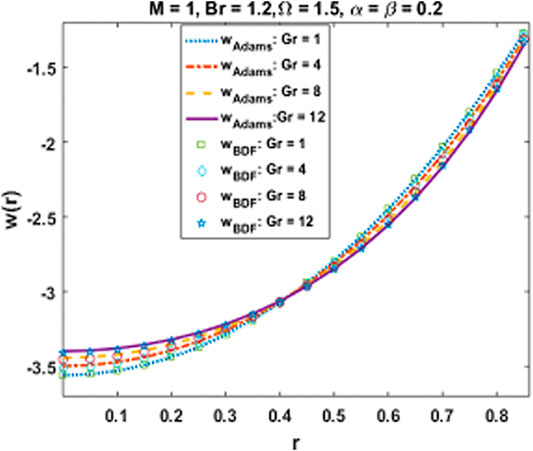
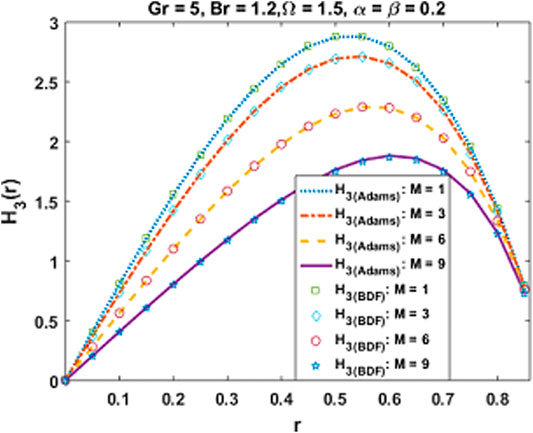
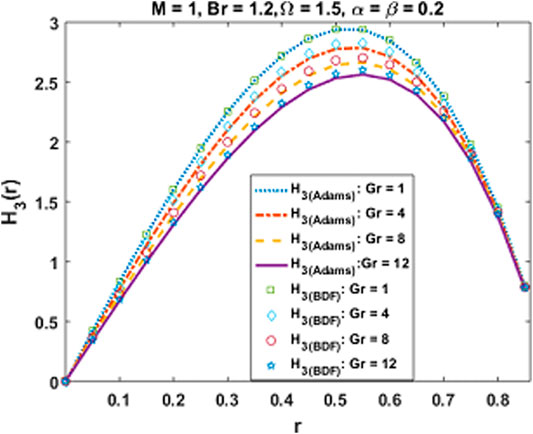
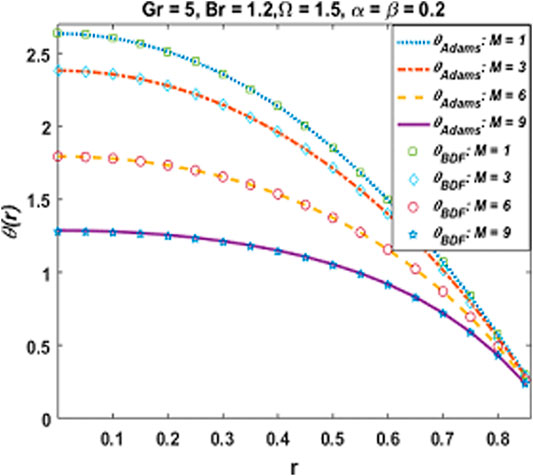
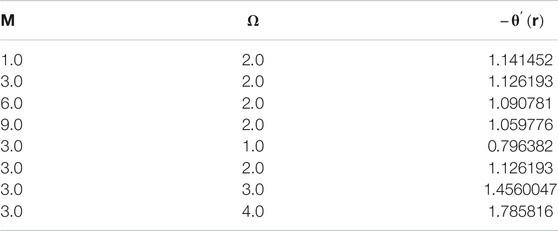
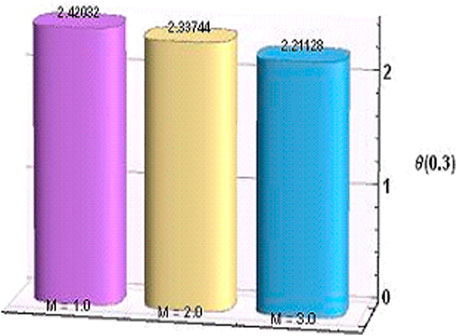
The coupled differential equations system is executed numerically, and the outcomes are figured out graphically to understand physical behaviors against engrossing parameters. The variation in axial velocity and magnetic induction profile for escalating values of pertinent parameters are depicted in Figures 7–10, respectively. As the magnetic parameter grows up, an enhancement in the velocity profile occurs in the central region of the cylindrical tube due to more dominant induction effects than magnetic diffusion and increases the flow rate. While it decreases near the ciliated wall because cilia resist the flow and the existence of magnetic effects increases the retarding behavior due to no slip velocity condition as observed in Figure 7. This effect of MHD is applicable in the biomedical engineering, in the treatment of different neurotic disorders, drug delivery for cancer treatment, and as an advance therapeutic concept to damage the tumor cells by providing local heat through induced magnetic field in presence of injected hybrid nanofluid. A similar trend is noticed for the velocity against Gr > 0 i.e., for cooling Newtonian in Figure 8. As Gr is directly linked with kinetic energy and hence velocity, its mounting values result in accelerating velocity at the center of the tube. Moreover, a conflicting behavior near the boundary is due to increasing frictional effects caused by the continuous beating of cilia. Further, velocity plots indicate that there exists a point of intersection inside the tube where these parameters show no influence on velocity. The variational behavior of axial induced magnetic field H3 for values of magnetic parameter M and Grashof number Gr are explored in Figures 9, 10 having maximum values between the center and boundary of cylindrical tube. Large values of M indicate high magnetic Reynolds number which causes fast advection process, therefore increasing flow rate reduces the magnetic induction profile. Moreover, Gr show diminishing trend as well. Behavior of temperature in peristalsis of nanohybrids through symmetric channel depends on many physical quantities as well as the system’s geometry. The physical impact of emerging parameters on the temperature of the fluid is deduced in Figures 11–14. Figure 11 reveals that mounting values of M gradually decline temperature which implies a considerable rise in the thermal exchange rate. This is due to the fact that as larger values of M show strong induction effects, fluid particles gain more kinetic energy by converting thermal energy which reduces fluid temperature.
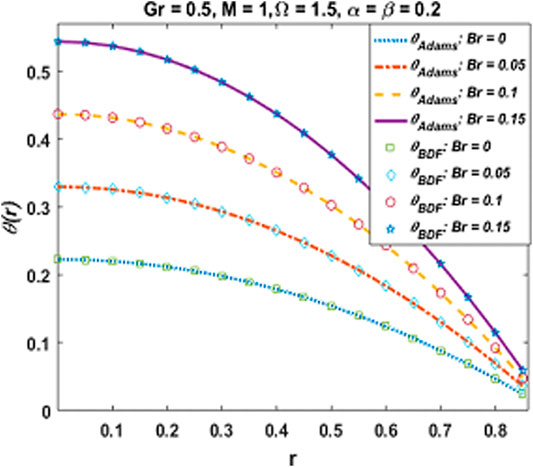
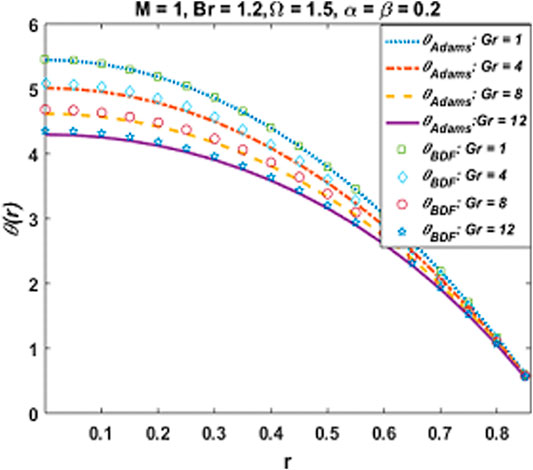
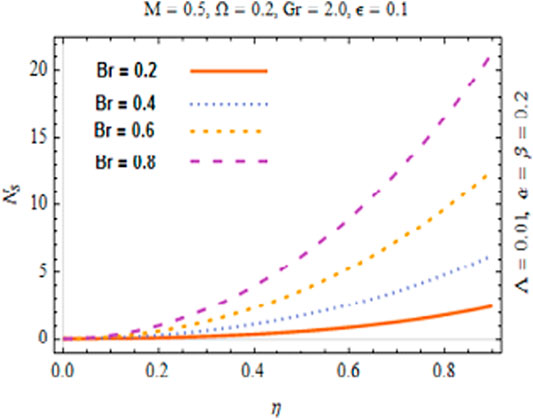
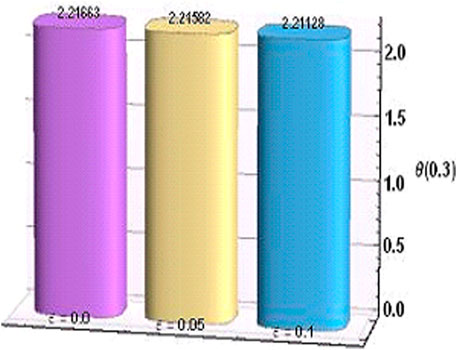
An increasing response of temperature of fluid toward Br is experienced in Figure 12. Since larger values of Br signify low viscous forces and high kinetic energy of fluid molecules which enhances molecular collision and results in temperature rise. Temperature of Cu-Al2O3/H2O hybrid nanofluid decreases due to enhancing buoyancy forces for high magnitude of Gr as explicated in Figure 13. Furthermore, the variation in temperature verses the heat generation parameter
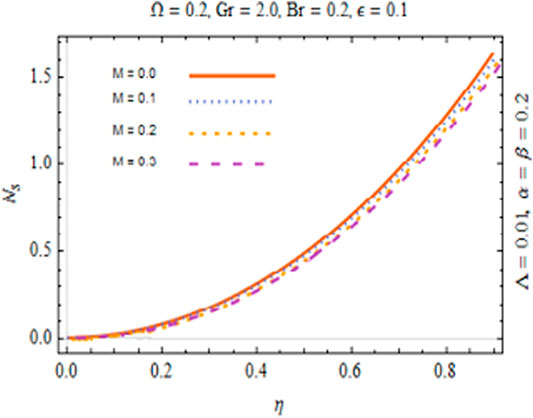
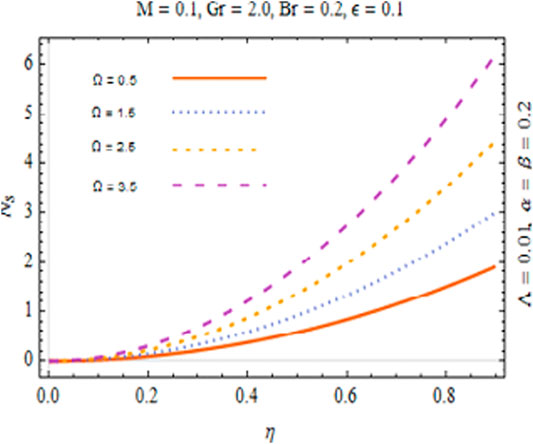
The most engrossing part of this section is irreversibility analysis. Figures 15–18 are sketched to physically inspect mechanism of second law analysis against pertinent parameters. The effect of magnetic parameter on Ns is figured out in Figure 15. It is observed that entropy in the fluid declines. It is of true significance physically since the fluid flow accelerates instantly with the increasing magnitude of M and heat transfer rate increases. Consequently, thermal energy of the system reduces. Therefore, the entropy of the system drops off. The role of Br and
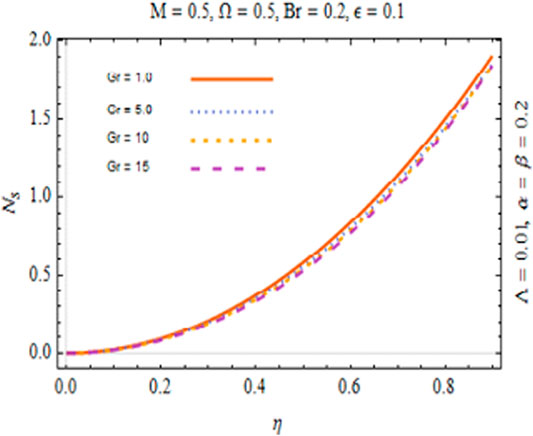
Further, Ns profile reduces with boosting values of Gr as shown in Figure 18. A physical interpretation of this performance is that the elevation in Gr enhances the temperature difference as well as the average kinetic energy of fluid particles which consequently reduce the viscous forces between fluid particles. Thus, Gr serves to reduce entropy production. Moreover, an inspection of all these plots reveals that the physical parameters show a negligible impact on Ns profile in the central region of the channel while it is sensitive to vary near the boundary. Also, entropy changes from zero to its maximum value as one move from the center of the tube toward the ciliated wall.
Besides this, Table 1 displays experimental values for the thermophysical characteristics of base fluid and nanomaterials. Tables 2, 3 are prepared and portrayed for numerical values of velocity and temperature for radial distance against escalating parameters
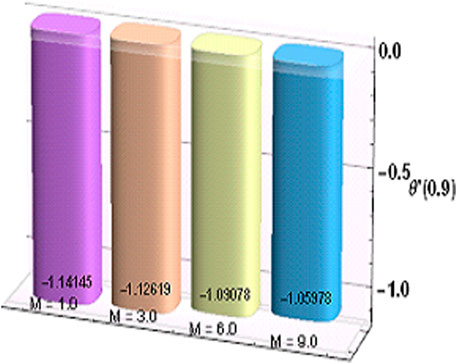
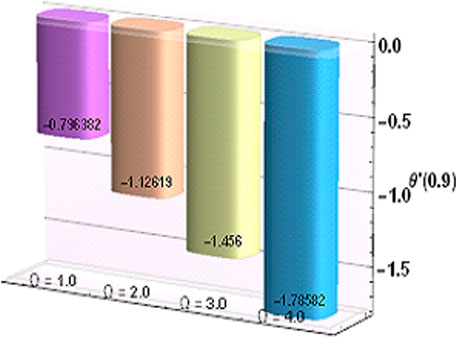
The behavior of the heat transfer rate for increasing magnitudes of magnetic parameter and heat generation parameter is depicted in Table 4. It can be observed that the magnetic parameter has an effect of decreasing heat transfer rate while an opposite variational trend is noticed for the heat generation parameter.
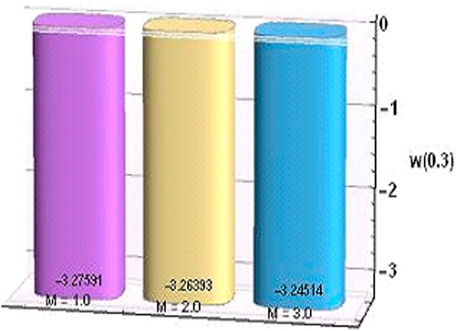
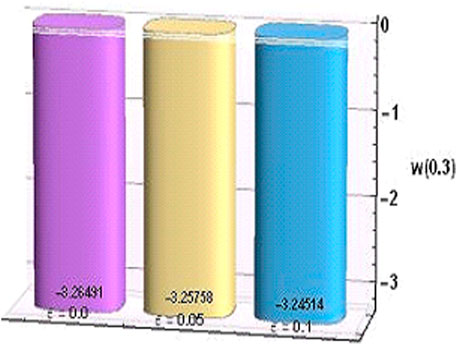
Furthermore, bar charts as represented in Figures 19–22 which are prepared to examine the behaviors of temperature and velocity for increasing values of M and
Convergence and Complexity Analysis
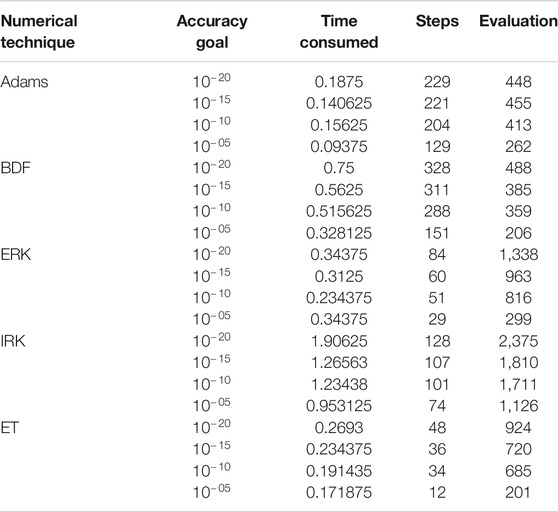
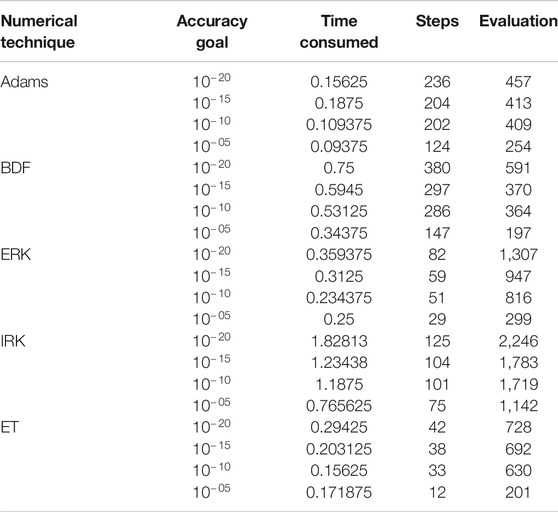
Stability analysis is performed based on various levels of accuracy goals for different numerical methods in this section. Additionally, Tables 5, 6 present the comparison of complexity analysis for Adams method (AM), Explicit Runge-Kutta approach (ERK), implicit Runge-Kutta method (IRK), extrapolation technique (ET) and backward difference method (BDF).
Results of complexity analysis along with stability analysis are performed for AM, ERK, IRK, ET and BDF on the bases of stiff and non-stiff goals of accuracy and achieved results for variation of M & Br of a hybrid nanofluidic model are given in Tables 5.
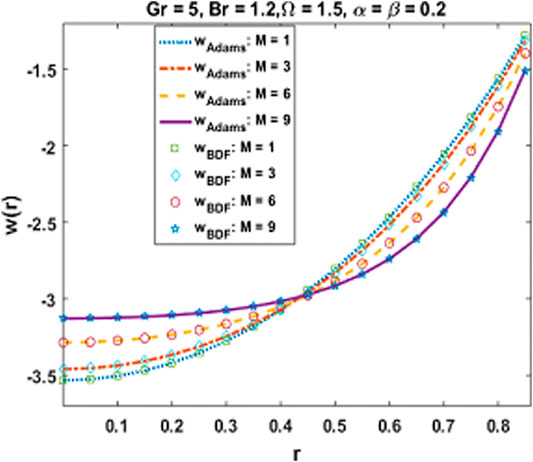
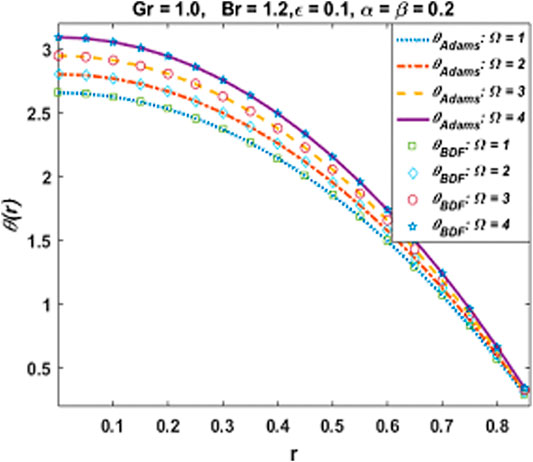
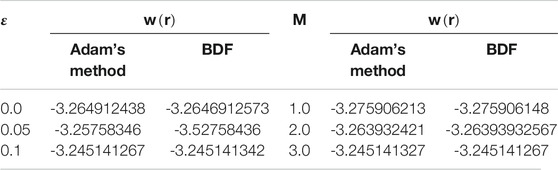
It is observed that all numerical computing algorithms are applicable for both non-stiff as well as stiff goals of accuracy for all variants of hybrid nanofluidic model which prove the analysis of stability and convergence of numerical computing algorithms. Furthermore, a complexity analysis comparison is performed based on time, steps, and function evaluations and it is examined that on the average, the Adams numerical method is the most competent as compared to the other numerical computing algorithms. Moreover, comparison of numerical results obtained by Adam’s method as well as backward difference method is provided in Table 7. It is witnessed that the outcomes are in good agreement. Mathematica and Matlab software package for the numerical experimentation presented in this study.
Concluding Remarks
Analysis of entropy rate and heat transfer in peristalsis due to cilia with magnetic induction effects via numerical techniques is of main concern in this study. Viscous and Newtonian heating factors are considered. Key findings are:
• Error analysis exhibits quite a negligible magnitude of absolute errors in the solutions which guarantee the validity of results of preferred numerical technique.
• Velocity profile show increasing behavior in the central part of the tube while a conflicting behavior is noted near the ciliated boundary for M and Gr along with a point of intersection in the region. Magnetic induction profile shows opposite trend vs. M and Gr. This effect of magnetic induction is helpful in modern drug delivery systems to guide the drugs suspended with hybrid nanoparticles to destroy tumor by the mechanism of hyperthermia and cryosurgery.
• Temperature of hybrid nanofluid turns down for M and Gr while an opposite trend is observed against Br and
• Second law analysis reveals that entropy rate reduces for M and Gr whereas more irreversibility generates for rising magnitudes of Br,
Heat transfer analysis exposes that Nu decreases for M while accelerates for
• Tabulated results for velocity and temperature of hybrid nanofluid portray that both profiles have conflicting behavior vs. radius of the cylindrical ciliated tube.
• Stability and convergence analysis is executed for various numerical techniques to attain accuracy goals and revealed that Adams method gives more accurate solutions as compared to other numerical techniques.
In the future, one may investigate modern intelligent computing-based stochastic solvers [62–66] for numerical solutions of the model representing the nanofluid [67–70] and magnetic induction effects on ciliary induced peristaltic transport of hybrid nanomaterials.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
SA, MA, and MR modelled the problem, SA, NP, and HA explore the solution and carried out numerical computations. WK and YH analyzed the finding of the study. All authors reviewed the manuscript.
Funding
This work was supported by the National Natural Science Foundation of China under Grant Nos. 51977153, 51977161, 51577046, State Key Program of National Natural Science Foundation of China under Grant No. 51637004, National Key Research and Development Plan (China) “important scientific instruments and equipment development” Grant No. 2016YFF010220, Equipment research project in advance (China) Grant No. 41402040301.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Glossary
Nomenclature
H0, Strength of Uniform magnetic field
g, Gravitational acceleration (N Kg-2 m2)
E, Electric field strength (N/C)
σ, Electrical conductivity (siemens per meter)
𝜃(r), Temperature profile
hnf, Hybrid nanofluid
nf, Nanofluid
f, Base fluid
References
2. Zhang L, Bhatti MM, Michaelides EE. Thermally developed coupled stress particle–fluid motion with mass transfer and peristalsis. J Therm Anal Calorim (2021) 143:2515–2524. doi:10.1007/s10973-020-09871-w
3. Awais M, Bukhari U, Ali A, Yasmin H. Convective and peristaltic viscous fluid flow with variable viscosity. J Engin Thermophys (2017) 26(1):69–78. doi:10.1134/s1810232817010088
4. Abbas Z, Rafiq MY, Hasnain J, Umer H. Impacts of lorentz force and chemical reaction on peristaltic transport of Jeffrey fluid in a penetrable channel with injection/suction at walls. Alexandria Eng J (2020) 60(1):1113–22. doi:10.1016/j.aej.2020.10.035
5. Awais M, Kumam P, Parveen N, Ali A, Shah Z, Thounthong P. Slip and Hall effects on peristaltic rheology of copper-water nanomaterial through generalized complaint walls with variable viscosity. Front Phys (2020) 7:249. doi:10.3389/fphy.2019.00249
6. Abrar MN, Sagheer M, Hussain S. Entropy analysis of Hall current and thermal radiation influenced by cilia with single-and multi-walled carbon nanotubes. Bull Mater Sci (2019) 42(5):250. doi:10.1007/s12034-019-1822-4
7. Awais M, Shah Z, Perveen N, Ali A, Kumam P, Rehman Hu., et al. MHD effects on ciliary-induced peristaltic flow coatings with rheological hybrid nanofluid. Coatings (2020) 10:186. doi:10.3390/coatings10020186
8. Saleem A, Qaiser A, Nadeem S. Physiological flow of biomedical compressible fluids inside a ciliated symmetric channel. Adv Mech Eng (2020) 12(7):1–11. doi:10.1177/1687814020938478
9. Butt AW, Akbar NS, Mir NA. Heat transfer analysis of peristaltic flow of a Phan-Thien-Tanner fluid model due to metachronal wave of cilia. Biomech Model Mechanobiol (2020) 19(5):1925–33. doi:10.1007/s10237-020-01317-4
10. Nadeem S, Khan MN, Muhammad N, Ahmad S. Mathematical analysis of bio-convective micropolar nanofluid. J Comput Des Eng (2019) 6(3):233–42. doi:10.1016/j.jcde.2019.04.001
11. Muhammad N, Nadeem S, Mustafa MT. Hybrid isothermal model for the ferrohydrodynamic chemically reactive species. Commun Theor Phys (2019) 71:384–92. doi:10.1088/0253-6102/71/4/384
12. Khan MN, Nadeem S, Muhammad N. Micropolar fluid flow with temperature‐dependent transport properties. Heat Transfer (2020) 49(4):2375–89. doi:10.1002/htj.21726
13. Zhang L, Bhatti MM, Michaelides EE. Electro-magnetohydrodynamic flow and heat transfer of a third-grade fluid using a Darcy-Brinkman-Forchheimer model. Int J Numer Methods Heat Fluid Flow (2020) [Epub ahead of print]. doi:10.1108/HFF-09-2020-0566
14. Arain MB, Bhatti MM, Zeeshan A, Saeed T, Hobiny A. Analysis of Arrhenius kinetics on multiphase flow between a pair of rotating circular plates. Math Probl Eng (2020). doi:10.1155/2020/2749105
15. Nadeem S, Ahmad S, Muhammad N. Analysis of ferrite nanoparticles in liquid. Pramana (2020) 94(1):1–9. doi:10.1007/s12043-019-1913-1
16. Wang J, Ijaz Khan M, Khan WA, Abbas SZ, Imran Khan M. Transportation of heat generation/absorption and radiative heat flux in homogeneous-heterogeneous catalytic reactions of non-Newtonian fluid (Oldroyd-B model). Comput Methods Programs Biomed (2020) 189:105310. doi:10.1016/j.cmpb.2019.105310
17. Ali Z, Zeeshan A, Bhatti MM, Hobiny A, Saeed T. Insight into the dynamics of Oldroyd-B fluid over an upper horizontal surface of a paraboloid of revolution subject to chemical reaction dependent on the first-order activation energy. Arabian J Sci Eng (2021) 1–10. doi:10.1007/s13369-020-05324-6
18. Ahmad S, Nadeem S, Muhammad N, Khan MN. Cattaneo–Christov heat flux model for stagnation point flow of micropolar nanofluid toward a nonlinear stretching surface with slip effects. J Therm Anal Calorim (2020) 143:1187–99. doi:10.1007/s10973-020-09504-2
19. Choi SUS, Eastman J. Enhancing thermal conductivity of fluids with nanoparticles. In: ASME international mechanical engineering congress & exposition; 1995 Nov 12–17; San Francisco, CA (1995) 66. p. 99–105.
20. Muhammad N, Nadeem S. Ferrite nanoparticles Ni-ZnFe2O4, Mn-ZnFe2O4 and Fe2O4 in the flow of ferromagnetic nanofluid. Eur Phys J Plus (2017) 132:377. doi:10.1140/epjp/i2017-11650-2
21. Awais M, Hayat T, Muqaddass N, Ali A, Aqsa SE, Awan SE Nanoparticles and nonlinear thermal radiation properties in the rheology of polymeric material. Results Phys (2018) 8:1038–45. doi:10.1016/j.rinp.2018.01.041
22. Muhammad N, Nadeem S, Mustafa MT. Analysis of ferrite nanoparticles in the flow of ferromagnetic nanofluid. PLoS One (2018) 13(1):e0188460. doi:10.1371/journal.pone.0188460
23. Ahmad S, Nadeem S, Muhammad N, Issakhov A. Radiative SWCNT and MWCNT nanofluid flow of Falkner-Skan problem with double stratification. Physica A (2020) 547:124054. doi:10.1016/j.physa.2019.124054
24. Muhammad N, Nadeem S, Issakhov A. Finite volume method for mixed convection flow of Ag-ethylene glycol nanofluid flow in a cavity having thin central heater. Physica A (2020) 537:122738. doi:10.1016/j.physa.2019.122738
25. Li F, Muhammad N, Abohamzeh E, Hakeem AKA, Hajizadeh MR, Li Z, et al. Finned unit solidification with use of nanoparticles improved PCM. J Mol Liquids (2020) 314:113659. doi:10.1016/j.molliq.2020.113659
26. Khan MI, Alzahrani F. Activation energy and binary chemical reaction effect in nonlinear thermal radiative stagnation point flow of Walter-B nanofluid: numerical computations. Int J Mod Phys B (2020) 34:2050132. doi:10.1142/S0217979220501325
27. Awais M, Awan SE, Raja MAZ, Shoaib M. Effects of gyro-tactic organisms in bio-convective nano-material with heat immersion, stratification, and viscous dissipation. Arabian J Sci Eng (2020) 1–14. doi:10.1007/s13369-020-05070-9
28. Khan MI, Alzahrani F, Hobiny A, Ali Z. Modeling of Cattaneo-Christov double diffusions (CCDD) in Williamson nanomaterial slip flow subject to porous medium. J Mater Res Technol (2020) 9(3):6172–7. doi:10.1016/j.jmrt.2020.04.019
29. Nadeem S, Alblawi A, Muhammad N, Alarifi IM, Issakhov A, Mustafa MT. A computational model for suspensions of motile micro-organisms in the flow of ferrofluid. J Mol Liquids (2020) 298:112033. doi:10.1016/j.molliq.2019.112033
30. Nayak MK, Shaw S, Ijaz Khan M, Pandey VS, Nazeer M. Flow and thermal analysis on Darcy-Forchheimer flow of copper-water nanofluid due to a rotating disk: a static and dynamic approach. J Mater Res Technol (2020) 9(4):7387–408. doi:10.1016/j.jmrt.2020.04.074
31. Khan MI, Alzahrani F, Hobiny A. Heat transport and nonlinear mixed convective nanomaterial slip flow of Walter-B fluid containing geotactic microorganisms. Alexandria Eng J (2020) 59:1761–9. doi:10.1016/j.aej.2020.04.042
32. Khan MI, Alzahrani F, Hobiny A. Simulation and modeling of second order velocity slip flow of micropolar ferrofluid with Darcy-Forchheimer porous medium. J Mater Res Technol (2020) 9(4):7335–40. doi:10.1016/j.jmrt.2020.04.079
33. Ali A, Saleem S, Mumraiz S, Awais M, Marwat DNK. Investigation on TiO2–Cu/H2O hybrid nanofluid with slip conditions in MHD peristaltic flow of Jeffrey material. J Therm Anal Calorim (2021) 143:1985–1996. doi:10.1007/s10973-020-09648-1
34. Mumraiz S, Ali A, Awais M, Shutaywi M, Shah Z. Entropy generation in electrical magnetohydro dynamic flow of Al2O3–Cu/H2O hybrid nanofluid with non-uniform heat flux. J Therm Anal Calorim (2021) 143:2135–2148. doi:10.1007/s10973-020-09603-0
35. Lund LA, Omar Z, Raza J, Khan I. Magnetohydrodynamic flow of Cu–Fe3O4/H2O hybrid nanofluid with effect of viscous dissipation: dual similarity solutions. J Therm Anal Calorim (2020) 143:915–27. doi:10.1007/s10973-020-09602-1
36. Parveen N, Awais M, Mumraz S, Ali A, Malik MY. An estimation of pressure rise and heat transfer rate for hybrid nanofluid with endoscopic effects and induced magnetic field: computational intelligence application. Eur Phys J Plus (2020) 135:886. doi:10.1140/epjp/s13360-020-00874-y
37. Yang J, Abdelmalek Z, Muhammad N, Mustafa MT. Hydrodynamics and ferrite nanoparticles in hybrid nanofluid. Int Commun Heat Mass Transfer (2020) 118:104883. doi:10.1016/j.icheatmasstransfer.2020.104883
38. Abbas N, Nadeem S, Malik MY. Theoretical study of micropolar hybrid nanofluid over riga channel with slip conditions. Physica A: Stat Mech its Appl (2020) 551:124083. doi:10.1016/j.physa.2019.124083
39. Rehman KU, Malik MY, Al-Mdallal QM, Al-Kouz W. Heat transfer analysis on buoyantly convective non-Newtonian stream in a hexagonal enclosure rooted with T-Shaped flipper: hybrid meshed analysis. Case Stud Therm Eng (2020) 21:100725. doi:10.1016/j.csite.2020.100725
40. Farooq S, Ijaz Khan M, Waqas M, Hayat T, Alsaedi A. Transport of hybrid type nanomaterials in peristaltic activity of viscous fluid considering nonlinear radiation, entropy optimization and slip effects. Comput Methods Programs Biomed (2020) 184:105086. doi:10.1016/j.cmpb.2019.105086
41. Babar H, Ali HM. Towards hybrid nanofluids: preparation, thermophysical properties, applications, and challenges. J Mol Liquids (2019) 281:598–633. doi:10.1016/j.molliq.2019.02.102
42. Ellahi R, Hussain F, Asad Abbas S, Sarafraz MM, Goodarzi M, Shadloo MS. Study of two-phase Newtonian nanofluid flow hybrid with hafnium particles under the effects of slip. Inventions (2020) 5:6. doi:10.3390/inventions5010006
43. Saqib M, Khan I, Shafie S, Qureshi A. Recent advancement in thermophysical properties of nanofluids and hybrid nanofluids: an overview. Int J Comput Anal (2019) 1(2):16–25. doi:10.33959/cuijca.v3i2.27
44. Ali A, Shah Z, Mumraiz S, Kumam P, Awais M. Entropy generation on MHD peristaltic flow of Cu-water nanofluid with slip conditions. Heat Trans Asian Res (2019) 48(8):4301–19. doi:10.1002/htj.21593
45. Khan MI, Qayyum S, Kadry S, Khan WA, Abbas SZ. Irreversibility analysis and heat transport in squeezing nanoliquid flow of non-Newtonian (second-grade) fluid between infinite plates with activation energy. Arab J Sci Eng (2020) 45:4939–47. doi:10.1007/s13369-020-04442-5
46. Abbas SZ, Khan WA, Kadry S, Khan MI, Waqas M, Khan MI. Entropy optimized Darcy-Forchheimer nanofluid (Silicon dioxide, Molybdenum disulfide) subject to temperature dependent viscosity. Comput Methods Programs Biomed (2020) 190:105363. doi:10.1016/j.cmpb.2020.105363
47. Muhammad R, Khan MI, Jameel M, Khan NB. Fully developed Darcy-Forchheimer mixed convective flow over a curved surface with activation energy and entropy generation. Comput Methods Programs Biomed (2020) 188:105298. doi:10.1016/j.cmpb.2019.105298
48. Muhammad R, Khan MI, Khan NB, Jameel M. Magnetohydrodynamics (MHD) radiated nanomaterial viscous material flow by a curved surface with second order slip and entropy generation. Comput Methods Programs Biomed (2020) 189:105294. doi:10.1016/j.cmpb.2019.105294
49. Nayak MK, Abdul Hakeem AK, Ganga B, Ijaz Khan M, Waqas M, Makinde OD. Entropy optimized MHD 3D nanomaterial of non-Newtonian fluid: a combined approach to good absorber of solar energy and intensification of heat transport. Comput Methods Programs Biomed (2020) 186:105131. doi:10.1016/j.cmpb.2019.105131
50. Abbas SZ, Khan MI, Kadry S, Khan WA, Israr-Ur-Rehman M, Waqas M. Fully developed entropy optimized second order velocity slip MHD nanofluid flow with activation energy. Comput Methods Programs Biomed (2020) 190:105362. doi:10.1016/j.cmpb.2020.105362
51. Yasmeen S, Okechi NF, Anjum HJ, Asghar S. Peristaltic motion of magnetohydrodynamic viscous fluid in a curved circular tube. Results Phys (2017) 7:3307–14. doi:10.1016/j.rinp.2017.08.044
52. Awais M, Raja MAZ, Awan SE, Shoaib M, Ali HM. Heat and mass transfer phenomenon for the dynamics of Casson fluid through porous medium over shrinking wall subject to Lorentz force and heat source/sink. Alexandria Eng J (2020) 60(1):1355–63. doi:10.1016/j.aej.2020.10.056
53. Awais M, Aqsa MY, Malik MY, Awan SE. Generalized magnetic effects in a Sakiadis flow of polymeric nano-liquids: analytic and numerical solutions. J Mol Liquids (2017) 241:570–6. doi:10.1016/j.molliq.2017.06.046
54. Awan S, Awais M, Qayyum A, Rehman S, Khan A, Ali H, et al. Numerical computing paradigms for the dynamics of squeezing rheology of third grade fluid. Therm Sci (2020) 24(6B):4173–82. doi:10.2298/tsci190508160a
55. Awais M, Awan SE, Muqaddass N, Rehman SU, Raja MAZ. Numerical and analytical approach for Sakiadis rheology of generalized polymeric material with magnetic field and heat source/sink. Therm Sci (2020) 24(2):1183–94. doi:10.2298/tsci180426284a
56. Awan SE, Khan ZA, Awais M, Ur Rehman S, Raja MAZ. Numerical treatment for hydro-magnetic unsteady channel flow of nanofluid with heat transfer. Results Phys (2018) 9:1543–54. doi:10.1016/j.rinp.2018.04.068
57. Awan SE, Raja MAZ, Mehmood A, Niazi SA, Siddiqa S. Numerical treatments to analyze the nonlinear radiative heat transfer in MHD nanofluid flow with solar energy. Arab J Sci Eng (2020) 45:4975–94. doi:10.1007/s13369-020-04593-5
58. Awan SE, Raja MAZ, Gul F, Khan ZA, Mehmood A, Shoaib M. Numerical computing paradigm for investigation of micropolar nanofluid flow between parallel plates system with impact of electrical MHD and Hall current. Arab J Sci Eng (2020) 46(1):645–62. doi:10.1007/s13369-020-04736-8
59. Siddiqa S, Naqvi SB, Begum N, Awan SE, Hossain MA. Thermal radiation therapy of biomagnetic fluid flow in the presence of localized magnetic field. Int J Therm Sci (2018) 132:457–65. doi:10.1016/j.ijthermalsci.2018.06.023
60. Awan SE, Awais M, Rehman SU, Niazi SA, Zahoor Raja MA. Dynamical analysis for nanofluid slip rheology with thermal radiation, heat generation/absorption and convective wall properties. AIP Adv (2018) 8(7):075122. doi:10.1063/1.5033470
61. Ibrahim M, Ijaz Khan M. Mathematical modeling and analysis of SWCNT-Water and MWCNT-Water flow over a stretchable sheet. Comput Methods Programs Biomed (2020) 187:105222. doi:10.1016/j.cmpb.2019.105222
62. Khan JA, Raja MAZ, Syam MI, Tanoli SAK, Awan SE. Design and application of nature inspired computing approach for nonlinear stiff oscillatory problems. Neural Comput Applic (2015) 26(7):1763–80. doi:10.1007/s00521-015-1841-z
63. Mehmood A, Afsar K, Zameer A, Awan SE, Raja MAZ. Integrated intelligent computing paradigm for the dynamics of micropolar fluid flow with heat transfer in a permeable walled channel. Appl Soft Comput (2019) 79:139–62. doi:10.1016/j.asoc.2019.03.026
64. Sabir Z, Baleanu D, Shoaib M, Raja MAZ. Design of stochastic numerical solver for the solution of singular three-point second-order boundary value problems. Neural Comput Appl (2020) 1–17. doi:10.1007/s00521-020-05143-8
65. Shah Z, Raja MAZ, Chu Y-M, Khan WA, Waqas M, Shoaib M, et al. Design of neural network based intelligent computing for numerical treatment of unsteady 3D flow of Eyring-Powell magneto-nanofluidic model. J Mater Res Technol (2020) 9(6):14372–87. doi:10.1016/j.jmrt.2020.09.098
66. Awais M, Awan SE, Iqbal K, Khan ZA, Raja MAZ. Hydromagnetic mixed convective flow over a wall with variable thickness and Cattaneo-Christov heat flux model: OHAM analysis. Results Phys (2018) 8:621–7. doi:10.1016/j.rinp.2017.12.043
67. Wang J, Muhammad R, Khan MI, Khan WA, Abbas SZ. Entropy optimized MHD nanomaterial flow subject to variable thicked surface. Comput Methods Programs Biomed (2020) 189:105311. doi:10.1016/j.cmpb.2019.105311
68. Bhatti MM, Phali L, Khalique CM. Heat transfer effects on electro-magnetohydrodynamic Carreau fluid flow between two micro-parallel plates with Darcy–Brinkman–Forchheimer medium. Archive Appl Mech (2021) 1–13. doi:10.1007/s00419-020-01847-4
69. Ahmad S, Nadeem S, Muhammad N. Boundary layer flow over a curved surface imbedded in porous medium. Commun Theor Phys (2019) 71(3):344. doi:10.1088/0253-6102/71/3/344
Keywords: hybrid nanofluid, induced magnetic field, entropy generation, peristaltic motion, axisymmetric tube, metachronal waves, numerical treatment
Citation: Awan SE, Awais M, Raja MAZ, Parveen N, Ali HM, Khan WU and He Y (2021) Numerical Treatment for Dynamics of Second Law Analysis and Magnetic Induction Effects on Ciliary Induced Peristaltic Transport of Hybrid Nanomaterial. Front. Phys. 9:631903. doi: 10.3389/fphy.2021.631903
Received: 21 November 2020; Accepted: 26 January 2021;
Published: 05 April 2021.
Edited by:
Umberto Lucia, Politecnico di Torino, ItalyReviewed by:
M. Ijaz Khan, Riphah International University, PakistanSohail Nadeem, Quaid-i-Azam University, Pakistan
Muhammad Mubashir Bhatti, Shanghai University, China
Copyright © 2021 Awan, Awais, Raja, Parveen, Ali, Khan and He. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wasim Ullah Khan, a3dhc2ltODE0QHdodS5lZHUuY24=; Yigang He, eWdoZTEyMjFAd2h1LmVkdS5jbg==
 Saeed Ehsan Awan
Saeed Ehsan Awan Muhammad Awais2
Muhammad Awais2 Muhammad Asif Zahoor Raja
Muhammad Asif Zahoor Raja Nabeela Parveen
Nabeela Parveen Wasim Ullah Khan
Wasim Ullah Khan