Boosting and Taming Wave Breakup in Second Harmonic Generation

Modulation instability is a universal phenomenon that can be found in a wide variety of nonlinear systems where, in the presence of a noise seed, peaks of random intensities can be generated. Several dynamical systems admit exact solutions in the form of breathers or solitons on a finite background. The vast majority of soliton studies has been restricted so far to one-dimensional systems. In contrast, the occurrences of localized structures in fully spatiotemporal systems has been only sporadically explored. In this work, we experimentally study the conditions for the wave-breaking of spatially extended optical beams in the process of second harmonic generation. Whenever the pump energy of the picosecond-long fundamental beam reaches a critical level, the beam shape at the second harmonic in a KTP crystal breaks into small filaments. These filaments exhibit extreme local intensity peaks, and their statistical distribution can be modified by the input energy of the fundamental beam. Moreover, by analyzing similar wave-breaking dynamics in a PPLN crystal in the presence of a higher nonlinear quadratic response, we observe that the spatial beam breaking may even gradually vanish as the laser intensity grows larger, leading to a spatial reshaping into a smooth and wider beam, accompanied by a substantial broadening of its temporal spectrum.

Introduction

A wide class of nonlinear systems exhibits Modulation Instability (MI): the onset stage of the nonlinear dynamics of MI leads to an exponential growth of periodic perturbations [1]. Although in presence of a noise seed, MI can give rise to peaks of random intensities, exact solutions are known, including first-order ones such as Akhmediev breathers or Peregrine solitons. Interestingly, MI has been largely studied in single mode optical fibers in the presence of dispersion and Kerr nonlinearity, and solitons on a finite background take the form of pulses (in the time domain) evolving along the fiber [2, 3]. In this work we focus our attention on a wider class of higher-dimensional nonlinear systems that involve spatially extended optical beams, whose combined spatial and temporal instabilities are expected to stimulate a host of further studies on nonlinear waves.

Wave-breaking, a mechanism of disintegration of optical beams or temporal pulses, has been extensively studied in nonlinear optics. In materials with cubic (Kerr) nonlinearity, there are two principal mechanisms of wave breaking, namely, MI and gradient catastrophe (GC): they appear in either the focusing or the defocusing regime, respectively. Conversely, in materials with quadratic nonlinearities the MI and GC processes may even coexist [4].

It is well known that beam instabilities may arise in three-wave mixing interactions in the presence of dispersion and diffraction [5, 6]. When limiting the analysis to pure spatial waves having a dominant transverse dimension, such as it occurs in the case of elliptical beams, it is possible to reduce the description of the transverse beam evolution into a single spatial coordinate. In this limit, MI based on quadratic interactions in type-II second harmonic generation (SHG) may occur, see for instance Ref. [7]. Moreover, in the limit known as cascading, it is possible to reduce the three-wave mixing interaction to a single nonlinear Schrödinger equation; some direct analogies can be established with temporal effects in nonlinear fibers.

When considering the full two-dimensional (2D) nature of the spatial transverse domain, an extended version of MI is still possible. In particular, purely 2D MI was numerically and experimentally discussed in Ref. [8] for type-II SHG. In Ref. [8] the authors observed the dramatic breakup of the beam shape at the SH, leading to spatial pattern formation: by increasing the input power of the fundamental wave, they were able to move from the pump depletion regime (characterized by a localized energy exchange between the fundamental and SH) into the MI regime, leading to a complete breakup of the SH beam. Among other types of beam instabilities in quadratic nonlinear media, transverse MI in three-wave mixing was reported, by considering the vector nature of the nonlinear interaction [9]. Correspondingly, azimuthal MI was theoretically and experimentally studied in Ref. [10], again in a type-II SHG in potassium titanyl phosphate (KTP) crystal.

It is important to stress that, in the realm of beam instabilities in quadratic crystals, the spatial dimensions cannot be easily disjoined from the temporal/spectral dimensions. This is particularly true in the high-energy regime: the ultimate nature of MI in quadratic nonlinear media involves a coupling between spatial and temporal dimensions [11]. This means that MI in quadratic crystals cannot be described as a simple product of spatial filamentation and temporal breakup; consider for example the mechanism of colored conical emission [12].

The presence of spatiotemporal beam instabilities can be associated, in a phase space representation of the dynamic evolution of a wave system, with the exponential amplification of small initial perturbations. This means that it is also interesting to study the beam evolution in the nonlinear stage of the instabilities, that is beyond the initial wave breakup or in the depleted pump regime. For instance, it may occur that, once the multiple filaments are formed, they may subsequently self-organize or combine (e.g., in the case of multiple filaments in air [13]). It is also possible to observe clustering phenomena, involving the aggregation at large scales of fine-scale structures. In astrophysics, these phenomena are at the basis of the formation of galaxies. In this perspective, a detailed study for the case of saturable nonlinear media was reported in Ref. [14].

Beam instabilities often provide the mechanism for the generation of rogue waves in 2D nonlinear wave systems. This perspective is particularly interesting, for example, in the recently reported cases of caustics [15], and of rogue waves in ferroelectrics boosted by nonlinearity [16]. In the process of rogue wave generation, the role played by nonlinearity may be twofold. For instance, Ref. [17] describes a system in which the presence of a weak nonlinearity was responsible for enhancing rogue waves. Whereas the rogue wave statistics was quenched in the strongly nonlinear regime [17]. The generation of spatial extreme waves with non-Gaussian statistics in a nonlinear cavity with a liquid crystal light valve was studied for instance in Ref. [18].

In a recent related work [19], we studied the generation of 2D transverse rogue waves in the fundamental beam, as a result of type II SHG in a KTP quadratic nonlinear crystal. These represent a new class of transient, Peregrine-like 2D self-guided beams, which spontaneously appear from nowhere and then disappear, as the beam intensity grows larger. In the strong conversion regime, temporal reshaping followed by spatiotemporal wave breaking, acting against spatial focusing, was observed to destabilize beam trapping.

In this work we explore, by a series of experimental studies, the spatiotemporal beam breakup which occurs in the SH beam. Specifically, we observed that, in a regime close to phase matching of SHG, the SH spatial beam breaks up, leading to the formation of a multitude of filaments. Hereafter, we simply call filaments the nonlinear self-trapped and self-sustained solitary waves, or quasi-solitons, that spontaneously form (and disappear) in a non-integrable wave system. Unveiling a new mechanism for the generation of nonlinear extreme waves with peculiar statistical properties is of fundamental scientific interest. In addition, we envisage that these sources of structured light may also find interesting technological applications. Some applications of similar structured light sources are discussed for instance in Ref. [20], which points to the interest in generating speckled beams with statistics that differ from a classical Rayleigh distribution [21]. Nonlinear waves, including rogue waves have been also recently proposed as computing reservoirs [22].

Remarkably, in our experiments we observed an unexpected behavior in SH beam filamentation. Specifically, as the power of the fundamental wave grows larger, instead of clustering, the multitude of filaments composing the SH gradually sinks into a spatially wide, and nearly uniform beam. At that point, the SH beam partially recovers its brightness, both in the near and in the far-field. This effect was accompanied by a significant broadening of the temporal spectrum, ultimately evolving into a supercontinuum, similarly to what previously observed in the formation of a single, stable polychromatic filament [23]. The efficiency of SHG, which can be attained in similar crystals in the absence of nonlinear wave breaking, was recently discussed in Ref. [24].

Materials and Methods

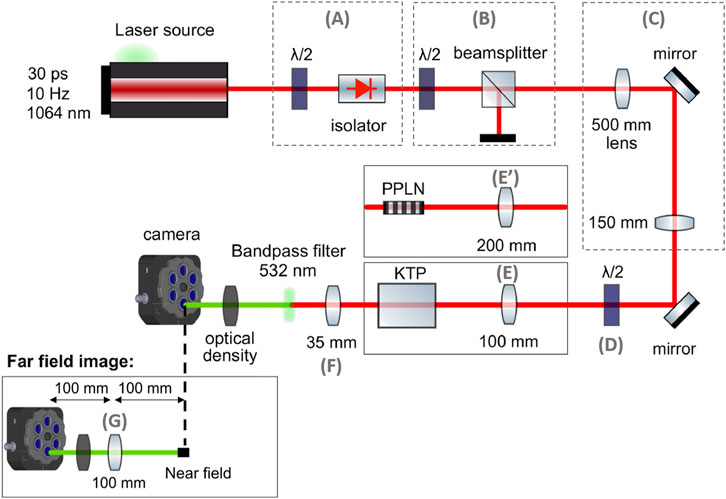
The experimental setup is illustrated in Figure 1. In all of our experiments, we used a Q-switched, mode-locked Nd:YAG laser (EKSPLA PL2250 series), delivering 30 ps duration high-energy pulses, at the central wavelength of 1064 nm, with a repetition rate of 10 Hz. The laser output was protected from back-reflections by means of a half-wave plate and a polarization sensitive isolator (A). The laser output beam was controlled by a second half-wave plate and a polarization beam splitter (B). An afocal system (C), composed by two lenses of 500 mm and 150 mm, respectively, reduced the Gaussian beam diameter by almost three times with respect to the original diameter of the laser beam.

FIGURE 1

FIGURE 1. Schematic of the experimental setup.

Two different crystals were used in our experiments. In a first series of measurements, we used a KTP crystal, manufactured by CASTECH. The KTP crystal was 30 mm long, 8 mm thick, and 8 mm wide. The SHG phase mismatch was controlled by means of two rotational axes (Newport gimbal optic mount). A half-wave plate (D) controlled the orientation of the input linear state of polarization (SOP). The crystal cut permitted phase-matching of type-II SHG for an input SOP at 45° between ordinary and extraordinary axes, for a light beam at normal input incidence (polar angles θ = 90°, Φ = 23.5°, with reference to the crystallographic axes).

In a second series of measurements, we replaced the KTP crystal by a PPLN crystal (manufactured by HCP Photonics Corporation), being 15 mm long, 1 mm thick, and 2 mm wide. The period of inversion of the ferroelectric domain was Λ_PPLN = 7.97 µm. For the PPLN crystal, SHG was obtained through the quasi-phase-matching (QPM) technique, and the phase mismatch was adjusted by changing the temperature of the oven in which the crystal was placed. The phase-matching of SHG was obtained at the temperature of 60°C, the linear SOP of the input laser light at the fundamental frequency was kept fixed, and aligned with the extraordinary axis of the PPLN crystal (type-0 QPM) by means of the half-wave plate (D).

The input laser beam was adapted to the crystal type. For the PPLN crystal, the pump beam was injected with an input diameter of 200 μm, measured at 1/e², by means of a 200 mm converging lens E’. For the KTP crystal, the input beam diameter was of 400 µm (1/e²), obtained with the help of a converging lens E with a 100 mm focal length. In both cases, the point of beam injection was located after the focal point of the lenses E or E’ for the KTP or the PPLN crystal, respectively. In both cases, the beam diffraction length at 1064 nm was much longer than the physical length of the crystal itself, so that, at low energy levels, i.e., in the absence of nonlinear effects, the laser beam could be considered as non-diverging along its propagation in the crystal.

At the output face of the crystals, the SHG beam at 532 nm at the output of the KTP crystal was filtered by means of a bandpass filter at 532 nm ± 3 nm. We also used a larger passband filter at 532 nm ± 10 nm for the experiments with the PPLN. The near-field at the crystal output was magnified by a 35 mm converging lens (F), and analyzed by a BC106N-VIS CCD Thorlabs camera, with a magnification of 4.56. The same setup was also used to analyze the near-field at the output of the PPLN crystal: in that case, the corresponding magnification was 8.375. To measure the far-field, we displaced the camera. A new converging lens G was interposed at equal distances between the camera and the near-field: such a distance was matched to the focal length of lens G (100 mm).

Results

We analyzed the output SH beam shape for different input intensities of the fundamental pump (we refer here to the peak intensities of the input beam at the fundamental wave I_FF). Specifically, by increasing the pump beam intensity, we observed a gradual spatial reshaping of the SH beam, which is induced by nonlinear beam propagation in the crystal. Figure 2 summarizes the results when using the KTP crystal, for six different levels of I_FF. The crystal orientation was kept fixed with an angular shift of ΔΦ = +0.33° from the phase-matching angles (θ = 90°, Φ = 23.5°). As can be seen in panels (a–c) of Figure 2, for input intensities close to 0.11 GW/cm², we observed a spatial focusing of the SH beam: its diameter at 1/e² dropped from 320 µm down to 50 µm (here the pump pulse energy was 2 µJ). Panels (d–f) of Figure 2 show that, when increasing the pump intensity I_FF above 1 GW/cm², we observed a breakup of the SH beam into a seemingly random pattern of tightly focalized light filaments. The resulting light intensity distribution is reminiscent of the speckled beams which result from beam propagation through random media. Such a nonlinear SH beam breakup was observed for both negative and positive values of the phase mismatch (we analyzed the range from ΔΦ = -1.67° to ΔΦ = +1.67°), and for nearly all orientations of the linear SOP of the input pump. SH beam breakup only vanished when the input SOP was aligned with the direction of either the ordinary or the extraordinary KTP axes, so that type-II three-wave mixing is not permitted.

FIGURE 2

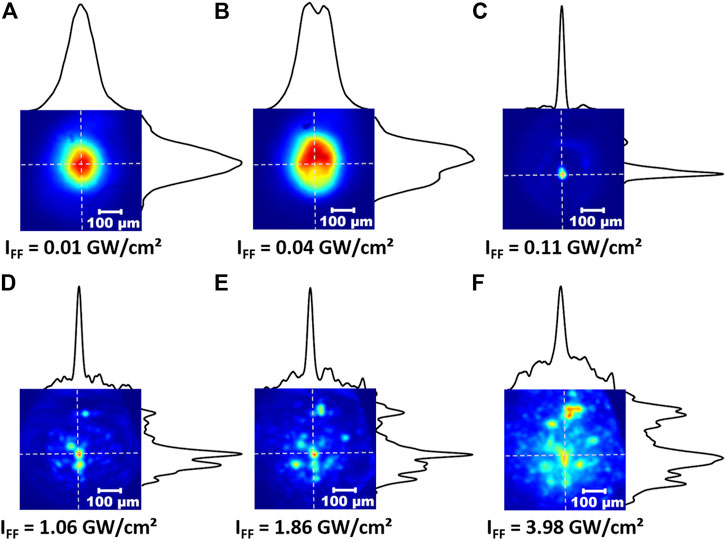
FIGURE 2. Near-field images of the SH beam at the output face of the KTP crystal. The SH beam shape is nearly Gaussian for an input intensity of 0.01 GW/cm²(A). The beam is depleted near the center of the Gaussian at 0.04 GW/cm² of input intensity (B) then, for a pump intensity of 0.11 GW/cm²(C), strong spatial compression of the SH beam is observed. Whereas for pump intensities above 1 GW/cm²(D)–(F) the output SH beam breaks in an irregular pattern of localized spots. These results refer to crystal orientations of θ = 90°, Φ = 23.5° + 0.33° (focusing case) and input SOP orientation of 47°. Colormaps are normalized to the local maximum intensity detected.

We characterized the random nature of the multiple filaments resulting from SH breakup by estimating the statistical distribution of the patterns of light spots in each image. For that purpose, we calculated the scintillation index of the SH as

$S_{SHG}= \frac{\langle I_{SHG}^2\rangle - {\langle I_{SHG}\rangle }^2}{ {\langle I_{SHG}\rangle }^2} (1)$

where <> denotes the average over the different pixel samples of a given image. For classical speckle patterns that obey Gaussian statistics, the scintillation index is equal to one. For the SH output intensity patterns in Figure 2, the SH scintillation index S_SHG is equal to 1.11 for I_FF = 1.1 GW/cm² pump intensity (Figure 2D). The SH scintillation index drops to S_SHG = 0.74 when the input beam intensity is increased up to I_FF = 1.9 GW/cm² (Figure 2E).

Figure 3 illustrates the statistics of pixel intensities upon different input beam powers. These statistics refer to the images reported in panels (c), (d), (e) and (f) of Figure 2. For each pump intensity level, we report the histogram of the SH intensity in linear and in log scale (square inset). For ease of comparison, the round insets reproduce the corresponding image over which the histogram is calculated. In Figures 3B,C, the dashed curves trace the negative-exponential probability density function (PDF) p(I) [21]:

$p\left(I\right)=\frac{1}{\langle I\rangle }{e}^{-\frac{I}{\langle I\rangle }}(2)$

FIGURE 3

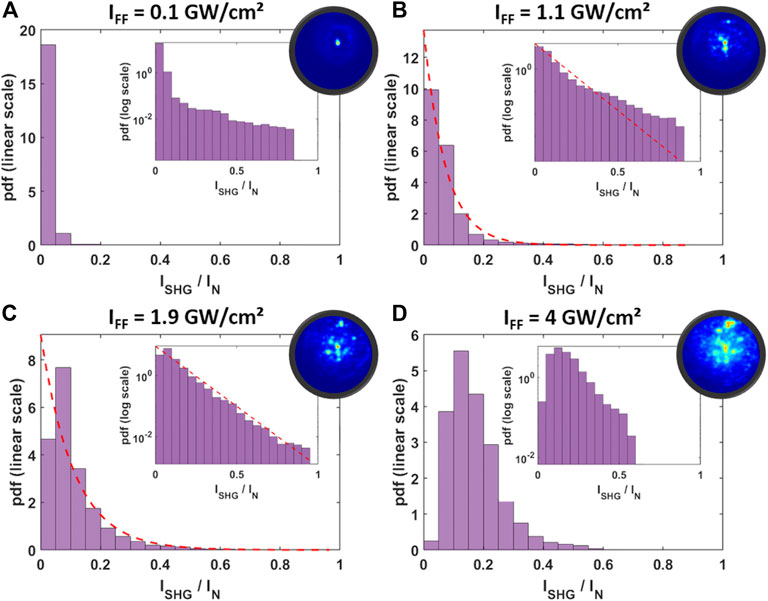
FIGURE 3. Statistics of the SH intensity levels, obtained in KTP for different input pump intensities I_FF. In the histograms the intensity axis of the SH is normalized to the maximum level permitted by the 8-bit camera. Note that the SH beam intensity was reduced by a variable attenuation to avoid saturation of the camera. The attenuation was modified for each value of I_FF(A, B). The circular insets are extracted from the corresponding cases of Figure 2. The red dashed curves represent the applications of Eq.2 for the different cases.

In order to measure the mean value of the speckle spots size, we also calculated the deterministic intensity correlations of the images shown in Figure 2 for three values of I_FF. From the image distribution I_SHG(x,y) of the SH, being x,y the coordinates of the pixel images, we calculated first the intensity deviation from its mean value $\delta I_{SHG}=I_{SHG}-\langle I_{SHG}\rangle$. Next, we calculated the corresponding deterministic intensity correlation CI (Δx, Δy).

$C_I\left(\text{Δ}x,\text{Δ}y\right)=\underset{-\infty }{\overset{+\infty }{{\displaystyle \mathrm{\iint }}}}\delta I_{SHG}\left(x,y\right)\delta I_{SHG}\left(x+\text{Δ}x,y+\text{Δ}y\right)\text{d}x\text{d}y (3)$

The results, for three selected intensity levels I_FF are illustrated in Figure 4.

FIGURE 4

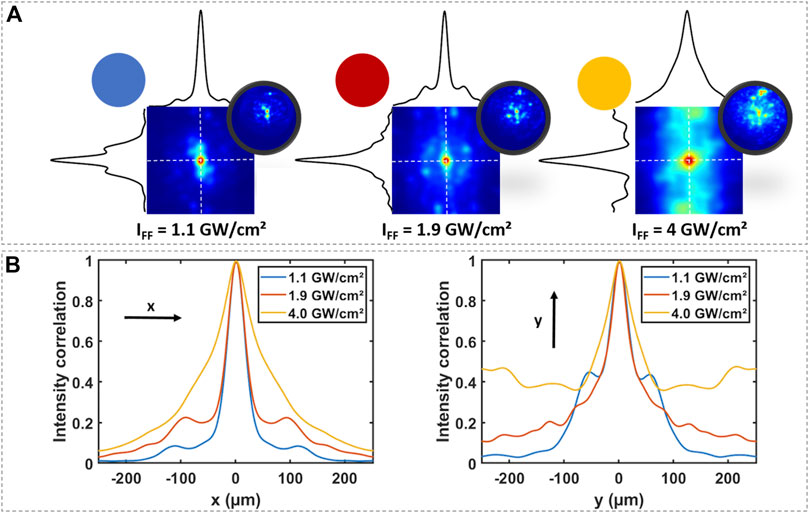
FIGURE 4. (A)—intensity correlations C_I of the near-field images of the SH beam at the output of the KTP crystal, (B)—comparison of the spatial profile of intensity correlations along the x and y directions, respectively. Data refer to a crystal orientation of θ = 90°, Φ = 23.5° + 0.33° and input polarization orientation of 47°. The circular insets are extracted from the corresponding cases of Figure 2.

In a second series of experiments, we analyzed nonlinear SH beam reshaping when replacing the KTP crystal by PPLN crystal, which results in a stronger nonlinear optical response. The experimental results illustrating the evolution of the output SH beam shape are reported in Figure 5. In particular, as shown in panel 5(a), we observed that the SH is fully broken in multiple filaments for a pump intensity I_FF = 2.7 GW/cm². We observed that the distribution of filaments evolves as the pump intensity is further increased. For pump intensities I_FF = 16 GW/cm² and higher, output SH filaments disappear: the spatial breakup is mitigated, and the SH beam increases its brightness both in the near and in the far-field (see Figure 5C for 51 GW/cm²). This type of SH spatial beam reshaping, which is not observed when using a KTP crystal, is accompanied by large spectral broadening of the SH, as illustrated by the series of spectra measurement which are reported in Figure 6.

FIGURE 5

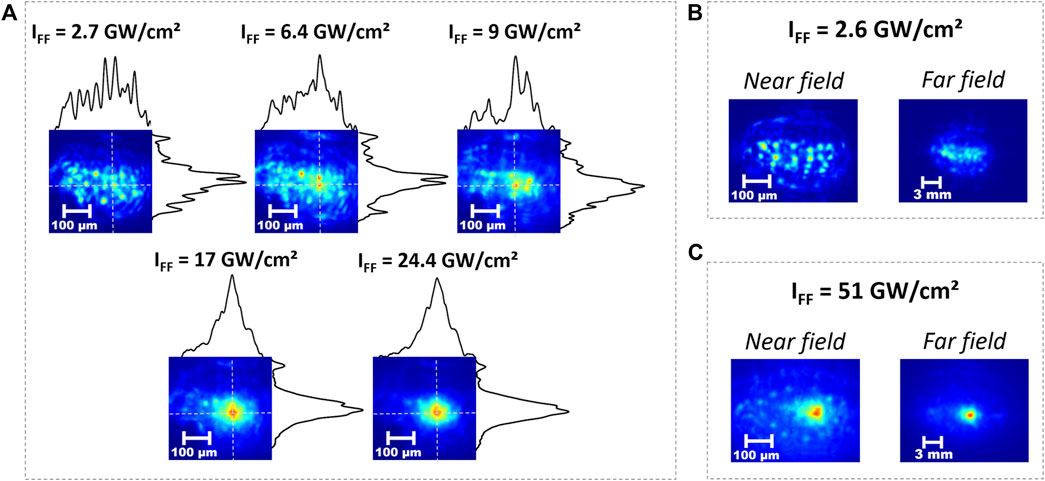
FIGURE 5. (A)—near field-images of the SH beam at the output face of the PPLN crystal for different pump intensities. Near and far-fields of SH beams for (B) I_FF = 2.6 GW/cm², (C) I_FF = 51 GW/cm². The scale in the far-field image is proportional to the spatial spectrum and it refers to the experimental setup described in Methods. These experimental results refer to a crystal temperature T = 60°C.

FIGURE 6

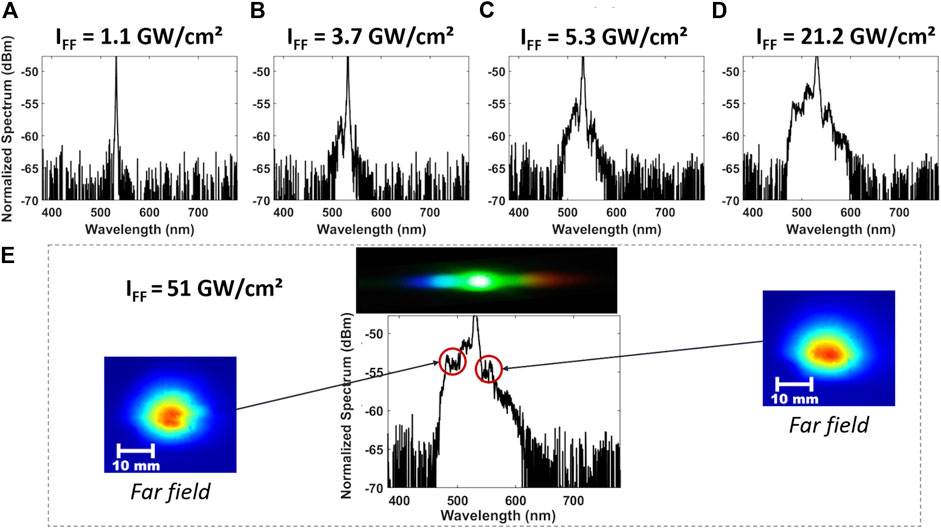
FIGURE 6. (A)–(D)—spectral evolution of the SH beam for different input pump intensities. (E)—spectrum of the SH beam at I_FF = 51 GW/cm² with corresponding photographic image. The two insets show the far-field beam shape of the two selected spectral components at 500 nm (left) and 550 nm (right), respectively.

Discussion

Our first series of experiments (carried out by using a KTP crystal, and illustrated in Figure 2) demonstrates an unexpected complex and strong spatial reshaping of SH beams in the process of type-II SHG. For relatively weak pump intensity levels (e.g., 0.04 GW/cm²), the output SH beam remains wide and nearly flat. Whenever the pump intensity reaches I_FF = 0.11 GW/cm² level, we observed a strong self-focusing of the SH beam, involving a significant compression of its diameter. When further increasing the input pump intensity I_FF by one order of magnitude, we observed the spatial breakup of the SH beam, and the formation of randomly distributed filaments. The presence of multiple filaments was confirmed till we reached the maximum available intensity I_FF = 4 GW/cm². The corresponding statistical analysis of the pixel intensities, corresponding to the four images of Figure 3, shows that the level of pump intensity has direct consequences on the PDF of the spatial intensity distribution of the SH beam. We underline that one could modify the speckles statistics by exploiting the mechanism of spatial nonlinear beam breaking, while otherwise keeping the KTP crystal unchanged.

As a possible perspective application of these results, we envisage the possibility to customize the statistics of filaments by exploiting nonlinear wave breaking, in alternative to other methods for modifying the speckle intensity statistics, e.g., by using a spatial light modulator [19]. Specifically, for an input pump intensity of 1.1 GW/cm², the speckles PDF in Figure 3B. agrees fairly well with the classical distribution of a Rayleigh speckle pattern. This is confirmed by the scintillation index, which is close to unity in that case. However, Figure 3D shows that, for input pump intensities I_FF as high as 4 GW/cm², the PDF of speckles strongly diverges from a Rayleigh PDF, and it even becomes not monotonic upon intensity. These changes in the intensity statistics reflect the different topologies of the pattern of filaments. A careful analysis of the PDF tails and their connection with extreme spatial waves (like the brightest filaments shown in Figures 2 and 5) will be the subject of future analysis.

In order to compare the typical size of the generated SH, we calculated for some of the images in Figure 2 the corresponding deterministic correlations for the beam pattern at SH, as shown in Figure 4. We considered three different intensities levels of I_FF. Figure 4 reveals that the short-range correlation, which is related to the typical size of speckles, remains very similar as the pump intensity increases from 1.1 GW/cm² up to 1.9 GW/cm², in spite of some differences in the PDFs of the SH beam intensity for these two cases. When further increasing the pump intensity up to 4 GW/cm², the deterministic spatial intensity correlation applied to the image shows that the filaments tend to increase their size. The long-range correlation is also gradually enhanced and the pump intensity grows larger. As a matter of fact, for I_FF = 4 GW/cm² we can see that the SH beam breakup is boosted by the large intensity of the fundamental beam. One may thus extrapolate that, by further increasing the pump intensity, one could gradually fill the gaps among different filaments, which would reduce the speckle contrast.

As illustrated in Figure 5, we repeated the study of the dependence of the SH beam breakup and its statistics by considering SHG in a PPLN crystal. In this case, the larger effective quadratic nonlinear response (about 15 pm/V to compare with 3 pm/V for KTP) and the absence of walk-off allow for a stronger nonlinear interaction. Again, we observed the presence of SH beam breakup, leading to the generation of filaments (see Figure 5, for pump intensities from 2.7 GW/cm² till 9 GW/cm²). Moreover, we revealed that the initial sea of filaments (some of them possessing extreme intensity values) becomes gradually interconnected via the generation of a broad intensity background. Eventually, SH filaments nearly disappear, and a spatially wide SH beam is observed for the largest values of the pump power (see Figure 5, for pump intensities from 17 GW/cm² up to 51 GW/cm²). In particular, it is important to notice in Figure 5 that both the near and the far-field patterns observed for a 51 GW/cm² pump intensity are strongly spatially localized, although the central spot is surrounded by a broad background. In this case, we can somehow see that the consequences of the spatial instability which leads to SH breaking into multiple filaments are eventually tamed by nonlinearity. It is important to notice that this nonlinear taming process takes place in the presence of a substantial broadening of the temporal spectrum around the SH wavelength. The mechanism of spectral broadening and supercontinuum generation in PPLN for a single smooth beam in PPLN was discussed, both experimentally and numerically, in Ref. [23]. In the present case, the spectral broadening is taking place out of a plurality of randomly distributed filaments, and it may possibly involve self-phase modulation, spatial and temporal MI. The detailed dynamics and the relative impact of these phenomena deserve to be further investigated with numerical and analytical studies. Figure 6 clearly illustrates the process of spectral broadening that accompanies spatial reshaping, which occurs in the present specific case, both in the near- and in the far-field. The photographic images in Figure 6E show that, for such pump intensity levels, spectral broadening emanated from the SH beam may cover both the blue and the red regions of the visible spectrum. These two insets show how the newly generated colors inherit the nearly bell-shape of the SH beam.

In conclusion, in this work we have experimentally shown how the beam shape obtained at the SH of a non-diverging pump beam can break into multiple filaments. Moreover, we carried out a statistical study of the intensity distribution of such filaments. We revealed that the statistical properties of SH filaments can be partially controlled by the level of intensity of the fundamental beam, while keeping fixed both the crystal and polarization beam orientations with respect to the crystallographic axes. The generation of multiple filaments with customized statistics may be of interest in all advanced applications requiring a structured light illumination, for example, in the fields of microscopy or reservoir computing. Moreover, we surprisingly observed that the aftermath of beam breakup can lead to a taming of spatiotemporal instabilities when the intensity of the fundamental beam is increased well above the instability threshold. Specifically, a re-localization of the SH beam is accompanied by a corresponding spectral broadening, leading to the generation of new colors in the visible. Such spatial beam reshaping accompanied by spectral broadening can be used to develop novel and versatile light sources in a variety of applications ranging from nonlinear fluorescence imaging to multispectral LIDAR measurements.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

RJ and VC conceived, planned and carried out the experiments, and interpreted the experimental results. SWe and TM carried out a complementary series of experiments to complete the interpretation of the results. AT, FB, BW, and SWa worked on the theoretical and bibliographic part and wrote part of the text. KK worked on a previous version of the setup and initial experimental results in PPLN crystal. All authors contributed to the preparation of the manuscript by providing critical feedback.

Funding

H2020 European Research Council (740355, 874596, 950618); CILAS (ArianeGroup) through the shared X-LAS laboratory; the French ANR through the “TRAFIC project: ANR-18-CE080016-01; the Investissements d’Avenir with the reference ANR-10-LABX-0074-01 Sigma-LIM; “Region Nouvelle Aquitaine” through projects F2MH, SCIR, SIP2 and Nematum.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Randoux S, Suret P, Chabchoub A, Kibler B, El G. Nonlinear spectral analysis of Peregrine solitons observed in optics and in hydrodynamic experiments. Phys Rev E (2018) 98:022219. doi:10.1103/PhysRevE.98.022219

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Dudley JM, Dias F, Erkintalo M, Genty G. Instabilities, breathers and rogue waves in optics. Nat Photon (2014) 8:755–64. doi:10.1038/nphoton.2014.220

CrossRef Full Text | Google Scholar

3. Dudley JM, Genty G, Dias F, Kibler B, Akhmediev N. Modulation instability, Akhmediev Breathers and continuous wave supercontinuum generation. Opt Express (2009) 17:21497–508. doi:10.1364/OE.17.021497

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Conforti M, Baronio F, Trillo S. Competing wave-breaking mechanisms in quadratic media. Opt Lett (2013) 38(10):1648–50. doi:10.1364/OL.38.001648

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Kanashov AA, Rubenchik AM. On diffraction and dispersion effect on three wave interaction. Physica D: Nonlinear Phenomena (1981) 4(1):122–34. doi:10.1016/0167-2789(81)90009-9

CrossRef Full Text | Google Scholar

6. Bespalov VI, Talanov VI. Filamentary structure of light beams in nonlinear liquids. J Exp Theor Phys Lett (1966) 3(12):307–10.

Google Scholar

7. Fuerst RA, Baboiu D-M, Lawrence B, Torruellas WE, Stegeman GI, Trillo S, et al. Spatial modulational instability and multisolitonlike generation in a quadratically nonlinear optical medium. Phys Rev Lett (1997) 78(14):2756–9. doi:10.1103/PhysRevLett.78.2756

CrossRef Full Text | Google Scholar

8. Delqué M, Fanjoux G, Gorza SP, Haelterman M. Spontaneous 2D modulation instability in second harmonic generation process. Opt Commun (2011) 284(5):1401–4. doi:10.1016/j.optcom.2010.10.098

CrossRef Full Text | Google Scholar

9. Boardman AD, Bontemps P, Xie K. Transverse modulation instability of vector optical beams in quadratic nonlinear media. J Opt Soc Am B (1997) 14(11):3119–26. doi:10.1364/JOSAB.14.003119

CrossRef Full Text | Google Scholar

10. Petrov DV, Torner L, Martorell J, Vilaseca R, Torres JP, Cojocaru C. Observation of azimuthal modulational instability and formation of patterns of optical solitons in a quadratic nonlinear crystal. Opt Lett (1998) 23(18):1444–6. doi:10.1364/OL.23.001787

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Salerno D, Jedrkiewicz O, Trull J, Valiulis G, Picozzi A, Di Trapani P. Noise-seeded spatiotemporal modulation instability in normal dispersion. Phys Rev E Stat Nonlin Soft Matter Phys (2004) 70:065603. doi:10.1103/PhysRevE.70.065603

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Trillo S, Conti C, Di Trapani P, Jedrkiewicz O, Trull J, Valiulis G, et al. Colored conical emission by means of second-harmonic generation. Opt Lett (2002) 27(16):1451–3. doi:10.1364/OL.27.001451

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Méchain G, Couairon A, Franco M, Prade B, Mysyrowicz A. Organizing multiple femtosecond filaments in air. Phys Rev Lett (2004) 93(3):035003. doi:10.1103/PhysRevLett.93.035003

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Chen Z, Sears SM, Martin H, Christodoulides DN, Segev M. Clustering of solitons in weakly correlated wavefronts. Proc Natl Acad Sci USA (2002) 99(8):5223–7. doi:10.1073/pnas.072287299

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Safari A, Fickler R, Padgett MJ, Boyd RW. Generation of caustics and rogue waves from nonlinear instability. Phys Rev Lett (2017) 119(20):203901. doi:10.1103/PhysRevLett.119.203901

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Pierangeli D, Di Mei F, Conti C, Agranat AJ, DelRe E. Spatial rogue waves in photorefractive ferroelectrics. Phys Rev Lett (2015) 115(9):093901. doi:10.1103/PhysRevLett.115.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Mattheakis M, Pitsios IJ, Tsironis GP, Tzortzakis S. Extreme events in complex linear and nonlinear photonic media. Chaos, Solitons & Fractals (2016) 84:73–80. doi:10.1016/j.chaos.2016.01.008

CrossRef Full Text | Google Scholar

18. Montina A, Bortolozzo U, Residori S, Arecchi FT. Non-Gaussian statistics and extreme waves in a nonlinear optical cavity. Phys Rev Lett (2009) 103(17):173901–4. doi:10.1103/PhysRevLett.103.173901

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Jauberteau R, Tonello A, Baronio F, Krupa K, Millot G, Wetzel B, et al. Observation of 2D spatiotemporal rogue events in a quadratic nonlinear medium. In: Conference on lasers and electro-optics, OSA technical digest; 2020 May 10-15; Washington, DC United States: Optical Society of America (2020) [paper JTu2F.18].

CrossRef Full Text | Google Scholar

20. Bender N, Yılmaz H, Bromberg Y, Cao H. Customizing speckle intensity statistics. Optica (2018) 5(5):595–600. doi:10.1364/OPTICA.5.000595

CrossRef Full Text | Google Scholar

21. Goodman JW. Some fundamental properties of speckle*. J Opt Soc Am (1976) 66(11):1145–50. doi:10.1364/JOSA.66.001145

CrossRef Full Text | Google Scholar

22. Marcucci G, Pierangeli D, Conti C. Theory of neuromorphic computing by waves: machine learning by rogue waves, dispersive shocks, and solitons. Phys Rev Lett (2020) 125(9):093901. doi:10.1103/PhysRevLett.125.093901

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Krupa K, Labruyère A, Tonello A, Shalaby BM, Couderc V, Baronio F, et al. Polychromatic filament in quadratic media: spatial and spectral shaping of light in crystals. Optica (2015) 2(12):1058–64. doi:10.1364/OPTICA.2.001058

CrossRef Full Text | Google Scholar

24. Krupa K, Fona R, Tonello A, Labruyère A, Shalaby BM, Wabnitz S, et al. Spatial beam self-cleaning in second-harmonic generation. Sci Rep (2020) 10:7204. doi:10.1038/s41598-020-64080-7

PubMed Abstract | CrossRef Full Text | Google Scholar