- Faculty of Engineering and the Institute of Nanotechnology and Advanced Materials, Bar Ilan University, Ramat Gan, Israel
Measuring physical phenomena in an experimental system is commonly limited by the detector. When dealing with spatially defined behaviors, the critical parameter is the detector size. In this work, we examine near-infrared (NIR) measurements of turbid media using different size detectors at different positions. We examine cylindrical and semi-infinite scattering samples and measure their intensity distribution. An apparent crossing point between samples with different scatterings was previously discovered and named the iso-pathlength point (IPL). Monte Carlo simulations show the expected changes due to an increase in detector size or similarly as the detector’s location is distanced from the turbid element. First, the simulations show that the intensity profile changes, as well as the apparent IPL. Next, we show the average optical pathlength, and as a result, the differential pathlength factor, are mostly influenced by the detector size in the range close to the source. Experimental measurements using different size detectors at different locations validate the influence of these parameters on the intensity profiles and apparent IPL point. These findings must be considered when assessing optical parameters based on multiple scattering models. In cases such as NIR assessment of tissue oxygenation, size and location may cause false results for absorption or optical path.
Introduction
Visible and near-infrared (NIR) light are commonly used to non-invasively study diffusive media, such as biological tissues [1, 2], wood [3], fruit [4], and more. The interaction of NIR light with human tissue allows the assessment of hemodynamics and oxidative metabolism for diagnosis purposes [5]. Quantitatively finding the relative concentration of chromophores within the tissue requires an estimation of the optical properties, namely the absorption coefficient (
Even though it is possible to estimate the optical properties in ideal systems, non-idealities in real measurement systems can cause variations [10–12]. From a theoretical standpoint, the accuracy of the measurement system depends strongly, but not solely, on how well the solution of the theoretical problem fits the experimental setup. Hence, curve-shape fitting methods mostly rely on calibration by phantoms with known optical properties to improve accuracy [5, 13]. However, while solving the practical problem, efforts still need to be made to understand the differences between theoretical and practical systems [14, 15].
During the last decade, many technological advancements for sources and detectors have been achieved [14, 16–18]. The signal to noise ratio is maximized by either increasing the detector size or positioning the detector close to the light source, since the maximal laser power is defined by the safety limits for skin. Further understanding of the influence of detector size and positioning when measuring diffused light could bridge the gap between theory and practice.
In this work, we test the influence of these parameters in NIR measurements. Specifically, we examine the change in the scattered light profile of cylindrical and semi-infinite scattering media. Previously we have demonstrated theoretically [19], numerically [20], and experimentally, first by phantoms [21] and then in human fingers [22], a unique optical phenomenon. This is the existence of an angle with minimal impact of the reduced scattering coefficient, named the iso-pathlength (IPL) point, dependent only on geometry. It also exists in semi-infinite geometry, more relevant in clinical applications of NIR spectroscopy on the head, arm, leg, etc. [23]. This phenomenon was demonstrated in a range of scatterings that fulfills the multiple scattering condition [24]. We have also shown that even though anisotropy also varies between different tissues, it does not change the IPL point [20]. Furthermore, absorption does not change the position of this point; it only attenuates the intensity [24]. It is therefore the optimal point for absorption measurements since it minimizes changes in optical pathlength [25]. Despite the fact that theoretical and numerical simulations are highly agreed, a consistent difference exists over experimental results [19]. This study explains this difference by examining experimental detector conditions and exploring the influence of the detector's size or equivalent position on three measurables: the angular intensity distribution, i.e. full scattering profile (FSP); the IPL point; and the optical pathlength (OPL).
Methods
Monte Carlo Simulations
First, MC simulations are used to find the influence of detector size on the intensity profile and OPL. The medium is characterized by the reduced scattering coefficient and anisotropy factor g. All photons enter the medium at (Z = −D/2, X = 0), and change their direction after a distance of dr according to the scattering coefficient with a probability of 1−exp (−
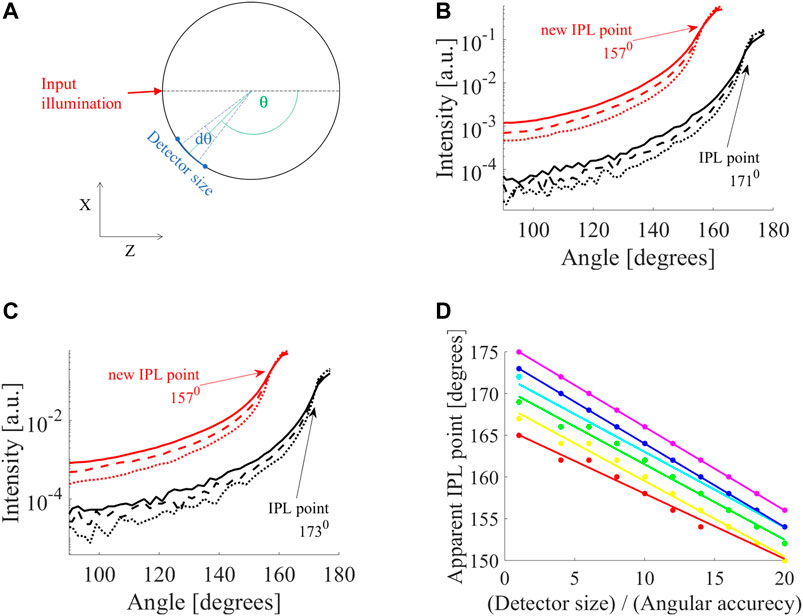
FIGURE 1. Influence of detector on apparent iso-pathlength point (IPL) point. (A) MC simulation of cylinder tissue of different scatterings (
We then simulated a scenario where the collection of photons takes place some distance from the air-tissue interface since this also effectively increases the detection area. Since most tissues are a half-infinite medium, we also carried out simulations of this kind. Each simulation launched 218 photons, and for simplicity, there was no absorption (
Experimental Setup
To validate our findings, an experimental system for FSP measurements was established [21]. A continuous wave (CW) He-Ne laser with a wavelength of 632.8 nm, and 0.8 mW power (Thorlabs, Japan) was used as an input source. A rail was placed on a rotation stage and a post was mounted on a rail carrier to allow adjustments of the distance between the sample and the detector. Different detectors were placed on the post holder. Samples were aligned to the center of the rotation stage and measured in two ways. First, a silicon photodetector (PD, SM05PD2B, Thorlabs), with an active area of 13 mm2, was placed close to the sample (not touching). Next, a multimode fiber, with a core diameter of 1.5 mm (M107L02, Thorlabs) was placed on the post at a similar distance.
The cylindrical samples were prepared from Intralipid (IL) in different concentrations as a scattering component and 1% agarose for solidification [27]. After heating the agarose, the IL was added and poured into glass cylindrical tubes with a diameter of 13 mm. The liquid was cooled under vacuum to avoid bubbles.
Results
MC Study of the Influence on Intensity Profile
In the following results, the solid, dashed, and dotted lines of the intensity profiles correspond to reduced scattering coefficients of μs' = 10,16 and 26 cm−1. First, we examined the influence of detector size (defined in Figure 1A). For example, two selected diameters, 10 mm (Figure 1B) and 12 mm (Figure 1C), show a loss in accuracy. A small detector (black lines in Figures 1B,C) shows different IPL points for each diameter (171°, for D = 10 mm, and 173° for D = 12 mm). However, when increasing the detector size by a factor of two or more, there is a change in the FSPs and the apparent IPL point seems the same. For example, when increasing the detector by a factor of eight (red lines in Figures 1B,C) the apparent IPL points for both diameters are identical (157° for both diameters) and shift to a lower angle (moving away from the light source). This emphasizes that this is not just an attenuation or linear shift, but rather a loss of spatial information and accuracy. To fully understand this, we looked at the change in apparent IPL point as the detector size increases for different diameters (D = 6,7,8,10,12 and 14 mm are red, yellow, green, cyan, blue and violet lines in Figure 1D). Each diameter presents a different slope of decrease so that as the detector size increases, the range of apparent IPL points decreases as well.
The influence of the location of the detector in respect to the air-tissue interface was also examined (Figure 2A). While moving away from the interface of an 8 mm diameter cylinder (Figure 2B) the IPL point moves from 168° (black lines) to 166° at a distance of 0.5 mm from the surface (blue lines), and 165° at a distance of 1 mm from the surface (red lines).
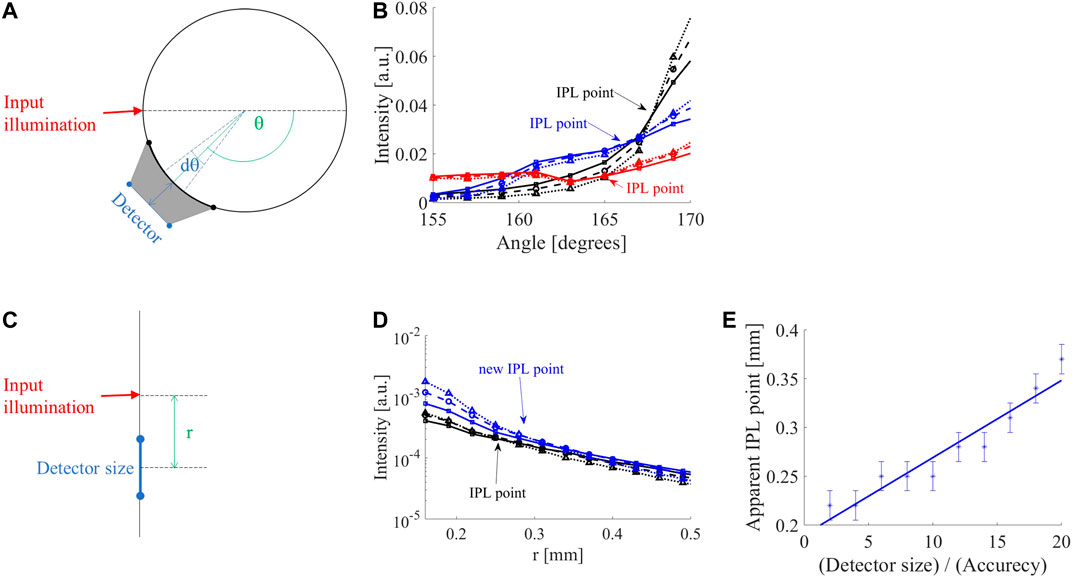
FIGURE 2. Influence of detector position and size. (A) In case the detector is distant from the surface of a cylindrical sample, the detector collects from a larger angular range (gray area), hence the detector acts as if it was larger than its physical size. (B) FSPs of 8 mm diameter cylinder adjacent to the air-tissue interface (black lines) in comparison to 0.5 mm (blue lines) and 1 mm (red lines) away from the interface. The original iso-pathlength point (IPL) point of 168° (black lines) moves to 166° at a distance of 0.5 mm (blue lines) and 165° at a distance of 1 mm (red lines). (C) MC simulation of the semi-infinite geometry demonstrate a similar behavior of the intensity as a function of distance (r), i.e., diffusion reflection profile. (D) While increasing the detector size, the IPL point moves from its original location (0.22 mm) further away from the input; for a 12-fold increase in detector size, the new IPL is at 0.28 mm (blue lines). (E) The apparent IPL point linearly increases with the detector size in the semi-infinite case.
Since many clinical applications involve large tissue dimensions, MC simulations of a semi-infinite medium were examined (Figure 2C). As in the cylindrical geometry, the IPL point moves away from the source (Figure 2D). Given a step size of 30 μm, the IPL point measured for a 30 μm detector is r = 0.22 mm (black lines), compared to a 360 μm detector where the IPL point is at r = 0.28 mm (blue lines). The change in the apparent IPL point of the semi-infinite geometry (Figure 2E) has a similar linear behavior as the cylindrical geometry (Figure 1D). Note that a decrease in angle is an increase in distance from the light source (according to the definition of the angle in Figure 1A).
MC Study of the Influence on Optical Pathlength
Next, we looked at the change in OPL (Figure 3A) and consequently differential pathlength factor (DPF) (Figure 3B), defined as
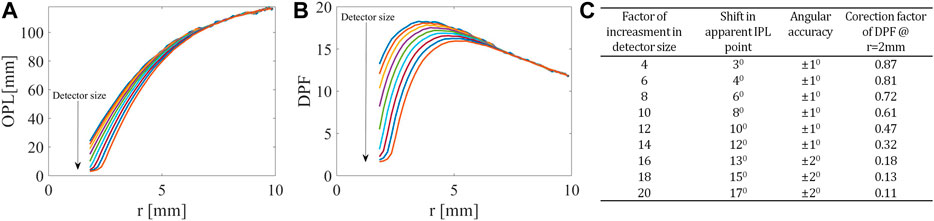
FIGURE 3. Influence of detector on OPL and DPF. At the closer distances from the light source, related to the higher angles in the FSPs, (A) the OPL and (B) the PDF decrease as the detector size increases. (C) Table summarizing the influence of detector size on both IPL point and DPF.
Experimental Results
The experimental system (Figure 4A) was used to measure the FSPs of the different scatterings (solid squares, dashed circles, and dotted triangles in Figure 4B represent
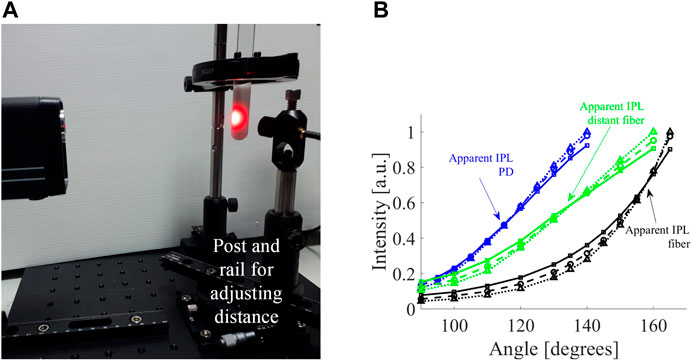
FIGURE 4. Experimental measurement of influence of detector on apparent IPL point. (A) The optical system includes a rail placed on a rotation stage and a post was mounted on the rail carrier to allow adjustments of the distance between the sample and the detector. (B) The FSPs of cylindrical tissue mimicking phantoms with different scatterings (
Let us consider the fiber from the experiment, which has a core diameter of 1.5 mm and a NA of 0.5. After moving the position of the fiber 2 cm away from its original position - the apparent IPL point moved 25°. Given the NA of the fiber (0.5 corresponds to an angle of 30°), a 2 cm distance translates to a factor of 4.85 of collected angular range compared to the core diameter. This translates to a factor of 24 increase in the detection area. The experimental data shows a shift of 25° ± 5°, which is consistent with the values from the simulation (Table in Figure 3C).
Discussion
In this work, we examined the influence of the detector size and positioning on measurements of cylindrical and semi-infinite scattering samples. We performed a MC study of the averaging effect increasing the detector size compared to the angular accuracy in different cylinder diameters. The increased detection range changed the FSPs and shifted the apparent IPL point further away from the light source. This also occurred when moving the detector away from the surface of the media, since this similarly increases the collection area. The increase in the detector indicates a loss in angular or special resolution. Furthermore, we simulated the influence of detector size on apparent OPL. Since the OPL is directly related to the DPF, both demonstrated a similar behavior. At closer distances to the light source, r, the OPL, and DPF decreased with the increase in detector size. This type of behavior, of the higher sensitivity of experimental measurements of OPL in the close range from the light source, is supported by previous reports [14, 28–30]. To further validate these findings, we performed CW measurements of the FSPs of cylindrical scattering phantoms. First, we measured the same phantoms by two detectors: by a PD and using a fiber. Since these detectors have different geometries, the apparent IPL point shifted from a theoretical one according to size. While the PD is larger and hence has improved signal to noise ratio and dynamic range, the fiber presents an IPL closer to the theoretical one. Nonetheless, using the larger detector, while considering the influence it has on the diffused light seems optimal in our opinion, giving the best of all worlds. Note that in the MC simulations the detector size was increased in one axis only, hence the experimental change in detector size in two dimensions had a stronger effect. As simulated, for a similar reason, while using the same detector and moving it further away from the sample surface, the apparent IPL point shifted further from the light source.
Conclusion
The findings of this work help the transition of NIR methods from research to clinical settings. Clinical applications of photoplethysmography, NIR diffuse optical imaging, and spectroscopy are increasingly adopted in the medical community as multimodal imaging has become more popular in recent years [10, 11, 14]. However, the diversity of responses of different medical instruments and the need for calibration complicates their use. This study highlights factors that should be considered in such instruments to allow quantitative, reliable, and sensitive physiological measurements.
Data Availability Statement
The original contributions presented in the study are included in the article, further inquiries can be directed to the corresponding author.
Author Contributions
This research conceptualization was formed by DF and HD. DF was responsible for the project administration, funding acquisition and research supervision methodology. The software, investigation, and formal analysis were done by HD The experiments were performed by IF and final validation was conducted by HD. The writing of the original draft was performed by HD, and DF was responsible for the review and editing for improving the paper.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Wang L, Ayaz H, Izzetoglu M, Onaral B. Evaluation of light detector surface area for functional Near Infrared Spectroscopy. Comput Biol Med (2017) 89:68–75. doi:10.1016/j.compbiomed.2017.07.019
2. Durduran T, Choe R, Baker WB, Yodh AG. Diffuse optics for tissue monitoring and tomography. Rep Prog Phys (2010) 73:076701. doi:10.1088/0034-4885/73/7/076701
3. Bargigia I, Nevin A, Farina A, Pifferi A, D'Andrea C, Karlsson M, et al. Diffuse optical techniques applied to wood characterization. J Near Infrared Spectrosc (2013) 21:259–68. doi:10.1255/jnirs.1068
4. Bellincontro A, Taticchi A, Servili M, Esposto S, Farinelli D, Mencarelli F. Feasible application of a portable NIR-AOTF tool for on-field prediction of phenolic compounds during the ripening of olives for oil production. J Agric Food Chem (2012) 60:2665–73. doi:10.1021/jf203925a
5. Re R, Pirovano I, Contini D, Spinelli L, Torricelli A. Time domain near infrared spectroscopy device for monitoring muscle oxidative metabolism: custom probe and in vivo applications. Sensors (2018) 18:264. doi:10.3390/s18010264
6. Cheong WF, Prahl SA, Welch AJ. A review of the optical properties of biological tissues. IEEE J Quan Electron (1990) 26:2166–85. doi:10.1109/3.64354
7. Piao D, Patel S. Simple empirical master–slave dual-source configuration within the diffusion approximation enhances modeling of spatially resolved diffuse reflectance at short-path and with low scattering from a semi-infinite homogeneous medium. Appl Opt (2017) 56:1447–52. doi:10.1364/AO.57.007942
8. Bhatt M, Ayyalasomayajula KR, Yalavarthy PK. Generalized Beer-Lambert model for near-infrared light propagation in thick biological tissues. J Biomed Opt (2016) 21:76012. doi:10.1117/1.JBO.21.7.076012
9. Wang L, Jacques SL, Zheng L. MCML--Monte Carlo modeling of light transport in multi-layered tissues. Comput Methods Programs Biomed (1995) 47:131–46. doi:10.1016/0169-2607(95)01640-f
10. Pirovano I, Re R, Candeo A, Contini D, Torricelli A, Spinelli L. Instrument response function acquisition in reflectance geometry for time-resolved diffuse optical measurements. Biomed Opt Express (2020) 11:240–50. doi:10.1364/BOE.380996
11. Cubeddu R, Pifferi A, Taroni P, Torricelli A, Valentini G. Experimental test of theoretical models for time-resolved reflectance. Med Phys (1996) 23:1625–33. doi:10.1118/1.597739
12. Pifferi A, Torricelli A, Bassi A, Taroni P, Cubeddu R, Wabnitz H, et al. Performance assessment of photon migration instruments: the MEDPHOT protocol. Appl Opt (2005) 44:2104–14. doi:10.1364/ao.44.002104
13. Wabnitz H, Taubert DR, Mazurenka M, Steinkellner O, Jelzow A, Macdonald R, et al. Performance assessment of time-domain optical brain imagers, part 1: basic instrumental performance protocol. J Biomed Opt (2014) 19:086010. doi:10.1117/1.JBO.19.8.086010
14. Behera A, Di Sieno L, Pifferi A, Martelli F, Mora A. Instrumental, optical and geometrical parameters affecting time-gated diffuse optical measurements: a systematic study. Biomed Opt Express (2018) 9:5524–42. doi:10.1364/BOE.9.005524
15. Ntziachristos V, Chance B. Accuracy limits in the determination of absolute optical properties using time-resolved NIR spectroscopy. Med Phys (2001) 28:1115–24. doi:10.1118/1.1373674
16. Ohlídal I, Franta D, Ohlídal M, Navrátil K. Optical characterization of nonabsorbing and weakly absorbing thin films with the wavelengths related to extrema in spectral reflectances. Appl Opt (2001) 40:5711–7. doi:10.1364/ao.40.005711 |
17. Xu K, Chen Y, Okhai TA, Snyman LW. Micro optical sensors based on avalanching silicon light-emitting devices monolithically integrated on chips. Opt Mater Express (2019) 9:3985–97. doi:10.1364/OME.9.003985
18. Xu K. Silicon MOS optoelectronic micro-nano structure based on reverse-biased PN junction. Phys. Status Solidi A (2019) 216:1800868. doi:10.1002/pssa.201800868
19. Duadi H, Piao D, Fixler D. Self calibration iso-pathlength point in cylindrical tissue geometry: solution of steady-state photon diffusion based on the extrapolated zero-boundary. OSA Continuum (2019) 2:92–8. doi:10.1364/OSAC.2.000092
20. Duadi H, Feder I, Fixler D. Linear dependency of full scattering profile isobaric point on tissue diameter. J Biomed Opt (2014) 19:026007. doi:10.1117/1.JBO.19.2.026007
21. Feder I, Duadi H, Fixler D. Experimental system for measuring the full scattering profile of circular phantoms. Biomed Opt Express (2015) 6:2877–86. doi:10.1364/BOE.6.002877
22. Duadi H, Feder I, Fixler D. Near‐infrared human finger measurements based on self‐calibration point: simulation and in vivo experiments. J Biophotonics (2018) 11:e201700208. doi:10.1002/jbio.201700208
23. Feder I, Duadi H, Chakraborty R, Fixler D. Self-calibration phenomenon for near-infrared clinical measurements: theory, simulation, and experiments. ACS Omega (2018) 3:2837–44. doi:10.1021/acsomega.8b00018
24. Duadi H, Fixler D. Influence of multiple scattering and absorption on the full scattering profile and the isobaric point in tissue. J Biomed Opt (2015) 20:56010. doi:10.1117/1.JBO.20.5.056010
25. Feder I, Duadi H, Fixler D. Single wavelength measurements of absorption coefficients based on iso-pathlength point. Biomed Opt Express (2020) 11:5760–71. doi:10.1364/BOE.401591
26. Ankri R, Duadi H, Motiei M, Fixler D. In-vivo tumor detection using diffusion reflection measurements of targeted gold nanorods - a quantitative study. J Biophotonics (2012a) 5:263–73. doi:10.1002/jbio.201100120
27. Ankri R, Duadi H, Motiei M, Fixler D. In-vivo Tumor detection using diffusion reflection measurements of targeted gold nanorods - a quantitative study. J Biophotonics (2012b) 5:263–73. doi:10.1002/jbio.201100120
28. Ultman JS, Piantadosi CA. Differential pathlength factor for diffuse photon scattering through tissue by a pulse-response method. Math Biosci (1991) 107:73–82. doi:10.1016/0025-5564(91)90072-q
29. Kohl M, Nolte C, Heekeren HR, Horst S, Scholz U, Obrig H, et al. Determination of the wavelength dependence of the differential pathlength factor from near-infrared pulse signals. Phys Med Biol (1998) 43:1771. doi:10.1088/0031-9155/43/6/028
Keywords: Monte Carlo simulations, near-infrared measurements, turbid media, scattering measurements, light-tissue interactions
Citation: Duadi H, Feder I and Fixler D (2021) Influence of Detector Size and Positioning on Near-Infrared Measurements and Iso-pathlength Point of Turbid Materials. Front. Phys. 9:647281. doi: 10.3389/fphy.2021.647281
Received: 29 December 2020; Accepted: 18 January 2021;
Published: 11 March 2021.
Edited by:
Vicente Micó, University of Valencia, SpainReviewed by:
Kaikai Xu, University of Electronic Science and Technology of China, ChinaAbraham Hirshberg, Tel Aviv University, Israel
Copyright © 2021 Duadi, Feder and Fixler. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dror Fixler, RHJvci5GaXhsZXJAYml1LmFjLmls
 Hamootal Duadi
Hamootal Duadi Idit Feder
Idit Feder Dror Fixler
Dror Fixler