Quantitative Phase Imaging Using Deep Learning-Based Holographic Microscope

Digital holographic microscopy enables the measurement of the quantitative light field information and the visualization of transparent specimens. It can be implemented for complex amplitude imaging and thus for the investigation of biological samples including tissues, dry mass, membrane fluctuation, etc. Currently, deep learning technologies are developing rapidly and have already been applied to various important tasks in the coherent imaging. In this paper, an optimized structural convolution neural network PhaseNet is proposed for the reconstruction of digital holograms, and a deep learning-based holographic microscope using above neural network is implemented for quantitative phase imaging. Living mouse osteoblastic cells are quantitatively measured to demonstrate the capability and applicability of the system.

Introduction

Optical microscope is an effective diagnostic tool in modern healthcare which allows pathologists to clearly and qualitatively observe the details of cells and tissues, and make judgments based on experience. This technique is sufficient in most cases. However, a bright field optical microscope records the intensity information of the specimen and suffers from low contrast for transparent biological cells which presents minimal light absorption. Various labeling methods, including staining and fluorescent tagging, are designed to enhance the imaging effect of the microscope, but the dyes may cross-react with the biological processes and affect the objectivity of medical diagnosis [1]. Although phase contrast microscopy or differential interference contrast microscopy, which converts the sightless phase shifts introduced by the specimen of interest into observable intensity variations, provide an approach to survey phase specimens without labeling, they cannot provide quantitative phase information on the specimen-induced phase shifts for subsequent accurate diagnosis. Furthermore, their inherent contrast mechanism makes automated cell segmentation hardly robust.

In comparison, quantitative phase imaging techniques enable quantitative light field information and the visualization of transparent specimens [2–4]. As a typical representative of this technique, digital holographic microscopy (DHM) can be implemented for complex amplitude imaging and be used to investigate transparent specimens, such as biological samples including tissues, dry mass, membrane fluctuation, etc [5–8]. In DHM, a hologram that carries specimen information is recorded digitally first, and then the hologram is numerically reconstructed to extract the amplitude or phase of the specimens’ complex field [9–13]. After that, the quantitative phase information can be converted to dry mass density of the cell with extremely high accuracy which has been demonstrated so far as a valuable tool in hematological or cancer diagnosis. The label-free, submicron scale sensitivity, full-field, non-destructive, real-time, quantitative and three-dimensional imaging abilities of DHM present a variety of advantages for biomedical applications, especially for live cell imaging [14–16]. Nowadays, DHM has been an important and powerful tool for medical diagnoses.

In our previous work, a common-path digital holographic microscopy based on a beam displacer unit was proposed for quantitative and dynamic phase imaging of biological cells [17]. This implementation reduces the system requirement for the light source coherence, realizes the convenient adjustment of the light beams and achieves an excellent temporal stability. However, its hologram reconstruction algorithms are often time consuming for obtaining satisfactory complex amplitude information of the specimen, which usually has certain requirements for computer hardware and need complicated tuning of user-defined parameters, such as the reconstruction distance, area and position in the frequency domain, etc. It is necessary to develop a new holographic reconstruction algorithm to improve the efficiency of common-path digital holographic microscopy.

In recent years, deep learning technology has developed rapidly, and very significant achievements have been made in areas such as autonomous driving, natural language processing, computer vision and many more. Currently, deep learning has also made remarkable achievements in computational imaging, and it has already been applied to various important tasks in coherent imaging, such as phase unwrapping [18], phase recovery [19–22], holograms reconstruction [23–27], and so on.

In this paper, an optimized structural convolution neural network PhaseNet is proposed for the reconstruction of digital holograms, and a deep learning-based holographic microscope (DLHM) using PhaseNet is implemented for quantitative phase imaging. Living mouse osteoblastic cells are quantitatively measured to demonstrate the capability and applicability of the system.

Methods

Suppose the intensity of the recorded digital hologram in DHM is I (x,y), the complex amplitude of the object light field U (ξ,η) can be numerically reconstructed by using the scalar diffraction theory,

$U\left(\xi ,\eta \right)={\displaystyle {\int }_{-\infty }^{\infty }{\displaystyle {\int }_{-\infty }^{\infty }I\left(x,y\right)}}R\left(x,y\right)g\left(\xi ,\eta ,x,y\right)\mathrm{d}x\mathrm{d}y,(1)$

where R (x,y) is the reconstruction reference light field and g (ξ,η; x,y) is the impulse response function [28–30].

The hologram is usually reconstructed using convolution algorithm, corresponding reconstructed object light field U (ξ, η) can be expressed as

$U\left(\xi ,\eta \right)=IFFT\left\{FFT\left\{I\left(x,y\right)R\left(x,y\right)\right\}\cdot FFT\left\{g\left(\xi ,\eta ,x,y\right)\right\}\right\},(2)$

where FFT and IFFT represent the Fourier and inverse Fourier transform operations, respectively.

And then, the intensity and phase information of the specimen can be calculated subsequently by

$I\left(\xi ,\eta \right)={\left|U\left(\xi ,\eta \right)\right|}^2(3)$

and

$\phi \left(\xi ,\eta \right)=\arctan \frac{\mathrm{Im}\left[U\left(\xi ,\eta \right)\right]}{\mathrm{Re}\left[U\left(\xi ,\eta \right)\right]}\left(\mathrm{mod}2\text{π}\right)(4)$

where Re and Im represent the real and imaginary parts of the object light field, respectively. Further by eliminating the 2π ambiguity due to the argument operation, the true phase information of the original object wavefield can be obtained.

After the object beam passes through the biological specimen, the optical path difference ΔOPD will be introduced due to the phase difference Δφ and the difference of refractive index (RI) between the cells and the culture medium, which is dependent on the laser wavelength λ, the RI of the surrounding medium n_medium, the cell thickness d and integral mean RI n_specimen. Therefore, the ΔOPD can be calculated as

$\Delta \text{OPD}=\left(n_{specimen}-n_{medium}\right)\cdot d=\frac{\lambda }{2\pi }\cdot \Delta \phi .(5)$

The ΔOPD is an integral effect of the optical path along the optical axis. Different parts of the cell have different RI resulting in different ΔOPD. Thus, in a certain sense, the ΔOPD represents the thickness of the cell.

Deep Learning-Based Holographic Microscope

The proposed deep learning-based holographic microscope includes a set of digital holographic microscope for the hologram recording and a deep neural network PhaseNet for the numerical reconstruction of digital holograms.

Digital Holographic Microscope

The main body of the proposed DLHM is a common-path digital holographic microscope as shown in Figure 1, which is modified based on a commercial microscope. The light source of the microscope was replaced by a fiber-coupled DPSS laser (Cobolt Samba, 532 nm). Then the laser beam is focused by a lens L to illuminate the specimen and magnified by a ×20 long working distance microscope objective MO. The transmitted light beam travels through a polarizer P1 and enters into the beam displacer BD, in which it’s separated into two orthogonally polarized beams with a small displacement. The two output beams pass through a polarizer P2 and interfere with each other at the lateral shearing region of BD. The polarization direction of P2 is set at 45° with the two output polarized beams, respectively. Thus, the two output beams interfere with each other in their overlap part and an off-axis digital hologram is recorded by a white-black CCD camera (target size of 5.95 mm × 4.46 mm, 1,280 × 960 pixels, pixel size 4.65 μm × 4.65 μm). The BD and two polarizers are assembled together as a simple, low-cost and compact beam displacer unit, as shown in Figure 1B. In fact, benefiting from the simple optical structure and common-path design, the commercial microscope has been improved to a digital holographic microscope for promising and potential applications in quantitative phase measurement.

FIGURE 1

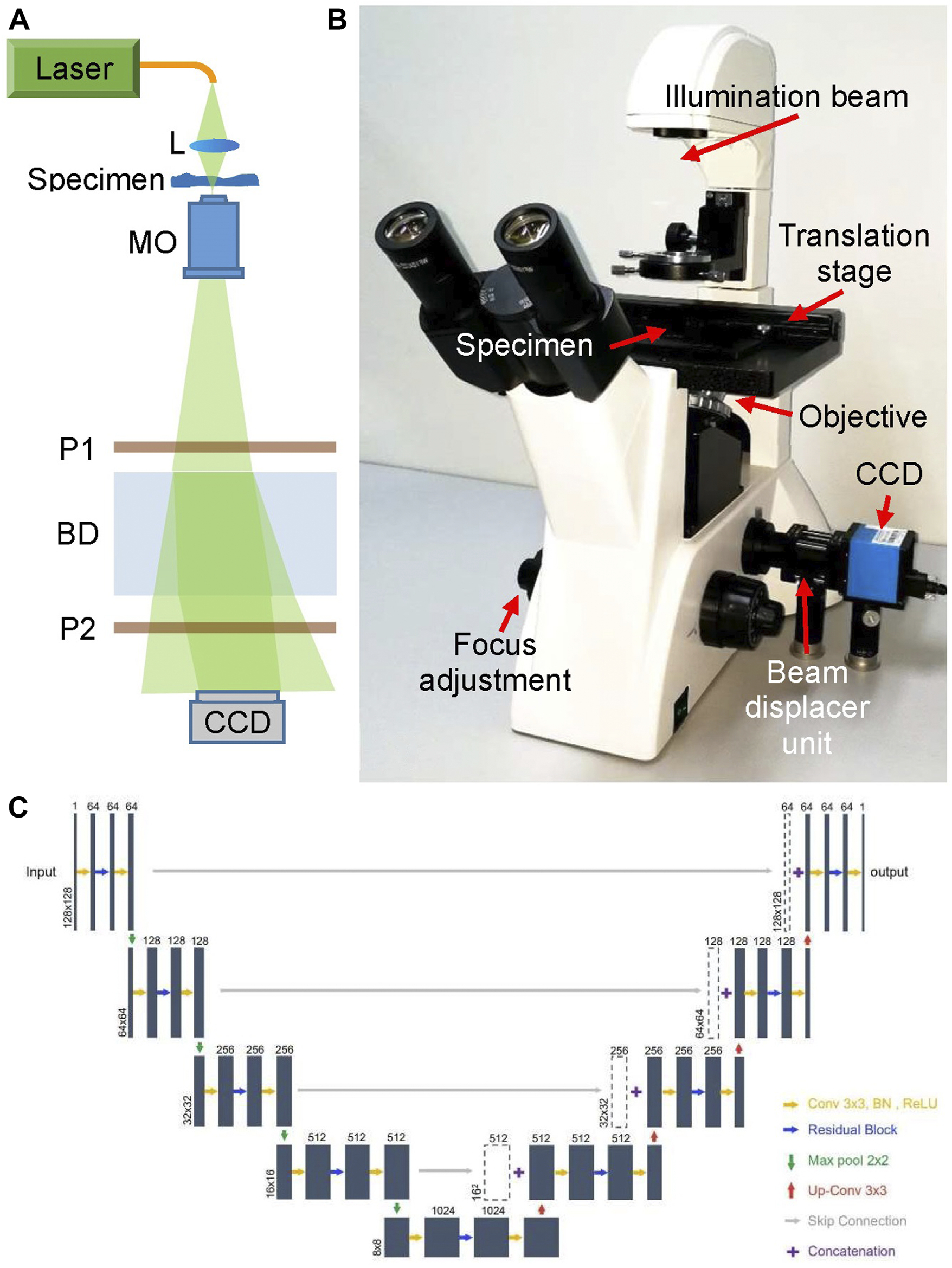
FIGURE 1. Deep learning-based holographic microscope and PhaseNet architecture. (A) Optical schematic of the common-path digital holographic microscope based on a beam displacer unit; (B) deep learning-based holographic microscope; (C). Detailed schematic of PhaseNet architecture. Each blue box corresponds to a multi-channel feature map. The number of channels is provided on top of the box. The x–y-size is denoted at the lower left edge of the box. White boxes represent copied feature maps.

PhaseNet

PhaseNet is one of the core components of data processing system of DLHM. It completes the intelligent reconstruction of the hologram and obtains the three-dimensional phase information of the specimens replacing the traditional convolution algorithm or the Fresnel transform algorithm in DHM. Figure 1C shows the detailed schematic of PhaseNet architecture which is an optimized structural CNN proposed for phase unwrapping [18]. This architecture contains three parts: down-sampling, bridge and up-sampling paths. The down-sampling path consists of five repeated use of two 3 × 3 convolutions followed by a BN and a ReLU, a residual block [31], and a 2-stride 2 × 2 max pooling operation for downsampling. The feature channels are increased by the first convolution of each repeat (first from 1 to 64 channels, the rest for double channels). By removing the max pooling from the down-sampling path, the bridge path is obtained. Each step in up-sampling consists of a transposed convolution for upsampling, a concatenation with the corresponding feature map from the down-sampling path by skip connection, two 3 × 3 convolutions followed by a BN and a ReLU, and a residual block between the two convolutions. The first two convolutions in each repeat decrease the number of feature channels (the last from 64 to 1 channel, the rest for halving channels). The residual blocks include two repeated use of 3 × 3 convolution followed by a BN and a ReLU. The skip connection is introduced to prevent the network performance degradation by summing the input and output. The down-sampling path extracts and advances the features of the sinogram, while the up-sampling path reconstructs the phase from the high-level features. The channels from the first two layers are increased from 1 to 64, which is to ensure that a sufficient number of low-level features are extracted for use in the later layers. The skip connections are added to improve the efficiency of gradient transmission.

Work Procedure

The work procedure of the proposed DLHM are as follows:

1. Hologram recording and reconstruction. Using DLHM to record off-axis digital holograms of the biological cells.

2. Phase information acquisition. Reconstructing the holograms by use of convolution algorithm to calculate the phase information of the biological cells.

3. PhaseNet training and testing. The holograms and phase results of each cell are used as input and ground truth, respectively, to train the PhaseNet. 9,000 pairs images are used for training, 1,000 pairs images for testing. Gaussian noise with random standard deviations from 0 to 25 is added into the holograms of the training dataset for better robustness. The ADAM-based optimization with an initial learning rate of 0.001 (dropping to the previous 0.75 every five epochs) is adopted to update PhaseNet’s parameters. The network is trained for 200 epochs.

4. Network output obtaining. In the network training process, the PhaseNet output is calculated according to the input of the network.

5. Loss function calculation. The mean squared error (MSE) of the PhaseNet output with ground truth (the phase information of biological cells) is calculated and used as the loss function. And the loss function is back-propagated through the network.

6. Quantitatively phase imaging of the biological cells. After finishing the above operations, the network training can be finally completed, and a neural network PhaseNet matching this DLHM can be obtained. Then, the digital hologram recorded by DLHM can be randomly input PhaseNet and the quantitative phase images of the specimen can be rapidly output. The network reconstruction time for a phase image is ∼0.014 s.

For PhaseNet implementing, Pytorch framework based on Python 3.6.1 is used. The network training and testing are performed on a PC with Core i7-8700K CPU, using NVIDIA GeForce GTX 1080Ti GPU. The training process takes ∼4 h for 100 epochs (∼10,000 pairs images size of 128 × 128 pixels in a batch size of 48).

Experiment Results and Discussions

The living mouse osteoblastic cells are measured by the DLHM. These mouse osteoblastic cells IDG-SW3 are cultured in Alpha minimum essential medium (αMEM, gibco by life technologies). They stick to the bottom of the petri dish while maintaining activity and are placed on the DLHM for measurement in room temperature environment.

Figure 2 shows the numerical reconstruction results of one mouse osteoblastic cell. Figure 2A is one of the recorded digital holograms of the cells in which its partially enlarged view clearly shows the interference fringes. In order to reconstruct the hologram numerically, Fourier transform is required to complete the spectral filtering. The spectrum of the hologram is shown in Figure 2B. After completing the numerical reconstruction and phase unwrapping, we can finally obtain the mouse osteoblastic cells’ intensity and phase information. Figure 2C shows the quantitative two-dimensional phase map of one mouse osteoblastic cell during the mitotic phase. This phase map represents the ΔOPD caused by the cell thickness, and it can also be called optical thickness of cells. In Figure 2C, some synapses are surrounding the cell. At this time, the cell is about to finish dividing and has become two cells. The biggest phase value in the central part of the two cells represents a maximum cell thickness and it’s where the nucleuses are located. These are shown very clearly in the three-dimensional phase map of Figure 2D. The RI of the αMEM is n_medium = 1.3377 calibrated by an Abbe refractometer, and by assuming a constant and homogeneous cellular RI n_specimen = 1.375, we can estimate that a phase difference of 1 rad corresponds to a cellular thickness of 2.27 μm according to Eq. 5. Figure 2E shows the profile map along with the dash lines A, B and C in Figure 2C. The maximum phase difference is about 7 rad which can be translated to an optical thickness of 15.89 μm.

FIGURE 2

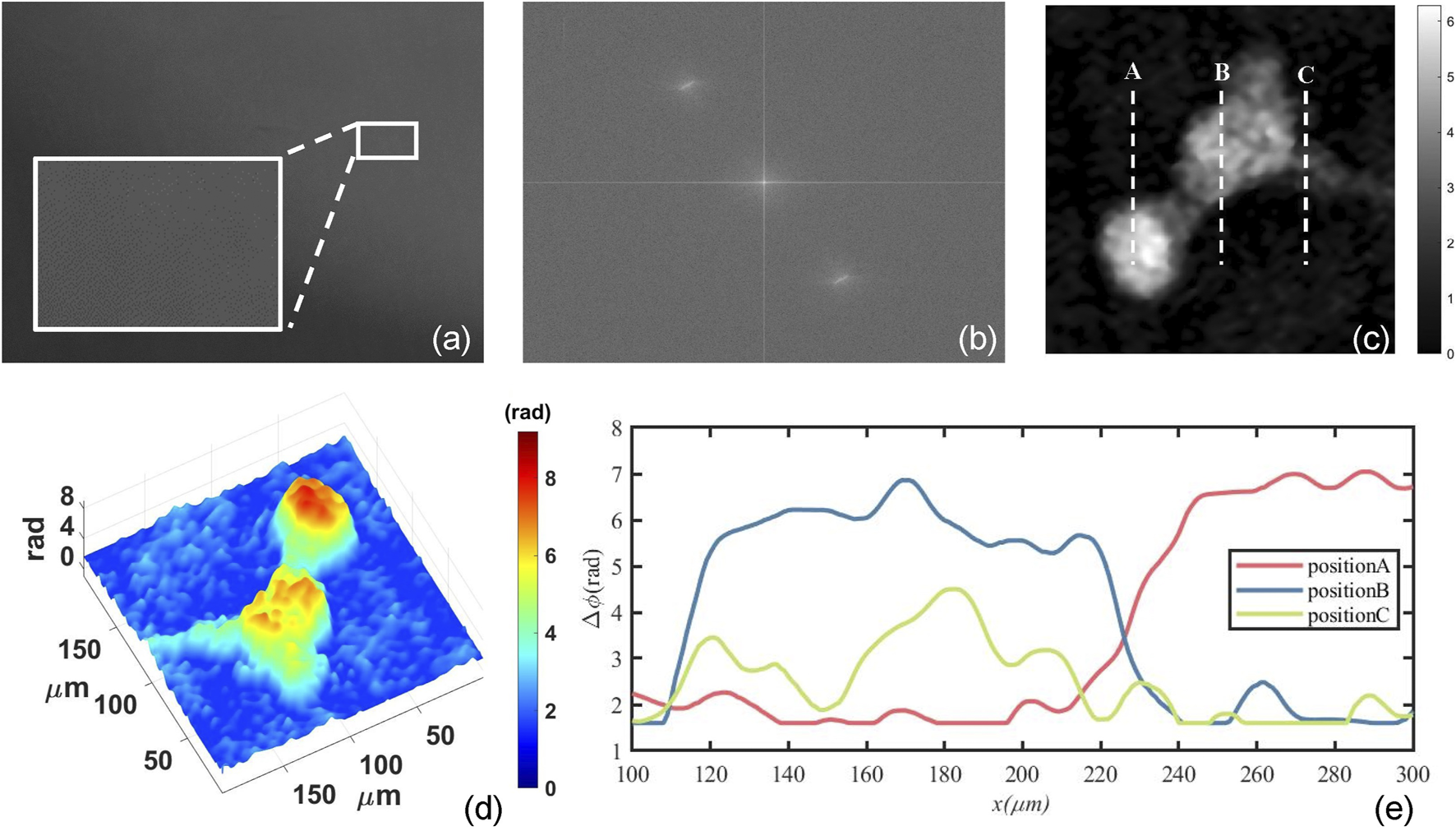
FIGURE 2. Numerical reconstruction results of mouse osteoblastic cells by use of convolution algorithm. (A) The digital holograms of a living mouse osteoblastic cell; (B) The spectrum of the hologram; (C) The quantitative two-dimensional phase map of one mouse osteoblastic cell; (D) three-dimensional phase map; (E) The profile map along with the dash lines A, B and C in (C).

1990 holograms of mouse osteoblastic cells are taken with DLHM. Then the phase images are recovered by traditional convolution algorithm. In order to improve the generalization ability of the neural network, data augmentation is a standard method. The dataset including 1990 holograms and corresponding phase images is expanded to 10,000 by flipping, rotating, etc. After that, the holograms and phase images of each cell are used as input and ground truth, respectively. Figure 3 shows part of the dataset. Among all the data, 90% are used for training, 10% for testing. Then we can use the prepared dataset to train the neural network PhaseNet.

FIGURE 3

FIGURE 3. Dataset examples. The upper part shows the holograms as input, and the lower part shows the phase results as ground truth.

As the training progresses, the MSE of the ground truth and the output are back-propagated to the network, and parameters such as weights are updated by gradient descent. After 100 epoch training, the network reaches the convergence state. In the beginning, the loss function drops the fastest, as the epoch progresses, it becomes slower and slower, and the speed is close to zero at 100 epochs.

After training, we feed the holograms in the test set to PhaseNet, and the corresponding phase results are quickly reconstructed. Part of the results is visualized in Figure 4. Figures 4A,B are the ground truth and corresponding reconstruction results, respectively. From the two-dimensional phase images of the cell, we can see that the results of the network reconstruction are very close to the ground truth. More quantitatively, we calculated its structural similarity index measure (SSIM), which is used for measuring the similarity between two images and is a perception-based model that considers image degradation as perceived change in structural information, while also incorporating important perceptual phenomena, including both luminance masking and contrast masking terms. Finally, the SSIM of the phase results obtained using PhaseNet can reach 0. 9404. This shows that PhaseNet can replace traditional algorithms to achieve the numerical reconstruction of holograms. Figure 4C shows the three-dimensional phase images of the cells obtained by PhaseNet.

FIGURE 4

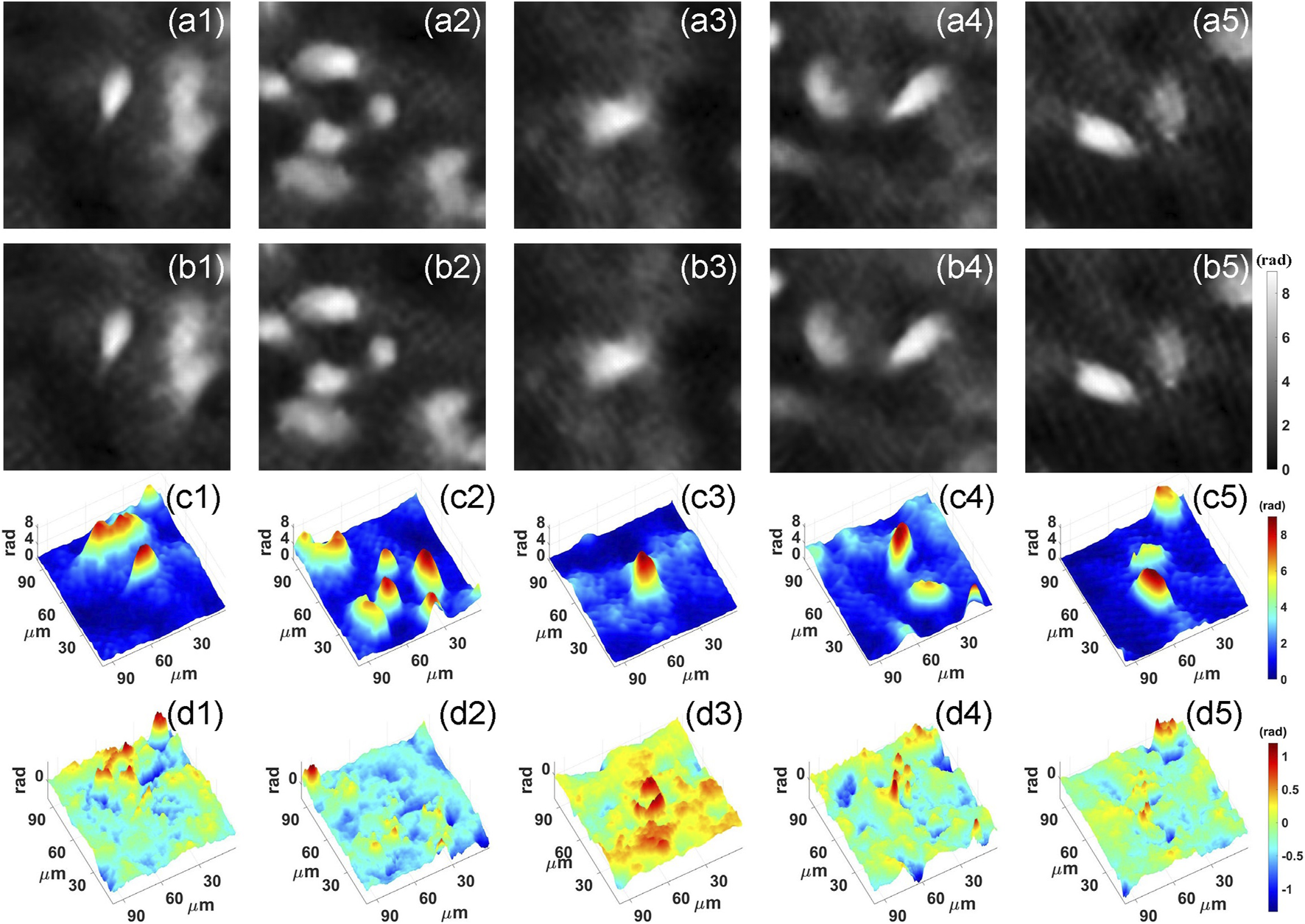
FIGURE 4. Neural network reconstruction results. (A) Ground truth; (B) PhaseNet reconstruction result; (C) Three-dimensional image of PhaseNet reconstruction result; (D) Three-dimensional image of error maps between Ground truth and PhaseNet reconstruction result.

After completing the network training, the deep learning-based holographic microscope is feasible for quantitative phase measurement of living biological cells. It can completely replace the traditional digital holographic microscope for label-free cell imaging. At the same time, due to the use of neural networks, the acquisition of three-dimensional information of specimens can be completed more quickly.

In conclusion, we proposed PhaseNet for the reconstruction of digital holograms, based on which the DLHM is implemented for quantitative phase imaging of biological specimens. In order to verify the capability and applicability of DLHM, we used the living mouse osteoblastic cells as samples to generate dataset and train PhaseNet. The testing results show that the average SSIM index of DLHM can reach 0.9404.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

JD and JZ conceived and supervised the project. YL and KW performed experiments and data analysis. KW, JW and JT contributed to data analysis. KW, JW and JD wrote the draft of the manuscript; All the authors edited the manuscript.

Funding

This work was supported by National Natural Science Foundation of China (NSFC) (62075183, 61927810) and NSAF (U1730137).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Park Y, Depeursinge C, Popescu G. Quantitative phase imaging in biomedicine. Nat Photon (2020) 12:578–89. doi:10.1364/cleo_si.2012.ctu3j.5

CrossRef Full Text | Google Scholar

2. Ahmad A, Dubey V, Singh G, Singh V, Mehta DS. Quantitative phase imaging of biological cells using spatially low and temporally high coherent light source. Opt Lett (2016) 41:1554–7. doi:10.1364/ol.41.001554

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Creath K, Goldstein G. Dynamic quantitative phase imaging for biological objects using a pixelated phase mask. Biomed Opt Express (2012) 3:2866–80. doi:10.1364/boe.3.002866

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Popescu G, BP Jena. Quantitative phase imaging of nanoscale cell structure and dynamics. Methods Cel Biol (2008) 90:87. doi:10.1016/S0091-679X(08)00805-4

CrossRef Full Text | Google Scholar

5. Fan X, Healy JJ, O’Dwyer K, Hennelly BM. Label-free color staining of quantitative phase images of biological cells by simulated Rheinberg illumination. Appl Opt (2019) 58:3104–14. doi:10.1364/ao.58.003104

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Doblas A, Sanchez-Ortiga E, Martinez-Corral M, Saavedra G, Garcia-Sucerquia J. Accurate single-shot quantitative phase imaging of biological specimens with telecentric digital holographic microscopy. J Biomed Opt (2014) 19:29. doi:10.1117/1.jbo.19.4.046022

CrossRef Full Text | Google Scholar

7. Marquet P, Rappaz B, Magistretti PJ, Cuche E, Emery Y, Colomb T, et al. Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy. Opt Lett (2005) 30:468–70. doi:10.1364/ol.30.000468

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Rong L, Latychevskaia T, Chen C, Wang D, Yu Z, Zhou X, et al. Terahertz in-line digital holography of human hepatocellular carcinoma tissue. Scientific Rep (2015) 5:33. doi:10.1038/srep08445

CrossRef Full Text | Google Scholar

9. Gao P, Yao B, Min J, Guo R, Ma B, Zheng J, et al. Autofocusing of digital holographic microscopy based on off-axis illuminations. Opt Lett (2012) 37:3630–2. doi:10.1364/ol.37.003630

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Ma J, Yuan C, Situ G, Pedrini G, Osten W. Resolution enhancement in digital holographic microscopy with structured illumination. Chin Opt Lett (2013) 11:124. doi:10.3788/col201311.090901

CrossRef Full Text | Google Scholar

11. Guo R, Yao B, Gao P, Min J, Zhou M, Han J, et al. Off-axis digital holographic microscopy with LED illumination based on polarization filtering. Appl Opt (2013) 52:8233–8. doi:10.1364/ao.52.008233

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Gao P, Pedrini G, Osten W. Structured illumination for resolution enhancement and autofocusing in digital holographic microscopy. Opt Lett (2013) 38:1328–30. doi:10.1364/ol.38.001328

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Weng J, Zhong J, Hu C. Digital reconstruction based on angular spectrum diffraction with the ridge of wavelet transform in holographic phase-contrast microscopy. Opt Express (2008) 16:21971–81. doi:10.1364/oe.16.021971

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Di J, Li Y, Xie M, Zhang J, Ma C, Xi T, et al. Dual-wavelength common-path digital holographic microscopy for quantitative phase imaging based on lateral shearing interferometry. Appl Opt (2016) 55:7287–93. doi:10.1364/ao.55.007287

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Min J, Yfao B, Ketelhut S, Engwer C, Greve B, Kemper B. Simple and fast spectral domain algorithm for quantitative phase imaging of living cells with digital holographic microscopy. Opt Lett (2017) 42:227–30. doi:10.1364/ol.42.000227

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Zhong Z, Zhao HJ, Cao LC, Shan MG, Liu B, Lu WL, et al. Automatic cross filtering for off-axis digital holographic microscopy. Results Phys (2020) 16:6. doi:10.1016/j.rinp.2019.102910

CrossRef Full Text | Google Scholar

17. Di J, Li Y, Wang K, Zhao J. Quantitative and dynamic phase imaging of biological cells by the use of the digital holographic microscopy based on a beam displacer unit. IEEE Photon J (2018) 10(4):6900510. doi:10.1109/jphot.2018.2839878

CrossRef Full Text | Google Scholar

18. Wang K, Li Y, Kemao Q, Di J, Zhao J. One-step robust deep learning phase unwrapping. Opt Express (2019) 27:15100–15. doi:10.1364/oe.27.015100

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Rivenson Y, Zhang Y, Gnaydin H, Teng D, Ozcan A. Phase recovery and holographic image reconstruction using deep learning in neural networks. Light-Science Appl (2018) 7:127. doi:10.1038/lsa.2017.141

CrossRef Full Text | Google Scholar

20. Wang K, Di J, Li Y, Ren Z, Kemao QJ. Transport of intensity equation from a single intensity image via deep learning. Opt Lasers Eng (2020) 134:106233. doi:10.1016/j.optlaseng.2020.106233

CrossRef Full Text | Google Scholar

21. Zhao F, Bian Y, Wang H, Lyu M, Pedrini G, Osten W, et al. Phase imaging with an untrained neural network. Light-Science Appl (2020) 9:127. doi:10.1038/s41377-020-0302-3

CrossRef Full Text | Google Scholar

22. Zhou W-J, Guan X, Liu F, Yu Y, Zhang H, Poon T-C, et al. Phase retrieval based on transport of intensity and digital holography. Appl Opt (2018) 57:A229–A234. doi:10.1364/ao.57.00a229

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Rivenson Y, Wu Y, Ozcan A. Deep learning in holography and coherent imaging. Light-Science Appl (2019) 8:44. doi:10.1038/s41377-019-0196-0

CrossRef Full Text | Google Scholar

24. Wang K, Dou J, Kemao Q, Di J, Zhao J. Y-Net: a one-to-two deep learning framework for digital holographic reconstruction. Opt Lett (2019) 44:4765–8. doi:10.1364/ol.44.004765

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Wang K, Kemao Q, Di J, Zhao J. Y4-Net: a deep learning solution to one-shot dual-wavelength digital holographic reconstruction. Opt Lett (2020) 45:4220–3. doi:10.1364/ol.395445

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Yan K, Yu Y, Huang C, Sui L, Qian K, Asundi A. Fringe pattern denoising based on deep learning. Opt Commun (2019) 437:148–52. doi:10.1016/j.optcom.2018.12.058

CrossRef Full Text | Google Scholar

27. Ren Z, So HK-H, Lam EY. Fringe pattern improvement and super-resolution using deep learning in digital holography. IEEE Trans Ind Inf (2019) 15:6179–86. doi:10.1109/tii.2019.2913853

CrossRef Full Text | Google Scholar

28. Di J, Zhao J, Sun W, Jiang H, Yan X. Phase aberration compensation of digital holographic microscopy based on least squares surface fitting. Opt Commun (2009) 282(19):3873–7. doi:10.1016/j.optcom.2009.06.049

CrossRef Full Text | Google Scholar

29. Sun W, Zhao J, Di J, Wang Q, Wang L. Real-time visualization of Karman vortex street in water flow field by using digital holography. Opt Express (2009) 17(22):20342–8. doi:10.1364/oe.17.020342

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Di J, Yu Y, Wang Z, Qu W, Cheng CY, Zhao J. Quantitative measurement of thermal lensing in diode-side-pumped Nd:YAG laser by use of digital holographic interferometry. Opt Express (2016) 24(25):28185–93. doi:10.1364/oe.24.028185

PubMed Abstract | CrossRef Full Text | Google Scholar

31. He K, Zhang X, Ren S, Sun J. Deep residual learning for image recognition. IEEE Conf. Comput. Vis. Pattern Recognit (2016) 14:770–8. doi:10.1109/cvpr.2016.90

CrossRef Full Text | Google Scholar