A New Deep Learning-Based Zero-Inflated Duration Model for Financial Data Irregularly Spaced in Time

Introduction

In the electronic security trading system, limit orders are offered by potential buyers and sellers. A trade will be executed only if the maximum bid price from the buy limit orders is higher than the minimum asked price from the sell limit orders. This results in a high uncertainty of trade duration. During the continuous trading process, less waiting time means less risk of price drift, which is particularly important for the traders who need to execute a large number of trades while maintaining a basically stable price [1]. Hence, the prediction of trade duration can provide important liquidity information for market participants to make trade decisions. In order to model the duration sequences, researchers most use the autoregressive conditional duration (ACD) model [2], in which the duration is assumed to be the multiplication of conditional mean duration and an error term. Following this work, various studies were conducted to extend the classic ACD model from two perspectives. From one perspective, the researchers in Refs. [3–6] focused on extending the linear equation of conditional mean duration to non-linear cases. From the other perspective, the ACD family models proposed in Refs. [7–11] try to choose a more suitable distribution to characterize the uncertainty of the error term. In 2018, a new ZIACD [12] model based on the zero-inflated negative binomial distribution was proposed to address the problem of excessive zero values.

Recently, financial researchers have paid more and more attention to machine learning methods, which succeed in natural language processing (NLP) and computer vision (CV) tasks. Random forests (RF), support vector regression (SVR), and deep neural networks (DNN) are successively applied to financial prediction tasks [13, 14]. Moreover, long short-term memory (LSTM) networks were deployed for constructing a hedge strategy in the financial market and achieved the highest returns compared with benchmark models, including RF, DNN, and logistic regression classifier (LOG) [15]. Although, the machine learning methods mentioned above can forecast future expectation, in many situations, we need to manage the risk of forecasting values (e.g., the financial volatility, the maximum loss given a probability level) simultaneously, which requires an accurate forecast in conditional duration distribution. Consequently, various studies [16–21] have been conducted to combine the machine learning methods and classic statistical models to realize this target. For instance, Peng et al. [20] used SVR to estimate the mean and the volatility equations of a conventional GARCH model, and the proposed SVR-GARCH model outperformed all the common models from the GARCH family in volatility prediction.

In this study, we extend the ZIACD model to establish a new hybrid model called “DL-ZIACD” for conditional duration distribution, utilizing a specially designed deep learning (DL) network. The established hybrid DL-ZIACD model is applied to nearly all constituent stocks of the Chinese Shenzhen Stock Exchange 100 Index (SZSE 100), and the results show that our DL-ZIACD model is superior to the benchmark models in forecasting conditional duration distribution. The contributions of this paper can be summarized as follows:

(1) We propose a new hybrid zero-inflated duration model by building a deep learning network to forecast the time-varying parameters of conditional duration distribution.

(2) The behavioral difference of large traders and small individual traders is taken into consideration when building the deep learning architecture of our DL-ZIACD model.

(3) The proposed model is applied to a large-scale dataset, and fixed hyper parameters are adopted for all SZSE 100 constituents to reduce the impact of manual tuning.

The remains of this paper are organized as follows: In section Related Work, we review the related work of this paper. Section Methodology provides a detailed description of our proposed DL-ZIACD model. Section Empirical Research applied our proposed model to a large-scale dataset, and section Conclusion concludes this paper.

Related Work

ACD Family Models

In order to estimate the conditional duration, the researchers most use the autoregressive conditional duration (ACD) model proposed by Engle et al. [2]. The classic version of the ACD model can be mathematically described as follows:

$\begin{array}{ll}{y}_i={\mu }_i{\epsilon }_i& (1)\end{array}$

$\begin{array}{ll}{\mu }_i=\omega +{\displaystyle \sum _{j=1}^p}{\alpha }_j{y}_{i-j}+{\displaystyle \sum _{h=1}^q}{\beta }_h{\mu }_{i-h}& (2)\end{array}$

$\begin{array}{ll}{\epsilon }_i~Exp(1)& (3)\end{array}$

In Equation (1), duration y_i is assumed as the multiplication of the expectation μ_i and an error term ε_i. In Equation (2), the expectation μ_i is linearly dependent on the duration of the lagged periods and the lagged terms of itself. p and q in Equation (2) represent orders of the lags, and the model defined by the above formulas can be labeled as ACD (p, q). Besides, exogenous variables can also be added as the independent variables and are represented as the term $\sum _{l=1}^r{\gamma }_l{x}_l$ in Equation (3). In this paper, the ACD (p, q) model with exogenous variables is written as Exv-ACD (p, q) for short.

$\begin{array}{ll}{\mu }_i=\omega +{\displaystyle \sum _{j=1}^p}{\alpha }_j{y}_{i-j}+{\displaystyle \sum _{h=1}^q}{\beta }_h{\mu }_{i-h}+{\displaystyle \sum _{l=1}^r}{\gamma }_l{x}_l& (4)\end{array}$

Based on the work of Engle et al. [2], various studies were proposed to extend the classic ACD model by utilizing non-linear functions to fit the conditional mean equation or choosing more suitable distributions for the error term. Shi et al. [21] has reviewed the two types of extensions based on the classic ACD model in detail. In a recent study, authors in Blasques et al. [12] have utilized the zero-inflated negative binomial distribution [see Equation (5)] to address the excessive zero values of duration y_iand characterize the dynamics of the time-varying location parameter with the general autoregressive score (GAS) model.

$\begin{array}{ll}\begin{array}{c}{y}_i~0withprobability\pi ,\\ y_i~NB({\mu }_i,\alpha )withprobability1-\pi .\end{array}& (5)\end{array}$

Machine Learning Methods Applied to Financial Data

In recent years, more and more researchers have tried to capture the complexity of financial time series data, utilizing machine learning methods. Serjam and Sakurai [22] chose the SVR model to predict the price movement in 1 min and got good results in simulated trading in the currency market. Kumar and Thenmozhi [13] compare the performance of the linear discriminant analysis, logit, artificial neural network, random forestand SVM in terms of predicting the direction of stock index daily movement. Chong et al. [14] systematically analyzed the potential of deep neural networks for stock market prediction at high frequencies and found that the DNN method can extract additional information from the residuals of the autoregressive model, not vice versa. In Fischer and Krauss [15], LSTM networks are employed to financial market predictions in order to recognize temporal information of sequential data more effectively. However, these methods cannot assess the risk of the forecasted values. Therefore, the hybrid models combining machine methods and statistical models are proposed to realize this target while retaining the strong fitting ability.

Hybrid Models

Many hybrid models have been proposed to forecast the future state and assess the corresponding risk simultaneously. In 2003, Perez-Cruz et al. [16] utilized the SVM algorithm to give a better estimation for the parameters of the Generalized Autoregressive Conditional Heteroskedasticity (GARCH) model than the regular maximum likelihood method. In Refs. [17, 18], the output of the GARCH model was added to the input variables of ANN to improve the volatility prediction of three stock exchange indexes and oil price, respectively. Following the work of Refs. [17, 18], Kim and Won [19] used the parameters of the multiple GARCH-type models and other explanatory variables as the input of stacked LSTM layers to reduce prediction errors. In Peng et al. [20], the mean and volatility equations in the GARCH model are extended to the non-linear SVR decision function, and the proposed SVR-GARCH was applied to the high frequency data of three cryptocurrencies and traditional currencies. Inspired by these works, Shi et al. [21] extended the mean equation of the classic ACD model, utilizing LSTM networks to propose the LSTM-ACD model. The architecture of LSTM-ACD with the attention layer added is abbreviated to LSTM-ACD (attention) in this paper. However, the problem of excessive zero values is ignored in the work of Shi et al. [21].

In the ZIACD model proposed by Blasques et al. [12], a zero-inflated negative binomial distribution was chosen to describe the discrete duration with excessive zeros. However, this model required the assumptions that the time-varying location parameter followed the specification of GAS, and other parameters were assumed to be static, which are hard to fulfill in realistic situations. In a research for assisting clinical decision-making, Kabeshova et al. [23] built a deep learning architecture based on zero-inflated mixture of multinomial distributions (ZiMM) to predict long-term and blurry relapses.

In this paper, we also establish a hybrid model based on zero-inflated distribution to forecast conditional duration distribution. Compared with the ZIACD model proposed by Blasques et al. [12], we choose a zero-inflated exponential distribution as the underlying distribution because the research data are recorded with millisecond precision. In addition, the dynamics of the time-varying parameters of the zero-inflated distribution is modeled by the specially designed deep learning (DL) networks, which take the behavioral difference between large investors and small individual investors into consideration.

Methodology

In this section, the process of establishing the DL-ZIACD model is described in two steps. First, we introduce a zero-inflated exponential distribution to address the problem of excessive zero values for the duration with millisecond precision. Second, a specially designed deep learning architecture is proposed to predict the time-varying parameters of the zero-inflated exponential distribution.

Zero-Inflated Exponential Distribution

When researchers analyze the ultrahigh frequency financial data, zero values account for a large proportion in the transaction duration even if the duration is recorded with precision of milliseconds. In the distributions used to describe the error terms of the ACD family models, zero values usually have zero density, and estimations problems may arise correspondingly [12]. Therefore, the zero-inflated negative binomial distribution is utilized in Blasques et al. [12] to characterize the duration with excessive zeros. However, treating the duration with a count distribution is not a proper way if the transaction data are recorded with precision of milliseconds.

In this study, we deal with the duration via zero-inflated exponential distribution, which is a hybrid of one-point distribution and exponential distribution. The following equation [Equations (6, 7)] describe the zero-inflated exponential distribution mathematically:

$\begin{array}{l}{y}_i~0withprobability{p}_i,\\ y_i~E({\lambda }_i)withprobability1-p_i.& (6)\end{array}$

$\begin{array}{l}P\left(y_i|p_i,{\lambda }_i\right)=p_i,y_i=0,\\ f\left(y_i|p_i,{\lambda }_i\right)=(1-p)\lambda e^{-\lambda y_i},y_i>0.& (7)\end{array}$

For convenience, we introduce an indicator variable z_i, defined as

$\begin{array}{ll}{z}_i=\{\begin{array}{cc}0,& y_i>0,\\ 1,& y_i\text{= 0.}\end{array}& (8)\end{array}$

Then the log likelihood function based on the distribution is calculated as follows:

$\begin{array}{ll}l={\displaystyle \sum _{i=1}^n}((1-z_i)log((1-p_i){\lambda }_i{e}^{-{\lambda }_{i}x})+z_{i}log(p_i))& (9)\end{array}$

In this study, λ_i and p_i are both supposed to be time-varying parameters, which are dependent on the historical data. The dependency relationship will be characterized by a specially designed deep learning architecture.

The Proposed DL-ZIACD Model

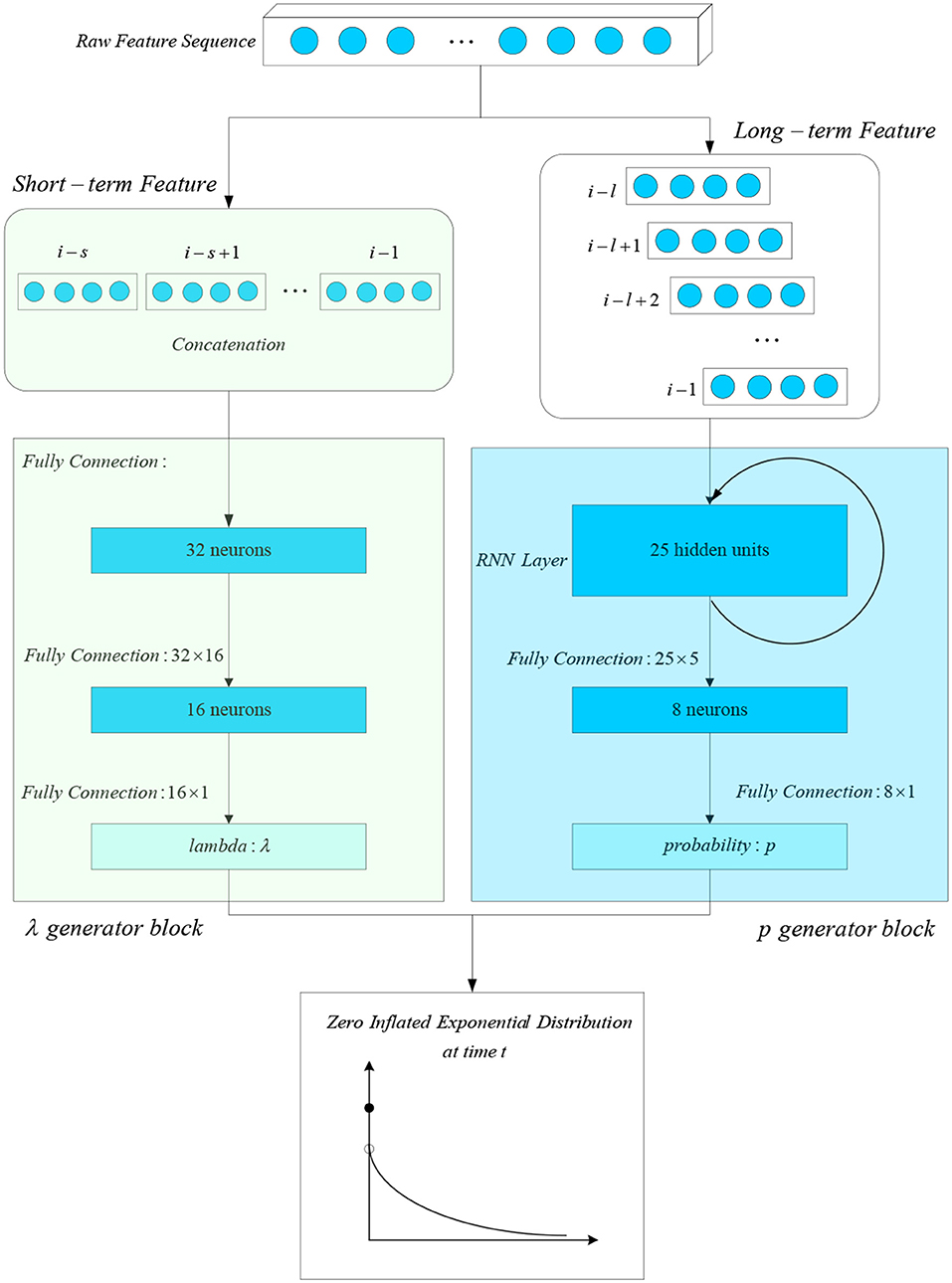
There are two reasons that can explain the presence of excessive zero duration. One reason is that a large-volume trade may be broken into several smaller trades and executed at the same time. The other reason for zero duration is that algorithmic traders, who can react instantly to the arbitrage opportunity by the trading program. The orders with large volume are usually offered by large traders such as institutional traders, and the algorithmic traders can also be viewed as a type of institutional traders. Therefore, the probability of zero duration p_i is highly related to the behavior of the large traders, who can make a decision based on a long sequence of historical data. Besides, a large-volume order means a high risk, which also drives the traders to spend more time on analyzing the historical data. We take these factors into consideration and design a p generator block, consisting of a LSTM layer and a fully connected layer to predict the probability of zero value one step ahead. Contrastingly, the parameter λ_iis more likely decided by the behavioral pattern of small individual traders, who provide the most liquidity for the stock market. Since the small individual traders are much less professional than the large traders, a two-layer fully connected network is utilized to predict the λ_i parameter.

As shown in Figure 1, we feed a long-term feature to the p generator block and a short-term feature to the λ generator block. We denote the raw feature sequence for the ith duration as F_i:{f_j| j = 1, 2, 3, ⋯ , i}, where, the f_j represents the raw feature vector of the jth transaction and consists the variables of volume, duration, price, etc., The long-term feature is sequential data of last l raw feature vectors selected from F_i. At the same time, we concatenate the last s raw feature vectors to get the short-term feature for the λ generator block. Then we can acquire the distribution of the next duration based on the output of the two blocks.

FIGURE 1

Figure 1. Architecture of the DL-ZIACD model.

We train the weights of the λ generator block and the p generator block jointly. The objective function is the negative value of the log likelihood function l, defined in Equation (9). In addition, the last 30% of the available data is selected as the test set. The remaining data are split into the training set and the validation set according to the ratio of 7:3, and we make use of the early stopping method to prevent the overfitting problem. The detailed training process of our DL-ZIACD model is presented in Algorithm 1.

Empirical Research

Data

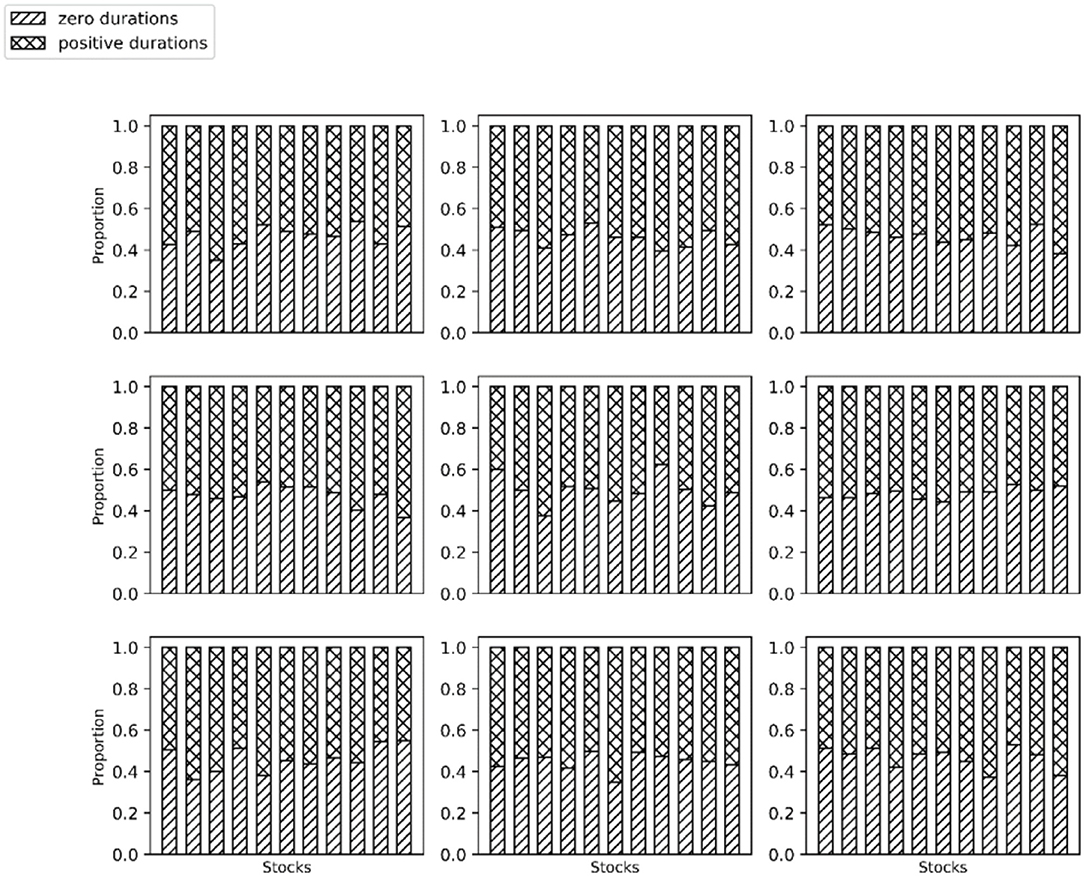
The widely quoted Shenzhen Stock Exchange 100 Index (SZSE 100) is a weighted index of 100 leading companies with large market capitalization and good liquidity in the Chinese Shenzhen Stock Exchange market. The data sample used in our study cover all the constituents of the Shenzhen Stock Exchange 100 Index (SZSE 100) released on December 31st, 2016. For each stock, the first 100,000 transactions executed during the consecutive auction session in 2017 are selected for the experiment, and 30% of the transactions are used as the test set. We exclude the stock of TIANJINZHONGHUAN SEMICONDUCTOR CO., LTD. from the data sample as this stock was suspended for all the year in 2017. Hence, the sample used in this study consists of 99 constituent stocks of SZSE 100 and has a data scale of 9,900,000 transactions. As shown in Figure 2, for most of the stocks studied, the proportion of zero duration exceeds 40%. Therefore, it is theoretically inappropriate to ignore the problem of excessive zero values.

FIGURE 2

Figure 2. The proportion of zero duration and positive duration.

Evaluation Criteria

By training the parameters of the DL-ZIACD model based on Algorithm 1, we can forecast the conditional duration distribution function ${\stackrel{\wedge }{g}}_i$ for each transaction in the future and acquire the quantiles of ${\stackrel{\wedge }{g}}_i$. Being less likely to be affected by the extreme values of right-skewed distributions, the median (50% quantile) is chosen to predict the value of the next trade duration. The prediction performance for the kth stock is measured by mean absolute error (MAE), which can be calculated by Equation (10):

$\begin{array}{ll}MA{E}_k^{duration}=\frac{1}{N}{\displaystyle \sum _{i=1}^N}|{\stackrel{\wedge }{y}}_i-y_i|& (10)\end{array}$

By averaging the MAE of the SZSE 100 constituent stocks, we get the MAE^duration metric:

$\begin{array}{ll}{\overline{MAE}}^{duration}=\frac{1}{99}{\displaystyle \sum _{k=1}^{99}}MA{E}_k^{duration}& (11)\end{array}$

To further measure the agreement between the forecasted distribution ${\stackrel{\wedge }{g}}_i$ and the real distribution g_i, we also evaluate the prediction performance of quantiles at different probability levels generated from ${\stackrel{\wedge }{g}}_i$. The quantile of the i-th trade duration at the upper α level is denoted by Q_{α, i} and defined by the following equation:

$\begin{array}{ll}\alpha =P(y_i<Q_{\alpha ,i})& (12)\end{array}$

Then the violation rates (VR) [11] can be given by

$\begin{array}{ll}\stackrel{\wedge }{\alpha }=\frac{1}{N}{\displaystyle \sum _{i=1}^N}I(y_i>Q_{\alpha ,i})& (13)\end{array}$

where I represents an indicator function, which takes value 1 when duration y_i exceeds the quantile Q_{α, i} and takes value 0 in other cases. We calculate the ratio of $\stackrel{\wedge }{\alpha }$ to α by $R_{\alpha }=\stackrel{\wedge }{\alpha }/\alpha$. The closer R_α is to 1, the better the performance is. As shown in Equation (14), $theMA{E}_{\alpha }^{ratio}$ metric is used to summarize the quantile forecasting performance on the 99 constituents of SZSE 100, where R_{α, k} denotes the $\stackrel{\wedge }{\alpha }/\alpha$ for the kth stock.

$\begin{array}{ll}MA{E}_{\alpha }^{ratio}=\frac{1}{99}{\displaystyle \sum _{k=1}^{99}}|R_{\alpha ,k}-1|& (14)\end{array}$

In addition, the loss function QL defined in Koenker and Bassett [24] to evaluate the performance of quantile regression is also chosen to assess the quantile forecasting performance in this paper. The quantile loss function for each stock can be calculated as follows:

$\begin{array}{ll}Q{L}_{\alpha }={\displaystyle \sum _{i=1}^N}(y_i-Q_{\alpha ,i})\left[(1-\alpha )-I(y_i<Q_{\alpha ,i})\right]& (15)\end{array}$

Similar to the MAE^ratio metric, we also average the QL_α of the SZSE 100 constituent stocks to acquire the ${\overline{QL}}_{\alpha }$, which reflects the overall performance of quantile forecasting.

Performance

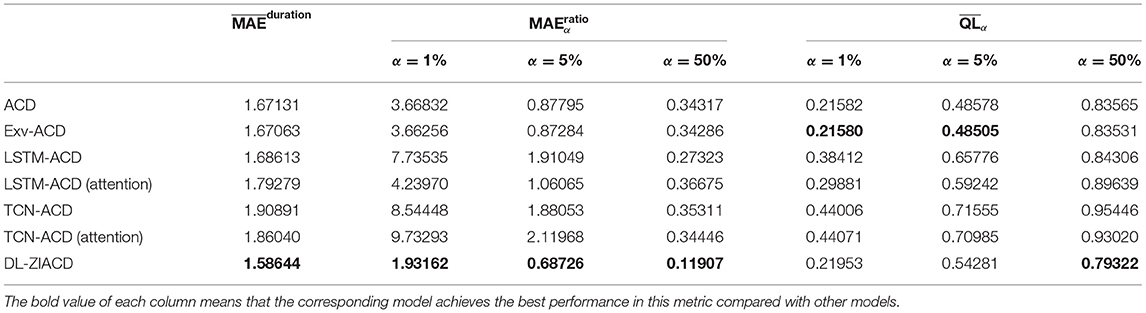
In section Related Work, the ACD, Exv-ACD, LSTM-ACD, and LSTM-ACD (attention) model have been introduced. In this paper, trade volume is specified as the exogenous variable for the Exv-ACD model. In the application of the ACD model and the Exv-ACD model, we choose the best order from (1, 1), (1, 2), (2, 1), and (2, 2) for each stock according to Akaike information criterion (AIC) [26]. As the temporal convolutional network (TCN) [25] architecture has exhibited superiority over the recurrent architectures in many sequence modeling tasks, we can also extend the mean equation of the classic ACD model by TCN architecture to propose a TCN-ACD model. In addition, the attention layer can also be added to the TCN-ACD to establish a TCN-ACD (attention) model. We set a number of filters to 16, dilation to [2, 3, 5, 9], and kernel size to 2. In this paper, the ACD, Exv-ACD, LSTM-ACD, LSTM-ACD (attention), TCN-ACD, TCN-ACD (attention) models are chosen as the benchmark models. The empirical results of the models are summarized in Table 1.

TABLE 1

Table 1. Overall performance of distribution forecasting.

As shown in Table 1, our proposed DL-ZIACD model clearly outperforms all the other models in ${\overline{MAE}}^{duration}$, which exhibits the superiority of the DL-ZIACD model over forecasting the center location of conditional duration distribution. Because ${\overline{MAE}}^{duration}$ is the average value of 99 MAE, we count the number of stocks on which the DL-ZIACD performs best. As can be seen in the following Figure 3, the DL-ZIACD is superior to the other six models on more than 60 of the SZSE 100 constituents, which validates the robustness of DL-ZIACD. The TCN-ACD (attention) model places second and achieves the lowest MAE^duration on 15 stocks.

FIGURE 3

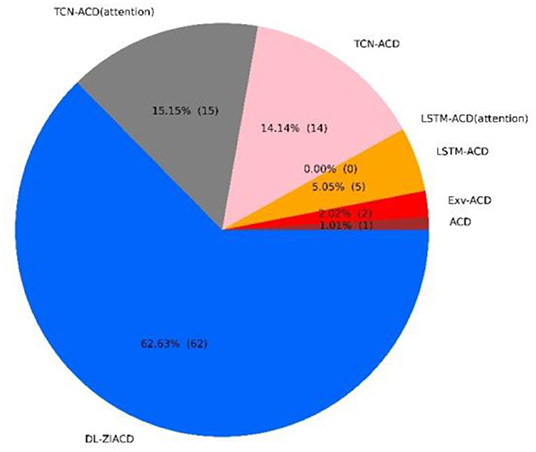
Figure 3. Detailed comparison of the seven models in MAE^duration by a pie chart [the size of each pie slice represents the percentage (number) of stocks on which the corresponding model achieves the lowest MAE^duration].

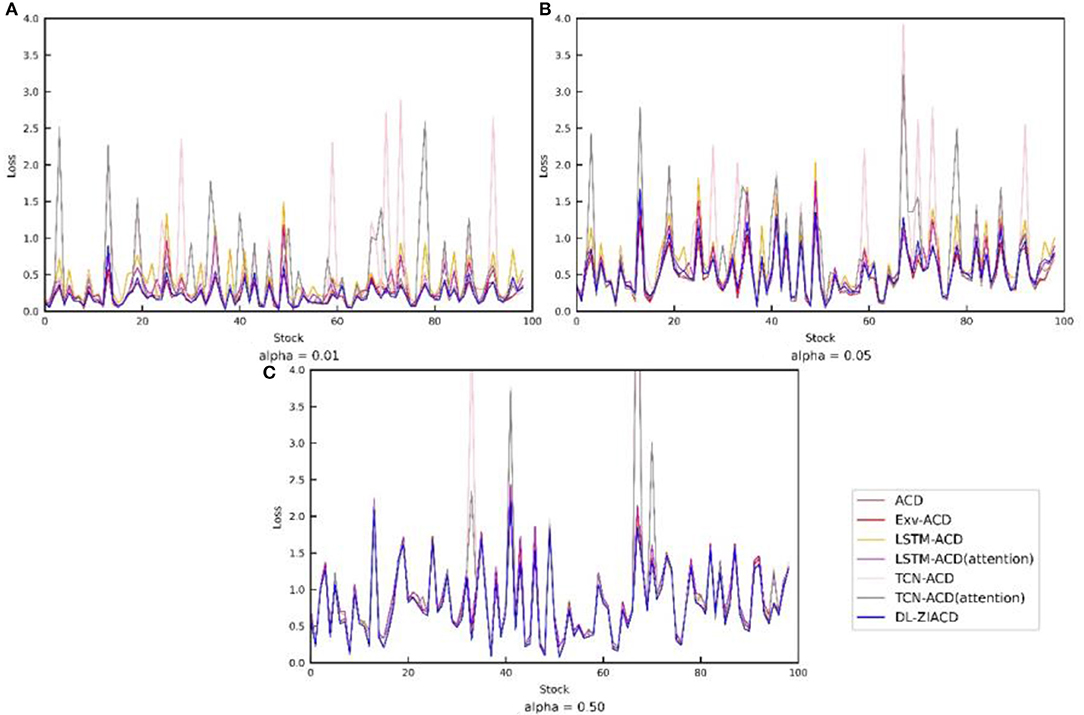
In terms of metric $MA{E}_{\alpha }^{ratio}$, the DL-ZIACD model also exhibits the best performance at all three α levels. From Figure 4, we can see that the R_α lines (blue color) of DL-ZIACD are also apparently closer to the horizontal line at 1 value, compared with other lines in all subfigures. This indicates the excellent and robust performance of our DL-ZIACD model in quantile forecasting.

FIGURE 4

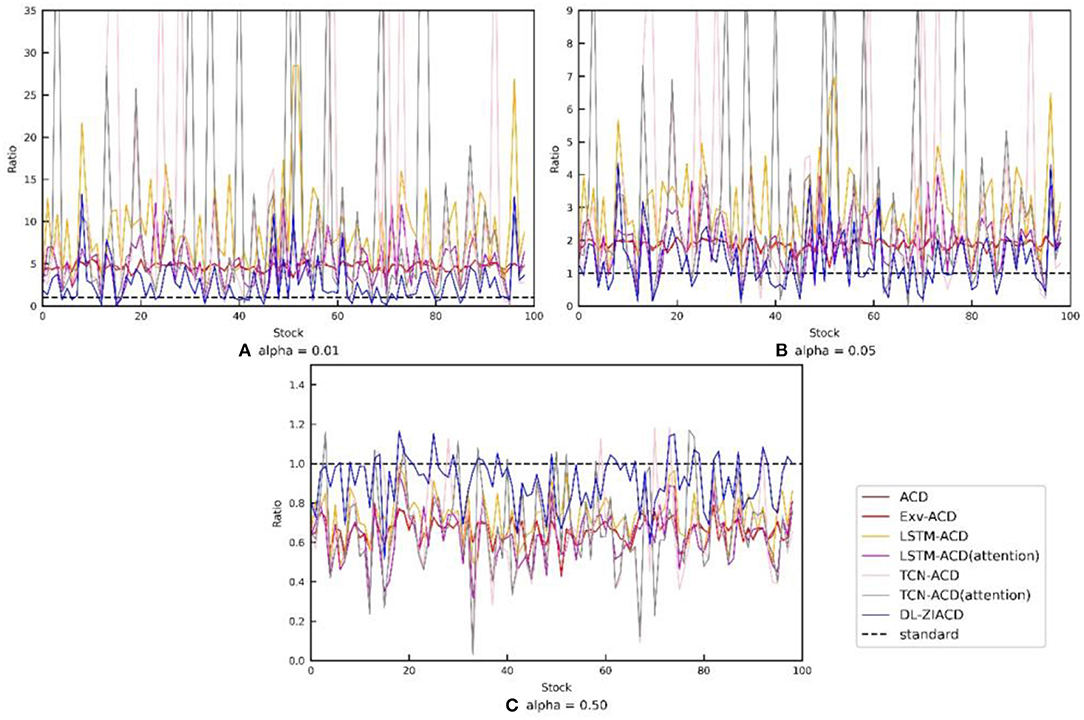
Figure 4. Detailed comparison of the 7 models in $R_{\alpha }=\stackrel{\wedge }{\alpha }/\alpha$ by a line chart. (Each full line is plotted by connecting the R_α value from the corresponding model on each stock, while each black dotted line is a horizontal line at 1 value).

The ${\overline{QL}}_{\alpha }$ is another type of a metric for evaluating quantile forecasting performance. We can see from Table 1 that DL-ZIACD achieves the lowest QL when α = 50%, places third when α = 1%, and when α = 5%. From Figure 5, we can find that DL-ZIACD achieves the lowest QL on more stocks than all the other six models, when α = 1% and 50%. From Figure A1 in the Appendix part, we also find that DL-ZIACD provides a robust quantile forecasting result as no extreme large QLvalues appear in the application of the DL-ZIACD model. Therefore, the DL-ZIACD model can provide accurate forecasts in both central location and extreme quantiles, which validates the agreement between the forecasted conditional duration distribution and the real distribution.

FIGURE 5

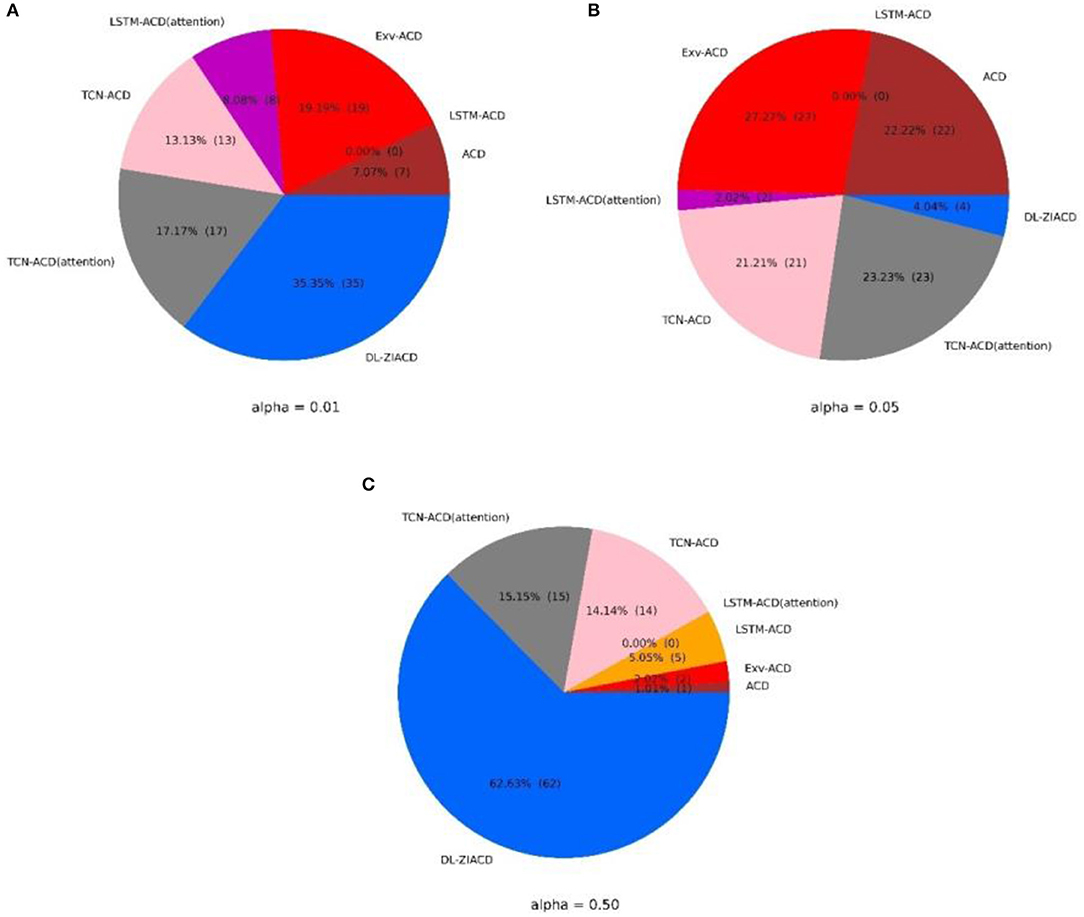
Figure 5. Detailed comparison of the seven models in QL_α by a pie chart [the size of each pie slice represents the percentage (number) of stocks on which the corresponding model achieves the lowest QL_α].

Conclusion

In this paper, a DL-ZIACD model is established to forecast the conditional distribution for financial transaction duration. The problem of excessive zero duration is addressed by the zero-inflated exponential distribution, the time-varying parameters of which are forecasted by a specially designed deep learning architecture that takes the behavioral differences between the large traders and the small individual traders into consideration. The proposed DL-ZIACD model is able to utilize the strong fitting ability of deep learning methods while retaining the ability of providing a probabilistic output.

We apply the DL-ZIACD model, as well as the benchmark models, to a large dataset, including all the constituents of SZSE 100 with a data scale of 9,900,000 transactions. Meanwhile, fixed hyper parameters are chosen for all the stocks to reduce the effect of manual tuning. Empirical results show that the DL-ZIACD model can provide accurate and robust forecasts in both central location and extreme quantiles for the conditional duration distribution. From the perspective of overall performance, the DL-ZIACD achieves the best results in most of the overall metrics (e.g., $MA{E}_{1\%}^{ratio}$). In addition, the DL-ZIACD model outperforms all the benchmark models on most of the constituent stocks in MAE^duration and R_α at all probability levels. That means a high degree of agreement between the forecasted distribution and the real distribution.

The scope of using our DL-ZIACD model is not limited to analyze the financial transaction duration. The proposed DL-ZIACD model can also be utilized to study the inter-times of arriving of queueing system. In this study, the historical data of fixed length are fed to the λ generator block of the deep learning architecture. For future research, it is possible to treat the length of the historical data as a parameter to improve the generalization ability of the model.

Data Availability Statement

Publicly available datasets were analyzed in this study. The datasets analyzed for this study can be purchased from Shanghai Wind Information Co., Ltd. (https://www.wind.com.cn/).

Author Contributions

YS: resources, supervision, and funding acquisition. WD: formal analysis, software, visualization, and writing - original draft. WL: conceptualization, methodology, and writing - review & editing, and validation. All authors have read and agreed to the published version of the manuscript.

Funding

This work was supported by National Natural Science Foundation of China (Nos. 71771204 and 71932008).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

1. Moallemi CC, Yuan K. A Model for Queue Position Valuation in a Limit Order Book. SSRN. (2016) doi: 10.2139/ssrn.2996221

CrossRef Full Text | Google Scholar

2. Engle RF, Russell JR. Autoregressive conditional duration: a new model for irregularly spaced transaction data. Econometrica. (1998) 66:1127–62. doi: 10.2307/2999632

CrossRef Full Text | Google Scholar

3. Bauwens L, Giot P. The logarithmic ACD model: an application to the bid-ask quote process of three NYSE stocks. Ann DÉconomie Stat. (2000) 60:117–49. doi: 10.2307/20076257

CrossRef Full Text | Google Scholar

4. Zhang MY, Russell JR, Tsay RS. A non-linear autoregressive conditional duration model with applications to financial transaction data. J Econom. (2001) 104:179–207. doi: 10.1016/S0304-4076(01)00063-X

CrossRef Full Text | Google Scholar

5. Bauwens L, Giot P. Asymmetric ACD models: introducing price information in ACD models. Empir Econ. (2003) 28:709–31. doi: 10.1007/s00181-003-0155-7

CrossRef Full Text | Google Scholar

6. Meitz M, Teräsvirta T. Evaluating models of autoregressive conditional duration. J Bus Econ Stat. (2006) 24:104–24. doi: 10.1198/073500105000000081

CrossRef Full Text | Google Scholar

7. Lunde A. A Generalized Gamma Autoregressive Conditional Duration Model. ResearchGate. (1999) Available online at: https://www.researchgate.net/publication/228464216 (accessed July 30, 2020).

Google Scholar

8. Hautsch N. The Generalized F ACD Model. Mimeo: University of Konstanz. (2001).

Google Scholar

9. De Luca G, Gallo GM. Mixture processes for financial intradaily durations. Stud Nonlinear Dyn Econom. (2004) 8:1223. doi: 10.2202/1558-3708.1223

CrossRef Full Text | Google Scholar

10. De Luca G, Zuccolotto P. Regime-switching pareto distributions for ACD models. Comput Stat Data Anal. (2006) 51:2179–91. doi: 10.1016/j.csda.2006.08.019

CrossRef Full Text | Google Scholar

11. Yatigammana RP, Chan JSK, Gerlach RH. Forecasting trade durations via ACD models with mixture distributions. Quant Finance. (2019) 19:2051–67. doi: 10.1080/14697688.2019.1618896

CrossRef Full Text | Google Scholar

12. Blasques F, Holý V, Tomanová P. Zero-inflated autoregressive conditional duration model for discrete trade durations with excessive zeros. arXiv [Preprint]. (2018). doi: 10.2139/ssrn.3314218

CrossRef Full Text | Google Scholar

13. Kumar M, Thenmozhi M. Forecasting Stock Index Movement: A Comparison of Support Vector Machines and Random Forest. ResearchGate (2006) Available online at: https://www.researchgate.net/publication/228265807 (accessed November 15, 2020).

Google Scholar

14. Chong E, Han C, Park FC. Deep learning networks for stock market analysis and prediction: methodology, data representations, case studies. Expert Syst Appl. (2017) 83:187–205. doi: 10.1016/j.eswa.2017.04.030

CrossRef Full Text | Google Scholar

15. Fischer T, Krauss C. Deep learning with long short-term memory networks for financial market predictions. Eur J Oper Res. (2018) 270:654–69. doi: 10.1016/j.ejor.2017.11.054

CrossRef Full Text | Google Scholar

16. Pérez-cruz F, Afonso-rodríguez JA, Giner J. Estimating GARCH models using support vector machines. Quant Finance. (2003) 3:163–72. doi: 10.1088/1469-7688/3/3/302

CrossRef Full Text | Google Scholar

17. Kristjanpoller W, Fadic A, Minutolo MC. Volatility forecast using hybrid Neural Network models. Expert Syst Appl. (2014) 41:2437–42. doi: 10.1016/j.eswa.2013.09.043

CrossRef Full Text | Google Scholar

18. Kristjanpoller W, Minutolo MC. Forecasting volatility of oil price using an artificial neural network-GARCH model. Expert Syst Appl. (2016) 65:233–41. doi: 10.1016/j.eswa.2016.08.045

CrossRef Full Text | Google Scholar

19. Kim HY, Won HC. Forecasting the volatility of stock price index: a hybrid model integrating lstm with multiple garch-type models. Expert Syst Appl. (2018) 103:25–37. doi: 10.1016/j.eswa.2018.03.002

CrossRef Full Text | Google Scholar

20. Peng Y, Albuquerque PHM, Camboim de Sá JM, Padula AJA, Montenegro MR. The best of two worlds: forecasting high frequency volatility for cryptocurrencies and traditional currencies with Support Vector Regression. Expert Syst Appl. (2018) 97:177–92. doi: 10.1016/j.eswa.2017.12.004

CrossRef Full Text | Google Scholar

21. Shi Y, Dai W, Long W, Li B. Improved ACD-based financial trade durations prediction leveraging LSTM networks and attention mechanism. Math Prob Eng. (2021) 2021:7854512. doi: 10.1155/2021/7854512

CrossRef Full Text | Google Scholar

22. Serjam C, Sakurai A. Analyzing performance of high frequency currency rates prediction model using linear kernel SVR on historical data. In: Asian Conference on Intelligent Information and Database Systems. Kanazawa: Springer (2017). p. 498–507. doi: 10.1007/978-3-319-54472-4_47

CrossRef Full Text | Google Scholar

23. Kabeshova A, Yu Y, Lukacs B, Bacry E, Gaïffas S. ZiMM: a deep learning model for long term and blurry relapses with non-clinical claims data. J Biomed Inform. (2020) 110:103531. doi: 10.1016/j.jbi.2020.103531

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Koenker R, Bassett G. Regression quantiles. Econometrica. (1978) 46:33–50. doi: 10.2307/1913643

CrossRef Full Text | Google Scholar

25. Bai S, Zico Kolter J, Koltun V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv [Preprint]. (2018).

Google Scholar

26. Akaike H. Information Theory and an Extension of the Maximum Likelihood Principle Budapest. (1998). doi: 10.1007/978-1-4612-1694-0_15

CrossRef Full Text | Google Scholar

Appendix

FIGURE A1

Figure A1. Detailed comparison of the seven models in QL_α by a line chart. (Each full line is plotted by connecting the QL_α value from the corresponding model on each stock).