Study on the Relationship Between Symmetric Property of Optical Orbital Angular Momentum Spectrum and Critical Points of Phase in an Inhomogeneous Non-Random Media

In the aero-optic turbulent boundary layer (TBL), there exist very rich air flow structures that fall into a wide range of scales, with the smallest being roughly of the order of the optical wavelength. However, these fine spatial variations cannot be neglected when one is dealing with light propagation through such structures, since both the amplitude and phase of a light wave undergo modulations. In this study, we studied the influence of TBL on the angular momentum spectrum of light and found that there exists critical point of the azimuthal distribution of the disturbance phase that determines the symmetric properties of the expansion spectrum.

1 Introduction

Allen discovered that Laguerre–Gaussian beams carry orbital angular momentum (OAM) [1], which is associated with their helical wave front. Since then, optical beams with OAM and helical phase structures have garnered increasing research interest. Owing to the infinite number of eigenmodes, beams of this type have found applications in fields such as laser and quantum communications [2–4]. Intense efforts have been put into the measurement of OAM, especially regarding the evolution and the spiral spectrum during light propagation.

For quite a long time, it was believed that there exists a close interconnection between the spiral spectrum and phase vortex structures. However, Charnotskii’s recent research showed that such a connection does not exist [5]. A tricky scenario is propagation in inhomogeneous media. Even if the incident wave consists of only one eigenmode, its spiral spectrum can spread during propagation [6–8], a phenomenon called cross-talk. Light with OAM propagating through inhomogeneous media is an important topic that is employed across many applications.

V. P. Aksenov and Ch. E. Pogutsa gave the mathematical form of the total OAM of a propagating light field, from which they were able to prove that the total OAM for homogeneous media is conserved, while it can change for inhomogeneous media [9]. Such a change is closely related to the spatial distribution of the refractive index (RI).

According to the traditional turbulence theory, provided the fluid is far away from the boundary and has a very high Reynolds number, the physical parameters of the turbulence can be treated as random fields. The properties of turbulence can be described through the statistical moment of fluid parameters [10]. Consequently, by introducing statistical theory and assuming the media to be statistically homogeneous, it is deduced that the ensemble average of total OAM is conserved [5, 9], while the spiral spectrum demonstrates a symmetric distribution with respect to the original [6–8]. Darryl J. Sanchez and Denis W. Oesch tentatively discussed the physical mechanism of the phenomenon: the kinetic energy of free turbulence dissipates as heat, which makes the spatial distribution of RI in turbulence inhomogeneous. According to the cascade theory of turbulence, the RI distribution is statistically homogeneous, so that photons carrying the new OAM must appear in pairs [11].

With the development of fluid mechanics and the progress of numerical techniques, researchers now have a new understanding of fluid motion, especially for fluids close to a definite solid boundary, for example, the turbulence around an airborne plane. Such regions are called the turbulent boundary layer (TBL). E. Jumper [12] pointed out that the power spectrum model cannot be used to describe the characteristics of turbulence in TBL because the model has definite structural properties [13, 14] and is not completely random. Research in this field has evolved to become the so-called aero-optics [15]. The properties of the total OAM and spiral spectrum distribution in TBL are our main focus in this study. In our task, the transmission medium was deterministic and inhomogeneous. Charnotskii calculated the total OAM in turbulence, and his result showed that $\langle L_z^2\rangle \ne 0$. This implies that for a single realization of turbulence, the total OAM usually varies. Lingfei Xu [16] calculated the total OAM and the spiral spectrum of OAM modes in a typical TBL by numerical methods and found that the instantaneous total OAM is not conserved and the spiral spectrum of OAM spreads in an asymmetric way. These behaviors are related to the typical structure of RI distribution in TBL.

Although numerical methods can present the evolution characteristics of OAM, it is still challenging to discuss the connection between OAM and the RI spatial distribution. The lack of an analytic form of the spatial structure makes it difficult to study the evolution mechanism. In this study, we do not rely on the concrete form and try to analyze the problem analytically. Hence, our idea is to obtain the asymptotic form of the spiral spectrum of OAM modes. Tow case is concerned: the fluctuation of refractive index is weak or much stronger. By such a mathematical method, we found that the symmetry of the spiral spectrum depends on the distribution of critical points in the scattered light’s phase. Based on such mathematical results, we discuss the mechanism of the influence and propose a method for analyzing the spiral spectrum spread. Our main aim was to analyze the asymptotic behavior of the spiral spectrum.

2 Asymptotic Behavior of the Scattered Light’s Spiral Spectrum

The complex amplitude of light propagating in the turbulent boundary layer can be obtained by the Rytov approximation:

$U\left(\mathbf{s}\right)=U_0\left(\mathbf{s}\right)\exp \left[\text{Ψ}\left(\mathbf{s}\right)\right],(1)$

where $\mathbf{s}=\left(\rho ,\theta \right)$, $U_0\left(\mathbf{s}\right)$ denotes the diffracted complex amplitude, and $\text{Ψ}\left(\mathbf{s}\right)$ denotes the Rytov disturbance. In general, the Rytov disturbance can be written as follows:

$\exp \left[\text{Ψ}\left(\rho ,\theta \right)\right]=\sqrt{T\left(\rho ,\theta \right)}\exp \left[ikP\left(\rho ,\theta \right)\right],(2)$

where $k=2\pi /\lambda$ is the wavenumber of light. $T\left(\rho ,\theta \right)$ and $P\left(\rho ,\theta \right)$ denote the disturbance on the amplitude and phase, respectively, and the coefficient for each spiral spectrum of OAM modes is given by the following equation: [16]

$C_{\text{Δ}l}={{\displaystyle \int }}^{\text{}}\rho \left|R_l\left(\rho ,z\right){|}^{2}d\rho \right|{{{\displaystyle \int }}^{\text{}}}_0^{2\pi }\exp \left[\text{Ψ}\left(\rho ,\theta \right)\right]\exp \left(i\text{Δ}l\theta \right)d\theta {|}^2,(3)$

where we write the complex amplitude of LG beam as follows: $U_{LG}\left(\rho ,\theta ,z\right)=R_l\left(\rho ,z\right)\text{exp}\left(il\theta \right)$. $\text{Δ}l$ denotes the difference between the spiral spectrum of OAM modes and initial beam’s OAM mode. In order to analyze the asymptotic of Eq. 3, we divide the analysis into two cases: 1), the disturbance phase that is much small; and2) the disturbance phase that is very large.

2.1 Asymptotic Behavior of C_Δl for $\mathit{P}\to 0$

In the weak fluctuating turbulence, the disturbance on the amplitude of beam can be ignored since the turbulent energy at high spatial frequency is really small. So, $T\left(\mathbf{s}\right)$ can be approximately equal to 1. $P\left(\mathbf{s},z^{\prime }\right)$ is also small, hence it will be a good approximation if the Rytov complex disturbance is written as follows:

$\exp \left[ikP\left(\mathbf{s}\right)\right]\approx =1+ikP\left(\mathbf{s}\right),(4)$

substituting Eq. 4 into Eq.3, we can obtain

$C_{\text{Δ}l}={{\displaystyle \int }}^{\text{}}\rho \left|R_l\left(\rho ,z\right){|}^{2}d\rho \right|2\pi \delta \left(\text{Δ}l\right)+ik{{{\displaystyle \int }}^{\text{}}}_0^{2\pi }P\left(\rho ,\theta \right)\text{exp}\left(i\text{Δ}l\theta \right)d\theta {|}^2,(5)$

where $\delta (\cdot )$ is the Dirac function. Because $P\left(\rho ,\theta \right)$ is a real function, from Eq.5, the following conclusion can be immediately obtained: $C_{\text{Δ}l}=C_{-\text{Δ}l}$.

2.2 Asymptotic Behavior for Large P

In this case, the distribution properties of the spiral spectrum are much more complex. It is difficult to analyze and examine the symmetry of the spiral spectrum distribution since the mathematical form of P is hardly obtained in the turbulence boundary layer. Hence, instead of obtaining the precise solution of Eq.3, we tend to discuss the spiral spectrum of OAM modes based on the asymptotic form obtained from Eq. 3. The key point is to discuss the asymptotic behavior of the integral:

$I={{{\displaystyle \int }}^{\text{}}}_0^{2\pi }\text{exp}\left(i\text{Δ}l\theta \right)\sqrt{T\left(\rho ,\theta \right)}{e}^{ikP\left(\rho ,\theta \right)}d\theta .(6)$

We can use the stationary phase method [17]. By using the stationary phase, we can obtain

$I\approx {\left(\frac{2\pi }{k}\right)}^{\frac{1}{2}}{\displaystyle \sum }_j\frac{{\mathit{ϵ}}_j\sqrt{T\left(\rho ,{\theta }_j\right)}}{\sqrt{|{\partial }^{2}P/\partial {\theta }^2{|}_{\theta ={\theta }_j}}}\text{exp}\left(i\text{Δ}l{\theta }_j\right)e^{ikP\left(\rho ,{\theta }_j\right)},(7)$

where ${\mathit{ϵ}}_j=e^{\pm i\frac{\pi }{4}}$, the symbol depends on $\frac{{\partial }^{2}P}{\partial {\theta }^2}{|}_{\theta ={\theta }_j}\mathrm{\gtrless }0$. ${\theta }_j$ is the critical point of the first kind: $\frac{\partial P}{\partial \theta }=0$. Here, we used the fact that $\frac{\partial P}{\partial \theta }{|}_{\theta =0}=\frac{\partial P}{\partial \theta }{|}_{\theta =2\pi }$ and $\text{exp}\left(i\text{Δ}l\times 0\right)=\text{exp}\left(i\text{Δ}l\times 2\pi \right)$. Thus, the contributions from the critical point of the second kind ($\theta =0$ and $\theta =2\pi$) is zero. Hence, there is

$\begin{array}{c}|I{|}^2=\frac{2\pi }{k}{\displaystyle \sum }_j\frac{T\left(\rho ,{\theta }_j\right)}{\left|{P^{″}}_j\right|}+\frac{2\pi }{k}{\displaystyle \sum }_n{\displaystyle \sum }_{m^{\prime }>n}\frac{2\sqrt{T\left(\rho ,{\theta }_n\right)}\sqrt{T\left(\rho ,{\theta }_{m^{\prime }}\right)}}{\sqrt{\left|{P^{″}}_{m^{\prime }}\right|\left|{P^{″}}_n\right|}}\left\{\text{cos}[\text{Δ}l\left({\theta }_{m^{\prime }}-{\theta }_n\right)+\hspace{0.17em}k\left(P_{m^{\prime }}-P_n\right)]\right\}\\ +\frac{2\pi }{k}{\displaystyle \sum }_n{\displaystyle \sum }_{m^{\prime \prime }>n}\frac{2\sqrt{T\left(\rho ,{\theta }_n\right)}\sqrt{T\left(\rho ,{\theta }_{m^{″}}\right)}}{\sqrt{\left|{P^{″}}_{m^{″}}\right|\left|{P^{″}}_n\right|}}\left\{\text{sin}[\text{Δ}l\left({\theta }_{m^{″}}-{\theta }_n\right)+k\left(P_{m^{″}}-P_n\right)]\right\},\end{array}(8)$

where ${P^{″}}_{m^{\prime }}=\frac{{\partial }^{2}P}{\partial {\theta }^2}{|}_{\theta ={\theta }_{m\prime }}$ and $P_{m^{\prime }}=P\left(\rho ,{\theta }_{m^{\prime }}\right)$. $\left\{m^{\prime }\right\}$ are the subscripts of such critical points of the first kind whose ${P^{″}}_{m^{\prime }}\cdot {P^{″}}_n>0$ and $\left\{m^{\prime }\right\}$ are the subscripts of the critical points of the first kind whose ${P^{″}}_{m^{″}}\cdot {P^{″}}_n<0$.

We will discuss about the case wherein the number of the first kind critical points is two or more. Equation 8 indicates that, in general, the spiral spectrum of the OAM modes is asymmetric. It will be symmetric if the terms of $\text{sin}\left[\text{Δ}l\left({\theta }_i-{\theta }_j\right)\right]$ in Eq. 8 vanish, for example, (i), the azimuthal difference between each of the two critical points of first kind is $n\pi$, where $n=0,\text{or }1$; or,(ii) the phase difference between each of the two first kind critical points is equal to $n\pi$ for ${P^{″}}_{m^{\prime }}\cdot {P^{″}}_n>0$ and $\frac{2n+1}{2}\pi$ for ${P^{″}}_{m^{\prime }}\cdot {P^{″}}_n<0$.

Equation 8 gives us a way to analyze the symmetric properties of the scattered light’s spiral spectrum. If the scale of coherent structures in the turbulent boundary layer is much larger than the wavelength of light, the disturbance on the phase is approximately equal to the integral of the refractive index difference: $P\left(\mathbf{s}\right)\approx {{{\displaystyle \int }}^{\text{}}}_0^L\text{Δ}n\left(\mathbf{s},z^{\prime }\right)d{z}^{\prime }$, where $\text{Δ}n\left(\mathbf{s},z^{\prime }\right)$ denotes the difference between the RI in the turbulent boundary and in the free space. $T\left(\mathbf{s}\right)$ can be treated as 1 approximately. Then, by Eq. 8, the symmetric properties can be analyzed by examining the critical points of RI distribution even when the exact scattered complex amplitude is not solved.

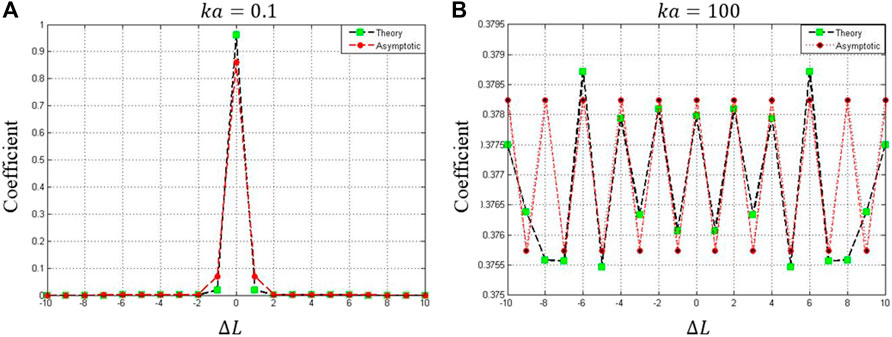
3 Verification With a Well-Known Case: Phase Tilt

The influence on the light’s OAM and the spiral spectrum of OAM modes is widely studied in the case in which the phase is tilted. The conclusion is well known: the spiral spectrum of OAM modes is expanded in a symmetric way. Here, we assume that the additional phase is tilted along with one direction, said, $\text{exp}\left(ikax\right)$, where, a is the tilt degree. Hence, the spiral spectrum of OAM modes is given by the following equation:

$C_{\text{Δ}l}={{\displaystyle \int }}^{\text{}}\rho \left|R_l\left(\rho \right){|}^{2}d\rho \right|{{{\displaystyle \int }}^{\text{}}}_0^{2\pi }\text{exp}\left[ika\rho \text{cos}\left(\theta \right)\right]\text{exp}\left(i\text{Δ}l\theta \right)d\theta {|}^2=4{\pi }^2{{\displaystyle \int }}^{\text{}}\rho \left|R_l\left(\rho \right){|}^2\right|J_{\text{Δ}l}\left(ka\rho \right){|}^{2}d\rho ,(9)$

where $J_{\text{Δ}l}(\cdot )$ is the $\text{Δ}l$-th order Bessel function. Equation 9 shows that the spiral spectrum of OAM modes is symmetric with the help of $J_{\text{Δ}l}(\cdot )={\left(-1\right)}^{\text{Δ}l}{J}_{-\text{Δ}l}(\cdot )$. The symptomatic behavior of Bessel function is given by the following equation:

$J_p\left(z\right)\sim \frac{{\left(z/2\right)}^p}{p!},z\to 0^{+},(10)$

$J_p\left(z\right)\sim \sqrt{\frac{2}{\pi z}}\text{cos}[z-\left(p+\frac{1}{2}\right)\frac{\pi }{2}],\left|z\right|\gg 1.(11)$

Substituting Eq. 10 and Eq. 11 into Eq. 9, the symptomatic behavior of spiral spectrum can be obtained as follows:

$C_{\text{Δ}l}\approx 4{\pi }^2{{\displaystyle \int }}^{\text{}}\rho |R\left(\rho \right){|}^2\frac{{\left(ka\rho \right)}^{2\left|\text{Δ}l\right|}}{4^{\left|\text{Δ}l\right|}\left|\text{Δ}l\right|!}d\rho ,\text{for small }a(12)$

$\begin{array}{c}{C}_{\text{Δ}l}=\frac{8\pi }{ka}{{\displaystyle \int }}^{\text{}}|R_l\left(\rho \right){|}^2{\text{cos}}^2[ka\rho -\left(\text{Δ}l+\frac{1}{2}\right)\frac{\pi }{2}]d\rho \\ =\frac{4\pi }{ka}{{\displaystyle \int }}^{\text{}}|R_l\left(\rho \right){|}^2{[\text{cos}\left(ka\rho \right)+{\left(-1\right)}^{\text{Δ}l}\text{sin}\left(ka\rho \right)]}^{2}d\rho ,\text{for large }a.\end{array}(13)$

Equations 12, 13 give the asymptotic behavior of spiral spectrum from its exact mathematical form (Eq. 9). Now, we will examine the asymptotic behavior of the spiral spectrum from Eq.5 to Eq. 8. By Eq.5, for a small a,

$\begin{array}{c}{C}_{\text{Δ}l}=4{\pi }^2\delta \left(\text{Δ}l\right){{\displaystyle \int }}^{\text{}}\rho |R\left(\rho \right){|}^{2}d\rho +k^2{a}^2{{\displaystyle \int }}^{\text{}}{\rho }^3|R\left(\rho \right){|}^{2}d\rho {{{\displaystyle \int }}^{\text{}}}_0^{2\pi }\text{cos}\left(\theta \right)\text{exp}\left(i\text{Δ}l\theta \right)d\theta \\ =4{\pi }^2\delta \left(\text{Δ}l\right){{\displaystyle \int }}^{\text{}}\rho |R\left(\rho \right){|}^{2}d\rho +\hspace{0.17em}{k}^2{a}^2{\pi }^2\delta \left(\left|\text{Δ}l\right|-1\right){{\displaystyle \int }}^{\text{}}{\rho }^3|R\left(\rho \right){|}^{2}d\rho .\end{array}(14)$

Equation 14 shows the following:

$\begin{array}{l}{C}_0=4{\pi }^2\delta \left(\text{Δ}l\right){{\displaystyle \int }}^{\text{}}\rho |R\left(\rho \right){|}^{2}d\rho \\ C_{\pm 1}=k^2{a}^2{\pi }^2{{\displaystyle \int }}^{\text{}}{\rho }^3|R\left(\rho \right){|}^{2}d\rho ,\end{array}(15)$

which coincides with Eq. 12 when $\text{Δ}l=0,\text{or},\pm 1$. $C_{\text{Δ}l}$ is extremely small for a large value of $\text{Δ}l$, and we can say that two kinds of asymptomatic behavior are same in the case of small a.For a large a, according to the method of the stationary phase, we have to calculate critical point of the first kind of $P=a\rho \text{cos}\left(\theta \right)$. It is extremely easy to find two critical points ${\theta }_1=0$ and ${\theta }_2=\pi$. Additionally, $P_1=a\rho$, $P_2=-a\rho$, $P^{″}1=-a\rho ,$ and $P^{″}2=a\rho$. Substituting into Eq. 8, we get the following:

$|I{|}^2=\frac{4\pi }{ka\rho }[1+2{\left(-1\right)}^{\text{Δ}l}\text{sin}\left(2ka\rho \right)]=\frac{4\pi }{ka\rho }{[\text{cos}\left(ka\rho \right)+{\left(-1\right)}^{\text{Δ}l}\text{sin}\left(ka\rho \right)]}^2,(16)$

therefore, the coefficient of the spiral spectrum is given as follows:

$C_{\text{Δ}l}=\frac{4\pi }{ka}{{\displaystyle \int }}^{\text{}}|R\left(\rho \right){|}^2{[\text{cos}\left(ka\rho \right)+{\left(-1\right)}^{\text{Δ}l}\text{sin}\left(ka\rho \right)]}^{2}d\rho ,(17)$

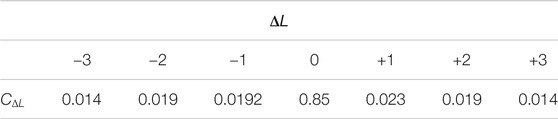
which also coincides with Eq. 13. We also give the comparisons between the theoretical results of Eq. 9 and the asymptomatic results, (Figure 1). By comparison between the asymptomatic results and the numerical simulation result, it can be found that the asymptomatic method can describe the behavior of the spiral spectrum with a minor error, which is about $3\text{\%}$. For the small $\text{Δ}L$, the errors will be smaller.

FIGURE 1

FIGURE 1. The spiral spectrum of OAM mode for phase tilt. $ka=0.1$ for (A) and $ka=100$ for for (B).

4 Symmetric Property of Spiral Spectrum in Some Simple Structured Media

Vortex is the basic structures in the turbulence. The refractive index of a vortex flow field can be treated as a Gaussion distribution. In order to avoid solving Navier–Stokes equations, we prefer to use such a simple vortex structure to discuss the symmetric property of the spiral spectrum by the method proposed in Section 2. According to Section 2.1, if the disturbance phase is small, the spiral spectrum of the scattered light is always symmetric. Hence, in this section, the symmetric property of light with strong phase disturbance is discussed. Moreover, the disturbance on the amplitude is ignored, assuming that the scale of vortex is much larger than that of the wavelength. Of course, it is immediately obtained by Eq. 3 that if the vortex flow field is on axis, the spiral spectrum will not expand at all. Hence, we choose a single vortex structure, the center of which is off-axis. The disturbance phase P can be written as follows:

$P\left(\rho ,\theta \right)=ka\exp [-{\rho }^2-{\rho }_0^2+2\rho {\rho }_0\cos \theta ].(18)$

The critical points of the first kind of Eq. 18 are ${\theta }_1=0$ and ${\theta }_2=\pi$. Thus, the spiral spectrum of the OAM modes is, of course, symmetric. The normalized RI distribution and spiral spectrum are shown in Figure 2; Table 1 gives the numerical results for $C_{\text{Δ}L}$ from $-3$ to $+3$. An interesting example is given by two off-axis vortex structures. The phase disturbance can be written as follows:

$P\left(\rho ,\theta \right)=ka\exp [-{\rho }^2-{\rho }_0^2+2\rho {\rho }_0\cos \theta ]+ka\exp [-{\rho }^2-{\rho }_0^2-2\rho {\rho }_0\cos \theta ].(19)$

Such structures are composed by two off-axis Gaussian vortex structure. The center of one vortex is at $x=1$ and another is at $x=-1$. The phase distribution is shown as Figure 3. Following the proposed method in Section 2.2, the critical point of such distribution can be obtained as: ${\theta }_1=0$, ${\theta }_2=\pi$, ${\theta }_3=\pi /2$, and ${\theta }_4=3\pi /2$. There are four critical points. Calculating P and $P^{\mathrm{″}}$ for each critical point, we have the following:

$\begin{array}{l}{P}_1=P_2=ka\exp [-{\left(\rho -{\rho }_0\right)}^2]+ka\exp [-{\left(\rho +{\rho }_0\right)}^2],\\ P_3=P_4=2ka\exp \left(-{\rho }^2-{\rho }_0^2\right),\\ P_1^{″}=P_2^{″}=ka\exp \left(-{\rho }^2-{\rho }_0^2\right)[\text{exp}\left(-2\rho {\rho }_0\right)-\text{exp}\left(2\rho {\rho }_0\right)]<0,\\ P_3^{″}=P_4^{″}=4ka{\rho }^2{\rho }_0^2\exp \left(-{\rho }^2-{\rho }_0^2\right)>0.\end{array}(20)$

Hence, the asymptotic behavior of Eq. 6 is as follows:

$\begin{array}{c}I=A_1{e}^{-i\frac{\pi }{4}}{e}^{i{P}_1}[1+{\left(-1\right)}^{\text{Δ}l}]+A_3{i}^{\text{Δ}l}{e}^{i\frac{\pi }{4}}{e}^{i{P}_3}[1+{\left(-1\right)}^{\text{Δ}l}]\\ =[1+{\left(-1\right)}^{\text{Δ}l}]\left(A_1{e}^{-i\frac{\pi }{4}}{e}^{i{P}_1}+A_3{i}^{\text{Δ}l}{e}^{i\frac{\pi }{4}}{e}^{i{P}_3}\right),\end{array}(21)$

where $A_1={\left(\frac{2\pi }{k{P}_1^{″}}\right)}^{\frac{1}{2}}$ and $A_3={\left(\frac{2\pi }{k{P}_3^{″}}\right)}^{\frac{1}{2}}$. From Eq. 21, the distribution of the spiral spectrum of the OAM modes is symmetric. Equation 21 also demonstrates that if $\text{Δ}l$ is odd, $C_m$ will be vanished at $m=l\pm \text{Δ}l$. The spiral spectrum can be directly calculated by Eq. 3, shown as Figure 4; Table 2 gives the precise numerical results. It expands in a symmetric way and vanished at the position where $\text{Δ}l$ is odd. Such conclusions coincide with those obtained by the proposed method in Section 2.2. So far, we can conclude that the symmetric property is related to the critical point of the phase distribution. In order to make this conclusion more credible, a special phase is constructed according to the rule of symmetry affected by the critical point proposed in Section 2.2:

$P\left(x,y\right)=ka\left(-\frac{1}{2}xy-\frac{1}{2}x\sqrt{x^2+y^2}+x^2+y^2\right).(22)$

The critical points can be calculated at ${\theta }_1=\pi /6$, ${\theta }_2=5\pi /6$, and ${\theta }_3=3\pi /2$. After tedious calculation, we obtain the following:

$\begin{array}{c}|I{|}^2=\frac{1+2\sqrt{3}}{{\rho }^2}+\frac{\sqrt{2}}{{\rho }^2}\text{sin}\left(\frac{2\pi }{3}\text{Δ}l+\frac{3\sqrt{3}}{4}{\rho }^2\right)+\frac{\sqrt{\sqrt{3}-1}}{{\rho }^2}\text{cos}\left(\frac{4\pi }{3}\text{Δ}l+\frac{3\sqrt{3}}{8}{\rho }^2\right)\\ -\frac{\sqrt{\sqrt{3}+1}}{{\rho }^2}\text{sin}\left(\frac{2\pi }{3}\text{Δ}l-\frac{3\sqrt{3}}{8}{\rho }^2\right).\end{array}(23)$

Under the integral for ρ, as shown in Eq.3, the $\text{sin}$ terms will not vanish in general. Thus, the spiral spectrum appears asymmetric. The phase distribution and spiral spectrum calculated by Eq. 3 are shown in Figure 5; Table 3.

FIGURE 2

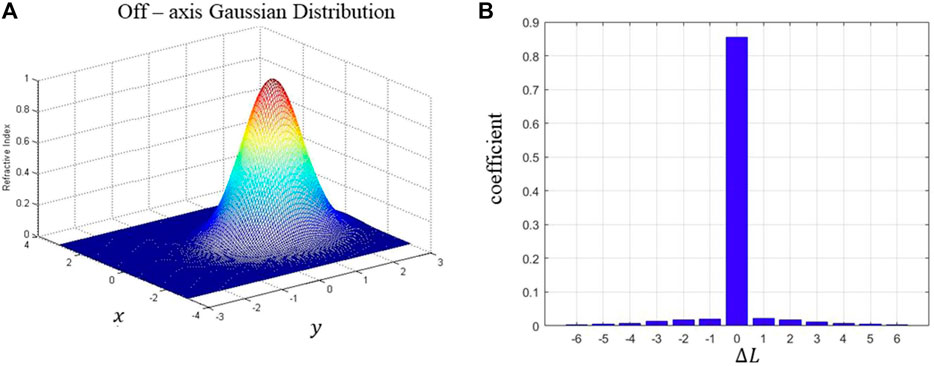
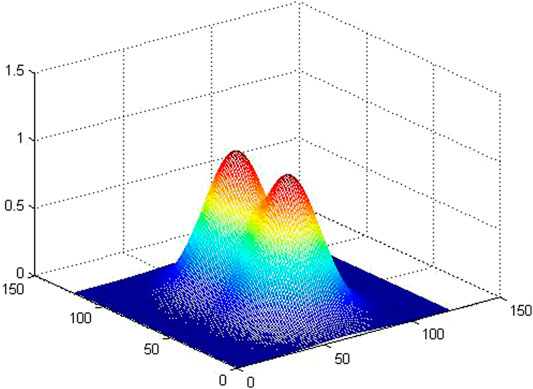
FIGURE 2. The spiral spectrum of OAM mode for the single Gaussion distribution.(A) The given phase distribution with ${\rho }_0=1$. (B) The spiral spectrum distribution calculated by Eq. 3.

TABLE 1

TABLE 1. Coefficients of spiral spectrum modes for single Gaussion vortex structure.

FIGURE 3

FIGURE 3. Two off-axis Gaussian vortex structures.

FIGURE 4

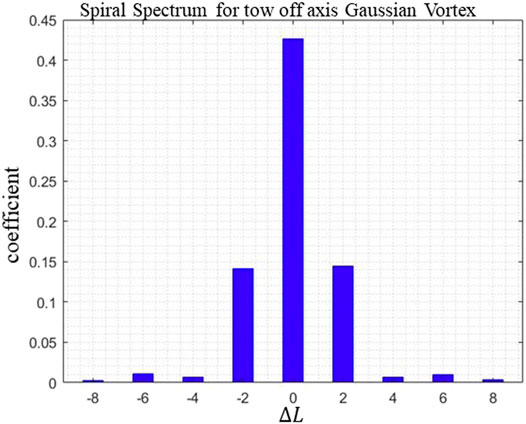
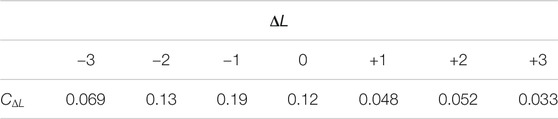
FIGURE 4. The spiral spectrum of light propagating through two off-axis Gaussian vortex structures, calculated by Eq. 3.

TABLE 2

TABLE 2. Coefficients of spiral spectrum modes for two off-axis Gaussian vortex structures.

FIGURE 5

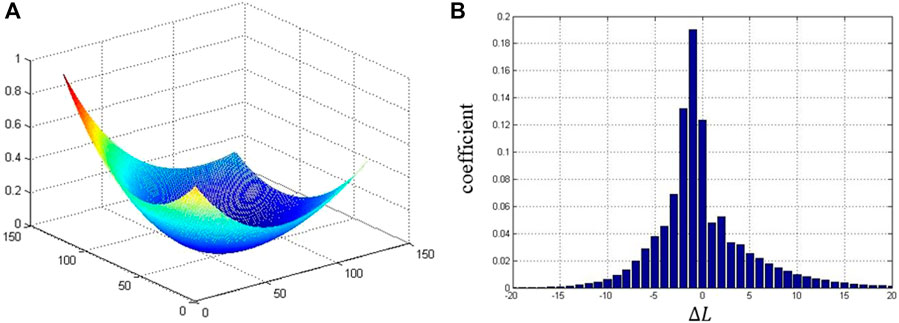
FIGURE 5. The case of asymmetric spiral spectrum of light. (A) The phase distribution and (B) The spiral spectrum calculated by Eq. 3.

TABLE 3

TABLE 3. Coefficients of spiral spectrum modes for an astigmatism phase.

The critical point distribution makes the spiral spectrum asymmetric. In this case, such critical point distribution is mainly affected by the term $xy$, which is known as astigmatism.

5 Conclusion

We studied the symmetric property of light’s spiral spectrum propagating through a non-random inhomogeneous media. Without losing the generality, instead of using the calculated phase aberration, we treated the unknown continuous distribution function of phase disturbance in a formal way. Through asymptotic methods, we found that there exists a critical point that determines the symmetric property of the spiral spectrum. The position and refractive index, along with its second derivative, determine the spectrum distribution.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author Contributions

LX conceived the research and derived equations about the asymptotic form; JH and ZZ wrote the computational codes, computed the numerical results, and made the figure plots; TR organized the article; and the four authors wrote the article.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank Cunfeng Gu in our department for their helpful discussions.

References

1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (1992) 45:8185–9. doi:10.1103/physreva.45.8185

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Gibson G, Courtial J, Padgett MJ, Vasnetsov M, Pas'ko V, Barnett SM, et al. Free-space information transfer using light beams carrying orbital angular momentum. Opt Express (2004) 22:5448–56. doi:10.1364/opex.12.005448

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Majumdar A, Riclkin JC. Free-space laser communications: principles and advances. Berlin, Germany: Springer (2007).

4. Wang JY, Yang IM, Fazal NA, Yan Y, Huang H, Ren Y, et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat Photon (2012) 6:488–96. doi:10.1038/nphoton.2012.138

CrossRef Full Text | Google Scholar

5. Charnotskii M. Transverse linear and orbital angular momenta of beam waves and propagation in random media. J Opt (2017) 20:025602. doi:10.1088/2040-8986/aa9f50

CrossRef Full Text | Google Scholar

6. Cheng M, Guo L, Li J, Huang Q, Cheng Q. Propagation of an optical vortex carried by a partially coherent Laguerre-Gaussian beam in turbulent ocean. Appl Opt (2016) 55:4642–8. doi:10.1364/ao.55.004642

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Yan X, Zhang PF, Zhang JH, Chun HQ, Fan CY. Decoherence of orbital angular momentum tangled photons in non-kolmogorov turbulence. J Opt Soc Am A (2016) 33:1831–5. doi:10.1364/josaa.33.001831

CrossRef Full Text | Google Scholar

8. Chen C, Yang H, Tong S, Lou Y. Changes in orbital-angular-momentum modes of a propagated vortex Gaussian beam through weak-to-strong atmospheric turbulence. Opt Express (2016) 24:6959–75. doi:10.1364/oe.24.006959

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Aksenov VP, Pogutsa CE. Fluctuations of the orbital angular momentum of a laser beam, carrying an optical vortex, in the turbulent atmosphere. Quan Electron. (2008) 45:343–8. doi:10.1070/qe2008v038n04abeh013576

CrossRef Full Text | Google Scholar

10. Sanchez DJ, Oesch DW. Localization of angular momentum in optical waves propagating through turbulence. Opt Express (2011a) 19:25388–96. doi:10.1364/oe.19.025388

CrossRef Full Text | Google Scholar

11. Sanchez DJ, Oesch DW. Orbital angular momentum in optical waves propagating through distributed turbulence. Opt Express (2011b) 19:24596–608. doi:10.1364/oe.19.024596

CrossRef Full Text | Google Scholar

12. Siegenthaler JP, Jumper EJ. Atmospheric propagation vs. aero-optics. Reston, VA: AIAA (2008).

CrossRef Full Text

13. Jumper EJ, Gordeyev S. Physics and measurement of aero-optical effects: past and present. Annu Rev Fluid Mech (2017) 49:419–41. doi:10.1146/annurev-fluid-010816-060315

CrossRef Full Text | Google Scholar

14. Elsinga GE, van Oudheusden BW, Scarano F. Evaluation of aero-optical distortion effects in piv. Exp Fluids (2005) 39:246–56. doi:10.1007/s00348-005-1002-8

CrossRef Full Text | Google Scholar

15. Kirmse T, Gardner AD, Krombholz C. Density effects in model deformation measurements on a naca 0010 profile in a transonic flow. In: 14th international symposium on flow visualization; 2010 Jun 21–24; Daegu, Korea (2010).

Google Scholar

16. Xu L, Zhou Z, Ren T, Yu X, Han B. Propagation characteristics of orbital angular momentum and its time evolution carried by a laguerre-Gaussian beam in supersonic turbulent boundary layer. Opt Express (2020) 28:4032–47. doi:10.1364/oe.382421

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wolf E, Born M. Principles of optics - electromagnetic theory of propagation, interference and diffraction of light. 7th ed. New York, NY: Cambridge University Press (1999).