Translation-Invariant Bipolarons and Charge Density Waves in High-Temperature Superconductors

Introduction

Presently, there is no agreement about the microscopic nature of the high-temperature superconductivity (HTSC). At the same time, there are phenomenological models such as a Ginzburg–Landau model [1], a model of charge density waves (CDWs) or pair density waves (PDWs) (the recent review on the theory and experiment with CDW/PDW in high-temperature superconductors, ultracold atomic gases, and mesoscopic devices was published by Agterberg et al. [2]) and a model of spin density waves which enable one to describe numerous HTSC experiments [3]. These models are silent on the nature of paired states taking part in SС. In author’s works [4–7], paired states mean translation invariant (TI) bipolaron states formed by a strong electron–phonon interaction similar to Cooper pairs (for the review of earlier pioneering works devoted to superconductivity based on the theory of small-radius bipolarons, see [8]). TI bipolarons are plane waves with a small correlation length capable of forming a Bose–Einstein condensate with high transition temperature which possesses SC properties. A correlation between the Bardeen–Cooper–Schrieffer (BCS) theory [9] and the Ginzburg–Landau theory was established by Gor’kov [10]. The aim of this work was to establish a correlation between the TI-bipolaron theory of SC and CDW (PDW).

Results

General Relations for the Spectrum of a Moving TI Bipolaron

TI bipolarons are formed at a temperature $T^{\ast }$which is much higher than that of an SC transition $T_c$ (Refs. [4–7]). For $T_c<T<T^{\ast }$ and in the absence of a Fermi surface with a sharp boundary, an ensemble of TI bipolarons would be an ideal gas whose particles would have a spectrum $s=\left\{{\nu }_k^2\left(\overrightarrow{\mathcal{P}}\right)\right\},$ determined by the dispersion equation (Refs. [4–7]):

$\begin{array}{l}1=\frac{2}{3}{\displaystyle \sum }_k\frac{k^2{\left|f_k\right|}^2{\omega }_k}{s-{\omega }_k^2},\\ {\omega }_k={\omega }_0\left(\overrightarrow{k},\overrightarrow{\mathcal{P}}\right)-\frac{\overrightarrow{k} \overrightarrow{\mathcal{P}}}{M}+\frac{k^2}{2M}-\frac{\overrightarrow{k}}{M}{\displaystyle \sum }_{k^{\text{'}}}\overrightarrow{k}{\left|f_{k^{\text{'}}}\right|}^2,\end{array}(1)$

$f_k=f_k\left(\overrightarrow{k},\overrightarrow{\mathcal{P}}\right)$ are parameters determining the ground state energy $E_{bp}\left(\overrightarrow{\mathcal{P}}\right)$ of a TI-bipolaron, $\overrightarrow{\mathcal{P}}$ is the total momentum of a TI bipolaron, $M=2m$, where $m$is the mass of a band electron (hole), and ${\omega }_0\left(\overrightarrow{k},\overrightarrow{\mathcal{P}}\right)$ is the phonon frequency in an electron gas around TI bipolarons.

In describing the Kohn anomaly, one usually proceeds from Frӧhlich Hamiltonian of the following form [11]:

$H={\displaystyle \sum }_p\epsilon \left(\overrightarrow{p}\right)c_{\overrightarrow{p}}^{+}{c}_{\overrightarrow{p}}+{\displaystyle \sum }_{\overrightarrow{p}}\mathit{ħ}\tilde{\omega }\left(k\right)b_{\overrightarrow{k}}^{+}{b}_{\overrightarrow{k}}+{\displaystyle \sum }_{\overrightarrow{p}\overrightarrow{k}}g\left(\overrightarrow{k}\right)c_{\overrightarrow{p}+\overrightarrow{k}}^{+}{c}_{\overrightarrow{p}}\left(b_{-\overrightarrow{k}}^{+}+b_{\overrightarrow{k}}\right),(2)$

where the first term corresponds to a free electron gas; $c_p^{+}, c_p$ are the operators of the birth and annihilation of an electron with energy $\epsilon \left(\overrightarrow{p}\right)$, respectively. The second term corresponds to Hamiltonian of the lattice; $b_{\overrightarrow{k}}^{+},b_{\overrightarrow{k}}$ are operators of the birth and annihilation of lattice oscillations with energy $\tilde{\omega }\left(k\right)$, respectively. The third term describes interactions of electrons with the lattice; $g\left(k\right)$ is the matrix element of the interaction.

Renormalization of phonon frequencies corresponding to (2) is determined by the expression [11]:

${\omega }^2\left(\overrightarrow{k}\right)=\tilde{\omega }{\left(\overrightarrow{k}\right)}^2+2\tilde{\omega }\left(\overrightarrow{k}\right){\left|g\left(\overrightarrow{k}\right)\right|}^{2}Re\left[\chi \left(\overrightarrow{k}\right)\right],(3)$

where $\omega \left(\overrightarrow{k}\right)$ are phonons renormalized by an interaction with an electron gas whose polarizability is determined by $\chi \left(\overrightarrow{k}\right)$.

The Kohn anomaly describes vanishing of renormalized phonon modes $\omega \left(k\right)$ for $k={\mathcal{P}}_{CDW}$.

In the TI-bipolaron theory of SC [4–7], bipolarons are believed to be immersed into an electron gas. The properties of such bipolarons are also described by Fröhlich Hamiltonian of the form (2), but with a field of already renormalized phonons with energies $\omega \left(k\right)$ and, accordingly, a matrix element of the interaction $V\left(\overrightarrow{k}\right)$ instead of $g\left(\overrightarrow{k}\right)$.

It should be noted that spectral equation 1 is independent of the form of $V\left(\overrightarrow{k}\right)$.

The experimental evidence of the occurrence of renormalized phonons with zero energy in layered HTSC cuprates is the absence of a gap in the nodal direction in these materials which, by definition, is the phonon frequency in the TI bipolaron theory of SC.

The wave function of a TI-bipolaron with the wave vector $\overrightarrow{\mathcal{P}}$ will have the following form:

$\left|\Psi \left(\overrightarrow{\mathcal{P}}\right){\rangle }_{bp}=e^{i\overrightarrow{\mathcal{P}}\overrightarrow{R}}\right|\Psi \left(0\right){\rangle }_{bp},(4)$

where $\overrightarrow{R}$ comprises coordinates of the bipolaron mass center. The explicit form of the wave function $|\Psi \left(0\right){\rangle }_{bp}$with zero momentum is well established [12]. An expression for $\overrightarrow{\mathcal{P}}$ can be derived by calculating the mathematical expectation of the operator of the total momentum $\widehat{\mathcal{P}}$:

$\overrightarrow{\mathcal{P}}=\langle \Psi \left(\overrightarrow{\mathcal{P}}\right)\left|\widehat{\mathcal{P}}\right|\Psi \left(\overrightarrow{\mathcal{P}}\right)\rangle =M\overrightarrow{u}+{\displaystyle \sum }_k\overrightarrow{k}{\left|f_k\right|}^2,(5)$

where $\overrightarrow{u}$ is the velocity of a TI bipolaron. Assuming that $\overrightarrow{\mathcal{P}}=M_{bp}\overrightarrow{u},$ where $M_{bp}$ is the bipolaron mass, we can rewrite (5) and express $M_{bp}$ as follows:

$M_{bp}=\frac{M}{1-\mathrm{\eta }} , \mathrm{\eta }=\frac{\overrightarrow{\mathcal{P}}}{{\mathcal{P}}^2}{\displaystyle \sum }_k\overrightarrow{k}{\left|f_k\right|}^2.(6)$

With the use of (6) expression for ${\omega }_k$ from (1) can be rewritten as follows:

${\omega }_k={\omega }_0\left(\overrightarrow{k},\overrightarrow{\mathcal{P}}\right)+\frac{k^2}{2M}-\frac{\overrightarrow{k} \overrightarrow{\mathcal{P}}}{M_{bp}}.(7)$

It follows from (6) that in the case of a weak and intermediate coupling (when TI-bipolaron states are metastable for $\overrightarrow{\mathcal{P}}=0$), the exact form of $f_k\left(\overrightarrow{k,}\overrightarrow{\mathcal{P}}\right)$ is known [13], and in the case of bipolaron, it is equal to

$f_k\left(\overrightarrow{k,}\overrightarrow{\mathcal{P}}\right)=-\frac{V_k}{{\omega }_0\left(\overrightarrow{k}\overrightarrow{,\mathcal{P}}\right)-\frac{\overrightarrow{k}\overrightarrow{\mathcal{P}}}{2M}\left(1-\eta \right)+\frac{k^2}{2M}},$

where $V_k$ is the electron–phonon matrix element, and the expression for the TI-bipolaron effective mass will have the simple form: $M_{bp}=M(1+\alpha /6),$ where α is a constant of the electron–phonon interaction; that is, mass $M_{bp}$ is equal to the sum of masses of individual polarons. For a large α, good approximations for $f_k$ are available only for $\overrightarrow{\mathcal{P}}=0$. For this reason, the calculation of the effective mass of a TI bipolaron is rather difficult.

TI Bipolarons and Charge Density Waves

Subject to availability of a Fermi surface with a sharp boundary, the TI-bipolaron gas under consideration will have some peculiarities. Thus, if there are rather large fragments on this surface which can be superimposed by transferring one of them onto vector $\overrightarrow{\mathcal{P}}$, then if the size of these fragments is rather large, the coupling between them will be rather strong, which will lead to the Peierls deformation of the lattice in the direction of this nesting. A loss of energy associated with the lattice deformation will be compensated by a gain in the energy of a bipolaron gas which forms a charge density wave with the wave vector $\overrightarrow{\mathcal{P}}={\overrightarrow{\mathcal{P}}}_{CDW.}$ The fact of a gain in the energy of a TI bipolaron follows from Equation 1, whose solution leads to the spectrum of a TI-bipolaron $E_k\left(\overrightarrow{\mathcal{P}}\right),$ where

$E_k\left(\overrightarrow{\mathcal{P}}\right)=\{\begin{array}{c}{E}_{bp}\left(\overrightarrow{\mathcal{P}}\right), k=0\\ E_{bp}\left(\overrightarrow{\mathcal{P}}\right)+{\omega }_0\left(\overrightarrow{\mathcal{P}},\overrightarrow{k}\right)+\frac{k^2}{2M}-\frac{\overrightarrow{k}\overrightarrow{\mathcal{P}}}{M_{bp}}, k\ne 0\end{array},(8)$

that is, $E_k=E_{bp}+{\omega }_k, \text{and }{v}_k={\omega }_k for k\ne 0$.

The gain in the energy is caused by the above considered Kohn anomaly [14] which implies that for $\mathcal{P}={\mathcal{P}}_{CDW}$ (in 1D–metal ${\mathcal{P}}_{CDW}=2k_F, {\omega }_0\left(2k_F\right)=0,$ where $k_F$ is a Fermi momentum), the phonon frequency ${\omega }_0\left({\mathcal{P}}_{CDW},k\right)={\omega }_{CDW}$ softens, and, as a consequence, the energy $E_{bp}$ greatly decreases due to a sharp increase in the constant of the electron–phonon interaction $\alpha \sim 1/{\omega }_{CDW}^{1/2}$. For ${\omega }_{CDW}\to 0, {\alpha }_{CDW}\to \infty ,$ accordingly $M_{bp}\to \infty$ and CDWs appears to be practically immobile.

The general expression for $E_{bp}\left(\overrightarrow{\mathcal{P}}\right)$ is complicated, and even in the case of $\overrightarrow{\mathcal{P}}=0$, there are only variational estimates for it [12]. It can be assumed that the general form of the $E_{bp}$ dependence on $\mathcal{P}$ will be δ-shaped, in which the δ-shaped minimum will correspond to $\mathcal{P}={\mathcal{P}}_{CDW }$ (Figure 1).

FIGURE 1

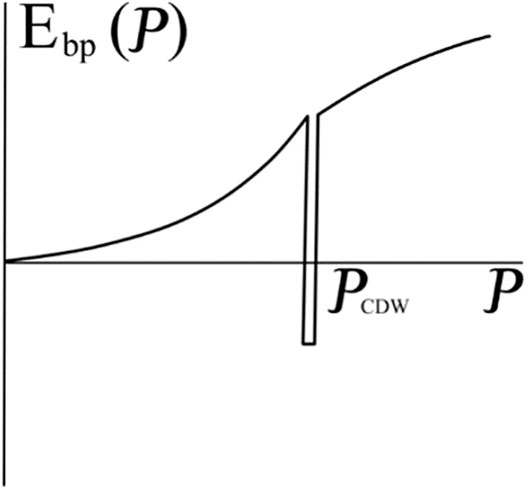
FIGURE 1. The suggested TI-bipolaron spectrum for a charge density wave. It looks as the roton spectrum, but is sharper at $\overrightarrow{\mathcal{P}}={\overrightarrow{\mathcal{P}}}_{CDW}$ due to the Kohn anomaly.

For this spectrum, TI bipolarons will pass on to the state with the energy minimum $E_{bp}\left({\mathcal{P}}_{CDW}\right)$ to form a single charge density wave consisting of paired states and determined by expression (4).

Hence, for $T_{CDW, } T_{bp}>T_C,$ where $T_{CDW }=\left|E_{bp}\left({\mathcal{P}}_{CDW}\right)-E_{bp}\left(0\right)\right|, T_{bp}=\left|E_{bp}\left(0\right)-2E_p\left(0\right)\right|, E_p\left(0\right)$ is the polaron ground state energy, the pseudogap precedes the SC. If in this case the condition $T_{CDW }>T_{bp}$ is fulfilled, then the pseudogap is a coherent pseudophase, and for $T_{bp}>T_{CDW}$, a coherent pseudophase is preceded by a non-coherent phase of free pairs. If the inequality $T_{CDW}, T_{bp}>T_C$ is not fulfilled, then the smallest quantity ($T_{CDW}$ or $T_{bp}$) becomes equal to $T_C$. In any case, the superconducting phase coexists with the pseudogap one which disappears for $T=0$, when all the pairs are in a Bose condensate and the CDW amplitude vanishes.

Energetical advantageousness of а condensate phase follows from expressions (7), (8), which suggest that a homogeneous Bose condensate has a lower energy on condition:

$\mathcal{P}<M_{bp}\sqrt{2{\omega }_0\left(\mathcal{P},k\right)/M}.(9)$

It should be noted that the scenario considered is close in many respects to the Fröhlich superconductivity model [15]. In the Frӧhlich model, it was assumed that two electrons with opposite momenta (as in BCS) on the Fermi surface are connected by a phonon with the wave vector ${\mathcal{P}}_{CDW}$ ($2k_F$ in 1D case), thereby forming a charged phonon. Being bosons, such phonons, in a macroscopic number, can be in the same state with the wave vector ${\mathcal{P}}_{CDW}$ to form a CDW (Fröhlich charge wave). Such a wave, however, will not be superconducting, since pinning which always takes place in real crystals or its scattering by normal carriers will hinder such a wave. The main difference between the TI-bipolaron description and Fröhlich approach is in the formation of a Bose condensate of TI bipolarons (which form a wave of Fröhlich charged phonons), which is just responsible for superconductivity.

Discussion—Comparison With Experiment

To be more specific, let us consider the case of a HTSC such as YBCO. The vector of a CDW in YBCO lies in ab-plane and has two equally likely directions: along the a-axis $\left({\overrightarrow{\mathcal{P}}}_{CDW,x}\right)$ and along the b-axis $\left({\overrightarrow{\mathcal{P}}}_{CDW,y}\right)$, corresponding to antinodal directions. For $T_c<T<T^{\ast }$, these directions of ${\overrightarrow{\mathcal{P}}}_{CDW}$ correspond to nonzero soft phonon modes ${\omega }_0\left({\mathcal{P}}_{CDW},k\right)$. The occurrence of a CDW in these directions in YBCO was detected in a lot of experiments including those on nuclear magnetic resonance [16–18], resonant inelastic X-ray scattering [19–21], resonant scattering, and diffraction of hard X-rays [22, 23]. Relevant softening of phonon modes in the course of a CDW formation was also observed [24].

Still greater softening of phonon modes can be expected for $T<T_c$. A phonon mode corresponding to a nodal direction can vanish, which corresponds to a lack of a gap in the nodal direction. This fact was confirmed experimentally [22] for $B{i}_{2}S{r}_{2-x}L{a}_{x}Cu{O}_{6+\delta }$ with the use of combined methods of resonant X-ray scattering, scanning tunneling microscopy, and angle-resolved photoelectron spectroscopy. In the case of YBCO with ${\omega }_0\left({\mathcal{P}}_{CDW},k\right)={\Delta }_0\left|\cos k_{x}a-\cos k_{y}a\right|$ (absolute value of CDW pairing amplitudes or energy gap [25, 26] which are the renormalized phonon frequency in a TI-bipolaron theory) according to (9), any value of ${\mathcal{P}}_{CDW}$ leads to instability of a CDW and the formation of an SC phase in this direction while retaining the pseudogap state in the antinodal direction.

It should be noted that in the approach suggested, a difference between CDWs and PDWs disappears and ${\mathcal{P}}_{CDW}={\mathcal{P}}_{PDW}$ (Ref. [27]).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

VL contributed to conception and design of the study, wrote the manuscript, read, and approved the submitted version.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Larkin A, Varlamov A. Theory of Fluctuations in Superconductors. Oxford UK: Oxford University Press (2005). doi:10.1093/acprof:oso/9780198528159.001.0001

CrossRef Full Text

2. Agterberg DF, Séamus Davis JC, Edkins SD, Fradkin E, Van Harlingen DJ, Kivelson SA, et al. The Physics of Pair-Density Waves: Cuprate Superconductors and beyond. Annu Rev Condens Matter Phys (2020) 11:231–70. doi:10.1146/annurev-conmatphys-031119-050711

CrossRef Full Text | Google Scholar

3. Grüner G. Density Waves in Solids. Reading: Addison-Wesley (1994). doi:10.1201/9780429501012

CrossRef Full Text

4. Lakhno VD. Superconducting Properties of 3D Low-Density Translation-Invariant Bipolaron Gas. Adv Condensed Matter Phys (2018) 2018:1380986. doi:10.1155/2018/1380986

CrossRef Full Text | Google Scholar

5. Lakhno V. Superconducting Properties of a Nonideal Bipolaron Gas. Physica C: Superconductivity its Appl (2019) 561:1–8. doi:10.1016/j.physc.2018.10.009

CrossRef Full Text | Google Scholar

6. Lakhno VD. Superconducting Properties of 3D Low-Density TI-Bipolaron Gas in Magnetic Field. Condensed Matter (2019) 4(2):43. doi:10.3390/condmat4020043

CrossRef Full Text | Google Scholar

7. Lakhno VD. Translational-Invariant Bipolarons and Superconductivity. Condensed Matter (2020) 5(2):30. doi:10.3390/condmat5020030

CrossRef Full Text | Google Scholar

8. Micnas R, Ranninger J, Robaszkiewicz S. Superconductivity in Narrow-Band Systems with Local Nonretarded Attractive Interactions. Rev Mod Phys (1990) 62:113. doi:10.1103/RevModPhys.62.113

CrossRef Full Text | Google Scholar

9. Bardeen J, Cooper LN, Schrieffer JR. Theory of Superconductivity. Phys Rev. (1957) 108:1175. doi:10.1103/PhysRev.108.1175

CrossRef Full Text | Google Scholar

10. Gor'kov LP. Microscopic Derivation of the Ginzburg-Landau Equations in the Theory of Superconductivity. Sov Phys JETP (1959) 9:1364. http://www.jetp.ras.ru/cgi-bin/e/index/e/9/6/p1364?a=list.

Google Scholar

11. Grimvall G. The Electron-Phonon Interaction in Metals. ISBN: 9780444861054. Amsterdam: North-Holland Publ. Comp. (1981).

12. Lakhno VD. Pekar's Ansatz and the strong Coupling Problem in Polaron Theory. Phys.-Usp. (2015) 58:295–308. doi:10.3367/UFNe.0185.201503d.0317

CrossRef Full Text | Google Scholar

13. Lee TD, Low FE, Pines D. The Motion of Slow Electrons in a Polar crystal. Phys Rev (1953) 90:297. doi:10.1103/PhysRev.90.297

CrossRef Full Text | Google Scholar

14. Kohn W. Image of the Fermi Surface in the Vibration Spectrum of a Metal. Phys Rev Lett. (1959) 2:393. doi:10.1103/PhysRevLett.2.393

CrossRef Full Text | Google Scholar

15. Fröhlich H. On the Theory of Superconductivity: the One-Dimensional Case. Proc R Soc Lond A (1954) 223:296–305. doi:10.1098/rspa.1954.0116

CrossRef Full Text | Google Scholar

16. Wu T, Mayaffre H, Krämer S, Horvatić M, Berthier C, Hardy WN, et al. Magnetic-field-induced Charge-Stripe Order in the High-Temperature Superconductor YBa2Cu3Oy. Nature (2011) 477:191–4. doi:10.1038/nature10345

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Wu T, Mayaffre H, Krämer S, Horvatić M, Berthier C, Kuhns PL, et al. Emergence of Charge Order from the Vortex State of a High-Temperature Superconductor. Nat Commun (2013) 4:2113. doi:10.1038/ncomms3113

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Wu T, Mayaffre H, Krämer S, Horvatić M, Berthier C, Hardy WN, et al. Incipient Charge Order Observed by NMR in the normal State of YBa2Cu3Oy. Nat Commun (2015) 6:6438. doi:10.1038/ncomms7438

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ghiringhelli G, Le Tacon M, Minola M, Blanco-Canosa S, Mazzoli C, Brookes NB, et al. Long-Range Incommensurate Charge Fluctuations in (Y,Nd)Ba2Cu3O6+x. Science 337(6096), 821–5. (2012). doi:10.1126/science.1223532

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Achkar AJ, Sutarto R, Mao X, He F, Frano A, Blanco-Canosa S, et al. Distinct Charge Orders in the Planes and Chains of Ortho-III-Ordered YBa2Cu3O6+δ Super Conductors Identified by Resonant Elastic X-ray Scattering. Phys Rev Lett 109, 167001 (2012). doi:10.1103/PhysRevLett.109.167001

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Blackburn E, Chang J, Hücker M, Holmes AT, Christensen NB, Liang R, et al. X-Ray Diffraction Observations of a Charge-Density-Wave Order in Superconducting Ortho-II YBa2Cu3O6.54 Single Crystals in Zero Magnetic Field. Phys Rev Lett 110, 137004 (2013). doi:10.1103/PhysRevLett.110.137004

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Comin R, Frano A, Yee MM, Yoshida Y, Eisaki H, Schierle E, et al. Charge Order Driven by Fermi-Arc Instability in Bi2Sr2-xLaxCuO6+δ. Science 343 (6169), 390–2. (2014). doi:10.1126/science.1242996

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Chang J, Blackburn E, Holmes AT, Christensen NB, Larsen J, Mesot J, et al. Direct Observation of Competition between Superconductivity and Charge Density Wave Order in YBa2Cu3O6.67. Nat Phys (2012) 8:871–6. doi:10.1038/nphys2456

CrossRef Full Text | Google Scholar

24. Le Tacon M, Bosak A, Souliou SM, Dellea G, Loew T, Heid R, et al. Inelastic X-ray Scattering in YBa2Cu3O6.6 Reveals Giant Phonon Anomalies and Elastic central Peak Due to Charge-Density-Wave Formation. Nat Phys (2014) 10:52–8. doi:10.1038/nphys2805

CrossRef Full Text | Google Scholar

25. Comin R, Sutarto R, He F, da Silva Neto EH, Chauviere L, Fraño A, et al. Symmetry of Charge Order in Cuprates. Nat Mater (2015) 14:796–800. doi:10.1038/nmat4295

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Chowdhury D, Sachdev S. Density-wave Instabilities of Fractionalized Fermi Liquids. Phys Rev B 90, 245136 (2014). doi:10.1103/PhysRevB.90.245136

CrossRef Full Text | Google Scholar

27. Hamidian MH, Edkins SD, Joo SH, Kostin A, Eisaki H, Uchida S, et al. Detection of a Cooper-pair Density Wave in Bi2Sr2CaCu2O8+x. Nature (2016) 532:343–7. doi:10.1038/nature17411

PubMed Abstract | CrossRef Full Text | Google Scholar