Quantifying Legal Entropy

Many scholars have employed the term “entropy” in the context of law and legal systems to roughly refer to the amount of “uncertainty” present in a given law, doctrine, or legal system. Just a few of these scholars have attempted to formulate a quantitative definition of legal entropy, and none have provided a precise formula usable across a variety of legal contexts. Here, relying upon Claude Shannon's definition of entropy in the context of information theory, I provide a quantitative formalization of entropy in delineating, interpreting, and applying the law. In addition to offering a precise quantification of uncertainty and the information content of the law, the approach offered here provides other benefits. For example, it offers a more comprehensive account of the uses and limits of “modularity” in the law—namely, using the terminology of Henry Smith, the use of legal “boundaries” (be they spatial or intangible) that “economize on information costs” by “hiding” classes of information “behind” those boundaries. In general, much of the “work” performed by the legal system is to reduce legal entropy by delineating, interpreting, and applying the law, a process that can in principle be quantified.

Introduction

It goes without saying that the law and legal systems are uncertain to a significant degree. Several scholars (e.g., Katz and Bommarito [1]; Friedrich et al. [2]) have attempted to determine the uncertainty (and related complexity) of legal systems by formulating measures of the “entropy” of words in legal texts, including statutes and other legal authorities. Although measuring the ambiguity of words in texts can be valuable in many situations, it does not provide a comprehensive measure of the uncertainty in interpreting legal rules, much less a “system-wide” measure of the uncertainty of the law and legal system and subsystems more generally. Other scholars (e.g., Dworkin [3], Parisi [4, 5], Ruhl and Ruhl [6]) have focused their efforts on more general notions of legal entropy and related concepts, but have done little to nothing to formalize those notions in mathematical terms.

This article provides several important contributions to the literature by formalizing the notion of legal entropy. First, it offers a conceptual framework to quantify the entropy of legal systems that extends beyond legal text to capture how the law actually functions in real-world situations, including not only legal interpretation, but also the entropy and related information costs in formulating and applying the law. Second, although some previous works have foreshadowed the possibility of a quantitative description of legal entropy (e.g., D'Amato [7]), the formalization offered here provides a fully mathematical formulation as it applies to legal systems and disputes. Third, the mathematical model proposed here offers a potential template for how legal AI systems can measure and store information about the uncertainty of legal systems. Fourth, the model helps to explain more fully the nature and function of important concepts in the law, including the so-called “modularization” of the law and legal concepts, as proposed in the seminal works on the topic by Smith [8–10] and follow-on works by others (e.g., Newman [11]), as a well as the Coase Theorem [12] and the indeterminacy of legal rules [13].

The article proceeds as follows. Part 2 provides a brief background of the notion of entropy in physics and information theory, particularly Shannon's [14] formulation of information entropy. Part 3 describes previous attempts to describe legal entropy, including descriptive notions of legal entropy and measures of the word entropy found in legal texts. It explains the limitations inherent in these previous treatments. In Part 4, relying on Shannon [14] and the theoretical work of Hohfeld [15], it introduces a formal mathematical description of legal entropy, as it applies to a particular legal issues and disputes as well as across legal systems and subsystems. Specifically, Part 4 proposes models for quantifying entropy in formulating and interpreting the law, as well as applying the law to a set of facts. In Part 5, the article applies its formal model to important theoretical and practical issues in the law, including legal indeterminacy, modularity, and the Coase Theorem. In so doing, it discusses practical problems in “measuring” legal entropy. Finally, the article concludes with some suggestions for further research.

Entropy in Physics and Information Theory

The concept of entropy in physics traces to the work of Clausius [16] in the mid-nineteenth century to describe a property of the transfer of heat, ΔQ, from a heat source at a certain temperature, T, to an idealized engine in a so-called reversible process.¹ In this situation, according to Clausius, the entropy of the system increases by ΔQ/T. Similarly, entropy decreases by such an amount when an idealized engine loses heat ΔQ to a heat sink at temperature T. In other words, as heat enters a thermodynamic system, entropy increases—particularly, if the system is cold, less if the system is already hot.

In the 1870s, Boltzmann [17] offered a molecular (i.e., microscopic) description of Clausius's notion of entropy. Specifically, Boltzmann [17] postulated that Clausius's macroscopic description of entropy could be explained in relation to microscopic states. Because heat at a macroscopic level is essentially a “disordered” collection of microscopic particles, the exact behavior or which is unknown at the macroscopic level, the entropy of the system can be viewed roughly as a measure of macroscopic disorder. As a cold system becomes hotter, its ordered, stable microscopic state of particles in fixed positions yields to a frenzy of quickly moving particles. Although in a classical system, the position and momentum of microscopic particles is measurable in principle, merely measuring the temperature and other macroscopic properties of a system would be insufficient to determine the precise position and momentum of each and every particle. As more heat enters a system, the more difficult it becomes to use macroscopic measures to determine the position and momentum of each particle that the system comprises. This increasing uncertainty results because the microscopic particles could be in a greater number of potential states (i.e., of position and momentum) in an increasingly hotter system than an increasingly colder system, where particles are relatively motionless. If a system is already hot, introducing a bit more heat increases the uncertainty of the microscopic states much less than if the system begins cold.

Boltzmann [17] was able to formulate a microscopic definition of entropy along these lines, S = k_b ln W, that explained Clausius's macroscopic definition. According to Boltzmann's Equation, the entropy S of an ideal gas is simply the natural logarithm (introduced for mathematical convenience) of the number of microstates, W, of the system corresponding to the gas's macrostate multiplied by a constant k_b (Boltzmann's constant).² In other words, the number of different position and momentum arrangements the microscopic particles may occupy for a given macroscopic state effectively explains the macroscopic entropy of the system.

Boltzmann [18] and later Gibbs [19] generalized his equation to take into account that certain microstates are more or less probable than others. In this case, weighting is necessary to take account of the variable probability of certain microstates that correspond to a given macrostate. In this case, using a well-known mathematical approximation, the so-called Gibbs entropy becomes:

$\begin{array}{ll}S={-k}_B\sum p_{i}ln{p}_i& (1)\end{array}$

Roughly speaking, the Gibbs entropy reflects a weighted average of the number of microstates corresponding to a given macrostate, where p_i is the probability for a certain microstate to occur. In this regard, note that ln p_i (for p_i < 1) is negative and decreases as p_i approaches zero. Thus, a state i with a seemingly small probability of occurrence may significantly contribute to overall entropy.

The Gibbs entropy is in effect a special case of a more general phenomena in which some “macroscopic” state of a generalized system, call it M, may be instantiated by W different “microscopic” states of the generalized system (Jaynes [20]). For instance, the “macroscopic” state of having 10 cents in one's hand can be instantiated by four “microscopic” states: (1) 10 pennies; (2) a nickel and 5 pennies; (3) two nickels; or (4) one dime. In other words, knowing the “macroscopic” state (here, the total monetary value) generally will be insufficient to specify the “microscopic” state (here, the precise coins used to achieve the total monetary value).

The greater the uncertainty in microscopic configuration, the greater the entropy. In other words (and using log base 2 to capture the number of bits of entropy), S = k log₂ W. Setting k = 1 for simplicity, and reducing W in the same manner as the Gibbs entropy, one arrives at the formula for Shannon [14] entropy in bits:

$\begin{array}{ll}S=-\sum p_i{log}_2{p}_i& (2)\end{array}$

If we suppose that each of the four microstates in our example are equally likely, the Shannon entropy of 10 cents is−4 x 0.25 × log₂ (0.25) = 2 bits of information.³ This is sensible since there are only four choices, which we can label 00, 01, 10, or 11. This more generalized notion of entropy as the uncertainty over a range of informational microstates, as reflected in the Shannon entropy, will play a central role in quantifying legal entropy herein.

Previous Treatments of Entropy in Legal Systems

Many scholars have applied the concept of entropy to legal systems. All of these treatments can be classified into two categories: (1) metaphorical uses of the concept of entropy; and (2) uses of formal mathematical and physical definitions to measure the “entropy” of legal texts.

Although the first category of scholarship (metaphor) can often be useful in thinking about the disorder, complexity, and uncertainty present in legal systems, it fails to offer any formal quantification of legal entropy. For instance, in a well-known article, Parisi [4] contends that real property is subject to a fundamental law of entropy that leads to increasing fragmentation of property interests, but fails to quantify the notion. Lewis [22] applies thermodynamic principles, including entropy, to the explain corporate reorganizations but, like other treatments, does not extend his notions beyond the level of metaphor. Ferrara and Gagliotti [23] purport to develop a conceptual “mathematical” approach to the law, including a notion that has “somewhat to do with the concept” of entropy in information theory, but their scheme is devoid of formal definition and thus reduces to metaphor. Ultimately, all previous treatments of the broad of concept of legal entropy (see also Berg [24], Edgar [25], Fromer [26], King [27], Moran [28], Stephan [29], as examples) fail to quantify the notion.⁴

Perhaps the treatment that comes closest to any quantification of legal entropy is that of D'Amato [7], who recognizes that entropy is at a maximum when the outcome of a legal dispute is equally likely for each part, further remarking that “[i]n order to use entropy in law directly, the legal scientist would have to embed the collection of predictions we call law into an abstract space that exhibited the variations in the level of uncertainty of the predictions.” Yet, immediately following this insight, D'Amato [7] states that “Since law cannot be completely transcribed into words, it cannot be transcribed into symbols and spaces either.” D'Amato's [7] statement is deficient in two important respects. First, to the extent one is concerned about the probabilities of outcomes in legal disputes, as is D'Amato [7], although it may be practically difficult to “transcribe” disputes into probability spaces, it is not impossible. Indeed, attorneys regularly the estimates the odds of winning and losing cases. Moreover, recent developments in legal artificial intelligence have vastly expanded the promise of more automated approaches to predicting legal outcomes (e.g., Katz et al. [32]; Branting et al. [33]). Second, aside from practical interest, it may be theoretically illuminating to devise mathematical models of the operation of the law. In this regard, such theoretical modeling is in turn arguably critical to practical advances in legal artificial intelligence.

The second category of articles relies on measures of entropy from computational linguistics and related fields, typically derived from Shannon [14, 34], to measure the uncertainty or ambiguity that is present in the text of statutes, regulations, and legal documents. For instance, Katz and Bommarito [1] measure legal complexity based on linguistic entropy present in U.S. federal statutes. In a similar vein, Friedrich et al. [2] examine the word and document entropy of opinions from the U.S. Supreme Court and the German Bundegerichtshof in order to measure and compare the textual ambiguity present in the courts' opinions.⁵

Although these text-based endeavors are important contributions to the literature, especially by formalizing previous metaphorical treatments, they are limited to what I term the “interpretive entropy” of legal systems—namely, the entropy and associated information costs involved in interpreting the law prior to its application to a particular set of facts. Moreover, because this scholarship tends to focus on the language of statutes and regulations, it measures only a portion of the interpretive entropy, because interpretation also involves the consultation of authoritative legal opinions, administrative interpretations, legislative and regulatory history, the text of other statutes and regulations, and not infrequently, general facts about the world (e.g., social norms, scientific facts, etc.).⁶

The present article adds to the literature by formalizing the metaphorical treatments in the first category. Like the articles examining the entropy of legal texts, it relies on formal mathematical and physical definitions, but it extends beyond the mere words of laws to provide more general, quantitative definitions of legal entropy.⁷

Formalizing Legal Entropy

This section relies on the work of Shannon [14], Hohfeld [15], and others to introduce a basic mathematical formalization of the entropy involved in the formulation, interpretation, and application of a law to a given set of facts involving a single legal actor, as well as system-wide entropy across multiple laws and facts concerning many legal actors. In so doing, it begins to overcome the theoretical limitations of the prior literature described earlier.

The Entropy of Legal Systems

As noted, although formal measures of the ambiguity of words in legal documents through measures of word entropy is useful to analyze and parse legal texts, it does not measure the entire extent of interpretive entropy, much less the entropy of legal systems more generally. Rather, one would like to quantify the ambiguity across the entire range of the formulation, interpretation, and application of particular laws to particular behavior.

For instance, the tax laws are notorious for being uncertain in delineation, interpretation, and application (Osofsky [37]). Regarding application, just small variations in the underlying facts relating to a particular tax provision can lead to large changes in the likelihood that the applicable legal actor is obligated to pay taxes or not. Similarly, patent infringement disputes are often difficult to predict, and like tax issues, are sensitive to small variations in the underlying law and facts (Sichelman [38]). Moreover, even if one can quantify the “entropy” of a particular application of law to facts involving a single legal actor, is it possible to quantify the entropy of a legal system and its subsystems encompassing many laws and many legal actors?

Thus, it becomes incumbent to conceptualize the different domains of entropy that arise in legal systems. Delineative entropy involves the ambiguity and related information costs in formulating the law in the first instance, typically into written symbols, in a constitution, statutes, regulations, judicial decisions, and the like. As noted earlier, interpretive entropy concerns the ambiguity in interpreting the written symbols in legal documents, including not only constitutions, statutes, and regulations, but also judicial decisions. Such an endeavor is not merely textual in nature, but will often involve relying upon institutional and social norms, which themselves can be uncertain. Finally, applicative entropy is roughly the uncertainty involved in applying an interpreted law to a given set of facts.⁸ Each type of legal entropy is considered in turn, along with a proposed formal quantification of each.⁹

Delineative Entropy

Formulating the law involves many different types of transaction costs. For instance, legislators must be paid to meet, investigate, negotiate, deliberate, and so forth. Similar transaction costs are borne by regulatory agencies and judges in formulating the law. Political scientists and economists have regularly modeled the delineation of law, including related transaction costs, in terms of public choice, game theoretic, and related models (e.g., Benson and Engen [42], Crump [43]). Yet, some of these transaction costs involve information costs that potentially relate to reducing the legal entropy involved in formulating the law, and scholars have yet to provide quantitative measures of such.¹⁰

What information costs reduce entropy? According to Shannon [14], the entropy of a system is precisely the number of informational bits needed to encode the microstates of the system. When the microstates themselves are unknown, such encoding involves an information cost in determining the precise informational bits of the microstates. As explained more fully in Part 5, actors within the legal system—such as lawyers, lawmakers, judges, law enforcement and others—regularly perform work by incurring information costs to encode microstates—typically, in order to reduce legal entropy by selecting one of the microstates, or at least by reducing the uncertainty in which microstate will be selected. In general, all information costs that genuinely generate new “legal” information about the microstates of some legal system or subsystem will reduce that system's or subsystem's legal entropy (see Part 5). Delineating the law involves many activities that generate new legal information and, in turn, reduce legal entropy. Here, I examine just a portion of those activities. A fuller account of delineative entropy would systematically review each and every one of them.

To begin with, lawmakers must determine which actions, roughly speaking, of legal actors not subject to law should be subject to law and, at conversely, which actions currently subject to law should not be subject to law (or should be subject to amended laws). Ex ante, there will be uncertainty in which categories of human behavior should be subject to law, not subject to law, or subject to legal amendment. Ultimately, this boils down to whether a category of human behavior should be subject to a general change in state with respect to the law.

Astute observers, perhaps aided by legal artificial intelligence, could estimate the probability that some given area of human behavior, especially those relating to newly arising technologies, should be subject to a change in legal state. Suppose it is first day of Nakamoto's [48] now-famous article on bitcoin, and just a few observers know about it. Eventually, information spreads—including from information costs incurred generally unrelated to legal entropy—and lawmakers learn about it but want to know more. At this time, whether activities related to cryptocurrency will be regulated is highly uncertain, probably close to 50%. The lawmakers expend information costs, including formal hearings with experts, to learn more about the economic and social ramifications of bitcoin and whether it should be subject to law.

After much expenditure, legal observers estimate that the probability is 80% that it will be subject to regulation in the near-term within some legal jurisdiction. At each stage during the investigative and deliberative process, one can in theory construct a “near-term” Shannon entropy related to whether some category of human behavior will be subject to law, call it “deontic” entropy,¹¹ which will be one form of overall delineative entropy.¹²

Specifically, for a “single” human behavior (e.g., whether cryptocurrency usage will be regulated), one can calculate the near-term Shannon deontic entropy by summing across the probability that the category will be subject to law. So, assuming 80%, we arrive at

$\begin{array}{l}S=-\sum p_i{log}_2{p}_i=-[(0.8)lo{g}_2(0.8)+(0.2)lo{g}_2(0.2)]\\ =0.72bits\end{array}$

Such entropy may appear at first blush low, but one must sum across all categories of human behavior to determine the total deontic entropy. Indeed, the level of abstraction at which we categorize human behavior will have a substantial effect on the total deontic entropy. For instance, within the category of cryptocurrency usage, there may be hundreds of distinct behaviors, of which may be subject to law. Thus, conditional on the category being subject to law, one may want to know the probabilities and associated entropy with specific behaviors within the category being subject to law, and for some areas of human behavior, even more fine-grained analyses. Here, in theory, one can use the formal notion of conditional entropy—described further below—to quantify the amount of entropy at every level of abstraction.

Of course, in practice, perfectly quantifying the entropy of hundreds of distinct behaviors at multiple levels of abstraction will be impossible. But contrary to D'Amato's [7] pessimistic suggestion that we give up on the endeavor entirely, as noted earlier, conceptualizing how we should formulate various types of legal entropy, even if practically difficult, serves important purposes. First, it provides an ideal model and, thus, a proper roadmap as to how one should build out a practical approach to modeling entropy. For instance, with respect to cryptocurrency, one may build out a rough model of various behaviors and categories potentially subject to law to generate a rough quantification of deontic entropy. Increasingly, these processes may be aided by legal artificial intelligence and related mechanisms. Second, building out these models may help us to understand law, from a theoretical perspective, in a more coherent and precise fashion. Indeed, the history of science is rife with models that are initially rough and thus difficult to solve, model, or explain, but later become subject to rigorous modeling and application. Notable examples are the development of the atomic theory of matter [50], the theory of evolution [51], and the theory of gravitation [52].

Once lawmakers determine that a given category of human behavior should be subject to law, the question becomes how to specifically draft statutes, regulations, or judicial decisions, particularly at a conceptual level, but even at a textual level, that instantiate the aims of the lawmakers. Specifically, if one begins with a concept (or set of concepts) that lawmakers or judges seek to instantiate into written law (or some other more concrete expression), there will exist multiple ways of instantiating the concept into written law.

Often, this involves the particularization of a more general concept (e.g., “Though shall not kill”) into a main rule that specifies the conditions under which the law is violated (e.g., “The killing of another person with malice aforethought,” etc., etc.) and sets of exceptions (e.g., except in self-defense, legitimately as a soldier in war, etc.). In other situations, it involves aggregating multiple concepts (e.g., the types of prohibited interferences of third parties against a landowner's permitted uses) into a single rule (e.g., the law against trespass). Quantifying the amount of uncertainty in how to specify the law, generally in text, is useful to understand how delineative entropy and the associated information costs in reducing that entropy play a role in formulating the law—particularly to illustrate how that process differs across different legal domains (e.g., torts vs. real property). In general, one can term this form of delineative entropy as “specificative” entropy.

Suppose there is a single, general concept of interest (e.g., “Thou shall not kill”) and astute observers have determined that there are roughly 50 different ways in which the lawmakers could conceptually instantiate the law. These 50 different ways may represent the various degrees of crimes (e.g., 1st vs. 2nd degree murder, voluntary and involuntary homicide), mens rea requirements (e.g., malice aforethought, intent, recklessness, and gross negligence), available defenses (e.g., self-defense and duress), and other potentially relevant aspects of the crime (e.g., transferred intent). In general, there may be a large number of permutations of how to instantiate a single concept, either as a single criminal rule, or a large set of related criminal rules.

The line between deontic entropy and specificative entropy is not bright. Although arriving at the applicable concept (e.g., “Thou shall not kill”) is squarely in the deontic entropy box, determining the permutations of instantiations under consideration (e.g., 50 forms) and the viability of each of those instantiations can be related both to deontic and specificative entropy. Once the likelihood of each instantiation is estimated, we can calculate the residual specificative entropy, again using Shannon entropy:

$\begin{array}{ll}S=-\sum p_i{log}_2{p}_i& (3)\end{array}$

For instance, returning to the bitcoin example, suppose that lawmakers are debating three different bills to regulate bitcoin and other cryptocurrencies. Experts estimate that the first bill has a 50% chance of passage, the second bill a 30% chance, and the third bill, a 20% chance, all subject to the earlier 20% chance that no bill passes.

In this case, we can first calculate the specificative entropy as:

$\begin{array}{l}S=-{\displaystyle \sum p_{i}lo{g}_2{p}_i=-[0.5lo{g}_2(0.5)+(0.3)lo{g}_2(0.3)}\\ +0.2lo{g}_2(0.2)]=2.006 bits\end{array}$

Note that the total delineative entropy will be a form of conditional entropy, on which the specificative entropy is conditional upon the deontic entropy, for if a given category of human behavior is not going to be subject to regulation, then lawmakers need not expend any effort to regulate it. In this bitcoin example, there is only an 80% chance that any bill will pass, which resulted in a deontic entropy of 0.72 bits. How should one combine the deontic and specificative entropy into an overall delineative entropy value?

Because the specificative entropy is conditional on the deontic entropy, one cannot simply add them together. Rather, the chain rule for conditional information entropy [53] applies:

$\begin{array}{ll}H(X,Y)=H(X)+H(Y|X)& (4)\end{array}$

where H(X,Y) is the joint (or combined) entropy of two random variables conditional upon one another, H(X) is the entropy solely due to random variable X and H(Y|X) is entropy of Y, conditional upon some specific X (i.e., X = x) occurring.¹³

In other words, the joint (or combined) entropy of a second random variable (Y) that is conditional on a first random variable (X) is the entropy of X plus the entropy of Y conditional on X.¹⁴ In our bitcoin example this results in the following total delineative entropy:

$\begin{array}{l}H(X,Y)=H(X)+H(Y|X)=0.72bits+(0.8){}^{*}(2.006bits)\\ =2.33bits\end{array}$

Note that this is less than simply adding the deontic and specificative entropy together. This is because the specificative entropy only plays a role conditional upon the deontic entropy resulting in the passage of a bill, which happens 80% of the time. Thus, in this simple example, one effectively adds the deontic entropy to chance that the specificative entropy will be meaningful.

Interpretive Entropy

As noted earlier, once a law is formulated—in a constitution, statute, regulation, judicial decision, or some other legal text—it must typically be interpreted to understand its scope and applicability. In this regard, other types of intermediate legal documents, such as contracts and patents, must be interpreted to determine their legal effect. Legal interpretation is fraught with ambiguity, which can be conceptualized in the framework of information entropy as interpretive entropy. Specifically, if one considers the legal rule under consideration the legal “macrostate,” then the “microstates” are all of the possible interpretations of the legal rule.¹⁵ Thus, the interpretive entropy is again expressed by the Shannon information entropy, where each state i is a potential interpretation, and the probability of i being the interpretation adopted by the legal institution of interest (e.g., a court or regulatory agency), p_i:

$\begin{array}{l}S=-\sum p_{i}lo{g}_2{p}_i\end{array}$

If the only step involved in this process were to interpret the express text of a legal rule with a standard dictionary, then techniques using word and related forms of linguistic entropy would provide a fairly accurate value of the interpretive entropy. For instance, one could measure the word entropy of legal texts that measures the ambiguity inherent in each word using a standard corpus (cf. Piantadosi et al. [54]).

Yet, legal interpretation extends well-beyond textual interpretation with a standard dictionary. As an initial matter, many legal terms are “terms of art,” requiring interpretation by specialized, legal dictionaries. Quantifying interpretive entropy using text-based measures of entropy must rely therefore not on a standard corpus, but a specialized one. More problematic, legal interpretation typically draws upon the language of other legal rules, which necessitates determining how those other rules' affect the entropy of the rule-at-issue. And even more problematic, interpreting rules draw on yet more disconnected sources, such as legislative history, judicial decisions, and even general policies and social norms. Not to mention that interpretive entropy applies not only to the interpretation of legal rules, but also legal documents more generally, such as patents and contracts, which introduce further interpretive issues.

In the face of such complexity, following D'Amato [7], one might throw up one's hands and abandon the quantitative endeavor entirely. However, while complex, legal rules ultimately are interpreted, and experienced attorneys regularly estimate the likelihood of a court interpreting a rule in one fashion or another. Indeed, so much has been recognized since at least Holmes [55]. Moreover, new approaches in legal analytics—like those in sports analytics—are likely to be paradigm-shifting in the ability to predict the outcomes of disputes and related aspects of the law more generally (cf. Katz et al. [32]; Branting et al. [33]).

Finally, the notions of joint and conditional entropy described in the context of delineative entropy similarly allow for interpretive entropy in principle to be broken into discrete parts and recomposed. For instance, courts and others interpreting legal documents usually only turn to sources other than the words when there is some ambiguity in specific words or phrases. If a word or phrase is entirely clear on its face, then typically legal interpreters will adopt a textual interpretation. Thus, the text-based techniques described earlier (e.g., Friedrich et al. [2]) and others can be used as initial cut to determine those words and phrases subject to some latent ambiguity. Words without such ambiguity can either be assumed to have zero entropy or simply the entropy calculated on the basis of the text-based methods. For those words or phrases with latent ambiguity, the text-based score may roughly be considered a primary variable upon which other sources for interpretation (e.g., other statutes or regulations, case decisions, social norms, and the like) can be considered secondary variables conditioned on the primary variables, allowing for the use of joint and conditional entropy as explained earlier. Although the precise nature of this staged approach is beyond the scope of this paper, the general contours sketched here should provide the beginnings of a more comprehensive and realizable method to quantifying interpretive entropy.

Applicative Entropy

Once a legal rule has been interpreted, in order to understand how it specifically regulates human behavior, it must be applied to a specific situation, or set of facts.¹⁶ Even though the applicable legal rule has been fully interpreted, residual indeterminacy in the application of the law may remain and can be quantified by applicative entropy. This indeterminacy can arise from “uncertainty as to the impact evidence will have on the decisionmaker,” idiosyncratic behavior in adjudication by a decisionmaker such as a judge or jury, and the influence of extra-legal factors on the regulatory and judicial process [56].

Applying the law typically results in the imposition of liability (or no liability), plus some form of remedy in the event liability is imposed. Again, Shannon entropy can be used to measure the entropy of liability and the conditional entropy to measure the entropy present in the range of remedies in the event liability is imposed. Before turning to these specifics, it is instructive to examine the typology of Hohfeld [15], as it offers a sound, quantitative conceptual basis to describe the entropy of composite legal systems and subsystems, which is illustrated well by applicative entropy.

Hohfeld's (Probabilistic) Typology

Rather than try to describe the entire formalism of Hohfeld [15], for purposes of this article, is straightforward enough to explain two Hohfeldian relations: a Hohfeldian right (that is, a right in the strict sense, hereinafter “strict-right”) and a Hohfeldian power (see generally Sichelman [57] for a detailed exposition).

Specifically, a legal actor, X, who holds a positive strict-right vis-à-vis Y, with respect to some action A, implies that Y is legally obligated vis-à-vis X to perform that action. For instance, X may hold a contractual strict-right that Y deliver to X's warehouse 100 widgets by the following Wednesday. If X holds a negative strict-right vis-à-vis X with respect to some action A, then Y is obligated to refrain from performing that action (in other words, Y is prohibited from performing the action). For instance, X may hold strict-right in tort that Y not punch X on the nose without justification (e.g., in self-defense).

In Hohfeld [15], whether a first actor X holds a strict-right vis-a-vis a second actor Y can be answered only in a binary fashion such as by a classical bit of information.¹⁷ In other words, if the strict-right is positive in nature, Y either has an obligation to perform some action A or not. Adjudication in the sense of Hohfeld [15] thus involves a determination by the court (or other adjudicatory body) if the application of a law to a given set of facts results in a strict-right/obligation for X and Y or a no-right/no-obligation for X and Y.

For convenience, we will label a strict-right as r₁ and the absence of a strict-right as ~r_1. In this fashion, one can represent a strict-right as an “on-bit” (in binary notation, the number “1”) and a no-right as an “off-bit” (in binary notation, the number “0”). In order to more easily manipulate these bits mathematically, it is useful to adopt an equivalent vector formalism, wherein:

$\begin{array}{l}{r}_1=\left(\begin{array}{c}0\\ 1\end{array}\right)\text{ and }~r_1=\left(\begin{array}{c}1\\ 0\end{array}\right)(\text{matrix notation})\end{array}$

Hohfeldian powers alter, terminate, or create other legal relations. For instance, by changing the applicable law, the legislature in effect may change X's right vis-à-vis Y that Y perform some action A to no obligation for Y perform the action. In mathematical terms, the legislature's power would be akin to second-rank permutation tensor (here, a 2 × 2 permutation matrix) that changes X's right vector into its negation (a Hohfeldian “no-right”) corresponding to the lack of any obligation (a Hohfeldian “privilege”) on the part of Y (Sichelman [59]).

Similarly, higher-order powers may change lower-order powers. For instance, a new constitutional amendment may eliminate a previously held second-order power of the legislature. One such example is the passage of the controversial Proposition 209, which amended the California Constitution to prohibit the government, including the legislature, from “discriminat[ing] against, or grant[ing] preferential treatment to, any individual or group on the basis of race, sex, color, ethnicity, or national origin in the operation of public employment, public education, or public contracting” (Cal. Const. art. I, § 31).

In this instance, the amendment would act as a higher-rank tensor that flips the legislature's second-order permutation tensor to a second-rank identity tensor. This is because an identity tensor that operates on first-order right/obligation relations would have no effect on these relations. In other words, a second-order identity tensor is emblematic of the lack of (a second-order) power (a Hohfeldian “disability”). More generally, higher-order powers can be described mathematically as higher-rank tensors that operate on lower-rank tensors (lower-order legal relations) (Sichelman [59]). In this regard, it is important to recognize that vectors are simply lower-rank tensors—thus, a first-order Hohfeldian strict-right is simply a lower-order Hohfeldian power. Thus, all Hohfeldian relations can simply be expressed in terms of legal powers and well-known mathematical relations.

A probabilistic version of Hohfeld's [15] schema may also be developed (Sichelman [59]). Here, instead of legal relations being described by a classical binary bit, the states can exist in probabilistic superpositions, better described by a quantum bit (i.e., qubit). The probabilistic nature of the legal relation may be a result of lack of knowledge of the underlying system or due to inherent indeterminacy in the system itself prior to judgment (a form of system measurement), or a combination of both reasons.¹⁸ Using the qubit formalism, one can specify a probabilistic Hohfeldian relation in the following form:

$\begin{array}{ll}|j{>}_{\text{n}}=a_n|j_{\text{r}}{>}_{\text{n}}+b_n|j_{~\text{r}}{>}_{\text{n}}& (5)\end{array}$

Where |j_r > _n is a legal power (or right, to first-order), |j_~r>_n is the negation of a legal power, P(j_r)_n = |a_n|² is the probability of a legal power obtaining upon judgment, P(j_~r)_n = |b_n|² is the probability of the negation, |a_n|² + |b_n|² = 1, and n is the order of the legal relation. In other words, probabilistic Hohfeldian relations, be they first-order strict-rights and obligations or higher-order powers and liabilities, can be characterized by the qubit formalism,¹⁹ where there is a probability |a_n|² that the legal relation will be measured (i.e., adjudicated) in the “power” state and 1–|a_n|² = |b_n|² in the negation (or lack) of the “power” state. The indeterminacy regarding the state of the system prior to judgment can be quantified as a form of applicative legal entropy.²⁰

Quantifying Applicative Entropy

As noted earlier, a legal judgment with respect to a first-order relation (strict-right/obligation) will either result in a finding that the defendant had an obligation (is liable) or not. Less frequently, a judgment may concern whether a legal actor holds a higher-order relation (power) or not. Prior to this judgment, the indeterminacy in the judgment again can be quantified using the Shannon entropy:

$\begin{array}{l}S=-\sum p_{i}lo{g}_2{p}_i\end{array}$

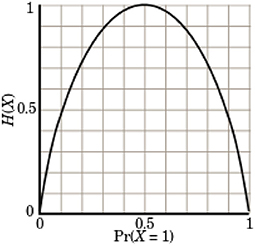
As there are only two potential outcomes in judgment, this reduces to the binary Shannon entropy:

$\begin{array}{ll}S=-plo{g}_{2}p-(1-p)lo{g}_2(1-p)& (6)\end{array}$

where p is the probability that a court finds a power (right to first-order) and corresponding liability (obligation to first-order) on the part of the defendant. In general, as discussed earlier, this entropy is maximum when there is a 50% chance of liability and a 50% of chance of no liability (see Figure 1).

FIGURE 1

Figure 1. Binary shannon entropy vs. probability of an event occurring.

Conditional upon a finding of liability, Shannon entropy can be applied to the range of potential remedies. In the event the remedies are discrete in nature, the ordinary Shannon entropy formula may be used. However, because remedies are usually continuous,²¹ it becomes necessary to use the differential or continuous entropy [53]:

$\begin{array}{ll}h(Y)=-{\displaystyle {\int }_Y}f\left(y\right)lnf\left(y\right)dy& (7)\end{array}$

where f(y) is a probability density function of the potential remedies. For instance, f(y) may represent the likelihoods of various lengths of prison sentences or the amount of damages owed.

For example, suppose that the likelihood of sentences follows a typical bell curve function:

$\begin{array}{ll}f(y)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(y-\mu )}^2}{{2\sigma }^2}}& (8)\end{array}$

where μ is the mean of the distribution and σ is the standard deviation of the curve. In this instance, the differential entropy is:

$\begin{array}{ll}h(Y)=-{\displaystyle {\int }_Y}\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(y-\mu )}^2}{{2\sigma }^2}}ln\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{(y-\mu )}^2}{{2\sigma }^2}}dy& (9)\end{array}$

With some rearranging, this reduces to the simple expression [61]:

$\begin{array}{ll}h(Y)=2\text{ ln}(2\pi \text{e}{\sigma }^2)& (10)\end{array}$

The total applicative entropy of a given dispute can then be calculated by the chain rule discussed in Part 4.2:

$\begin{array}{ll}H(X,Y)=H(X)+H(Y|X)& (11)\end{array}$

Here, H(X) is applicative entropy related to whether liability will be found or not, and H(Y|X) is the applicative entropy related to the remedy, conditional upon liability being found.

Systemwide Entropy

The previous discussion of legal entropy, be it delineative, interpretive, or applicative entropy, has involved one or a narrow set of rules, interpretations, and applications. An immediate question arises as to how to derive the entropy of a legal system or subsystem that encompasses numerous legal relations (in the Hohfeldian sense). Although a full treatment of systemwide legal entropy is beyond the scope of this article, some preliminary remarks may be made.

First, the Hohfeldian mathematical formalization of relations into vectors and tensors is particularly helpful in conceptualizing the quantitative state and related entropy of a system. Recall that the general probabilistic state of a legal relation can be described as the following:

$\begin{array}{ll}|j{>}_{\text{n}}=a_n|j_{\text{r}}{>}_{\text{n}}+b_n|j_{~\text{r}}{>}_{\text{n}}& (12)\end{array}$

For a first-order relation (a Hohfeldian strict-right), the state of a single legal relation is simply a 2-D vector in a “Hohfeldian” state space. As the vector rotates in the state space, the a_n and b_n—and, hence, the relative probabilities of a right being found—change in time. This rotation may be due to the operation on the vector by a power (i.e., a tensor) or simply by the change in external circumstances (e.g., changing underlying facts). For the higher-order relations (a Hohfeldian power), the state of a single relation is a multi-dimensional tensor in the Hohfeldian state space. Like the vector, these tensors may rotate (in a higher-dimensional sense) in the state space, with corresponding changes in the relative probabilities of liability being found (or not).

In theoretical terms, one can imagine the complete Hohfeldian state space as a collection of a multitude of vectors and tensors corresponding to every possible action and states of the world affected by law (and a complement space of all of those actions and states not so affected). In other words, any action or state of the world with a non-zero probability of being subject to a power (including a first-order, power, i.e., strict-right) has an associated vector (or tensor) in the state space representing that specific probability.²² The complement state space represents all actions and states of the world with a zero probability of being subject to a power (including a strict-right).

Of course, listing every possible action and state of the world potentially subject to law and determining how those states change over time is essentially an impossible task.²³ However, for discrete subspaces, it is certainly possible to construct such a space, measuring entropy and other useful properties of the system. For instance, a patent typically will contain multiple, separate claims, each of which describes a slightly different instantiation of the invention. In this sense, each claim provides a separate legal right to prevent third parties from making, using, and selling the corresponding claimed invention. One claim in a patent may relate to a product, the sale of which infringes that claim, while another claim in a patent may relate to the performance of a method with the product that infringes the claim. Although the two claims are related, actions that infringe one claim (e.g., the product claim) may not infringe the other claim (e.g., the method claim).

The legal subspace of interest may be all of the claims of the patent as they apply to the activity of a potential infringer. For an accused infringer to be found liable, the claim must both be valid and enforceable (which typically does not depend on the specific activity of the infringer²⁴) and infringed (by the particular activity of the infringer). Thus, using Shannon entropy, one can first determine the probability that each claim will be found valid and enforceable, using that to determine the entropy related to validity/enforceability, and conditional upon a positive determination, the probability that the claim is infringed by the accused infringer, which then can be used to calculate the conditional entropy and, ultimately, total entropy of each claim (again, according to the chain rule described earlier).

If the decision for each patent claim is statistically independent, then one can simply add the entropy for each claim together. However, whether a given patent claim is valid, enforceable, and infringed is typically correlated to other patent claims in the same patent. When the judgment of particular claims is correlated, the joint entropy of the claims in combination can be used to determine the total entropy.

Specifically, the joint entropy of a set of multiple, random, discrete variables that are potentially correlated can be written as [53]²⁵:

$\begin{array}{l}H(X_1,\dots ,X_n)=-{\displaystyle \sum _{x_1}}\dots {\displaystyle \sum _{x_n}}P(x_1,\dots ,x_n){log}_{2}P(x_1,\dots ,x_n)\end{array}$

Here, P (x₁, … x_n) is the joint probability that each event occurs together. For instance, if there are only two patent claims, X and Y, then the possible outcomes are defendant is liable on X and Y (outcome 1); liable on X but not Y (outcome 2); liable on Y but not X (outcome 3); and liable on neither (outcome 4). If the probability of outcome 1 is 1/4, outcome 2 is 1/3, outcome 3 is 1/6, and outcome 4 is 1/4, then the joint entropy for the two patent claims is:

$\begin{array}{l}-(1/4)\text{ lo}{\text{g}}_2(1/4)+(1/3)\text{ lo}{\text{g}}_2(1/3)+(1/6)\text{ lo}{\text{g}}_2(1/6)\\ +(1/4)\text{ lo}{\text{g}}_2(1/4)=0.96\text{ bits}\end{array}$

Note that the underlying probabilities of liability—and, hence, legal entropy—may change in time due to the exercise of a second-order power by a legislature or some external set of circumstances. For instance, Congress passed the America Invents Act in 2011, which effectively changed the probability that a given patent claim would be found invalid. In this instance, the legislative change would immediately rotate all patent claim vectors in state space, resulting in different probabilities and, in turn, a different subsystem entropy. Similarly, exogenous changes in societal norms, technology, economics, and so forth, may affect the underlying probabilities of legal claims (e.g., Cooter [64]), again, rotating vectors in state space as these changes take effect. For instance, the advent of the Internet arguably changed how judges view software patent claims as a whole, which in turn led to a diminished role for software patents more generally (e.g., Barzel [65]).

These concepts can be extended to the legal system as a whole. First, divide the legal system into independent legal subsystems (To the extent the law is truly a “seamless web,” skip this step.) The entropy of any legal subsystem can be constructed in principle by using the joint and conditional entropies of individual states within the subsystem. (Even if the law is a seamless web, at some point, the correlations among states is so low, they can be ignored and the legal system treated as if it is composed of independent subsystems.)

Again, in practice, this will be nearly impossible, but for certain subsystems of interest—e.g., a patent—certainly possible, especially with improvements in AI approaches for modeling the law. And, again, in the very least, it provides a conceptual framework for richer jurisprudential understandings of the law. The next part considers the beginnings of these richer accounts in a few notable areas.

Practical Uses of Legal Entropy

Legal Indeterminacy

There is an extensive literature on the notion of legal indeterminacy (see Solum [13] for a discussion). One camp, particularly those in the critical legal studies vein, argue for radical indeterminacy of legal doctrine and judicial decisionmaking (e.g., Kennedy [66], D'Amato [7], Singer [67]). Another argues for minimal determinacy, at least in principle (e.g., Dworkin [3]). And the last camp takes an intermediate position (e.g., Kress [68]). Yet, despite the numerous articles on the topic of legal indeterminacy, only a handful of pieces attempt to quantify it—some by examining the ambiguity of legal language using measures from computational linguistics (e.g., Katz and Bommarito [1]) and others by analyzing reversal rates and dissents as a possible proxy of indeterminacy (e.g., Lefstin [69]). Yet, none attempt a wholesale quantification of the amount of indeterminacy present in legal rules and adjudication. This lacuna is notable, because filling it may help to solve many of the recurring debates and disagreements regarding legal indeterminacy in the literature.

For instance, Kress [68] contends, “The pervasiveness of easy cases undercuts critical scholars' claim of radical indeterminacy.” Interpretive and applicative entropy measured across numerous legal rules and related disputes provide a quantitative test of this assertion. Of course, practically quantifying these types of entropy is no simple feat, but a combination of human-coded and automated methods—including those using advances in AI (e.g., Branting et al. [70]; Katz et al. [32]; Branting et al. [33])²⁶—could certainly provide a precise quantitative metric for at least a particular field or doctrine in the law. As machine learning and other automated techniques in legal document classification and analysis continue to improve, arguably, the previous impasse among scholars regarding the “indeterminacy” of the law should yield to at least a modicum of agreement. Regardless, quantitative approaches to legal entropy can provide a deeper understanding of this core issue in the law.

Legal Entropy, Modularity, and Work

Refining Legal Modularity With Legal Temperature and Work

As noted earlier, the original concept of entropy in thermodynamics resulted from investigations regarding an ideal engine and how the transfer of heat, ΔQ, from a heat source at a certain temperature, T, to an idealized engine in a so-called reversible process, increased the entropy of the system by an amount ΔQ/T. Recall that Boltzmann [17] provided a microscopic picture of the macroscopic entropy, whereby heat is essentially a “disordered” collection of microscopic particles, the introduction of which increases the system disorder by a measure of ΔQ/T. According to Boltzmann [17] this ratio can be captured by the total number of microstates of a system corresponding to a given macrostate.

To gain a deeper appreciation of legal entropy, it is useful to construct the notion of legal heat and legal temperature. For simplicity, consider the context of applicative legal entropy with respect to first-order Hohfeldian relations (i.e., strict-right/obligation), where a fully interpreted legal rule is subject to judgment. Recall that each legal relation can be depicted as a vector in state space, such that if the vector does not lie upon one of the axes, there is indeterminacy in the judgment, such that:

$\begin{array}{ll}|j>=a|j_{\text{r}}>+b|j_{~\text{r}}>& (13)\end{array}$

where |j_r> is a legal right, |j_~r> is the negation of a right, P(j_r) = |a|² is the probability of a legal right obtaining upon judgment, P(j_~r) = |b|² is the probability of the negation obtaining, and |a|² + |b|² = 1. Also recall that the entropy in this situation is:

$\begin{array}{l}S=-plo{g}_{2}p-(1-p)lo{g}_2(1-p)=-|a{|}^{2}lo{g}_2|a{|}^2\\ -|b{|}^{2}lo{g}_2|b{|}^2\end{array}$

As legal “heat” enters a legal system, the entropy of the system increases by increasing the underlying uncertainty in outcome. For instance, in the context of applicative entropy (i.e., judgments), increasing uncertainty in the underlying facts constitutes legal “heat” that shifts the Hohfeldian state vector away from vertical or horizontal and into a diagonal position, maximizing entropy when the state vector is at a perfect diagonal, |a|² = |b|², with the corresponding result that judgment is a coin flip (50/50).

Incoming legal heat will have less effect the higher the legal temperature. For instance, if a legal system is at its maximum applicative entropy (50/50), the introduction of more heat cannot increase the entropy of the system. For instance, suppose that the adjudicator—the judge or jury—has already decided to flip a coin to determine the outcome of a dispute. Thus, increasing uncertainty in the underlying facts will have no effect on the ultimate outcome. Because the change in entropy is proportional to the change in heat divided by the background system temperature, at least for applicative entropy, we can see that background system temperature is directly proportional to the background entropy. In other words, when the background entropy is very low, the background temperature is low, and the introduction of legal heat will be more meaningful.

The notion of legal heat, temperature, and entropy can be useful in explaining important theoretical concepts in the law at a more quantitative and arguably deeper level. Importantly, the insightful work of Smith [8–10] on the role of modularity in legal systems can be refined using these concepts. Specifically, Smith [8–10] posits that information costs play an integral role in the “modularity” of legal systems—namely, the use of “boundaries” in the law (be they spatial or intangible) to “economize on information costs” by “hiding” classes of information “behind” the boundaries.

Smith's concept can also be understood in terms of legal entropy. Specifically, as the entropy of a legal subsystem increases, more information—and, hence, more information costs—are required to encode and resolve disputes concerning the legal subsystem. For instance, consider a piece of real property, and the potential uses of an “owner” and “third parties” with respect to the property. One could list out every potential use of the owner and third parties with respect to the property, determining whether such use “improperly” interferes with the owner's or a third party's “rights,” where the rights and interference thereof are defined by some set of background laws and principles. Each step in this use-by-use analysis would be fraught with substantial indeterminacy, generating high entropy and hence large information costs to resolve whether each use is “rightful” (cf. Smith [8–10]). Similarly, a use-by-use approach would involve large costs in delineating and interpreting the law.

As an alternative, the boundary of the property may be used as a proxy to define rightful and wrongful uses to substantially reduce systemwide entropy and, hence, information costs in delineating, interpreting, and applying the law. In other words, in the terms of Smith [8–10], the boundary effectively hides the owner's (unspecified) interests in using the land from legal consideration in the investigation of actions by a third party. To determine if a third party unreasonably interfered with the owner's interests, instead of examining whether a particular action on the part of the third party interfered with particular uses of the owner, the law generally assumes that when a third party unjustifiably crosses the boundary, an interference occurs. This assumption economizes on information costs by using the boundary as a reliable proxy for actual interference with the owner's and third parties' specific interests.

Of course, erecting boundaries as proxies can introduce error costs in allocating rights and duties, so it is important to place some constraints on the modularization of law. The notions of legal temperature and entropy can also perform important work in imposing such constraints. Namely, it is only when the legal system inside the boundary has relatively low temperature and entropy, especially when compared to the temperature and entropy near or outside the boundary, that modularity will serve its role to reduce information costs without imposing significant error costs. If, on the other hand, entropy and temperature were to rise inside the boundary—for instance, as the result of substantial, ever-changing and indeterminate State regulation as to the uses that the owner could undertake—then the modularity of an “exclusionary” approach to property becomes less attractive, instead yielding to a more particularized “governance” approach (Smith [8–10]). Using the information-theoretic concepts of legal entropy and temperature not only helps to more fully explain modularity, but also provides a means to quantify how modularity functions, and when exclusionary regimes should yield to governance regimes [see generally (Sichelman and Smith, unpublished)²⁷].

Reducing Legal Entropy and the “Work” of the Legal System

As the discussion of modularity shows, the legal system can in effect reduce legal entropy by reducing the uncertainty and related information costs in delineating, interpreting, and applying the law. More generally, lawyers and the legal system expend “work” by drafting and interpreting constitutions, laws, regulations, contracts, patents, and other legal documents to reduce the amount of uncertainty in whether particular actions that legal actors may perform are permitted, forbidden, or obligated (in deontic terms) and in whether particular laws are valid or not (i.e., can effectuate a power in Hohfeldian terms).

Legal “work” expends transaction costs in the time and effort required to draft, interpret, and apply the law, which often encompasses time and effort in negotiation, the collection of facts, the investigation of background law, and so forth.²⁸ A portion of these transaction costs are “information costs” in the sense of Smith [8–10]. The efficient level of information costs can be specifically quantified as the amount of entropy reduction in a legal system or subsystem performed by legal work.²⁹ Specifically:

$\begin{array}{ll}\Delta W_I=-\Delta S_L& (14)\end{array}$

In other words, the amount of legal work efficiently expended in information costs directly reduces the legal entropy by the same amount.³⁰ The legal entropy is the sum of the delineative, interpretive, and applicative entropy defined in earlier, as well as other types of legal entropy not discussed here (e.g., enforcement entropy).

The direct relationship between legal work, information costs, and entropy reduction provides a direct linkage between legal entropy and the economic theory of law, importantly including Coase's Theorem. Specifically, because information costs are a class of transaction costs, one can postulate a Coasean world in which the only transaction costs are information costs.

In a world solely of information costs, the efficient allocation of legal rights will depend on the amount of legal work the legal system must expend on reducing the entropy of the system from one in which both actors hold Hohfeldian privileges (i.e., the absence of a duty) to one in which the actors are subject to one or more duties. As Parisi [4] notes, it is only in the hypothetical absence of transaction costs that delineation is costless and entropy may effectively be disregarded.

Importantly, Coase [12] abstracted away from the fact that the initial delineation of legal entitlements between legal actors itself expends transaction (including information) costs (Lee and Smith [76]). Instead, Coase posited an artificial world of zero transaction costs only after the initial assignment of “property rights,” assuming such assignment is costless. Indeed, as Lee and Smith [76] properly recognize, Coase's [12] notion of “property rights” is more akin to “thin,” costly-to-delineate contractual rights than the usually “lumpy,” less-costly property rights. In this sense, Coase [12] obscured an important aspect of the relationship between transaction costs and the assignment of legal rights. Namely, because “pre-Coasean” transaction costs must be expended in the delineation of the law itself, it will only be efficient to randomly delineate and assign a right to one legal actor or another when these pre-Coasean transaction (including information) costs in so doing are symmetric and, thus, equal.

However, in many, if not most, cases, the transaction costs of delineation are not symmetric in the assignment of entitlements, which implies that an efficient allocation of entitlements will not occur even if transaction costs following that allocation are zero.³¹ This is particularly so for well-defined legal entitlements, a key assumption of the Coasean, post-assignment, transaction cost-less world.³²

In sum, even before the Coasean world comes into being, transaction costs typically play a fundamental role. Thus, postulating a world with no transaction costs only subsequent to the allocation of entitlements does not necessarily imply that the initial assignment is always efficient. An understanding of the delineation entropy involved in the assignment of rights prior to the Coasean world of zero transaction costs is central to a deeper understanding of how transaction costs bear on the efficiency of the legal system.

Conclusion

Numerous legal scholars have discussed the notion of legal entropy, but few have attempted to quantify it. Those attempts to quantify the notion have been limited to analyzing the ambiguity of legal texts by measuring the entropy of words. Although certainly useful, these approaches fail to capture the multifaceted nature of legal entropy. In this article, relying upon the work of Shannon [14, 31] and Hohfeld [15], I have proposed the beginnings of a mathematical framework to quantify legal entropy more broadly. The model proposed offers several useful benefits. First, it offers a potential template for how legal AI systems can measure and store information about the uncertainty of legal systems. Second, the model helps to explain more fully the nature and function of so-called legal indeterminacy as well as the “modularization” of the law and Coasean notions of how transaction costs affect the allocation of legal entitlements. To be certain, the model fails to address important practical details concerning how to assess the underlying probabilities necessary to calculate legal entropy, but hopefully increasing advances in legal AI will lead to the wide-scale realization of such a model in the near future.

Data Availability Statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

I am grateful to my research assistant, Millicent Whitemore, and my research associate, Yuksel Calli, for assembling sources and their detailed review of an earlier version of the manuscript. I also thank Michael Bommarito, Philip Glass, Daniel Martin Katz, Francesco Parisi, Anita Parkash, Henry Smith, and Marika Taylor for helpful comments and questions. I thank Daniel Martin Katz, J. B. Ruhl, and Pierpaolo Vivo for hosting and inviting me to present this article at The Physics of the Law: Legal Systems Through the Prism of Complexity Science.

Footnotes

1. ^The discussion in this section is designed to offer a concise and simplified qualitative background of the notion of entropy in physics and information theory in order to set the stage for the following discussion of legal entropy, and thus should not be viewed as a precise technical account.

2. ^Because the log (AB) = log A + log B, by defining the entropy in terms of a logarithm (such as the natural logarithm), it becomes simpler to calculate entropy as the number of microstates increases, particularly when two systems are combined.

3. ^Another way to conceptualize Shannon entropy is in terms of “surprise,” which typically is defined as the unlikelihood of an event occurring, i.e., 1/p [21]. Since the log (1/p) = –log p, we can rewrite Shannon entropy as proportional to the sum over states of p_i log₂ (1/p_i). Thus, information entropy is driven by a combination of the logarithm of the level of surprise (i.e., improbability) of a given microstate and the probability of the microstate occurring, summed across all microstates.

4. ^Loevinger [30] cites Shannon and Weaver [31] and offers an “equation,” which is best characterized as tongue-and-cheek. Namely, Loevinger [30] states: “The second law of sociodynamics is the law of the conservation of entropy. Entropy, in social as in physical phenomena, is a measure of disorder, uncertainty or confusion. The law of the conservation of entropy in sociodynamics states that the amount of entropy concerning any social problem remains constant regardless of the number of agencies or entities to which it is referred while the time required for decision or action on the problem increases in geometrical proportion to the number of agencies or entities whose concurrence is required. This law can be expressed as T = NC², where “W” is the time required for decision or action and ‘NC' is the number of agencies or entities whose concurrence is required.”

5. ^Other studies use legal documents as inputs and measure entropy unrelated to legal entropy. For instance, Zhang et al. [35] extend the application of Shannon entropy from text to patent indicators, including citation counts, number of patent families, and similar indicators, to measure the importance of particular patents in technological innovation. Although such approaches may be useful for determining the economic “information” content and, hence, the economic importance signified by a particular legal document, they do not measure legal entropy, that is, the uncertainty or ambiguity of a legal document or broader legal relation within the legal system.

6. ^As D'Amato [7] insightfully remarks, “For example, a statute that seemed to mean one thing may be construed by a court to mean something different. Although the court will usually say that it is clarifying the statute, it does not always do so. It may create an exception, an exemption, a privilege; it might construe the rule narrowly to avoid constitutional problems, or broadly to give effect to an unnoticed legislative intent buried in the legislative history. The court's decision becomes a part of the meaning of the rule, so that the rule now becomes more complex—it is a statute plus a judicial decision. The more complex rule may invite further adjudication and more inventive subsequent constructions by courts.”

7. ^Lee et al. [36] propose a statistical mechanics-based model of voting within groups using a maximum entropy model, applying it to the U.S. Supreme Court. This approach is more in the vein of political science than law per se and, as such, is somewhat orthogonal to the discussion here, but it could be useful in quantifying applicative entropy for disputes to be resolved by a group of adjudicators (e.g., on appeal).

8. ^In this regard, contracts also may be considered as a form of “private lawmaking” [39], subject to delineative, interpretative, and applicative entropy. In other instances, law may be formulated in unwritten ways, such as through oral tradition or even social symbols (e.g., Weyrach and Bell [40]), again, subject to all forms of legal entropy.

9. ^Another type of legal entropy is enforcement entropy, which stems from the uncertainty in the enforcement of a given law. I abstract away from enforcement entropy in this treatment for simplicity, but the same types of approaches discussed herein would apply to enforcement entropy (see generally Lederman and Sichelman [41]).

10. ^Dinga et al. [44] provide a conceptual model of “social entropy,” briefly addressing legislation, but do not quantify social entropy in any manner. Although there is a substantial literature regarding “entropy economics” and “economic complexity,” that literature does not address the legal domain (see, e.g., Golan [45], Gold and Smith [46], Hausmann et al. [47]).

11. ^Deontic logic concerns the logic of normative concepts, including obligations (see generally Hilpinen [49]).

12. ^Alternatively, one might imagine a hypothetical in which lawmakers investigate whether some behavior previously subject to legal restrictions should no longer be subject to them—for instance, the use of a previously illegal drug—resulting in similar deontic probabilities. More generally, deontic entropy concerns the uncertainty regarding whether some set of human behavior should be subject to a change in the law, from no regulation to regulation, from regulation to no regulation, or some intermediate set of changes.

13. ^In this regard, the term p(y|x) means the probability of event y given that event × occurs [12].

14. ^Formally, the joint entropy H(x, y) of a pair of discrete random variables (X, Y) with a joint distribution p(x, y) is defined [12] as $H\left(X,Y\right)=-\sum _{x\in X}\sum _{y\in Y}p\left(x,y\right)logp\left(x,y\right)$. The conditional entropy is formally defined [12] as $H(Y|X)=-\sum _{x\in X}\sum _{y\in Y}p(x,y)logp(y|x)$.

15. ^Of course, one must also determine where a legal rule begins and ends to interpret the rule. Sometimes, this process is fraught with difficulty, which itself may introduce a form of interpretive entropy. Here, I abstract away from this potentially additional layer of entropy.

16. ^Of course, some laws apply to the process of lawmaking, enforcement, and adjudication itself. The discussion of applicative entropy here extends to these legal rules as well. Relatedly, it also applies to the application of an interpreted contract, patent, or similar legal document to a set of facts.

17. ^See Marinescu and Marinescu [58] for a detailed discussion of classical information theory.

18. ^In the event the indeterminacy results from mere lack of knowledge, the state of the system can be described wholly by classical probability theory. However, the qubit formalism can easily model both the lack of knowledge and inherent indeterminacy in a given system prior to measurement. Like the difference between classical and quantum mechanics (i.e., in physics), the conceptual difference between mere lack of knowledge and inherent indeterminacy for legal relation states may—in certain conceptions—lead to quantum-like legal effects, such as legal “entanglement” of states, that can distinguish “classical” legal indeterminacy (i.e., lack of knowledge) from “quantum” legal indeterminacy (i.e., inherent indeterminacy). For simplicity, however, I rely upon the classical entropy formulas herein.

19. ^Note that the for the higher-order relations, the states |j_r>_n and |j_~r>_n are 2nd-rank and higher-rank tensors, not simply vectors, as in the standard quantum formalism.

20. ^In this regard, note that while the Von Neumann entropy—which in effect measures the indeterminacy of a mixed quantum state with respect to its entangled substates—is zero for a pure quantum state, there is nonetheless Shannon information entropy for a pure state with respect to the indeterminacy of its potential measurement outcomes prior to a measurement [60].

21. ^In general, outcomes in legal contexts are discrete and small in number, e.g., one of a small number of potential formulations, interpretations, and applications of the law. Even potential remedies are often discrete, though as noted, in some cases, remedies may form a continuous distribution. Enforcement likelihoods may also form a continuous distribution, but as noted, this paper abstracts away from enforcement for simplicity. Of course, empirical studies of legal systems may construct effectively continuous distributions from large datasets (e.g., of words in statutes), but this paper explores legal entropy from an internal perspective of the legal system itself. Of course, it should be straightforward given the discussion here to apply its concepts to such external empirical studies.

22. ^Cf. Gold and Smith [45, 46] (“In other words, we pick the costlier-to-provide legal relation where Shannon entropy is higher and the cheaper signal (sometimes doing almost nothing) for where it is lower.”).

23. ^For a discussion of how one might model the changing information nature of legal rights and related interests over time using an evolutionary approach, see Alston and Mueller [62] and Ruhl [63].

24. ^Sometimes the enforceability of a patent claim turns on facts unique to a given dispute, but for simplicity, I assume here that it is a general determination—i.e., that it applies across all disputes.

25. ^For continuous variables, such as remedies, the differential joint entropy may be used [53].

26. ^Branting et al. [33] uses “maximum entropy” classification models to predict outcomes of a variety motions in federal district court. Although Branting et al. [33] does not discuss legal entropy as that term is used here, maximum entropy models as applied to legal disputes implicitly concern interpretive and applicative entropy. Specifically, Branting et al. [33] attempt to predict outcomes for three different types of motions using the following features: “the party filing the motion, the judge ruling on the motion, the sub-type of motion, and alphanumeric character sequences having non-alphanumeric characters on both the left and right sequence borders that occur in the text of the motion.” As Berger et al. [50] explain, a maximum entropy approach “model[s] all that is known and assume[s] nothing about that which is unknown.” Thus, if one has no information about the result of a motion in court, one assumes the “maximum entropy,” which would give each side a 50% chance of winning. In modeling legal outcomes with maximum entropy models, one begins with one bit of interpretive and applicative entropy per decision and works to reduce the overall entropy—and, thus, increase predictability—by incorporating more and more (training) information by fitting that information to the known data through a series of logistic regressions (see, e.g., Yu et al. [71]).

27. ^Sichelman T, Smith HE. Measuring Legal Modularity. On file with author (2021).

28. ^Another set of information costs (and associated entropy) arises from enforcement of the law. As noted earlier, this article abstracts away from such concerns for simplicity, but they are certainly important, and susceptible to the approaches described herein.

29. ^Here, the “efficient level of information costs” assumes that it is efficient to increase legal certainty; in some situations, legal uncertainty may be economically efficient. Cf. Kaplow [72] (describing potential benefits of uncertainty in legal rules).

30. ^Parisi [5] is apparently the earliest work to associate legal entropy with positive, asymmetric transaction and strategic costs. The model offered in the present article provides a more precise relationship between legal entropy and transaction costs; namely, it posits that transaction costs arise from activities that reduce legal entropy. In other words, information (a form of transaction) costs are expended to make a legal system or set of entitlements more predictable. Cf. Yang [73] (noting that costs to acquire information in the context of an economic coordination game reduce informational entropy). However, in economic parlance, transaction costs may be viewed as a form of economic “friction,” burning up surplus in a metaphorical manner that reduces the amount of available energy (i.e., analogous to surplus) with a concomitant increase in systemwide entropy. More precisely, the burning of surplus in the form of transaction costs will lead to economic uncertainty in the sense of Shannon entropy if the number of microstates corresponding to suboptimal, high-transaction cost welfare regimes is higher than the number of microstates corresponding to relatively optimal, low-transaction cost welfare regimes. (For general reflections on the notion of entropy in economics, see Rosser [74].) Moreover, economic transactions are achieved by physical activities that generate transaction costs, including information costs, and may result in real-world, physical entropy (e.g., the use of a computer) (see, e.g., Georgescu-Roegen [75]). Nonetheless, economic and physical frictions are not the type of “frictions” of concern to legal entropy in the sense used in the present article. In other words, each form of entropy (e.g., legal, economic, physical) is an independent instantiation of the general notion of entropy embodied in the Shannon entropy formula (cf. Jaynes [20]).

31. ^Parisi [77] offers a revision to the Coase Theorem based on a conceptual approach to entropy that focuses on how asymmetric transaction costs in the transfer of property rights affect remedies, rather than the asymmetric costs in the delineation of legal entitlements in the first instance (see also Luppi and Parisi [78]).

32. ^Barzel [65] notes that “[i]t is evident, however, that costless transacting results in the perfect delineation of rights and that it is redundant to also require that rights are well defined,” but does not extend this observation to its effects on the Coase Theorem in the first instance (see also Barzel [79]). Cheung [80] makes a similar observation, stating “private property rights cannot coexist with zero transaction costs.” Cheung [80] criticizes the Coase Theorem on these and other grounds, but does not discuss how these costs might be incorporated into an extended notion of the Coase Theorem.

References

1. Katz DM, Bommarito MJ. Measuring the complexity of the law: the United States Code. Artif Intell Law. (2014) 22:337–74. doi: 10.1007/s10506-014-9160-8

CrossRef Full Text | Google Scholar

2. Friedrich R, Luzzatto M, Ash E. Entropy in legal language. In: CEUR Workshop Proceedings. (2020). p. 25–30.

Google Scholar

3. Dworkin R. Law's Empire. Belknap Press (1986).

Google Scholar

4. Parisi F. Entropy in property. Am J Comparat Law. (2002) 50:595–632. doi: 10.2307/841063

CrossRef Full Text | Google Scholar

5. Parisi F. Freedom of contract and the laws of entropy. Supreme Court Econ Rev. (2003) 10:65–90. doi: 10.1086/scer.10.1147138

CrossRef Full Text | Google Scholar

6. Ruhl JB, Ruhl HJ. The arrow of the law in modern administrative states: using complexity theory to reveal the diminishing returns and increasing risks the burgeoning of law poses to society. UC Davis Law Rev. (1997) 30:407–82.

Google Scholar

7. D'Amato A. Legal uncertainty. Cal Law Rev. (1983) 71:1–55. doi: 10.2307/3480139

CrossRef Full Text | Google Scholar

8. Smith HE. Modularity in contracts: boilerplate and information flow. Mich Law Rev. (2006) 104:1175–222.

Google Scholar

9. Smith HE. Intellectual property as property: delineating entitlements in information. Yale Law J. (2007) 116:1742–822. doi: 10.2307/20455776

CrossRef Full Text | Google Scholar

10. Smith HE. Property as the law of things. Harv Law Rev. (2012) 125:1691–726.

Google Scholar

11. Newman CM. A license is not a ‘contract not to sue': disentangling property and contract in the law of copyright licenses”. Iowa Law Rev. (2013) 98:1101–62. doi: 10.2139/ssrn.2010853

CrossRef Full Text | Google Scholar

12. Coase RH. The problem of social cost. J Law Econ. (1960) 3:1–44. doi: 10.1086/466560

CrossRef Full Text | Google Scholar

13. Solum L. Indeterminacy. In: Patterson D, editor. A Companion to Philosophy of Law and Legal Theory. Oxford: Blackwell Publishing, Ltd (1999). p. 488–502. doi: 10.1111/b.9780631213291.1999.00034.x

CrossRef Full Text | Google Scholar

14. Shannon CE. A mathematical theory of communication. Bell Syst Techn J. (1948) 27:379–423. doi: 10.1002/j.1538-7305.1948.tb01338.x

CrossRef Full Text | Google Scholar

15. Hohfeld W. Some fundamental legal conceptions as applied in judicial reasoning. Yale Law J. (1913) 23:16–59. doi: 10.2307/785533

CrossRef Full Text | Google Scholar

16. Clausius R. Über eine veränderte Form des zweiten Hauptsatzes der mechanischen Wärmertheorie. Poggendorffs Annalen Phys Chem. (1854) 93:481–506. doi: 10.1002/andp.18541691202

CrossRef Full Text | Google Scholar

17. Boltzmann L. Weitere Studien uber das Warmegleichgewicht unter Gasmolekulen. Sitzungsb Akad Wissen Wien Ber. (1872) 66:275–370.

Google Scholar

18. Boltzmann L. Über die Beziehung zwischen dem zweiten Hauptsatze der mechanischen Wärmetheorie und der Wahrscheinlichkeitsrechnung respektive den Sätzen über das Wärmegleichgewicht. Wien Ber. (1877) 76:373–435.

Google Scholar

19. Gibbs JW. On The Equilibrium of Heterogeneous Substances. Connecticut Academy of Arts and Sciences (1874). doi: 10.5479/sil.421748.39088007099781

CrossRef Full Text | Google Scholar

20. Jaynes ET. Information theory and statistical mechanics. Phys Rev. (1957) 106:620–30. doi: 10.1103/PhysRev.106.620

CrossRef Full Text | Google Scholar

21. Stone J. Information Theory: A Tutorial Introduction. Tutorial Introductions (2015).

Google Scholar

22. Lewis PB. Bankruptcy and thermodynamics. Florida Law Rev. (1998) 50:329–84.

Google Scholar

23. Ferrara M, Gagliotti RA. Legal values and legal entropy: a suggested mathematical model. Int J Math Models Methods Appl Sci. (2012) 3:490–8.

Google Scholar

24. Berg L. System of legal impact from social entropy to legal development. Rev Quid. (2018) 2 (Special Issue):133–7.

Google Scholar

25. Edgar C. Struggling against entropy: monetary patent infringement damages after eBay. Drake Law Rev. (2018) 66:45–67.

Google Scholar

26. Fromer J. An information theory of copyright law. Emory Law J. (2014) 64:71–128.

Google Scholar

27. King JH Jr. Deus ex machina and the unfulfilled promise of New York Times v. Sullivan: applying the times for all seasons. Ky Law J. (2007) 95: 650-714.

Google Scholar

28. Moran J. Postmodernism's misguided place in legal scholarship: chaos theory, deconstruction, and some insights from Thomas Pynchon's fiction. South Calif Interdiscip Law J. (1997):155–99.

Google Scholar

29. Stephan PB. One voice in foreign relations and federal common law. Va J Int Law. (2019) 60:1–79.

Google Scholar

30. Loevinger L. Politics and the regulatory agencies. Columb Law Rev. (1968) 68:371–83. doi: 10.2307/1120891

CrossRef Full Text | Google Scholar

31. Shannon CE, Weaver W. The Mathematical Theory Of Communication. Urbana, IL: The University of Illinois Press (1949).

Google Scholar

32. Katz B, Bommarito MJ, Blackman M. A general approach for predicting the behavior of the supreme court of the United States. PLoS ONE. (2017) 12:e0174698. doi: 10.1371/journal.pone.0174698

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Branting LK, Yeh A, Weiss B, Merkhofer EM, Brown B. Inducing predictive models for decision support in administrative adjudication. In: AICOL International Workshops. AI Approaches to the Complexity of Legal Systems, Vol. 10791. Springer (2017). p. 465–77. doi: 10.1007/978-3-030-00178-0_32

CrossRef Full Text | Google Scholar

34. Shannon CE. Prediction and entropy of printed english. Bell Syst Techn J. (1951) 30:50–64. doi: 10.1002/j.1538-7305.1951.tb01366.x

CrossRef Full Text | Google Scholar

35. Zhang Y, Qian Y, Huang Y, Guo Y, Zhang G, Lu J. An entropy-based indicator system for measuring the potential of patents in technological innovation: rejecting moderation. Scientometrics. (2017) 111:1925–46. doi: 10.1007/s11192-017-2337-7

CrossRef Full Text | Google Scholar

36. Lee ED, Broedersz CP, Bialek W. Statistical mechanics of the US supreme court. J Stat Phys. (2015) 160:275–301. doi: 10.1007/s10955-015-1253-6

CrossRef Full Text | Google Scholar

37. Osofsky L. The case against strategic tax law uncertainty. Law Rev. (2011) 64:489–538.

Google Scholar

38. Sichelman T. Myths of (un)certainty at the federal circuit. Loyola Los Angeles Law Rev. (2010) 43:1161–94.

Google Scholar

39. Slawson WD. Standard form contracts and democratic control of lawmaking power. Harv Law Rev. (1971) 84:529–66. doi: 10.2307/1339552

CrossRef Full Text | Google Scholar

40. Weyrach WO, Bell MA. Autonomous lawmaking: the case of the “Gypsies”. Yale Law J. (1993) 103:323–99. doi: 10.2307/797098

CrossRef Full Text | Google Scholar

41. Lederman L, Sichelman T. Enforcement as substance in tax compliance. Wash Lee Law Rev. (2013) 70:1679–749.

Google Scholar

42. Benson BL, Engen EM. The market for laws: an economic analysis of legislation. South Econ J. (1988) 54:732–45. doi: 10.2307/1059016

CrossRef Full Text | Google Scholar

43. Crump D. Game theory, legislation, and the multiple meanings of equality. Harv J Legis. (2001) 38:331.

Google Scholar

44. Dinga E, Tanaescu CR, Ionescu GM. Social entropy and normative network. Entropy. (2020) 22:1051. doi: 10.3390/e22091051

CrossRef Full Text | Google Scholar

45. Golan A. Information and entropy econometrics — a review and synthesis. Foundat Trends Econometr. (2008) 2:1–145. doi: 10.1561/0800000004

CrossRef Full Text | Google Scholar

46. Gold A, Smith HE. Scaling up legal relations. In: Balganesh S, Sichelman T, Smith H, editors. The Legacy of Wesley Hohfeld: Edited Major Works, Select Personal Papers, and Original Commentaries. Cambridge, MA: Cambridge University Press (2021).

Google Scholar

47. Hausmann R, Hidalgo C, Bustos S, Coscia M, Simoes A. The Atlas of Economic ComplexityL Mapping Paths to Prosperity. Cambridge, MA: MIT Press (2014). doi: 10.7551/mitpress/9647.001.0001

CrossRef Full Text | Google Scholar

48. Nakamoto S. Bitcoin: A Peer-to-Peer Electronic Cash System. (2008). Available online at: http://www.bitcoin.org/bitcoin.pdf

Google Scholar

49. Hilpinen R (ed). Deontic logic: introductory systematic readings. In: Synthese Library, Vol. 33. Dordrecht: Springer (1971). doi: 10.1007/978-94-010-3146-2

CrossRef Full Text | Google Scholar

50. Berger AL, Della Pietra SA, Della Pietra VJ. A maximum entropy approach to natural language processing. Comput Linguist. (1996) 22:39–71.

Google Scholar

51. Smith JM. The Theory of Evolution. Cambridge, MA: Cambridge University Press (1993).

Google Scholar

52. Sachs M. Quantum Mechanics and Gravity. Berlin: Springer (2004) doi: 10.1007/978-3-662-09640-6

CrossRef Full Text | Google Scholar

53. Cover TM, Thomas JA. Elements of Information Theory. Wiley (2012).

Google Scholar

54. Piantadosi ST, Tily H, Gibson E. The communicative function of ambiguity in language. Cognition. (2012) 122:280–91. doi: 10.1016/j.cognition.2011.10.004

CrossRef Full Text | Google Scholar

55. Holmes OW. The path of the law. Harv Law Rev. (1897) 10:457–78. doi: 10.2307/1322028

CrossRef Full Text | Google Scholar

56. Yablon CM. The good, the bad, and the frivolous case: an essay on probability and rule 11. UCLA Law Rev. (1996) 44:65–107.

Google Scholar

57. Sichelman T. Some fundamental conceptions as applied in judicial reasoning. In: Hohfeld WN, editors. Wesley Hohfeld One Hundred Years Later: Edited Major Work. Cambridge: Cambridge University Press (2021).

Google Scholar

58. Marinescu DC, Marinescu GM. Classical and Quantum Information. Burlington, MA: Academic Press (2011) doi: 10.1016/B978-0-12-383874-2.00003-5

CrossRef Full Text | Google Scholar

59. Sichelman T. The Mathematical Structure of the Law (2021).

Google Scholar

60. Bjork G. Information gain when measuring an unknown qubit. Eur J Phys. (2018) 39:015403. doi: 10.1088/1361-6404/aa94e4

CrossRef Full Text | Google Scholar

61. Norwich K. Information, Sensation, and Perception. Biopsychology.org (2003).

Google Scholar

62. Alston L, Mueller B. Towards a more evolutionary theory of property rights. Iowa Law Rev. (2015) 100:2255–73.

Google Scholar

63. Ruhl JB. The fitness of law: using complexity theory to describe the evolution of law and society and its practical meaning for democracy. Vanderbilt Law Rev. (1996) 49:1407–90.

Google Scholar

64. Cooter R. Structural adjudication and the new law merchant: a model of decentralized law. Int Rev Law Econ. (1994) 14:215–31. doi: 10.1016/0144-8188(94)90020-5

CrossRef Full Text | Google Scholar

65. Barzel Y. The capture of wealth by monopolists and the protection of property rights. Int Rev Law Econ. (1994) 14:393–409. doi: 10.1016/0144-8188(94)90023-X

CrossRef Full Text | Google Scholar

66. Kennedy D. Form and substance in private law adjudication. Harv Law Rev. (1976) 89:1685–778. doi: 10.2307/1340104

CrossRef Full Text | Google Scholar

67. Singer JW. The player and the cards: nihilism and legal theory. Yale Law J. (1984) 94:3–70. doi: 10.2307/796315

CrossRef Full Text | Google Scholar

68. Kress K. Legal indeterminacy. Calif Law Rev. (1989) 77:283–337. doi: 10.2307/3480606

CrossRef Full Text | Google Scholar

69. Lefstin JA. The measure of the doubt: dissent, indeterminacy, and interpretation at the federal circuit. Hastings Law J. (2007) 58:1025–1094.

Google Scholar

70. Branting K, Weiss B, Brown B, Pfeifer C, Chakraborty A, Ferro L, et al. Semi-supervised methods for explainable legal prediction. In: Seventeenth International Conference on Artificial Intelligence and Law. (2019). p. 22–31. doi: 10.1145/3322640.3326723

CrossRef Full Text | Google Scholar

71. Yu HF, Huang FL, Lin CJ. Dual coordinate descent methods for logistic regression and maximum entropy models. Mach Learn. (2011) 85:41–75. doi: 10.1007/s10994-010-5221-8

CrossRef Full Text | Google Scholar

72. Kaplow L. A model of the optimal complexity of legal rules. J Law Econ Organ. (1995) 11:150–63.

Google Scholar

73. Yang M. Coordination with flexible information acquisition. J Econ Theory. (2015) 158:721–38. doi: 10.1016/j.jet.2014.11.017

CrossRef Full Text | Google Scholar

74. Rosser JB. Entropy and econophysics. Eur Phys J Special Topics. (2016) 225:3091–104. doi: 10.1140/epjst/e2016-60166-y

CrossRef Full Text | Google Scholar

75. Georgescu-Roegen N. The Entropy Law and the Economic Process. Cambridge, MA: Harvard University Press (1971). doi: 10.4159/harvard.9780674281653

CrossRef Full Text | Google Scholar

76. Lee BA, Smith H. The nature of coasean property. Int Rev Econ. (2012) 59:145–55. doi: 10.1007/s12232-012-0152-2

CrossRef Full Text | Google Scholar

77. Parisi F. The Asymmetric Coase Theorem: Dual Remedies for Unified Property. SSRN (2001). doi: 10.2139/ssrn.264314

CrossRef Full Text | Google Scholar

78. Luppi B, Parisi F. Toward an asymmetric coase theorem. Euro J Law Econ. (2011) 31:111–22. doi: 10.1007/s10657-010-9201-z

CrossRef Full Text | Google Scholar

79. Barzel Y. Economic Analysis of Property Rights, 2nd ed. New York, NY: Cambridge University Press (1997). doi: 10.1017/CBO9780511609398

CrossRef Full Text | Google Scholar

80. Cheung SNS. The transaction costs paradigm. Econ Inq. (1998) 36:514–21. doi: 10.1111/j.1465-7295.1998.tb01733.x

CrossRef Full Text | Google Scholar