- 1INAF–Istituto di Astrofisica e Planetologia Spaziali, Rome, Italy
- 2INAF–Osservatorio Astronomico di Trieste, Trieste, Italy
- 3ASI–Italian Space Agency, Rome, Italy
The interaction between the interplanetary medium and planetary environments gives rise to different phenomena on several temporal and spatial scales. Here, we propose for the first time, the application of the Hilbert-Huang Transform (HHT) to characterize both the local and global properties of Mercury's environment as seen during two Mercury Surface, Space Environment, Geochemistry and Ranging (MESSENGER) flybys. In particular, we compute the energy-time-frequency distribution of the observed magnetic field components and the reconstruction of these signals at large, magnetohydrodynamics (MHD) and kinetic scales through the empirical mode decomposition. We show that the HHT analysis allows to capture and reproduce some interesting features of the Hermean environment such as flux transfer events (FTEs), Kelvin-Helmholtz vortices, and ultralow frequency (ULF) wave activity. Moreover, our findings support the ion kinetic nature of the Hermean plasma structures, the characterization of the magnetosheath by anisotropic ion-kinetic intermittent fluctuations, superimposed to both MHD fluctuations and large-scale field structure. Our approach has proven to be very promising for characterizing the structure and dynamics of planetary magnetic field at different scales, for identifying the boundaries, and for discriminating the different scale-dependent features of global and local source processes that can be used for modeling purposes.
1. Introduction
The interplanetary medium significantly affects the dynamics of planetary environments by means of energy and mass transfer processes [1]. This interaction involves several types of phenomena such as magnetic reconnection, plasma instabilities, magnetic flux transport, particle precipitation, turbulence, and waves [2]. The main features of planetary magnetospheres are usually described in the magnetohydrodynamic (MHD) approximation, although some assumptions are not valid for properly describing the ionospheres, i.e., the electrically non-neutral layers of planetary environments [2]. In addition, almost all planetary environments are also characterized by sub-ion/kinetic processes [3, 4] such as wave-particle interactions, damping processes, and stochastic heating [5, 6], thus not properly described in the MHD framework [7]. The basic structure of the magnetosphere of the planets is quite similar and can be understood by scaling the Earth's case, although the dynamical features peculiar to the specific body are completely dependent on its intrinsic/induced nature [8], on the different particle population and plasma composition (especially the presence of heavy ions) [9–11], and on the effects of solar transient phenomena impacting their boundaries [12, 13] and affecting planetary exospheres [14] and environments [15, 16]. Indeed, planetary ionospheres play a key role in planets with small and/or no significant internal magnetic field (such as Venus and Mars) in deflecting solar wind plasma and forming induced magnetospheres; on the contrary, planets with intrinsic main magnetic fields (such as Earth and Mercury) stand off the solar wind plasma flow that modifies its bipolar shape into a comet-like one [17]. Whether induced or intrinsic, these systems are characterized by a wide variety of phenomena occurring on different temporal and spatial scales, as well as in different surrounding regions, which need to be properly identified and investigated [1, 17].
A feasible way to characterize the existence of different dynamical processes within complex systems such as planetary magnetospheres is the investigation of scale-invariant features, allowing proper identification of different regimes by deriving global information on a common description of the fundamental features [18]. However, when measurements come from different surrounding planetary regions, a global investigation only can lead to misleading results due to the fact that scale-invariant properties, structures, and phenomena are localized (i.e., have a smaller spatial scale). This warning/limit needs to be carefully considered when investigating dynamical features at the boundaries of planetary magnetospheres, for example, when crossing the bow shock surface or the magnetopause [3, 8, 19]. Indeed, the local properties of the ambient solar wind could be completely different with respect to the nearest regions, e.g., the foreshock region, which could in turn be different from the magnetosheath and/or the inner magnetosphere. These options mark serious concerns also on theoretical and modeling implications for understanding fundamental mechanisms of turbulence, intermittency, magnetic reconnection, particle acceleration, and transport in space plasmas [17, 20]. Thus, suitable data analysis methods that take into account local features of data, and at the same time allow to characterize global characteristics and scale-invariant features, should be considered for the investigation of the dynamical features of the different regions of planetary environments and of the ambient solar wind [21].
In this paper, we provide the first application of the Hilbert-Huang Transform (HHT) to investigate the near-Mercury electromagnetic environment as observed during two Mercury Surface, Space Environment, Geochemistry and Ranging (MESSENGER) flybys. Our results look encouraging also in light of the next flybys around Mercury by BepiColombo (the first in October 2021). Our goal is to provide a useful tool for discerning between the different regions crossed by spacecraft during planetary flybys. Indeed, our findings will help to characterize the structure and dynamics of planetary magnetic field at different scales as well as to identify some interesting features of the Hermean environment such as flux transfer events (FTEs), Kelvin-Helmholtz vortices, and ultralow frequency (ULF) wave activity, or to detect the “effective” planetary magnetic field that can be used for modeling purposes.
The paper is organized as follows: section 2 presents data used in this study, while section 3 describes the HHT method. Section 4 shows the results of our analysis and discusses different features and outcomes. Finally, a summary of our main findings and future perspectives are given in section 5.
2. Data
The MESSENGER mission has been designed to investigate the features of Hermean environment, the chemical composition of its surface, and the nature of Mercury's exosphere and magnetosphere [22]. MESSENGER was launched on August 3, 2004 at 06:15 UT and reached Mercury's orbit on March 18, 2011, after a sequence of Earth, Venus and Mercury flybys. In the following, we concentrate on the first and the second Mercury flybys on January 14, 2008 and October 6, 2008, respectively, for which measurements at the highest resolution are available. Among the whole list of MESSENGER instruments we used, data collected from the magnetometer (MAG) instrument, a miniature three-axis ring-core fluxgate magnetometer with low-noise electronics, sampling magnetic field values simultaneously by three 20-bit analog-to-digital converters at Δf = 20 Hz and having a fine range of ±1,530 nT full scale (0.047-nT resolution) [23]. MAG data are released at the highest resolution of 20 Hz without applying digital filters, at lower resolutions between 1 and 10 Hz by means of the use of digital filters at Nyquist frequency, and sub-sampled in the frequency range 0.01–0.5 Hz by using a 0.5-Hz filter [23]. During both periods of interest MAG collected data at the highest frequency resolution of 20 Hz which have been retrieved from the automated multi-dataset analysis (AMDA) DataBase at http://amda.irap.omp.eu/desktop.php. We considered a 6-h length time interval centered at the time of the closest approach, corresponding to the time intervals 16:00–22:00 UT and 06:00–12:00 UT for both flybys, respectively. Figure 1 reports the trajectories of both flybys, while MAG data are reported in Figure 2 in the Mercury Solar Orbital (MSO) reference system (i.e., X pointing from Mercury to the Sun, Z pointing northward and orthogonal to Mercury's orbital plane, and Y oriented according to a right-handed orthogonal coordinate system).
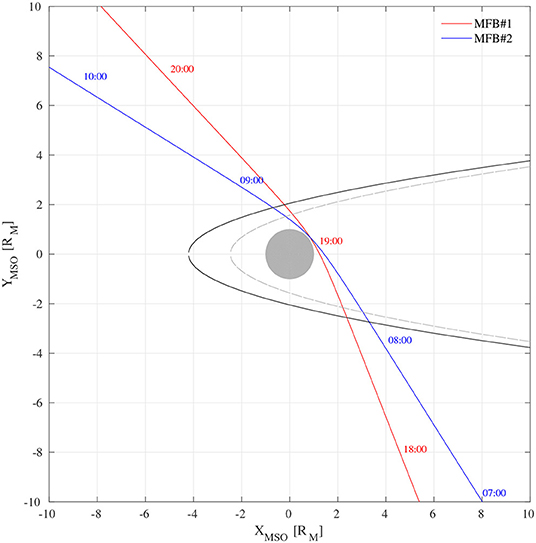
Figure 1. The trajectories in the XMSO − YMSO plane for the first (red) and the second (blue) Mercury flyby, respectively. The gray and the black lines refer to the bow shock and magnetopause models [3, 24], respectively. Time labels refer to the 2 days (i.e., January 14, 2008 and October 6, 2008) and are expressed in UT.
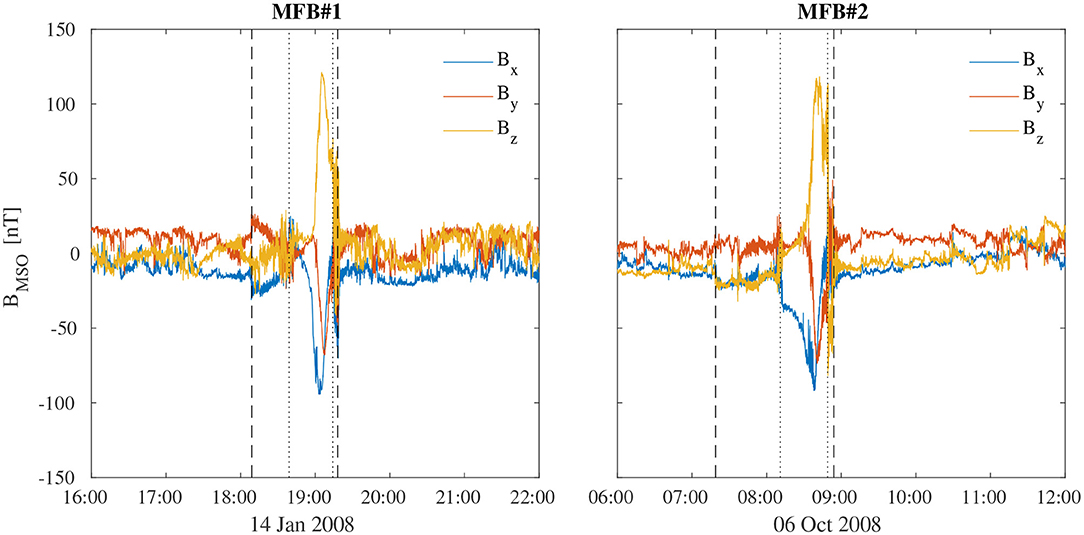
Figure 2. Magnetic field components in the MSO reference frame measured during the first (left) and the second (right) Mercury flyby. The vertical dashed and dotted lines refer to the bow shock and magnetopause crossings, respectively.
As it can be seen in the left panel of Figure 2, during the first Mercury flyby, the MESSENGER crossed the bow shock surface in the inbound and outbound at 18:08 and 19:18 UT on January 14, 2008, respectively, while the inbound and outbound magnetopause crossings occurred at 18:43 and 19:14 UT, respectively. The closest approach was at an altitude of ~200 km and occurred near the local midnight [3]. Several kinds of processes were observed during this flyby as FTEs at the boundary of the magnetosheath, ULF wave activity, and Kelvin-Helmholtz vortex-like structures [3, 4]. Moreover, MESSENGER passed near the center of the cross-tail current sheet and registered the highest value of the magnetic field intensity as the closest approach was reached, with the inner magnetosphere region (see Figure 1) dominated by the bipolar planetary magnetic field of mercury, then decreased until the MESSENGER exited the magnetosphere and went toward the ambient solar wind [3, 23].
The second Mercury flyby was characterized by a similar nightside near-equatorial magnetosphere trajectory, slightly tilted with respect to the first one, again approaching Mercury from the flanks and exiting the magnetosphere not far from the magnetopause and bow shock nose. The inbound and outbound bow shock and magnetopause crossings occurred at 07:19 and 08:54 UT and at 08:11 and 08:49 UT, respectively (right panel of Figure 2, [20]). The spacecraft again passed near the cross-tail current sheet and the closest approach occurred at an altitude of ~250 km. During this transit, the mean interplanetary magnetic field was southward and two FTEs were also observed just inside the dawn magnetopause and in the magnetosheath [25].
3. The Hilbert-Huang Transform
The HHT is a powerful and relatively novel method designed for investigating the instantaneous (local) features of time series by combining the Empirical Mode Decomposition (EMD) and the Hilbert Spectral Analysis (HSA) [26]. It works very well with non-stationary and nonlinear data due to its empirical approach, rather than as a theoretical tool for other common transforms (Lomb-Scargle, Fourier, and Wavelets) [26]. Indeed, by means of the concept of instantaneous frequency introduced by the HHT, it is possible to overcome some limitations of common data analysis methods that are not suitable to carry out local information, producing misleading results and requiring many components to build up a decomposition that corresponds to non-stationary data [27]. Below, we briefly recall the main characteristics of the EMD and the HSA procedures.
3.1. Empirical Mode Decomposition
The EMD is the fundamental part of the HHT since it allows to derive embedded components that are suitable for the next step of the HSA [26]. The EMD allows to decompose any complicated dataset into a finite and small number of oscillating components and a non-oscillating residue as
Each empirical mode or intrinsic mode function is a function having the same (or differing at most by one) number of extrema and zero crossings and a zero-average mean envelope derived from local maxima and minima envelopes. They are derived via an iterative process, known as sifting process, without leaving the time domain. As a consequence, EMD is adaptive, highly efficient, free of any a-priori constraints, and can be applied to nonlinear and non-stationary processes [26]. The sifting process is an iterative algorithm which exploits the local properties of time series to derive embedded oscillations known as intrinsic mode functions or empirical modes. The first step is to derive a zero-mean signal
being 〈…〉 the time average, and to identify its local maxima and minima . Then, they are separately interpolated by using a cubic spline to derive the so-called upper and lower envelopes, from which the mean envelope is obtained as
At this stage a candidate “intrinsic mode function” is obtained as . However, after the first round of sifting, new extrema can be generated such that cannot satisfy the requirements to be classified as an intrinsic mode function, i.e., having the same (or differing at most by one) number of extrema and zero crossings whose envelopes are symmetric with respect to zero [26]. Thus, is now treated as a new time series whose upper , lower , and mean envelops are derived, thus producing another candidate intrinsic mode function . The above steps are repeated n times until the so-called candidate “intrinsic mode function” satisfies the requirements to be classified as an intrinsic mode function, thus obtaining the first empirical mode [26]. Then, is subtracted to the zero-mean signal and, since the new signal still contains longer period oscillations, it requires to be subjected to the same sifting process as described above. The sifting process ends when no more oscillating functions can be extracted out, e.g., when the final residue of the decomposition is obtained [26]. Since an infinite number of iterations is ideally required to derive the decomposition basis, Huang et al. [26] proposed to stop the sifting process when the sum of the difference between successive steps defined as
is less than a fixed value ϵ ∈ [0.2, 0.3]. This criterion has been refined by Flandrin et al. [28] by the so-called threshold method based on two thresholds, θ1 and θ2, to guarantee globally small fluctuations (as in [26]) and to avoid locally large excursions [28]. For our analysis we used the threshold method proposed by Huang et al. [26] by setting ϵ = 0.2, although no significant differences, both in terms of the extracted number of IMFs and their shapes, are found between the two criteria [27, 28].
3.2. Hilbert Spectral Analysis
The derived empirical modes guarantee a well-behaved HSA, i.e., the use of the Hilbert Transform (HT) to write each as modulated both in amplitude and in phase [26]. Thus, given an empirical mode , its Hilbert Transform is defined as:
where is the Cauchy principal value. Basically, this is the convolution of with 1/t. By defining the complex signal
we obtain
where and Φk(t) are the instantaneous amplitude and phase of the k−th empirical mode, respectively. Equations (5)–(8) are also known as the Carson-Gabor representation of time series, allowing to represent signals in the time-frequency plane in terms of so-called “information diagrams” [29, 30]. In this way we are able to carry out local information on the amplitude and phase variability, being both and Φk(t) time-dependent [26]. Moreover, also a novel concept of instantaneous frequency [31, 32] immediately comes out as:
from which a typical mean timescale of oscillation can be derived for each empirical mode as:
These two novel concepts of instantaneous amplitude and phase are fundamental for avoiding a-priori mathematical assumptions, thus allowing to derive local features in time. Indeed, the time-dependent amplitude is particularly suitable for correctly dealing with nonlinear features of time series, while the time-dependent phase Φ(t) is efficient for deriving non-stationary characteristics. Moreover, the sifting algorithm allows to obtain oscillating components on different timescales, thus properly investigating processes of different origin and with different features [26].
Thus, after performing the Hilbert transform on each empirical mode we may write the original data as
enabling us to represent the overall energy of the time series in a time–frequency plane by contouring the squared amplitude of the whole set of empirical mode, thus defining the so-called Hilbert-Huang energy spectrum [26]. In this way, local (temporal) information at different frequencies can be simply derived (thus providing a powerful measure of the instantaneous contribution of the different processes [26]). The Hilbert-Huang energy spectrum is exactly equivalent to a spectrogram, i.e., a visual representation of the spectrum of frequencies of a signal as it varies with time, as obtained for other transforms (e.g., Fourier or Wavelet, although usually termed “scalogram”). Moreover, global information at different frequencies can be easily exploited by defining the marginal power spectral density as the time-integrated version of , e.g.,
offers a measure of the total energy contribution from each frequency value, representing the cumulated energy over the entire data span, in a similar way to the Fourier power spectral density [26]. The concept can be rapidly expanded to all statistical moments q ≥ 0 by defining
allowing us to investigate scale-invariant features and scaling-law behavior, since in case of scale-invariance, we have:
being ξ(q) the Hilbert-based scaling exponent, which can be easily associated with the classical scaling exponent ζ(q) obtained via the structure function analysis as ζ(q) = ξ(q) − 1. This approach has been widely applied to characterize scale-invariant properties of fluid turbulence (e.g., [33]), also in the case of passive scalar turbulence (e.g., [34]), as well as, space plasma turbulence (e.g., [21]).
4. Results and Discussions
Applying the EMD we obtained a set of N1 = {20, 23, 24} and N2 = {23, 25, 26} empirical modes for each magnetic field component measured during the first and the second Mercury flybys, respectively. It is important to note that the EMD acts as a sort of dyadic filter [28], and it is expected to filter out a number of empirical modes of the order of log2(Nt), where Nt is the number of points of the considered time series. In our case Nt= 432,000 (i.e., 6 h at 1/20 s sampling time), thus log2(Nt) ~ 18. Since the number of extracted modes is larger than the expected one, the studied time series have a more complex structure and store a larger information content than a purely stochastic noise [28, 35–37]. Thus, they can be used as representatives of fluctuations in a specific range of scales, and can be related to a wide class of physical processes [35]. However, the evidence of this power-law behavior only provides global information on the overall dynamical features of the Hermean electromagnetic environment as observed during the two flybys. To derive local information in the time-frequency (scale) plane, we evaluated the Hilbert-Huang energy spectrum for each magnetic field component as shown in Figure 3.
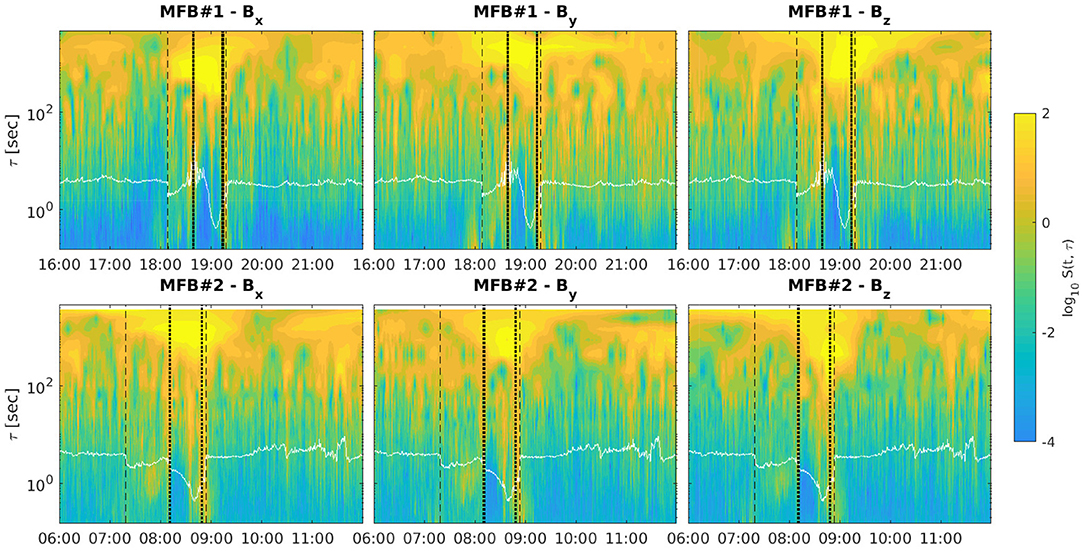
Figure 3. The Hilbert-Huang energy spectrum for each magnetic field component (Bx, By, and Bz, in the left, middle, and right panels) for the first (top) and the second (bottom) Mercury flybys, respectively. The white line corresponds to the ion-cyclotron scale τci = 1/fci, while the vertical dashed and dotted lines refer to the bow shock and magnetopause crossings, respectively. The instrument noise is <20 pT/Hz1/2 at 1-Hz intrinsic noise level [23]. For optimal visualization, data are shown within the logarithmic range [−4, 2], allowing the colormap saturation above 2.
It can be noted that both flybys' measurements are characterized by highly non-stationary features since the Hilbert-Huang energy spectrum shows a clear dependence on time across the whole scale range [26]. It is also evident from Figure 3 that the energy increases on the whole scale spectrum as the MESSENGER approached the inner magnetosphere, reaching its maximum around the closest approach time (bright yellow area). This can be simply related to the difference in terms of magnetic field intensity in the inner magnetosphere, being about 1–2 orders of magnitude higher than ambient solar wind (few nT vs. tens/hundreds of nT). Moreover, a significant increase is found for magnetic field fluctuations at shorter scales [below the ion-cyclotron scale τci = 1/fci = mi/(qiB)] in the magnetosheath which could be the effect of the rich diversity of non-MHD–type fluctuations [4] (see the region below the white line in Figure 3).
If we look at the different regions separately some additional features can be noticed. The ambient solar wind shows classical signatures of the MHD fluctuations within the so-called MHD (inertial) range (τ ∈ [τci, τf], being s the large-scale break usually associated with the beginning of the large-scale forcing–dominated regime) [21, 38], together with less pronounced non-MHD fluctuations. It is apparent in Figure 3 that the Mercury's magnetosheath is clearly dominated by kinetic fluctuations at τ < τci, especially in the outbound region when the MESSENGER approached again the ambient solar wind (i.e., 19:14–19:18 and 08:49–08:54 UT for the first and the second flyby, respectively), mixed with both MHD fluctuations and large-scale processes (τ ≳ τf) which can drive topological changes of the magnetic field configuration, quite similar to the Earth's magnetosheath ones [39]. This region is indeed characterized by small-scale processes associated with the development of ULF wave activity and MHD-like processes such as instabilities and flux-transfer phenomena [3]. Finally, the inner magnetosphere is characterized by large-scale high-energy fluctuations, representative of the main structure of the magnetosphere, and MHD-type processes when the innermost regions are crossed. Interestingly, the clear difference between the Hermean magnetosphere and the ambient solar wind across the whole frequency range seems to support the existence of two distinct regions within a stable and steady-state overall configuration of the near-Mercury electromagnetic environment. Furthermore, the high energy detected at non-MHD scales support previous findings on the key role of non-MHD effects and processes of the Hermean environment [4].
By keeping in mind the above features, we also investigated the time-dependent features of the different dynamical regimes (i.e., the large-scale, the MHD, and the ion-kinetic regimes) by summing up empirical modes into the different scaling ranges. The ion-kinetic regime can be easily identified by summing up empirical modes whose local timescales are below the ion-cyclotron timescale τci (except for the first mode which is found to be not significant). The break τf between the large-scale and MHD regimes is instead locally evaluated by means of the scaling-law behavior across the different frequencies for each time t. Thus, the MHD regime is obtained by empirical mode reconstructions whose timescales are within the ion-cyclotron timescale τci and the large-scale break τf, while the large-scale reconstruction corresponds to summing up empirical modes with τ > τf. Thus, for the i−th magnetic field component we can define:
The sub-ion, MHD, and large-scale reconstructions for each magnetic field component and for both flybys are displayed in Figure 4. It is easy to note that large-scale range (magenta lines in Figure 4) allows us to characterize properly the profile of the main magnetic field, clearly increasing as the planet is approached due to the intensification of the intrinsic main field. This reconstruction can be really helpful for testing numerical models reproducing the behavior of the main field. In fact, it is free of any higher frequency dynamics of different origin, and the “effective” planetary magnetic field may be identified. Moreover, this reconstruction also allows a correct characterization of the magnetosheath large-scale behavior as well as to investigate and localize the boundaries. The MHD range dynamics (cyan lines in Figure 4) is instead characterized by localized fast amplitude enhancements, especially for the magnetosheath region of Mercury. This could be helpful for characterizing and investigating some localized phenomena inside planetary magnetospheres as the FTEs [40], possibly identified at the boundary of the inbound magnetosheath, or dynamical processes affecting the diamagnetic decrease or the ion boundary layer. Moreover, this range can be helpful for investigating magnetospheric turbulence, reconnection-driven processes in the plasma sheet, plasma convection processes, and turbulent vortices stability [4]. Finally, the sub-ion/kinetic range dynamics (green lines in Figure 4) is particularly helpful for investigating kinetic processes occurring in the inner magnetosphere and surrounding regions, where significant increases in amplitudes are found at these scales. It can also allow us to investigate physical processes affecting the magnetosheath of Mercury, and the interplay between foreshock and magnetosheath processes (as kinetic Alfvén waves or whistler waves or ULF waves, if simultaneous plasma and magnetic field measurements can be provided, or different kinds of plasma instabilities [4]).
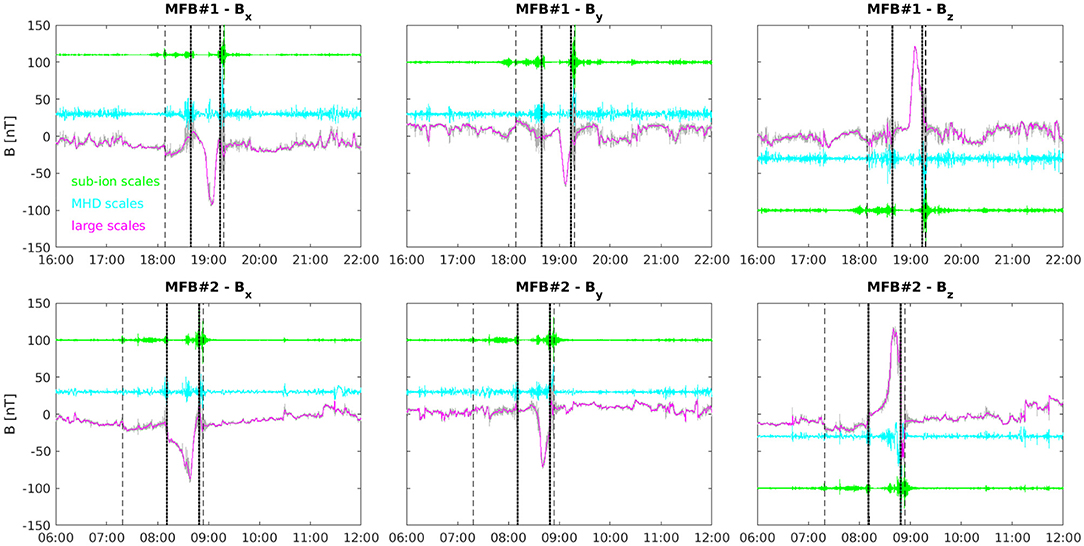
Figure 4. The sub-ion (green), the MHD (cyan), and the large-scale (magenta) reconstructions for each magnetic field component (Bx, By, and Bz, in the left, middle, and right panels) for the first (top) and the second (bottom) Mercury flybys, respectively. The gray line corresponds to the raw data, while the vertical dashed and dotted lines refer to the bow shock and magnetopause crossings, respectively. An offset is applied to the sub-ion and MHD reconstructions for visual purposes.
To assess the suitability of the empirical modes and their local properties in correctly reproducing some interesting features of planetary environments, we also investigate how the different reconstructions of empirical modes in the “sub-ion range,” “MHD range,” and “large-scale range” behave during some selected time intervals of the both Mercury flybys as also described in [3]. We focus on four time periods characterized by boundaries' crossings, a FTE, the vortex-like structures related to the Kelvin-Helmholtz instability at the magnetopause boundary, and the ULF wave activity in the outbound magnetosphere. The results for selected magnetic field components are shown in Figure 5.
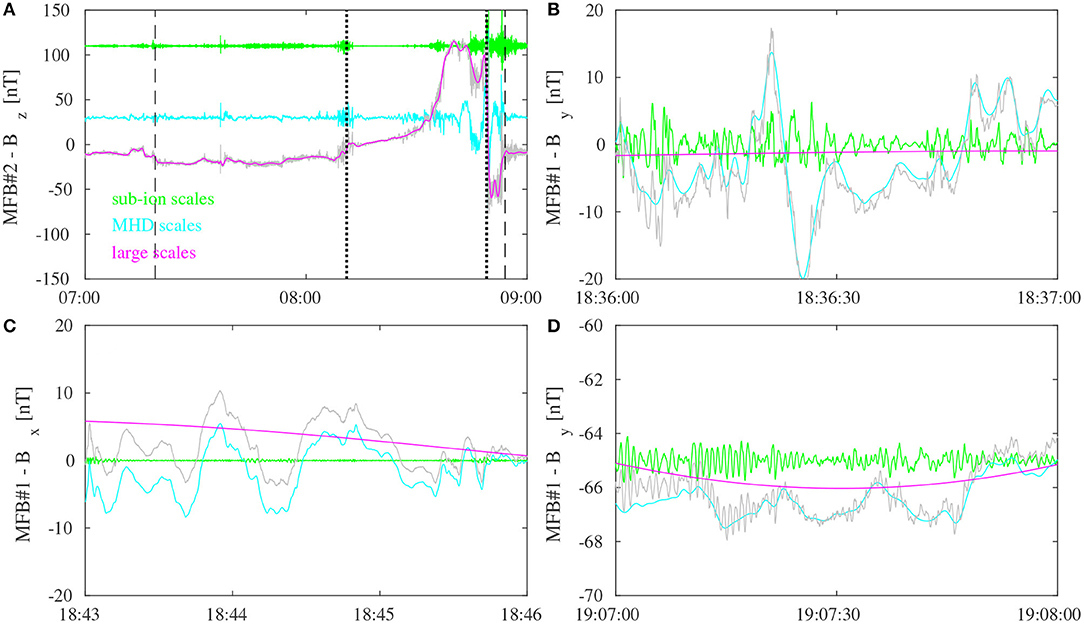
Figure 5. The comparison between the original time series (gray lines) and the different reconstructions (colored lines) for selected magnetic field components during some selected intervals corresponding to (A) the near-Hermean electromagnetic environment, (B) a flux transfer event (FTE), (C) Kelvin-Helmholtz vortex-like structures, and (D) ULF waves. Green, cyan, and magenta lines refer to the kinetic, MHD, and large-scale ranges, respectively. The vertical dashed and dotted lines in (A) refer to the bow shock and magnetopause crossings, respectively. An offset is applied to the sub-ion and MHD reconstructions for visual purposes in (A,D).
4.1. Large-Scale Features and Boundaries
During the second flyby MESSENGER crossed the inbound bow shock surface at 07:19 UT, leaving the Hermean electromagnetic environment at 08:54 UT, entering again in the ambient solar wind. These boundaries are indicated by the dashed lines in Figure 5A where the z component of the magnetic field is illustrated (gray line), together with its sub-ion (green line), MHD (cyan line), and large-scale (magenta line) reconstructions. The large-scale reconstruction is particularly efficient to identify not only the main magnetic field contribution due to the inner core of the planet but also its changes at the bow shock and the magnetopause crossings. This is especially evident for the outbound magnetopause and bow shock crossings at 08:49 UT and 08:54 UT, respectively. We can clearly see a fast decrease of Bz when crossing the outbound magnetopause and an increase when the outbound bow shock is crossed. Moreover, we also observe amplitude enhancements near the magnetopause surface for the MHD reconstructions during both the inbound and outbound crossings, being representative of MHD processes occurring near the magnetopause boundary (see below for more details). Furthermore, the MHD reconstruction seems also to be able to characterize a vortex-like structure, associated with the sudden change in the Bz sign, observed near the outbound magnetopause crossing at 08:45 UT, together with amplitude increases at sub-ion/kinetic scales. Finally, the outbound magnetosheath is clearly characterized by high-amplitude enhancements at sub-ion scales (see the green line in Figure 5A) with respect to the inbound one, being the reflection of ion-kinetic processes occurring in this region. These findings seem to support the suitability of using the EMD reconstructions to characterize and identify different surrounding planetary regions in terms of the different scale-dependent processes occurring into these locations as well as boundaries' crossings.
4.2. Flux Transfer Event
A FTE is observed in the By component between 18:36:21 and 18:36:25 of the first MESSENGER flyby during its passage through the magnetosheath (Figure 5B). The typical signature of a FTE is its helical structure with a clear bipolar By signature [41], as it can be easily noted in Figure 5B, typically produced by localized magnetic reconnection between the interplanetary magnetic field and the planetary one. This feature is well-reproduced by means of the “MHD range” reconstruction of empirical modes (the cyan line). An interesting feature emerging from the HHT analysis is that in correspondence of the FTE there is also a non-negligible contribution at sub-ion/kinetic scales (see green lines in Figure 5B), while a constant large-scale reconstruction is observed. According to previous observations, multiple macroscale FTEs can consist of numerous small-scale ones, leading to complex structures within the flux rope [42]. Nevertheless, our finding suggest that sub-ion/kinetic processes can be generated and enclosed within the MHD-scale flux rope that is responsible of the FTE. However, further statistical investigations are needed to go deeper into this binomial sub-ion/kinetic–MHD nature of FTEs.
4.3. Kelvin-Helmholtz Vortices
Near the interface between the flanks of the plasma sheet and the magnetosheath, the MESSENGER observed several rotations of the magnetic field caused by vortices driven by the Kelvin-Helmholtz instability. Figure 5C reports typical examples of Kelvin-Helmholtz vortices in the Bx component [3] observed at the flanks of the plasma sheet and the magnetosheath [43]. As for the FTE case, the “MHD range” reconstruction allows to reproduce the main features of the vortex-like structures, thus supporting their description in terms of MHD-like processes in a region with a strong northward large-scale magnetic field (magenta lines). However, differently from the FTE there are no enhancements into the sub-ion/kinetic reconstructions, thus suggesting a purely MHD nature of Kelvin-Helmholtz vortices. This seems also be in agreement with MHD numerical simulations that are able to correctly describe Kelvin-Helmholtz vortices with respect to FTEs [44, 45].
4.4. Ultra Low Frequency Wave Activity
Furthermore, during its closest approach MESSENGER also observed ion cyclotron waves and other plasma-wave modes in the ULF band, namely on frequencies below the ion cyclotron frequency [46]. As shown in Figure 5D these oscillations are well-reproduced by the “kinetic range” reconstruction (the green line), as expected since it involves empirical modes with mean timescales larger than the ion-cyclotron scale τci, as especially evidenced in the By component. This occurs while the original time series are also characterized by MHD-like and large-scale structures which can be associated with both magnetospheric turbulence and the dipolar internal magnetic field of Mercury. Further analysis is required to better characterize these findings by means of bulk plasma properties [3].
4.5. Interplanetary Medium vs. Hermean Magnetosheath Scaling Properties
As a final step of our analysis we investigate the scaling properties of the near-Hermean solar wind with respect to those of the Hermean magnetosheath region. To do this we investigate the high-order statistics in terms of scaling exponents ζ(q) for the two regions by means of evaluating the generalized Hilbert spectra as in Equation (13) for q ∈ [0, 4], then evaluating the Hilbert-based scaling exponents ξ(q) over the MHD inertial range, and deriving the classical scaling exponents ζ(q) = ξ(q) − 1. This is for two different reasons: (i) the MHD range is characterized by stationary increments (fluctuations), thus being the best suitable frequency range for scaling law purposes [47], and (ii) scaling exponents can be directly compared with theoretical results derived from the statistics of increments [18, 48]. As usual, if ζ(q) is a linear function of q then the system shows monofractal features, while if ζ(q) is a nonlinear convex function of q then the system has a multifractal character. Moreover, meaningfully high-order moments scaling exponents can be obtained up to a maximum order qmax = log10(Nt) − 1 = log10(432,000)−1 = 4 [49], thus explaining our choice on the range of q ∈ [0, 4]. Figure 6 shows the scaling exponents ζ(q) of the MHD range for the first Mercury flyby in the solar wind and the magnetosheath.
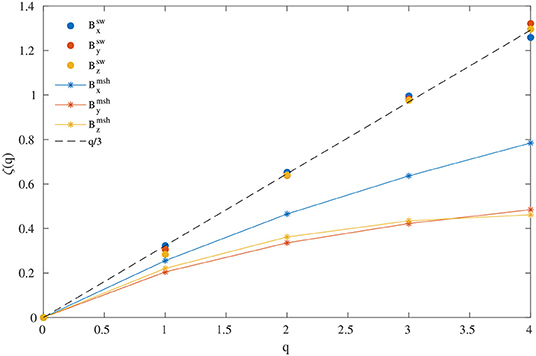
Figure 6. Scaling exponents ζ(q) of the MHD range for the first Mercury flyby in the solar wind and the magnetosheath, respectively. Blue, orange, and yellow symbols refer to the magnetic field components. Filled circles correspond to the solar wind, while asterisks refer to the magnetosheath, respectively. The dashed black line refers to the theoretical scaling of q/3 [48].
The results suggest that solar wind magnetic fluctuations are characterized by scaling exponents ζ(q) that linearly behave with q near Mercury (instead of being a nonlinear convex function of q as observed at larger heliocentric distances [21]). The linear behavior suggests a monofractal nature of solar wind magnetic field fluctuations near Mercury that can be interpreted as the evidence of the self-similarity for high-order statistics, while a multifractal nature is observed, due to the emergence of intermittency, at larger heliocentric distances [21, 50]. Conversely, the complexity of near-Mercury environment shows completely different features, being the magnetosheath characterized by a nonlinear convex behavior for all q, with a high degree of intermittency, especially for both By and Bz, that could indicate a strong anisotropic turbulent environment characterized by intermittent fluctuations, similar to the terrestrial magnetosheath [39]. This can be interpreted as a two-dimensional magnetic field fluctuations topology due to intermittent phenomena taking place into the Hermean magnetosheath, being the magnetic field directed along the x-axis with more organized fluctuations. This seems to suggest stronger anisotropic intermittent fluctuations for the Hermean magnetosheath with respect to the terrestrial one [39]. Furthermore, by strictly referring to the second-order scaling exponent, there seems to be a different nature of the energy transfer across the inertial range domain, being ζ(2) for the solar wind larger than that observed into the Hermean magnetosheath. This points toward a different nature of turbulent fluctuations, being not only more intermittent than the corresponding solar wind ones, but also characterized by faster kinetic energy decaying mechanisms [4]. Indeed, the magnetosheath region of Mercury has been shown to be quite similar to the Earth's one [39], although energy-transfer mechanisms are faster (of the order of seconds/minutes) than those at the Earth (hundreds of minutes). This implies that plasma instabilities developing at the boundaries of Mercury can lead to a more intermittent nature than the ambient solar wind due to localized processes occurring at the boundaries as mirror/ion-cyclotron/firehose instabilities or Alfvén vortex filaments [4, 39].
5. Conclusions
In this paper we provided a study of the dynamical features of the near-Mercury environment as described from magnetic field measurements collected by the MESSENGER during two Mercury's flybys. The main novelty of this work is given by the use of the HHT method to investigate the magnetic field variability across different regions. The HHT is particularly suitable for investigating local features, in terms of amplitude enhancements and processes, occurring over a wide range of frequencies and of possible different origin, as observed in planetary environments [37]. This analysis is performed both in terms of local and global properties, as well as in terms of scaling law behaviors. It is the first time that this type of analysis is used to characterize the different regions of planetary environments, although widely used for investigating the near-Earth regions [51]. The main results can be summarized as follows:
1. The near-Mercury environment presents different features with respect to the ambient solar wind. Locally, the largest energy is found at lower frequencies when the MESSENGER resided into the inner magnetosphere (from few nT to hundreds of nT), as an effect of the large-scale internal magnetic field of Mercury. High-frequency enhancements are observed in the magnetosheath, in the central plasma sheet and in the ion boundary layer adjacent to the outbound magnetopause, due to the rich diversity of non-MHD–type fluctuations [4]. In detail, the foreshock region is characterized by both large-scale structure and ion-kinetic intermittent fluctuations [4]; the magnetosheath shows kinetic fluctuations, especially in the outbound region, mixed with MHD fluctuations, possibly associated with FTEs produced by localized magnetic reconnection [3, 40]; and the inner magnetosphere is characterized by large-scale fluctuations, being representative of the main structure of the magnetosphere, MHD-type processes in the innermost regions [3], and ion-kinetic processes near the ion boundary layer.
2. By using the HHT, three different dynamical regimes can be identified: (i) the large-scale range for τ > τf, (ii) the MHD or inertial range for τci < τ < τf, and (iii) the sub-ion/kinetic range (non-MHD) for τ < τci. The first one can reproduce the behavior of the internal main magnetic field, thus the “effective” planetary magnetic field. It can be used for modeling purposes, since it is free of any higher frequency dynamics of different origin. The intermediate range allows to characterize the inertial range dynamics as FTEs, magnetospheric turbulence, reconnection-driven processes in the plasma sheet, plasma convection processes, and turbulent vortices stability [4]. Finally, the kinetic range dynamics allows to reproduce the non-MHD features and can allow to investigate several types of ion-kinetic processes as kinetic Alfvén waves and plasma instabilities. Hence, being able to capture and reproduce some interesting features of the Hermean environment as FTEs, Kelvin-Helmholtz vortices, and ULF wave activity, the HHT is a suitable method for characterizing physical processes of a different nature.
3. The high-order statistics of the inertial range dynamics highlights some interesting features of the different regions in the surrounding planetary space. Firstly, the ambient solar wind near Mercury is characterized by a linear dependency of ζ(q) on q, thus indicating a monofractal nature of solar wind magnetic field fluctuations. This analysis seems to confirm that a breakdown of the statistical self-similarity due to the emergence of intermittency in the inertial range of solar wind turbulence is observed through the interplanetary space at larger distances (e.g., >0.4 AU) than the Mercury's orbit [21]. Secondly, the magnetosheath of Mercury is instead characterized by a multifractal intermittent nature, different from the surrounding solar wind. In particular, a higher degree of intermittency is found with respect to the terrestrial magnetosheath [39] that could indicate a stronger anisotrpic turbulent environment characterized by intermittent fluctuations, especially in the Y-Z plane [4].
The role of the three dynamical regimes into the different near-Hermean regions can be explicitly seen in Figure 7 reporting the magnetic field intensity (in logarithmic scale) into the sub-ion/kinetic (BK), the MHD/inertial (BI), and the large-scale (BL) regimes along the two flybys trajectories.
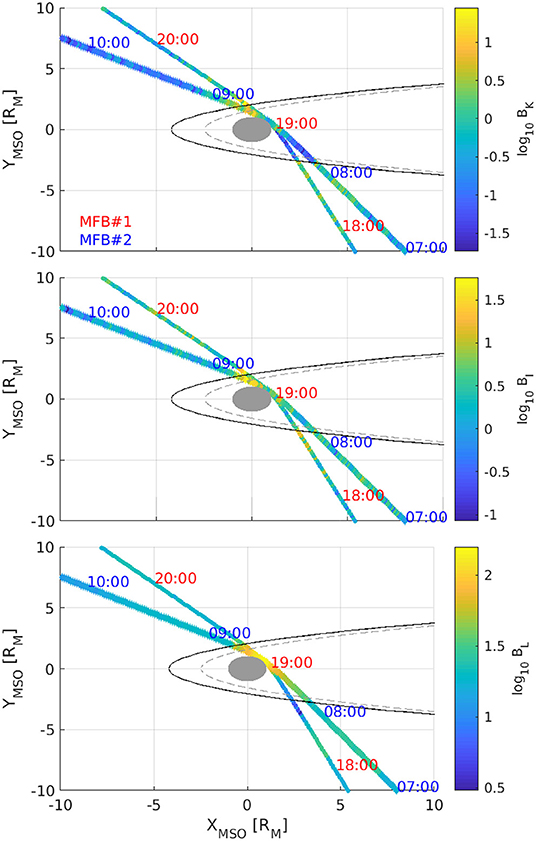
Figure 7. The sub-ion/kinetic BK (top), the MHD/inertial BI (middle), and the large-scale BL (bottom) reconstructions for the magnetic field intensity (in logarithmic scale) along the trajectories of both Mercury flybys. The gray and the black lines correspond to the bow shock and magnetopause models [3, 24]. Time labels refer to the 2 days (i.e., January 14, 2008 and October 6, 2008) and are expressed in UT.
It is evident that large-scale magnetic field fluctuations intensified into the inner magnetosphere, especially approaching the lowest altitude. Conversely, MHD fluctuations enhance at the bow shock and magnetopause crossings, being the reflection of MHD plasma instabilities developing at the boundaries (e.g., FTEs and K-H vortices), while sub-ion/kinetic processes mostly characterize the outbound magnetosheath region.
Our results can be particularly useful for the characterization of the structure and dynamics of planetary magnetic field into the different dynamical regimes, thus investigating physical processes of different origin. The potential of the HHT is still far from being fully explored. In fact, future investigation are surely required on different parameters, as for example, the distribution of the different particle populations, the plasma parameters (density, temperature, and velocity), or the electric field, combined with magnetic field observations. Moreover, also high-resolution measures and different scenarios should be explored as for example the effects of a solar perturbation on the different planetary surrounding regions.
In this view, the ESA/JAXA BepiColombo mission will help to provide new high resolution measurements by means of the two magnetometers onboard two separate spacecraft, the Mercury Planetary Orbiter (MPO) and the Mercury Magnetospheric Orbiter (Mio). In particular, the MPO will orbit closer to the planet and study the surface and internal composition of the planet, while Mio will have larger orbit to study Mercury's magnetosphere. MPO and MIO will offer a more complete and simultaneous view of the different magnetospheric regions for a deeper characterization of Mercury's environment in terms of high resolution (up to 128 Hz) magnetic field measurements [52] as well as of neutral and ionized particle distribution via the SERENA package [53], and other ion and electron sensors onboard to provide a global view of the Hermean environment.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author/s.
Author Contributions
TA planned the manuscript, provided data analysis, and drafted the manuscript. AMi planned the manuscript, interpreted the results, and drafted the manuscript. ML, SM, and SI interpreted the results and reviewed the manuscript. AI, CP, ED, VM, AMu, SO, and RR contributed to the scientific discussions and reviewed the manuscript draft. All authors contributed to the article and approved the submitted version.
Funding
This work was supported by the ASI-SERENA contract no. 2018-8-HH.O Partecipazione scientifica alla missione BEPICOLOMBO SERENA Fase E and the ESA contract (RFP/NC/ IPL-PSS/JD/258.2016) Expert Support to SERENA Science Operations.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
1. Russell CT. Magnetic fields of the terrestrial planets. J Geophys Res. (1993) 98:18681–96. doi: 10.1029/93JE00981
3. Slavin JA, Acuna MH, Anderson BJ, Baker DN, Benna M, Gloeckler G, et al. Mercury's magnetosphere after MESSENGER's first flyby. Science. (2008) 321:85. doi: 10.1126/science.1159040
4. Uritsky VM, Slavin JA, Khazanov GV, Donovan EF, Boardsen SA, Anderson BJ, et al. Kinetic-scale magnetic turbulence and finite Larmor radius effects at Mercury. J Geophys Res. (2011) 116:A09236. doi: 10.1029/2011JA016744
5. Hadid LZ, Sahraoui F, Kiyani KH, Retinó A, Modolo R, Canu P, et al. Nature of the MHD and kinetic scale turbulence in the magnetosheath of saturn: cassini observations. Astrophys J. (2015) 813:L29. doi: 10.1088/2041-8205/813/2/L29
6. Sahraoui F, Hadid L, Huang S. Magnetohydrodynamic and kinetic scale turbulence in the near-Earth space plasmas: a (short) biased review. Rev Modern Plasma Phys. (2020) 4:4. doi: 10.1007/s41614-020-0040-2
7. Vörös Z, Yordanova E, Khotyaintsev YV, Varsani A, Narita Y. Energy conversion at kinetic scales in the turbulent magnetosheath. Front Astron Space Sci. (2019) 6:60. doi: 10.3389/fspas.2019.00060
8. Anderson BJ, Johnson CL, Korth H, Purucker ME, Winslow RM, Slavin JA, et al. The global magnetic field of mercury from MESSENGER orbital observations. Science. (2011) 333:1859. doi: 10.1126/science.1211001
9. Milillo A, Wurz P, Orsini S, Delcourt D, Kallio E, Killen RM, et al. Surface-exosphere-magnetosphere system of mercury. Space Sci Rev. (2005) 117:397–443. doi: 10.1007/s11214-005-3593-z
10. Mura A, Milillo A, Orsini S, Massetti S. Numerical and analytical model of Mercury's exosphere: Dependence on surface and external conditions. Planet Space Sci. (2007) 55:1569–83. doi: 10.1016/j.pss.2006.11.028
11. Orsini S, Mangano V, Mura A, Turrini D, Massetti S, Milillo A, et al. The influence of space environment on the evolution of Mercury. Icarus. (2014) 239:281–90. doi: 10.1016/j.icarus.2014.05.031
12. Mangano V, Massetti S, Milillo A, Plainaki C, Orsini S, Rispoli R, et al. THEMIS Na exosphere observations of Mercury and their correlation with in-situ magnetic field measurements by MESSENGER. Planet Space Sci. (2015) 115:102–9. doi: 10.1016/j.pss.2015.04.001
13. Orsini S, Mangano V, Milillo A, Plainaki C, Mura A, Raines JM, et al. Mercury sodium exospheric emission as a proxy for solar perturbations transit. Sci Rep. (2018) 8:928. doi: 10.1038/s41598-018-19163-x
14. Massetti S, Mangano V, Milillo A, Mura A, Orsini S, Plainaki C. Short-term observations of double-peaked Na emission from Mercury's exosphere. Geophys Res Lett. (2017) 44:2970–7. doi: 10.1002/2017GL073090
15. Milillo A, Fujimoto M, Kallio E, Kameda S, Leblanc F, Narita Y, et al. The BepiColombo mission: an outstanding tool for investigating the Hermean environment. Planet Space Sci. (2010) 58:40–60. doi: 10.1016/j.pss.2008.06.005
16. Milillo A, Fujimoto M, Murakami G, Benkhoff J, Zender J, Aizawa S, et al. Investigating mercury's environment with the two-spacecraft BepiColombo mission. Space Sci Rev. (2020) 216:93. doi: 10.1007/s11214-020-00712-8
17. Kivelson MG, Bagenal F. Chapter 7 - Planetary magnetospheres. In: Spohn T, Breuer D, Johnson TV, editors. Encyclopedia of the Solar System, 3rd Edn. Boston, MA: Elsevier (2014). p. 137–57. Available online at: http://www.sciencedirect.com/science/article/pii/B9780124158450000074. doi: 10.1016/B978-0-12-415845-0.00007-4
18. Frisch U. Turbulence: The Legacy of A.N. Kolmogorov. Cambridge: Cambridge University Press (1995). doi: 10.1017/CBO9781139170666
19. DiBraccio GA, Slavin JA, Imber SM, Gershman DJ, Raines JM, Jackman CM, et al. MESSENGER observations of flux ropes in Mercury's magnetotail. Planet Space Sci. (2015) 115:77–89. doi: 10.1016/j.pss.2014.12.016
20. Raines JM, DiBraccio GA, Cassidy TA, Delcourt DC, Fujimoto M, Jia X, et al. Plasma sources in planetary magnetospheres: mercury. Space Sci Rev. (2015) 192:91–144. doi: 10.1007/s11214-015-0193-4
21. Alberti T, Laurenza M, Consolini G, Milillo A, Marcucci MF, Carbone V, et al. On the scaling properties of magnetic-field fluctuations through the inner heliosphere. Astrophys J. (2020) 902:84. doi: 10.3847/1538-4357/abb3d2
22. Solomon SC, McNutt RL, Gold RE, Domingue DL. MESSENGER mission overview. Space Sci Rev. (2007) 131:3–39. doi: 10.1007/s11214-007-9247-6
23. Anderson BJ, Acuna MH, Lohr DA, Scheifele J, Raval A, Korth H, et al. The magnetometer instrument on MESSENGER. Space Sci Rev. (2007) 131:417–50. doi: 10.1007/s11214-007-9246-7
24. Shue JH, Chao JK, Fu HC, Russell CT, Song P, Khurana KK, et al. A new functional form to study the solar wind control of the magnetopause size and shape. J Geophys Res. (1997) 102:9497–512. doi: 10.1029/97JA00196
25. Slavin JA, Lepping RP, Wu CC, Anderson BJ, Baker DN, Benna M, et al. MESSENGER observations of large flux transfer events at Mercury. Geophys Res Lett. (2010) 37:L02105. doi: 10.1029/2009GL041485
26. Huang NE, Shen Z, Long SR, Wu MC, Shih HH, Zheng Q, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc R Soc Lond Ser A. (1998) 454:903–98. doi: 10.1098/rspa.1998.0193
27. Huang NE, Wu Z. A review on Hilbert-Huang transform: method and its applications to geophysical studies. Rev Geophys. (2008) 46:RG2006. doi: 10.1029/2007RG000228
28. Flandrin P, Rilling G, Goncalves P. Empirical mode decomposition as a filter bank. IEEE Signal Process Lett. (2004) 11:112–4. doi: 10.1109/LSP.2003.821662
29. Carson JR, Fry TC. Variable frequency electric circuit theory with application to the theory of frequency-modulation. Bell Syst Tech J. (1937) 16:513–40. doi: 10.1002/j.1538-7305.1937.tb00766.x
30. Gabor D. Theory of communication. Part 1: the analysis of information. J Instit Electr Eng. (1946) 93:429–41. doi: 10.1049/ji-3-2.1946.0074
31. Wilkinson TD. Hilbert transforms in signal processing, by Stefan L. Hahn. Opt Photon News. (1998) 9:65.
32. Huang H, Pan J. Speech formant frequency estimation method based on Hilbert-Huang transform. Acoust Soc Am J. (2005) 118:1929. doi: 10.1121/1.4780727
33. Huang YX, Schmitt FG, Hermand JP, Gagne Y, Lu ZM, Liu YL. Arbitrary-order Hilbert spectral analysis for time series possessing scaling statistics: comparison study with detrended fluctuation analysis and wavelet leaders. Phys Rev E. (2011) 84:016208. doi: 10.1103/PhysRevE.84.016208
34. Huang YX, Schmitt FG, Gagne Y, Lu ZM, Liu YL. Application of arbitrary-order hilbert spectral analysis to passive scalar turbulence. J Phys Conf Ser. (2011) 318:042003. doi: 10.1088/1742-6596/318/4/042003
35. Wu Z, Huang NE. A study of the characteristics of white noise using the empirical mode decomposition method. Proc R Soc Lond Ser A. (2004) 460:1597–611. doi: 10.1098/rspa.2003.1221
36. De Michelis P, Consolini G, Tozzi R. On the multi-scale nature of large geomagnetic storms: an empirical mode decomposition analysis. Nonlin Process Geophys. (2012) 19:667–73. doi: 10.5194/npg-19-667-2012
37. Alberti T, Consolini G, De Michelis P, Laurenza M, Marcucci MF. On fast and slow Earth's magnetospheric dynamics during geomagnetic storms: a stochastic Langevin approach. J Space Weath Space Clim. (2018) 8:A56. doi: 10.1051/swsc/2018039
38. Verdini A, Grappin R, Pinto R, Velli M. On the origin of the 1/f spectrum in the solar wind magnetic field. Astrophys J Lett. (2012) 750:L33. doi: 10.1088/2041-8205/750/2/L33
39. Yordanova E, Vaivads A, André M, Buchert SC, Vörös Z. Magnetosheath plasma turbulence and its spatiotemporal evolution as observed by the cluster spacecraft. Phys Rev Lett. (2008) 100:205003. doi: 10.1103/PhysRevLett.100.205003
40. Imber SM, Slavin JA, Boardsen SA, Anderson BJ, Korth H, McNutt RL, et al. MESSENGER observations of large dayside flux transfer events: do they drive Mercury's substorm cycle? J Geophys Res. (2014) 119:5613–23. doi: 10.1002/2014JA019884
41. Russell CT, Elphic RC. Initial ISEE magnetometer results: magnetopause observations (article published in the special issues: advances in magnetospheric physics with GEOS- 1 and ISEE - 1 and 2.). Space Sci Rev. (1978) 22:681–715. doi: 10.1007/BF00212619
42. Zhong J, Wei Y, Lee LC, He JS, Slavin JA, Pu ZY, et al. Formation of macroscale flux transfer events at mercury. Astrophys J Lett. (2020) 893:L18. doi: 10.3847/2041-8213/ab8566
43. Fairfield DH, Otto A, Mukai T, Kokubun S, Lepping RP, Steinberg JT, et al. Geotail observations of the Kelvin-Helmholtz instability at the equatorial magnetotail boundary for parallel northward fields. J Geophys Res. (2000) 105:21,159–21,173. doi: 10.1029/1999JA000316
44. Ivanovski S, Kartalev M, Dobreva P, Vatkova G, Chernogorova T. Coupled Kelvin-Helmholtz and tearing mode instabilities in the magnetopause layer. J Theor Appl Mech. (2011) 41:31–42.
45. Aizawa S, Delcourt D, Terada N, André N. Statistical study of non-adiabatic energization and transport in Kelvin-Helmholtz vortices at mercury. Planet Space Sci. (2020) 193:105079. doi: 10.1016/j.pss.2020.105079
46. Glassmeier KH, Klimushkin D, Othmer C, Mager P. ULF waves at Mercury: earth, the giants, and their little brother compared. Adv Space Res. (2004) 33:1875–83. doi: 10.1016/j.asr.2003.04.047
47. Vassilicos JC, Brasseur JG. Self-similar spiral flow structure in low Reynolds number isotropic and decaying turbulence. Phys Rev E. (1996) 54:467–85. doi: 10.1103/PhysRevE.54.467
48. Kolmogorov A. The local structure of turbulence in incompressible viscous fluid for very large reynolds' numbers. Akad Nauk SSSR Doklady. (1941) 30:301–5.
49. Dudok de Wit T. Can high-order moments be meaningfully estimated from experimental turbulence measurements? Phys Rev E. (2004) 70:055302. doi: 10.1103/PhysRevE.70.055302
50. Chen CHK, Bale SD, Bonnell JW, Borovikov D, Bowen TA, Burgess D, et al. The evolution and role of solar wind turbulence in the inner heliosphere. Astrophys J Suppl Ser. (2020) 246:53. doi: 10.5194/egusphere-egu2020-11550
51. Alberti T, Giannattasio F, De Michelis P, Consolini G. Linear versus nonlinear methods for detecting magnetospheric and ionospheric current systems patterns. Earth Space Sci. (2020) 7:e00559. doi: 10.1029/2019EA000559
52. Glassmeier KH, Auster HU, Heyner D, Okrafka K, Carr C, Berghofer G, et al. The fluxgate magnetometer of the BepiColombo mercury planetary orbiter. Planet Space Sci. (2010) 58:287–99. doi: 10.1016/j.pss.2008.06.018
Keywords: ion-kinetic physics, Hilbert-Huang transform, mercury, messenger (spacecraft), magnetic field, magnetohydradynamics
Citation: Alberti T, Milillo A, Laurenza M, Massetti S, Ivanovski SL, Ippolito A, Plainaki C, De Angelis E, Mangano V, Mura A, Orsini S and Rispoli R (2021) Multiscale Features of the Near-Hermean Environment as Derived Through the Hilbert-Huang Transform. Front. Phys. 9:668098. doi: 10.3389/fphy.2021.668098
Received: 15 February 2021; Accepted: 12 March 2021;
Published: 12 April 2021.
Edited by:
Luca Sorriso-Valvo, Institute for Space Physics (Uppsala), SwedenReviewed by:
Yasuhito Narita, Austrian Academy of Sciences (OeAW), AustriaChristian L. Vásconez, National Polytechnic School, Ecuador
Copyright © 2021 Alberti, Milillo, Laurenza, Massetti, Ivanovski, Ippolito, Plainaki, De Angelis, Mangano, Mura, Orsini and Rispoli. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tommaso Alberti, dG9tbWFzby5hbGJlcnRpQGluYWYuaXQ=
 Tommaso Alberti
Tommaso Alberti Anna Milillo
Anna Milillo Monica Laurenza
Monica Laurenza Stefano Massetti1
Stefano Massetti1 Valeria Mangano
Valeria Mangano