Secrecy Performance Analysis of Hybrid RF/VLC Dual-Hop Relaying Systems

1 Introduction

In the past ten years, the research on conventional radio frequency (RF) wireless communication has intensified [1]. With the rapid development of solid-state lighting, the visible light communication (VLC) technology has emerged as a promising technology in recent years [2]. VLC has a wider modulation bandwidth, less susceptibility to electromagnetic interference, and a larger capacity than RF communications. In VLC, both illumination and communication are simultaneously implemented [3]. The performance of VLC, however, heavily depends on the line-of-sight (LoS) connection, and it also has a limited coverage area. Therefore, the performance of VLC suffers severe degradation in the absence of the LoS link. Moreover, the light emitted by a light-emitting diode (LED) in VLC is easily blocked by obstacles [4]. In contrast, RF communication has higher transmission reliability even in the absence of the LoS link [5–10]. To address the issues mentioned above, hybrid VLC/RF technology is proposed to tackle the aforementioned problems. The VLC technology can overcome the shortcomings of RF spectrum shortage and large power consumption, while the RF technology compensates for the dependence of VLC on LoS to improve the communication coverage and also reduces the power consumption. Besides, VLC and RF signals do not interfere with each other [7].

There are several studies on hybrid wireless systems combining RF and VLC technologies. In reference [3], a random geometric framework for the coexistence of VLC and RF networks was proposed, and its coverage and achievable rate analysis for typical users were studied. In reference [5], the power and bandwidth allocation problem for the energy efficiency maximization of the VLC/RF hybrid system was solved, and the impact of the system parameters on the energy efficiency of the mixed system was investigated. The research in reference [7] showed that compared with the network that only uses RF or VLC, a hybrid RF/VLC network can reduce the probability of interruption by reducing the area power consumption. An effective beamforming design was also discussed in reference [8].

Since the physical layer security (PLS) utilizes the randomness of the wireless channel and noise, it is often considered to be a viable solution to ensure secure communication and prevent eavesdropping and jamming attacks [11]. In reference [9], PLS characteristics of the hybrid RF/VLC system were studied, the problem of minimizing the power consumption was also studied, and a zero-forcing beamforming strategy and a minimum power allocation algorithm were proposed. The PLS of indoor heterogeneous VLC/RF networks based on known and unknown channel state information (CSI) was further analyzed in reference [12]. In reference [13], the PLS transmission for VLC with simultaneous lightwave information and power transfer was investigated.

Besides, dual-hop relay technology has been considered to be another efficient technology that can be used to increase the capacity and expand the coverage of low-power wireless networks [14]. In such systems, the signal propagates from the source node to the destination node through a relay node, so that the connection can be realized in the case of high path loss and deep attenuation in the traditional direct transmission between the source node and the destination node. In references [4, 10], the dual-hop hybrid systems with energy harvesting relays were investigated. Specifically, the authors of reference [4] optimized the VLC/RF hybrid system from the perspective of maximizing the data rate, while the authors of reference [10] investigated the data packet transmission performance of the VLC/RF hybrid system. Furthermore, in reference [14], the performance of hybrid free-space optical (FSO) communication and RF dual-hop systems based on amplify-and-forward relaying and CSI-assisted relaying were analyzed, and the closed-form expressions for the outage probability and the average bit error rate were derived in the high signal-to-noise ratio (SNR) regime. In reference [15], the expressions of the outage probability, bit error rate, and average capacity of the hybrid RF/FSO system were derived for the first time. For amplify-and-forward relay, the outage probability and bit error probability of the hybrid RF/FSO system were also obtained in reference [16]. There are many studies on the PLS of the dual-hop system. It is noteworthy that the authors of references [17–20] considered the mixed RF/FSO transmission systems. The lower bound of the secrecy outage probability (SOP) and the closed-form expression of the probability of strictly positive secrecy capacity (SPSC) when an eavesdropper is eavesdropping on the FSO link were derived in reference [17]. Furthermore, for a mixed RF/FSO downlink simultaneous wireless information and power transfer system, reference [18] derived the exact and asymptotic expressions of the SOP. The closed-form expressions for the lower bound of the SOP and the exact average secrecy capacity of mixed RF/FSO systems were also derived in reference [19], where an eavesdropper node eavesdrops on the FSO hop. In reference [20], the secrecy outage performance of a mixed RF/FSO system with imperfect CSI was analyzed. To the best of the authors’ knowledge, in the aforementioned works, Shannon’s capacity is often employed to evaluate the performance of the VLC link [11, 12]. However, in the actual VLC environment, the visible-light signal is an optical intensity signal, which means that the signal amplitude of the VLC system is non-negative. Furthermore, in the VLC system, it is necessary to consider illumination while transmitting data; therefore, the average optical intensity should be a fixed value according to the users’ dimming requirement [21]. Therefore, Shannon’s capacity is not suitable for VLC. Based on the considerations above, it is necessary to analyze the secrecy performance of the hybrid RF/VLC dual-hop relaying systems.

In this study, we analyze the PLS performance of a hybrid RF/VLC system. The main contributions are summarized as follows:

• Based on the system model, when the VLC link is eavesdropped upon, the probability density functions (PDFs) of the channel gain for the RF and VLC channels are derived, respectively. Using those PDFs, we then derive the closed-form expressions for the lower bound of the SOP and the probability of SPSC. It is also shown that the performance gap between theoretical results and simulation results is small, which verifies the accuracy of the derived expression. Moreover, the SOP increases with the noise standard deviation of Bob and decreases with the noise standard deviation of Eve. The SNR threshold degrades the system secrecy performance. The performance of the probability of SPSC mainly depends on the VLC, which deteriorates with Bob’s noise standard deviation and improves with Eve’s noise standard deviation or the radius of the floor.

• For the case when the RF link is eavesdropped upon, the PDFs and cumulative distribution functions (CDFs) of the instantaneous SNR at the relay node and the Eve node have been derived. Based on these statistic distributions, we also derive the closed-form expressions for the lower bound of the SOP and the probability of SPSC. The results further show that the performance gap between theoretical results and simulation results is also small, which verifies the accuracy of the derived expressions. In this case, the performance of the probability of SPSC mainly depends on the RF link, and all theoretical results of the probability of SPSC match the simulation results very well. Numerical results further confirm that the system secrecy performance is degraded with the distance between the Alice and relay nodes and the channel fading factor and improved by increasing the path loss exponent.

This article is arranged as follows. In Section 2, the system model of the hybrid VLC/RF system is presented. In Section 3, we derive the lower bound of the SOP and the exact expression of the probability of SPSC when the VLC link is eavesdropped upon. The secrecy performance analysis when the RF link is eavesdropped upon is presented in Section 4. Section 5 presents some numerical results. Finally, the conclusion of this article is given in Section 6.

2 System Model

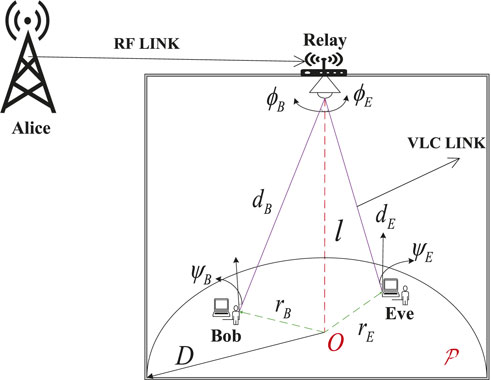
As shown in Figure 1, we consider a dual-hop hybrid RF/VLC network, which includes an outdoor RF link and an indoor VLC link. The hybrid network is composed of a source node (Alice), a relay node, an eavesdropper (Eve), and a legitimate receiver (Bob). The relay node includes an outdoor component and an indoor component, which are connected by using a wired medium. In this study, we assume that the outdoor component receives and recovers information by using the DF relaying scheme and then transmits it to the indoor component. The indoor component converts the received electrical signal to an optical signal by using an LED. There is no direct communication between Alice and Bob; information must be transmitted through the relay node. The communication arranges two transmission time slots. In the first time slot, Alice transmits confidential information x to the outdoor component of the relay over the RF channel. In the second time slot, the indoor component of the relay forwards the optical signal X to Bob through the indoor VLC channel. Both Bob and Eve deploy photodiodes to receive information and perform photoelectric conversion. When Alice transmits to Bob, Eve attempts to intercept the secret information.

FIGURE 1

FIGURE 1. RF/VLC hybrid communication network.

2.1 RF Link

In the first time slot, the received signal at the relay can be written as follows:

$y=\sqrt{P_{\mathrm{s}}}{h}_{\mathrm{SR}}x+n_{\mathrm{R}},(1)$

where $P_s$ represents the transmission power at Alice, $h_{\text{SR}}$ represents the channel gain of the RF link, x is the transmitted confidential information, and $n_{\text{R}}$ is additive white Gaussian noise (AWGN) with zero mean and variance $N_0$.

The instantaneous SNR ${\gamma }_{\text{SR}}$ at the relay is given by the following:

${\gamma }_{\text{SR}}=P_{\text{s}}|h_{\text{SR}}{|}^2/N_0.(2)$

In the RF link, $|h_{\text{SR}}{|}^2$ in Eq. 2 can be expressed as follows:

$|h_{\text{SR}}{|}^2=|g_{\text{R}}{|}^2{G}_{\text{R}},(3)$

where $g_{\text{R}}$ and $G_{\text{R}}$ denote the fast fading and path loss, respectively. It should be noted that the two terms are independent of each other. The envelope of $g_{\text{R}}$ is assumed to experience a Nakagami-m fading, and thus the squared envelope $|g_{\text{R}}{|}^2$ follows a gamma distribution. Therefore, the PDF of $|g_{\text{R}}{|}^2$ can be written as follows [22]:

$f_{{\left|g_{\text{R}}\right|}^2}\left(x\right)=\frac{x^{m_{\text{R}}-1}}{\text{Γ}\left(m_{\text{R}}\right)}{m}_{\text{R}}^{m_{\text{R}}}\text{exp}\left(-m_{\text{R}}x\right),x\ge 0,(4)$

where $m_{\text{R}}$ represents the fading factor, and $\Gamma \left(m_R\right)={\displaystyle {\int }_0^{+\infty }{x}^{m_R-1}{e}^{-x}dx}$ represents the gamma function.

Furthermore, $G_{\text{R}}$ in Eq. 3 can be modeled as follows [22]:

$G_{\text{R}}={\left(\frac{d_0}{d_1}\right)}^{\lambda },(5)$

where λ denotes the path loss exponent, $d_0$ denotes the reference distance, and $d_1$ is the distance between Alice and the relay.

Therefore, the PDF of $|h_{\text{SR}}{|}^2$ can be written as follows:

$\begin{array}{l}{f}_{{\left|h_{\text{SR}}\right|}^2}\left(y\right)=\frac{1}{G_{\text{R}}}{\left(\frac{y}{G_{\text{R}}}\right)}^{m_{\text{R}}-1}\frac{1}{\text{Γ}\left(m_{\text{R}}\right)}{m}_{\text{R}}^{m_{\text{R}}}\\ \times \exp (-m_{\text{R}}\cdot \frac{y}{G_{\text{R}}}),y\ge 0.\end{array}(6)$

By using (8.351.1) in reference [23], the cumulative distribution function (CDF) of $|h_{\text{SR}}{|}^2$ can be written as follows:

$F_{{\left|h_{\text{SR}}\right|}^2}\left(y\right)=\frac{1}{\text{Γ}\left(m_{\text{R}}\right)}\gamma \left(m_{\text{R}},\frac{m_{\text{R}}y}{P_{\text{R}}}\right),y\ge 0,(7)$

where $\gamma (\cdot ,\cdot )$ is the lower incomplete gamma function defined by (8.350.1) in reference [23].

2.2 VLC Link

In the second time slot, we consider an indoor VLC link. To facilitate the analysis, it is assumed that the receiving area $\mathcal{P}$ is a disk with a radius D. As shown in Figure 1, the LED is projected at the center of the disk. Besides, we assume that both Bob and Eve are uniformly distributed within the area $\mathcal{P}$. According to the settings above, the PDF of Bob’s (or Eve’s) position is given by the following:

$f_U\left(u\right)=\frac{1}{\pi D^2},u\in \mathcal{P},(8)$

$f_W\left(w\right)=\frac{1}{\pi D^2},w\in \mathcal{P},(9)$

where U represents the position of Bob and W represents the position of Eve.

In the second time slot, the received signals at Bob and Eve can be expressed as follows:

$Y_k=H_{k}X+Z_k,k=\text{B}\text{for}\text{Bob},k=\text{ E}\text{for}\text{Eve},(10)$

where X represents the input optical intensity, $Z_k\sim N\left(0,{\sigma }_k^2\right)$ is the AWGN at Bob (or Eve), and ${\sigma }_k^2$ is the variance of the corresponding noise.

Because the information is modulated as the instantaneous optical intensity, X must meet the non-negative constraint as follows [21]:

$X\ge 0.(11)$

Although the optical intensity can be adjusted according to the dimming requirements, the average optical intensity cannot change with time. Therefore, the dimmable average optical intensity constraint is given by the following [21]:

$E\left(X\right)=\xi P,(12)$

where ξ indicates the dimming target, and P indicates the nominal optical intensity of the LED. Because the user can adjust the optical intensity at will, the dimming target must satisfy the following [21]:

$0\le \xi \le 1.(13)$

Without loss of generality, we assume that both Bob and Eve can be illuminated by the LED, and thus, the illumination angle ${\psi }_k$ cannot exceed the field of view of the PD ${\text{Ψ}}_{\text{c}}$, that is, $0<{\psi }_k<{\text{Ψ}}_{\text{c}}$. In indoor VLC, the channel gain $H_k$ can be written as follows [24]:

$H_k=\frac{\left(m+1\right)A}{2\pi d_k^2}{T}_{S}g{\text{cos}}^m\left({\varphi }_k\right)\text{cos}\left({\psi }_k\right),k=\text{B}\text{or}\text{E},(14)$

where $d_k$ and ${\varphi }_k$ represent the distance and the irradiance angle between the LED and Bob (or Eve), A is the physical area of the PD, m denotes the order of the Lambertian emission, g is the PD’s concentrator gain, and $T_S$ represents the optical filter gain. Also, assuming that the normal vector between the transceiver plane and the ceiling is vertical, we can obtain $\text{cos}\left({\varphi }_k\right)=\text{cos}\left({\psi }_k\right)=l/d_k$, where l represents the vertical distance between the LED and the receiving plane. Therefore, the channel gain in Eq. 14 can be further written as follows:

$H_k=\frac{\left(m+1\right)A{T}_{S}g{l}^{m+1}}{2\pi }{\left(r_k^2+l^2\right)}^{-\frac{m+3}{2}},(15)$

where $r_k$ is the distance between the projection point O and the $k^{\text{th}}$ receiver.

According to Eqs. 8 and 9, the CDF of $r_k$ can be expressed as follows:

$\begin{array}{l}{F}_{r_k}\left(r_k\right)=\mathrm{Pr}\left\{r\le r_k\right\}\\ =\mathrm{Pr}\left\{\rho \le r_k,0\le \theta \le 2\pi \right\}\\ ={\displaystyle {\int }_0^{2\pi }{\displaystyle {\int }_0^{r_k}\frac{1}{\pi D^2}\rho \mathrm{d}\rho \mathrm{d}\theta }}\\ =\frac{r_k^2}{D^2},0<r_k\le D.\end{array}(16)$

Furthermore, the PDF of $r_k$ can be obtained as follows:

$f_{r_k}\left(r_k\right)=\frac{\text{d}{F}_{r_k}\left(r_k\right)}{\text{d}{r}_k}=\frac{2r_k}{D^2},0\le r_k\le D,(17)$

where $\frac{\text{d}{F}_{r_k}\left(r_k\right)}{\text{d}{r}_k}$ is the derivative of $F_{r_k}\left(r_k\right)$ with respect to $r_k$.

The PDF of the channel gain $H_k$ is then written as follows:

$f_{H_k}\left(h\right)=\left|\frac{\text{d}}{\text{d}h}{r}_k\right|f_{r_k}\left(r_k\right),(18)$

where $|.|$ is a symbol for the absolute value.

Substituting Eq. 15 and Eq. 17 into Eq. 18, we can obtain the PDF of $H_k$ as follows:

$f_{H_k}\left(h\right)=\text{Ξ}{h}^{-\frac{2}{m+3}-1},v_{\text{min}}\le h\le v_{\text{max}},(19)$

where $\text{Ξ}$, $v_{\text{min}}$, and $v_{\text{max}}$ are given by the following:

$\text{Ξ}=\frac{2}{\left(m+3\right)D^2}{\left(\frac{\left(m+1\right)A{T}_{S}g{l}^{m+1}}{2\pi }\right)}^{\frac{2}{m+3}},(20)$

$v_{\text{min}}=\frac{\left(m+1\right)A{T}_{S}g{l}^{m+1}}{2\pi }{\left(D^2+l^2\right)}^{-\frac{m+3}{2}},(21)$

$v_{\text{max}}=\frac{\left(m+1\right)A{T}_{\text{S}}\text{g}{l}^{m+1}}{2\pi }{l}^{-\left(m+3\right)}.(22)$

3 Secrecy Performance Analysis When VLC Link Is Eavesdropped Upon

3.1 SOP Analysis

In this subsection, we analyze the SOP of the hybrid RF/VLC system. Because there are no eavesdroppers in the RF link, the instantaneous SC of the first hop is its instantaneous channel capacity, that is,

$\begin{array}{c}{C}_{\text{hop},1}=\frac{1}{2}\text{ln}\left(1+{\gamma }_{\text{SR}}\right)\\ =\frac{1}{2}\text{ln}\left(1+\frac{P_{\text{s}}}{N_0}|h_{\text{SR}}{|}^2\right).\end{array}(23)$

In the VLC link, we need to consider the average and non-negative constraints simultaneously. Therefore, Shannon’s capacity is not applicable to the VLC link [25]. For VLC with constraints as in Eqs 11, 12, a lower bound on the instantaneous SC is given by the following [26]:

$\begin{array}{c}{C}_{\text{hop},2}=\frac{1}{2}\text{ln}\left(\frac{{\sigma }_{\text{E}}^2}{2\pi {\sigma }_{\text{B}}^2}\cdot \frac{e{\xi }^2{P}^2{H}_{\text{B}}^2+2\pi {\sigma }_{\text{B}}^2}{H_{\text{E}}^2{\xi }^2{P}^2+{\sigma }_{\text{B}}^2}\right)\\ =\frac{1}{2}\text{ln}\left(\frac{1+J_{\text{B}}}{1+J_{\text{E}}}\right).\end{array}(24)$

Furthermore, according to Eq. 19, $J_{\text{B}}=\frac{e{\xi }^2{P}^2{H}_{\text{B}}^2}{2\pi {\sigma }_{\text{B}}^2}$ and $J_{\text{E}}=\frac{{\xi }^2{P}^2{H}_{\text{E}}^2}{{\sigma }_{\text{E}}^2}$, the PDFs of $J_{\text{B}}$ and $J_{\text{E}}$ are given by the following [13]:

$\{\begin{array}{c}{f}_{J_{\text{B}}}\left(j\right)=\frac{\text{Ξ}}{2}{\left(\frac{2\pi {\sigma }_{\text{B}}^2}{e{\xi }^2{P}^2}\right)}^{-\frac{1}{m+3}}{j}^{-\frac{1}{m+3}-1},J_{\text{B},\text{min}}\le j\le J_{\text{B},\text{max}},\\ f_{J_{\text{E}}}\left(j\right)=\frac{\text{Ξ}}{2}{\left(\frac{{\sigma }_{\text{E}}^2}{{\xi }^2{P}^2}\right)}^{-\frac{1}{m+3}}{j}^{-\frac{1}{m+3}-1},J_{\text{E},\text{min}}\le j\le J_{\text{E},\text{max}},\end{array}(25)$

where $J_{\text{B},\text{min}}=\frac{e{\xi }^2{P}^2{v}_{\text{min}}^2}{2\pi {\sigma }_{\text{B}}^2}$, $J_{\text{B},\text{max}}=\frac{e{\xi }^2{P}^2{v}_{\text{max}}^2}{2\pi {\sigma }_{\text{B}}^2}$, $J_{\text{E},\text{min}}=\frac{{\xi }^2{P}^2{v}_{\text{min}}^2}{{\sigma }_{\text{E}}^2}$, and $J_{\text{E},\text{max}}=\frac{{\xi }^2{P}^2{v}_{\text{max}}^2}{{\sigma }_{\text{E}}^2}$.

As is known, the hybrid system is equivalent to a series network, so the capacity of the system is determined by the worse channel [27]. Therefore, the instantaneous SC of the entire hybrid system is the minimum of $C_{\text{hop},1}$ and $C_{\text{hop},2}$, which can be expressed as follows¹:

$C_{\text{I}}=\text{min}\left\{C_{\text{hop},1},C_{\text{hop},2}\right\}.(26)$

The SOP is an important performance metric to evaluate the PLS of a wireless communication system. It is defined as the probability that the instantaneous SC is lower than the target capacity $C_{\text{th}}$. Therefore, SOP can be expressed as follows:

$P_{\text{SOP}}=\text{Pr}\left\{C_{\text{I}}<C_{\text{th}}\right\}.(27)$

Substituting Eq. 26 into Eq. 27, the SOP is rewritten as follows:

$\begin{array}{c}{P}_{\text{SOP}}=\text{Pr}\left\{\text{min}\left(C_{\text{hop},1},C_{\text{hop},2}\right)<C_{\text{th}}\right\}\\ =1-\text{Pr}\left\{\text{min}\left(C_{\text{hop},1},C_{\text{hop},2}\right)\ge C_{\text{th}}\right\}\\ =1-\text{Pr}\left\{C_{\text{hop},1}\ge C_{\text{th}}\right\}\text{Pr}\left\{C_{\text{hop},2}\ge C_{\text{th}}\right\},\end{array}(28)$

where $\text{Pr}\left\{C_{\text{hop},1}\ge C_{\text{th}}\right\}$ is given by the following:

$\begin{array}{l}\text{Pr}\left\{C_{\text{hop},1}\ge C_{\text{th}}\right\}\hfill \\ =\text{Pr}\left\{\frac{1}{2}\text{ln}\left(1+\frac{P_{\text{s}}}{N_0}{\left|h_{\text{SR}}\right|}^2\right)\ge C_{\text{th}}\right\}\hfill \\ =1-\text{Pr}\left\{\frac{1}{2}\text{ln}\left(1+\frac{P_{\text{s}}}{N_0}{\left|h_{\text{SR}}\right|}^2\right)<\frac{1}{2}\text{ln}\left({\gamma }_{\text{th}}\right)\right\}\hfill \\ =1-\text{Pr}\left\{{\left|h_{\text{SR}}\right|}^2<\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right\}\hfill \\ =1-F_{{\left|h_{\text{SR}}\right|}^2}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right),\hfill \end{array}(29)$

and $\text{Pr}\left\{C_{\text{hop},2}\ge C_{\text{th}}\right\}$ is given by the following:

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},2}\ge C_{\text{th}}\right\}=1-\text{Pr}\left\{C_{\text{hop},2}<C_{\text{th}}\right\}\\ =1-\text{Pr}\left\{\frac{1}{2}\text{ln}\left(\frac{1+J_{\text{B}}}{1+J_{\text{E}}}\right)<\frac{1}{2}\text{ln}\left({\gamma }_{\text{th}}\right)\right\},\end{array}(30)$

where $C_{\text{th}}=\frac{1}{2}\text{ln}\left({\gamma }_{\text{th}}\right)$ denotes the threshold of the targeted SC and ${\gamma }_{\text{th}}\ge 1$ denotes the equivalent threshold of the SNR [13]. It should be noted that it is challenging to obtain a closed-form expression of Eq. 30. In indoor VLC, it is reasonable to assume that $J_{\text{B}}\gg 1$ and $J_{\text{E}}\gg 1$. When $J_{\text{B}}>J_{\text{E}}$, we have $\left(1+J_{\text{B}}\right)/\left(1+J_{\text{E}}\right)<J_{\text{B}}/J_{\text{E}}$. Therefore, an upper bound of Eq. 30 is given by the following:

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},2}\ge C_{\text{th}}\right\}\le 1-\text{Pr}\left\{J_{\text{B}}<J_{\text{E}}{\gamma }_{\text{th}}\right\}.\end{array}(31)$

From Eqs 28, 29, and 31, the SOP is lower-bounded by the following:

$\begin{array}{c}{P}_{\text{SOP}}=1-\left(1-F_{{\left|h_{\text{SR}}\right|}^2}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right)\times \left(1-\text{Pr}\left\{J_{\text{B}}<J_{\text{E}}{\gamma }_{\text{th}}\right\}\right)\\ \stackrel{\text{Δ}}{=}{P}_{{\text{SOP}}_{\text{L}}}.\end{array}(32)$

In Eq. 25, $J_{\text{B}}$ and $J_{\text{E}}$ are independent of each other. Moreover, the value of $P_{{\text{SOP}}_{\text{L}}}$ depends on the value of ${\gamma }_{\text{th}}$. Figure 2 shows four cases of the integral region of $\text{Pr}\left(J_{\text{B}}<J_{\text{E}}{\gamma }_{\text{th}}\right)$. Based on the four cases, $\text{Pr}\left(J_{\text{B}}<J_{\text{E}}{\gamma }_{\text{th}}\right)$ is derived as follows:

$\text{Pr}\left(J_{\text{B}}<J_{\text{E}}{\gamma }_{\text{th}}\right)=\{\begin{array}{ll}0,\hfill & \text{if}{\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}\hfill \\ D_1,\hfill & \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}<{\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}\hfill \\ D_2,\hfill & \text{if}\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{max}}}<{\gamma }_{\text{th}}<\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\hfill \\ 1,\hfill & \text{if}{\gamma }_{\text{th}}\ge \frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}},\hfill \end{array}(33)$

where $D_1$ and $D_2$ are given by the following:

$\begin{array}{l}{D}_1={\displaystyle {\int }_{\frac{J_{\text{B},\text{min}}}{{\gamma }_{\text{th}}}}^{J_{\text{E},\text{max}}}{f}_{J_{\text{E}}}\left(z\right)}{\displaystyle {\int }_{J_{\text{B},\text{min}}}^{{\gamma }_{\text{th}}z}{f}_{J_{\text{B}}}\left(y\right)\text{d}y}\text{d}z\\ =\epsilon {\left(m+3\right)}^2{J}_{\text{B},\text{min}}^{-\frac{1}{m+3}}\left[{\left(\frac{J_{\text{B},\text{min}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{1}{m+3}}-J_{\text{E},\text{max}}^{-\frac{1}{m+3}}\right]\\ -\frac{\epsilon }{2}{\left(m+3\right)}^2{\gamma }_{\text{th}}^{-\frac{1}{m+3}}\left[{\left(\frac{J_{\text{B},\text{min}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{2}{m+3}}-J_{\text{E},\text{max}}^{-\frac{2}{m+3}}\right]\end{array}(34)$

FIGURE 2

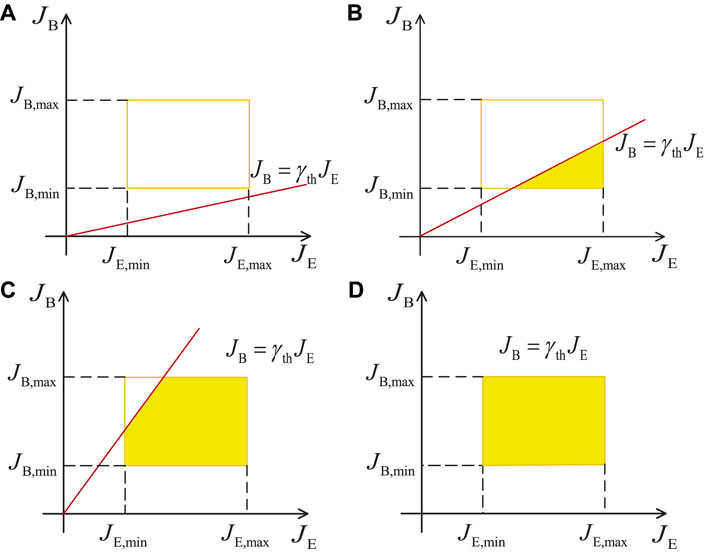
FIGURE 2. Four cases of the integral of $\text{Pr}\left(J_{\text{B}}<J_{\text{E}}{\gamma }_{\text{th}}\right)$. (A) ${\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}$. (B) $\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}<{\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}$. (C) $\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{max}}}<{\gamma }_{\text{th}}<\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}$. (D) ${\gamma }_{\text{th}}\ge \frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}$².

and

$\begin{array}{c}{D}_2={\displaystyle {\int }_{J_{\text{E},\text{min}}}^{\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}}{f}_{J_{\text{E}}}\left(z\right)}{\displaystyle {\int }_{J_{\text{B},\text{min}}}^{{\gamma }_{\text{th}}z}{f}_{J_{\text{B}}}\left(y\right)\text{d}y\text{d}z}+{\displaystyle {\int }_{\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}}^{J_{\text{E},\text{max}}}{f}_{J_{\text{E}}}\left(z\right)}{\displaystyle {\int }_{J_{\text{B},\text{min}}}^{J_{\text{B},\text{max}}}{f}_{J_{\text{B}}}\left(y\right)\text{d}y\text{d}z}\\ =\epsilon {\left(m+3\right)}^2{J}_{\text{B},\text{min}}^{-\frac{1}{m+3}}[J_{\text{E},\text{min}}^{-\frac{1}{m+3}}-{\left(\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{1}{m+3}}]-\frac{\epsilon }{2}{\left(m+3\right)}^2{\gamma }_{\text{th}}^{-\frac{1}{m+3}}[J_{\text{E},\text{min}}^{-\frac{2}{m+3}}-{\left(\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{2}{m+3}}]\\ +\epsilon {\left(m+3\right)}^2\left(J_{\text{B},\text{min}}^{-\frac{1}{m+3}}-J_{\text{B},\text{max}}^{-\frac{1}{m+3}}\right)\times [{\left(\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{1}{m+3}}-J_{\text{E},\text{max}}^{-\frac{1}{m+3}}],\end{array}(35)$

where $\epsilon =\frac{{\text{Ξ}}^2}{4}{\left(\frac{2\pi {\sigma }_{\text{B}}^2{\sigma }_{\text{E}}^2}{e{\xi }^4{P}^4}\right)}^{-\frac{1}{m+3}}$.

The lower bound of the SOP can be further derived as follows:

$P_{{\text{SOP}}_{\text{L}}}=\{\begin{array}{cc}{F}_{{\left|h_{\text{SR}}\right|}^2}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right),& \text{if}{\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}\\ 1-\left(1-F_{{\left|h_{\text{SR}}\right|}^2}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right)\left(1-D_1\right),& \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}<{\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}\\ 1-\left(1-F_{{\left|h_{\text{SR}}\right|}^2}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right)\left(1-D_2\right),& \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}<{\gamma }_{\text{th}}<\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\\ 1,& \text{if}{\gamma }_{\text{th}}\ge \frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}},\end{array}(36)$

Substituting Eq. 34 and Eq. 35 into Eq. 36, the expression for the lower bound of the SOP can be obtained as Eq. 37, as shown below:

$P_{{\text{SOP}}_{\text{L}}}=\{\begin{array}{cc}\frac{P_{\text{R}}}{\text{Γ}\left(m_{\text{R}}\right)}\gamma \left(m_{\text{R}},\frac{m_{\text{R}}}{P_{\text{R}}}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right),& \text{if}{\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}\\ \begin{array}{c}1-\frac{P_{\text{R}}}{\text{Γ}\left(m_{\text{R}}\right)}\gamma \left(m_{\text{R}},\frac{m_{\text{R}}}{P_{\text{R}}}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right)+\frac{P_{\text{R}}}{\text{Γ}\left(m_{\text{R}}\right)}\gamma \left(m_{\text{R}},\frac{m_{\text{R}}}{P_{\text{R}}}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right)\\ \times \epsilon {\left(m+3\right)}^2{J}_{\text{B},\text{min}}^{-\frac{1}{m+3}}\left[{\left(\frac{J_{\text{B},\text{min}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{1}{m+3}}-J_{\text{E},\text{max}}^{-\frac{1}{m+3}}\right]\\ -\frac{\epsilon }{2}{\left(m+3\right)}^2{\gamma }_{\text{th}}^{-\frac{1}{m+3}}\left[{\left(\frac{J_{\text{B},\text{min}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{2}{m+3}}-J_{\text{E},\text{max}}^{-\frac{2}{m+3}}\right],\end{array}& \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}<{\gamma }_{\text{th}}\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}\\ \begin{array}{c}1-\frac{P_{\text{R}}}{\text{Γ}\left(m_{\text{R}}\right)}\gamma \left(m_{\text{R}},\frac{m_{\text{R}}}{P_{\text{R}}}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right)+\frac{P_{\text{R}}}{\text{Γ}\left(m_{\text{R}}\right)}\gamma \left(m_{\text{R}},\frac{m_{\text{R}}}{P_{\text{R}}}\left(\frac{\left({\gamma }_{\text{th}}-1\right)N_0}{P_{\text{s}}}\right)\right)\\ \times \epsilon {\left(m+3\right)}^2{J}_{\text{B},\text{min}}^{-\frac{1}{m+3}}\left[J_{\text{E},\text{min}}^{-\frac{1}{m+3}}-{\left(\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{1}{m+3}}\right]\\ -\frac{\epsilon }{2}{\left(m+3\right)}^2{\gamma }_{\text{th}}^{-\frac{1}{m+3}}\left[J_{\text{E},\text{min}}^{-\frac{2}{m+3}}-{\left(\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{2}{m+3}}\right]\\ +\epsilon {\left(m+3\right)}^2\left(J_{\text{B},\text{min}}^{-\frac{1}{m+3}}-J_{\text{B},\text{max}}^{-\frac{1}{m+3}}\right)\times \left[{\left(\frac{J_{\text{B},\text{max}}}{{\gamma }_{\text{th}}}\right)}^{-\frac{1}{m+3}}-J_{\text{E},\text{max}}^{-\frac{1}{m+3}}\right],\end{array}& \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}<{\gamma }_{\text{th}}<\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\\ 1,& \text{if}{\gamma }_{\text{th}}\ge \frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\end{array}(37)$

Remark 1.According toEq. 33, with the increase in${\sigma }_B$, the channel gain$H_B$decreases, and the integral range of$\text{Pr}\left(J_B<J_E{\gamma }_{th}\right)$is enlarged. In this circumstance, the value of SOP inEq. 37increases with${\sigma }_B$. Similarly, we can conclude that the SOP degrades with the increase in${\sigma }_E$.

Remark 2.With the increase in${\gamma }_{th}$, the value of the lower bound of the SOP inEq. 37is enlarged. Moreover, when${\gamma }_{th}\ge J_{B,max}/J_{E,min}$, the lower bound of the SOP becomes one; hence, the information cannot be transmitted securely.

3.2 Probability of SPSC Analysis

In secure communications, the probability of SPSC is a fundamental benchmark that is employed to emphasize the existence of SC [17]. In this subsection, we derive the probability of SPSC of the hybrid RF/VLC system. The probability of SPSC is defined as follows:

$\begin{array}{c}{P}_{\text{SPSC}}=\text{Pr}\left\{\text{min}\left(C_{\text{hop},1},C_{\text{hop},2}\right)>0\right\}\\ =\text{Pr}\left\{C_{\text{hop},1}>0\right\}\text{Pr}\left\{C_{\text{hop},2}>0\right\}.\end{array}(38)$

According to Eq. 23, $\text{Pr}\left\{C_{\text{hop},1}>0\right\}$ is expressed as follows:

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},1}>0\right\}=\text{Pr}\left\{\frac{1}{2}\text{ln}\left(1+\frac{P_{\text{s}}}{N_0}{\left|h_{\text{SR}}\right|}^2\right)>0\right\}\\ =\text{Pr}\left\{\frac{P_{\text{s}}}{N_0}{\left|h_{\text{SR}}\right|}^2>0\right\}\\ =1,\end{array}(39)$

and $\text{Pr}\left\{C_{\text{hop},2}>0\right\}$ is expressed as follows:

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},2}>0\right\}=\text{Pr}\left\{\frac{1}{2}\text{ln}\left(\frac{1+J_{\text{B}}}{1+J_{\text{E}}}\right)>0\right\}\\ =\text{Pr}\left\{J_{\text{B}}>J_{\text{E}}\right\}.\end{array}(40)$

Remark 3.Since$\text{Pr}\left\{C_{hop,1}>0\right\}$is always equal to one, the performance of the probability of SPSC mainly depends on the VLC link.

It should be noted that the value of Eq. 40 also depends on the integral region. Figure 3 shows four cases of the integral region in Eq. 40. Based on the four cases, the probability of SPSC in Eq. 40 can be written as follows:

$P_{\text{SPSC}}=\{\begin{array}{ll}1,\hfill & \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}\ge 1\hfill \\ C_1,\hfill & \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}<1\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}\hfill \\ C_2,\hfill & \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}<1<\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\hfill \\ 0,\hfill & \text{if}\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\le 1.\hfill \end{array}(41)$

Since $J_{\text{B}}$ and $J_{\text{E}}$ are independent of each other, $C_1$ and $C_2$ are given by the following:

$\begin{array}{c}{C}_1=1-{\displaystyle {\int }_{J_{\text{B},\text{min}}}^{J_{\text{E},\text{max}}}{f}_{J_{\text{E}}}\left(z\right)}{\displaystyle {\int }_{J_{\text{B},\text{min}}}^z{f}_{J_{\text{B}}}\left(y\right)\text{d}y\text{d}z}\\ =1+\epsilon {\left(m+3\right)}^2{J}_{\text{B},\text{min}}^{-\frac{1}{m+3}}\left[J_{\text{E},\text{max}}^{-\frac{1}{m+3}}-J_{\text{B},\text{min}}^{-\frac{1}{m+3}}\right]-\frac{\epsilon }{2}{\left(m+3\right)}^2\left[J_{\text{E},\text{max}}^{-\frac{2}{m+3}}-J_{\text{B},\text{min}}^{-\frac{2}{m+3}}\right]\end{array}(42)$

and

$\begin{array}{c}{C}_2={\displaystyle {\int }_{J_{\text{E},\text{min}}}^{J_{\text{B},\text{max}}}{f}_{J_{\text{E}}}\left(z\right)}{\displaystyle {\int }_z^{J_{\text{B},\text{max}}}{f}_{J_{\text{B}}}\left(y\right)\text{d}y\text{d}z}\\ =\epsilon {\left(m+3\right)}^2\left[J_{\text{B},\text{max}}^{-\frac{2}{m+3}}-J_{\text{B},\text{max}}^{-\frac{1}{m+3}}{J}_{\text{E},\text{min}}^{-\frac{1}{m+3}}\right]-\frac{\epsilon }{2}{\left(m+3\right)}^2\left[J_{\text{B},\text{max}}^{-\frac{2}{m+3}}-J_{\text{E},\text{min}}^{-\frac{2}{m+3}}\right].\end{array}(43)$

Finally, the closed-from expression of the probability of SPSC can be expressed as follows:

$P_{\text{SPSC}}=\{\begin{array}{cc}1,& \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}\ge 1\\ 1+\epsilon {\left(m+3\right)}^2{J}_{\text{B},\text{min}}^{-\frac{1}{m+3}}\left[J_{\text{E},\text{max}}^{-\frac{1}{m+3}}-J_{\text{B},\text{min}}^{-\frac{1}{m+3}}\right]-\frac{\epsilon }{2}{\left(m+3\right)}^2\left[J_{\text{E},\text{max}}^{-\frac{2}{m+3}}-J_{\text{B},\text{min}}^{-\frac{2}{m+3}}\right],& \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}<1\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}\\ \epsilon {\left(m+3\right)}^2\left[J_{\text{B},\text{max}}^{-\frac{2}{m+3}}-J_{\text{B},\text{max}}^{-\frac{1}{m+3}}{J}_{\text{E},\text{min}}^{-\frac{1}{m+3}}\right]-\frac{\epsilon }{2}{\left(m+3\right)}^2\left[J_{\text{B},\text{max}}^{-\frac{2}{m+3}}-J_{\text{E},\text{min}}^{-\frac{2}{m+3}}\right],& \text{if}\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}<1<\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\\ 0,& \text{if}\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}\le 1.\end{array}(44)$

FIGURE 3

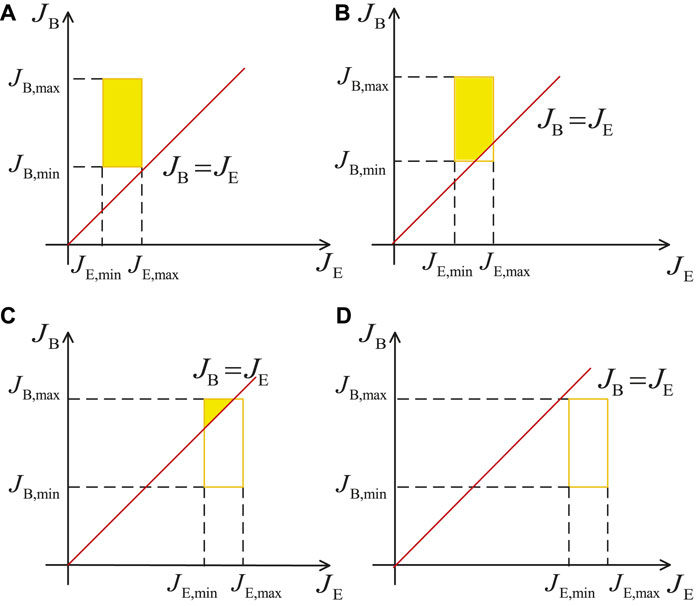
FIGURE 3. Four cases of the integral of $\text{Pr}\left\{C_{\text{RD}}>0\right\}$. (A) $1\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}$. (B) $\frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{max}}}<1\le \frac{J_{\text{B},\text{min}}}{J_{\text{E},\text{min}}}$. (C) $\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{max}}}<1<\frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}$. (D) $1\ge \frac{J_{\text{B},\text{max}}}{J_{\text{E},\text{min}}}$³.

Remark 4.Opposite to Remark 1, with the increase in${\sigma }_B$, the channel gain$H_B$is decreased, and the integral range of$\text{Pr}\left\{C_{hop,2}>0\right\}$is enlarged. In this circumstance, the value of the probability of SPSC can decrease with the increase in${\sigma }_B$. Besides, we can conclude that the probability of the SPSC can increase with the increase in${\sigma }_E$.

Remark 5.As the radius D increases, the probability of Eve being placed far away from Bob increases and the probability of Eve eavesdropping on confidential information decreases. Therefore, the channel gain$H_B$is decreased, and the integral range of$\text{Pr}\left\{C_{hop,2}>0\right\}$is enlarged. According to Remark 3, the performance of the probability of SPSC mainly depends on the VLC link. Therefore, the performance of the system will be improved.

4 Secrecy Performance Analysis When RF Link Is Eavesdropped Upon

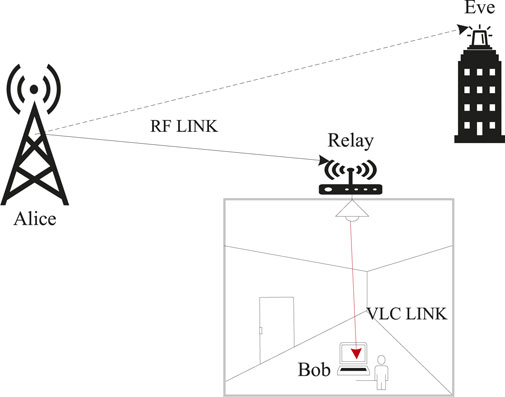
In Section 3, the SOP and the probability of the SPSC have been analyzed when the VLC link is eavesdropped upon. However, in practice, the RF link is more vulnerable to unauthorized users, so it is necessary to analyze the secrecy performance of the hybrid RF/VLC system when the RF link is eavesdropped upon. The system model is shown in Figure 4.

FIGURE 4

FIGURE 4. RF/VLC hybrid communication network when the RF link is eavesdropped upon.

4.1 SOP Analysis

In this subsection, we analyze the SOP of a hybrid RF/VLC system when the RF link is eavesdropped upon. The instantaneous SC of the first hop is given by the following:

$\begin{array}{c}{C}_{\text{hop},1}^{\text{′}}={\left\{\frac{1}{2}\left(\text{ln}\left(1+{\gamma }_{\text{SR}}\right)-\text{ln}\left(1+{\gamma }_{\text{SE}}\right)\right)\right\}}^{+}\end{array},(45)$

where ${\left\{x\right\}}^{+}=\text{max}\left\{x,0\right\}$, ${\gamma }_{\text{SE}}$ represents the instantaneous SNR at Eve and it can be expressed as follows:

$\begin{array}{c}{\gamma }_{\text{SE}}=P_{\text{s}}|h_{\text{SE}}{|}^2/N_0\end{array}.(46)$

Similarly, the $h_{\text{SE}}$ represents the channel gain between Alice and Eve, where $|h_{\text{SE}}{|}^2$ can be written as follows:

$\begin{array}{c}{\left|h_{\text{SE}}\right|}^2={\left|g_{\text{R}}^{\text{′}}\right|}^2{G}_{\text{E}}\end{array},(47)$

where the PDF of $|g_{\text{R}}^{\text{′}}{|}^2$ is as follows:

$\begin{array}{c}{f}_{|g_{\text{R}}^{\text{′}}{|}^2}\left(x\right)=\frac{x^{m_{\text{E}}-1}}{\text{Γ}\left(m_{\text{E}}\right)}{m}_{\text{E}}^{m_{\text{E}}}\text{exp}\left(-m_{\text{E}}x\right),x\ge 0\end{array},(48)$

where $m_{\text{E}}$ represents the fading factor between Alice and Eve. Furthermore, $G_{\text{E}}$ in Eq. 47 can be modeled as follows [22]:

$G_{\text{E}}={\left(\frac{d_0}{d_1^{\prime }}\right)}^{\lambda },(49)$

where $d_1^{\prime }$ is the distance between Alice and Eve. Therefore, the PDF and the CDF of ${\gamma }_{\text{S}j}$ ($j\in \left\{\text{R},\text{E}\right\}$) are as follows:

$\{\begin{array}{ll}{f}_{{\gamma }_{\text{S}j}}\left(z\right)=\frac{N_0}{P_{\text{s}}{G}_j}{\left(\frac{N_0}{P_{\text{s}}{G}_j}z\right)}^{m_j-1}\frac{1}{\text{Γ}\left(m_j\right)}{m}_j^{m_j}\text{exp}\left(-\frac{m_j{N}_0}{P_{\text{s}}{G}_j}z\right),\hfill & z\ge 0\hfill \\ F_{{\gamma }_{\text{S}j}}\left(z\right)=\frac{1}{\text{Γ}\left(m_j\right)}\gamma \left(m_j,\frac{m_j{N}_0}{P_{\text{s}}{G}_j}z\right),\hfill & z\ge 0.\hfill \end{array}(50)$

Because there are no eavesdroppers in the VLC link, the instantaneous SC of the first hop is its instantaneous channel capacity, that is, a lower bound on the instantaneous SC of the second hop is written by using the following [21]:

$\begin{array}{c}{C}_{\text{hop},1}^{\prime }=\frac{1}{2}\text{ln}\left(1+\frac{e}{2\pi }{\left(\frac{H_{\text{B}}\xi P}{{\sigma }_{\text{B}}}\right)}^2\right)=\frac{1}{2}\text{ln}\left(1+J_{\text{B}}\right)\end{array}.(51)$

Similarly, the instantaneous SC of the entire hybrid system is the minimum of $C_{\text{hop},1}^{\prime }$ and $C_{\text{hop},2}^{\prime }$, which is expressed as follows:

$C_{\text{I}}^{\prime }=\text{min}\left\{C_{\text{hop},1}^{\prime },C_{\text{hop},2}^{\prime }\right\}.(52)$

We have known that SOP can be given by $P_{\mathrm{SOP}}=\mathrm{Pr}\left\{C_{\mathrm{I}}^{\prime }<C_{\mathrm{th}}\right\}$. Furthermore, the SOP can be rewritten as follows:

$\begin{array}{c}{P}_{\text{SOP}}=\text{Pr}\left\{\text{min}\left(C_{\text{hop},1}^{\prime },C_{\text{hop},2}^{\prime }\right)<C_{\text{th}}\right\}\\ =1-\text{Pr}\left\{C_{\text{hop},1}^{\prime }\ge C_{\text{th}}\right\}\text{Pr}\left\{C_{\text{hop},2}^{\prime }\ge C_{\text{th}}\right\},\end{array}(53)$

where

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},1}^{\prime }\ge C_{\text{th}}\right\}\\ =\text{Pr}\left\{\frac{1}{2}\text{ln}\left(\frac{1+{\gamma }_{\text{SR}}}{1+{\gamma }_{\text{SE}}}\right)\ge \frac{1}{2}\text{ln}{\gamma }_{\text{th}}\right\}\\ =1-\text{Pr}\left\{{\gamma }_{\text{SR}}<{\gamma }_{\text{th}}{\gamma }_{\text{SE}}+{\gamma }_{\text{th}}-1\right\}\end{array}(54)$

and

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},2}^{\prime }\ge C_{\text{th}}\right\}=\text{Pr}\left\{\frac{1}{2}\text{ln}\left(1+J_{\text{B}}\right)\ge \frac{1}{2}\text{ln}{\gamma }_{\text{th}}\right\}\\ =1-\text{Pr}\left\{J_{\text{B}}<{\gamma }_{\text{th}}-1\right\}.\end{array}(55)$

Substituting Eqs 54 and 55 into Eq. 53, we have the following:

$P_{\text{SOP}}=\{\begin{array}{c}\begin{array}{c}{\displaystyle {\int }_0^{\infty }{F}_{{\gamma }_{\text{SR}}}\left({\gamma }_{\text{SE}}{\gamma }_{\text{th}}+{\gamma }_{\text{th}}-1\right)f_{{\gamma }_{\text{SE}}}\left({\gamma }_{\text{SE}}\right)\text{d}{\gamma }_{\text{SE}},}\end{array}\\ \text{if}{\gamma }_{\text{th}}-1<J_{\text{B},\text{min}}\\ \begin{array}{c}1-\left(1-{\displaystyle {\int }_0^{\infty }{F}_{{\gamma }_{\text{SR}}}\left({\gamma }_{\text{SE}}{\gamma }_{\text{th}}+{\gamma }_{\text{th}}-1\right)f_{{\gamma }_{\text{SE}}}\left({\gamma }_{\text{SE}}\right)\text{d}{\gamma }_{\text{SE}}}\right)\left(1-{\displaystyle {\int }_{J_{\text{B},\text{min}}}^{{\gamma }_{\text{th}}-1}{f}_{J_{\text{B}}}\left(y\right)\text{d}y}\right),\end{array}\\ \text{if}{J}_{\text{B},\text{min}}\le {\gamma }_{\text{th}}-1<J_{\text{B},\text{max}}\\ \begin{array}{c}1-\left(1-{\displaystyle {\int }_0^{\infty }{F}_{{\gamma }_{\text{SR}}}\left({\gamma }_{\text{SE}}{\gamma }_{\text{th}}+{\gamma }_{\text{th}}-1\right)f_{{\gamma }_{\text{SE}}}\left({\gamma }_{\text{SE}}\right)\text{d}{\gamma }_{\text{SE}}}\right)\left(1-{\displaystyle {\int }_{J_{\text{B},\text{min}}}^{J_{\text{B},\text{max}}}{f}_{J_{\text{B}}}\left(y\right)\text{d}y}\right),\end{array}\\ \text{if}{\gamma }_{\text{th}}-1\ge J_{\text{B},\text{max}}.\end{array}(56)$

It is mathematically difficult to obtain the exact close-form expression for SOP as shown in Eq. 56. Therefore, we alternatively evaluate the lower bound of SOP. We assume that ${\gamma }_{\text{SE}}\gg 1$ and ${\gamma }_{\text{SR}}\gg 1$, and when ${\gamma }_{\text{SR}}>{\gamma }_{\text{SE}}$, we have $\left(1+{\gamma }_{\text{SR}}\right)/\left(1+{\gamma }_{\text{SE}}\right)<{\gamma }_{\text{SR}}/{\gamma }_{\text{SE}}$. Therefore, we can derive the lower bound of SOP as follows:

$P_{\text{SOP}}\ge P_{{\text{SOP}}_{\text{L}}}\stackrel{\text{Δ}}{=}\{\begin{array}{c}A,\text{if}{\gamma }_{\text{th}}-1<J_{\text{B},\text{min}}\\ A+{\epsilon }^{\prime }[J_{\text{B},\text{min}}^{-\frac{1}{m+3}}-{\left({\gamma }_{\text{th}}-1\right)}^{-\frac{1}{m+3}}]\times \left(1-A\right),\text{if}{J}_{\text{B},\text{min}}\le {\gamma }_{\text{th}}-1<J_{\text{B},\text{max}}\\ A+{\epsilon }^{\prime }[J_{\text{B},\text{min}}^{-\frac{1}{m+3}}-J_{\text{B},\text{max}}^{-\frac{1}{m+3}}]\times \left(1-A\right),\text{if}{\gamma }_{\text{th}}-1\ge J_{\text{B},\text{max}},\end{array}(57)$

where

$\begin{array}{c}A=\frac{1}{\text{Γ}\left(m_{\text{R}}\right)}\frac{1}{\text{Γ}\left(m_{\text{E}}\right)}{\left(\frac{m_{\text{E}}{G}_{\text{R}}}{{\gamma }_{\text{th}}{m}_{\text{R}}{G}_{\text{E}}}\right)}^{m_{\text{E}}}\frac{\text{Γ}\left(m_{\text{R}}+m_{\text{E}}\right)}{m_{\text{R}}{\left(1+\frac{m_{\text{E}}{G}_{\text{R}}}{{\gamma }_{\text{th}}{m}_{\text{R}}{G}_{\text{E}}}\right)}^{m_{\text{R}}+m_{\text{E}}}}\times F\left(1,m_{\text{R}}+m_{\text{E}};1+m_{\text{R}};\frac{1}{\frac{m_{\text{E}}{G}_{\text{R}}}{{\gamma }_{\text{th}}{m}_{\text{R}}{G}_{\text{E}}}+1}\right)\end{array}.(58)$

${\epsilon }^{\prime }=\left(m+3\right)\frac{\text{Ξ}}{2}{\left(\frac{2\pi {\sigma }_{\text{B}}^2}{e{\xi }^2{P}^2}\right)}^{-\frac{1}{m+3}}$, $F\left(a,b;c;z\right)$ is the Gauss hypergeometric function.

Remark 6.With the increase in$d_1$, the Alice–relay link path loss is reduced, which results in the decreasing of the instantaneous SNR${\gamma }_{SR}$, and the value of the$\text{Pr}\left\{C_{hop,1}^{\prime }\ge C_{th}\right\}$is reduced due to the channel advantages of the Alice–relay link over the Alice–Eve. Therefore, the value of the lower bound of the SOP also increased.

Remark 7.According toEqs 2, 46, and 54, it is seen that by increasing λ, the value of the$\text{Pr}\left\{C_{hop,1}^{\prime }\ge C_{th}\right\}$is also increased, and then the lower bound of the SOP is decreased.

Remark 8.By increasing$m_E$, the value of the$C_{hop,1}^{\prime }$is decreased and the value of the$\text{Pr}\left\{C_{hop,1}^{\prime }\ge C_{th}\right\}$is also decreased. According toEq. 53, we can conclude that the value of the SOP is increased.

4.2 Probability of SPSC Analysis

Similarly, the probability of SPSC of the hybrid RF/VLC system when an eavesdropper eavesdrops on the RF link can be written as follows:

$\begin{array}{c}{P}_{\text{SPSC}}=\text{Pr}\left\{\text{min}\left(C_{\text{hop},1}^{\prime },C_{\text{hop},2}^{\prime }\right)>0\right\}\\ =\text{Pr}\left\{C_{\text{hop},1}^{\prime }>0\right\}\text{Pr}\left\{C_{\text{hop},2}^{\prime }>0\right\}.\end{array}(59)$

According to Eq. 45, $\text{Pr}\left\{C_{\text{hop},1}^{\prime }>0\right\}$ is expressed as follows:

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},1}^{\prime }>0\right\}=\text{Pr}\left\{\frac{1}{2}\text{ln}\left(\frac{1+{\gamma }_{\text{SR}}}{1+{\gamma }_{\text{SE}}}\right)>0\right\}\\ =\text{Pr}\left\{{\gamma }_{\text{SR}}>{\gamma }_{\text{SE}}\right\},\end{array}(60)$

and $\text{Pr}\left\{C_{\text{hop},2}^{\prime }>0\right\}$ is expressed as follows:

$\begin{array}{c}\text{Pr}\left\{C_{\text{hop},2}^{\prime }>0\right\}=\text{Pr}\left\{\frac{1}{2}\left(1+J_{\text{B}}\right)>0\right\}\\ =\text{Pr}\{J_{\text{B}}>0\}=1.\end{array}(61)$

Based on Eqs 60 and 61, the closed-from expression of the probability of SPSC in Eq. 59 can be written as follows:

$\begin{array}{c}{P}_{\text{SPSC}}=\frac{1}{\text{Γ}\left(m_{\text{R}}\right)}\frac{1}{\text{Γ}\left(m_{\text{E}}\right)}{\left(\frac{G_{\text{R}}{m}_{\text{E}}}{m_{\text{R}}{G}_{\text{E}}}\right)}^{m_{\text{E}}}\frac{\text{Γ}\left(m_{\text{R}}+m_{\text{E}}\right)}{m_{\text{E}}{\left(1+\frac{G_{\text{R}}{m}_{\text{E}}}{m_{\text{R}}{G}_{\text{E}}}\right)}^{m_{\text{R}}+m_{\text{E}}}}F\left(1,m_{\text{R}}+m_{\text{E}};1+m_{\text{E}};\frac{\frac{G_{\text{R}}{m}_{\text{E}}}{m_{\text{R}}{G}_{\text{R}}^{\prime }}}{\frac{G_{\text{R}}{m}_{\text{E}}}{m_{\text{R}}{G}_{\text{E}}}+1}\right).\end{array}(62)$

Remark 9.Similar to Remark 6, the probability of the SPSC decreases by increasing$d_1$. However, with the increase in$d_1^{\prime }$, the value of the$\text{Pr}\left\{C_{hop,1}^{\prime }>0\right\}$is also increased. Therefore, the probability of the SPSC is increased by increasing$d_1^{\prime }$.

Remark 10.Since the value of the$\text{Pr}\left\{C_{hop,2}^{\prime }>0\right\}$is always equal to one, the probability of SPSC mainly depends on the RF link.

5 Numerical Results

In this section, we present the numerical results of hybrid RF/VLC systems. Here, the theoretical results of the derived lower bound of the SOP and the probability of SPSC are verified by using Monte-Carlo simulation, which is performed by generating ${10}^4$ random samples. Unless otherwise specified, the main simulation parameters of the hybrid system are listed in Table 1. It should be noted that all numerical results are obtained by using MATLAB.

TABLE 1

TABLE 1. Main simulation parameters.

5.1 Results When VLC Link Is Eavesdropped Upon

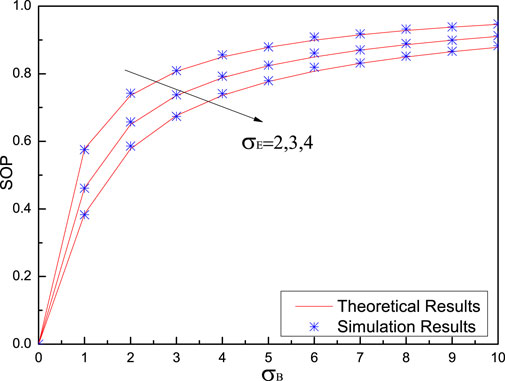
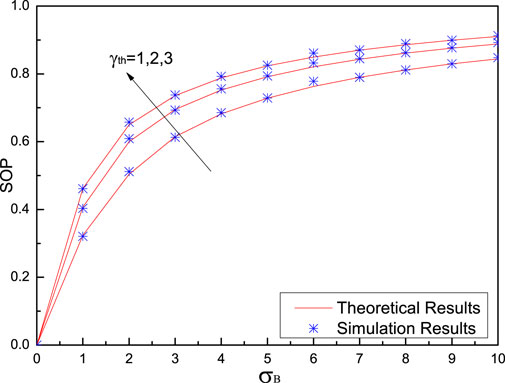
Figure 5 shows the SOP versus Bob’s noise standard deviation ${\sigma }_{\text{B}}$ with different Eve’s noise standard deviations ${\sigma }_{\text{E}}$ when P = 60 dB, ξ = 0.2, and ${\gamma }_{\text{th}}$ = 3. It is seen that the SOP performance deteriorates with the increase in ${\sigma }_{\text{B}}$, and this is because the larger the value of ${\sigma }_{\text{B}}$, the smaller the channel gain $H_{\text{B}}$. A larger $H_{\text{B}}$ also leads to better secrecy performance, while a smaller $H_{\text{B}}$ degrades the secrecy performance. Besides, with the increase in ${\sigma }_{\text{E}}$, the value of SOP is reduced; therefore, by increasing ${\sigma }_{\text{E}}$, $H_{\text{E}}$ is reduced, and a smaller $H_{\text{E}}$ leads to higher secrecy as in Remark 1.

FIGURE 5

FIGURE 5. SOP versus ${\sigma }_{\text{B}}$ with different ${\sigma }_{\text{E}}$ when P = 60 dB, ξ = 0.2, and ${\gamma }_{\text{th}}$ = 3.

Figure 6 shows the SOP versus Bob’s noise standard deviation ${\sigma }_{\text{B}}$ with different ${\gamma }_{\text{th}}$ when P = 60 dB, ξ = 0.2, and ${\sigma }_{\text{E}}$ = 3. As it is seen, the SOP increases with the increase in ${\sigma }_{\text{B}}$, which is consistent with that in Figure 5. Moreover, it can be observed that the value of SOP becomes larger with the increase in ${\gamma }_{\text{th}}$, which means that the system secrecy performance is degraded, which coincides with Remark 2.

FIGURE 6

FIGURE 6. SOP versus ${\sigma }_{\text{B}}$ with different ${\gamma }_{\text{th}}$ when P = 60 dB, ξ = 0.2, and ${\sigma }_{\text{E}}$ = 3.

From Figure 5 and Figure 6, it can be clearly observed that simulation results are in close agreement with the theoretical results, which validates our theoretical analysis of SOP as correct.

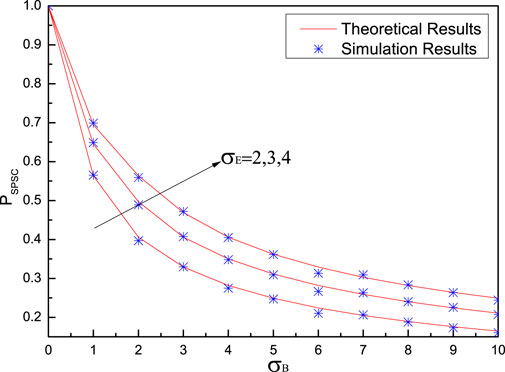
Figure 7 shows the probability of SPSC versus Bob’s noise standard deviation ${\sigma }_{\text{B}}$ with different Eve’s noise standard deviations ${\sigma }_{\text{E}}$ when P = 60 dB and ξ = 0.2. It can be seen that the performance of the probability of SPSC deteriorates with the increase in ${\sigma }_{\text{B}}$, and this is because a larger value of ${\sigma }_{\text{B}}$ results in a smaller channel gain $H_{\text{B}}$. A larger $H_{\text{B}}$ leads to better secrecy performance, whereas a smaller value leads to worse secrecy performance. Moreover, it can be observed from the plot that the probability of SPSC is increased by increasing ${\sigma }_{\text{E}}$ from ${\sigma }_{\text{E}}$ = 2 to ${\sigma }_{\text{E}}$ = 4. This means that by increasing ${\sigma }_{\text{E}}$, $H_{\text{E}}$ is reduced, and a smaller $H_{\text{E}}$ leads to better secrecy performance. This is consistent with Remark 4.

FIGURE 7

FIGURE 7. $P_{\text{SPSC}}$ versus ${\sigma }_{\text{B}}$ with different ${\sigma }_{\text{E}}$ when P = 60 dB and ξ = 0.2.

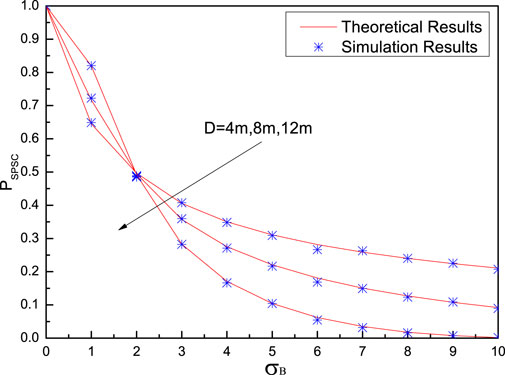
Figure 8 shows the probability of SPSC versus Bob’s noise standard deviation ${\sigma }_{\text{B}}$ with different floor radii D when P = 60 dB and ξ = 0.2. It can be seen from Figure 8 that when ${\sigma }_{\text{B}}\le 2$, the probability of SPSC decreases with the increase in D. This is because when ${\sigma }_{\text{B}}\le 2$, a larger ${\sigma }_{\text{E}}$ (${\sigma }_{\text{E}}=3$) leads to a smaller $H_{\text{E}}$, and thus, secrecy performance mainly depends on Bob’s and Eve’s SNRs. When ${\sigma }_{\text{B}}>2$, it is seen that by increasing D from 4 to 12 m, the value of the probability of SPSC is increased. This is also consistent with Remark 5. Expanding the floor radius, D, also decreases the probability of Eve eavesdropping on information, which improves the performance of the hybrid system.

FIGURE 8

FIGURE 8. $P_{\text{SPSC}}$ versus ${\sigma }_{\text{B}}$ with different D when P = 60 dB and ξ = 0.2.

Moreover, it can be found from Figure 7 and Figure 8 that all theoretical results match simulation results very well, which indicates the correctness of the theoretical analysis.

5.2 Results When RF Link Is Eavesdropped Upon

Figure 9 shows SOP versus the distance between nodes Alice and relay $d_1$ with different path loss exponents λ when P = 60 dB, $m_{\text{E}}$ = 2, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $d_1^{\prime }$ = 2 (eavesdropping on the RF link). It can be seen that the SOP performance is deteriorated by increasing $d_1$, which is intuitive because a larger value of $d_1$ results in a smaller channel gain, $h_{\text{SR}}$, which then results in a worse secrecy performance. This conclusion is consistent with Remark 6. Moreover, with the increase in path loss exponent λ, the value of SOP becomes smaller, which means that the system secure transmission performance is improved. This verifies the conclusion in Remark 7.

FIGURE 9

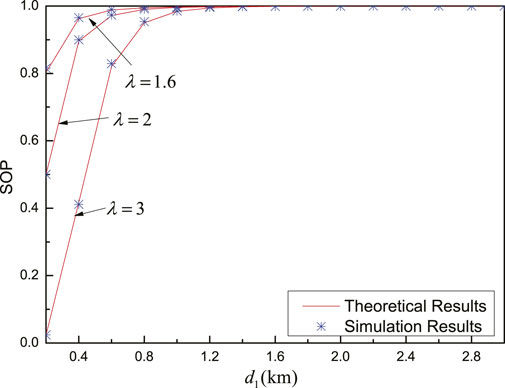
FIGURE 9. SOP versus $d_1$ with different λ when P = 60 dB, $m_{\text{E}}$ = 2, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $d_1^{\prime }$ = 2 (eavesdropping on the RF link).

Figure 10 shows the SOP versus the distance between nodes Alice and relay $d_1$ with different Alice–Eve channel fading factors $m_{\text{E}}$ when P = 60 dB, λ = 3, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $d_1^{\prime }$ = 2 (eavesdropping on the RF link). As it is seen, by increasing $d_1$, the SOP performance is degraded with the increase in $d_1$. This is also consistent with that in Figure 9. Besides, by increasing $m_{\text{E}}$, the value of SOP also becomes large. This is because the larger the value of $m_{\text{E}}$, the smaller the Alice–Eve channel fading which, in turn, deteriorates the secrecy performance. This verifies the conclusion in Remark 8.

FIGURE 10

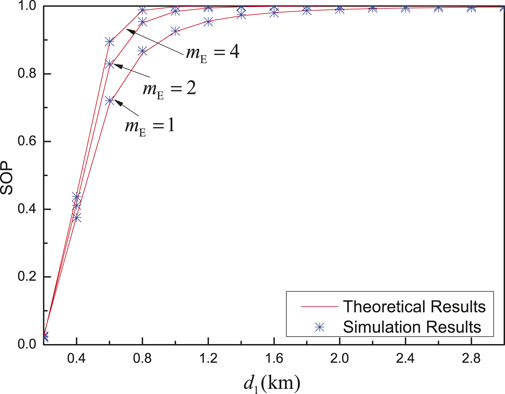
FIGURE 10. SOP versus $d_1$ with different $m_{\text{E}}$ when P = 60 dB, λ = 3, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $d_1^{\prime }$ = 2 (eavesdropping on the RF link).

From Figure 9 and Figure 10, it should be emphasized that the performance gap between theoretical results and simulation results is small, which verifies the accuracy of the derived expression, which indicates that the scaling for the lower bound of SOP is reasonable.

Figure 11 shows the probability of SPSC versus the distance between nodes Alice and relay $d_1$ with different distances between node Alice and Eve $d_1^{\prime }$ when P = 60 dB, λ = 3, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $m_{\text{E}}$ = 2 (eavesdropping on the RF link). It is seen that the SPSC performance is decreased by increasing $d_1$. This also indicates that the system secrecy performance is reduced when the relay node receives less confidential information. This conclusion is consistent with that in Figure 9. By increasing $d_1^{\prime }$, Eve eavesdrops on less information. Therefore, the larger the value of $d_1^{\prime }$, the better the performance. This is also consistent with Remark 9.

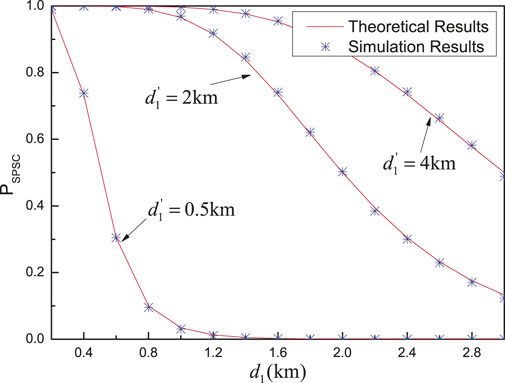
FIGURE 11

FIGURE 11. $P_{\text{SPSC}}$ versus $d_1$ with different $d_1^{\prime }$ when P = 60 dB, λ = 3, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $m_{\text{E}}$ = 2 (eavesdropping on the RF link).

Figure 12 shows the probability of SPSC versus the distance between nodes Alice and relay $d_1$ with different Alice–Eve channel fading factors $m_{\text{E}}$ when P = 60 dB, λ = 3, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $d_1^{\prime }$ = 2 (eavesdropping on the RF link). Similar to Figure 11, the probability of the SPSC performance degrades with the increase in $d_1$. Moreover, for $m_{\text{E}}$ smaller than 1.6 (km), the probability of the SPSC increases with the increase in the Alice–Eve channel fading factor $m_{\text{E}}$. However, if $d_1$ is larger than 1.6 (km), the probability of the SPSC increases with the decrease in the Alice–Eve channel fading factor $m_{\text{E}}$. This is because for small $d_1$, the relay node has a stronger ability to receive confidential information than Eve. For a larger $d_1$, Eve eavesdrops on more confidential information.

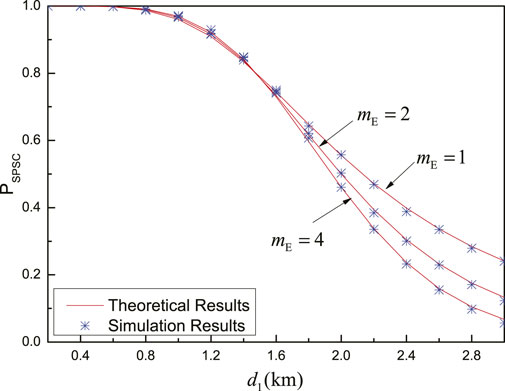
FIGURE 12

FIGURE 12. $P_{\text{SPSC}}$ versus $d_1$ with different $d_1^{\prime }$ when P = 60 dB, λ = 3, ${\sigma }_{\text{B}}$ = 2, $m_{\text{B}}$ = 2, and $d_1^{\prime }$ = 2 (eavesdropping on the RF link).

From Figure 11 and Figure 12, all theoretical results of the probability of the SPSC match the simulation results very well, which verifies the accuracy of the derived theoretical expression of the probability of the SPSC. Therefore, the derived expression can be used directly to evaluate the system performance with time-intensive simulations.

5.3 Comparisons for Systems With and Without Eavesdroppers

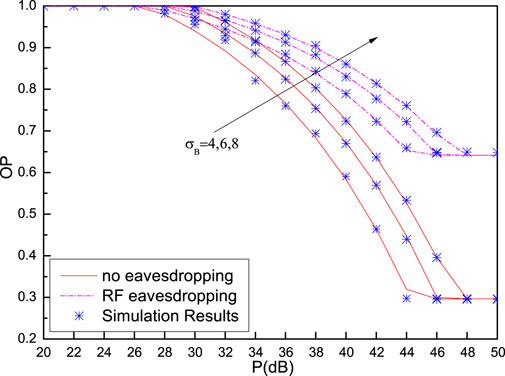
Figure 13 depicts OP performance for systems with and without an RF eavesdropper when ξ = 0.2 and ${\gamma }_{\text{th}}$ = 3. It is seen that the OP performance decreases with the increase in P, and this is because the larger the value of P, the larger the capacity of the second hop becomes. Besides, with the increase in larger ${\sigma }_{\text{B}}$, the OP performance is deteriorated, which is consistent with Remark 1. Furthermore, for fixed P and ${\sigma }_{\text{B}}$, the system with an RF eavesdropper achieves worse OP performance than the system without an eavesdropper. It is because the existence of the eavesdropper increases the security risk of the system.

FIGURE 13

FIGURE 13. OP performance of systems with and without an RF eavesdropper when ξ = 0.2 and ${\gamma }_{\text{th}}$ = 3.

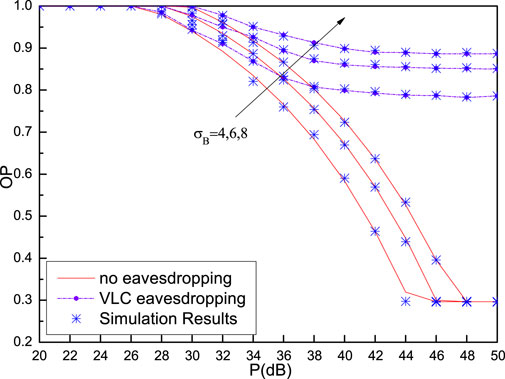
Figure 14 illustrates the OP performance for systems with and without a VLC eavesdropper when ξ = 0.2 and ${\gamma }_{\text{th}}$ = 3. As it is seen, the value of OP decreases with the increase in P, which is consistent with that in Figure 13. Moreover, it can be observed that for fixed ${\sigma }_{\text{B}}$ and P, the value of OP becomes larger when the VLC link is eavesdropped upon.

FIGURE 14

FIGURE 14. OP performance of systems with and without a VLC eavesdropper when ξ = 0.2 and ${\gamma }_{\text{th}}$ = 3.

6 Conclusion

In this article, we have studied the performance of a hybrid RF/VLC DF-based relaying network, in which two scenarios are taken into account: in one scenario, the VLC link is wiretapped, and in the other scenario, the RF link is wiretapped. The major conclusions of the study are given as follows:

1. We assume that the RF link experiences Nakagami-m fading and has path loss, and the non-negative and average optical intensity constraint in the VLC link is considered. The closed-form expressions of the lower bound of SOP and the probability of SPSC are derived, respectively. Numerical results show that theoretical results match simulation results well.

2. When the VLC link is eavesdropped upon, Bob’s (or Eve’s) noise standard deviation ${\sigma }_{\text{B}}$ (or ${\sigma }_{\text{E}}$), the equivalent threshold of the SNR ${\gamma }_{\text{th}}$, and the floor radius D have strong impacts on the performance of SOP or the probability of SPSC. The increase in the ${\sigma }_{\text{B}}$ and ${\gamma }_{\text{th}}$ degrades the system secrecy performance, while the increase in ${\sigma }_{\text{E}}$ and D will improve the secrecy performance.

3. If the RF link is eavesdropped upon, we can conclude that with the increase in $d_1$, the system secrecy performance is degraded, whereas the increase in λ and $d_1^{\text{'}}$ improves the secrecy performance.

4. The derived theoretical expressions in this study will enable communication system designers to quickly and accurately evaluate PLS performance of the hybrid RF/VLC system without time-intensive and laborious Monte-Carlo simulations.

In this study, the secrecy performance of the hybrid RF/indoor VLC system is analyzed. In future work, we will establish the channel model for outdoor VLC and continue to study the secrecy performance of the hybrid RF/outdoor VLC system. Moreover, we will also explore some secrecy performance improvement schemes of the hybrid system.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding authors.

Author Contributions

JW and QW designed the research. JW, QW, and JL contributed with data acquisition, analysis, and discussion of results. BZ contributed to the data analysis. JL wrote the manuscript with input from all other authors.

Funding

This work is supported by the National Nature Science Foundation of China (61701254 and 11604133), the Science and Technology Plan of Youth Innovation Team for Universities of Shandong Province (2019KJJ019), the Introduction and Cultivation Plan of Youth Innovation Talents for Universities of Shandong Province, the Fund of the Shandong Key Laboratory of Optical Communication Science and Technology in Liaocheng University (SDOC201901), and the Open Project of Shanghai Key Laboratory of Trustworthy Computing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Note that the instantaneous SC in reference [18] is defined as the difference of channel capacities between the Alice–relay–Bob channel and the Alice–relay–Eve channel. Different from reference [18], the instantaneous SC in our study is defined as the minimum SC of the two hops, which is similar to that in reference [17].

²The orange rectangle in Figure 2 is determined by J_B and J_E, and the red straight line represents $J_{\text{B}}={\mathrm{\gamma }}_{\text{th}}{J}_{\text{E}}$. The integral region is the yellow enclosed area enclosed by the red straight line and the orange rectangle in Figure 2. The four cases in Figure 2 depend on the slope γ_th of the line and the ratio of JB and JE. According to mathematical knowledge, the value of $\mathrm{Pr}\left(J_{\text{B}}<J_{\text{E}}{\mathrm{\gamma }}_{\text{th}}\right)$ is actually equal to the double integral on the integral region, and the calculation of the double integral is realized by the repeated integral.

³Similarly to Figure 2, the orange rectangle in Figure 3 is also determined by J_B and J_E, and the red straight line represents J_B = J_E. The integral region is also the yellow enclosed area enclosed by the red straight line and the orange rectangle in Figure 3. The four cases in Figure 3 depend on the slope 1 of the line and the ratio of J_B and J_E. According to mathematical knowledge, the value of Pr {J_B > J_E} is actually equal to the double integral on the integral region, and the calculation of the double integral is realized by the repeated integral.

References

1. Yang Z, Chen M, Wong KK, Poor HV, Cui S. Federated Learning for 6G: Applications, Challenges, and Opportunities. arXiv preprint arXiv:2101.01338 (2021).

Google Scholar

2. Wang J-Y, Yang Z, Wang Y, Chen M. On the Performance of Spatial Modulation Based Optical Wireless Communications. IEEE Photon Technol Lett (2016) 28:1. doi:10.1109/LPT.2016.2585502

CrossRef Full Text | Google Scholar

3. Tabassum H, Hossain E. Coverage and Rate Analysis for Co-existing RF/VLC Downlink Cellular Networks. IEEE Trans Wireless Commun (2018) 17:2588–601. doi:10.1109/TWC.2018.2799204

CrossRef Full Text | Google Scholar

4. Rakia T, Yang H-C, Gebali F, Alouini M-S. Optimal Design of Dual-Hop VLC/RF Communication System with Energy Harvesting. IEEE Commun Lett (2016) 20:1979–82. doi:10.1109/LCOMM.2016.2595561

CrossRef Full Text | Google Scholar

5. Kashef M, Ismail M, Abdallah M, Qaraqe KA, Serpedin E. Energy Efficient Resource Allocation for Mixed RF/VLC Heterogeneous Wireless Networks. IEEE J Select Areas Commun (2016) 34:883–93. doi:10.1109/JSAC.2016.2544618

CrossRef Full Text | Google Scholar

6. Hammouda M, Akin S, Vegni AM, Haas H, Peissig J. Link Selection in Hybrid RF/VLC Systems under Statistical Queueing Constraints. IEEE Trans Wireless Commun (2018) 17:2738–54. doi:10.1109/TWC.2018.2802937

CrossRef Full Text | Google Scholar

7. Kong J, Ismail M, Serpedin E, Qaraqe KA. Energy Efficient Optimization of Base Station Intensities for Hybrid RF/VLC Networks. IEEE Trans Wireless Commun (2019) 18:4171–83. doi:10.1109/TWC.2019.2922611

CrossRef Full Text | Google Scholar

8. Hsiao Y-C, Wu Y-C, Lin C. Energy-efficient Beamforming Design for MU-MISO Mixed RF/VLC Heterogeneous Wireless Networks. IEEE Trans Signal Process (2019) 67:3770–84. doi:10.1109/TSP.2019.2920612

CrossRef Full Text | Google Scholar

9. Marzban MF, Kashef M, Abdallah M, Khairy M. Beamforming and Power Allocation for Physical-Layer Security in Hybrid RF/VLC Wireless Networks. In: 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC). Piscataway, New Jersey: IEEE (2017). p. 258–63.

CrossRef Full Text | Google Scholar

10. Rakia T, Yang HC, Gebali F, Alouini MS. Dual-hop VLC/RF Transmission System with Energy Harvesting Relay under Delay Constraint. In: 2016 IEEE Globecom Workshops (GC Wkshps). Piscataway, New Jersey: IEEE (2016). p. 1–6.

CrossRef Full Text | Google Scholar

11. Al-Khori J, Nauryzbayev G, Abdallah MM, Hamdi M. Secrecy Performance of Decode-And-Forward Based Hybrid RF/VLC Relaying Systems. IEEE Access (2019) 7:10844–56. doi:10.1109/ACCESS.2019.2891678

CrossRef Full Text | Google Scholar

12. Kumar A, Garg P, Gupta A. PLS Analysis in an Indoor Heterogeneous VLC/RF Network Based on Known and Unknown CSI. IEEE Syst J (2021) 15:68–76. doi:10.1109/JSYST.2020.2964033

CrossRef Full Text | Google Scholar

13. Wang J-Y, Qiu Y, Lin S-H, Wang J-B, Wang Q, Zhang B. Performance Analysis and Improvement for Secure VLC with SLIPT and Random Terminals. IEEE Access (2020) 8:73645–58. doi:10.1109/ACCESS.2020.2988470

CrossRef Full Text | Google Scholar

14. Zedini E, Soury H, Alouini M-S. On the Performance Analysis of Dual-Hop Mixed FSO/RF Systems. IEEE Trans Wireless Commun (2016) 15:3679–89. doi:10.1109/TWC.2016.2524685

CrossRef Full Text | Google Scholar

15. Yang L, Hasna MO, Gao X. Performance of Mixed RF/FSO with Variable Gain over Generalized Atmospheric Turbulence Channels. IEEE J Select Areas Commun (2015) 33:1913–24. doi:10.1109/JSAC.2015.2432471

CrossRef Full Text | Google Scholar

16. Soleimani-Nasab E, Uysal M. Generalized Performance Analysis of Mixed RF/FSO Cooperative Systems. IEEE Trans Wireless Commun (2016) 15:714–27. doi:10.1109/TWC.2015.2477400

CrossRef Full Text | Google Scholar

17. Pan X, Ran H, Pan G, Xie Y, Zhang J. On Secrecy Analysis of DF Based Dual Hop Mixed RF-FSO Systems. IEEE Access (2019) 7:66725–30. doi:10.1109/ACCESS.2019.2914227

CrossRef Full Text | Google Scholar

18. Lei H, Dai Z, Park K-H, Lei W, Pan G, Alouini M-S. Secrecy Outage Analysis of Mixed RF-FSO Downlink SWIPT Systems. IEEE Trans Commun (2018) 66:6384–95. doi:10.1109/TCOMM.2018.2865944

CrossRef Full Text | Google Scholar

19. Lei H, Dai Z, Ansari IS, Park K-H, Pan G, Alouini M-S. On Secrecy Performance of Mixed RF-FSO Systems. IEEE Photon J. (2017) 9:1–14. doi:10.1109/JPHOT.2017.2723422

CrossRef Full Text | Google Scholar

20. Lei H, Luo H, Park K-H, Ren Z, Pan G, Alouini M-S. Secrecy Outage Analysis of Mixed RF-FSO Systems with Channel Imperfection. IEEE Photon J. (2018) 10:1–13. doi:10.1109/JPHOT.2018.2835562

CrossRef Full Text | Google Scholar

21. Wang J-B, Hu Q-S, Wang J, Chen M, Wang J-Y. Tight Bounds on Channel Capacity for Dimmable Visible Light Communications. J Lightwave Technol (2013) 31:3771–9. doi:10.1109/JLT.2013.2286088

CrossRef Full Text | Google Scholar

22. Simon MK, Alouini MS. Digital Communication over Fading Channels. 2nd ed., Vol. 95. Hoboken, New Jersey: John Wiley & Sons (2005).

23. Jeffrey A, Zwillinger D. Table of Integrals, Series, and Products. Amsterdam, Netherlands: Elsevier (2007).

24. Komine T, Nakagawa M. Fundamental Analysis for Visible-Light Communication System Using LED Lights. IEEE Trans Consumer Electron (2004) 50:100–7. doi:10.1109/TCE.2004.1277847

CrossRef Full Text | Google Scholar

25. Yin L, Haas H. Physical-layer Security in Multiuser Visible Light Communication Networks. IEEE J Select Areas Commun (2018) 36:162–74. doi:10.1109/JSAC.2017.2774429

CrossRef Full Text | Google Scholar

26. Wang J-Y, Liu C, Wang J-B, Wu Y, Lin M, Cheng J. Physical-layer Security for Indoor Visible Light Communications: Secrecy Capacity Analysis. IEEE Trans Commun (2018) 66:6423–36. doi:10.1109/TCOMM.2018.2859943

CrossRef Full Text | Google Scholar

27. Ai Y, Mathur A, Cheffena M, Bhatnagar MR, Lei H. Physical Layer Security of Hybrid Satellite-FSO Cooperative Systems. IEEE Photon J (2019) 11:1–14. doi:10.1109/JPHOT.2019.2892618

CrossRef Full Text | Google Scholar