Fluids Alter Elasticity Measurements: Porous Wave Propagation Accounts for Shear Wave Dispersion in Elastography

In shear wave elastography, rotational wave speeds are converted to elasticity measures using elastodynamic theory. The method has a wide range of applications and is the gold standard for non-invasive liver fibrosis detection. However, the observed shear wave dispersion of in vivo human liver shows a mismatch with purely elastic and visco-elastic wave propagation theory. In a laboratory phantom experiment we demonstrate that porosity and fluid viscosity need to be considered to properly convert shear wave speeds to elasticity in soft porous materials. We extend this conclusion to the clinical application of liver stiffness characterization by revisiting in vivo studies of liver elastography. To that end we compare Biot’s theory of poro-visco-elastic wave propagation to Voigt’s visco-elastic model. Our results suggest that accounting for dispersion due to fluid viscosity could improve shear wave imaging in the liver and other highly vascularized organs.

1 Introduction

Shear wave elastography is a fast, non-invasive method to estimate tissue elasticity in vivo. Its first clinical application has been the estimation of liver fibrosis, and it is more and more used as a replacement for liver puncture, the current gold standard. The method is quantitative through in situ measurement of the shear wave speed by ultrasonic or magnetic resonance imaging. An estimate of tissue elasticity is retrieved through inversion of the wave speed. Clinical applications as of today include ultrasonic 1D elasticity estimation (FibroScan, Echosens, Paris, France), ultrasonic 2D elasticity mapping (e.g., Aixplorer, SuperSonic Imagine, Aix-en-Provence, France; GE Logiq, Boston, United States; Canon Aplio, Canon Medical Systems, Tochigi, Japan) and magnetic resonance 2D and 3D elasticity mapping (e.g., General Electric/Philips/Siemens Healthcare). Linear elastic or visco-elastic theory is commonly assumed for the elasticity inversion. However, the order of magnitude of the shear modulus retrieved from elastography and other measurement methods, such as dynamic mechanical analysis (DMA), differs [1]. Furthermore, ex vivo and in vivo elastography measurements vary, making a standardization difficult [2, 3]. Finally, the observed in vivo shear wave velocity dispersion with frequency of the liver is badly predicted by visco-elastic theory, and recent in vivo studies [4, 5] challenge the commonly assumed correlation of viscosity with fibrosis [6]. As of today questions remain concerning the physical processes behind the observed dispersion. This ambiguity has led recent studies (e.g., [7]) to drop the rheological model in favor of a model-independent dispersion slope as the “viscous” parameter. Our work attempts to explain the observed discrepancies between theory and in vivo elastography data by considering the liver as a porous biphasic medium, which is described by Biot theory, instead of a homogeneous visco-elastic solid. The introduction of a fluid phase introduces a new loss mechanism, the viscosity of the fluid, as well as a change in the effective density of the solid part. Proper physical modeling of the of the shear wave dispersion is key to a quantitative elasticity reconstruction and ultimately might reduce false positives and negatives in elastography liver characterization. We postulate that to properly account for the observed shear wave dispersion in the liver, porous theory needs to be taken into account. This hypothesis is based on our experimental results in a porous phantom and theoretical considerations which are compared to existing in vivo data. The paper is structured as follows:

In Section 1.1 we report various approaches to model the liver as a porous material. Publications in elastography which regard the liver as a poro-elastic Biot medium are scarce and consequently the investigated literature spans includes from anatomy, dynamic mechanical analysis, surgery simulation, tissue engineering and numerical fluid dynamics. In Section 3.1 we confirm the results of [8] who found that the shear wave dispersion in a soft porous material is described by poro-elastic wave propagation theory. This is unambiguously shown by comparing the shear wave dispersion in a soft porous phantom saturated by a Xanthan solution with the dispersion of the same phantom saturated by water. The observed results are exclusively explained by poro-visco-elastic theory, which is introduced as Biot’s theory in Section 2.1.1. Furthermore, a more intuitive interpretation of Biot’s theory is given in Section 2.1.2 and the experimental results are compared to Biot’s model in Section 3.1.1. The experimental results are followed by analytic modeling of the liver as a porous material in Section 3.2. We use literature values for the poro-visco-elastic parameters (Section 2.6.1) to compare the theoretical dispersion of a model liver with previously reported in vivo shear wave dispersion measurements (Section 4.2). The analytic modeling shows that changes in the porous parameters can account for measured variations in shear wave speed that visco-elasticity fails to explain (Section 3.2.1, Section 4.2.1). We conclude by comparing Biot theory with commonly used rheological models in Section 4.3.1. Finally, we present challenges for future research in Section 4.3 and a common conclusion in Section 5.

1.1 The Liver-A Sponge?

Recently, we have shown experimentally that Biot’s theory of poro-elastic wave propagation well predicts the shear wave dispersion in a melamine sponge [8]. In Biot’s theory of poro-elastic wave propagation shear wave dispersion is caused by the viscosity of the fluid saturating the connected pore space. Several organs that are of interest to elastography imaging have been described as porous materials, e.g., the lung, spleen, brain and liver. The liver is the foremost organ to be clinically imaged using shear wave elastography. Here, it is usually modeled as an elastic or visco-elastic solid. However, fresh liver grafts clearly show the presence of at least one liquid phase: the blood. In fact, the liver is one of the blood-richest organs and has previously been depicted as a fluid-filled sponge by several research groups [9–11]. Together with other organs, such as the spleen, the liver serves as a specific blood reservoir of the body [12]. It is thus justified to regard it as a soft porous material saturated by a viscous fluid. Furthermore, blood saturation or liver perfusion and blood viscosity are not constants. Both vary among individuals as well as with time for each individual. Perfusion and viscosity are known to be dependent on many factors such as hydration, diet, health and physical fitness. Liver diseases do not only alter the elasticity of the cellular matrix of the liver but are known to affect the porous parameters, notably porosity and permeability, as well. These insights led different groups to numerically model the liver as a poro-elastic or poro-visco-elastic material in the last decade [1, 9, 13–19]. However, albeit early realization of interstitial fluid flow as an dissipative mechanism for acoustic waves [20], few attempts to link the shear wave dispersion in the liver to its porous and fluid properties have been made to our knowledge. Some recent studies investigated the influence of pore pressure on shear wave speed in the liver [21–23], and [24] describes a 2-parameter pore channel flow model for shear wave dispersion. The first group focuses on pressure effects. The second develops a model that incorporates flow in the constitutive equations, similar to Biot’s first porous theory, the theory of consolidation [25], and to earlier work in compression elastography [26]. Recently [27], model the liver as a hyper-poro-visco-elastic but focus on hyper-elastic deformation and the fluid pressure effect on the shear wave velocity by assuming low porosities and permeabilities. The effect of the viscous fluid on the dynamic wave propagation however, as developed by [28–31] and presented in Section 2.1.1, seems to have been overlooked by the ultrasound elastography community. Hence, the application of Biot theory to ultrasound shear wave elastography seems overdue.

2 Materials and Methods

2.1 Porous Wave Propagation Theory

2.1.1 Biot Theory

A non-phenomenological theory that models porous wave propagation based on the physics of fluid-solid interaction is Biot’s theory of poro-elastic wave propagation [28, 29]. Biot’s shear wave dispersion is governed by the characteristics of the porous structure and the pore filling fluid. As a consequence, the expression for the wave speed differs significantly from that of a purely elastic monophasic wave propagation model. Instead of a single homogeneous density, the model takes into account the fluid density ρ_fl and the density of the solid frame ρ_fr, which is expressed in terms of bulk density of the solid material ρ_s and the porosity ϕ as ρ_fr = ρ_s (1 − ϕ). The mean density is expressed as $\tilde{\rho }={\rho }_s(1-\varphi )+{\rho }_{fl}\varphi$. Furthermore, the model accounts for inertial and viscous coupling between the displacements of the two phases.

The consideration of viscous effects through the fluid viscosity η_f leads to the frequency dependence of the shear wave speed, which is expressed in terms of wavenumber and angular frequency:

$\begin{array}{ll}\hfill v_s& =\frac{1}{\mathfrak{R}\sqrt{{\left(\frac{{\omega }_s}{k_s}\right)}^{-2}}}\hfill \end{array}(1)$

$\begin{array}{ll}\hfill {\left(\frac{{\omega }_s}{k_s}\right)}^{-2}& =\frac{q\tilde{\rho }-{\rho }_{fl}^2}{q{\mu }_{fr}},\hfill \end{array}(2)$

where μ_fr is the shear modulus of the foam. The term q can be expressed in terms of the solid, fluid and porous parameters as:

$\begin{array}{c}\hfill q=\frac{\alpha {\rho }_{fl}}{\varphi }+\frac{i\eta F(\zeta )}{{\omega }_s\kappa },\end{array}(3)$

where κ is permeability, α is tortuosity and F(ζ) expresses the frequency dependence of the viscosity, or the deviation from Poiseuille flow [32]. The permeability is measured in m² and is a measure of fluid transmission through a sample. It is defined as the proportionality constant in Darcy’s law of the volumetric flow rate. The tortuosity takes into account the pore shape. It is generally assumed for cylindrical pores and is evaluated as the total length of the pore divided by the shortest path connecting its ends or in other words: “the ratio of the arc length of a curve relative to its end-to-end distance” [16]. It also accounts for the inertial coupling of the solid and fluid phase, where inertial coupling signifies that an accelerating solid drags parts of the surrounding fluid with it [33]. The solid moving in the fluid thus acquires an additional mass due to the deflection of the surrounding fluid volume, which can be seen as a renormalization process (see [34] 1.3.4). The virtual mass of the solid is thus ρ_virt = ρ_fr + ρ_a = (1 − ϕ)ρ_s + ρ_a, where the additional or apparent mass is calculated as ρ_a = (α − 1)ϕρ_fl.

The derivation from first principles and a detailed description of Biot’s theory are beyond the scope of this work and can be found in the cited references as well as several textbooks, e.g., [35–37]. In order to follow our reasoning we find it however helpful to give an intuitive interpretation that is accessible to the reader who was unfamiliar with poro-elastic theory before reading the present manuscript.

2.1.2 Loss Mechanism and Significance of Biot’s Theory

When compared to linear-elastic or visco-elastic theory some results of Biot’s theory might seem counter-intuitive. We can however understand the complex inertial and viscous effects of the fluid in terms of classic elastic theory by looking at the extreme ends of the dispersion curves when ω → 0 and ω → ∞. If we consider that the shear modulus μ_fr stays constant with frequency and we want to find an equivalent to Biot’s wave speed in terms of the elastic shear wave speed expression $v_s=\sqrt{\frac{\mu }{\rho }}$, we immediately see that the density ρ needs to be replaced by an effective density ρ_eff (ω → 0) and ρ_eff (ω → ∞). At very low frequency, when ω → 0 Hz, the solid and the fluid phase are locked together through viscous coupling. This signifies that due to the viscous drag they move in phase without relative movement between the two. The wave speed is then defined by the true shear modulus of the solid and an effective density made up of the densities of the solid and the fluid phase (${\rho }_{eff}=\tilde{\rho }={\rho }_s(1-\varphi )+{\rho }_{fl}\ast \varphi$). In the case of biological tissues, those densities are approximately equal and the low-frequency limit is thus the velocity which we would have calculated using linear elasticity or visco-elasticity and the true shear modulus. At very high frequencies, when ω → ∞ Hz, which is conceptually similar to the case when the porous material is saturated by a superfluid, the shear wave velocity reaches its maximum value. Because of the lack of viscosity, the fluid is not dragged along by viscous coupling and rests on average¹. The fluid and solid displacements are thus out-of-phase and the shear wave experiences a different effective density: the solid frame density plus an apparent density due to the remaining added mass effect of the fluid. The added mass effect stems from the fact that the fluid is considered to be at rest on average, while there is relative movement between the accelerating solid and the fluid phase (see [38] I, 11). Ignoring the inertial coupling described in ¹, the expression for the effective density is then: ρ_eff = (1 − ϕ)ρ_s + ρ_a. The higher the porosity of the medium, the lower the solid frame density and consequently due to $v_s=\sqrt{\frac{\mu }{{\rho }_{eff}}}$, the higher the shear wave speed in the high-frequency limit. Even for biological tissue, where fluid and solid densities are very similar, the shear wave speed at higher frequencies differs thus strongly from the elastic shear wave speed. While the idealized viscous-less case defines the high-frequency limit of the shear wave velocity and the phase-locked case defines the low frequency limit of the shear wave speed, it is obvious from the gap between the two values that a different physical mechanism is required to explain the evolution from low to high frequency. This is done through fluid viscosity, which introduces dissipation and defines the form of the dispersion curve in between the low and high frequency limits. Eqs 2, 3 account for the frequency dependence: $\tilde{\rho }$ is scaled by the factor q which is a frequency dependent function of the fluid viscosity. To stay within the effective density model, the term $q\bar{\rho }$ could be interpreted as an effective density which is given through the frequency dependence of q(ω).

2.2 Visco-elastic Wave Propagation

In Section 3 we compare the poro-visco-elastic model to a simple visco-elastic model. The shear wave speed of the visco-elastic model is calculated using Voigt’s model:

$\begin{array}{ll}\hfill \mu & ={\mu }_0+i\omega {\mu }_1\hfill \end{array}(4)$

$\begin{array}{ll}\hfill v_s& =\sqrt{\frac{\mu }{\rho }},\hfill \end{array}(5)$

with μ₀ being solid elasticity and μ₁ being solid viscosity. In the present work we explicitly make the choice to compare Biot’s model only to a simple visco-elastic model. Viscosity is still not widely inferred for in clinical practice [39] and most in vivo studies employ a Voigt model with limited success [7]. As a consequence, a model independent measure of the dispersion slope has been proposed as diagnostic value [7] and more complex visco-elastic models, such as Zener’s model are being investigated [7, 40]. However, these include more springs and dampers and require complex inversions. One key difference between viscous and porous models is: the porous parameters in Biot’s model are physical parameters that can be measured independently or determined from physical considerations [40], while the visco-elastic model is phenomenological. Hence, if we were to measure the porous and fluid parameters independently of shear wave elastography, the Voigt and Biot model would exhibit the same number of free parameters, the solid elasticity and viscosity. Note that [40] finds an equivalence of the Zener and Biot model for low frequency shear waves. However, this does not hold for deviations from Poiseuille flow and Zener’s model does not explain the secondary longitudinal wave recently shown in a soft porous tissue [8].

2.3 Parameter Inversion

In order to fit the experimental data to the Biot and Voigt model we perform a constraint global minimization using the Basinhopping algorithm [41] of the Python library Scipy. The global method was chosen instead of a local method to avoid local minima in the optimization. In short, the Basinhoppin algorithm performs a multitude of local minimizations though the L-BFGS-B (Broyden-Fletcher-Goldfarb-Shanno) algorithm, which is a quasi-Newton method [42]. For each minimization it uses varying starting values and keeps or rejects the result. In Section 3 all minimizations are performed on the least squares [42] of the experimental and analytic shear wave speed of the investigated frequency range:

$\mathit{ϵ}=\sum _{i=1}^N\frac{{[v_{exp}({\omega }_i)-v_{sim}({\omega }_i)]}^2}{N},(6)$

where N is the number of frequencies at which the shear wave speed was measured, v_exp is the experimental phase velocity, v_sim is the analytic phase velocity and ω_i is a experimentally measured frequency. Eq. 2 is used to calculate the poro-visco-elastic shear wave speed v_sim. The shear wave speed v_sim of the visco-elastic model is calculated using Voigt’s model from Eq. 5. The bounds for the different minimizations performed in Section 3 are listed in Table 3.

2.4 Penetration Depth

The penetration depth is comparable to the skin depth in electromagnetics and relates the mathematical model outcome of any attenuation model to physical wave propagation (see [40] 2.3.2.2). For example, a model with an elasticity μ₀ → 0 and viscosity μ₁ ≫ μ₀ will result in a calculated wave speed v_s > 0 but a penetration depth δ_skin → 0. Hence, the wave is a non-propagating one. We use the penetration depth as a physical constraint on the feasibility of a proposed model with:

${\delta }_{skin}=\frac{\omega }{2\mathit{\pi }{v}_s{\alpha }_s},(7)$

where α_s is the shear wave attenuation, v_s is the shear wave speed and ω is the frequency for which the physicality of wave propagation is investigated. We classify a model as being physical if δ_skin > 0.5λ. The theoretical penetration depth separating a diffusion from a propagating wave is lower (see [40] 2.3.2), but we judge time of flight and phase velocity measurements on less than half a wavelength as unreasonable in shear wave elastography because near-field effects are likely to dominate the wave-field [43, 44].

2. 5 Shear Wave Propagation in a Foam

2. 5.1 Experiment

Similar to [8] we saturate a rectangular Basotect® melamine resin foam and analyze the shear wave dispersion through the phase velocity measurement of a frequency sweep. Robust results are achieved through ultrafast shear wave imaging of plane shear waves inside the foam. Figure 1 shows the experimental setup: The foam of dimensions 30 × 18 × 12 cm is immersed in a water tank. A metal rod driven by a piston (ModalShop Inc. K2004E01) excites shear waves in the frequency range from 100 to 250 Hz. The chosen frequency range ensures sufficient wave propagation and avoids guided waves which exist at lower frequencies due to the finite sample size. The resulting wavefield is imaged in the x − z plane using shear wave elastography. Ultrasonic plane waves are emitted orthogonal to the direction of shear wave propagation at 4,000 fps using a Verasonics Vantage™ scanner and a Philips L7-4 probe. Phase-based motion estimation [45] of the ultrasound reflection images results in retrieval of the z-component of the particle velocity throughout the imaging plane. Because the shear wave speed in the sample is two orders of magnitude lower than the ultrasonic wave speed, the particle displacement induced by the shear wave propagation is well resolved in time. The shear wave excitation is exemplary shown in Figure 1A) and the imaging principle in Figure 1B). Because the wave excitation source is extended in z, the resulting wave front is planar, which is visible in the insets in Figure 1. Hence, we sum the particle velocities along the z-axis in order to increase Signal-to-Noise Ratio. The resulting 2D space-time wavefield is then Fourier transformed using Matlab’s™ FFT in order to measure the phase velocities of the frequency sweep. Because a plane wave evolves according to e^i(kx−ωt), the phase of a single frequency evolves linear in space. The phase velocity can thus be measured from the linear fit of the phase along the spatial dimension for each frequency. The phase is fitted using the Random Sample Consensus (RANSAC) algorithm [46, 47] adapted from [48]. The benefit of the RANSAC algorithm lies in defining a set of inlier points which are taken into account for slope estimation and a set of outlier points which are disregarded. We employ a coefficient of determination (R²) larger than 0.98 and 70% inliers for each frequency. With ϕ_meas ∈ Inlier, the phase velocity is thus measured as:

$\begin{array}{ll}\hfill {\varphi }_{meas}(\omega )& =\beta x+C\hfill \end{array}(8)$

$\begin{array}{ll}\hfill v_{s_{\varphi (\omega )}}& =\frac{\omega }{\beta },\hfill \end{array}(9)$

where ϕ is the phase, β is the linear slope of the phase, x is the coordinate of the spatial dimension, C is a Constant and ω is the frequency investigated. In contrast to our previous work reported in [8], we perform two experiments that differ only in the viscosity of the saturating fluid. For the high viscosity fluid we choose a 0.1% solution of Xanthan (E415) in water and measure the dispersion at 40 °C, where 40 °C ensures a good mixing of Xanthan with water. For the low viscosity fluid we measure the dispersion in water at 40°.

FIGURE 1

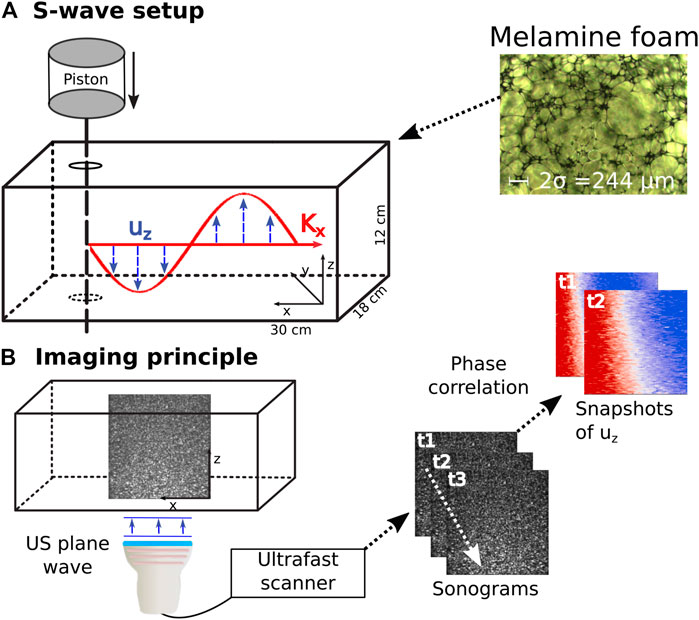
FIGURE 1. Experimental setup. (A) Shear waves are excited in a water saturated melamine foam through a frequency sweep of a metal rod. The inset shows a microscopic image of the melamine foam used for the experiment. (B) Schematic sketch of the imaging principle in ultrasonic shear wave elastography. 2D snapshots of the plane wave ultrasonic reflection images are acquired at a high pulse repetition frequency. Particle movement of the shear wave induces changes in the sonograms and is retrieved through phase correlation. u_z is displacement along z, K_x is the wave vector in propagation direction. US is the abbreviation for ultrasound, t signifies timestep and σ is the viscous length.

2.5.2 Poro-Visco-Elastic Dispersion Modeling in Melamine Foam

The Biot parameters of the foam were independently measured using the acoustic impedance tube method [49] and a Johnson-Champoux-Allard-Lafarge model [49–52] for [8]. For the different methods detailed in [49], the porosity ϕ was found between 96.7 and 99.7%, the tortuosity α between 1 and 1.02 and the permeability κ between 1.28 × 10^–9 and 2.85 × 10^–9 m². The viscous length σ is between 11.24 × 10^–5 and 13.02 × 10^–5 m as indicated in the microscopic photo at the top of Figure 1, and the density is 8.8 kg m⁻³ ± 1 kg m⁻³. The viscous length is typically employed in modeling air filled porous materials and not needed in the classical Biot model. The other quantities were fixed to ϕ = 99%, κ = 1.276 × 10^–9 m² and α = 1.02.

The elastic parameters are unknown and are likely to have been altered since the experiments performed by [8] on the same foam sample due to degassing, compression, immersion in water and aging. To investigate if Biot’s theory can explain the observed dispersion we perform a joint least squares inversion [53] on the unknown parameters μ_fr (shear modulus of the foam frame) and η_f (fluid viscosity). To account for viscosity of the foam itself we introduce the complex shear modulus μ_fr = μ₀ + iωμ₁, where the range for μ₁ is taken from the values given for melamine in [54]. This extended Biot theory, including solid relaxation mechanisms, has been described by Biot [31], and shown to be consistent with the Kramers-Kronig relations by Turgut [55]. We jointly invert using Eq. 6 and Python’s Scipy package [56] as detailed in Section 2.3. Because we use the same foam sample at equal temperature in both experiments, μ_fr is constrained to be identical for both experiments. In contrast, the fluid viscosity is bounded to 0.1–100 mPas for the Xanthan experiment and fixed to 0.6 mPas (viscosity of water at 40°) for the foam in the water experiment.

2.6 Shear Wave Propagation in the Liver

2.6.1 Porous Parameter Values of the Liver

The liver can be roughly separated into hepatocytes, blood vessels, bile ducts and space of disse or perisinusoidal space. The latter is part of the interstitial space and contains extracellular fluid. The blood vessels follow a hierarchical tree-like structure with the central vein and portal arteriole at the top and the liver sinusoids at the bottom. The meso- and micro-circulation are exemplary show in Figure 2, which is reproduced with permission from [57], and are gained from a liver corrosion cast. The macro-, meso- and microscopic structures exhibit different scales of porosity and permeability. While the portal vein for example can be seen as a tubular conduct with a very high Darcy permeability (1 × 10^–3–1 × 10^–2 m² [58]), the permeability of the sinusoidal space has been modeled with permeabilities as low as 1.56 × 10^–14 m² and the interstitial space with 3.12 × 10^–17 m² [13, 59]. Most studies reporting liver permeability values take a microstructure approach, investigating single liver lobules or the permeability across vessel walls. A more general approach was taken by [17], who modeled a 3D liver using a tissue permeability of 1.44 × 10^–9–2.5 × 10^–9 m² and a vascular permeability of 5.0 × 10^–9 m². Here, tissue permeability is the permeability derived from the sinusoids. A permeability of 1.4 × 10^–9 m² for an avascular model was also found by [60] for a poro-visco-elastic liver model. These relatively high values are not surprising, considering that the blood flow into the liver sinusoids equals about 1.35 Lmin⁻¹ at a pressure drop of 1.2 kPa [12]. As is the case of the permeability, care has to be taken when comparing literature values for porosity. Considering only sinusoidal porosity, [61] find 7.4 ± 1.1% while [13, 62] state values ranging from 14% for a healthy to 24.6% for a cirrhotic liver. According to [10], total liver porosity values range from 50 vol% to 70 mass% of total free fluid, including blood, water and bile.

FIGURE 2

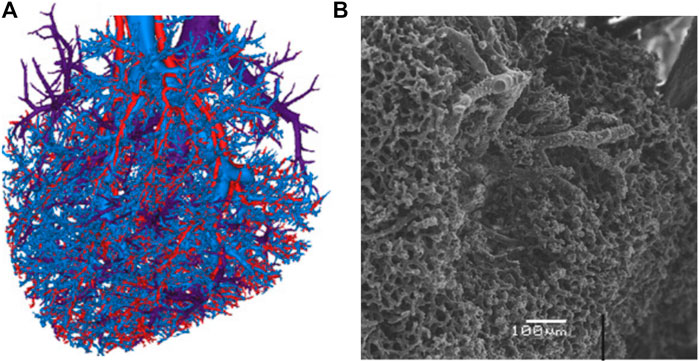
FIGURE 2. Visualization of the liver vasculature as presented by [57]. The blood vessels, present at all scales, constitute the main source of porosity in our poro-visco-elastic liver model. (A). Reconstruction of three mesovascular trees (hepatic artery, portal vein and hepatic venous system) from liver vascular corrosion casts. Reproduced with permission from Fig. 2 e) in [57]. (B). Scanning electron microscopic image of the sinusoidal microcirculation. Reproduced with permission from Fig. 1 c) in [57].

These porosity and permeability values are higher than those used recently by [27] in a poro-hyper-visco-elastic model. They base their consideration on the values by [13], who modeled micro-circulatory or sinusoidal permeability based on hexagonal liver lobules. We believe however, that the sinusoidal permeability is not the relevant quantity for shear wave elastography. The region of interest for any liver elastography method is in the centimeter range and far exceeds the scale of a liver lobule (0.15³ mm³ in [13]). Therefore, one should take into account mesocirculation and potentially macrocirculation for proper modeling of the permeability and porosity in shear wave elastography.

2.6.2 Variability of Porous Parameter Values

For the average adult the normal blood volume in the liver equals about one third of its mass [63] or 450 ml. However, experiments in cats have shown that the liver can account for up to 400 ml of additional blood per kg of liver and rapidly expel half of the stored blood from the liver [63, 64]. Concordantly, [12] states that the human liver can occasionally store up to 0.5–1 L of additional blood in the hepatic vein and sinusoids. Using ultrasonic measurements [65] found mean diurnal variations of 17% in human liver volume. Recently [66], found that mice liver volume oscillates with the feeding and circadian cycle, gaining and loosing 34% each day. Furthermore, fibrosis and cirrhosis have been shown to change the capillarization and thus the porous microstructure of the liver [67–69]. For harmonic ultrasound elastography, [70] found that water uptake leads to a change in the hepatic shear wave velocity. They conclude that the shear wave speed is most likely related to a change in vascular load after water intake. These blood volume variations on short timescales for a single organism as well as pathologic changes due to liver disease influence the shear wave speed as predicted by poro-visco-elastic theory. They notably alter the porosity and permeability parameters in Biot’s model. Furthermore, the higher the porosity, the more Biot’s model becomes sensitive to the fluid viscosity. Our research revealed few studies reporting the tortuosity of the liver pore space. For rat liver sinusoids it was found to be 1.04–1.11 by [71].

The above cited studies give the range of available literature values for the porous parameters of the liver and will serve as input to the analytic modeling of the liver as a poro-visco-elastic solid in Section 3.2. Table 1 summarizes the porous and elastic parameter values reported for the liver.

TABLE 1

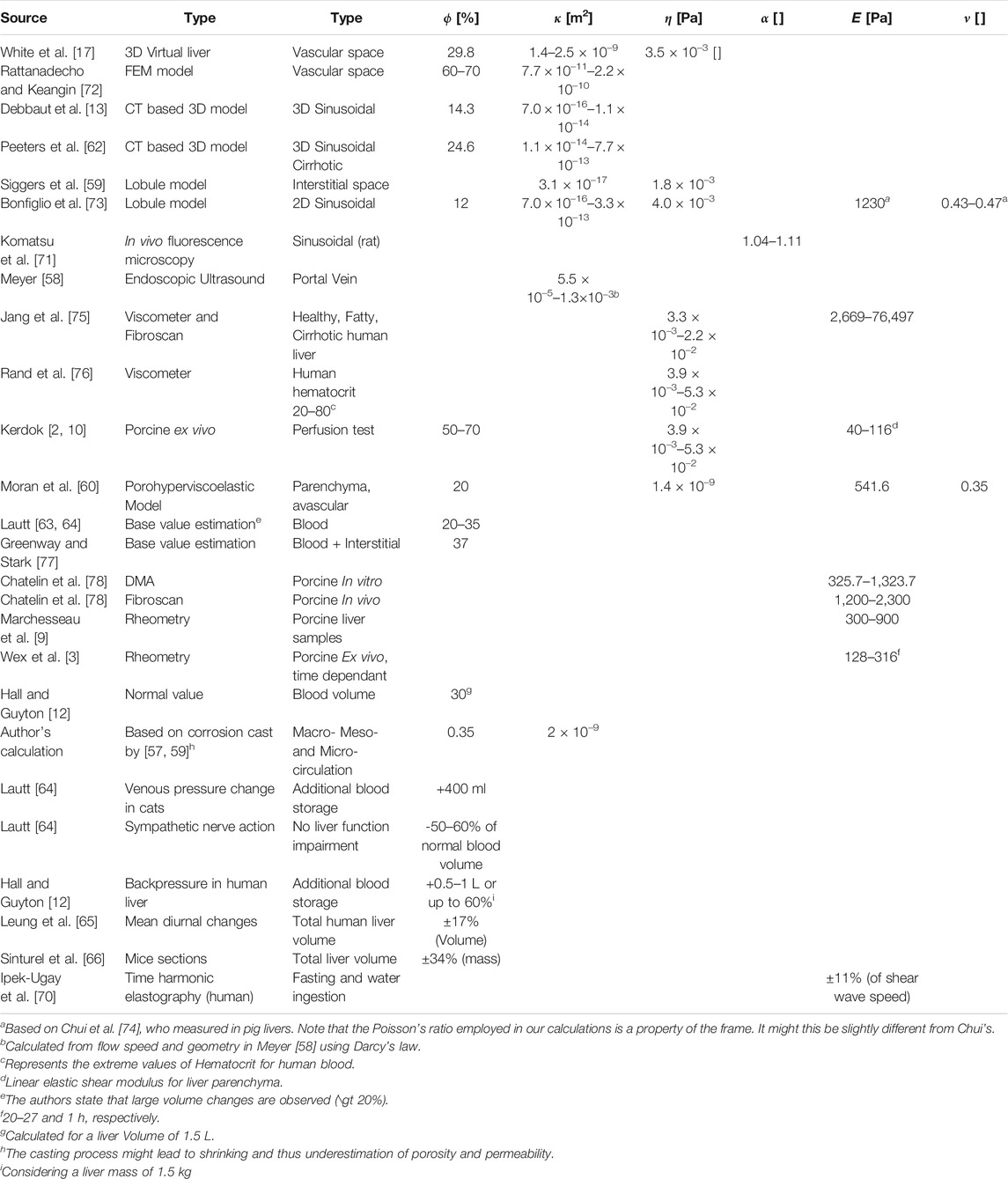
TABLE 1. Literature values for the poro-elasatic parameters of the liver. ϕ is porosity, κ is permeability, η is viscosity, α is tortuosity, E is Young’s modulus and ν is Poisson’s ratio. The different groups focus on different applications and use different approximations and assumptions, partly explaining the large variability of values. The most crucial point when refering to literature values with regards to elastography is if the microcirculation only or the meso- and macro-circulation are considered. The liver lobule model seems to focus on single lobules and micro-circulation in most of the literature we reviewed. For detailed description of measurements, approximations and error estimations, please see the provided references.

2.6.3 Permeability Calculation

The permeability of a porous sample with tubular pores of a single fixed radius r is given as [79]:

$\kappa =\varphi \frac{r^2}{8}.(10)$

Following [80], a more realistic permeability can be calculated as:

$\kappa ={\int }_0^{\infty }\frac{\varphi }{8}{a}_{\mu }^{2}f(a)da,(11)$

where a_μ is the mean radius of capillary tubes and f(a) is the probability distribution density function of the tube radius. In Section 4.3.1, we use Eq. 11 to calculate the permeability of the liver corrosion cast of [57].

2.6.4 Poro-Visco-Elastic Liver Model

In Section 3.2, we analytically model how the shear wave dispersion in the liver is influenced by the porosity and fluid phase in the poro-visco-elastic wave propagation model. The liver is regarded as a homogeneous solid saturated by a Newtonian fluid according to Biot’s theory ( [31, 55]. We compare these analytic curves of a hypothetical liver with some exemplary literature values of in vivo elastography measurements. The measurements are displayed in Figure 4 and stem from Figure 1 of [81]. The data was read off manually by taking seven and nine points from the experimental curves for the F1 and F3 curve, respectively. Finally, we compare the results to a best fit of the experimental results with Voigt’s model. The poro-visco-elastic modeling is equivalent to the melamine foam modeling presented in Section 2.5.2. However, the foam parameters are now replaced by liver values from the literature.

Regarding blood as a Newtonian fluid is of course a simplification, albeit one that is commonly made. A more accurate description of blood is a non-Newtonian visco-elastic shear thinning fluid or sol where the viscosity depends on shear stress, oscillation frequency and Hematocrit [82]. Shear rate is a function of flow and vessel diameter, which vary widely throughout the liver [83]. We thus explicitly make the choice of reducing the model complexity by assuming an average Newtonian blood viscosity under systolic conditions as for example measured by [75]. The Biot parameters are inter-related, hence the sensitivity of the shear wave speed on one parameter depends on the choice of the others. This leads to a variety of possible dispersion curves within the range of literature values given in Section 2.6.1. Exploiting the parameter space is beyond the scope of this manuscript. Instead, in Section 3.2 we present the dispersion curves for a low and a high porosity with changing viscosity. This shows the variety of dispersion curves which are covered by the porous model with fixed elastic and changing porous parameters.

To reduce complexity and because the Biot model is less sensitive towards tortuosity than to porosity ϕ, permeability κ, and fluid viscosity η_f we fix the tortuosity to 1.05 throughout our calculations, which is in the range reported in Section 2.6.1.

In Section 3.2 we use the same modeling method to compare the poro-visco-elastic model to statistics of experimental shear wave dispersion data acquired by [81] and to Voigt’s model. Equivalent to how [81] measure the experimental dispersion, the dispersion of the analytic model is evaluated using the slope of the linear fit between 73 and 250 Hz. With this range we account for the experimental conditions of the measurements of Figure 5 [81]: The stated problems at low frequencies and the fact that the upper frequency for the fit of each point in Figure 5 varied depending on the quality of the experimental data. The five parameter optimization of the Biot model exposes the ambiguity every multi-parameter inversion suffers. We do not claim to find the true values explaining the experimental data here, but merely want to evaluate if physical changes in porous parameters as reported in Section 2.6.2 are able to explain the experimental trend observed by [81]. We thus explicitly compare with a two parameter, and thus less ambiguous, Voigt model, only. To facilitate the multi-parameter inversion for Biot’s parameters we put further physical a priori constraints. The aim of the multi-parameter inversion here is to see if the observed statistical trend in the dispersion data can be explained by changes in the Biot model. We thus restrict the solid viscosity of the Biot model to not exceed that of the point with the lowest Dispersion, effectively fixing the Voigt viscosity for the entire observed data. Furthermore, we suppose increasing porosity and permeability for increasing dispersion, which is reflected in the optimization bounds. The latter results from Eq. 11: a higher porosity must be accompanied by a higher permeability if no geometry changes happen.

3 Results

3.1 Experimental Shear Wave Dispersion in Melamine Foam

The red and blue crosses in Figure 3 show the shear wave dispersion curves for high and low viscosity fluids. The dispersion for the foam in water (blue) differs significantly from the dispersion of the same foam in Xanthan solution (red). For example, the measured phase velocity in the foam saturated by the Xanthan solution at 125 Hz is 2 m s⁻¹ (>20%) lower than that of the foam saturated by water.

FIGURE 3

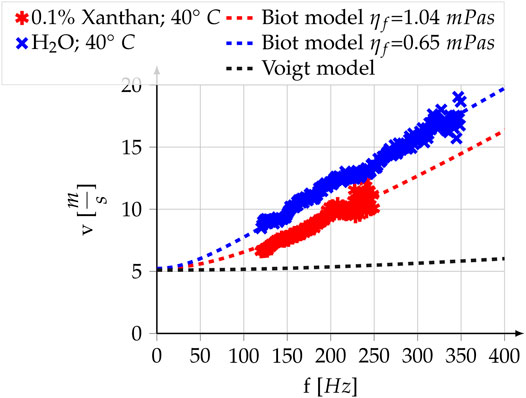
FIGURE 3. Poro-visco-elastic model, visco-elastic model and experimental measurements for the melamine foam. In the two realizations of Biot’s model all parameters are equal, except for the fluid viscosity. For all parameter values see Table 2. The Voigt model is displayed to highlight the differences with the poro-visco-elastic model. It is not a fit but uses the same shear modulus, solid viscosity and average density $\tilde{\rho }={\rho }_s(1-\varphi )+{\rho }_{fl}\varphi$ as the Biot model.

3.1.1 Poro-Visco-Elastic Dispersion Modeling in Melamine Foam

An inversion for the free parameters μ₀ and μ₁ of the Biot model, as described in Section 2.3, is performed on both experimental curves. The parameter bounds and values for the fixed parameters of the Biot model can be found in Section 2.5.2. The result is a μ₀ of 27.3 kPa, a μ₁ of 8.2 Pas for the foam and a fluid viscosity of 1.04 mPas for the Xanthan solution. The resulting analytic dispersion curves are shown as dotted lines in Figure 3 and expose a good fit with the experimental results. The only parameter changing between the two experiments is the viscosity of the fluid and hence solid elasticity and solid viscosity, the two free parameters of the Voigt model, stay constant throughout both experiments. As a consequence, we only model one dispersion curve for the Voigt model. It is displayed as the dashed black line and represents the dispersion resulting from a Voigt model, which uses the same elastic parameters as the Biot model. Due to the Voigt’s model incapacity of modeling both curves, we did not perform a purely visco-elastic fit on the experimental data here.

3.2 Porous Dispersion in the Liver

Figure 4 shows the modeling results for a liver with different values of porosity and permeability and an identical set of visco-elastic parameters. The exact parameter values can be found in Table 2. The blue dashed curve represents a low porosity-low fluid viscosity liver, while the blue straight curve represents a high porosity-low fluid viscosity curve. The superimposed black curves are two exemplary shear wave dispersion curves in the liver acquired through ARFI/SWEI with an Siemens SONOLINE Antares scanner and a CH4–1 transducer (Siemens Healthcare, Ultrasound Business Unit, Mountain View, CA), taken from [81]. The dashed curve represents a liver classified with Fibrosis stage F1 and the straight curve represents a liver classified with Fibrosis stage F3. The least-squares best fit of the visco-elastic Voigt model and the experimental data in the frequency range of 100–400 Hz are plotted in red. Both, the poro-visco-elastic model results and the visco-elastic model results respect a penetration depth superior to 0.5 λ (see Section 2.4). The drop-off of the experimentally measured wave speeds at low frequencies is attributed to a roll-off of the Fourier transform by Ref. [81]. They express confidence in their measurements for values >73 Hz. Within this confidence interval the measurements show an inflection at 100 and 150 Hz, which the Voigt model is incapable of reproducing without boosting μ₁ to large values that lead to a penetration depth <0.5λ. In contrast to that, the observed inflection is an intrinsic property of the Biot model with steeper slope at lower frequencies for smaller fluid viscosity.

FIGURE 4

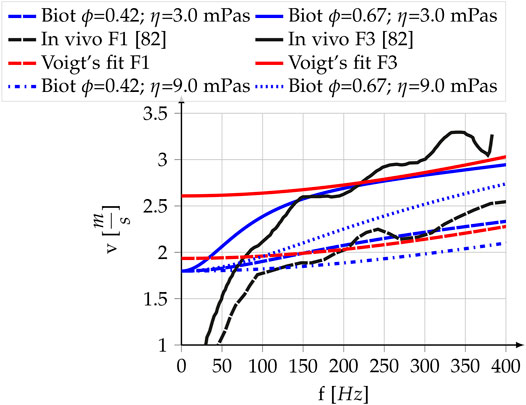
FIGURE 4. Experimental and theoretical shear wave dispersion curves for the liver. Black: Data acquired with ARFI/SWEI. Values are reproduced from Figure 1 in [81]. “-” F3 Fibrosis classification, “- -” F1 Fibrosis classification; Blue: Poro-visco-elastic model developed in this paper, “-” high porosity and permeability, “- -”, low porosity and permeability,”⋅⋅” same as “-” with tripled fluid viscosity, “⋅-” same as “- -” with tripled fluid viscosity; Red: Voigt’s visco-elastic model, “-” high shear modulus, “- -” low shear modulus. The parameter values for the analytic curves are reported in Table 2.

TABLE 2

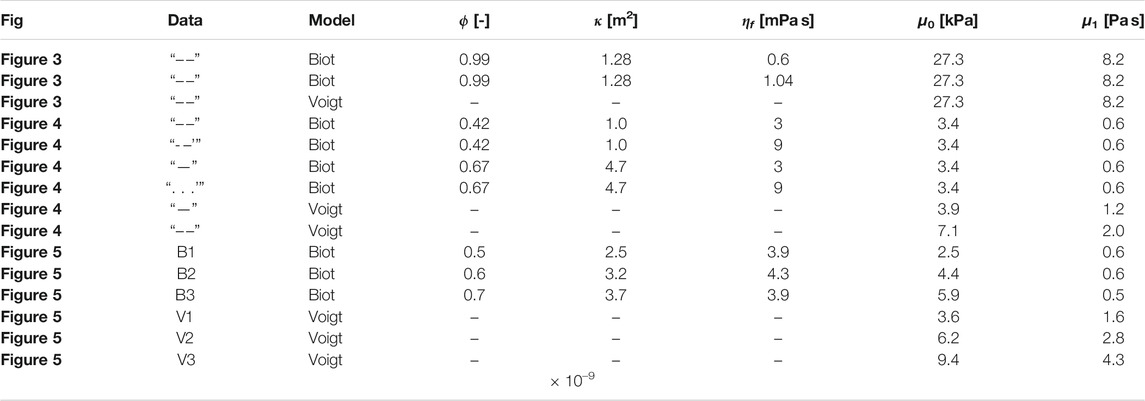
TABLE 2. Modeling parameter values for the poro-elastic and visco-elastic models. The fluid density and the mean density are set to 1,050 kgm⁻³, which is the reported value of arterial blood [100]. ϕ-porosity, κ-permeability, η_f-fluid viscosity, μ₀-shear modulus, μ₁-solid viscosity.

The dotted blue curve represents the modeling result of using the same set of parameters as for the straight blue line except for the fluid viscosity η_f. Fluid viscosity is tripled for the dotted blue curve, leading to a significant decrease of the shear wave speed. The dash-dotted blue line was achieved likewise from the model of the dashed blue line. At 200 Hz, a commonly taken shear wave speed reference frequency, the difference between the low porosity-high fluid viscosity (dash-dotted) and the high porosity-low fluid viscosity (straight) model reaches 0.8  ms⁻¹ or 42% of the lower value.

3.2.1 Experimental Support for the Poro-Visco-Elastic Liver Model

Reference [81] conducted a statistical analysis of in vivo measurements of shear wave dispersion slope at 200 Hz versus shear wave speed at 200 Hz for healthy and fibrotic human livers. In Figure 6 of [81], which is replotted in our Figure 5, one can observe a positive correlation (R² = 0.3) of the steepness of the dispersion slope with the measured speed at 200 Hz [81]. Eyeballing the trend we set three dispersion-speed target pairs for the inversion: 2.0 ms⁻¹–0.25$\frac{{\mathrm{m}\mathrm{s}}^{-1}}{100\mathrm{H}\mathrm{z}}$, 2.5  ms⁻¹–0.45$\frac{{\mathrm{m}\mathrm{s}}^{-1}}{100\mathrm{H}\mathrm{z}}$, 3.0 ms⁻¹–0.65$\frac{{\mathrm{m}\mathrm{s}}^{-1}}{100\mathrm{H}\mathrm{z}}$. Using Eq. 6 and the Basinhopping algorithm [41] (see Section 2.3) the inversion for Voigt’s model results in the points V1,V2, and V3 of Figure 5. They represent the least squares best fits of the Voigt model and the speed-dispersion pairs. Using the same speed - dispersion pairs, the least squares fit using the poro-visco-elastic model results in the points B1, B2 and B3. The exact parameter values for V1,V2, V3 and B1,B2, B3 can be found in Table 2 and the bounds for the inversion in Table 3.

FIGURE 5

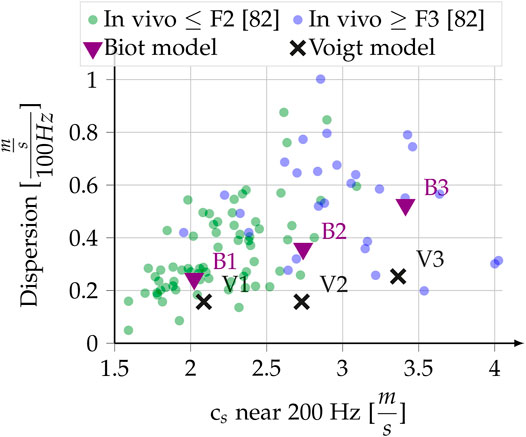
FIGURE 5. In vivo liver dispersion measurements, redrawn from Figure 6 in [81], with Fibrosis classification. The dispersion slope close to 200 Hz is plotted against the shear wave speed around 200 Hz. Superimposed are the results of our modeling, which tries to reproduce the eyeballed trend as described in Section 2.6.4 and Section 3.2.1.

TABLE 3

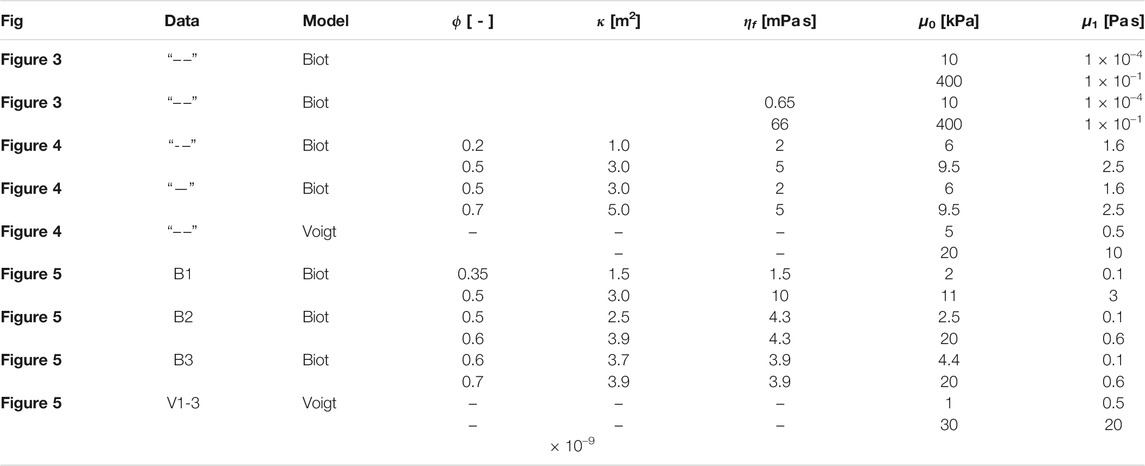
TABLE 3. Modeling parameter bounds for the poro-elastic and visco-elastic models. ϕ-porosity, κ-permeability, η_f-fluid viscosity, μ₀-shear modulus, μ₁-solid viscosity.

4 Discussion

4.1 Poro-Elastic Loss Mechanism of Melamine Foam

The experiment confirms the results by [8] that the shear wave dispersion in a highly porous soft phantom is governed by the viscosity of the fluid. Since the dispersion of the foam in Xanthan solution and in water differ significantly at the same temperature, viscous effects of the solid matrix cannot be the single reason for the wave dispersion. The experiment clearly shows that the difference in dispersion is due to the changed viscosity of the pore filling fluid. As a consequence, it is impossible for Voigt’s model to reproduce the observed difference in the dispersion curves. Thus, modeling of shear wave propagation in soft porous materials by poro-elastic theory is justified. Biot’s non-phenomenological theory of poro-elastic wave propagation takes the fluid viscosity into account by introducing a mechanism of fluid-solid interaction [28, 29].

It should be noted that the rheology of Xanthan solutions is non-Newtonian and as such Xanthan shares the shear dependency of the viscosity with blood. However, Biot’s approximation of a Newtonian fluid with one constant apparent viscosity is sufficient for the small frequency range investigated herein, and in order to show that fluid viscosity is the single parameter which alters the shear wave dispersion. The good fit of the dispersion curves, which was retrieved by restricting the elastic and viscous parameters to lie within the range of the literature values for melamine foam, indicates that Biot’s theory is well suited to explain the observed shear wave dispersion.

Our experiments show a fundamental difference between porous theory and other rheological models such as Voigt’s model: the effect of a change in viscosity. A higher value of the fluid viscosity (Biot) leads to a smaller slope of the dispersion curve while a higher solid viscosity (Voigt) leads to a steeper slope of the dispersion curve. This can be understood in the following way: A higher fluid viscosity signifies stronger solid-fluid coupling. As a consequence, the shear wave encounters an increased effective density.

The experimental results were gained on a melamine sponge, which is an artificial, highly porous, soft solid. Melamine sponge has already been used to mimic ultrasonic scattering in biological porous tissue, namely the lung [84]. While the results of [8] and the experimental results presented herein show that Biot theory can explain shear wave dispersion in soft porous materials, its applicability on in vivo organs will be discussed in the following.

4.2 Porous Liver Modeling

The analytic shear wave dispersion curves in Figure 4 are modeled without a change of the elastic parameters and cover the experimental curves for a F1 and F3 fibrosis stage liver. While the Voigt model requires a near two-fold increase of the elasticity and solid viscosity, the poro-visco-elastic model can reproduce both curves without a change in neither the elasticity nor the solid viscosity. Hence, the measurements above 73 Hz could in principle be explained without a change in solid visco-elasticity by using poro-visco-elastic theory. Since fibrosis classification by elastography relies on changes in shear modulus, this would indicate the possibility of false positives in fibrosis classification due to varying liver saturation. If the poro-visco-elastic model can be confirmed in vivo, shear wave elasticity imaging should thus take the porous parameters into account. Considering that perfusion and blood viscosity have been shown to be highly variable on short timescales (see Section 2.6.2), we think that these modeling results should be considered in future clinical research.

The fluid viscosity in the poro-visco-elastic model is 3.1 mPas, which is below the commonly assumed whole blood viscosity of 3.5 mPas but above the viscosities given for microcirculation and interstitial fluid in the liver by [59]. In a recent study [75], observed an anti-correlation of blood viscosity with liver stiffness as measured by transient elastography. The authors suggested pathologic changes as the source of this anti-correlation. The viscosity induced changes in shear wave speed of our porous modeling indicate the possibility of a different explanation. The correlation could be rooted in the inherent effect of the fluid viscosity on the shear wave speed, and as such be an artifact of the elasticity inversion.

4.2.1 Experimental Support for the Poro-Visco-Elastic Liver Model

Our hypothesis that the poro-visco-elastic model is more appropriate than Voigt’s model to explain shear wave dispersion in the liver is supported by the analysis of the experimental results by [81] reported in Figure 5. In Voigt’s model, an increase in the elasticity modulus will lead to an increase in measured speed at 200 Hz, but to a decrease of the dispersion slope. A much larger increase in solid viscosity (μ₁) than in elasticity (μ₀) could reproduce the correlation, but to our knowledge no such physical mechanism is known. On the contrary, the predominance of μ₀ for liver elastic behavior is well documented [78]. Furthermore, such an increase in solid viscosity leads to very low penetration depths, effectively making the modeled wave a non-propagating one. Unlike Voigt’s model, Biot’s poro-visco-elastic model is able to reproduce a correlation of increased shear wave speed with increased dispersion slope for the reported in vivo measurements.

Ex vivo measurements do not reproduce this correlation of dispersion slope with shear wave speed [85]. This could be owed to the fact that ex vivo livers are partially drained. The drainage changes the porous properties, which adds to other factors, such as fluid pressure, that are inhibiting ex vivo experiments from properly reproducing the physics that govern shear wave dispersion in vivo.

While assuming the purely visco-elastic model, the porous and liquid properties of the liver might thus have largely been overlooked previously. Studies supporting this statement were conducted by [21–23, 86], who compared confined and unconfined ex vivo liver samples and found that the pressure on the fluid in the liver influences the shear wave speed. Reference [24] employed a microchannel flow model equivalent to Darcy’s law and noted that it is superior to Kelvin-Voigt models, because it is based on tissue architecture instead of a priori information on springs and dampers. Both findings strongly support our deduction that porosity plays a crucial role in shear wave propagation in the liver. However, they do not discuss the main loss mechanism shown in Section 3.1: the viscosity of the fluid in the Biot model. While these works deduce elasticity changes from increased pressure on the tissue, we introduce the direct role of the fluid phase through porous physics into the calculation of the shear wave speed.

4.3 Future Research

4.3.1 Biot Parameter Measurements

Why should we introduce another multi-parameter rheological model? From a mathematical point of view, the introduction of additional model parameters improves model fit but also increases model ambiguity. The critical reader might thus question the benefit of introducing another complex multi-parameter model. We agree of course, that conforming to Occam’s razor [87], a simpler model is to be preferred over a complex model whenever sufficient experimental data for the model parameters is lacking. Biot’s model however exhibits several traits that differentiate it from other complex rheological models such as Zener’s model or a fractional Kelvin-Voigt model.

First, it is an entirely non-phenomenological model which is derived from first principles and the porous parameters can in principle all be measured independently. This is the main reason why it is widely applied in geophysical applications, e.g., in oil and gas exploration. Second, both the liver porosity and permeability depend heavily on blood vessel size and are not independent variables. The porosity, i.e., the space occupied by free fluids, can be estimated as the total volume of blood and extracellular fluid. Tubes are a good approximation for the average blood vessel shape and as a consequence permeability and porosity can be calculated from the knowledge of the distribution of vessel sizes with Eq. 11.

Reference [69] analyzed the 3D micro and mesoscopic structure of the hepatic blood vessel tree using high resolution Computer Tomography of a liver cast. As a final check for the Biot model we create a normally distributed probability function for each vessel generation based on their values of the mean and standard deviation of the pore size and length per vessel generation. For the interstitial fluid we assume a pore radius of 0.25  µm, a value derived by [59] for the space of disse, and a Volume percentage of 12% [77, 88]. Integrating over the permeabilities for each vessel generation we retrieve κ ≈ 2e⁻⁹m² and ϕ ≈ 0.35. Theses values are in the lower range of the literature values [17], which is in accordance with the assumption that the cast represents an un- or normally perfused liver. Reference [57] also evoke a possible shrinking of the blood vessel diameters due to the casting process.

We assume that a change in liver perfusion in vivo is reached through vaso-dilatation or vaso-contraction [63, 64, 89]. We can then calculate the necessary dilatational factor to reach the maximum porosity of 70% for the poro-visco-elastic model: For example, increasing the radius of the smallest 8 vessel generations by two and of the remaining generations by 1.2 as well as their lengths by 1.5 for the smallest 8 and by 1.2 for the remaining generations gives a porosity of 70% and a permeability of 5.6 × 10^–9 m². This rough estimation is in accordance with the upper limits of the literature². Furthermore, the dilatational factors are not purely speculative, since [68] found a dilatational factor for the sinusoids of nearly two in cirrhotic rat livers.

As of now, these theoretical porous parameter values are estimated from the liver cast and the literature, but recent imaging advances in ultrasound [90–92] and MRI imaging [93] have shown that porosity and blood vessel size estimation in vivo are becoming feasible. Another approach that might advance the imaging of porous properties with shear wave elastography was recently presented by [94]. They suggest to use Bayesian inference to deduce microstructure properties from effective wave parameters. Hence, poro-visco-elastic shear wave speed estimation could in the future replace the phenomenological springs and dampers of the currently applied rheological models with a physical loss mechanism that is determined by measurable porous parameters. From a physicist point of view, the added model complexity is then well justified by a reduction in the model ambiguity. If the poro-visco-elastic model will also result in improved disease classification compared to more complex visco-elastic models will have to be evaluated in the future.

4.3.2 Low-Frequency Dispersion

References [95, 96] show, that in the case of magnetic resonance shear wave elastography of the brain, a poro-elastic finite element model following [97–99] is more accurate than a visco-elastic model at very low frequencies. Physical reasoning for the observed low speeds at low frequencies requires much lower elastic moduli than are commonly inverted for in transient elastography. An elastography independent measurement of such low elastic moduli is given by [9, 78] for in vitro porcine liver. They find storage moduli as low as 300 Pa, using dynamic mechanical analysis (DMA). Similar values are reported for ex vivo bovine livers by [3] on fresh porcine liver grafts, using a rheometer and a fractional Kelvin-Voigt model, and by [60], who employed a poro-hyper-elastic model. Even lower elastic moduli are reported for in-vivo mimicking perfusion tests on ex-vivo liver samples. Reference [10] report linear elastic shear modulus values of less than 100 Pa for liver parenchyma.

These results in combination with poro-visco-elastic modeling indicate that the entire observable dispersion range, including the low frequencies, needs to be taken into account in order to accurately retrieve the elasticity of the liver. Future in vivo studies of the liver should thus focus on acquiring shear wave speeds over a large bandwidth. At very low frequencies, frequency dependent fluid viscosity and permeability should be taken into account due to the pronounced visco-elastic properties of blood.

5 Conclusion

Our results show, that for fluid saturated, soft porous materials, the porous parameters need to be taken into account to properly model shear wave dispersion. The shear moduli retrieved from simple visco-elastic models are prone to overestimations in the presence of porosity. Fluid viscosity, permeability, and porosity of the diseased as well as the healthy liver can vary inter- and intra-individual on short timescales. It is thus justified to assume that the wide range of observed shear wave dispersion curves in the in vivo liver is partly owed to changes in the porous properties of the liver. Our comparison of poro-visco-elastic and simple visco-elastic modeling shows, that porous parameter changes can easily be the reason for false positives in visco-elastic shear modulus inversion. In the here presented porous liver model porosity dominates at low frequencies, and solid viscosity is dominant at high frequencies. Furthermore, the stiffer the matrix of the liver, the more sensitive the shear wave dispersion becomes to the porous parameters in the Biot model.

Compared to more complex visco-elastic models, the poro-visco-elastic model does not require further phenomenological parameters. Instead it relies on directly measurable quantities. Furthermore, it gives a physical explanation for the observed shear wave dispersion in the liver. If our results are confirmed in vivo, they are likely to have implications for elasticity imaging of other porous organs, such as the spleen, the kidney and the brain.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

JA and SC contributed equally to conception and design of the study. JA conducted the experiments, literature search and analytical modeling and SC participated therein. JA wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported in part by the Plan Cancer ARC-2018-PhysiCancer-BPALP.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We want to thank Olivier Rouvière for discussions on liver diagnosis, Vahid Rezania for discussing liver porosity and permeability with us, and Paul Greiller for his support in the laboratory. We further thank the reviewers for their remarks that greatly improved the quality of the present manuscript.

Footnotes

¹This is an oversimplification, in Biot’s theory some rotation, which diminishes the added mass, is induced in the fluid by inertial coupling. The rotation is included in the calculation of the effective density by multiplying it with $(1-\frac{{\rho }_a^2}{((1-\varphi ){\rho }_s+{\rho }_a)(\varphi {\rho }_f+{\rho }_a)})$.

²The largest two vessel generations, e.g., the hepatic vein, are ignored, assuming that these are avoided by the practitioner in shear wave elastography. The radii of the biliary tree are also neglected, since its estimated volume percentage of 1.2% is relatively low.

References

1. Sparks JL. Liver Tissue Engineering. Tissue Engineering for Artificial Organs: Regenerative Medicine. Smart Diagn Personalized Med (2016) 1-2:297–324. doi:10.1002/9783527689934.ch9

CrossRef Full Text | Google Scholar

2. Kerdok AE, Ottensmeyer MP, Howe RD. Effects of Perfusion on the Viscoelastic Characteristics of Liver. J Biomech (2006) 39:2221–31. doi:10.1016/j.jbiomech.2005.07.005

CrossRef Full Text | Google Scholar

3. Wex C, Stoll A, Fröhlich M, Arndt S, Lippert H. How Preservation Time Changes the Linear Viscoelastic Properties of Porcine Liver. Biorheology (2013) 50:115–31. doi:10.3233/BIR-130632

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Chen S, Urban M, Pislaru C, Kinnick R, Greenleaf J. Liver Elasticity and Viscosity Quantification Using Shearwave Dispersion Ultrasound Vibrometry (SDUV). In: Annual International Conference of the IEEE Engineering in Medicine and Biology Society; 2009 Sep. 3–6; Minneapolis, MN, United States. IEEE (2009) p. 2252–5. doi:10.1109/IEMBS.2009.5334992

CrossRef Full Text | Google Scholar

5. Lin H, Zhang X, Shen Y, Zheng Y, Guo Y, Zhu Y, et al. Model-dependent and Model-independent Approaches for Evaluating Hepatic Fibrosis in Rat Liver Using Shearwave Dispersion Ultrasound Vibrometry. Med Eng Phys (2017) 39:66–72. doi:10.1016/j.medengphy.2016.10.007

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Rus G, Faris IH, Torres J, Callejas A, Melchor J. Why Are Viscosity and Nonlinearity Bound to Make an Impact in Clinical Elastographic Diagnosis? Sensors (Switzerland) (2020) 20:1–35. doi:10.3390/s20082379

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Sugimoto K, Moriyasu F, Oshiro H, Takeuchi H, Yoshimasu Y, Kasai Y, et al. Clinical Utilization of Shear Wave Dispersion Imaging in Diffuse Liver Disease. Ultrasonography (2019) 39:3–10. doi:10.14366/usg.19031

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Aichele J, Giammarinaro B, Reinwald M, Moign GL, Catheline S. Capturing the Shear and Secondary Compression Wave: High Frame Rate Ultrasound Imaging in Saturated Foams. Phys Rev Lett (2019) 123:148001. doi:10.1103/PhysRevLett.123.148001

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Marchesseau S, Heimann T, Chatelin S, Willinger R, Delingette H. Fast Porous Visco-Hyperelastic Soft Tissue Model for Surgery Simulation: Application to Liver Surgery. Prog Biophys Mol Biol (2010) 103:185–96. doi:10.1016/j.pbiomolbio.2010.09.005

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Kerdok AE. Characterizing the Nonlinear Mechanical Response of Liver to Surgical Manipulation. Cambridge, MA: Ph.D. thesisHarvard University (2006).

11. Grisham JW. Organizational Principles of the Liver. In: The Liver: Biology and Pathobiology. 5th ed. Chicester, United Kingdom: John Wiley & Sons Ltd (2009) p. 1–15. doi:10.1002/9780470747919.ch1

CrossRef Full Text | Google Scholar

12. Hall JE, Guyton AC. Guyton and Hall Textbook of Medical Physiology. 13th ed. edn. Philadelphia, PA: Elsevier (2016).

13. Debbaut C, Vierendeels J, Casteleyn C, Cornillie P, Van Loo D, Simoens P, et al. Perfusion Characteristics of the Human Hepatic Microcirculation Based on Three-Dimensional Reconstructions and Computational Fluid Dynamic Analysis. J Biomechanical Eng (2012) 134:011003. doi:10.1115/1.4005545

CrossRef Full Text | Google Scholar

14. Rezania V, Marsh R, Coombe D, Tuszynski J. A Physiologically-Based Flow Network Model for Hepatic Drug Elimination II: Variable Lattice Lobule Models. Theor Biol Med Model 10 (2013) 1. doi:10.1186/1742-4682-10-53

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Rezania V, Marsh R, Coombe D, Tuszynski J. A Physiologically-Based Flow Network Model for Hepatic Drug Elimination I: Regular Lattice Lobule Model. Theor Biol Med Model (2013) 10:52. doi:10.1186/1742-4682-10-52

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Rezania V, Coombe D, Tuszynski J. Liver Bioreactor Design Issues of Fluid Flow and Zonation, Fibrosis, and Mechanics: A Computational Perspective. J Funct Biomater (2020) 11:13. doi:10.3390/jfb11010013

PubMed Abstract | CrossRef Full Text | Google Scholar

17. White D, Coombe D, Rezania V, Tuszynski J. Building a 3D Virtual Liver: Methods for Simulating Blood Flow and Hepatic Clearance on 3D Structures. PLoS ONE (2016) 11:1–24. doi:10.1371/journal.pone.0162215

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Raghunathan S, Evans D, Sparks JL. Poroviscoelastic Modeling of Liver Biomechanical Response in Unconfined Compression. Ann Biomed Eng (2010) 38:1789–800. doi:10.1007/s10439-010-9957-x

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ricken T, Dahmen U, Dirsch O. A Biphasic Model for Sinusoidal Liver Perfusion Remodeling after Outflow Obstruction. Biomech Model Mechanobiology (2010) 9:435–50. doi:10.1007/s10237-009-0186-x

CrossRef Full Text | Google Scholar

20. Mak AF. Unconfined Compression of Hydrated Viscoelastic Tissues: A Biphasic Poroviscoelastic Analysis. Biorheology (1986) 23:371–83. doi:10.3233/BIR-1986-23406

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Rotemberg V, Palmeri ML, Rouze NC, Nightingale R, Nightingale KR. Comparison between Acoustic Radiation Force Impulse (ARFI)-based Hepatic Stiffness Quantification in Deformed and Undeformed Pressurized Canine Livers. In: 2011 IEEE International Ultrasonics Symposium; 2011 Oct 18–21; Orlando, FL, United States. IEEE (2011) p. 2090–2093. doi:10.1109/ULTSYM.2011.0518

CrossRef Full Text | Google Scholar

22. Rotemberg V, Palmeri M, Nightingale R, Rouze N, Nightingale K. The Impact of Hepatic Pressurization on Liver Shear Wave Speed Estimates in Constrained versus Unconstrained Conditions. Phys Med Biol (2012) 57:329–41. doi:10.1088/0031-9155/57/2/329

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Rotemberg V, Byram B, Palmeri M, Wang M, Nightingale K. Ultrasonic Characterization of the Nonlinear Properties of Canine Livers by Measuring Shear Wave Speed and Axial Strain with Increasing portal Venous Pressure. J Biomech (2013) 46:1875–81. doi:10.1016/j.jbiomech.2013.04.027

CrossRef Full Text | Google Scholar

24. Parker KJ. A Microchannel Flow Model for Soft Tissue Elasticity. Phys Med Biol (2014) 59:4443–57. doi:10.1088/0031-9155/59/15/4443

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Biot MA. General Theory of Three-Dimensional Consolidation. J Appl Phys (1941) 12:155–64.

CrossRef Full Text | Google Scholar

26. Konofagou EE, Harrigan TP, Ophir J, Krouskop TA. Poroelastography: Imaging the Poroelastic Properties of Tissues. Ultrasound Med Biol (2001) 27:1387–97. doi:10.1016/S0301-5629(01)00433-1

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Zheng Y, Jiang Y, Cao Y. A Porohyperviscoelastic Model for the Shear Wave Elastography of the Liver. J Mech Phys Sol (2021) 150:104339.

CrossRef Full Text | Google Scholar

28. Biot MA. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. I. Low-Frequency Range. The J Acoust Soc America (1956) 28:168–78. doi:10.1121/1.1908239

CrossRef Full Text | Google Scholar

29. Biot MA. Theory of Propagation of Elastic Waves in a Fluid-Saturated Porous Solid. II. Higher Frequency Range. J Acoust Soc America (1956) 28:179–91. doi:10.1121/1.1908241

CrossRef Full Text | Google Scholar

30. Biot MA. Mechanics of Deformation and Acoustic Propagation in Porous media. J Appl Phys (1962) 33:1482–98. doi:10.1063/1.1728759

CrossRef Full Text | Google Scholar

31. Biot MA. Generalized Theory of Acoustic Propagation in Porous Dissipative Media. J Acoust Soc America (1962) 34:1254–64. doi:10.1121/1.1918315

CrossRef Full Text | Google Scholar

32. Berryman JG. Confirmation of Biot’s Theory. Appl Phys Lett (1980) 37:382–384. doi:10.1063/1.91951

CrossRef Full Text | Google Scholar

33. Hughes ER, Leighton TG, Petley GW, White PR, Chivers RC. Estimation of Critical and Viscous Frequencies for Biot Theory in Cancellous Bone. Ultrasonics (2003) 41:365–8. doi:10.1016/S0041-624X(03)00107-0

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Falkovich G. Fluid Mechanics A Short Course for Physicists. New York: Cambridge University Press (2011).

35. Bourbié T, Coussy O. Acoustics of Porous Media. Paris: (Institut Français Du Pétrole Publications) (Editions TECHNIP) (1987).

36. Allard J, Atalla N. Propagation of Sound in Porous Media: Modelling Sound Absorbing Materials. 2nd ed. Chicester, United Kingdom: John Wiley & Sons Ltd (2009).

37. Mavko G, Mukerji T, Dvorkin J. The Rock Physics Handbook - Tools for Seismic Analysis of Porous Media. 2nd ed. New York, United States: Cambridge University Press (2009).

38. Landau L, Lifshitz E. Fluid Mechanics. Oxford: Pergamon Books Ltd. (1987).

39. Lee DH, Lee JY, Bae JS, Yi NJ, Lee KW, Suh KS, et al. Shear-wave Dispersion Slope from US Shear-Wave Elastography: Detection of Allograft Damage after Liver Transplantation. Radiology (2019) 293:327–33. doi:10.1148/radiol.2019190064

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Holm S. Waves with Power-Law Attenuation. Cham, Switzerland: Springer Nature Switzerland AG (2019) doi:10.1007/978-3-030-14927-7

CrossRef Full Text

41. Wales DJ, Doye JPK. Global Optimization by Basin-Hopping and the Lowest Energy Structures of Lennard-Jones Clusters Containing up to 110 Atoms. The J Phys Chem A (1997) 101:5111–6.

CrossRef Full Text | Google Scholar

42. Chapra SC, Canale RP. Numerical Methods for Engineers, Vol. 33. New York: McGraw-Hill (1991).

43. Sandrin L. The Role of the Coupling Term in Transient Elastography. J Acoust Soc Am (2004) 115:73–83. doi:10.1121/1.1635412

CrossRef Full Text | Google Scholar

44. Catheline S, Benech N. Longitudinal Shear Wave and Transverse Dilatational Wave in Solids. J Acoust Soc America (2015) 137:EL200. doi:10.1121/1.4907742

CrossRef Full Text | Google Scholar

45. Pinton G, Dahl J, Trahey G. Rapid Tracking of Small Displacements with Ultrasound. IEEE Ultrason Symp (2005) 4:2062–5. doi:10.1109/ULTSYM.2005.1603285

CrossRef Full Text | Google Scholar

46. Fischler MA, Bolles RC. Random Sample Consensus: A Paradigm for Model Fitting with Applications to Image Analysis and Automated Cartography. Commun ACM (1981) 24:381–95.

CrossRef Full Text | Google Scholar

47. Torr PH, Zisserman A. MLESAC: A New Robust Estimator with Application to Estimating Image Geometry. Computer Vis Image Understanding (2000) 78:138–56. doi:10.1006/cviu.1999.0832

CrossRef Full Text | Google Scholar

48. Kovesi PD. MATLAB and Octave Functions for Computer Vision and Image Processing, 10 (2020) p. 43. Available at: https://www.peterkovesi.com/matlabfns/.accessed 07 11. 2020.

CrossRef Full Text | Google Scholar

49. Niskanen M, Groby J, Duclos A, Dazel O, Le Roux JC, Poulain N, et al. Deterministic and Statistical Characterization of Rigid Frame Porous Materials from Impedance Tube Measurements. J Acoust Soc America (2017) 2407:14255. doi:10.1121/1.5008742

CrossRef Full Text | Google Scholar

50. Johnson DL, Koplik J, Dashen R. Theory of Dynamic Permeability and Tortuosity in Fluid Saturated Porous media. J Fluid Mech (1987) 176:379–402. doi:10.1017/S0022112087000727

CrossRef Full Text | Google Scholar

51. Champoux Y, Allard JF. Dynamic Tortuosity and Bulk Modulus in Air-Saturated Porous media. J Appl Phys 70 (1991) 1975. doi:10.1063/1.349482

CrossRef Full Text | Google Scholar

52. Lafarge D, Lemarinier P, Allard JF, Tarnow V. Dynamic Compressibility of Air in Porous Structures at Audible Frequencies. J Acoust Soc America (1997) 102:1995. doi:10.1121/1.419690

CrossRef Full Text | Google Scholar

53. Nocedal J, Wright SJ. Numerical Optimization, Vol. 17. New York: Springer (2006). doi:10.1007/978-0-387-40065-5

CrossRef Full Text

54. Deverge M, Renault A, Jaouen L. Elastic and Damping Characterizations of Acoustical Porous Materials: Available Experimental Methods and Applications to a Melamine Foam. Appl Acoust (2008) 69:1129–40. doi:10.1016/j.apacoust.2007.11.008

CrossRef Full Text | Google Scholar

55. Turgut A. An Investigation of Causality for Biot Models by Using Kramers-Krönig Relations. Shear Waves Mar Sediments (2011) 21–8. doi:10.1007/978-94-011-3568-9_3

CrossRef Full Text | Google Scholar

56. Virtanen P, Gommers R, Oliphant TE, Haberland M, Reddy T, Cournapeau D, et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat Methods (2020) 17:261–72.

PubMed Abstract | CrossRef Full Text | Google Scholar

57. Debbaut C, Segers P, Cornillie P, Casteleyn C, Dierick M, Laleman W, et al. Analyzing the Human Liver Vascular Architecture by Combining Vascular Corrosion Casting and Micro-CT Scanning: A Feasibility Study. J Anat (2014) 224:509–17. doi:10.1111/joa.12156

CrossRef Full Text | Google Scholar

58. Meyer E. Beurteilung Der Pfortader Mittels Endoskopischen Ultraschall (EUS) Bei Patienten Mit Leberzirrhose Und Einem Kontrollkollektiv. Bochum: Ruhr – Universität Bochum (2013).

59. Siggers JH, Leungchavaphongse K, Ho CH, Repetto R. Mathematical Model of Blood and Interstitial Flow and Lymph Production in the Liver. Biomech Model Mechanobiology (2014) 13:363–78. doi:10.1007/s10237-013-0516-x

CrossRef Full Text | Google Scholar

60. Moran EC, Raghunathan S, Evans DW, Vavalle NA, Sparks JL, Leroith T, et al. Porohyperviscoelastic Model Simultaneously Predicts Parenchymal Fluid Pressure and Reaction Force in Perfused Liver. J Biomechanical Eng 134 (2012) 1. doi:10.1115/1.4007175

CrossRef Full Text | Google Scholar

61. Hoehme S, Brulport M, Bauer A, Bedawy E, Schormann W, Hermes M, et al. Prediction and Validation of Cell Alignment along Microvessels as Order Principle to Restore Tissue Architecture in Liver Regeneration - Supporting Information. Proc Natl Acad Sci United States America (2010) 107:10371–6. doi:10.1073/pnas.0909374107

CrossRef Full Text | Google Scholar

62. Peeters G, Debbaut C, Cornillie P, De Schryver T, Monbaliu D, Laleman W, et al. A Multilevel Modeling Framework to Study Hepatic Perfusion Characteristics in Case of Liver Cirrhosis. J Biomechanical Eng (2015) 137:051007. doi:10.1115/1.4029280

CrossRef Full Text | Google Scholar

63. Lautt WW. Hepatic Vasculature: A Conceptual Review. Gastroenterology (1977) 73:1163–9. doi:10.1016/s0016-5085(19)31879-7

PubMed Abstract | CrossRef Full Text | Google Scholar

64. Lautt WW. Hepatic Circulation. Colloquium Ser Integrated Syst Physiol Molecule Funct (2009) 1:1–174. doi:10.4199/C00004ED1V01Y200910ISP001

CrossRef Full Text | Google Scholar

65. Leung NW, Farrant P, Peters TJ. Liver Volume Measurement by Ultrasonography in normal Subjects and Alcoholic Patients. J Hepatol (1986) 2:157–64. doi:10.1016/S0168-8278(86)80074-5

CrossRef Full Text | Google Scholar

66. Sinturel F, Gerber A, Mauvoisin D, Wang J, Gatfield D, Stubblefield JJ, et al. Diurnal Oscillations in Liver Mass and Cell Size Accompany Ribosome Assembly Cycles. Cell (2017) 169:651–63. doi:10.1016/j.cell.2017.04.015

PubMed Abstract | CrossRef Full Text | Google Scholar

67. Bhunchet E, Fujieda K. Capillarization and Venularization of Hepatic Sinusoids in Porcine Serum-Induced Rat Liver Fibrosis: A Mechanism to Maintain Liver Blood Flow. Hepatology (1993) 18:1450–8. doi:10.1002/hep.1840180626

PubMed Abstract | CrossRef Full Text | Google Scholar

68. Moeller M, Thonig A, Pohl S, Ripoll C, Zipprich A. Hepatic Arterial Vasodilation Is Independent of Portal Hypertension in Early Stages of Cirrhosis. PLoS ONE (2015) 10.

PubMed Abstract | CrossRef Full Text | Google Scholar

69. Debbaut C, Vierendeels J, Siggers JH, Repetto R, Monbaliu D, Segers P. A 3D Porous media Liver Lobule Model: The Importance of Vascular Septa and Anisotropic Permeability for Homogeneous Perfusion. Comput Methods Biomech Biomed Eng (2014) 17:1295–310. doi:10.1080/10255842.2012.744399

CrossRef Full Text | Google Scholar

70. Ipek-Ugay S, Tzschätzsch H, Hudert C, Marticorena Garcia SR, Fischer T, Braun J, et al. Time Harmonic Elastography Reveals Sensitivity of Liver Stiffness to Water Ingestion. Ultrasound Med Biol (2016) 42:1289–94. doi:10.1016/j.ultrasmedbio.2015.12.026

PubMed Abstract | CrossRef Full Text | Google Scholar

71. Komatsu H, Koo A, Guth PH. Leukocyte Flow Dynamics in the Rat Liver Microcirculation. Microvasc Res (1990) 40:1–13. doi:10.1016/0026-2862(90)90002-9

PubMed Abstract | CrossRef Full Text | Google Scholar

72. Rattanadecho P, Keangin P. Numerical Study of Heat Transfer and Blood Flow in Two-Layered Porous Liver Tissue during Microwave Ablation Process Using Single and Double Slot Antenna. Int J Heat Mass Transfer (2013) 58:457–70. doi:10.1016/j.ijheatmasstransfer.2012.10.043

CrossRef Full Text | Google Scholar

73. Bonfiglio A, Leungchavaphongse K, Repetto R, Siggers JH. Mathematical Modeling of the Circulation in the Liver Lobule. J Biomechanical Eng (2010) 132:111011. doi:10.1115/1.4002563

CrossRef Full Text | Google Scholar

74. Chui C, Kobayashi E, Chen X, Hisada T, Sakuma I. Combined Compression and Elongation Experiments and Non-linear Modelling of Liver Tissue for Surgical Simulation. Med Biol Eng Comput (2004) 42:787–98. doi:10.1007/BF02345212

PubMed Abstract | CrossRef Full Text | Google Scholar

75. Jang B, Han JW, Sung PS, Jang JW, Bae SH, Choi JY, et al. Hemorheological Alteration in Patients Clinically Diagnosed with Chronic Liver Diseases. J Korean Med Sci (2016) 31:1943–8. doi:10.3346/jkms.2016.31.12.1943

PubMed Abstract | CrossRef Full Text | Google Scholar

76. Rand PW, Lacombe E, Hunt HE, Austin WH. Viscosity of normal Human Blood. J Appl Physiol (1963) 19:117–22.

Google Scholar

77. Greenway CV, Stark RD. Hepatic Vascular Bed. Physiol Rev (1971) 51:23–65. doi:10.1152/physrev.1971.51.1.23

PubMed Abstract | CrossRef Full Text | Google Scholar

78. Chatelin S, Oudry J, Périchon N, Sandrin L, Allemann P, Soler L, et al. In Vivo liver Tissue Mechanical Properties by Transient Elastography: Comparison with Dynamic Mechanical Analysis. Biorheology (2011) 48:75–88. doi:10.3233/BIR-2011-0584

PubMed Abstract | CrossRef Full Text | Google Scholar

79. Yamamoto T, Turgut A. Acoustic Wave Propagation through Porous media with Arbitrary Pore Size Distributions. J Acoust Soc America (1988) 83:1744–51. doi:10.1121/1.396507

CrossRef Full Text | Google Scholar

80. Cui ZW, Liu JX, Wang KX. Elastic Waves in Non-newtonian (Maxwell) Fluid-Saturated Porous media. Waves Random Media (2003) 13:191–203. doi:10.1088/0959-7174/13/3/304

CrossRef Full Text | Google Scholar

81. Nightingale K, Rouze N, Rosenzweig S, Wang M, Abdelmalek M, Guy C, et al. Derivation and Analysis of Viscoelastic Properties in Human Liver: Impact of Frequency on Fibrosis and Steatosis Staging. IEEE Trans Ultrason Ferroelectrics, Frequency Control (2015) 62:165–75. doi:10.1109/TUFFC.2014.006653

CrossRef Full Text | Google Scholar

82. Thurston GB, Henderson NM. Viscoelasticity of Human Blood. In: OK Baskurt, MR Hardeman, MW Rampling, and HJ Meiselman, Editors. Handbook of Hemorheology and Hemodynamics. (Washington, DC: IOS Press) (2007). p. 72–90.

Google Scholar

83. Cho YI, Cho DJ. Hemorheology and Microvascular Disorders. Korean Circ J (2011) 41:287–95. doi:10.4070/kcj.2011.41.6.287

PubMed Abstract | CrossRef Full Text | Google Scholar

84. Mohanty K, Blackwell J, Egan T, Muller M. Characterization of the Lung Parenchyma Using Ultrasound Multiple Scattering. Acoust Soc America (2016) 140:3186–7. doi:10.1016/j.ultrasmedbio.2017.01.011

CrossRef Full Text | Google Scholar

85. Parker KJ, Partin A, Rubens DJ. What Do We Know about Shear Wave Dispersion in normal and Steatotic Livers? Ultrasound Med Biol (2015) 41:1481–7. doi:10.1016/j.ultrasmedbio.2015.01.002

PubMed Abstract | CrossRef Full Text | Google Scholar

86. Nazari N, Barbone P. Shear Wave Speed in Pressurized Soft Tissue. J Mech Phys Sol (2018) 119:60–72. doi:10.1016/j.jmps.2018.06.009

CrossRef Full Text | Google Scholar

87.Occam’s Razor — Origin, Examples, & Facts. Encyclopedia Britannica Available at: https://www.britannica.com/topic/Occams-razor (Accessed October 12, 2020).

Google Scholar

88. Jr Jjp , Bull JL. Imaging the Mechanical Properties of Porous Biological Tissue. In: Handbook of Thermal Science and Engineering. Springer International Publishing (2017) doi:10.1007/978-3-319-32003-8

CrossRef Full Text | Google Scholar

89. McCuskey RS. Morphological Mechanisms for Regulating Blood Flow through Hepatic Sinusoids. Liver (2000) 20:3–7. doi:10.1034/j.1600-0676.2000.020001003.x

PubMed Abstract | CrossRef Full Text | Google Scholar

90. Pinter SZ, Lacefield JC. Detectability of Small Blood Vessels with High-Frequency Power Doppler and Selection of Wall Filter Cut-Off Velocity for Microvascular Imaging. Ultrasound Med Biol (2009) 35:1217–28. doi:10.1016/j.ultrasmedbio.2009.01.010

PubMed Abstract | CrossRef Full Text | Google Scholar

91. Weng L, Phillips WH. Apparatus and Method for Detecting Blood Vessel Size and Direction for Doppler Flow Measurement System. United States Patent No. US00555588.6A (1996).

92. Lähivaara T, Kärkkäinen L, Huttunen JMJ, Hesthaven JS. Deep Convolutional Neural Networks for Estimating Porous Material Parameters with Ultrasound Tomography. J Acoust Soc America (2018) 143:1148–58. doi:10.1121/1.5024341

CrossRef Full Text | Google Scholar

93. Lilaj L, Fischer T, Guo J, Braun J, Sack I, Hirsch S. Separation of Fluid and Solid Shear Wave fields and Quantification of Coupling Density by Magnetic Resonance Poroelastography. Magn Reson Med (2020) 28507. doi:10.1002/mrm.28507

CrossRef Full Text | Google Scholar

94. Klessens W, Vasconcelos I, Jiao Y. AI-driven Bayesian Inference of Statistical Microstructure Descriptors from Finite-Frequency Waves (2021). arXiv:2104.08114 [cond-mat, physics:physics].

95. McGarry MD, Johnson CL, Sutton BP, Georgiadis JG, Van Houten EE, Pattison AJ, et al. Suitability of Poroelastic and Viscoelastic Mechanical Models for High and Low Frequency MR Elastography. Med Phys (2015) 42:947–57. doi:10.1118/1.4905048

PubMed Abstract | CrossRef Full Text | Google Scholar

96. McGarry M, Van Houten E, Solamen L, Gordon-Wylie S, Weaver J, Paulsen K. Uniqueness of Poroelastic and Viscoelastic Nonlinear Inversion MR Elastography at Low Frequencies. Phys Med Biol (2019) 64:075006. doi:10.1088/1361-6560/ab0a7d

PubMed Abstract | CrossRef Full Text | Google Scholar

97. Perrinez PR, Marra SP, Kennedy FE, Paulsen KD. 3D Finite Element Solution to the Dynamic Poroelasticity Problem for Use in MR Elastography. Med ImagingPhysiology, Funct Struct Med Images (2007) 6511:65111B. doi:10.1117/12.709786

CrossRef Full Text | Google Scholar

98. Perrinez P, Kennedy F, Van Houten E, Weaver J, Paulsen K. Modeling of Soft Poroelastic Tissue in Time-Harmonic MR Elastography. IEEE Trans Biomed Eng (2009) 56:598–608. doi:10.1109/TBME.2008.2009928

PubMed Abstract | CrossRef Full Text | Google Scholar

99. Perrinez PR, Kennedy FE, Van Houten EE, Weaver JB, Paulsen KD. Magnetic Resonance Poroelastography: An Algorithm for Estimating the Mechanical Properties of Fluid-Saturated Soft Tissues. IEEE Trans Med Imaging (2010) 29:746–55. doi:10.1109/TMI.2009.2035309

PubMed Abstract | CrossRef Full Text | Google Scholar

100. Kenner T. The Measurement of Blood Density and its Meaning. Basic Res Cardiol (1989) 84:111–24. doi:10.1007/BF01907921

PubMed Abstract | CrossRef Full Text | Google Scholar