- 1SIGMA Weather Group, State Key Laboratory for Space Weather, National Space Science Center, Chinese Academy of Sciences, Beijing, China
- 2College of Earth and Planetary Sciences, University of Chinese Academy of Sciences, Beijing, China
In the solar coronal numerical simulation, the coronal heating/acceleration and the magnetic divergence cleaning techniques are very important. The coronal–interplanetary total variation diminishing (COIN-TVD) magnetohydrodynamic (MHD) model is developed in recent years that can effectively realize the coronal–interplanetary three-dimensional (3D) solar wind simulation. In this study, we focus on the 3D coronal solar wind simulation by using the COIN-TVD MHD model. In order to simulate the heating and acceleration of solar wind in the coronal region, the volume heating term in the model is improved efficiently. Then, the influence of the different methods to reduce the
Introduction
The 3D COIN-TVD MHD model which was proposed in [1–3] and was improved in [4–8] in recent years can effectively realize the coronal–interplanetary 3D solar wind simulation. This model uses the TVD Lax–Friedrichs (TVD-LF) scheme uniformly in the corona region and the interplanetary space region, and a combination of Open Multi-Processing (OpenMP) based on shared memory and Message Passing Interface (MPI) based on distributed memory has been successfully used to study the solar wind background from the corona to the interplanetary space.
The solar energy is stored in the solar nucleus, and the generated radiant energy spreads from the inside to the outside. The solar temperature should theoretically decrease with the increase of the heliocentric distance. However, the temperature of the upper atmosphere corona is much higher than that of the lower atmosphere (photosphere). The reason for the abnormal warming of the atmosphere has not yet been investigated. Therefore, coronal heating/acceleration is a central issue in the solar coronal simulation and has been discussed by many researchers (e.g., [9–16]). Parker proposed a basic theory for the problem of heating an expanding solar corona [17–19]. Later, various methods for solar wind acceleration and coronal heating have been developed. For example, the Alfvén wave heating method (AHM) can accelerate solar wind through the exchange of momentum and energy between large-scale Alfvén wave turbulence and solar wind plasma [10]. The turbulent heating method (THM) assumes that the turbulent free energy is transformed into the energy accelerated by the solar wind when the turbulent free energy changes with the heliocentric distance [10]; By adding momentum and energy source terms to the MHD equations [16], the volume heating method (VHM) has been widely used in solar wind simulation (e.g., [15, 20, 21].
In the MHD simulation, the divergence of the magnetic field should be strictly controlled to zero. The nonzero divergence of the magnetic field can lead to the
In this study, we adopt the COIN-TVD model to simulate the coronal solar wind. Similar to [20, 21], we use the volume heating sources to model the solar wind heating/acceleration process in the simulation.
In Governing Equations of Coronal Interplanetary-Total Variation Diminishing Model, we introduce the equations of the COIN-TVD MHD model. Mesh Grid System and Numerical Scheme describes mesh grid system and boundary conditions. Volume Heating Method and Magnetic Field Divergence Cleaning Methods presents the VHM method and three magnetic field divergence processing methods. Numerical Results shows the results of numerical simulation and comparisons of three methods for processing magnetic field divergence. In Conclusions and Discussions, we make the conclusion and discussion.
Governing Equations of Coronal–Interplanetary Total Variation Diminishing Model
The ideal MHD equations are used to simulate the coronal solar wind. Under the Corotating coordinate system, equations can be written as:
where
Mesh Grid System and Numerical Scheme
Mesh Grid System
In the spherical coordinate, the range of the calculation area is expressed as 1
Numerical Scheme
In the COIN-TVD model, all of the physical quantities are computed from the TVD-LF numerical scheme in a face-centered grid structure (e.g., [7, 8]). And this scheme is performed in the six-component mesh grid system.
The inner boundary is located on the surface of the Sun, where the inner boundary setting depends on local fluid conditions (e.g., [2]; 2007, [16, 21, 33]). When
The Carrington Rotation (CR) 2199 is chosen for background establishment. The initial magnetic field B0 is given by using the potential field source surface (PFSS) model [35, 36], the spherical harmonics coefficients were used to obtain the initial PFSS solution is 6. And other initial parameters, such as plasma density
Volume Heating Method and Magnetic Field Divergence Cleaning Methods
In this section, we introduce the numerical schemes of the volume heating method and three methods to constrain
Volume Heating Method
Due to the limitations of observation and theory, there is no mature theoretical model to describe the mechanism of coronal heating and solar wind acceleration. Here, we use the volume heating method to solve the issue of coronal heating and solar wind acceleration. We add the source terms of momentum SM and energy QE to the MHD Eq. 1, Eq. 2, Eq. 3, and Eq. 4 as follows:
According to the work in [7, 39–41], we set energy and momentum source terms as follows:
Here,
Here, r is the heliocentric distance,
Following [20, 44, 45], the source term QE also contains a heat conduction term, the expression of the heat conduction term is
Powell Method
The Powell method to maintain the magnetic divergence cleaning constraint is given as follows.
Two divergence source terms,
In this way, the divergence of the magnetic field can be propagated to the boundary to reduce the numerical error of
This means that the
Diffusive Method
The diffusive method is proposed to reduce the error of the magnetic divergence, in which an artificial diffusivity is added at each time step as
Here,
For satisfying the condition
Composite Diffusive/Powell Method
We combined the Powell method and the diffusive method together in the MHD calculation in the composite diffusive/Powell method for the first time, and this method can further control the error of the magnetic field divergence.
The composite diffusive/Powell method adds two divergence source terms,
Numerical Results
In this section, we show the numerical results of the solar coronal simulation from 1RS to 22.5RS for CR2199, which are obtained by executing the methods introduced in Volume Heating Method and Magnetic Field Divergence Cleaning Methods.
It takes about 100 h in physical time to obtain the steady state in our simulation. Figures 1,2 present the distribution of the magnetic field lines, the radial velocity, the number density and the temperature on the meridional plane at Φ = 180°–0° from model A and model B, respectively. From these figures, it can be seen that the high latitude areas always have fast speed, high temperature, and low density. On the contrary, the radial speed is slower, the temperature is lower, and the number density is higher at lower latitudes around the heliospheric current sheet (HCS), and this is the characteristic feature of the solar wind in the corona [47]. Model B is successful in simulating the acceleration and heating of the solar wind in the corona, as shown in Figure 2. Compared with Figure 1, we can find that both the radial speed and temperature in Figure 2 are higher than those in Figure 1 obviously. This result indicates that the VHM can accelerate and heat the coronal solar wind, and the parameters
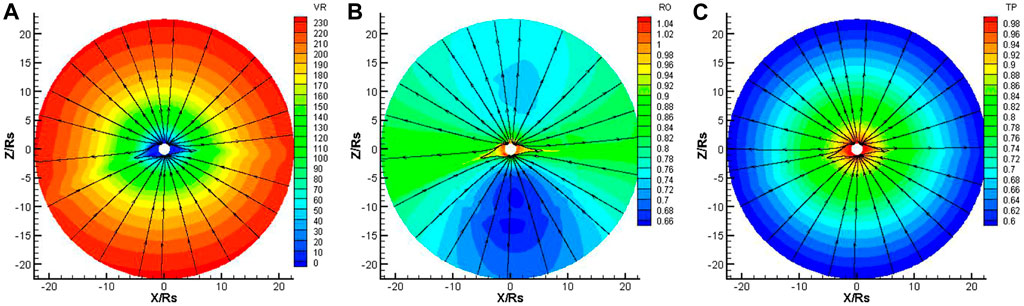
FIGURE 1. The distribution of the radial speed VR (km/s) (A), density RO × 108 (/cm3) (B) and temperature TP × 106 (K) (C) on the meridional plane of Φ = 180°–0° from 1 to 22.5Rs, deduced from model A. The streamline represents the magnetic field lines.
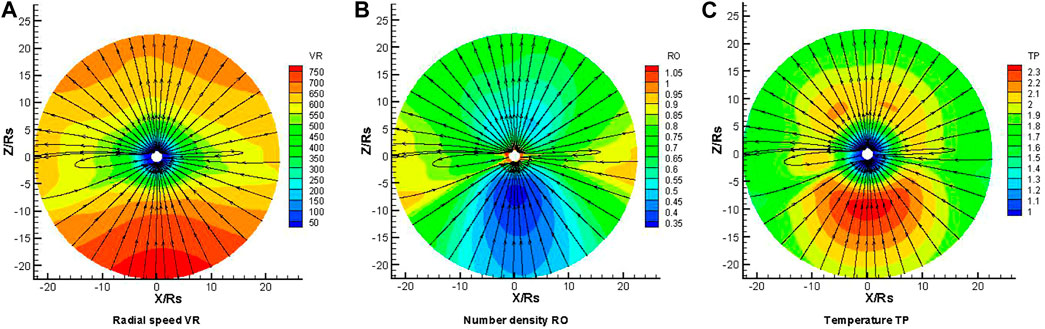
FIGURE 2. The distribution of the radial speed VR (km/s) (A), density RO × 108 (/cm3) (B) and temperature TP × 106 (K) (C) on the meridional plane of Φ = 180°–0° from 1 to 22.5Rs, deduced from model B. The streamline represents the magnetic field lines.
Then, we present the simulation results of the coronal solar wind with three magnetic divergence cleaning methods. Figures 3–5, respectively, show the variation in the radial speed, the number density, and the temperature along heliocentric distance from 1 to 22.5 Rs with different latitudes of θ = −80° and θ = −10° at the same longitude of Φ = 0°, where θ = −80° locates at the open field region and θ = −10° locates at the HCS region. Comparing the three figures, we can find that the radial speed in the open field region is larger than that in the HCS region, the temperature is higher in the open field, and the number density is smaller in the high latitude region.
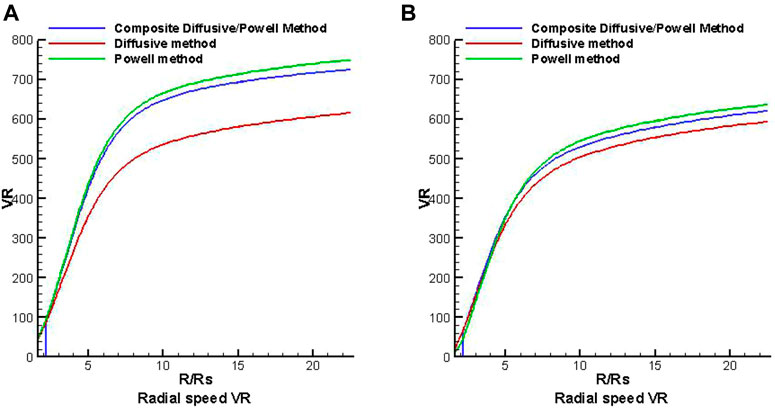
FIGURE 3. The distribution of radial speed VR (km/s) along heliocentric distance with different latitudes of θ = −80° (A) and θ = −10° (B) at the same longitude Φ = 0° from three divergence methods.
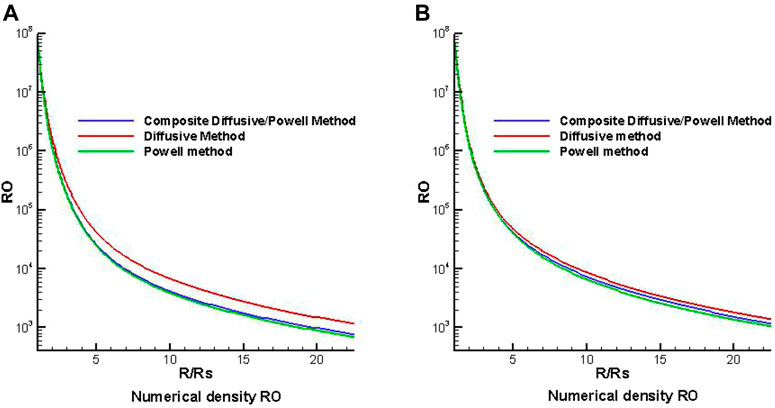
FIGURE 4. The distribution of density RO (/cm3) along heliocentric distance with different latitudes of θ = −80° (A) and θ = −10° (B) at the same longitude Φ = 0° from three divergence methods.
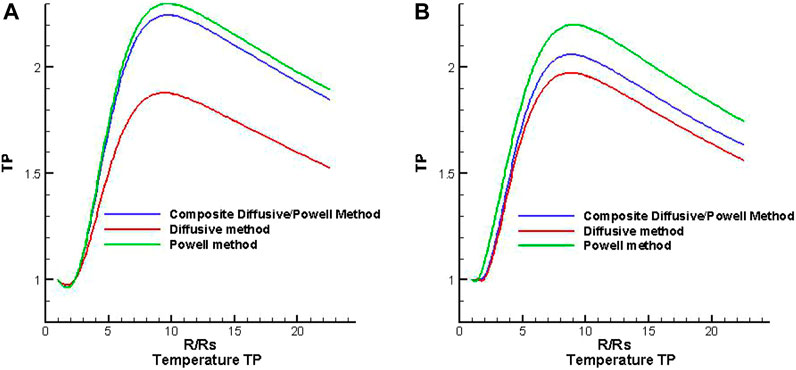
FIGURE 5. The distribution of temperature TP × 106 (K) along heliocentric distance with different latitudes of θ = −80° (A) and θ = −10° (B) at the same longitude Φ = 0° from three divergence methods.
The composite diffusive/Powell method which combines the diffusive method and the Powell method is our new try to handle the
To quantitatively see how
Here,
To investigate how the three magnetic divergence cleaning methods control the
Figures 6,7 show the distributions of the Error(B) on the different meridional planes of Φ = 180°–0° and Φ = 270°–90°, respectively, for the steady-state solar wind. The three panels in Figures 6, 7 present the results from the composite diffusive/Powell method, the diffusive method and the Powell method, from left to right, respectively. It is obvious that the Error(B) deduced from the composite diffusive/Powell method is lower than that from the other two methods, on both meridional planes. This indicates that the composite diffusive/Powell method is the most effective method among the three methods in dealing with the magnetic field divergence.
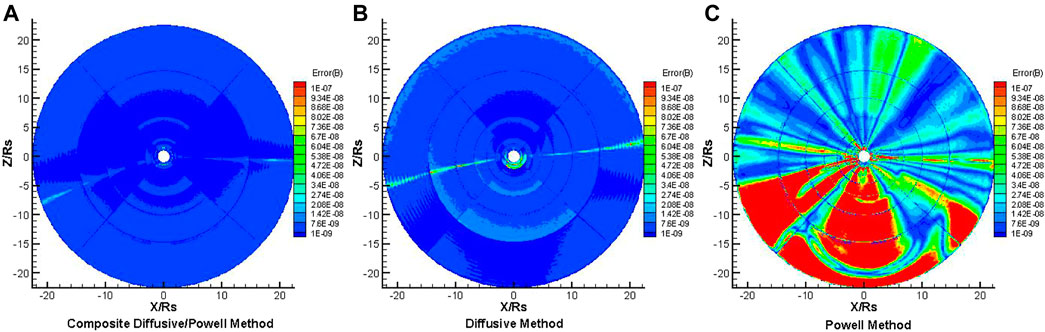
FIGURE 6. The distribution of Error(B) on the meridional plane of Φ = 180°–0° from 1 to 22.5RS, from composite diffusive/Powell method (A), diffusive method (B), and Powell method (C), respectively.
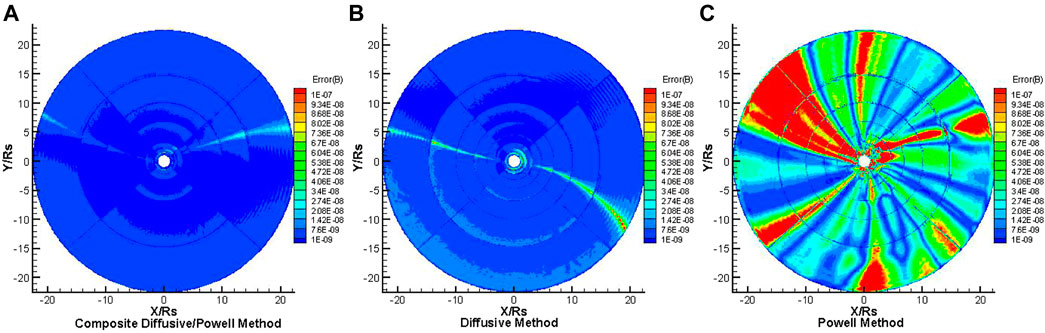
FIGURE 7. The distribution of Error(B) on the meridional plane of Φ = 270°–90° from 1 to 22.5RS, the results from composite diffusive/Powell method (A), diffusive method (B) and Powell method (C), respectively.
Here, we use the following metric for measuring divergence, which was also adopted by other research studies (e.g., [33, 47]):
where M is the total number of grid points in the computational domain. We know that there are other metrics that can be used to measure the divergence. As pointed in [49], the metric defined by Eq. 14 may rely on the spatial resolution. However, in this simulation, we make the comparison among the three cases with the same mesh system and the same metric definition; therefore, the influence of the spatial resolution on the comparison of the metric by Eq. 14 can be ignored.
Figure 8 shows the evolution of the Error(B)ave with time deduced from the three methods. It can be recognized that the value of the Error(B)ave from the composite diffusive/Powell method is around 10–8.7–10–8.5, from the diffusive method is around 10–8.6–10–8.2, and from the Powell method is around 10–8.6–10–7.1. The composite diffusive/Powell method has the smallest Error(B)ave, and this method is a new try to maintain the magnetic divergence-free constraint. From Figure 8, we can also find that the Error(B)ave from the composite diffusive/Powell method and diffusive method is smaller than that from the Powell method obviously. Moreover, the Error(B)ave from the composite diffusive/Powell method keeps on decreasing after 60 h and is significantly smaller than that from the diffusive method near 100 h. Overall, we can find that all the divergence cleaning methods can keep the related errors under control, though the divergence errors of the Powell method are larger than those of the other methods, the divergence errors shown in Figures 6–8 are indeed small, and the largest worst number is 10–7, shown as the orange and red colors in Figures 6,7. The Error(B)ave from the Powell method is about 10–7.3, from the diffusive method is 10–8.4, and from the composite diffusive/Powell method is 10–8.7 near 100 h. The composite diffusive/Powell method is the best method to reduce the error of magnetic divergence among the three methods in this research.
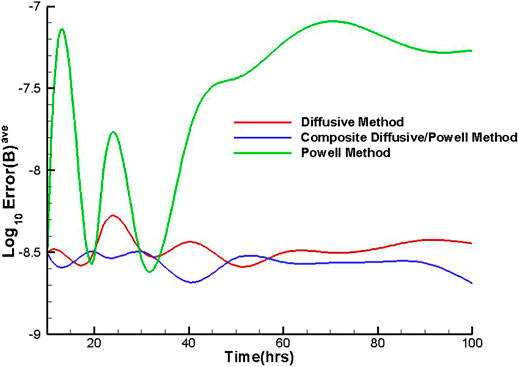
FIGURE 8. The temporal evolution of the Log10Error(B)ave from the three divergence cleaning methods.
Conclusions and Discussions
In this study, by using the 3D COIN-TVD MHD model, we simulate the solar wind in the coronal region, in which the divergence cleaning and coronal heating/acceleration methods are included. The volume heating method is an effective way for coronal heating, in which the parameters can be adjusted according to the WSA model in the simulation of the coronal solar wind. In the COIN-TVD MHD model, increasing the parameters
For the divergence cleaning methods, here we choose the diffusive method, the Powell method and the composite diffusive/Powell method. We compared the numerical characteristics of the combination of each method for handling the divergence of the magnetic field and the COIN-TVD MHD model in the solar coronal simulation. The numerical results show that all of them can produce large-scale structured solar wind and reduce the divergence of the magnetic field more or less. The difference between the three divergence cleaning methods is summarized as follows:
1) The Powell method is relatively simple to apply. It only needs to add two items to the source term of the MHD equations. In this study, the Powell method can reduce the error of the relative magnetic field divergence, but it is less effective than the other two methods in dealing with magnetic divergence.
2) The diffusive method also has a good effect on reducing magnetic field divergence error in this study. It reduces the error of divergence by adding a source term in the induction equation and the
3) The composite diffusive/Powell method is a preliminary new try in this study, and it combines the Powell method and the diffusive method during the simulation. It has been proven that this composite method is the most efficient way to reduce the relative divergence errors among the three methods we used. Moreover, it also ensures the conservation of the MHD equations during the simulation.
In addition to the methods we mentioned, there are many other methods to simulate the coronal heating and the solar wind acceleration process and to control the divergence of the magnetic field. For example, both the Alfvén wave heating method and the turbulent heating method are effective for coronal heating. The Powell method can also company with other methods to control the magnetic divergence, which may be implemented in the future. Moreover, although these simulations are performed for the background solar corona, these methods can also be used for the simulation of CME initiation and propagation in the interplanetary space.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary files, further inquiries can be directed to the corresponding author/s.
Author Contributions
FS provided the thesis research topic, FS and YL provided the code for the three-dimensional solar wind numerical simulation. CL modified the code, ran the program code, and drew pictures based on the data. FS, CL, and MZ participated in the analysis of the results and the writing of the manuscript. XL modified the manuscript.
Funding
This work was jointly supported by the Strategic Priority Research Program of the Chinese Academy of Sciences, Grant no. XDB 41000000, National Natural Science Foundation of China (Grant nos 41774184 and 41974202), and State Key Laboratory of Special Research Fund Project.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Acknowledgments
We acknowledge the use of synoptic magnetogram from the Global Oscillation Network Group (GONG). The numerical simulation of the model uses Tianhe-1A supercomputing machine.
References
1. Feng X, Wu ST, Wei F, Fan Q. A Class of Tvd Type Combined Numerical Scheme for Mhd Equations and its Application to Mhd Numerical Simulation. Chin J Space Sci (2002) 22(4):300–8. doi:10.3969/j.issn.0254-6124.2002.04.002
2. Feng X, Wu ST, Wei F, Fan Q. A Class of TVD Type Combined Numerical Scheme for MHD Equations with a Survey about Numerical Methods in Solar Wind Simulations. Space Sci Rev (2003) 107:43–53. doi:10.1023/A:1025547016708
3. Feng X, Xiang CQ, Zhong DK, Fan QL. A Comparative Study on 3-D Solar Wind Structure Observed by Ulysses and MHD Simulation. Chin Sci Bull (2005) 50:672–8. doi:10.1360/982004-293
4. Shen F, Feng XS, Wang Y, Wu ST, Song WB, Guo JP, et al. Three-dimensional MHD Simulation of Two Coronal Mass Ejections' Propagation and Interaction Using a Successive Magnetized Plasma Blobs Model. J Geophys Res (2011) 116:A9. doi:10.1029/2011JA016584
5. Shen F, Feng XS, Wu ST, Xiang CQ, Song WB. Three-dimensional MHD Simulation of the Evolution of the April 2000 CME Event and its Induced Shocks Using a Magnetized Plasma Blob Model. J Geophys Res (2011) 116:A4. doi:10.1029/2010JA015809
6. Shen F, Wu ST, Feng X, Wu C-C. Acceleration and Deceleration of Coronal Mass Ejections during Propagation and Interaction. J Geophys Res (2012) 117:A11. doi:10.1029/2012JA017776
7. Shen F, Shen C, Zhang J, Hess P, Wang Y, Feng X, et al. Evolution of the 12 July 2012 CME from the Sun to the Earth: Data-Constrained Three-Dimensional MHD Simulations. J Geophys Res Space Phys (2014) 119:7128–41. doi:10.1002/2014JA020365
8. Shen F, Yang Z, Zhang J, Wei W, Feng X. Three-dimensional MHD Simulation of Solar Wind Using a New Boundary Treatment: Comparison with In Situ Data at Earth. ApJ (2018) 866:18. doi:10.3847/1538-4357/aad806
9. Aschwanden MJ, Burlaga LF, Kaiser ML, Ng CK, Reames DV, Reiner MJ, et al. Theoretical Modeling for the Stereo mission. Space Sci Rev (2008) 136:565–604. doi:10.1007/s11214-006-9027-8
10. Usmanov AV, Goldstein ML, Besser BP, Fritzer JM. A Global MHD Solar Wind Model with WKB Alfvén Waves: Comparison with Ulysses Data. J Geophys Res (2000) 105:12675–95. doi:10.1029/1999JA000233
11. Zel'Dovich YB, Raizer YP, Hayes WD, Probstein RF, Gill SP. Physics of Shock Waves and High-Temperature Hydrodynamic Phenomena. J Appl Mech (1967)(4) 34. doi:10.1016/B978-0-12-395672-9.X5001-2
12. Roussev II, Gombosi TI, Sokolov IV, Velli M, Manchester W, DeZeeuw DL, et al. A Three-Dimensional Model of the Solar Wind Incorporating Solar Magnetogram 15 Observations. Astrophysical J Lett (2003) L57(61):595. doi:10.1086/378878
13. Cohen O, Sokolov IV, Roussev II, Arge CN, Manchester WB, Gombosi TI, et al. A Semiempirical Magnetohydrodynamical Model of the Solar Wind. ApJ (2006) 654:L163–L166. doi:10.1086/511154
14. Cohen O, Sokolov IV, Roussev II, Gombosi TI. Validation of a Synoptic Solar Wind Model. J Geophys Res (2008) 113:A3. doi:10.1029/2007JA012797
15. Suess ST, Poletto G, Wang A-H, Wu ST, Cuseri I. The Geometric Spreading of Coronal Plumes and Coronal Holes. Solar Phys (1998) 180:231–46. doi:10.1023/A:1005001618698
16. Hansen KC, Gombosi TI, DeZeeuw DL, Groth CPT, Powell KG. A 3D Global MHD Simulation of Saturn's Magnetosphere. Adv Space Res (2000) 26:1681–90. doi:10.1016/S0273-1177(00)00078-8
17. Parker EN. Dynamics of the Interplanetary Gas and Magnetic Fields. ApJ (1958) 128:664. doi:10.1086/146579
19. Parker EN. Dynamical Properties of Stellar Coronas and Stellar Winds. III. The Dynamics of Coronal Streamers. ApJ (1964) 139(8):690. doi:10.1086/147795
20. Feng X, Yang L, Xiang C, Wu ST, Zhou Y, Zhong D. Three-dimensional Solarwindmodeling from the Sun to Earth by a Sip-Cese Mhd Model with a Six-Component Grid. ApJ (2010) 723:300–19. doi:10.1088/0004-637X/723/1/300
21. Feng X, Zhang M, Zhou Y. A New Three-Dimensional Solar Wind Model in Spherical Coordinates with a Six-Component Grid. ApJS (2014) 214:6. doi:10.1088/0067-0049/214/1/6
22. Dedner A, Kemm F, Kröner D, Munz C-D, Schnitzer T, Wesenberg M. Hyperbolic Divergence Cleaning for the MHD Equations. J Comput Phys (2002) 175:645–73. doi:10.1006/jcph.2001.6961
23. Dedner A, Rohde C, Wesenberg M. A New Approach to Divergence Cleaning in Magnetohydrodynamic Simulations. In: TY Hou, and E Tadmor, editors. Hyperbolic Problems: Theory, Numerics, Applications. Berlin; Heidelberg: Spring-Verlag (2003). p. 509–18. doi:10.1007/978-3-642-55711-8-4710.1007/978-3-642-55711-8_47
24. Susanto A, Ivan L, De Sterck H, Groth CPT. High-order central ENO Finite-Volume Scheme for Ideal MHD. J Comput Phys (2013) 250:141–64. doi:10.1016/j.jcp.2013.04.040
25. Evans CR, Hawley JF. Simulation of Magnetohydrodynamic Flows - A Constrained Transport Method. ApJ (1988) 332:659–77. doi:10.1086/166684
26. Ziegler U. A Semi-discrete central Scheme for Magnetohydrodynamics on Orthogonal-Curvilinear Grids. J Comput Phys (2011) 230:1035–63. doi:10.1016/j.jcp.2010.10.022
27. Ziegler U. Block-Structured Adaptive Mesh Refinement on Curvilinear-Orthogonal Grids. SIAM J Sci Comput (2012) 34:C102–C121. doi:10.1137/110843940
28. Brackbill JU, Barnes DC. The Effect of Nonzero ∇ · B on the Numerical Solution of the Magnetohydrodynamic Equations. J Comput Phys (1980) 35:426–30. doi:10.1016/0021-9991(80)90079-0
29. Brandenburg A, Rädler KH, Rheinhardt M, Käpylä PJ. Magnetic Diffusivity Tensor and Dynamo Effects in Rotating and Shearing Turbulence. ApJ (2008) 676:740–51. doi:10.1086/527373
30. Manabu Y, Kanako S, Yosuke M. Development of a Magnetohydrodynamic Simulation Code Satisfying the Solenoidal Magnetic Field Condition. Comput Phys Commun (2009) 180:1550–7. doi:10.1016/j.cpc.2009.04.010
31. Powell KG, Roe PL, Linde TJ, Gombosi TI, De Zeeuw DL. A Solution-Adaptive Upwind Scheme for Ideal Magnetohydrodynamics. J Comput Phys (1999) 154:284–309. doi:10.1006/jcph.1999.6299
32. Hayashi K. Magnetohydrodynamic Simulations of the Solar Corona and Solar Wind Using a Boundary Treatment to Limit Solar Wind Mass Flux. Astrophys J Suppl S (2005) 161:480–94. doi:10.1086/491791
33. Feng X, Liu X, Xiang C, Li H, Wei F. A New MHD Model with a Rotated-Hybrid Scheme and Solenoidality-Preserving Approach. ApJ (2019) 871:226. doi:10.3847/1538-4357/aafacf
34. Feng X, Zhang S, Xiang C, Yang L, Jiang C, Wu ST. A Hybrid Solar Wind Model of the Cese+hll Method with a Yin-Yang Overset Grid and an Amr Grid. ApJ (2011) 734:50. doi:10.1088/0004-637X/734/1/50
35. Schatten KH, Wilcox JM, Ness NF. A Model of Interplanetary and Coronal Magnetic fields. Sol Phys (1969) 6(3):442–55. doi:10.1007/BF00146478
36. Altschuler MD, Newkirk G. Magnetic fields and the Structure of the Solar corona. Solar Phys (1969) 9(1):131–49. doi:10.1007/BF00145734
37. Lee CO, Arge CN, Odstrčil D, Millward G, Pizzo V, Quinn JM, et al. Ensemble Modeling of CME Propagation. Sol Phys (2013) 285:349–68. doi:10.1007/s11207-012-9980-1
38. Moguen Y, Bruel P, Perrier V, Dick E. Non-reflective Inlet Conditions for the Calculation of Unsteady Turbulent Compressible Flows at Low Mach Number. Mech Industry (2014) 15(3):179–89. doi:10.1051/meca/2014027
39. Nakamizo A, Tanaka T, Kubo Y, Kamei S, Shimazu H, Shinagawa H. Development of the 3-D MHD Model of the Solar corona-solar Wind Combining System. J Geophys Res (2009) 114:A7. doi:10.1029/2008JA013844
40. Feng X, Jiang C, Xiang C, Zhao X, Wu ST. A Data-Driven Model for the Global Coronal Evolution. ApJ (2012) 758:62. doi:10.1088/0004-637X/758/1/62
41. Feng X, Yang L, Xiang C, Jiang C, Ma X, Wu ST, et al. Validation of the 3D AMR SIP-CESE Solar Wind Model for Four Carrington Rotations. Sol Phys (2012) 279:207–29. doi:10.1007/s11207-012-9969-9
42. Arge CN, Pizzo VJ. Improvement in the Prediction of Solar Wind Conditions Using Near-Real Time Solar Magnetic Field Updates. J Geophys Res (2000) 105(A5):10465–79. doi:10.1029/1999ja000262
43. Arge CN, Luhmann JG, Odstrcil D, Schrijver CJ, Li Y. Stream Structure and Coronal Sources of the Solar Wind during the May 12th, 1997 CME. J Atmos Solar-Terrestrial Phys (2004) 66:1295–309. doi:10.1016/j.jastp.2004.03.018
44. Suess ST, Wang A-H, Wu ST. Volumetric Heating in Coronal Streamers. J Geophys Res (1996) 101(A9):19957–66. doi:10.1029/96JA01458
45. Yang L, Feng X, Xiang C, Zhang S, Wu ST. Simulation of the Unusual Solar Minimum with 3D SIP-CESE MHD Model by Comparison with Multi-Satellite Observations. Sol Phys (2011) 271:91–110. doi:10.1007/s11207-011-9785-7
46. Spitzer L. Physics of Fully Ionized Gases. 2nd ed., 359. New York: Interscience (1962). 3559. doi:10.1126/science.139.3559.1045
47. Zhang M, Feng X. A Comparative Study of Divergence Cleaning Methods of Magnetic Field in the Solar Coronal Numerical Simulation. Front Astron Space Sci (2016) 3:6. doi:10.3389/fspas.2016.00006
48. Pakmor R, Springel V. Simulations of Magnetic fields in Isolated Disc Galaxies. Month Notices R Astron Soc (2013) 432:176–93. doi:10.1093/mnras/stt428
Keywords: MHD simulation, corona heating and acceleration, magnetic divergence cleaning, solar wind, volumn heating
Citation: Liu C, Shen F, Liu Y, Zhang M and Liu X (2021) Numerical Study of Divergence Cleaning and Coronal Heating/Acceleration Methods in the 3D COIN-TVD MHD Model. Front. Phys. 9:705744. doi: 10.3389/fphy.2021.705744
Received: 06 May 2021; Accepted: 13 July 2021;
Published: 30 July 2021.
Edited by:
Qiang Hu, University of Alabama in Huntsville, United StatesReviewed by:
Keiji Hayashi, Stanford University, United StatesMehmet Yalim, University of Alabama in Huntsville, United States
Copyright © 2021 Liu, Shen, Liu, Zhang and Liu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Fang Shen, ZnNoZW5Ac3BhY2V3ZWF0aGVyLmFjLmNu
 Chang Liu
Chang Liu Fang Shen
Fang Shen Yousheng Liu1,2
Yousheng Liu1,2 Man Zhang
Man Zhang