Effects of Surface Tension on the Stability of Surface Nanobubbles

1 Introduction

Small bubble can exist everywhere in the nature and industrial liquid systems, which is a spherical void under or in the liquid. Nanobubbles include bulk nanobubbles and surface nanobubbles (SNBs) [1]. In all kinds of environments, SNBs survive with smaller contact angles of the gaseous phase and higher stability than the common-sized ones. Figure 1 shows a SNB of spherical cap on the solid substrate. Its contact angle is usually between 10 and 30° and lateral size is several or more than ten times of the height.

FIGURE 1

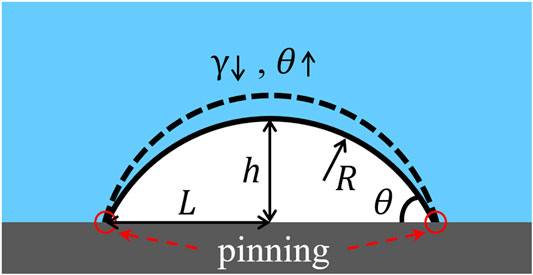
FIGURE 1. The sketch of a pinned surface nanobubble. θ is the gas-side contact angle, L is the lateral radius, h is the height, R is the radius of curvature, and γ is the surface tension of the gas-liquid interface.

Nanobubbles are usually generated by electrochemical reactions [2] or solvent exchange process [3]. They have been widely used in a number of technical fields and have recently been reported to have wide prospect in cancer treatment and medical imaging. The nanobubbles have obvious application effect in bio-medicine [4] and water oxygenation [1], and they are effective in creating slip boundary conditions in fluid transport [5, 6] and can increase the efficiency in mineral particle flotation [7]. However, a small bubble on the surface would also influence the electrochemical reaction processes [8], and decrease the efficiency of photocatalytic reactions in solar conversion [9] and cause decompression illness [10]. It is essential to understand the principle of nanobubbles for their utilization and to avoid their harmfulness.

The concept of SNBs and the relevant studies date back about 40 and 20 years, respectively. There has been a lot of investigations focus on the generation, the properties, and the applications of SNBs. The SNBs were firstly realized in the force measurement experiments between two surfaces [11]. When two hydrophobic surfaces are close to each other, and the relation between the force and the distance presents a ladder shape, which is different from the long-range gravity and electrostatic interaction. During a long time, the study progress of SNBs was limited by experimental conditions, and high-tech microscopes or other technical methods were needed to observe bubbles of nano scale. In 2000, Lou [12] and Ishida [13] got the first images of SNBs on different substrates using the atomic force microscope (AFM). These earliest experimental results verified the assumption of SNBs proposed by Parker [14] and laid a solid foundation for the later study of SNBs.

Researchers are interested in the extraordinary properties especially for the small gas-side contact angle θ [15–17] and the long-term stability of SNB [18–20]. On one hand, its gas-side contact angle is much smaller than the angle determined by Young’s equation [21], which is the criterion for the equilibrium of the three-phase contact point [22, 23]. On the other hand, the long surviving time is far more than the predicted by Epstein and Plesset’s theory [24]. For a nanobubble with curvature radius of 100 nm, the pressure inside (mainly Laplace pressure) is about 14 times of the standard atmosphere. It means that the bubble will shrink and disappear in ∼μs as soon as its appearance. However, experiments show that SNBs can exist for hours or even days [18–20]. It is several orders of magnitude greater than the above-mentioned theory.

In terms of theoretical research, a considerable amount of literature has been published discussing about SNBs. Most of these studies focus on their long-term life and other features and try to explain the amazing stability. Ducker argued that some contaminants are adsorbed on the interface of SNBs, which may lead to the decrease of surface tension and make the SNBs stable [16]. Das’ simulation showed that the surfactant will cut down the surface tension by half, but this is not enough for the stability [25]. However, all the theory was denied by the experiments which show that there is gas exchange across the interface [26]. Brenner firstly put forward the dynamic equilibrium model including the gas absorption on hydrophobic surface that the gas gets into the bubble near the substrate is the supplement for that gets out across the interface [27]. Yasui took the potential of Van Der Waals to improve the dynamic model, and showed that the density inside the bubble is not uniform [28]. Inspired by the coffee ring effect, several models involving contact line pinning were proposed by Liu [29, 30], Weijs [31] and Lohse [32]. Using the Popov’s solution for the evaporation of liquid droplet [33], Lohse and Zhang demonstrated the dynamic evolution to equilibrium of the SNBs with gas oversaturation in water [32]. It is a pity that this model cannot explain the stable bubbles in the under-saturated environment, which was found in some experiments [34, 35]. Tan combined the hydrophobic adsorption with contact line pinning-oversaturation theory to explain that bubbles can survive in under-saturated water, and also presented that how hydrophobicity and oversaturation work together to stabilize SNBs [36]. Furthermore, Tan got the timescale ∼1,000 s of bubble evolution with the dynamic gas concentration in water with height of 1 mm [37]. Recently, Petsev argued that the adsorption of gas molecules at the substrate modifies the energy of solid-gas interface, and thus reduces the gas-side contact angles and the pressure inside [38]. However, none of those models can account for all the outstanding properties of SNBs, especially their stability on the hydrophilic surface, such as mica or glass.

With the contact line pinning, as a surface nanobubble dissolves, its volume decreases, the curvature radius increases and the Laplace pressure reduces. The surface tension determines the internal pressure of the nanobubble and thus influences the dynamic evolution of nanobubble. Ducker and Das have shown that the interface containing some impurity can reduce the surface tension [16, 25]. In the calculations of the stabilization process, surface tension is a crucial parameter, determining the pressure inside and concentration around the bubble. In this work, we investigate the effects of variable surface tension on the evolution and stability of SNBs, which the surface tension follows the Tolman or state dependence. With the smaller surface tension in the gas-liquid interface, the results show that the SNBs can exist with larger contact angle in the same environment and even survive on a highly hydrophilic surface.

2 Hydrophobic Attraction Model of Surface Nanobubbles

The solubility of gas in liquid is a constant at certain pressure and temperature. Usually, the solubility increases with increasing pressure, but there is an inverse relation with temperature. The gas saturation ratio s and gas oversaturation ζ₀ are defined as fallow respectively

$s=\frac{c_{\infty }}{c_s},(1)$

${\zeta }_0=\frac{c_{\infty }}{c_s}-1=s-1,(2)$

where c_s is the gas solubility at standard atmospheric pressure, and normal temperature of T = 293K; c_∞ is the far-field dissolved gas concentration (environment concentration) which is a given condition and determines ζ₀. If the concentration c(z) along the z axis (height direction) is the same as c_∞, the gas oversaturation ζ(z) is also the same. Brenner [27] firstly used the hydrophobic attraction in the dynamic equilibrium mechanism of SNBs base on the results of some molecular dynamics (MD) simulations [39–41] and experiments [42, 43]. Those study demonstrate that there is a gas enrichment layer near solid hydrophobic surfaces when gas dissolves in the liquid, leading to a spatially distributed c(z). When the hydrophobic adsorption is taken into account, the gas concentration, as the solution of the diffusion equation, exists with the form as follow

$c\left(z\right)=c_{\infty }\exp \left(-\frac{{\varphi }_0{e}^{-z/\lambda }}{k_{B}T}\right),(3)$

In Equation 3, the attractive potential ϕ(z) = ϕ₀e^−z/λ is a function of the distance z, and ϕ₀ is a representation of the surface’s wettability (for hydrophilic, ϕ₀ > 0; hydrophobic, ϕ₀ < 0; neutral, ϕ₀ = 0), λ = 1 nm is the characteristic distance of the interaction, k_B is the Boltzmann constant and T is the temperature. And the gas oversaturation can be expressed as

$\zeta \left(z\right)=s\times \exp \left(-\frac{{\varphi }_0{e}^{-z/\lambda }}{k_{B}T}\right)-1.(4)$

In the SNBs’ evolution theory, the gas diffuses from the interface out to the infinity following the diffusion equation (Eq. 5) [31]. The well-known Young-Laplace’s law (Eq. 6) determines the pressure inside the bubble and Henry’s law (Eq. 7) defines the gas concentration around the gas-liquid interface.

$\frac{\partial c}{\partial t}=D\times {\nabla }^{2}c,(5)$

$P_b=P_0+\frac{2\gamma }{R},(6)$

$c\left(R,t\right)=\frac{P_b}{P_0}{c}_s,(7)$

where D is the diffusion constant, P₀ is the atmospheric pressure, γ is the surface tension, R is the curvature radius. R can be calculated by the bubble bottom radius L and the real-time contact angle using R = L / sin(θ).

With the concentration difference between in and out of the interface, the SNBs will dissolve or grow, and the concentration gradient determines the diffusion rate. The evolution problem of a dissolving pinned SNB under liquid is analogous to that of an evaporating pinned droplet. For this problem, Popov has derived the exact solution [33], which is consistent with the experiments. Lohse and Zhang extended this theory to calculate the evolution of pinned SNBs [32]. Tan embedded spatially varying oversaturation ζ (z) (Eq. 4) into the pinning-oversaturation stabilization theory about SNBs’ evolution and showed that the stability of SNBs does not necessarily require strict gas oversaturation [36]. With the above definitions, the hydrophobic attraction model (HA model) is used to calculate the evolution of the contact angle as follows. The mass changing rate of the gas in a spherical nanobubble with a fixed footprint radius L and any contact angle θ obeys

$\frac{dm}{dt}=-\frac{\pi LD{c}_s}{h}f\left(\theta \right){\displaystyle {\int }_0^h\left(\frac{2\gamma }{L{P}_0}\sin \theta -\zeta \left(z\right)\right)}dz,(8)$

where

$f\left(\theta \right)=\frac{\sin \theta }{1+\cos \theta }+4{\displaystyle {\int }_0^{\infty }\frac{1+\cosh 2\theta \xi }{\sinh 2\pi \xi }\tanh \left[\left(\pi -\theta \right)\xi \right]}d\xi ,(9)$

is a geometric term of Popov’s theory [33]. The total mass of bubble is calculated by the gas density ρ_g and the volume of spherical cap

$m=\frac{\pi L^3{\rho }_g\left({\cos }^3\theta -3\cos \theta +2\right)}{3{\sin }^3\theta }.(10)$

Then the changing rate of contact angle at any real-time θ is obtained by Eq. 8 and Eq. 10

$\frac{d\theta }{dt}=-\frac{D{c}_s}{{\rho }_g{L}^{2}h}{\left(1+\cos \theta \right)}^{2}f\left(\theta \right){\displaystyle {\int }_0^h\left(\frac{2\gamma }{L{P}_0}\sin \theta -\zeta \left(z\right)\right)}dz.(11)$

Given an initial contact angle θ₀ and L, the dynamic evolution of SNB can be calculated and plotted by Eq. 11. Note that the first part of the above expression before the integral part is negative, whether the contact angle increases or decreases entirely depends on the integral term, which is the difference between the gas getting in at the bottom and those getting out at the upside of the bubble. The integral term turning into zero means that the SNBs reach equilibrium. In this paper, the parameters are set as follows, D = 2 × 10^–9 m²/s, c_s = 0.017 kg/m³, ρ_g= 1.165 kg/m³, P₀ = 101,325 Pa, which are the same as the HA model.

3 Tolman and State-Dependent Surface Tension

Equations 8–11 show that the dynamic evolution of SNBs is entirely determined by the geometric parameters (L and θ), gas oversaturation ζ(z) along the z axis and some constants including surface tension γ. Surface tension is the tendency of liquid surface at rest to shrink into the minimum surface area possible. At liquid–air interface, surface tension results from the greater attraction of liquid molecules to each other (due to cohesion) than to the molecules in the air (due to adhesion), and for ambient water, it is 72 mN/m. Actually, surface tension is equal to surface energy per unit surface area and adhesion is the inevitable result of minimizing the surface free energy.

Both the recent experiments and molecular dynamics (MD) simulations demonstrate that the density of SNBs is much higher than that of gas at standard atmosphere [44, 45]. In addition, Luo puts forward that the interface between the gas and the liquid is a special layer, which is called coupled layer of gas and liquid, and its density is between the pure water and the gas [46]. With the curving interface between gas and liquid, the pressure inside the bubble is larger than outside P₀. The following points indicate that the surface tension decreases with the increasing internal pressure and density. The larger pressure, the little difference is in density and molecular attraction between the two phases, and the adhesion is getting larger while the cohesion remains unchanged; the larger pressure, the more gas is trapped on the surface of the liquid and the surface energy decreases; the larger pressure, the more gas diffuses into the water and the surface energy decreases. Whether the reduction of the difference between cohesion and adhesion, or of the surface energy would lead to a smaller surface tension.

In the above analysis, the surface tension of the bubble’s interface will decrease in some way and has effects on the dynamic model. In this paper, we introduce two variable forms of surface tension into the HA model, and conduct a study about the effects of surface tension on the stability of SNBs. One of the two forms is Tolman-dependent surface tension, the other is state-dependent, which are already proved and used in other study.

3.1 The Tolman-Dependence

In Manning’s theoretical analysis, the stability of nanobubbles is determined by mechanical equilibrium and thermodynamic stability [47]. The Laplace equation explains mechanical equilibrium, which is at the local free energy maximum or minimum. Bubbles with radius-dependent surface tension would obtain the thermodynamic stability at the local free energy minimums. The Tolman-dependent surface tension expression is [48].

$\gamma \left(R\right)={\gamma }_0\times \left(1-\frac{2\delta }{R}\right),(12)$

where δ is the Tolman length. The effect of Tolman length on nano-droplet and bubble is obvious [49–52]. And here we use δ = 17 nm as Manning [47], which is derived from the experimental pressure inside the bubble [53]. When this form of tension is used, the bubble can hold the thermodynamic stability. From the expression, there is a significant change in the surface tension if the scale of R is close to that of δ.

3.2 The State-Dependence

In 1994, Attard’s group firstly proposed the assumption that there are nanobubbles on the surface in the force measure experiments [14]. And then they conducted a series of thermodynamic analyses on the stability of the SNBs [54–57], and came up with a conclusion that the surface tension depends on the saturation degree, which is the ratio of the actual concentration of dissolved gas to the saturation concentration (Eq. 1). Computer simulations of the oversaturated liquid−vapor interface also show that the decrease in surface tension is in linear [54, 58] with a reasonable approximation

$\gamma \left(s\right)={\gamma }_0\frac{s^{\ast }-s}{s^{\ast }-1},(13)$

where γ₀ is 72 mN/m at normal atmospheric pressure, and s^*.is the spinodal values with the range of 3–6. Here, we use s* = 5 as Attard [56]. The surface tension decreases with increasing saturation ratio of the vapor phase, and then it vanishes while approaching the spinodal, which is intuitively appealing and consistent with earlier density functional results [59, 60].

In Attard’s thermodynamic analyses, the maximum of free energy along the path of mechanical equilibrium can be reduced by reducing the surface tension. And the critical radius of the bubble is

$R_{critical}=\frac{2\gamma }{\left(s-1\right)p_0},(14)$

This equation follows the principle of diffusive and mechanical equilibrium. It can be inferred that the bubbles can nucleate more readily and remain smaller sizes than predicted by classical nucleation theory if the decrease in surface tension with the saturation ratio s is considered. While the classical nucleation theory holds that the surface tension is a constant. The reduced surface tension is beneficial to the formation and stability of SNBs.

4 Results and Discussion

4.1 The Results of the Tolman-Dependence

For a SNB with an initial contact angle θ₀ = 20^o and footprint radius L = 100 nm, its curvature radius is R = 292.38 nm, which is almost ten times of 34 nm (2δ). The curvature radius R increases rapidly as the contact angle decreases, and soon it is far more than 2δ, as shown in Figure 2A. The surface tension is γ = 0.8837×γ₀ at t = 0 and later changes towards γ₀ with the rapidly growing radius R until reaching equilibrium, holding little effect on the changing rate of the contact angle. When the bubble reaches equilibrium, R is much larger (for hydrophobic surface with ϕ₀ = −2 k_BT, R = 677.47 nm; for neutral substrate with ϕ₀ = 0, R = 1,386.31 nm) than the beginning and the surface tension is just slightly smaller than γ₀. The angle of equilibrium looks like the same at ϕ₀ = 0 because the R is large enough and γ reaches 0.9755 × γ₀, while it gets a little larger at ϕ₀ = −2 k_BT. The contact angle of Tolman-dependence reaches equilibrium at about 22 and 27 µs, with ϕ₀ = −2 k_BT and ϕ₀ = 0, respectively. The bubbles cannot survive on a hydrophilic surface with ϕ₀ = 2 k_BT and shrink rapidly and dissolve completely in 20 µs. And the slightly small change in surface tension gives additional survivable time of only about 1 µs. It is similar in the case of L = 50 nm and L = 30 nm.

FIGURE 2

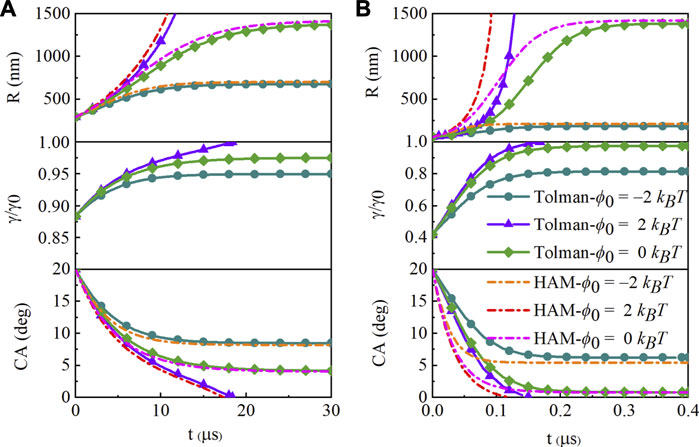
FIGURE 2. Evolution of the curvature radius, Tolman-dependence surface tension and contact angle (CA) with the initial contact angle θ₀ = 20^o and footprint radius (A)L = 100 nm, (B)L = 20 nm. The far-field concentration is c_∞ = 2c_s. The curves are for hydrophobic (ϕ₀ = −2 k_BT, circle symbol), hydrophilic (ϕ₀ = 2 k_BT, triangle symbol), and neutral (ϕ₀ = 0 k_BT, rhombus symbol) surfaces. The dashed ones are for hydrophobic attraction model (HAM) with the same surface.

When the radius is close to the Tolman length (L = 20 nm, R = 58.48 nm at t = 0), the surface tension changes significantly, and has a greater influence on the evolution process, as shown in Figure 2B. The most obvious is that the curves of the two models are much more different in the first half of the process. The contact angle of Tolman-dependence reaches equilibrium at about 0.28 and 0.3 µs, with ϕ₀ = −2 k_BT and ϕ₀ = 0, respectively. Since the surface tension is 0.4γ₀ at the beginning, the pressure is much smaller that the gas gets slower out of the bubble than the HA model. Compared with the results of L = 100 nm, the time scale is almost one 100th of that. The bubble shrinks so faster due to the larger pressure and smaller volume.

The effect of Tolman-dependent surface tension on the equilibrium contact angle depends on the radius at equilibrium. The hydrophobic surface allows the SNBs to maintain a larger contact angle, corresponding to a smaller radius. And the calculated pressure inside (L = 20 nm, P/P₀ = 7.29; L = 100 nm, P/P₀ = 2.99) is smaller than the HA model (L = 20 nm, P/P₀ = 7.74; L = 100 nm, P/P₀ = 3.03), while is the same on the neutral surface. The equilibrium contact angles are almost the same on the neutral surface, because the radius is large enough to ignore the change of tension at equilibrium.

4.2 The Results of the State-Dependence

When the saturation ratio s is 1, the surface tension remains constant as γ₀ and the evolution result is the same as HA model. In this model, the SNBs have long-term life on hydrophobic or neutral surface, while those shrink and disappear after about 20 microseconds on hydrophilic surface (ϕ₀ = 2 k_BT). Considering the state-dependence, the surface tension γ goes against the change of saturation ratio s. As s increases, there will be a corresponding change in the contact angle evolution under the same interaction of the gas and solid, as shown in Figure 3. On the neutral surface, the contact angle is getting larger, and the pressure inside is the same as HA model at the equilibrium. It can be inferred from that the concentration around the bubble determined by pressure inside must be equal to the saturated concentration in liquid when the bubble is stable, which is the same set in the two models. When the saturation ratio s equals 2 or 3, the internal pressure is two or three times the normal atmospheric pressure, even though the initial pressure and its changing rate are different because of the smaller state-dependent surface tension. When s equals 2, the contact angle of state-dependence reaches equilibrium at about 31 and 39 µs, with ϕ₀ = −2 k_BT and ϕ₀ = 0, respectively. While it is 28 and 50 μs with s = 3. And the SNB reaches equilibrium at about 78 μs on hydrophilic surface (ϕ₀ = 2 k_BT).

FIGURE 3

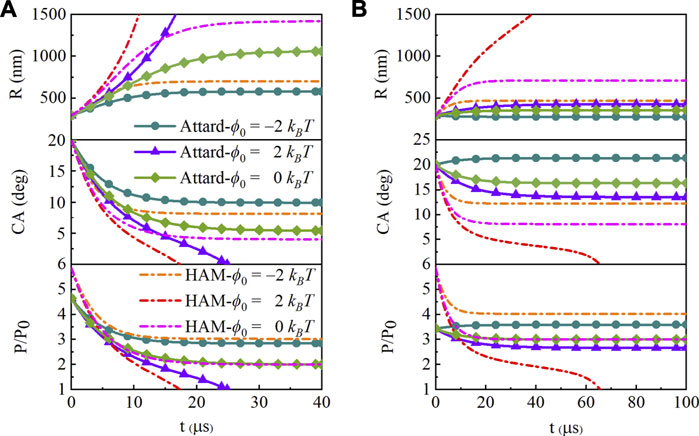
FIGURE 3. Evolution of the curvature radius, contact angle (CA) and pressure with state-dependent surface tension at L = 100 nm, initial contact angle θ₀ = 20^o and different saturation ratios of (A)s = 2, (B)s = 3. The curves are for hydrophobic (ϕ₀ = −2 k_BT, circle symbol), hydrophilic (ϕ₀ = 2 k_BT, triangle symbol), and neutral (ϕ₀ = 0 k_BT, rhombus symbol) surfaces. The dashed ones are for hydrophobic attraction model (HAM) with the same surfaces.

On the hydrophobic surface with the attraction potential of −2 k_BT, the contact angle is also larger and the pressure is a little smaller than HA model, which is calculated by Laplace’s equation with the surface tension and radius. It means that the decrease in surface tension can enhance the stability of SNBs. There is more gas staying in the bubble, leading to a larger contact angle (s = 2). The more gas coming in than the gas getting out means the growth of the bubble (s = 3). In this case, the smaller radius will lead to the larger inside pressure than that of s = 2.

There is a significant difference in the SNBs’ evolution between the two saturation ratios on a hydrophilic surface. When the saturation ratio is 2, the surface tension γ becomes 0.75γ₀, and the internal pressure decreases by the same proportion at t = 0, as shown in Figure 3A. The gas diffuses slower with the decreasing pressure, and so as the changing contact angle. The bubble cannot survive on a hydrophilic surface with a potential of 2 k_BT. However, it can survive on one with less than 0.8 k_BT (ϕ₀ = 0.8 k_BT, θ_e = 2.67^o; ϕ₀ = 0.7 k_BT, θ_e = 3.31^o) in the simulation, while with less than 0.7 k_BT in HA model (ϕ₀ = 0.7 k_BT, θ_e = 1.44^o). It can be inferred that SNBs may be able to survive on the more hydrophilic surface with the larger saturation ratio s. When the saturation ratio is 3, a nanobubble can survive with an angle of 13.57^o on the hydrophilic surface with attraction potential of 2 k_BT, while the nanobubble will shrink down and vanish within 70 μs in HA model, as shown in Figure 3B. Although HA model has demonstrated that SNBs can remain stable on a moderately hydrophilic surface with a sufficiently large saturation ratio, but state-dependent surface tension weakens the need of the degree of oversaturation. The nanobubble grows up with a little larger contact angle on the hydrophobic surface.

With the state-dependent surface tension, we also consider the effects of different potential values on SNBs under two saturation ratios. Figure 4 shows the contact angle evolution with two saturation ratios and potential ranges, which represent different surfaces, −4 k_BT to 4 k_BT with s = 2.5 and −4 k_BT to 10 k_BT with s = 3. When the saturation ratio is 2.5, the bubbles can survive on the surface with 1 k_BT, the same as HA model. Nevertheless, its equilibrium contact angle (7.82^o) is two times larger than HA model. The lower surface tension indicates that SNBs are more stable with larger contact angles. For a hydrophobic surface with −4 k_BT, the bubble can grow with angle up to 23.85^o while it will shrink to 17.74^o in HA model at the equilibrium. When the saturation ratio is 3, the decrease in surface tension can make the SNBs survivable on the hydrophilic surface with potential up to 5 k_BT. While the surface tension remains γ₀, the bubble can only survive up to 1.8 k_BT. This confirms the previous hypothesis that SNBs can survive on more hydrophilic surfaces with higher saturation degree.

FIGURE 4

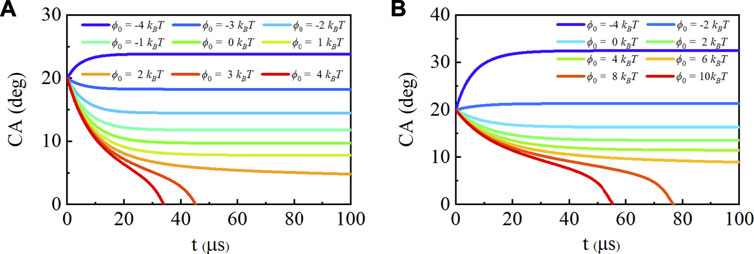
FIGURE 4. Contact angle (CA) evolution with different interaction of the gas and solid. The footprint radius is L = 100 nm, the initial contact angle is θ₀ = 20^o and the saturation ratio is (A)s = 2.5, (B)s = 3.

In the previous calculations, the contact rim radius was fixed at 100 nm. In fact, the SNBs observed in experiments exist with different sizes. Figure 5 shows equilibrium contact angles of SNBs of different sizes in the liquid with different saturation ratio s, compared with HA model. The SNBs of larger contact rim radius are with larger contact angles. On the surface with ϕ₀ = −2 k_BT, the reduced surface tension caused by saturation ratio s enlarges the equilibrium contact angle with the same L. When s is 2 or 3, the contact angle holds an apparent change. Stable SNBs must maintain the same pressure in the same environment and the Laplace’s law determines the inside pressure with the surface tension and radius. From the equation of R = L / sin(θ), if the pressure and L are the same in the two models, the larger angle is with state-dependent surface tension. The larger angle means that the bubbles are easier to exist or more stable.

FIGURE 5

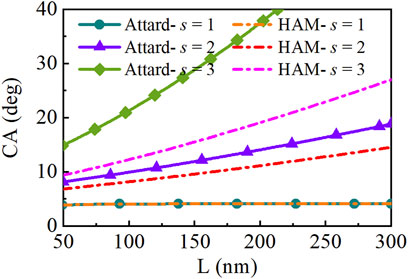
FIGURE 5. The relation between contact rim radius L and equilibrium contact angle (CA) with different saturation ratios in the two models: state-dependent surface tension model and hydrophobic attraction model (HAM).

5 Conclusion

Many researches about SNBs focus on their long life and small contact angles. The HA model reveals that only contact line pinning is required and the attractive hydrophobic potential can make a supplementary for the gas oversaturation, which is not a necessary condition for the stability of SNBs. In this work, we take the Tolman-dependent and state-dependent surface tension into the HA model. The surface tension changes with the curvature radius R or the saturation ratio s. It slows down the changing rate of evolution process, and enlarges the contact angle at the equilibrium. The SNBs are more stable on the hydrophobic or neutral surface with larger contact angle and even can survive on the highly hydrophilic surface under the same oversaturation degree.

The surface tension of Tolman-dependence related to the curvature radius R has little effect on the evolution of SNBs in large scale (such as L = 50 or 100 nm), while it has a great influence in small SNBs (such as L = 20 nm), in which the initial curvature radius R is close to the Tolman length. When the SNBs reach equilibrium, the surface tension maintains a constant and the SNBs hold larger contact angle. It is similar in the state-dependence, surface tension is beneficial to the stability of SNBs. With the saturation ratio s = 3, the bubbles on the highly hydrophilic surface (ϕ₀ = 1∼5 k_BT) can also be stable, and those on the hydrophobic surface grow up. In conclusion, the two variable surface tensions, which are verified providing SNBs’ mechanical equilibrium and thermodynamic stability, can make the SNBs holding larger contact angle and more stable. The present study enriches our understanding of the mechanism for the stability of SNBs. In the future, much more research is urgently needed on the phase interface’s surface tension, which is a new perspective on the SNB and closely related to its thermodynamic stability. At the same time, more experiments and simulation studies should be carried out to provide some guidance for theoretical analysis of the stability mechanism.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

This work was supported by the National Natural Science Foundation of China (Grant Nos. 11862003, 81860635, and 12062005), the Key Project of Guangxi Natural Science Foundation (Grant No. 2017GXNSFDA198038), Guangxi “Bagui Scholar” Teams for Innovation and Research Project, and Guangxi Collaborative Innovation Center of Multisource Information Integration and Intelligent Processing.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Temesgen T, Bui TT, Han M, Kim TI, Park H. Micro and Nanobubble Technologies as a New Horizon for Water-Treatment Techniques: A Review. Adv Colloid Interf Sci (2017) 246:40–50. doi:10.1016/j.cis.2017.06.011

CrossRef Full Text | Google Scholar

2. Yuan Y, Adimi S, Thomas T, Wang J, Guo H, Chen J, et al. Co3Mo3N-An Efficient Multifunctional Electrocatalyst. The Innovation (2021) 2:100096. doi:10.1016/j.xinn.2021.100096

CrossRef Full Text | Google Scholar

3. Zhou L, Wang S, Zhang L, Hu J. Generation and Stability of Bulk Nanobubbles: A Review and Perspective. Curr Opin Colloid Interf Sci (2021) 53(1):101439. doi:10.1016/j.cocis.2021.101439

CrossRef Full Text | Google Scholar

4. Zhang L, Zhang Y, Cheng J, Wang L, Wang X, Zhang M, et al. Inert Gas Deactivates Protein Activity by Aggregation. Sci Rep (2017) 7(1):10176. doi:10.1038/s41598-017-10678-3

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Wang Y, Bhushan B. Boundary Slip and Nanobubble Study in Micro/nanofluidics Using Atomic Force Microscopy. Soft Matter (2009) 6.

Google Scholar

6. Wen B, Zhang C, Tu Y, Wang C, Fang H. Galilean Invariant Fluid-Solid Interfacial Dynamics in Lattice Boltzmann Simulations. J Comput Phys (2014) 266(6):161–70. doi:10.1016/j.jcp.2014.02.018

CrossRef Full Text | Google Scholar

7. Sobhy A, Tao D. Nanobubble Column Flotation of fine Coal Particles and Associated Fundamentals. Int J Mineral Process (2013) 124(Complete):109–16. doi:10.1016/j.minpro.2013.04.016

CrossRef Full Text | Google Scholar

8. Shen G, Zhang XH, Ming Y, Zhang L, Zhang Y, Hu J. Photocatalytic Induction of Nanobubbles on TiO2 Surfaces. J Phys Chem C (2008) 112(11):4029–32. doi:10.1021/jp711850d

CrossRef Full Text | Google Scholar

9. Seh ZW, Kibsgaard J, Dickens CF, Chorkendorff I, Nørskov JK, Jaramillo TF. Combining Theory and experiment in Electrocatalysis: Insights into Materials Design. Science (2017) 355(6321):eaad4998. doi:10.1126/science.aad4998

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Vann RD, Butler FK, Mitchell SJ, Moon RE. Decompression Illness. The Lancet (2011) 377(9760):153–64. doi:10.1016/s0140-6736(10)61085-9

CrossRef Full Text | Google Scholar

11. Israelachvili J, Pashley R. The Hydrophobic Interaction Is Long Range, Decaying Exponentially with Distance. Nature (1982) 300(5890):341–2. doi:10.1038/300341a0

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Lou S-T, Ouyang Z-Q, Zhang Y, Li X-J, Hu J, Li M-Q, et al. Nanobubbles on Solid Surface Imaged by Atomic Force Microscopy. J Vac Sci Technol B (2000) 18(5):2573–5. doi:10.1116/1.1289925

CrossRef Full Text | Google Scholar

13. Ishida N, Inoue T, Miyahara M, Higashitani K. Nano Bubbles on a Hydrophobic Surface in Water Observed by Tapping-Mode Atomic Force Microscopy. Langmuir (2000) 16(16):6377–80. doi:10.1021/la000219r

CrossRef Full Text | Google Scholar

14. Parker JL, Claesson PM, Attard P. Bubbles, Cavities, and the Long-Ranged Attraction between Hydrophobic Surfaces. J Phys Chem (1994) 98(34):8468–80. doi:10.1021/j100085a029

CrossRef Full Text | Google Scholar

15. Seddon JRT, Kooij ES, Poelsema B, Zandvliet HJW, Lohse D. Surface Bubble Nucleation Stability. Phys Rev Lett (2011) 106(5):056101. doi:10.1103/PhysRevLett.106.056101

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Ducker WA. Contact Angle and Stability of Interfacial Nanobubbles. Langmuir (2009) 25(16):8907–10. doi:10.1021/la902011v

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Zhang L, Zhang X, Zhang Y, Hu J, Fang H. The Length Scales for Stable Gas Nanobubbles at Liquid/solid Surfaces. Soft Matter (2010) 6(18):4515–9. doi:10.1039/C0SM00243G

CrossRef Full Text | Google Scholar

18. Craig VSJ. Very Small Bubbles at Surfaces-The Nanobubble Puzzle. Soft Matter (2011) 7(1):40–8. doi:10.1039/C0SM00558D

CrossRef Full Text | Google Scholar

19. Alheshibri M, Qian J, Jehannin M, Craig VSJ. A History of Nanobubbles. Langmuir (2016) 32(43):11086–100. doi:10.1021/acs.langmuir.6b02489

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Lohse D, Zhang X. Surface Nanobubbles and Nanodroplets. Rev Mod Phys (2015) 87(3):981–1035. doi:10.1103/RevModPhys.87.981

CrossRef Full Text | Google Scholar

21. Young T. III. An Essay on the Cohesion of Fluids. Phil Trans R Soc (1805) 95:65–87. doi:10.1098/rstl.1805.0005

CrossRef Full Text | Google Scholar

22. He B, Qin C, Zhou S, Wen B. Analysis of Depinning Behavior of Drop on Chemically Heterogeneous Surface. Phys Rev Fluids (2020) 5(11). doi:10.1103/physrevfluids.5.114003

CrossRef Full Text | Google Scholar

23. Ji T, Pan Y, Shao Y, He B, Wen B. Lateral Drop Rebound on a Hydrophobic and Chemically Heterogeneous Surface. Langmuir (2021) 37(23):6905–14. doi:10.1021/acs.langmuir.1c00242

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Epstein PS, Plesset MS. On the Stability of Gas Bubbles in Liquid‐Gas Solutions. J Chem Phys (1950) 18:1505–9. doi:10.1063/1.1747520

CrossRef Full Text | Google Scholar

25. Das S. Effect of Impurities in the Description of Surface Nanobubbles: Role of Nonidealities in the Surface Layer. Phys Rev E (2011) 83(6 Pt 2):066315. doi:10.1103/PhysRevE.83.066315

PubMed Abstract | CrossRef Full Text | Google Scholar

26. German SR, Wu X, An H, Craig VSJ, Mega TL, Zhang X. Interfacial Nanobubbles Are Leaky: Permeability of the Gas/Water Interface. ACS Nano (2014) 8(6):6193–201. doi:10.1021/nn5016049

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Brenner MP, Lohse D. Dynamic Equilibrium Mechanism for Surface Nanobubble Stabilization. Phys Rev Lett (2008) 101(21):214505. doi:10.1103/PhysRevLett.101.214505

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Yasui K, Tuziuti T, Kanematsu W, Kato K. Advanced Dynamic-Equilibrium Model for a Nanobubble and a Micropancake on a Hydrophobic or Hydrophilic Surface. Phys Rev E (2015) 91(3):033008. doi:10.1103/PhysRevE.91.033008

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Liu Y, Zhang X. Nanobubble Stability Induced by Contact Line Pinning. J Chem Phys (2013) 138(1):014706. doi:10.1063/1.4773249

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Liu Y, Zhang X. A Unified Mechanism for the Stability of Surface Nanobubbles: Contact Line Pinning and Supersaturation. J Chem Phys (2014) 141(13):134702. doi:10.1063/1.4896937

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Weijs JH, Lohse D. Why Surface Nanobubbles Live for Hours. Phys Rev Lett (2013) 110(5):054501. doi:10.1103/PhysRevLett.110.054501

PubMed Abstract | CrossRef Full Text | Google Scholar

32. Lohse D, Zhang X. Pinning and Gas Oversaturation Imply Stable Single Surface Nanobubbles. Phys Rev E (2015) 91(3):031003. doi:10.1103/PhysRevE.91.031003

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Popov YO. Evaporative Deposition Patterns: Spatial Dimensions of the deposit. Phys Rev E Stat Nonlin Soft Matter Phys (2005) 71(3):036313. doi:10.1103/PhysRevE.71.036313

PubMed Abstract | CrossRef Full Text | Google Scholar

34. Qian J, Craig VSJ, Jehannin M. Long-Term Stability of Surface Nanobubbles in Undersaturated Aqueous Solution. Langmuir (2019) 35(3):718–28. doi:10.1021/acs.langmuir.8b03487

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Zhang X, Chan DYC, Wang D, Maeda N. Stability of Interfacial Nanobubbles. Langmuir (2013) 29(4):1017–23. doi:10.1021/la303837c

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Tan BH, An H, Ohl C-D. Surface Nanobubbles Are Stabilized by Hydrophobic Attraction. Phys Rev Lett (2018) 120(16):164502. doi:10.1103/PhysRevLett.120.164502

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Tan BH, An H, Ohl C-D. Stability, Dynamics, and Tolerance to Undersaturation of Surface Nanobubbles. Phys Rev Lett (2019) 122(13):134502. doi:10.1103/PhysRevLett.122.134502

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Petsev ND, Leal LG, Shell MS. Universal Gas Adsorption Mechanism for Flat Nanobubble Morphologies. Phys Rev Lett (2020) 125(14):146101. doi:10.1103/PhysRevLett.125.146101

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Dammer SM, Lohse D. Gas Enrichment at Liquid-Wall Interfaces. Phys Rev Lett (2006) 96(20):206101. doi:10.1103/PhysRevLett.96.206101

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Luzar A, Bratko D. Gas Solubility in Hydrophobic Confinement. J Phys Chem B (2005) 109(47):22545–52. doi:10.1021/jp054545x

PubMed Abstract | CrossRef Full Text | Google Scholar

41. Bratko D, Luzar A. Attractive Surface Force in the Presence of Dissolved Gas: a Molecular Approach. Langmuir (2008) 24(4):1247–53. doi:10.1021/la702328w

PubMed Abstract | CrossRef Full Text | Google Scholar

42. Zhang XH, Quinn A, Ducker WA. Nanobubbles at the Interface between Water and a Hydrophobic Solid. Langmuir (2008) 24(9):4756–64. doi:10.1021/la703475q

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Zhang XH, Khan A, Ducker WA. A Nanoscale Gas State. Phys Rev Lett (2007) 98(13):136101. doi:10.1103/PhysRevLett.98.136101

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Zhou L, Wang X, Shin H-J, Wang J, Tai R, Zhang X, et al. Ultrahigh Density of Gas Molecules Confined in Surface Nanobubbles in Ambient Water. J Am Chem Soc (2020) 142(12):5583–93. doi:10.1021/jacs.9b11303

PubMed Abstract | CrossRef Full Text | Google Scholar

45. Zhou L, Wang X, Zhang L, Hu J. Recent Developments in Nanobubble Research Based on Synchrotron Radiation Techniques. SCIENTIA SINICA Physica (2021) 1674–7275. doi:10.1360/SSPMA-2021-0091

CrossRef Full Text | Google Scholar

46. Luo QQ, Yang JM. Gas Adsorption and Accumulation on Hydrophobic Surfaces: Molecular Dynamics Simulations. Chin Phys B (2015) 24(009):392–8. doi:10.1088/1674-1056/24/9/096801

CrossRef Full Text | Google Scholar

47. Manning GS. On the Thermodynamic Stability of Bubbles, Immiscible Droplets, and Cavities. Phys Chem Chem Phys (2020) 22(31):17523–31. doi:10.1039/D0CP02517H

PubMed Abstract | CrossRef Full Text | Google Scholar

48. Tolman RC. The Effect of Droplet Size on Surface Tension. J Chem Phys (1949) 17(3):333–7. doi:10.1063/1.1747247

CrossRef Full Text | Google Scholar

49. Berg JK, Weber CM, Riegler H. Impact of Negative Line Tension on the Shape of Nanometer-Size Sessile Droplets. Phys Rev Lett (2010) 105(7):076103. doi:10.1103/PhysRevLett.105.076103

PubMed Abstract | CrossRef Full Text | Google Scholar

50. Wang JY, Betelu S, Law BM. Line Tension Approaching a First-Order Wetting Transition: Experimental Results from Contact Angle Measurements. Phys Rev E Stat Nonlin Soft Matter Phys (2001) 63(3):031601. doi:10.1103/PhysRevE.63.031601

PubMed Abstract | CrossRef Full Text | Google Scholar

51. Weijs JH, Marchand A, Andreotti B, Lohse D, Snoeijer JH. Origin of Line Tension for a Lennard-Jones Nanodroplet. Phys Fluids (2011) 23(2):021602. doi:10.1063/1.3546008

CrossRef Full Text | Google Scholar

52. Duncan D, Li D, Gaydos J, Neumann AW. Correlation of Line Tension and Solid-Liquid Interfacial Tension from the Measurement of Drop Size Dependence of Contact Angles. J Colloid Interf Sci (1995) 169(2):256–61. doi:10.1006/jcis.1995.1032

CrossRef Full Text | Google Scholar

53. Ohgaki K, Khanh NQ, Joden Y, Tsuji A, Nakagawa T. Physicochemical Approach to Nanobubble Solutions. Chem Eng Sci (2010) 65(3):1296–300. doi:10.1016/j.ces.2009.10.003

CrossRef Full Text | Google Scholar

54. Moody MP, Attard P. Curvature-Dependent Surface Tension of a Growing Droplet. Phys Rev Lett (2003) 91(5):056104. doi:10.1103/PhysRevLett.91.056104

PubMed Abstract | CrossRef Full Text | Google Scholar

55. Attard P. The Stability of Nanobubbles. Eur Phys J Spec Top (2013) 223(5):893–914. doi:10.1140/epjst/e2013-01817-0

CrossRef Full Text | Google Scholar

56. Pinning PA. Down the Reasons for the Size, Shape, and Stability of Nanobubbles. Langmuir (2016) 32:11138.

PubMed Abstract | Google Scholar

57. Attard P. Thermodynamic Stability of Nanobubbles. arXivPhysics (2015).

Google Scholar

58. He S, Attard P. Surface Tension of a Lennard-Jones Liquid under Supersaturation. Phys Chem Chem Phys (2005) 7(15):2928–35. doi:10.1039/b507106b

PubMed Abstract | CrossRef Full Text | Google Scholar

59. Cahn JW, Hilliard JE. Free Energy of a Nonuniform System. I. Interfacial Free Energy. J Chem Phys (1958) 28(2):258–67. doi:10.1063/1.1744102

CrossRef Full Text | Google Scholar

60. Oxtoby DW, Evans R. Nonclassical Nucleation Theory for the Gas-Liquid Transition. J Chem Phys (1988) 89(12):7521–30. doi:10.1063/1.455285

CrossRef Full Text | Google Scholar