Resilience of Nematode Connectomes Based on Network Dimension-reduced Method

The whole map of nematode connectomes provides important structural data for exploring the behavioral mechanism of nematodes, but to further reveal the functional importance and resilience pattern of nematode neurons, it is necessary to effectively couple the regulatory relationship between neurons and their topology. Here, with a typical signal excitation function we propose a model to capture the interacting relationship between the neurons, because a differential equation depicts the activity of a neuron, n neurons mean we need high-D differential equations to capture the neural network. With mean-field theory, we decouple this N-dimension question into a one-dimension problem mathematically. In our framework, we emphatically analyze the characteristics, similarities and differences of the structure and dynamical behaviors of the neuronal system for Caenorhabditis elegans and Pristionchus pacificus. The comparing results of simulating method and theoretical approach show that the most important homologous neurons between C.elegans and P.pacificus are I2 and NSM, which may lead to their different behavior characteristics of predation and prey. At the same time, we expect that the x_eff index can be used to reveal the importance of neurons for the functional evolution and degeneration of neural networks from a dynamic perspective. In the hermaphroditic and male C.elegans, we test the control level of the intermediate neuron groups over the output neuron groups and the single neuron. These results suggest that our theoretical approach can be used to reveal the effects of bio-connectivity groups, potentially enabling us to explore the interaction relationship of neural networks in humans and animals.

1 Introduction

Due to special physiological structure and easy modeling, nematode has become the primary model to reveal the neurons structure and functional mechanism for humans and animals [1, 2]. After four decades of exploration, nematodes are the first organisms, for which the wiring diagram of their entire nervous system has been mapped at the cellular level [3, 4]. Even Witvliet et al reconstructed full brain of eight isogenic Caenorhabditis elegans individuals across postnatal stages to investigate how it changes with age [5]. This contributes to a more detailed and accurate understanding and exploration of human and animal behavior at the neuronal level, as well as an analysis of the functional importance of individual neurons at the systemic level. Therefore, we coupled the structural information of the neuronal map of the nematode and the functional relationship between the neurons, predicted the functional involvement of specific neurons or synapses in defined behavioral responses [6, 7].

Resilience is system’s ability to retain its basic functionality while errors, failures and environmental changes occur, which universally presents in most dynamical systems [8]. Thanks to the rapid development of network theory, the description of the nonlinear dynamics that governs the interactions between the neurons have been extracted. According to external disturbance for neuron systems, deleting interneurons or synapses may disconnect the networks, or make a great impact on the individual behavior [9]. The methods to explore the nematode’s resilience mainly can be divided into two categories. 1) Biological experiments: such as the gene labeling and the neuron ablation. They can track some specific synapses or their function in detail. The labeling approach can capture the directionality of synaptic connections, and its quantitative analysis of synapse patterns display excellent concordance with electronic micrograph reconstructions [10, 11]. However, this approach takes a lot of energy and is not universal. 2) Theoretical experiments: using different mathematical methods and engineering mechanisms, which can abstractly study the function of outstanding nodes in nematodes [12–16]. For example, according to the theory of symmetry group, they found that the symmetry of the neural network has directly biological significance, and its correctness can be strictly proved by using the mathematical form of symmetry group. This form makes it possible to understand the importance of the structure-function relationship [17]. In addition, Yan also applied network control principles to the connectomes, which reveals both neurons with known importance and neurons which was previously unknown [18]. Within a network control principle, they add input signal to control the output of neurons by a linear framework. The results remain reliable with a small amount of disturbance to the reference connectors, but large disturbances are likely to cause distortion.

Here we construct a framework to explore the resilience of nematode connectomes: we use the signal excitation model to describe and solve quantitatively structure-function relationship of the nematode, which combines the biological behavior with dynamic behavior. The application of signal excitation mode is key to revealing how different behaviors, which contributes to understand the mapping from network structure to function [19]. Since the network contains a large number of neurons, each activity of synapse node or neuron node can be seen as a solution of the high-D differential equations. However, calculating the stable state of the neural system could be difficult or almost impossible, especially when the system is large-scale. With a network dimension-reduction method, we can derive an effective one-dimensional dynamic model which captures the system function of the neural networks. Finally, we use a weighted average activity x_eff to measure the neural performance of the whole nematodes. Meanwhile, we introduce a weighted average connectivity β_eff to express the structural strength of the nematode neuron system.

With the application of our framework into the neuron networks of P.pacificus and C.elegans, the differences between the predator and prey behaviors of these two nematodes can be clearly quantified at the neural network level, and the key neurons leading to the differences in nematode behaviors can be easily identified as well. Similarly, for hermaphroditic and male C.elegans, we apply our approach to discuss the core control of the intermediate neuron groups to output neuron groups. Core control means that the interneurons have great influence over the output neurons or all the neurons after neuronal perturbation.

Actually, our approach is a general mathematical framework, which couples the complex structure of the system with the nonlinear activation function, and enriches the research methods for exploring the functional behaviors of nematode. We can reveal the underlying principle of the neural network in this way. In the future, our theoretical methods can be applied to more specific linkage groups, to do targeted quantitative research [20].

2 Neural Model and Network Dimension-reduced Method

2.1 Neural Dynamics Model

There are nonlinear regulation relationships between each synapse in neural networks. Taking hyperbolic tangent excitation function as an example in this paper, we give a neural network decoupling method with a general network structure. For the stimulation relationships between the trillions of neuron synapses in human brain or animals, it would enable the individuals show a much more complex nonlinear phenomenon of affine transformation. The activation function can be used to describe the coupling mechanism among synapses as

$\frac{d{x}_i}{dt}=I-\frac{x_i}{R}+\frac{J}{2}\sum _{j=1}^N{A}_{ij}(1+\tanh (n(x_j-\alpha ))),(1)$

Where, x_i describes the activity of the neuron i, I is the basal activity of the neurons, R is the inverse of the death rate, α is the firing threshold, and J is the maximal interaction strength between pair of neurons. The adjacency matrix A depicts the topology of the neuron networks. The coefficient n governs the steepness of the sigmoid function, analogously to the Hill coefficient n in gene regulatory networks [18]. Actually, the Eq. 1 is made up of two parts: $I-\frac{x_i}{R}$ describes the growth rate of the neuron itself, $\frac{J}{2}{\sum }_{j=1}^N{A}_{ij}(1+tanh\left(n(x_j-\alpha )\right))$ describes the positive excitation effect of its neighbor neurons on neuron i.

2.2 Network Dimension-Reduced Method

When the system of Eq. 1 tends to a relatively stable state, which means that the activities of the N individuals in the network are constant values, so the N-dimensional nonlinear rate equations all equal to 0. However, calculating the stable state of the system requires to solve the N-dimensional nonlinear rate equations numerically or analytically, which could be very difficult, or almost impossible especially when the system is large-scale. We present a new dimensionality reduction to explore the interactive relationship between neuronal connectomes for nematodes with mean-field approximation. This approximation is exact in the limit where the node activities are uniformly distributed.

2.2.1 Theoretical Framework for Network Resilience

Once we get the value of x_i for the neuron i from the solutions of Eq. 1, we can quantify the performance and the connectivity strength of the neural networks with a weighted average metrics on the network topology following the way in [21]. Defining an operator for the degree sequence of A as

$\mathrm{\Gamma }\left(y\right)=\frac{1^{\top }Ay}{1^{\top }A1}={⟨⟨y⟩}_{nn}⟩=\frac{⟨s_j^{out}{y}_j⟩}{⟨s_j^{out}⟩}.(2)$

Here, y_i is a variable of neuron i, and $⟨y⟩$ is the weighted average of all the neurons. $s_j^{out}$ is the outdegree of neuron j. In contrast, $s_i^{in}$ represents the indegree of neuron i. This operator is used to calculate the weighted average y over all nearest neighbor nodes of network A.

In order to simplify the N-dimension of Eq. 1 and approximate it to 1D formalism, we use a mean field hypothesis. Here we define $I-\frac{x_i}{R}$ as F(x_i), define $(1+tanh\left(n(x_j-\alpha )\right))$ as G(x_i, x_j). Using Γ(G(x_i, x)) ≈ G(x_i, Γ(x)) approximate Eq. 1, we get

$\frac{d{x}_i}{dt}=I-\frac{x_i}{R}+s_i^{\mathrm{i}\mathrm{n}}\frac{J}{2}(1+\tanh (n(\mathrm{\Gamma }(\mathrm{x})-\alpha ))).(3)$

For the states of all nodes in the system, Eq. 3 can be rewritten by the Hadamard product as

$\frac{d\mathrm{x}}{dt}=I-\frac{\mathrm{x}}{R}+s^{in}◦\frac{J}{2}(1+\tanh (n(\mathrm{\Gamma }(\mathrm{x})-\alpha ))).(4)$

Where we used the Hadamard product ◦, namely a ◦ b$={({\mathrm{a}}_1{\mathrm{b}}_1,\dots ,{\mathrm{a}}_{\mathrm{N}}{\mathrm{b}}_{\mathrm{N}})}^{\mathrm{T}}$. Eq. 4 is an equation composed of N dimensions. In order to reduce the dimensionality of this set of equations, we apply $\mathrm{\Gamma }(\mathrm{x})=\frac{{\mathrm{1}}^{T}A\mathrm{x}}{{\mathrm{1}}^{T}A\mathrm{1}}$ to both sides of Eq. 4, namely

$\frac{\mathrm{d}\mathrm{\Gamma }(\mathrm{x})}{dt}=\mathrm{\Gamma }\left(I-\frac{\mathrm{x}}{R}+s^{in}◦\frac{J}{2}(1+\tanh (n(\mathrm{\Gamma }(\mathrm{x})-\alpha )))\right).(5)$

Using Γ(F(x)) ≈ F(Γ(x)) and Γ(G(x, Γ(x))) ≈ G(Γ(x), Γ(x)), we get the equation

$\frac{\mathrm{d}\mathrm{\Gamma }(\mathrm{x})}{dt}=I-\frac{\mathrm{\Gamma }(\mathrm{x})}{R}+\mathrm{\Gamma }(s^{in})\frac{J}{2}(1+\tanh (n(\mathrm{\Gamma }(\mathrm{x})-\alpha ))).(6)$

In the process of dimension reduction, we introduce two variables to describe the state of the system, where x_eff measures the neural performance of the whole nematodes, β_eff expresses the structural strength of the nematode neuron system,

$x_{\mathrm{e}\mathrm{ff}}=\mathrm{\Gamma }(\mathrm{x})=\frac{{\mathrm{1}}^{T}A\mathrm{x}}{{\mathrm{1}}^{T}A\mathrm{1}},(7)$

${\beta }_{\mathrm{e}\mathrm{ff}}=\mathrm{\Gamma }(s^{\mathrm{i}\mathrm{n}})=\frac{{\mathrm{1}}^{T}A{s}^{\mathrm{i}\mathrm{n}}}{{\mathrm{1}}^{T}A\mathrm{1}}=\frac{\langle s^{\mathrm{o}\mathrm{u}\mathrm{t}}{s}^{\mathrm{i}\mathrm{n}}\rangle }{\langle s\rangle }.(8)$

Lastly, we have successfully decouple this N-dimension question into a one-dimension problem mathematically. Bring Eqs 7, 8 into Eq. 6, one gets

$\frac{d{x}_{\text{eff}}}{dt}=I-\frac{x_{\text{eff}}}{R}+\frac{J}{2}{\beta }_{\text{eff}}(1+\tanh (n(x_{\text{eff}}-\alpha ))).(9)$

Subsequently, when the system comes to a stable state, it is obvious that $\frac{d{x}_{\text{eff}}}{dt}=0$. Hence, we can further get that

${\beta }_{\text{eff}}(x_{\text{eff}})=\frac{2}{J}\left(\frac{x_{\text{eff}}}{R}-I\right)\frac{1}{1+\tanh (n(x_{\text{eff}}-\alpha ))}.(10)$

Equation 10 describes the theoretical relationship between the topology of the neuron networks and its dynamical performance. Actually, by Eq. 10 we have decoupled the complex system of Eq. 1 into a 1D problem.

2.2.2 Simulation Method

From Eq. 10, we can obtain the theoretical curves of x_eff for β_eff. To verify the correctness of our dimension-reduced method for the system resilience of x_eff, we use the ODE45 function to solve the neural dynamics of Eq. 1, which can ensure we get the numerical results of x_i. Then, with the steady state vector x and Eq. 2, which can separate the system from the topology parameter β_eff and the behavior parameter x_eff. The steps to simulate the neural dynamics are following

1. use ODE45 function to solve Eq. 1. We can obtain the stable vector x. In our study we set I = n = 2, R = α = J = 1. The setting of this parameter we refer to [16]. Assuming the network has N neurons, the solution of the steady state vector is x = [x₁, x₂, …, x_N]. It is easy to know that in the steady state vector, the value of column i represents the steady state activity x_i of neuron i.

2. compute the x_eff and β_eff from Eq. 9. For the vector x obtained in step 1 and the network indegree sequence sⁱⁿ, we can get the system topology parameter β_eff and the behavior parameter x_eff with the operator $\mathrm{\Gamma }\left(y\right)$.

3. compare the simulation results with the theoretical solutions. From the theoretical curve of Eq. 10, we test whether the simulation values of β_eff and x_eff fall on the theoretical curves. In our experiments, the simulation points agree well with the theoretical curve, which shows the feasibility of our approach.

2.3 Datasets for Neural Networks

In this study, we used two data sets: pharyngeal nervous systems of C.elegans and P.pacifica [22], all neuronal connections of hermaphrodite and male C.elegans [3]. The groundbreaking work of Cook and Bumbarger et al. provides a wealth data of neural networks, which can help explore the wiring problem from the perspective of structure. We want to couple the information of structure and dynamical function, so as to probe into the complex wiring problem of nematode from the network function and system resilience.

The connection matrix for pharyngeal nervous systems of C.elegans and P.pacifica was derived from the data set used by Bumbarger in his earlier work [22]. The matrix contains neuron connections and weights. The data and its experiment are used for homology comparison of two nematode in our study.

In fact, because of the complex wiring of the nematodes, their neurons have a precise functional grouping: input neuron, intermediate neuron, output neuron. So, for the dataset of hermaphrodite and male C.elegans, instead of focusing on the function of a single node in the nematode network, we focus on the influence of the intermediate neurons on the output neurons.

Connectome adjacency matrices of hermaphrodite and male C.elegans are gap junction, which were provided by Steven J. Cook [3]. Notably, they presented the complete wiring diagram of an animal nervous system for the first time in 2019, including adult C.elegans of both sexes. It is an important milestone in the field of neuron science. The data corresponding to one connectome has the following information: the node, the weight, neuron names in each group. e.g., InterNeurons contains all the neurons that belong to the “InterNeurons” group, neuron names in each subgroup, e.g., InterNeurons_1 contains all the neurons that belong to the “InterNeurons_1” subgroup of the “InterNeurons” group.

3 Results

3.1 Resilience of C.elegans and P.pacificus

P.pacificus (Figure 1A) and C.elegans (Figure 1B) have highly similar synaptic structures, but quite different functions in the pharynx [23], we mainly explore the different connective structure and function in pharyngeal neurons.

FIGURE 1

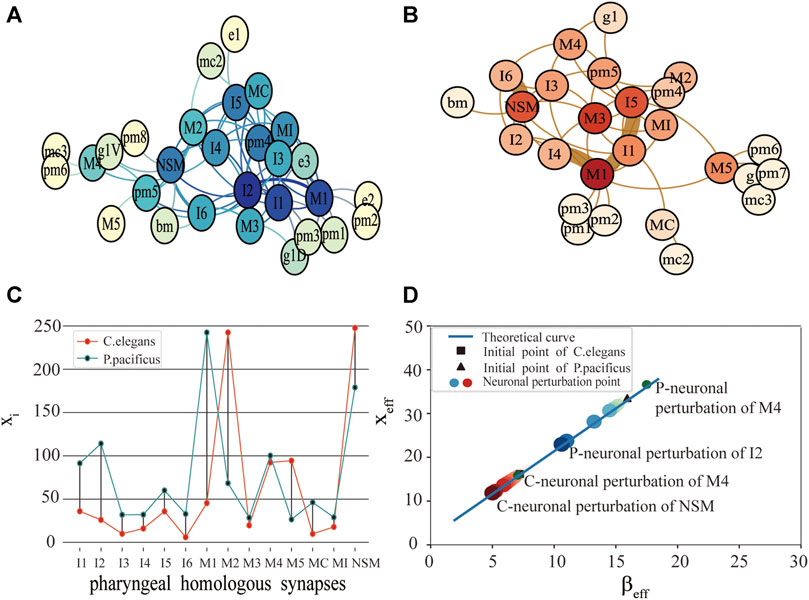
FIGURE 1. Comparison of function and structure of synaptic connectivity in C.elegans and P.pacificus. (A) Neuron network for P.pacificus. (B) Neuron network for C.elegans. (C) Activity of 14 homologous synapses between C.elegans and P.pacificus. (D) System performance of C.elegans and P.pacificus while the neurons are disturbed. The red circles represent the system resilience of C.elegans while the homologous synapses are disturbed. The blue circles represent the system resilience of P.pacificus. The darker the color, the greater the effect of the neuronal perturbation.

We measured the functional differences of the connective structure for C.elegans and P.pacificus with x_i. As shown in Figure 1C, by exploring the impact of the 14 pharyngeal homologous neurons, we found that the values of M1 for P.pacificus and C.elegans show the greatest difference, which means that M1 is the most functionally different synapse between the two nematodes. M1 is a motor neuron, and their structure centralities of M1 in C.elegans and P.pacificus are quite similar [22]. Our framework can help identify the potential critical neurons, which may be inconsistent with the traditional structural comparison.

Then, with the framework we explored the differences of the predation behavior for the two nematodes through the system resilience index x_eff. As shown in Figure 1D, first of all, the activities of C.elegans and P.pacificus were in good agreement with our predicted theoretical curves. Secondly, we were awared that the x_eff of the P.pacificus simulation point is much higher than C.elegans. That is to say, the total activity of the P.pacificus is much higher than C.elegans. Nematode feeding strategies differ greatly [24, 25]. P.pacificus have a necromenic association with scarab beetles [22]. Their dauer larvae rest on the insect and resume development after the beetle’s death to feed on microbes on the decaying carcass. P.pacificus can be easily cultured on bacteria [26], however, which is also predatory on other nematodes. In fact, the difference of predation strategy leads to the difference of neuron function. For example, differential but coordinated regulation of pm1 and pm3 in P.pacificus represents motor output that is specific to predatory feeding and does not exist in C.elegans [27, 28]. Actually, the key characteristic of P.pacificus is that it takes predation behavior actively for a long time [29, 30], while the C.elegans, which is preyed on, just eats the food around it. Thus, from the neural level, we can conclude that the system resilience index x_eff could be used to reveal the essential differences of the predation behavior for the two nematodes that C.elegans are prey, and P.pacificus is more likely to be predators [31].

Thirdly, we tested 14 pharyngeal neurons, which showed that NSM and I2 are the neuron with the greatest reduction compared with the original simulation point in Figure 1D. It meant that NSM and I2 are the two most important homologous neurons. I2 is an interneuron, which play the role of coordinating corpus and tooth contractions during predation. I2 are more highly connected in P.pacificus and may function as network hubs. Although there are no more detailed studies showing the important function of NSM neurons, the high impact of which on the system resilience in our results is sufficient for further attention of biological experiments. Compared with Bumbarger’s earlier biological experiments [22], the difference is that they concluded that I1 and I2 are the most important candidate neurons from the view of the system structure, but we found NSM and I2 are the two most important homologous neurons while considering the synaptic structural and functional characteristics simultaneously.

In addition, a phenomenon occurs in our experiment from Figure 1D, after neuronal perturbation (node deleting) of a few homozygous neurons, the x_eff of P.pacificus decreased, but x_eff of C.elegans increased. M4 is one of these special neurons. With its necromenic beetle association, P.pacificus has an intermediate position between the microbivorous C.elegans and true parasites [32, 33]. In other words, C.elegans are prey and P.pacificus is more likely to be predators. As one of the important feeding neurons in the pharynx, M4 is closely related to predation strategy. So we made a bold guess that M4 may degenerate in P.pacificus, but evolve in C.elegans. More details in the Discussion.

3.2 Quantitative Analysis of Control Model in Hermaphrodite and Male C.elegans

From the point of dynamics, the three-layer classification of neurons provides a good basis for the discussion of control. Here we see sensory neurons as input neurons, muscle neurons as output neurons, and other categories as intermediate neurons. We explore the control of the intermediate neurons over the output neurons.

At the beginning, we want to find a class of intermediate neurons that have core control over input neurons. Then, we can further get which of the intermediate neurons has the highest level of control. The control level is described by x_i. The interneurons ultimately serve all the neurons in the system, so we also explore the control of the intermediate neurons over all the neurons. In our experiment, aiming at a group of output neurons or all neurons, if a group of interneurons are removed, we should firstly calculate the x_i, the one changes greatest, indicating that the interneurons have core control level over the output neurons or all the neurons.

Originally, We found the intermediate neurons group with the greatest control over the output neuron group. For hermaphrodite C.elegans, there are two types of output neurons: SexSpecificCells-Muscle and BodyWallMuscles. As shown in Figure 2A, after perturbation of the OtherEndOrgan intermediate neurons, the x_i of the SexSpecificCells-Muscle have dropped mostly, this is to say, the OtherEndOrgan intermediate neurons have the maximum control level over the SexSpecificCells-muscle output neurons. By contrast, after perturbing of the intermediate neurons, the x_i of the BodyWallMuscles changes barely, which means that the intermediate neurons have no control over the BodyWallMuscles output neurons. Male C.elegans also has two output neurons: SexSpecificCells-BodyWallMuscles and SexSpecificCells-Muscle. As shown in Figure 2C, when perturbing the Sex-OtherOrgan intermediate neurons, the x_i of the SexSpecificCells-BodyWallMuscles and the SexSpecificCells-Muscle both decease sharply, so the sex-OtherOrgan intermediate neurons have the maximum control over the SexSpecificCells-BodyWallMuscles output neurons, and also have the maximum control over the SexSpecificCells-Muscle output neurons. The final result is shown in a three-layer model, as shown in Figures 2B–D.

FIGURE 2

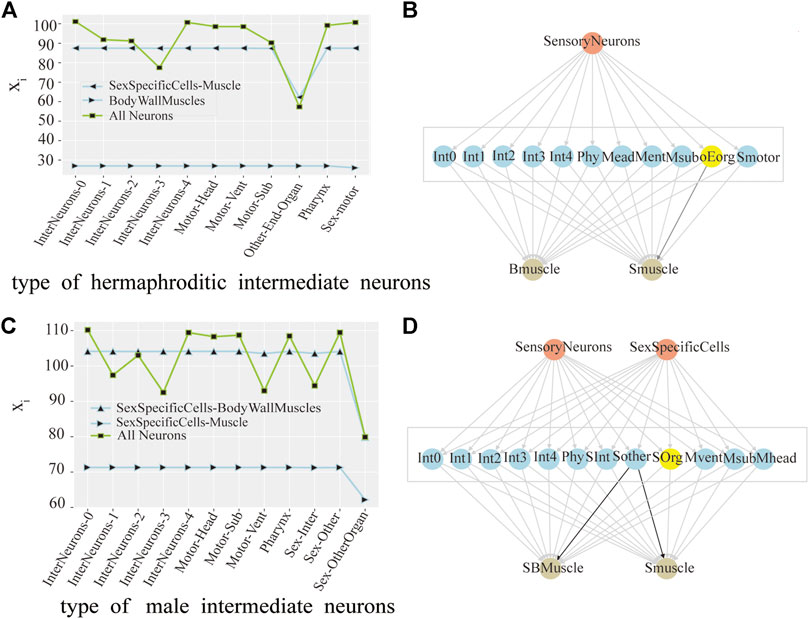
FIGURE 2. Control analysis of neuron group in hermaphrodite and male C.elegans. (A) Line chart of the change of the average activity by neuronal perturbation of the each interneurons group in hermaphroditic C.elegans. (pink as the input neuron, blue as the intermediate neuron, and yellow as the output neuron, same as below). (B) Model of the interneurons group with core control in hermaphroditic C.elegans. The groups of interneurons with maximum control were marked with yellow color, same as below. (C) Line chart of the change of the average activity by neuronal perturbation of the each interneurons group in male C.elegans. (D) Model of the interneurons group with core control in male C.elegans.

As shown in Figure 2A, in hermaphrodite C.elegans, no matter removing which group of interneurons, the line at the bottom of the Figure 2A is always stable, which means that the x_i of the BodyWallMuscles is steady. When removing the OtherEndOrgan intermediate neurons, what stands out in our results is the x_i of whole neurons (green line) decreases mostly. However, in Figure 2C, for the sexOtherorgan intermediate neurons in male C.elegans, all line corresponding to the sexOtherorgan drop sharply, which both have great effect on the neural network and the output neurons. As a result, we conclude that although these intermediate neurons have no direct control over the output neurons, they still play an important role in the overall functional mechanism of C.elegans. Hence, even though there is no decrease in the activity of the output neurons after the ablation experiment, the average activity of all neurons decreases significantly. In other words, the control mechanism over the output neurons and the whole neurons are not congruent.

Ultimately, we try to identify the intermediate neurons group with the greatest control level. We measure the neuron disturbance by degree in the intermediate group with core control, and calculate the effect of neuron control by the change of the mean value of x_i. In Figure 3, the neurons in Y-coordinate are arranged in degrees. As can be seen from the Figure 3A, in the case of male C.elegans’ sexOtherorgan intermediate group of neurons, the value decreases mostly after the removal of CEPshVR neurons. So CEPshVR has the maximum control over the SBmuscle output neurons group. As shown in Figure 3C, the value in male C.elegans’ sexOtherorgan intermediate neurons decreases sharply with the disturbance of Int neurons. Consequently, the Int neurons have the maximum control over the Smuscle output neurons group. Similarly, as shown in Figure 4A, in the case of hermaphrodite C.elegans’ OtherEndOrgan intermediate neurons, the HSNR neurons have the maximum control over the sexspecificcells-muscle output neurons group. Briefly, for most of the interneuron groups, the higher the degree, the bigger circle in Figures 3, 4, the greater the controlling impact. To illustrate more clearly, we mark in Figures 3B,D, 4B, The gray area in the middle displays the specific neurons of the interneuron group, where the neurons of the core control level are marked in yellow.

FIGURE 3

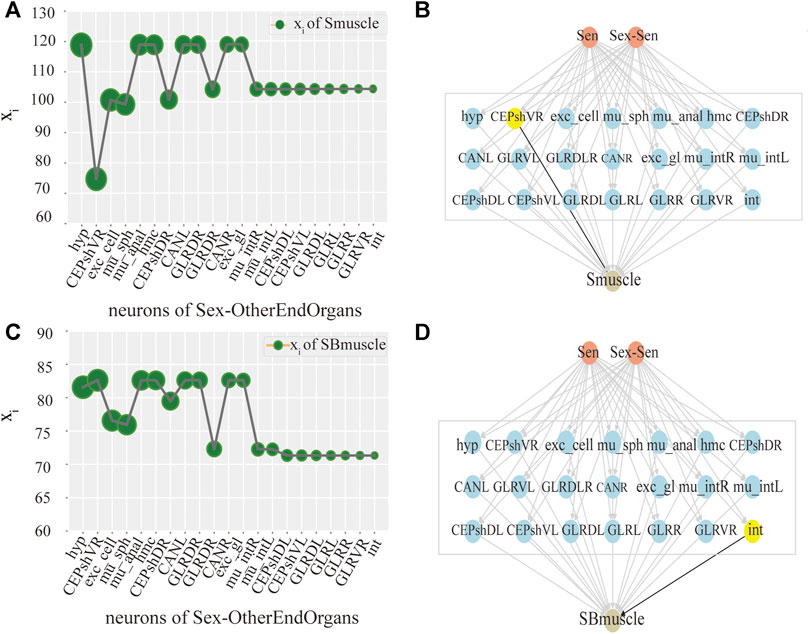
FIGURE 3. Control analysis of single neuron in male C.elegans. (A) Activity line chart of SBmuscle, after neuronal perturbation of the Sexotherorgan intermediate neuronal group in the male C.elegans by degree. Degree refers to the degree of the node in this nematode network, we calculated degree and sorted them. The order is shown in figure: The size of the green circle represents the size of degree, same as below. (B) Control model of SBmuscle by the Interneuron group of Sexotherorgan. The neurons with maximum control are shown in yellow color, same as below. (C) Activity line chart of Smuscle, after neuronal perturbation of the Sexotherorgan intermediate neuronal group in the male C.elegans by degree. (D) Control model of Smuscle by the Interneuron group of Sexotherorgan. (SensoryNeurons:Sen; SexSpecificCells-SensoryNeuron:Sex-Sen; SexSpecificCells -InterNeurons:Sex-Inter; SexSpecificCells -OtherEndorgans: Sex- OtherEndOrgans. Same as the others).

FIGURE 4

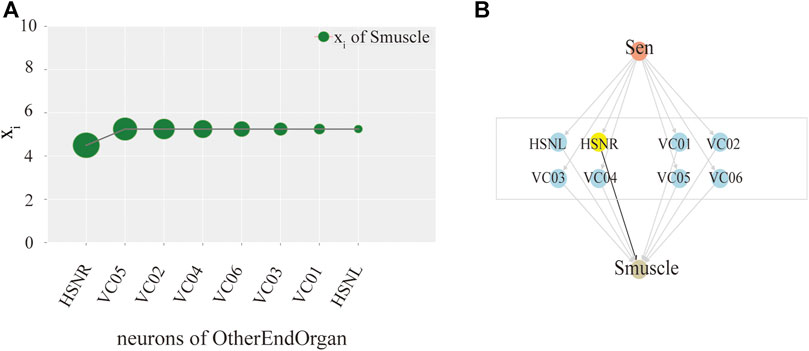
FIGURE 4. Model exploration of single neuron hermaphroditism in C.elegans.(A) Activity line chart of SexSpecficalCells-muscle, after neuronal perturbation of the SexSpecficalCells-motor intermediate neuronal group in the hermaphroditism C.elegans by degree. (B) Control model of SexSpecficalCells-muscle by the Interneuron group of SexSpecficalCells-motor.

4 Discussion

In our framework, the coupling method of network structure and dynamical interactions enables us to establish a dynamical model of neuron networks to explore the system performance. To quantitatively solve the high-dimension rate equations, we provide a way in which multi-dimensional features between neurons can be reduced into one-dimension equation. Our approach can help the realization of the mapping from structure to function, and the quantitative measurement from function to control for neuron systems.

Excepting this, we noticed that x_eff of the P.pacificus simulation point is much higher than C.elegans. With its necromenic beetle association, P.pacificus has an intermediate position between the microbivorous C.elegans and true parasites [34, 35]. The omnivorous feeder P.pacificus should have the most complex metabolic pathways for nutrition and protection against defense and prey, comparing with the microbivorous C.elegans [36, 37]. So we infer that the essence of this phenomenon is the distinction of predation behavior caused the difference of synaptic connection, which changes the structure of nematode network.

Furthermore, we hope that our research could be used to illustrate evolution and degeneration of neuron: M4 most likely degenerates in C.elegans, evolve in P.pacificus. Combining the differences in the two nematode predation strategies, and the functions of M4, our evidence is as follows: M4 are known to be one of the major excitatory neurons in C.elegans, which is required for posterior isthmus peristalsis [38–40], it meant that M4 plays a crucial role in the act of eating or swallowing in C.elegans. However, the ablation experiments made by Edelman and Garry have shown that MC are the only neurons required for rapid eating in P.pacificus. But the ablation of other cholinergic pharyngeal neurons, such as M2S and M4, only slightly reduced feeding rates [41, 42]. In addition, Trojanowski’s previous results demonstrate that this robust and evolutionarily adaptable network is highly degenerate at both the neural and genetic levels, the same behavior can be stimulated by multiple neurons and different types of receptors [41]. Avery and Horvitz even found out, in the C.elegans gene ced-3 Mutant, probably MSpaaaaap (the sister of M4), can sometimes take over M4’s function. Using a laser microbeam to kill cells, they found that one of the extra cells in ted-3 worms, tentatively identified as MSpaaaaap, could become a functioning M4 neuron about half of the time, although it rarely or never fully replaced M4 [38]. Given the above, we can not be absolutely sure that M4 most likely degenerates in C.elegans, evolve in P.pacificus, but we hope our theoretical framework can help explore the function of neurons in the evolution and degeneration process.

To illustrate the power of our framework, we analyzed the control model of hermaphroditic and male C.elegans. Based on the data of Cook et al [3], our experiment abstracted the neuron connection group from the real network to the theory level by a nonlinear dynamical model, and obtained a measurable control index of the intermediate neurons to the output neurons. The control between different functional groups need to take into account both structural and functional characteristics. It means that our framework may help design more targeted and accurate biological ablation experiments. To understand vividly, we mapped the control model of the three-layer neurons, which is accurate to the individual neurons [43, 44].

In sum, our theoretical research perfects the exploration of the functional structure of nematodes, and breaks the limitation of analyzing the function and control ability from the structure. Comparing with the linear control model to predict motor neuron controllability, Yan et al. use network control principles, we emphasize the growth rate of the node itself and the influence of its neighbors on the node [18, 45] Importantly, this is a more efficient way to quickly target groups of neurons, even individual neurons or synapses that have core controlling power. In this view, our theoretical approach contributes to exploring the importance and the evolution mechanism of the individual neurons, and proves how to calculate the control level with the dynamics. These observations are not limited to nematode, but are also applicable to connectome model organism with complete data and clear background. However, the real interactions of nematode connection network are much more complicated than our dynamical model [46, 47]. We use this model for theoretical exploration, there may be some difference between our parameter setting and the real system. We need to refer to more biological experiments for further parameter setting and to use more complex dynamical equations or generative models to capture the interactions in our next work.

Data Availability Statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://doi.org/10.1016/j.cell.2012.12.013 and https://doi.org//10.1038/s41586-019-1352-7.

Author Contributions

DD and WX performed the analysis. WX validated the analysis and drafted the manuscript. DD and SS reviewed the manuscript. WX designed this study. All authors have read and approved the content of the manuscript.

Funding

This work was supported by the National Natural Science Foundation of China (projects no. 72071153, the Natural Science Foundation of Shaanxi Province (project n.2020JM-486), the China Postdoctoral Science Foundation (project n.2017M613336).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Dirven L, Petersen M, Petersen MA, Aaronson NK, Chie W-C, Conroy T, et al. Development and Psychometric Evaluation of an Item Bank for Computerized Adaptive Testing of the Eortc Insomnia Dimension in Cancer Patients (Eortc Cat-Sl). Appl Res Qual Life (2019) 16:827–44. doi:10.1007/s11482-019-09799-w

CrossRef Full Text | Google Scholar

2. Bargmann CI. Genetic and Cellular Analysis of Behavior in C. Elegans. Annu Rev Neurosci (1993) 16:47–71. doi:10.1146/annurev.ne.16.030193.000403

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Cook SJ, Jarrell TA, Brittin CA, Wang Y, Bloniarz AE, Yakovlev MA, et al. Whole-animal Connectomes of Both Caenorhabditis elegans Sexes. Nature (2019) 571:63–71. doi:10.1038/s41586-019-1352-7

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Sarma GP, Lee CW, Portegys T, Ghayoomie V, Jacobs T, Alicea B, et al. Openworm: Overview and Recent Advances in Integrative Biological Simulation of Caenorhabditis elegans. Philos Trans R Soc Lond B Biol Sci (2018) 373(1758):20170382. doi:10.1098/rstb.2017.0382

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Witvliet D, Mulcahy B, Mitchell JK, Meirovitch Y, Berger DR, Wu Y, et al. Connectomes Across Development Reveal Principles of Brain Maturation. Nature (2021) 596:257–61. doi:10.1038/s41586-021-03778-8

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Morita S, Oshio K-i., Osana Y, Funabashi Y, Oka K, Kawamura K. Geometrical Structure of the Neuronal Network of Caenorhabditis elegans. Physica A: Stat Mech its Appl (2001) 298:553–61. doi:10.1016/s0378-4371(01)00266-7

CrossRef Full Text | Google Scholar

7. Alicea B. Raising the Connectome: The Emergence of Neuronal Activity and Behavior in Caenorhabditis elegans. Front Cel Neurosci (2020) 14(524791):524791. doi:10.3389/fncel.2020.524791

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Duan D, Lv C, Si S, Wang Z, Li D, Gao J, et al. Universal Behavior of Cascading Failures in Interdependent Networks. Proc Natl Acad Sci USA (2019) 116:22452–7. doi:10.1073/pnas.1904421116

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Chen BL, Hall DH, Chklovskii DB. Wiring Optimization Can Relate Neuronal Structure and Function. Proc Natl Acad Sci (2006) 103(12):4723–8. doi:10.1073/pnas.0506806103

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Lav R, Varshney LB, Chen EP, Hall DH, Chklovskii DB. Structural Properties of the Caenorhabditis elegans Neuronal Network. PLoS Comput Biol (2011) 7(2):e1001066. doi:10.1371/journal.pcbi.1001066

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chalfie M, Sulston J, White J, Southgate E, Thomson J, Brenner S. The Neural Circuit for Touch Sensitivity in Caenorhabditis elegans. J Neurosci (1985) 5(4):956–64. doi:10.1523/jneurosci.05-04-00956.1985

CrossRef Full Text | Google Scholar

12. Costa AC, Ahamed T, Stephens GJ. Adaptive, Locally Linear Models of Complex Dynamics. Proc Natl Acad Sci U S A (2019) 116(5):1501–10. doi:10.1073/pnas.1813476116

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Baltzley MJ, Gaudry Q, Kristan WB. Species-specific Behavioral Patterns Correlate with Differences in Synaptic Connections Between Homologous Mechanosensory Neurons. J Comp Physiol A (2010) 196(3):181–97. doi:10.1007/s00359-010-0503-y

CrossRef Full Text | Google Scholar

14. Liu Y, Sanhedrai H, Dong GG, Shekhtman LM, Wang F, Buldyrev SV, et al. Efficient Network Immunization Under Limited Knowledge. Natl Sci Rev (2020) doi:10.1093/nsr/nwaa229

CrossRef Full Text | Google Scholar

15. Dong G, Wang F, Shekhtman L, Danziger M, Fan J, Du R, et al. Optimal Resilience of Modular Interacting Networks. Proc Natl Acad Sci 118(22):e1922831118. doi:10.1073/pnas.1922831118

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Morone F, Del Ferraro G, Makse HA. The K-Core as a Predictor of Structural Collapse in Mutualistic Ecosystems. Nat Phys (2018) 15:95–102. doi:10.1038/s41567-018-0304-8

CrossRef Full Text | Google Scholar

17. Morone F, Makse HA. Symmetry Group Factorization Reveals the Structure-Function Relation in the Neural Connectome of Caenorhabditis elegans. Nat Commun (2019) 10(1):4961. doi:10.1038/s41467-019-12675-8

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Yan G, Vértes PE, Towlson EK, Chew YL, Walker DS, Schafer WR, et al. Network Control Principles Predict Neuron Function in the Caenorhabditis elegans Connectome. Nature (2017) 550(7677):519–23. doi:10.1038/nature24056

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Blaxter ML, De Ley P, Garey JR, Liu LX, Scheldeman P, Vierstraete A, et al. A Molecular Evolutionary Framework for the Phylum Nematoda. Nature (1998) 392:71–5. doi:10.1038/32160

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Duan D-L, Tao C, Wu X-X, Wu C, Shu-bin S, Gen-qing B. Identification of Unstable Individuals in Dynamic Networks. Chin Phys B (2021) 30(9):090501. doi:10.1088/1674-1056/abe92f

CrossRef Full Text | Google Scholar

21. Gao J, Barzel B, Al B. Universal Resilience Patterns in Complex Networks. Nature (2016) 530(7590):307–12. doi:10.1038/nature16948

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Bumbarger DJ, Riebesell M, Rödelsperger C, Sommer RJ, Sommer RJ. System-wide Rewiring Underlies Behavioral Differences in Predatory and Bacterial-Feeding Nematodes. Cell (2013) 152(1):109–19. doi:10.1016/j.cell.2012.12.013

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Franks CJ, Holden-Dye L, Bull K, Luedtke S, Walker RJ. Anatomy, Physiology and Pharmacology of Caenorhabditis elegans Pharynx: A Model to Define Gene Function in a Simple Neural System. Invert Neurosci (2006) 6(3):105–22. doi:10.1007/s10158-006-0023-1

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Mörck C, Axäng C, Pilon M. A Genetic Analysis of Axon Guidance in the C Elegans Pharynx. Dev Biol (1200) 260:158–75. doi:10.1016/s0012-1606(03)00238-0

CrossRef Full Text | Google Scholar

25. Pilon M. Developmental Genetics of the Caenorhabditis Eleganspharynx. Wires Dev Biol (2014) 3:263–80. doi:10.1002/wdev.139

CrossRef Full Text | Google Scholar

26. Gruninger TR, Gualberto DG, LeBoeuf B, Garcia L. Integration of Male Mating and Feeding Behaviors in Caenorhabditis elegans. J Neurosci (2006) 26:169–79. doi:10.1523/jneurosci.3364-05.2006

CrossRef Full Text | Google Scholar

27. Avery L, You YJ. C. elegans Feeding. WormBook (2012) 1–23:1–23. doi:10.1895/wormbook.1.150.1

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Avery L, Horvitzt HR. Pharyngeal Pumping Continues After Laser Killing of the Pharyngeal Nervous System of C. elegans. Neuron (1989) 3:473–85. doi:10.1016/0896-6273(89)90206-7

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Pervez , Rashid . Attraction of Allodorylaimus americanus (Nematoda: Dorylaimida) towards different prey nematodes and factors influencing this attraction. Archives of Phytopathology and Plant Protection 42:344–351. doi:10.1080/03235400601070421 (2009).

CrossRef Full Text | Google Scholar

30. Lichtman JW, Livet J, Sanes JR. A Technicolour Approach to the Connectome. Nat Rev Neurosci (2008) 9(6):417–22. doi:10.1038/nrn2391

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Haspel G, O'Donovan MJ, Hart AC. Motoneurons Dedicated to Either Forward or Backward Locomotion in the Nematode Caenorhabditis elegans. J Neurosci (2010) 30(33):11151–6. doi:10.1523/jneurosci.2244-10.2010

CrossRef Full Text | Google Scholar

32. Albertson D, Thomson JN. The Pharynx of Caenorhabditis elegans. Phil Trans R Soc Lond B (1976) 275:299–325. doi:10.1098/rstb.1976.0085

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Sherman D, Harel D. Deciphering the Underlying Mechanisms of the Pharyngeal Motions in Caenorhabditis elegans. Ithaca, NewYork: Neurons and Cognition (2019).

Google Scholar

34. Mapes CJ. Structure and Function in the Nematode Pharynx. Parasitology (1965) 55:583–94. doi:10.1017/s0031182000069286

CrossRef Full Text | Google Scholar

35. Mayer WE, Herrmann M, Sommer RJ. Phylogeny of the Nematode Genus Pristionchus and Implications for Biodiversity, Biogeography and the Evolution of Hermaphroditism. BMC Evol Biol (2007) 7:104. doi:10.1186/1471-2148-7-104

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Dieterich C, Clifton SW, Schuster LN, Chinwalla A, Delehaunty K, Dinkelacker I, et al. The Pristionchus Pacificus Genome Provides a Unique Perspective on Nematode Lifestyle and Parasitism. Nat Genet (2008) 40:1193–8. doi:10.1038/ng.227

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Stern S, Kirst C, Bargmann CI. Neuromodulatory Control of Long-Term Behavioral Patterns and Individuality across Development. Cell (2017) 171:1649–62. doi:10.1016/j.cell.2017.10.041

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Avery L, Horvitz HR. A Cell that Dies During Wild-type C. elegans Development Can Function as a Neuron in a Ced-3 Mutant. Cell (1987) 51(6):1071–8. doi:10.1016/0092-8674(87)90593-9

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Avery L, Horvitzt HR. Pharyngeal Pumping Continues After Laser Killing of the Pharyngeal Nervous System of C. elegans. Neuron (1989) 3(4):473–85. doi:10.1016/0896-6273(89)90206-7

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Wicks S, Rankin C. Integration of Mechanosensory Stimuli in Caenorhabditis elegans. J Neurosci (1995) 15(3):2434–44. doi:10.1523/jneurosci.15-03-02434.1995

CrossRef Full Text | Google Scholar

41. Trojanowski NF, Padovan-Merhar O, Raizen DM, Fang-Yen C. Neural and Genetic Degeneracy Underlies Caenorhabditis elegans Feeding Behavior. J Neurophysiol (2014) 112(4):951–61. doi:10.1152/jn.00150.2014

CrossRef Full Text | Google Scholar

42. Rudiger B, Colomb J, Pankratz B, Schröck A, Stocker RF Genetic Dissection of Neural Circuit Anatomy Underlying Feeding Behavior Indrosophila: Distinct Classes Ofhugin-Expressing Neurons. J Comp Neurol (2007) 502(5):848–56. doi:10.1002/cne.21342

CrossRef Full Text | Google Scholar

43. Whalen AJ, Brennan SN, Sauer TD, Schiff SJ. Observability and Controllability of Nonlinear Networks: The Role of Symmetry. Phys Rev X (2015) 5:011005. doi:10.1103/PhysRevX.5.011005

PubMed Abstract | CrossRef Full Text | Google Scholar

44. Tsalik EL, Hobert O. Functional Mapping of Neurons that Control Locomotory Behavior in Caenorhabditis Elegans. J Neurobiol (2003) 56(2):178–97. doi:10.1002/neu.10245

CrossRef Full Text | Google Scholar

45. Gao J, Liu YY, D'Souza RM, Barabási AL. Target Control of Complex Networks. Nat Commun (2014) 5:5415. doi:10.1038/ncomms6415

PubMed Abstract | CrossRef Full Text | Google Scholar

46. Stephens GJ, Johnson-Kerner B, Bialek W, Ryu WS. Dimensionality and Dynamics in the Behavior of C. elegans. Plos Comput Biol (2008) 4:e1000028. doi:10.1371/journal.pcbi.1000028

PubMed Abstract | CrossRef Full Text | Google Scholar

47. Zhen M, Samuel AD, Samuel T. C. elegans Locomotion: Small Circuits, Complex Functions. Curr Opin Neurobiol (2015) 33:117–26. doi:10.1016/j.conb.2015.03.009

PubMed Abstract | CrossRef Full Text | Google Scholar