Hepatitis B virus (HBV) is a serious threat to human health as it can cause the chronic hepatitis B, and eventually liver cancer. It also has become one of the major threats to public health in the world. In this paper, considering the rationality of using standard incidence in Caputo-Fabrizio fractional order HBV infection model, we propose a model with standard incidence. The analysis of local stability about the equilibrium and the simulation of global stability are given. We also use the real data to estimate the parameters of this model. The simulation results can fit the data well. Moreover, we propose an optimal control model and give the optimal therapy strategy, which show that optimal therapy can reduce the cost and side effects while ensuring the therapeutic effect.

1 Introduction

Hepatitis B virus (HBV) is a partially double-stranded DNA virus and can cause liver diseases such as hepatitis, cirrhosis and liver cancer, and eventually death. When the virus invades the human body, it enters the liver cells by binding to the receptor. Then, HBV-DNA is transported to the nucleus of liver cells and converted into cccDNA under the action of host enzymes. Since cccDNA is not easily degraded, chronic hepatitis B is difficult to be cured [1, 2]. Despite the highly effective recombinant vaccine has been available from 1981 [3], and more and more population are actively vaccinated, the number of the HBV infected is still increasing. More than two billion people have been infected worldwide, and 350 million people are suffering from chronic hepatitis B [4]. HBV has become a major threat to global public health.

Mathematical models can be used to simulate and predict the process of biodynamics. Researchers analyzed the dynamics of the model from different aspects. An immune model was given by Su et al. [5] and the existence, uniqueness and global stability of the model were also analyzed. Anwarud [6] proposed a HBV model with the effect of vaccine and treatment and gave the optimal control strategy. Li et al. [7] analyzed the network vulnerability based on Markov criticality and applied it in lots of biosystem networks. Kalyan [8] considered the intracellular delay in the production of the infected hepatocytes and incorporated a time lag in his model. The spatial diffusion was also used by Khalid [9]. However, most of the papers are limited in the classical integer order.

Fractional calculus is an arbitrary order generalization of classical integral calculus which has the characters of memory, history and nonlocality. There are many definitions of fractional calculus. Among them, Caputo order is one of the widely used types. Kai Diethel [10] summarized the application of Caputo in various field and the numerical methods of fractional order. Devendra [11] derived analysis and numerical solutions of nonlinear fractional problems in nanofluid dynamics, nanoscale heat conduction and carbon nanotube current. Ivan [12] gave a fractional order Ebola epidemic model to study its outbreak. Min Ma [13] considered the diffusion issue in fractional order models and gave the numerical method. Hatıra [14] proposed HIV model with Caputo and constant proportional Caputo operators. Fatmawati [15] gave the Caputo order model of HIV transmission with awareness effect. To reduce the transmission of HIV, Caputo order model for the transmission of HIV epidemic with optimal control was proposed by Parvaiz [16]. The theory of Caputo fractional order in dynamic system has also been derived. The local stability was similar to that in integer order and derived by E. Ahmed [17]. The global stability of fractional order was also given by Boukhouima [18]. And other theorems [19] of the Caputo order systems have been derived and widely used in papers. However, the singular kernel of the Caputo fractional derivative causes a lot of difficult problems both in integral calculation and discretization.

To avoid the shortage of the singular kernel, some researchers have proposed new definitions of fractional order. These definitions include the Caputo-Fabrizio derivative defined by an exponential decay law [20] and Atangana–Baleanu derivative defined by a Mittag–Leffler law [21]. Although Caputo-Fabrizio order does not conform to the traditional fractional calculus [22], it is also used in lots of biodynamic system. Esmehan [23] gave a cancer-immune system and discussed the model by adding IL-12 cytokine and anti-PD-L1 inhibitor. Elvin [24] proposed and analyzed a Caputo–Fabrizio fractional model for the HIV/AIDS epidemic which includes an antiretroviral treatment compartment. Human liver model involving Caputo–Fabrizio derivative was also proposed by Dumitru [25]. Hakimeh [26] proposed a Caputo–Fabrizio model for hearing loss due to Mumps virus with optimal control. The basic theorems of this order have also been proved, including the existence and uniqueness of the solution and the local stability of the equilibrium point [27].

Many papers study HBV with mathematic models. The earliest study can be traced back to the three-state model proposed by Novak et al. [28] and the analysis of the model and basic reproduction number were given. With the development of HBV, researchers have found that the bilinear incidence can not describe the real infection within body well. So Min et al. [29] modified βxv to $\frac{\beta xv}{x+y}$ which can be seen as the standard incidence. Similarly, Y. J. et al. [30] gave a model by using the standard incidence rate and the logistic function. They also gave the optimal therapy in its corresponding control model. The factional order is also used in HBV models. Salman proposed a within-host fractional order HBV model with Caputo order [31]. Compared with models above, this paper considered not only Caputo fractional order, but also the cure of infected hepatocytes. At the same time, Caputo-Fabrizio order can be also used in HBV models. Saeed Ahmad [32] gave a Caputo-Fabrizio order model describing the dynamics of hepatitis B infectious disease and used the Banach fixed point theory approach. Fei Gao [33] proposed the Caputo-Fabrizio with delay, analyzed and simulated the stability of its equilibrium points. However, the infection incidence is bilinear and the real data of HBV infection is not used in his model.

So far, almost no paper considered the Caputo-Fabrizio order model with standard incidence which is more reasonable. And Caputo-Fabrizio order also has the character of memory and can effectively avoid the singularity of Caputo order. Besides, there are seldom papers considered parameter estimation based on the real data and optimal control in Caputo Fabrizio order HBV infection models. Based on the above discussion, we first propose a Caputo-Fabrizio fractional order model with standard incidence. Then, we use the clinical data to estimate the parameters of our model. Finally, we propose an optimal control model based on the treatment for chronic hepatitis B and give the optimal therapy strategy. Using the actual data to estimate the parameters of the HBV model can make our model have medical significance. And the optimal treatment strategy can reduce the cost and side effects while ensuring the therapeutic effect.

2 Model Formulation

In general, the process of hepatitis B infection [34] mainly includes susceptible hepatocytes, infected hepatocytes, and hepatitis B virus. Uninfected hepatocytes are produced at a certain rate. HBV particles can invade hepatocytes through interaction with the receptors on the liver surface. They reproduce new viruses by various functions and release them into the bloodstream with the lysis of infected cells. The hepatitis B virus genes can naturally be lost which lead to a certain proportion of the infected cells transforming into uninfected hepatocytes. At the same time, liver cells and viruses will gradually die out. The simplified process is shown in Figure 1. And based on this process, we first give the Caputo-Fabrizio model based on the standard incidence as follows:

$\left\{\begin{array}{cc}\hfill {}_0{}^{CF}D_t^{\alpha }x& ={\lambda }^{\alpha }-d^{\alpha }x-{\beta }^{\alpha }\frac{xv}{x+y}+{\delta }^{\alpha }y\hfill \\ \hfill {}_0{}^{CF}D_t^{\alpha }y& ={\beta }^{\alpha }\frac{xv}{x+y}-a^{\alpha }y-{\delta }^{\alpha }y\hfill \\ \hfill {}_0{}^{CF}D_t^{\alpha }v& =k^{\alpha }y-{\mu }^{\alpha }v\hfill \end{array}\right.(1)$

Here $x\left(t\right)$, $y\left(t\right)$, $v\left(t\right)$ are the healthy hepatocytes, infected hepatocytes and hepatitis B virus respectively. α is the fractional order. Uninfected cells produce at a constant rate of λ^α. Healthy and infected hepatocyte die at the rate of d^αx and a^αy respectively. The infected rate is ${\beta }^{\alpha }\frac{xv}{x+y}$. Infected hepatocytes can be cured by noncytolytic processes at the rate of δ per cell. Free virus is produced from infected cells at the rate of k^αy and attenuated at the rate of μ^αv. The initial values are given as $x\left(t_0\right)=x_0,y\left(t_0\right)=y_0,v\left(t_0\right)=v_0$.

FIGURE 1

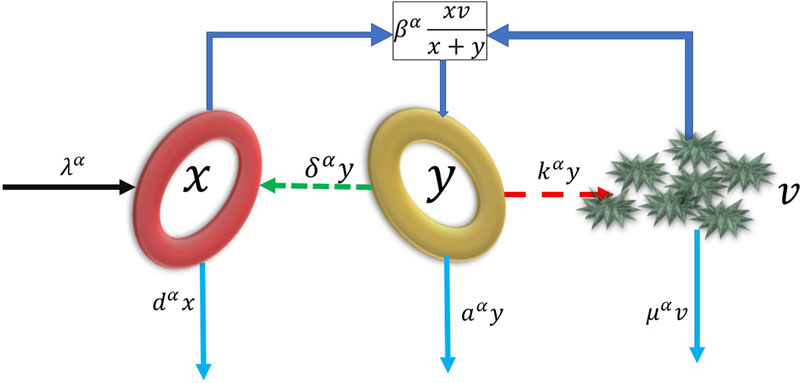
FIGURE 1. Diagram for basic virus dynamics model. x, y, v represent the healthy hepatocytes, infected hepatocytes and hepatitis B virus respectively. The healthy hepatocytes are produced at the rate of λ^α and die at d^α. At the same time, it can be invaded by hepatitis B virus and become infected hepatocytes at the rate of ${\beta }^{\alpha }\frac{xv}{x+y}$. Infected hepatocytes die at the rate a^α, lysis and release hepatitis B virus at the rate of k^αy. They also have the ability of self-healing and can transform into uninfected hepatocytes at the rate of δ^αy. Hepatitis B virus is degraded at the rate of μ^α.

Assume that λ = λ^α, d = d^α, β = β^α, δ = δ^α, a = a^α, k = k^α, μ = μ^α, model 1) will be transformed to model (2). And the meaning of parameters in our framework is given in Table 1.

$\left\{\begin{array}{cc}\hfill {}_0{}^{CF}D_t^{\alpha }x& =\lambda -dx-\beta \frac{xv}{x+y}+\delta y\hfill \\ \hfill {}_0{}^{CF}D_t^{\alpha }y& =\beta \frac{xv}{x+y}-ay-\delta y\hfill \\ \hfill {}_0{}^{CF}D_t^{\alpha }v& =ky-\mu v\hfill \end{array}\right.(2)$

Since our model is a fractional order model, CF represents the Caputo-Fabrizio order, and here we will give some basic definition of Caputo-Fabrizio fractional calculus in Definition 1 and 2.

TABLE 1

TABLE 1. The meaning of parameters in our framework.

Let $H^1\left(a,b\right)=\left\{f|f\in L^2\left(a,b\right)\right\}$ and $f^{\prime }\in L^2\left(a,b\right)$, where $L^2\left(a,b\right)$ is the space of square integrable functions on the interval $\left(a,b\right)$.

Definition 1 ([21]) The definition of Caputo-Fabrizio order differential was later modified by Losada and Nieto as

${}_a{}^{CF}D_t^{\alpha }f(t)=\frac{2\left(1-\alpha \right)}{\left(2-\alpha \right)M\left(\alpha \right)}{\int }_a^t{f}^{\prime }(x)\exp \left[-\alpha \frac{t-x}{1-\alpha }\right]dx.(3)$

Definition 2. ([21]) Let$\alpha \in \left[\mathrm{0,1}\right]$, then fractional integral ofαfor functionf(x) can be expressed as

${}_a{}^{CF}I_t^{\alpha }f\left(t\right)=\frac{2\left(1-\alpha \right)}{\left(2-\alpha \right)M\left(\alpha \right)}f\left(t\right)+\frac{2\alpha }{\left(2-\alpha \right)M\left(\alpha \right)}{\int }_a^{t}f\left(x\right)dx.(4)$

Remark 1. In Definition 1, the definition of Eq. 4 is the mean of $f\left(t\right)$and${\int }_a^{t}f\left(x\right)dx$. Therefore$\frac{2\left(1-\alpha \right)}{\left(2-\alpha \right)M\left(\alpha \right)}+\frac{2\alpha }{\left(2-\alpha \right)M\left(\alpha \right)}=1,$which implies$M\left(\alpha \right)=\frac{2}{2-\alpha },\alpha \in \left[\mathrm{0,1}\right]$. The rest of this paper is organized as follows. Section 3 gives the analysis and simulation of the local stability of equilibrium points. The parameter estimation are given in Section 4, and the last two sections give the theorems and simulation of optimal control model and our conclusion respectively.

3 Stability Analysis

In biology models, the stable analysis of the system can help us to understand the process of the biology phenomenon. The following two basic lemmas [35] can be used for stability analysis. Lemma 1 give the characteristic equation form of Caputo-Fabrizio order linear system. Lemma two give the criterion of local stability.

Lemma 1. Let$F\left(t\right)\in R^n$andM ∈ R^n×n, then the characteristic equation related to the linear system${}_{t_0}{}^{CF}D_t^{\alpha }F\left(t\right)=MF\left(t\right)$supplemented with the orderα ∈ (0, 1) is given by$\det \left[s{I}_{n\times n}-\left(1-\alpha \right)M-\alpha M\right]=0$.

Lemma 2. Suppose that the matrix$s{I}_{n\times n}-\left(1-\alpha \right)M-\alpha M$is invertible. Then, if and only if all roots of the characteristic equation have negative real parts, the fractional linear Caputo-Fabrizio system is asymptotically stable at the free equilibrium point. There are two equilibria in model (2): The disease-free equilibrium $E_0=\left(\frac{\lambda }{d},\mathrm{0,0}\right)$ and the endemic-free equilibrium $E_1=\left(\frac{\lambda }{R_{0}a-a+d},\frac{(R_0-1)\lambda }{R_{0}a-a+d},\frac{k}{\mu }\frac{(R_0-1)\lambda }{R_{0}a-a+d}\right)$. And the basic reproduction number [36] R₀ of system 2) is $\frac{\beta k}{\mu (a+\delta )}$. Here we will give the analysis of the two equilibria.

Theorem 1. The disease-free equilibriumE₀is locally asymptotically stable ifR₀ < 1. IfR₀ > 1, it is unstable.Proof. The Jacobian matrix at E₀ is given:

$J_1=\left[\begin{array}{ccc}\hfill -d\hfill & \hfill \delta \hfill & \hfill -\beta \hfill \\ \hfill 0\hfill & \hfill -a-\delta \hfill & \hfill \beta \hfill \\ \hfill o\hfill & \hfill k\hfill & \hfill -\mu \hfill \end{array}\right](5)$

From Lemma 1, the characteristic equation of system (2) is $s\left(I-\left(1-\alpha \right)J_1\right)-\alpha J_1=0$. We can denote three roots as

$s_1=\frac{\alpha }{-1+\alpha }$

$s_2=\frac{2\alpha \left(1-\alpha \right)\mu \left(a+\delta \right)\left(R_0-1\right)-c_1+\sqrt{{c_1}^2+4\mu \left(a+\delta \right)\left(R_0-1\right)}}{2\left(1+\left(1-\alpha \right)\left(a+\delta +\mu \right)+\left(1-R_0\right)\left(a+\delta \right){\left(1-\alpha \right)}^2\right.}$

$s_3=\frac{2\alpha \left(1-\alpha \right)\mu \left(a+\delta \right)\left(R_0-1\right)-c_1-\sqrt{{c_1}^2+4\mu \left(a+\delta \right)\left(R_0-1\right)}}{2\left(1+\left(1-\alpha \right)\left(a+\delta +\mu \right)+\left(1-R_0\right)\left(a+\delta \right){\left(1-\alpha \right)}^2\right.}(6)$

Here $c_1=\left(a+\delta +\mu \right)\alpha$. It is obvious to see that s₁ < 0 as 0 < α < 1. If R₀ < 1, s₂ < 0, s₃ < 0. Otherwise s₂ > 0 and s₃ > 0. From Lemma 2, it can be proved that when R₀ < 1, the disease free equilibrium E₀ is locally asymptotically stable. When R₀ > 1, E₀ is unstable. The local stability of disease-free equilibrium indicates that HBV infection will not persist. Basic reproduction number R₀ is an important index to measure whether the disease will die out. When R₀ < 1, the disease will die out, and when R₀ > 1, we will have the endemic equilibrium E₁. We give the analysis of the its stability in Theorem 2.

Theorem 2.IfR₀ > 1, the endemic equilibriumE₁is asymptotically stable.

Proof. The Jacobian matrix at E₁ is given as

$J_2=\left[\begin{array}{ccc}\hfill -d-\beta \frac{v_1{y}_1}{{\left(x_1+y_1\right)}^2}\hfill & \hfill \delta +\beta \frac{x_1{v}_1}{{\left(x_1+y_1\right)}^2}\hfill & \hfill -\beta \frac{x_1}{x_1+y_1}\hfill \\ \hfill \beta \frac{v_1{y}_1}{{\left(x_1+y_1\right)}^2}\hfill & \hfill -\beta \frac{x_1{v}_1}{{\left(x_1+y_1\right)}^2}-a-\delta \hfill & \hfill \beta \frac{x_1}{x_1+y_1}\hfill \\ \hfill o\hfill & \hfill k\hfill & \hfill -\mu \hfill \end{array}\right](7)$

From Lemma 1, the characteristic equation of system (2) is (I − (1 − α)J₂) −αJ₂ = 0 which can be rewritten as a₁s³ + a₂s² + a₃s¹ + a₄ = 0. Let $l_1=\beta \frac{v_1{y}_1}{{\left(x_1+y_1\right)}^2},l_2=\beta \frac{x_1{v}_1}{{\left(x_1+y_1\right)}^2},l_3=\beta \frac{x_1}{x_1+y_1}$, we will get that

$\begin{array}{cc}\hfill a_4& =\mu {\alpha }^3\left(a{l}_1+d{l}_2\right)\hfill \\ \hfill a_3& ={\alpha }^2\left(ad+d\delta +a{l}_1+d{l}_2+d\mu +l_1\mu +l_2\mu \right)+{\alpha }^2\left(1-\alpha \right)\left(3a{l}_1\mu +3d{l}_2\mu \right)\hfill \\ \hfill a_2& =\alpha \left(a+d+\delta +l_1+l_2+\mu \right)+{\left(1-\alpha \right)}^2\alpha \left(3a{l}_1\mu +3d{l}_2\mu \right)\hfill \\ \hfill & +2\left(1-\alpha \right)\left(ad+d\delta +a{l}_1+d{l}_2+d\mu +l_1\mu +l_2\mu \right)\hfill \\ \hfill a_1& =1+\left(1-\alpha \right)\left(a+d+\delta +l_1+l_2+\mu \right)+{\left(1-\alpha \right)}^3\left(3a{l}_1\mu +3d{l}_2\mu \right)\hfill \\ \hfill & +{\left(1-\alpha \right)}^2\left(d\left(a+\mu +\delta \right)+a{l}_1+d{l}_2+l_1\mu +l_2\mu \right)\hfill \end{array}(8)$

As 0 < α < 1, thus a₁, a₂, a₃, a₄ > 0. Set $d_1=\frac{a_2}{a_1},d_2=\frac{a_3}{a_1},d_3=\frac{a_4}{a_1}$, q = ad + dδ + al₁ + dl₂ + dμ + l₁μ + l₂μ, then

$\begin{array}{cc}\hfill a_2{a}_3-a_1{a}_4& =q\left(a+d+\delta +l_1+l_2\right)+\mu (ad+d\delta +d\mu +l_1\mu +l_2\mu )\hfill \\ \hfill & +{\left(1-\alpha \right)}^2\left({\alpha }^{2}2q\left(3a{l}_1\mu +4d{l}_2\mu \right)+{\alpha }^{3}2q\left(a{l}_1+d{l}_2\right)\right.\hfill \\ \hfill & +{\left(1-\alpha \right)}^3{\alpha }^3{\mu }^2\left(a{l}_1+d{l}_2\right)\left(8a{l}_1+11d{l}_2\right)\hfill \end{array}(9)$

As 0 < α < 1, a₂a₃ − a₁a₄ > 0 and $d_1{d}_2-d_3=\frac{a_2{a}_3-a_1{a}_4}{a_1^2}>0$. Thus we can prove the stability of E₁. The local asymptotic stability of the endemic equilibrium indicates the possible physical state of the patients without drug intervention. When R₀ > 1, the disease will always exist.

4 Simulation and Parameter Estimation

First we use the predictor-corrector Adams-Bashforth-Moulton (ABM) technique of the Caputo-Fabrizio equation to carry out the simulation. we will give the simulation results of equilibria E₀ and E₁. And the initial values are given in Table. 2.

TABLE 2

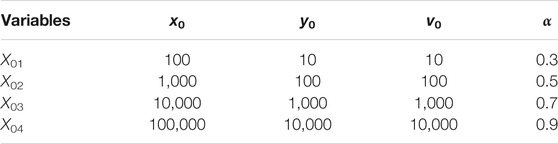
TABLE 2. The initial values of the simulation of E₀ and E₁. Here x₀, y₀, v₀ are the initial values of the healthy, infected hepatocyte and HBV.

For the disease-free equilibrium E₀, we select the parameters in Table. 3 which is satisfied the condition in Theorem 1. The simulation results are shown in Figure 2. As we have proved the local stability of the equilibrium in Section 3 and Figure 2 can also validates this proof. Here x can approach to 500 which is $\frac{\lambda }{d}$, y and v are 0. However, due to the lack of theory, it is difficult to prove the global stability. As we choose the initial values which is quite different from each other, the simulation results always tend to the same value. Therefore, we can think E₀ might be globally asymptotically stable. Similarly, we use the parameters in Table 4 to the simulate the endemic equilibrium E₁, the simulation results is shown in Figure 3 which shows the simulation results is consistent with Theorem 2.

TABLE 3

TABLE 3. The parameters using in the simulation of disease-free equilibrium E₀. The meaning of the parameters are in Table. 1. Here the basic reproduction number R₀ = 0.0075 < 1.

FIGURE 2

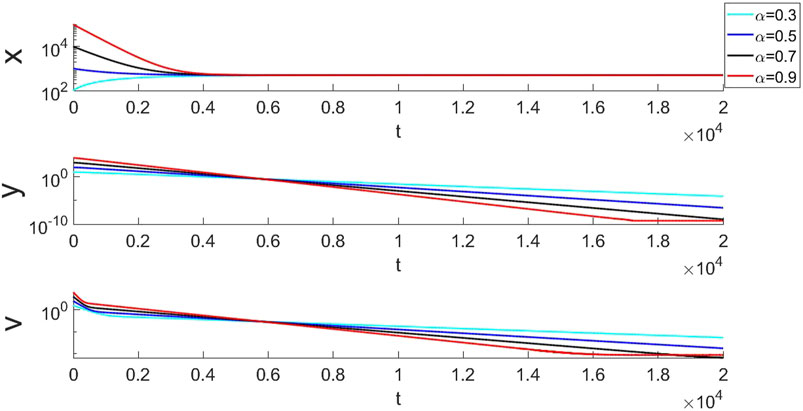
FIGURE 2. The simulation results of E₀ with four different set of initial values. Under different fractional orders and initial values, x can always approach to 500 with different initial values. y and v approaches to 0.

TABLE 4

TABLE 4. The parameters using in the simulation of endemic equilibrium E₁. The basic reproducion number R₀ = 2 > 1.

FIGURE 3

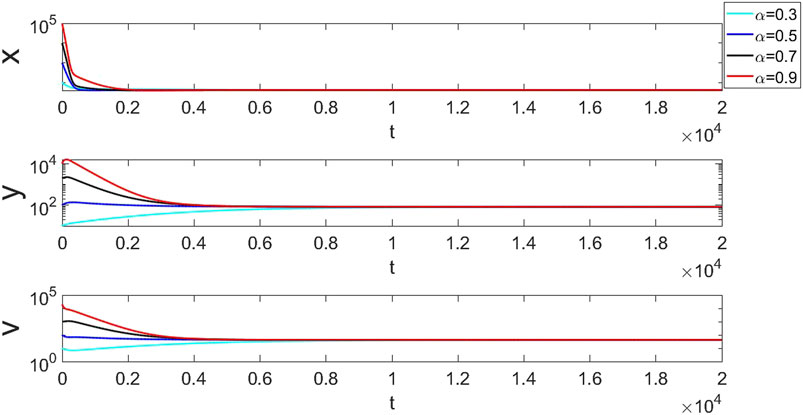
FIGURE 3. The simulation results of the endemic equilibrium E₁. In this simulation, x can always approach to 41.667. y, v are 81.3 and 41.667 respectively. This is consistent with our calculation of the value of the equilibrium point.

Then, we use the real data in Table 5 [37] to estimate the parameters of our model. The estimation range of parameters are $\left[1\times 10^5,1\times 10^7\right],\left(\mathrm{0,100}\right]$ for λ and k and $\left(\mathrm{0,1}\right)$ for others which are in line with the actual human physiological structure. Our estimated results are shown in Table 6 which make R₀ < 1 and simulation is shown in Figure 4. The fractional order is estimated as 0, 7,519, this shows that fractional order is applicable in the model. k is estimated as 0.0574 and μ is 0.799, this shows the drugs have been used and have obvious effect. The estimated results of a and d are 0.01 and 0.0038, which is similar to the data that is used in papers [30]. From Figure 4, we can see that our model can fit the data well. The hepatitis B virus can reduced rapidly in the first few weeks. And then it tends to a more gentle downward trend. However, the infected hepatocytes reduce exponentially, but decreasing rate is slower than that of hepatitis B virus. Due to the reduce of infected hepatocytes and hepatitis B virus, healthy hepatocytes are less likely infected, therefore they are in a state of first increasing and then regional stability. This phenomenon is consistent with Theorem 1.

TABLE 5

TABLE 5. The number of hepatitis B virus and the corresponding measurement time during the treatment of hepatitis B patients. The number of HBV here is shown in log format.

TABLE 6

TABLE 6. The estimated parameters by the least square method with using the read data of HBV virus and date. The parameters estimated here are in the normal range.

FIGURE 4

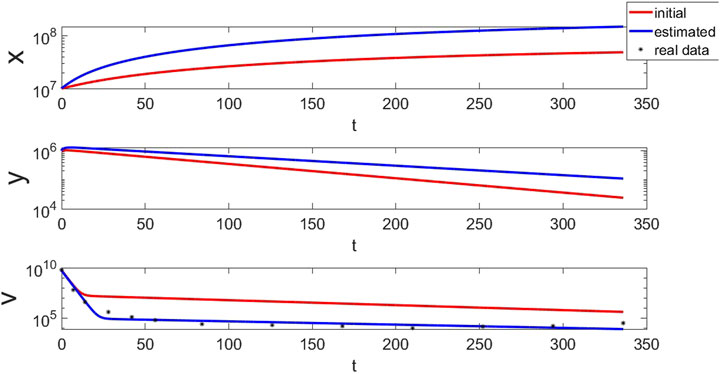
FIGURE 4. The simulation results using the estimated parameters in Table. 5. Although the simulation results of the initial parameters are quite different from the real data, it can fit real data well with the estimated parameters.

5 Optimal Control Problem

In paper [38], a combined treatment of HBV infection was designed with Entecavir (ETV) and Chinese herbal Tiaogan Jianpi Jiedu granules (TGJPJD). ETV can be used to reduce the replication of hepatitis B virus [39]. TGJPJD can kill hepatitis B virus by activating immunity. And based on the combined therapy of HBV, we propose our control model.

$\left\{\begin{array}{cc}\hfill {}_0{}^{CF}D_t^{\alpha }x& =\lambda -dx-\beta \frac{xv}{x+y}+\delta y\hfill \\ \hfill {}_0{}^{CF}D_t^{\alpha }y& =\beta \frac{xv}{x+y}-ay-\delta y\hfill \\ \hfill {}_0{}^{CF}D_t^{\alpha }v& =\left(1-u_1(t)\right)ky-\left(1+u_2(t)\right)\mu v\hfill \end{array}\right.(10)$

The parameters have the same meaning as given in Table. 1 u₁(t) (0 < u₁(t) < 1) and u₂(t) (0 < u₂(t) < 1) are the control variables and represent the drug effect of ETV and TGJPJD respectively. In order to achieve the therapeutic effect with lower the cost and side effects, we give the following objective function. Here a₂, a₃, b₂, b₃, c₁, c₂ represent the corresponding weight of each variable.

$J\left(u\right)=\frac{1}{2}\left(a_2{y}^2+a_3{v}^2\right)+\frac{1}{2}{\int }_0^{t_f}(b_2{y}^2+b_3{v}^2+c_1{u_1}^2+c_2{u_2}^2)dt.(11)$

The Hamilton function of $J\left(u\right)$ can be written as

$\begin{array}{cc}\hfill H& =p_1\left(\lambda -dx-\frac{\beta xv}{x+y}+\delta y\right)+p_2\left(\frac{\beta xv}{x+y}-ay-\delta y\right)\hfill \\ \hfill & +p_3\left((1-u_1)ky-(1+u_2)\mu v\right)+\left(b_2{y}^2+b_3{v}^2+c_1{u_1}^2+c_2{u_2}^2\right)\hfill \end{array}(12)$

Optimization process has many applications in dynamic systems [40–42]. In our paper, the optimal control problem is a process in which we find the best u(t) to minimize the performance index functional J(t). By using Pontryagin’s minimum principlex [43], we can transform the original problem into a constrained functional and find its theoretical optimization. And the optimal control therapy our model based the above theorem which can make J(u) minimum are given as follows:

$\left\{\begin{array}{c}\hfill u_1=\min \left[\max \left(\frac{ky{p}_3}{c_1},0\right),1\right]\\ \hfill u_2=\min \left[\max \left.\left(\frac{\mu p_{3}v}{c_2},0\right)\right],1\right]\end{array}\right.(13)$

Using the parameters as we estimated in Section 5, we give the simulation results in Figure 5 and Figure 6. From the simulation in Figure 5 and Figure 6, we can see that the dosage of the two drugs should be kept at the maximum at the initial stage, but the dosage of TGJPJD can be gradually reduced at about 138 days and will last 12 days. The dosage of ETV could be reduced at about 150 days, but the reduction of ETV would result in the rebound of virus, it is necessary to further strengthen the dosage of TGJPJD. So the dose of TGJPJD will increase at about 150 days and then reduce. Finally, it will be the lowest dose at about 174 days. With the enhancement of the immunity by TGJPJD, the two drugs can be maintained at a lower level to achieve better therapeutic effect.

FIGURE 5

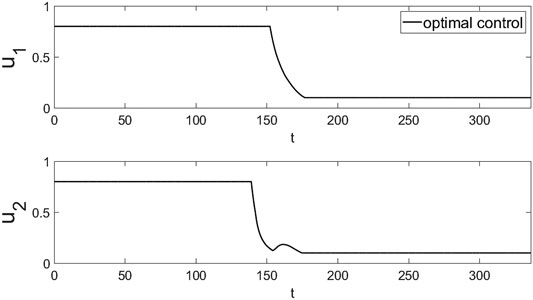
FIGURE 5. The optimal control results of the two drugs. Here u₁(t) is the drug dosage of ETV and u₂(t) is TGJPJD. And u₁ reduce at 152 days and will last until 177 days. u₂ will first reduce at about 138 days until 150 days. Then, due to the rebound of the virus, its dosage will increase in about 152 days and then decrease.

FIGURE 6

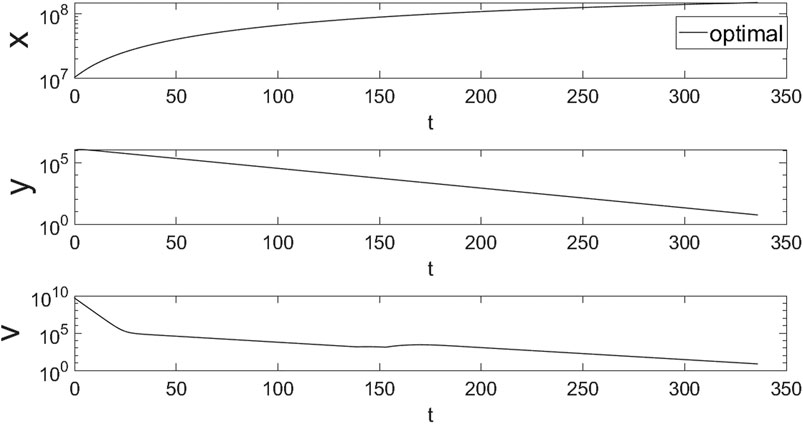
FIGURE 6. The simulation results of the hepatocytes and hepatitis B virus under the optimal control. Both y and v will finally reduce to a satisfying results. And v will have a rebound due to the decrease of ETV dose at about 150 days.

In Figure 6, the healthy hepatocytes will always keep increasing and then begin to stabilize. And the infected cells will reduce due to the drugs and the reduce of virus. hepatitis B virus will first reduce at about 150 days. And then due to the decrease of the ETV, the number of viruses showed a rebound trend. However, by adjusting the dosage of TGJPJD granule, the final number of virus can be reduced to less than 500, reaching the standard of cure.

In order to show the advantages of optimal control of therapeutic strategies, we also compare the objective function values of optimal as we give above with the maximizing drug dosage (u₁ = u₂ = 0.9) and minimizing drug dosage (u₁ = u₂ = 0.1), and show them in Table. 7. The results show that with the optimal therapy, the cost can be minimized, and the corresponding treatment effect can also be satisfying.

TABLE 7

TABLE 7. The comparasion of objective function J with different drug dosage. The maximum dosage is (u₁ = u₂ = 0.9) and the minimum dosage is (u₁ = u₂ = 0.1).

6 Conclusion

In this paper, a Caputo-Fabrizio fractional HBV model with standard incidence were proposed. The local stability of the equilibria were analyzed and global stability were simulated. At the same time, parameters were estimated based on the real data. With the estimated parameters, our model can simulate the data well. Finally, based on clinic combination therapy of HBV with ETV and TGJPJD, we proposed an optimal control model and gave the optimal therapy, which showed therapeutic effect can be achieved with lower drug dosage and side effects. However, cellular immunity and humoral immunity are not carefully considered in our model. In the optimal control model, the metabolism of drugs in the liver is not analyzed, and HBV replication in cells is not reflected. For our future work, we will apply the latest therapeutic regimens for chronic hepatitis B in our model and analyze it according to the corresponding clinical data. The metabolism of drugs should also be considered. Besides, we will consider the effect of cellular immunity and humoral immunity which is essential.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors conceived the study and performed the analyses. LY wrote the code. LY and YS wrote the article. All authors reviewed and revised the article.

Funding

This work is jointly supported by the Fundamental Research Funds for the Central Universities of China, grants 2020XD-A01-1, National Natural Science Foundation of China 71871233) and Beijing Natural Science Foundation (9182015), 2015 National traditional Medicine Clinical Research Base Business Construction Special Topics (JDZX2015299).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Le Mire MF, Miller DS, Foster WK, Burrell CJ, Jilbert AR. Covalently Closed Circular Dna Is the Predominant Form of Duck Hepatitis B Virus Dna that Persists Following Transient Infection. J Virol (2005) 79:12242–52. doi:10.1128/jvi.79.19.12242-12252.2005

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Hoofnagle JH, Doo E, Liang TJ, Fleischer R, Lok AS. Management of Hepatitis B: Summary of a Clinical Research Workshop. Hepatology (2007) 45:1056–75. doi:10.1002/hep.21627

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Huzair F, Sturdy S. Biotechnology and the Transformation of Vaccine Innovation: The Case of the Hepatitis B Vaccines 1968-2000. Stud Hist Philos Sci C Stud Hist Philos Biol Biomed Sci (2017) 64:11–21. doi:10.1016/j.shpsc.2017.05.004

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Who . Hepatitis B virues, WHO. Available at: https://www.who.int/news-room/fact-sheets/detail/hepatitis-b and accessed date: 27 July 2021.

Google Scholar

5. Su Y, Sun D, Zhao L. Global Analysis of a Humoral and Cellular Immunity Virus Dynamics Model with the Beddington-Deangelis Incidence Rate. Math Meth Appl Sci (2015) 38:2984–93. doi:10.1002/mma.3274

CrossRef Full Text | Google Scholar

6. Din A, Li Y, Liu Q. Viral Dynamics and Control of Hepatitis B Virus (Hbv) Using an Epidemic Model. Alexandria Eng J (2020) 59:667–79. doi:10.1016/j.aej.2020.01.034

CrossRef Full Text | Google Scholar

7. Li H-J, Wang L, Bu Z, Cao J, Shi Y. Measuring the Network Vulnerability Based on Markov Criticality. ACM Trans Knowl Discov Data 16 (2021). p. 1–24. doi:10.1145/3464390

CrossRef Full Text | Google Scholar

8. Manna K, Chakrabarty SP. Chronic Hepatitis B Infection and Hbv Dna-Containing Capsids: Modeling and Analysis. Commun Nonlinear Sci Numer Simulation (2015) 22:383–95. doi:10.1016/j.cnsns.2014.08.036

CrossRef Full Text | Google Scholar

9. Hattaf K, Yousfi N. A Generalized Hbv Model with Diffusion and Two Delays. Comput Math Appl (2015) 69:31–40. doi:10.1016/j.camwa.2014.11.010

CrossRef Full Text | Google Scholar

10. Diethelm K. The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type. Lecture Notes Math (2010) 2004:85–132. doi:10.1007/978-3-642-14574-2

Google Scholar

11. Kumar D, Singh J, Baleanu D. Numerical Computation of a Fractional Model of Differential-Difference Equation. J Comput Nonlinear Dyn (2016) 11. doi:10.1115/1.4033899

CrossRef Full Text | Google Scholar

12. Area I, Batarfi H, Losada J, Nieto JJ, Shammakh W, Torres Á. On a Fractional Order Ebola Epidemic Model. Adv Differ Equ, (2015) 2015 1–12. doi:10.1186/s13662-015-0613-5

CrossRef Full Text | Google Scholar

13. Ma M, Baleanu D, Gasimov YS, Yang XJ. New Results for Multidimensional Diffusion Equations in Fractal Dimensional Space. Rom J Phys (2016) 61:784–794.

Google Scholar

14. Günerhan H, Dutta H, Dokuyucu MA, Adel W. Analysis of a Fractional Hiv Model with Caputo and Constant Proportional Caputo Operators. Chaos, Solitons & Fractals (2020) 139:110053. doi:10.1016/j.chaos.2020.110053

CrossRef Full Text | Google Scholar

15. Fatmawati , Khan MA, Odinsyah HP. Fractional Model of Hiv Transmission with Awareness Effect. Chaos, Solitons & Fractals (2020) 138:109967. doi:10.1016/j.chaos.2020.109967

CrossRef Full Text | Google Scholar

16. Naik PA, Zu J, Owolabi KM. Global Dynamics of a Fractional Order Model for the Transmission of Hiv Epidemic with Optimal Control. Chaos, Solitons & Fractals (2020) 138:109826. doi:10.1016/j.chaos.2020.109826

CrossRef Full Text | Google Scholar

17. Ahmed E, El-Sayed AMA, El-Saka HAA. On Some Routh-Hurwitz Conditions for Fractional Order Differential Equations and Their Applications in Lorenz, Rössler, Chua and Chen Systems. Phys Lett A (2006) 358:1–4. doi:10.1016/j.physleta.2006.04.087

CrossRef Full Text | Google Scholar

18. Boukhouima A, Hattaf K, Yousfi N. Dynamics of a Fractional Order Hiv Infection Model with Specific Functional Response and Cure Rate. Int J Differential Equations (2017) 2017:1–8. doi:10.1155/2017/8372140

CrossRef Full Text | Google Scholar

19. Odibat ZM, Shawagfeh NT. Generalized Taylor's Formula. Appl Math Comput (2007) 186:286–93. doi:10.1016/j.amc.2006.07.102

CrossRef Full Text | Google Scholar

20. Caputo M, Fabrizio M. A New Definition of Fractional Derivative without Singular Kernel. Prog Fractional Differ Appl (2015) 1:487–497. doi:10.12785/pfda/010201

CrossRef Full Text | Google Scholar

21. Losada J, Nieto JJ. Properties of a New Fractional Derivative without Singular Kernel. Prog Fractional Differ Appl (2015) 1:87–92. doi:10.12785/pfda/010202 Available at https://www.who.int/news-room/fact-sheets/detail/hepatitis-b” [Accessed July 27, 2021]

CrossRef Full Text | Google Scholar

22. Ortigueira MD, Machado JT. A Critical Analysis of the Caputo–Fabrizio Operator. Commun Nonlinear Sci Numer Simulation 59 (2018). doi:10.1016/j.cnsns.2017.12.001

CrossRef Full Text | Google Scholar

23. Uçar E, Özdemir N. A Fractional Model of Cancer-Immune System with Caputo and Caputo–Fabrizio Derivatives. Eur Phys J Plus (2021) 136:1–17. doi:10.1140/epjp/s13360-020-00966-9

CrossRef Full Text | Google Scholar

24. Moore EJ, Sirisubtawee S, Koonprasert S. A Caputo–Fabrizio Fractional Differential Equation Model for Hiv/aids with Treatment Compartment. Adv Difference Equations (2019) 2019. doi:10.1186/s13662-019-2138-9

CrossRef Full Text | Google Scholar

25. Baleanu D, Jajarmi A, Mohammadi H, Rezapour S. A New Study on the Mathematical Modelling of Human Liver with Caputo–Fabrizio Fractional Derivative. Chaos, Solitons and Fractals (2020) 134:109705. doi:10.1016/j.chaos.2020.109705

CrossRef Full Text | Google Scholar

26. Mohammadi H, Kumar S, Rezapour S, Etemad S. A Theoretical Study of the Caputo–Fabrizio Fractional Modeling for Hearing Loss Due to Mumps Virus with Optimal Control. Chaos, Solitons and Fractals (2021) 144:110668. doi:10.1016/j.chaos.2021.110668

CrossRef Full Text | Google Scholar

27. Sene N. Stability Analysis of the Fractional Differential Equations with the Caputo-Fabrizio Fractional Derivative. J Fractional Calculus Appl (2020) 1:160–72.

Google Scholar

28. Nowak MA, Bangham CR. Population Dynamics of Immune Responses to Persistent Viruses. Science (1996) 272:74. doi:10.1126/science.272.5258.74

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Min L, Su Y, Kuang Y. Mathematical Analysis of a Basic Virus Infection Model with Application to Hbv Infection. Rocky Mountain J Math (2008) 38:1573–85. doi:10.1216/rmj-2008-38-5-1573

CrossRef Full Text | Google Scholar

30. Ji Y, Min L, Ye Y. Global Analysis of a Viral Infection Model with Application to Hbv Infection. J Biol Syst (2010) 18:325–37. doi:10.1142/S0218339010003299

CrossRef Full Text | Google Scholar

31. Salman S, Yousef A. On a Fractional-Order Model for Hbv Infection with Cure of Infected Cells. J Egypt Math Soc (2017) 25:445–451. doi:10.1016/j.joems.2017.06.003

CrossRef Full Text | Google Scholar

32. Ahmad S, ur Rahman M, Arfan M. On the Analysis of Semi-analytical Solutions of Hepatitis B Epidemic Model under the Caputo-Fabrizio Operator. Chaos, Solitons and Fractals (2021) 146:110892. doi:10.1016/j.chaos.2021.110892

CrossRef Full Text | Google Scholar

33. Gao F, Li X, Li W, Zhou X. Stability Analysis of a Fractional-Order Novel Hepatitis B Virus Model with Immune Delay Based on Caputo-Fabrizio Derivative. Chaos, Solitons and Fractals (2021) 142. doi:10.1016/j.chaos.2020.110436

CrossRef Full Text | Google Scholar

34. Iannacone M, Guidotti L. Immunobiology and Pathogenesis of Hepatitis B Virus Infection. Nat Rev Immunol (2021):1–14. doi:10.1038/s41577-021-00549-4

CrossRef Full Text | Google Scholar

35. Li H, Cheng J, Li HB, Zhong SM. Stability Analysis of a Fractional-Order Linear System Described by the Caputo-Fabrizio Derivative. Mathematics (2019) 7. doi:10.3390/math7020200

CrossRef Full Text | Google Scholar

36. Dreessche P, Watmough J. Reproduction Numbers and Sub-threshold Endemic Equilibria for Compartmental Models of Disease Transmission. Math Biosciences (2002) 180:29–48. doi:10.1016/S0025-5564(02)00108-6

CrossRef Full Text | Google Scholar

37. Young P, Woo J. The Adefovir-Lamivndine Combination Therapy Effectively Suppresses the Emergence of Geotypic Resistance to Adefovir in Lamivudine Resistant Hepatitis B. Hepatol Int (2009) 3:70–85. doi:10.1007/s12072-008-9120-z

Google Scholar

38. Li X, Zhou D, Chi X, Li Q, Wang L, Lu B, et al. Entecavir Combining Chinese Herbal Medicine for Hbeag-Positive Chronic Hepatitis B Patients: a Randomized, Controlled Trial. Hepatol Int (2020) 14:985–996. doi:10.1007/s12072-020-10097-z

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Park JY, Kim CW, Bae SH. Entecavir Plus Tenofovir Combination Therapy in Patients with Multidrug‐resistant Chronic Hepatitis B: Results of a Multicentre, Prospective Study [J]. Liver Int (2016) 36(8):1108–1115.

40. Li H, Bu Z, Wang Z, Cao J. Dynamical Clustering in Electronic Commerce Systems via Optimization and Leadership Expansion. IEEE Trans Ind Inform (2020) 16:5327–34. doi:10.1109/TII.2019.2960835

CrossRef Full Text | Google Scholar

41. Li H, Wang Z, Pei J, Cao J, Shi Y. Optimal Estimation of Low Rank Factors via Feature Level Data Fusion of Multiplex Signal Systems. IEEE Trans Knowledge Data Eng (2020) 1–24. doi:10.1109/TKDE.2020.3015914

CrossRef Full Text | Google Scholar

42. Brokate M. Pontryagin’s Principle for Control Problems in Age-dependent Population Dynamics. J Math Biol (1985) 23:75–101. doi:10.1007/bf00276559

PubMed Abstract | CrossRef Full Text | Google Scholar

43. Kirk DE. Optimal Control Theory: An Introduction. Posit Aware Monthly J Test Positive Aware Netw (2004) 23:13–8.

Google Scholar