Computing Edge Metric Dimension of One-Pentagonal Carbon Nanocone

1 Introduction

Carbon nanocones (CNC) made their first appearance in 1968, or perhaps earlier, on the surface of graphite occurring naturally [25]. These chemical structures are exciting due to their conceivable uses in gas sensors, gas storage, bio-sensors, energy storage, chemical probes, and nano-electronic devices, see [2, 3, 8, 17, 29]. Nanocones are the networks of the carbon that can be represented mathematically as cubic planar infinite graphs. Iijima [19], mainly addressed graphitic carbon helical microtubules. The existence of CNC and their combinatorial properties have been discussed in [14, 24]. Depending upon the positive signed curvature, Klein et al. [25] categorized CNC into eight groups. Brinkmann et al. have classified these structures [7]. Justus et al. [20] have given the expander constants and boundaries of these nanocones triangle patches. CNC has recently gained considerable scientific attention due to its peculiar properties and promising applications such as hydrogen storage and energy [7].

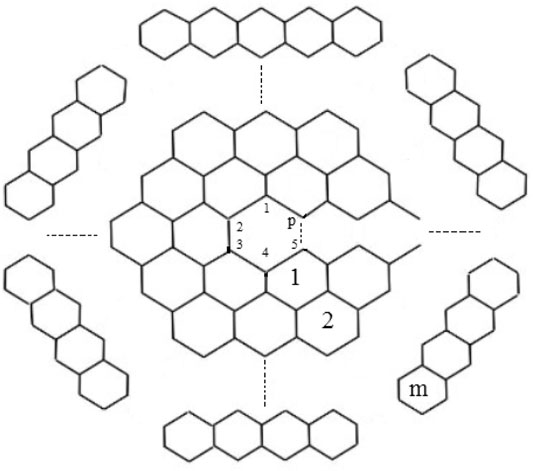
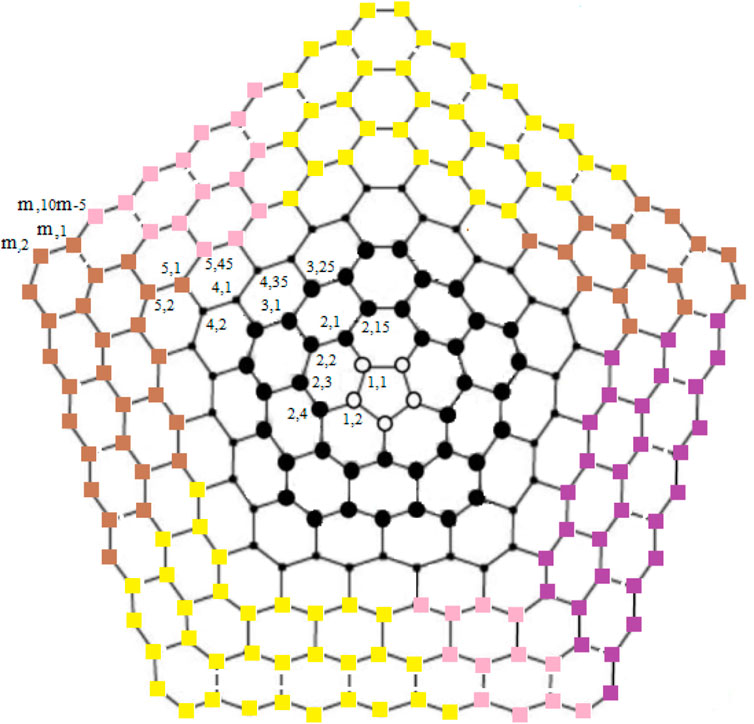
The chemical graph of carbon nanocones CNC_p[m], as shown in Figure 1, comprises of conical structures with a cycle of size and order p at their center and (m − 1)-layers of six-sided faces (hexagons) placed at the conical surface around its center. Here we are interested for the case p = 5 i.e., CNC₅[m]. When one pentagon is inserted in the honeycomb layer, a disclination defect in the graphenic plane is generated, resulting in the formation of a conic structure with positive curvature in which the pentagon is surrounded by the first belt of five hexagons. CNC₅[m] denotes an (m − 1)-dimensional one-pentagonal carbon nanocone (1-PCNC), where m represents (m − 1)-number of layers consisting of six-sided faces, which include the conical surface of the nanocone, and five denotes the presence of a single five-sided face on the tip known as its center. Along with it, a two-dimensional planar graph of a 1-PCNC is constructed, with carbon atoms representing vertices and bonds representing edges between them (see Figure 2).

FIGURE 1

FIGURE 1. CNC_p[m].

FIGURE 2

FIGURE 2. CNC₅[m].

Resolvability in graph theory aims to understand the behavior of real-world distance-based frameworks. It has been used in chemistry, molecular topology, industrial chemistry, and computer science. It attracts authors from various fields, including mathematics, because of the fascinating problems that arise from the symmetries and structures involved. It is always highly beneficial in an enigmatic network to identify uniquely the location of vertices (such as atoms) by establishing an identity with respect to a specific set. Such a specific set with minimum cardinality is called the metric basis and this cardinality is the metric dimension [16, 34]. These findings have been used effectively in drug patterns to access specific atoms.

The researchers are motivated by the fact that the metric dimension has a variety of practical applications in everyday life and so it has been extensively investigated. Metric dimension is utilized in a wide range of fields of sciences, including robot navigation [23], geographical routing protocols [27], connected joints in network and chemistry [10, 11], telecommunications [6], combinatorial optimization [31], network discovery and verification [6], etc. NP-hardness and computational complexity for the resolvability parameters are addressed in [15, 26].

Many authors have introduced and analyzed certain variations of resolving sets, such as local resolving set, partition resolving set, fault-tolerant resolving set, resolving dominating set, strong resolving set, independent resolving set, and so on. For further details the reader is referred to [1, 6, 10, 21, 22, 32, 33]. In addition to defining other variants of resolving sets in graphs, Kelenc et al. [22], introduced a parameter used to uniquely distinguish graph edges and called it the edge metric dimension. In general, a graph metric was used to describe each pair of edges based on distances to a specific set of vertices. This was based on the assumption that a minimum resolving set R of a connected graph G identifies uniquely all the vertices of G using distance-vector, but does not necessarily recognize all the edges of G.

CNCs are a significant class of carbon nanomaterials that have been discovered in 1994 by Ge and Sattler [23]. This class of CNC has recently received considerable attention. Bultheel and Ori [9], analyzed topological modeling techniques used to study 1-PCNC and obtained significant findings about the chemical reactivity and desired sizes. Moreover, they also addressed the topological roundness and efficiency of CNC₅[m] as the long-range topological potential whose local minima correspond to magic sizes of nanocones with a greater percentage of formation. In [36], Zhang et al. calculated analytic expressions of Hosoya polynomial and certain distance-related indices such as the hyper Harary and Weiner indices for 1-PCNC. Fereshteh and Mehdi [13], obtained the adjacent eccentric distance sum index of 1-PCNC. In [5], Ashrafi et al. proved that $W(CN{C}_5[m])=(\frac{62}{3})m^5+(\frac{310}{3})m^4+(\frac{1205}{6})m^3+(\frac{1135}{6})m^2+86m+15$.

In [30], Saheli et al. proved that $\xi (CN{C}_5[m])=5(10m^3+\frac{43}{2}{m}^2+\frac{31}{2}m+4)$. For more on CNC₅[m], one can refer to [4, 18, 28].

The flexibility and strength of carbon nanotubes make them suitable for manipulating another nanoscale structures, implying that they will play an important part in nanotechnology engineering. These 3D all-carbon architectures may be used to create the next generation of power storage, field emission transistors, photovoltaics, supercapacitors, biomedical devices & implants, and high-performance catalysis. Because of its applications, uses, and significance in numerous fields of study, we are interested in contributing more to this subject. For our purpose, in 1-PCNC bonds represent the edges and carbon atoms represent vertices. Recently, a study [17] reveals that 1-PCNC possesses the minimum metric generator of cardinality three correspondings to the atoms (vertices) therein. We now obtain some important results regarding the edges (bonds) present in 1-PCNC, as there is no such study regarding the edge metric dimension of 1-PCNC network. So, in this article, we study some basic properties of 1-PCNC along with its edge metric dimension.

The main results obtained are as follows:

• The edge metric dimension of 1-PCNC is three.

• Metric dimension (1-PCNC) = Edge metric dimension (1-PCNC).

• The resolving set and edge resolving set for 1-PCNC are independent.

The remainder of this paper is structured as: Section 2 introduces some basic concepts related to the metric dimension and the edge metric dimension. Some proven outcomes of 1-PCNC with respect to the metric dimension are also discussed. We study the edge metric dimension of 1-PCNC in Sect. 3 and discuss some of its properties. Finally, the conclusion and future work of the present study are discussed in Sect. 4.

2 Preliminaries

In this section, we list some basic properties of 1-PCNC, the definition of metric dimension & edge metric dimension, and recall some existing results regarding these notions.

Suppose G = (V, E) is a non-trivial, simple, and connected graph, where V represents a set of vertices and E represents a set of edges. The distance between two vertices u and w in an undirected graph G, denoted by d(u, w), is the length of a shortest u − w path in G.

Definition 1. Chemical Graph: A chemical graph (molecular graph) is a simple labeled graph in which the vertices correspond to the atoms of the molecule and the edges relate to chemical bonds.

Definition 2. One-Pentagonal carbon nanocone: 1-PCNC is denoted by CNC₅[m]; (m ≥ 2). CNC₅[m] consists of conical structures with a cycle of length five at its core and m represents m − 1 layers of hexagons placed at the conical surface around its center as shown in Figure 2. The bounded-face boundaries of CNC₅[m] comprises of one five-sided face and $\frac{5m(m-1)}{2}$ number of six sided faces. It has 5m² number of vertices (or atoms) and $5(m^2+\frac{m(m-1)}{2})$; m ≥ 1 number of edges (or bonds). By V(CNC₅[m]) and E(CNC₅[m]) respectively, we denote the vertex set and the edge set of 1-PCNC, where V(CNC₅[m]) = {u_i,1, u_i,2, u_i,3, u_i,4, …, u_i,10i−5|1 ≤ i ≤ m} and E(CNC₅[m]) = {u_i,1u_i,2, u_i,2u_i,3, u_i,3u_i,4, …, u_i,10i−7u_i,10i−6, u_i,10i−6u_i,10i−5, u_i,10i−5u_i,1|1 ≤ i ≤ m} ∪ {u_1,1u_2,1, u_1,2u_2,4, u_1,3u_2,7, u_1,4u_2,10, u_1,5u_2,13} ∪ {u_i,2u_i+1,1, u_i,2j+1u_i+1,2j+2|1 ≤ j ≤ i & 2 ≤ i ≤ m − 1} ∪ {u_i,2ju_i+1,2j+3|i + 1 ≤ j ≤ 2i & 2 ≤ i ≤ m − 1} ∪ {u_i,2j−1u_i+1,2j+4|2i + 1 ≤ j ≤ 3i & 2 ≤ i ≤ m − 1} ∪ {u_i,2j−2u_i+1,2j+5|3i + 1 ≤ j ≤ 4i & 2 ≤ i ≤ m − 1} ∪ {u_i,2j−3u_i+1,2j+6|4i + 1 ≤ j ≤ 5i − 1 & 2 ≤ i ≤ m − 1}.

Definition 3. Metric dimension: A vertex w ∈ V(G) resolves (recognize) a pair of distinct vertices w₁, w₂ ∈ V(G) if d(w, w₁) ≠ d(w, w₂). A set of vertices R ⊆ V(G) is said to be a resolving set for G if every pair of different vertices in G are recognized by at least one vertex from R. For a subset of distinct (ordered) vertices R = {w₁, w₂, w₃, …, w_z}⊆ V(G), the metric co-ordinate (code) of w ∈ V(G) with respect to R is the z-vector r(w) = r(w|R) = (d(w, w₁), d(w, w₂), d(w, w₃), …, d(w, w_z)). The metric dimension of G, denoted by dim(G), is defined as dim(G) = min{|R| : R is resoving set in G}. These notions were introduced, independently by Slater [34] and Harary and Melter [16].

Definition 4. Independent set: A set of vertices I in a graph G is said to be an independent set (also known as stable set) if no two vertices in I are adjacent [12].

Definition 5. Independent resolving set: A subset of vertices R in G is said to be an independent resolving set for G, if R_E is resolving as well as independent set [12].One can see that the metric dimension deals with the vertices of the graph by its definition, a similar concept dealing with the edges of the graph introduced by Kelenc et al. in [22], called the edge metric dimension of graph G, which uniquely identifies the edges related to graph G.

Definition 6. Edge metric dimension: For an edge e = cz and a vertex w the distance between them is defined as d(e, w) = min{d(c, w), d(z, w)}. A subset R_E is called an edge resolving set for G, if for any two distinct edges e₁ and e₂ of G are recognized by at least one vertex w of R_E. For a subset of distinct (ordered) vertices R_E = {w₁, w₂, w₃, …, w_z}⊆ V(G), the edge metric co-ordinate (edge code) of e ∈ E(G) with respect to R_E is the z-vector r_E(e) = r_E(e|R_E) = (d(e, w₁), d(e, w₂), d(e, w₃), …, d(e, w_z)). The edge resolving set with minimum cardinality is termed as edge metric basis, and that cardinality is known as the edge metric dimension of graph G, denoted by edim(G) [22].

Definition 7. Independent edge resolving set (IERS): A subset R_E of distinct vertices in G is said to be an IERS for G, if R_E is edge resolving as well as independent set.In [17], Hussain et al. obtained the metric dimension of CNC₅[m]. They proved that CNC₅[m] denotes a class of plane graph with constant and bounded metric dimension i.e., the metric dimension does not depend upon the value of m. For metric dimension, they gave the following result.

Proposition 1. dim (CNC₅[m]) = 3, for every m ≥ 1.Using the definition of an independent set and Theorem 2 in [17], we obtain the following result regarding CNC₅[m].

Proposition 2. For every m ≥ 2, the independent resolving number is three for CNC₅[m].

3 Main Results

Each chemical structure can be represented as a graph in chemical graph theory, where edges are alternated to bonds and atoms to vertices. The recent advanced topic is resolvability parameters of a graph, in which the entire structure is designed in such a way that each atom (bond) has a unique position. In this section, we show that the minimum edge resolving set for 1-PCNC has cardinality three, with atoms/vertices chosen from all possible atom/vertex combinations.

Theorem 1. edim (CNC₅[m]) ≥ 3, for every m ≥ 2.

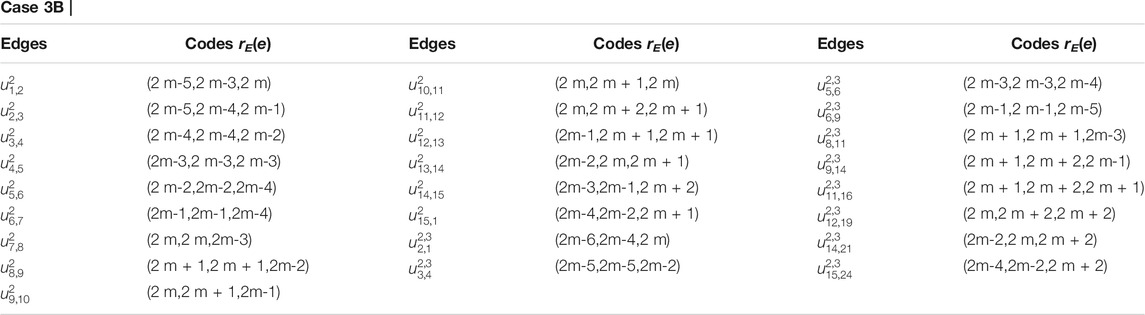
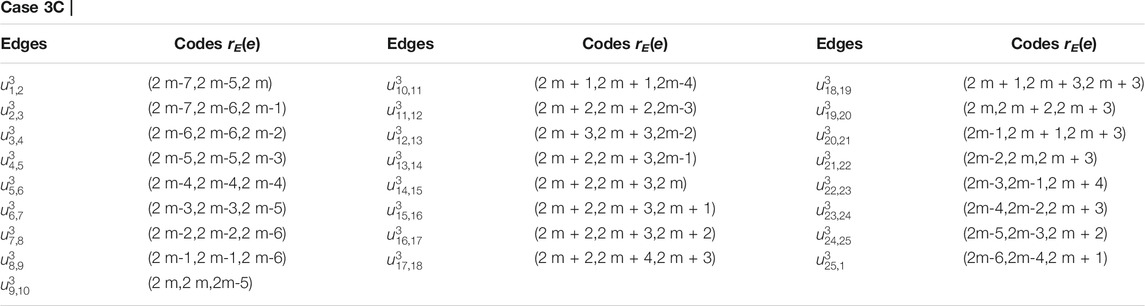
Proof. To show this, we have to prove that there exists no edge resolving set R_E for CNC₅[m] such that |R_E| ≤ 2. Since 1-PCNC is not a path graph, so the possibility of a singleton edge resolving set for CNC₅[m] is ruled out [32]. Next, suppose on the contrary that |R_E| = 2, such that R_E = {u_l,1, u_z,j}. Then, we have the following possibilities to be considered (see, Table 1, Table 2, and Table 3).

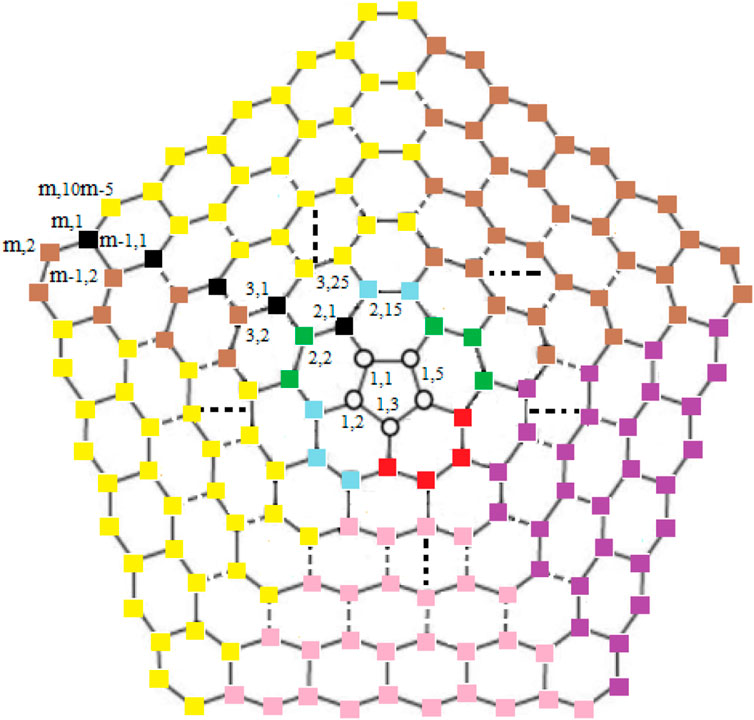
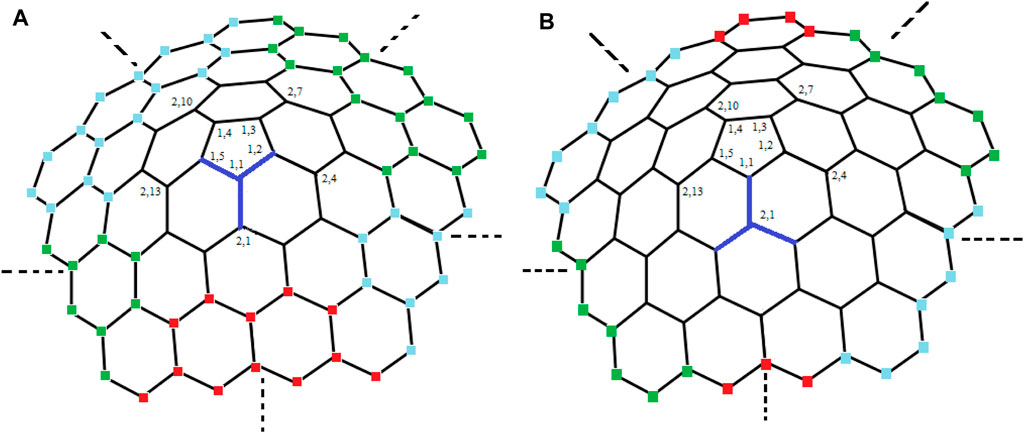
For subcases 1 and 2 (Table 1), one can find contradictions easily. Now, for 3 ≤ i ≤ m, we find that the vertex u_i,1 (in black color) and the vertices in yellow, brown, pink, and purple color on i^th cycle as shown in Figure 3 are at the same distance from the edges {u_i,1u_i,2, u_i,1u_i−1,2}, {u_i,1u_i,10i−5, u_i,1u_i−1,2}, {u_i,1u_i,2, u_i,1u_i,10i−5}, and {u_1,1u_1,2, u_1,2u_2,4} respectively, a contradiction.

TABLE 1

TABLE 1. Case 1: When both of the vertices u_l,1, u_z,j lie on the same i^th-cycle i.e., l = z = i

TABLE 2

TABLE 2. Case 2: When one vertex u_l,1 lies on i^th cycle and other u_z,j lies on the z = (i + 1)^th cycle.

TABLE 3

TABLE 3. Case 3: When the vertices u_l,1 and u_z,j lie on two distinct cycles that are not neighboring.

FIGURE 3

FIGURE 3. CNC₅ [m] for Case 1.

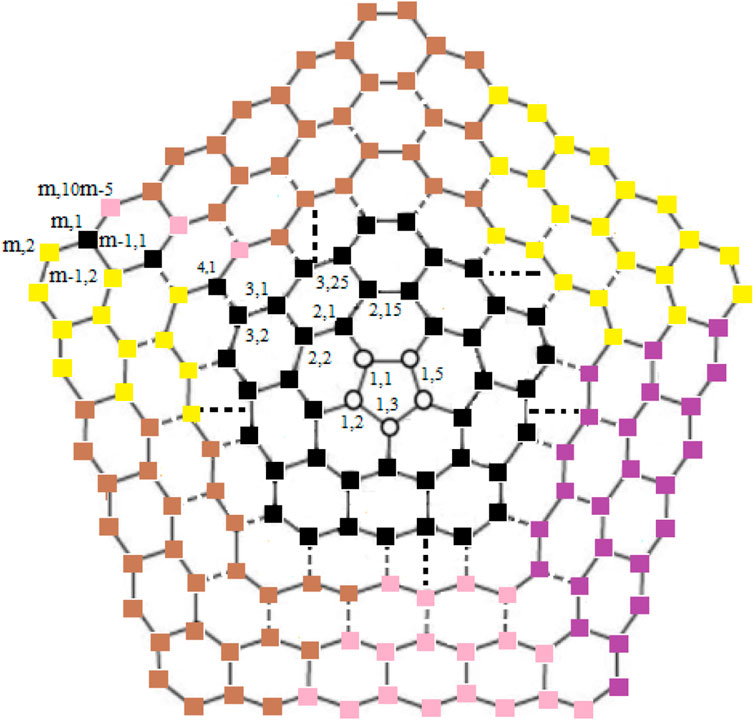
For subcases 1 and 2 (Table 2), one can find contradictions easily. Now, for 3 ≤ i ≤ m − 1, we find that the vertex u_i,1 (in black color) and the vertices in yellow, brown, pink, and purple color on (i + 1)^th cycle as shown in Figure 4 are at the same distance from the edges {u_i,1u_i−1,2, u_i,1u_i,10i−5}, {u_i,1u_i,2, u_i,1u_i−1,2}, {u_i,1u_i,2, u_i,1u_i,10i−5}, and {u_1,1u_1,2, u_1,2u_2,4} respectively, a contradiction.

FIGURE 4

FIGURE 4. CNC₅ [m] for Case 2.

From subcase 1 (Table 3), we find that the vertex u_1,1 and the vertices in red, green, and blue color on i^th (3 ≤ i ≤ m) cycle as shown in Figure 5A are at the same distance from the edges {u_1,1u_1,5, u_1,1u_1,2}, {u_1,1u_1,5, u_1,1u_2,1}, and {u_1,1u_2,1, u_1,1u_1,2} respectively, a contradiction.Next, from subcase 2, we find that the vertex u_2,1 and the vertices in red, green, and blue color on k^th (4 ≤ k ≤ m) cycle as shown in Figure 5B are at the same distance from the edges {u_2,1u_2,2, u_2,1u_2,15}, {u_2,1u_2,2, u_2,1u_1,1}, and {u_1,1u_2,1, u_2,1u_2,15} respectively, a contradiction.Finally, for subcase 3, we find that the vertex u_i,1 (for i = 3, see Figure 6) and the vertices on the k^th (i + 2 ≤ k ≤ m) cycle are at the same distance from the edges {u_i,1u_i−1,2, u_i,1u_i,2} or {u_i,1u_i−1,2, u_i,1u_i,10i−5} or {u_i,1u_i,2, u_i,1u_i,10i−5} or {u_1,1u_1,2, u_1,2u_2,4}, a contradiction.Now, by symmetry of graphs other relations can be obtain (i.e., for 4 ≤ i ≤ m − 2; i + 2 ≤ k ≤ m and 1 ≤ j ≤ 10k − 5), which shows the same kind of contradictions as we obtained for i = 3, a contradiction.Hence, from the above cases, we conclude that there is no edge metric generator R_E for 1-PCNC such that |R_E| = 2. However, symmetry of graphs can be used to derive alternative relations that show the same kind of contradictions. Therefore, we must have |R_E|≥ 3 i.e., edim (CNC₅[m]) ≥ 3.Next, we prove that the upper bound for the edge metric dimension of 1-PCNC is also three.

FIGURE 5

FIGURE 5. CNC₅ [m] for Case 3 (Subcase 1 (Panel A) and 2 (Panel B)).

FIGURE 6

FIGURE 6. CNC₅ [m] for Case 3 (Subcase 3).

Theorem 2. edim (CNC₅[m]) ≤ 3, for every m ≥ 2.

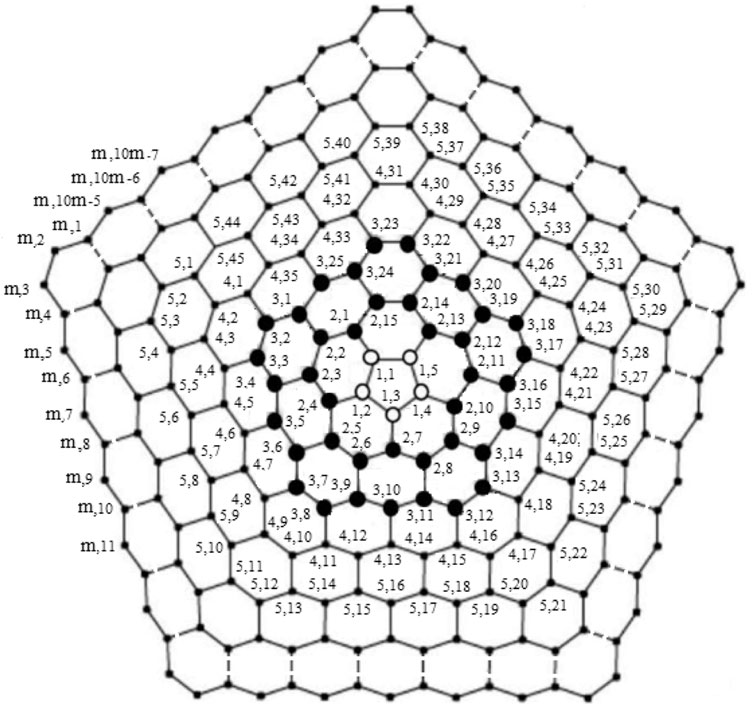
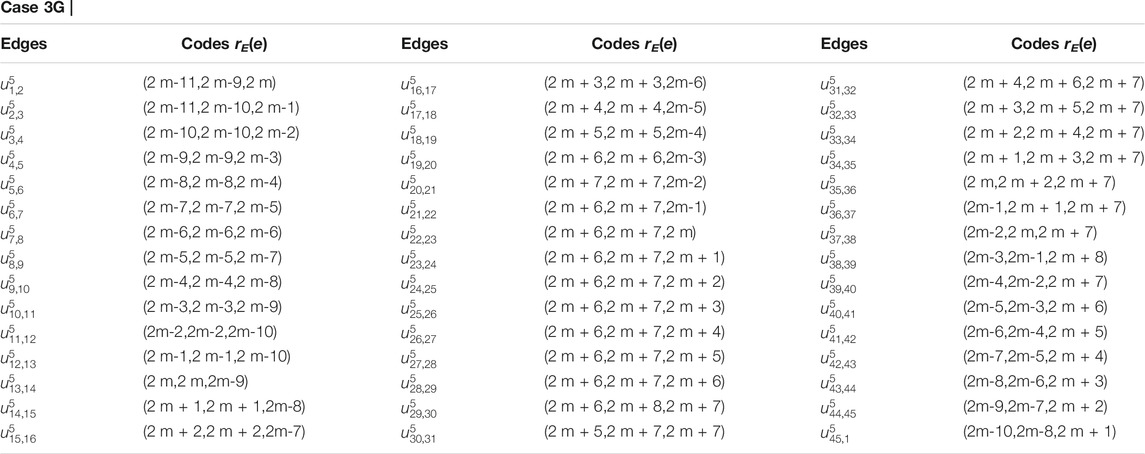
Proof. Suppose R_E is an edge resolving set for CNC₅[m]. To prove that the edge resolving set R_E of 1-PCNC has cardinality less than or equal to three (i.e., |R_E| = 3, because of Theorem 1), we have to show that the edge codes corresponding to R_E are distinct for any pair of different edges in CNC₅[m]. Let R_E = {u_m,1, u_m,3, u_m,2m+2}. Then, we will show that R_E is an edge resolving set for CNC₅[m] with cardinality three. Next, we give edge codes to every edge of CNC₅[m] with respect to R_E. For our convenience, we denote the edges on the CNC₅[m] by $u_{i,j}{u}_{i,k}=u_{j,k}^i$ and $u_{i,j}{u}_{k,l}=u_{j,l}^{i,k}$.The edge metric codes for the edges of first cycle and edges joining first and second cycles are as shown in Case 3A.The edge metric codes for the edges of second cycle and edges joining second and third cycles are as shown in Case 3B.The edge metric codes for the edges of third cycle are as shown in Case 3C.The edge metric codes for the edges joining the third and fourth cycle are as shown in Case 3D.The edge metric codes for the edges of fourth cycle are as Case 3E.The edge metric codes for the edges joining the fourth and fifth cycle are as shown in Case 3F.The edge metric codes for the edges of fifth cycle are Case 3G.Next, the edge metric codes for the edges joining the i^th and (i + 1)^th; (5 ≤ i ≤ m − 2) cycles are as shown in Case 3H.The edge metric codes for the edges joining the i = (m − 1)^th and i + 1 = m^th cycles are as shown in Case 3I.The edge metric codes for the edges of i^th (6 ≤ i ≤ m − 1) cycle are as shown in Case 3J.The edge metric codes for the edges of i = m^th cycle are as shown in Case 3K.From these edge codes, we find that these are distinct from one and another in at least one coordinate, implying R_E to be an edge resolving set with cardinality three for CNC₅[m]. Hence, edimCNC₅[m] ≤ 3.By using Theorem 1 and Theorem 2, we obtain the following result

CASE 3A

Case 3A

CASE 3B

Case 3B

CASE 3C

Case 3C

CASE 3D

Case 3D

CASE 3E

Case 3E

CASE 3F

Case 3F

CASE 3G

Case 3G

CASE 3H

Case 3H

CASE 3I

Case 3I

CASE 3J

Case 3J

CASE 3K

Case 3K

Theorem 3. edim (CNC₅[m]) = 3, for every m ≥ 2.Next, if the edge resolving set is independent for CNC₅[m], then we have the following important result.

Theorem 4. For every m ≥ 2, the independent edge resolving number is three for CNC₅[m].

Proof. For proof, refer to Theorem 3.

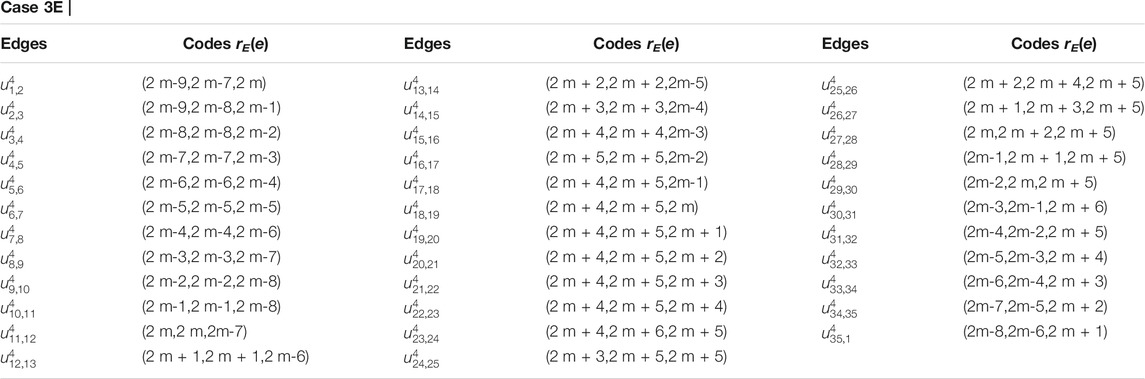
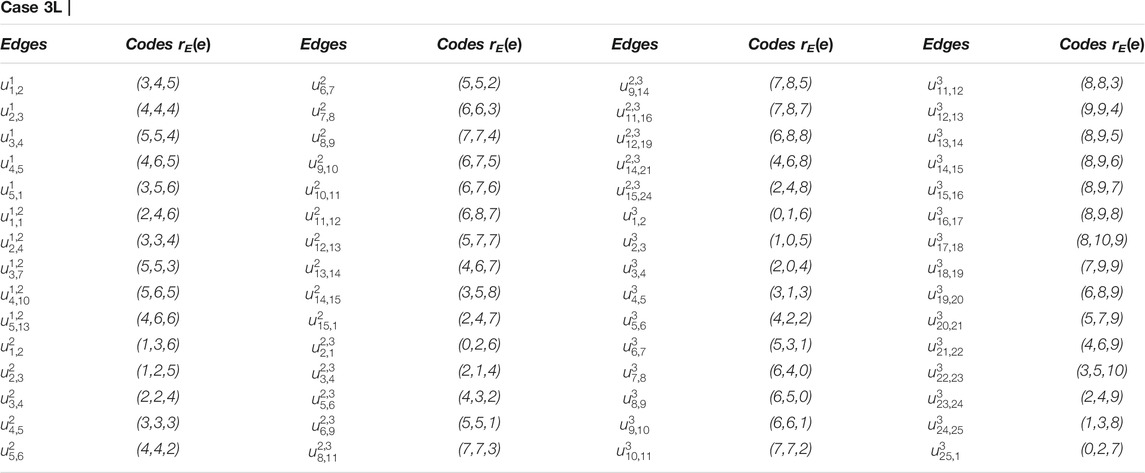
Example 3.1I. f m = 3 and R_E = {u_3,1, u_3,3, u_3,8}, the edge metric codes for CNC₅ [3] (Figure 7), are shown in Case 3L:

CASE 3L

Case 3L

FIGURE 7

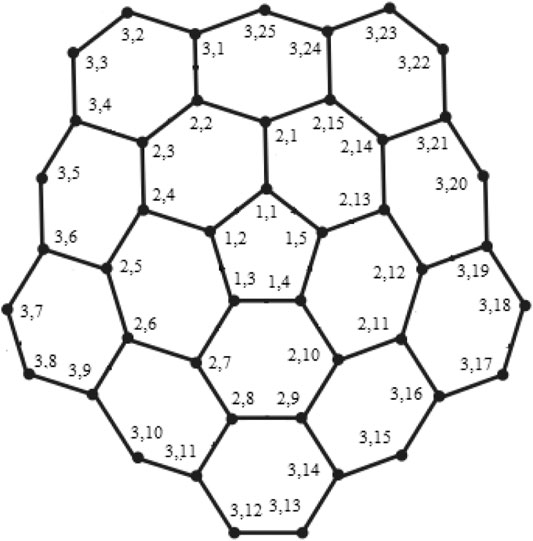
FIGURE 7. CNC₅ [3].

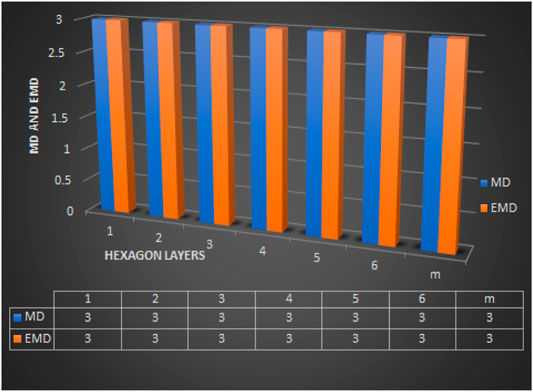
Remark 3.1. For 1-PCNC CNC₅[m], we find that edim(CNC₅[m]) = dim(CNC₅[m]) = 3 (using proposition 1 and Theorem 3). The comparison between metric dimension (MD) and edge metric dimension (EMD) of CNC₅[m] is clearly shown in Figure 8 and the value of these two dimensions are independent of the number of hexagon layers m and vertices in CNC₅[m].

FIGURE 8

FIGURE 8. Comparision between MD and EMD of CNC₅ [m].

4 Conclusion

Edge metric generators for a given connected chemical graph contain crucial information required for the identification of each bond (edge) present in the graph, uniquely. In this article, for an important class of carbon nanocone, viz., one-pentagonal carbon nanocone CNC₅[m], we prove that edim (CNC₅[m]) = 3 and it does not depend upon the value of m. We show that the minimum edge resolving set for 1-PCNC is also independent. The contributions of this research may be beneficial to those working in the fields of micro-devices built with CNC₅[m], nano-devices, nano-biotechnology, nano-engineering, and pharmacy. Following the metric dimension and edge metric dimension of CNC₅[m], the natural problem that arises from the text is:

What should be the minimal cardinality of mixed metric resolving set (edge, as well as vertex, resolving set [35]) for CNC₅[m]?

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Ethics statement

The present article does not contain any studies with human participants or animals performed by any of the authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication

Funding

The research of HR is supported by the post-doctoral funding under grant number 10-20-302-303.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

We would like to express our sincere gratitude to the referees for a very careful reading of this paper and for all their insightful comments/criticism, which have led to a number of significant improvements to this paper.

References

1. Ahsan M, Zahid Z, Zafar S, Rafiq A, Sindhu MS, Umar M. Computing the Edge Metric Dimension of Convex Polytopes Related Graphs. J Math Computer Sci (2021) 22:174–88.

Google Scholar

2. Andova V, Došlić T, Krne M, Lužar B, Škrekovski R. On the Diameter and Some Related Invariants of Fullerene Graphs. MATCH Commun Math Comput Chem (2012) 68:109–30.

Google Scholar

3. Andova V, Kardoš F, Škrekovski R. Sandwiching Saturation Number of Fullerene Graphs, MATCH Commun. Math Comput Chem (2015) 73:501–18.

Google Scholar

4. Ashrafi AR, Saati H. PI and Szeged Indices of One-Pentagonal Carbon Nanocones. Jnl Comp Theo Nano (2007) 4(4):761–3. doi:10.1166/jctn.2007.2363

CrossRef Full Text | Google Scholar

5. Ashrafi AR, Mohammad-Abadi Z. The Wiener Index of One-Pentagonal Carbon Nanocone. Fullerenes, Nanotubes and Carbon Nanostructures (2012) 20(8):688–95. doi:10.1080/1536383x.2011.552998

CrossRef Full Text | Google Scholar

6. Beerloiva Z, Eberhard F, Erlebach T, Hall A, Hoffmann M, Mihalák M, et al. Network Discovery and Verification. IEEE J Sel Area Commun (2006) 24:2168–81.

Google Scholar

7. Brinkmann G, Van Cleemput N. Classification and Generation of Nanocones. Discrete Appl Mathematics (2011) 159(15):1528–39. doi:10.1016/j.dam.2011.06.014

CrossRef Full Text | Google Scholar

8. Brinkmann G, Friedrichs OD, Lisken S, Peeters A, Cleemput NV. CaGe-a Virtual Environment for Studying Some Special Classes of Plane Graphs -an Update. MATCH Commun Math Comput Chem (2010) 63:533–52.

Google Scholar

9. Bultheel A, Ori O. Topological Modeling of 1-Pentagon Carbon Nanocones - Topological Efficiency and Magic Sizes. Fullerenes, Nanotubes and Carbon Nanostructures (2018) 26(5):291–302. doi:10.1080/1536383x.2018.1437543

CrossRef Full Text | Google Scholar

10. Chartrand G, Eroh L, Johnson MA, Oellermann OR. Resolvability in Graphs and the Metric Dimension of a Graph. Discrete Appl Mathematics (2000) 105:99–113. doi:10.1016/s0166-218x(00)00198-0

CrossRef Full Text | Google Scholar

11. Chartrand G, Poisson C, Zhang P. Resolvability and the Upper Dimension of Graphs. Comput Mathematics Appl (2000) 39:19–28. doi:10.1016/s0898-1221(00)00126-7

CrossRef Full Text | Google Scholar

12. Chartrand G, Saenpholphat V, Zhang P. The Independent Resolving Number of a Graph. Math Bohem (2003) 128:379–93. doi:10.21136/mb.2003.134003

CrossRef Full Text | Google Scholar

13. Fereshteh M, Mehdi A. The Adjacent Eccentric Distance Sum index of One Pentagonal Carbon Nanocones. J Comput Theoret Nanosci (2015) 12(10):3860–3.

Google Scholar

14. Gillot J, Bollmann W, Lux B. Cristaux de graphite en forme de cigare et a structure conique. Carbon (1968) 6:381–7. doi:10.1016/0008-6223(68)90033-x

CrossRef Full Text | Google Scholar

15. Hauptmann M, Schmied R, Viehmann C. Approximation Complexity of Metric Dimension Problem. J Discrete Algorithms (2012) 14:214–22. doi:10.1016/j.jda.2011.12.010

CrossRef Full Text | Google Scholar

16. Harary F, Melter RA. On the Metric Dimension of a Graph. Ars Comb (1976) 2:191–5.

Google Scholar

17. Hussain Z, Munir M, Ahmad A, Chaudhary M, Alam Khan J, Ahmed I. Metric Basis and Metric Dimension of 1-pentagonal Carbon Nanocone Networks. Sci Rep (2020) 10(1):19687–7. doi:10.1038/s41598-020-76516-1

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Hussain Z, Munir M, Nazeer W, Saleem MS, Min Kang S, Chel Kwun Y. Computational Aspects of Line Graph of Carbon Nanocones. J Natn Sci Found Sri Lanka (2019) 47(4):435–43. doi:10.4038/jnsfsr.v47i4.9681

CrossRef Full Text | Google Scholar

19. Iijima S. Helical Microtubules of Graphitic Carbon. Nature (1991) 354(6348):56–8. doi:10.1038/354056a0

CrossRef Full Text | Google Scholar

20. Justus C. Boundaries of triangle-patches and the Expander Constant of Fullerenes. Universität Bielefeld (2007).

Google Scholar

21. Kelenc A, Kuziak D, Taranenko A, G. Yero I. Mixed Metric Dimension of Graphs. Appl Mathematics Comput (2017) 314:429–38. doi:10.1016/j.amc.2017.07.027

CrossRef Full Text | Google Scholar

22. Kelenc A, Tratnik N, Yero IG. Uniquely Identifying the Edges of a Graph: the Edge Metric Dimension. Discrete Appl Mathematics (2018) 251:204–20. doi:10.1016/j.dam.2018.05.052

CrossRef Full Text | Google Scholar

23. Khuller S, Raghavachari B, Rosenfeld A. Landmarks in Graphs. Discrete Appl Mathematics (1996) 70:217–29. doi:10.1016/0166-218x(95)00106-2

CrossRef Full Text | Google Scholar

24. Klein D. Topo-combinatoric Categorization of Quasi-Local Graphitic Defects. Phys Chem Phys (2002) 4:209–11. doi:10.1039/b110618j

CrossRef Full Text | Google Scholar

25. Klein DJ, Balaban AT. The Eight Classes of Positive-Curvature Graphitic Nanocones. J Chem Inf Model (2006) 46(1):307–20. doi:10.1021/ci0503356

CrossRef Full Text | Google Scholar

26. Garey MR, Johnson DS. Computers and Intractability: A Guide to the Theory of NP-Completeness. New York, USA: W.H. Freeman and Co. (1983) 48(2):498–500. doi:10.2307/2273574

CrossRef Full Text

27. Liu K, Abu-Ghazaleh N. Virtual Coordinates with Backtracking for Void Traversal in Geographic Routing. Lect Notes Comput Sci (2006) 4104:46–59. doi:10.1007/11814764_6

CrossRef Full Text | Google Scholar

28. Nazeer W, Farooq A, Younas M, Munir M, Kang S. On Molecular Descriptors of Carbon Nanocones. Biomolecules (2018) 8(3):92. doi:10.3390/biom8030092

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Sagar TC, Chinthapenta V, Horstemeyer MF. Effect of Defect Guided Out-Of-Plane Deformations on the Mechanical Properties of Graphene. Fullerenes, Nanotubes and Carbon Nanostruct (2020) 28:1–7. doi:10.1080/1536383x.2020.1813720

CrossRef Full Text | Google Scholar

30. Saheli Z, Saati H, Ashrafi A. The Eccentric Connectivity index of One Pentagonal Carbon Nanocones. Optoelectron Adv Mater Rapid Commun (2010) 4(6):896–7.

Google Scholar

31. Sebo A, Tannier E. On Metric Generators of Graphs. Math Oper Res (2004) 29(2):383–93.

Google Scholar

32. Sharma SK, Bhat VK. Metric Dimension of Heptagonal Circular Ladder. Discrete Math Algorithms Appl (2021) 13(1):2050095. doi:10.1142/s1793830920500950

CrossRef Full Text | Google Scholar

33. Sharma SK, Bhat VK. Fault-Tolerant Metric Dimension of Two-fold Heptagonal-Nonagonal Circular Ladder. Discrete Math Algorithm Appl (2021) 2150132. doi:10.1142/S1793830921501329

CrossRef Full Text | Google Scholar

34. Slater PJ. Leaves of Trees. Congr Numer (1975) 14:549–59.

Google Scholar

35. Xing BH, Sharma SK, Bhat VK, Raza H, Liu JB. The Vertex-Edge Resolvability of Some Wheel-Related Graphs. J Math (2021). doi:10.1155/2021/1859714

CrossRef Full Text | Google Scholar

36. Zhang Q-X, Xu S-J, Chen H-Y. The Hosoya Polynomial of One-Pentagonal Carbon Nanocone. Fullerenes, Nanotubes and Carbon Nanostructures (2014) 22(10):866–73. doi:10.1080/1536383x.2013.812634

CrossRef Full Text | Google Scholar