- 1Key Laboratory of Geological Hazards in Three Gorges Reservoir Area, Ministry of Education, China Three Gorges University, Yichang, China
- 2Department of Civil Engineering, Yunnan Minzu University, Kunming, China
- 3State Key Laboratory of Safety and Health for Metal Mines, Sinosteel Ma’anshan Institute of Mining Research Co., Ltd., Ma’anshan, China
Gravelly soils exhibit complicated mechanical behaviours closely related to particle breakage and relative density state. To better capture the mechanical responses of gravelly soils, a generalised plastic model considering evolution of void ratio and particle breakage was developed within the framework of critical state soil mechanics. In the model, particle breakage effect was described by incorporating breakage index to deviate the critical state line off the ideal position. A differential equation relating increment of void ratio to variation of volumetric strain was used to depict the evolution of current void ratio. It indirectly reflected the relative density state of gravelly soils. The model was applied to conducting numerical simulations for a series of triaxial tests on four types of gravelly soils. Comparisons between the test data and the modelling results indicated that considerations of void ratio evolution and particle breakage could better simulate the stress-dependent dilatation/contraction behaviours of gravelly soils.
1 Introduction
Gravelly soils (including coarse-grained aggregates, rockfill materials and railway basalts) are widely used as construction materials in the various geotechnical projects (e.g. roadbeds and dams). Over the past several decades, researchers have made efforts to investigate the mechanical properties of gravelly soils [1]. Experimental studies have indicated that particle breakage greatly affects the mechanical behaviours of gravelly soils [2,3]. In a microstructure view, particle breakage changed the grain distributions. Then, the mechanical responses of gravelly soils have changed remarkably with the reconfiguration of particle grading [3].
Based on the fundamental observations, particle breakage has been generally taken into account to build the constitutive models for gravelly soils [3–6]. In the constitutive descriptions, effect of particle breakage was described using a variable of breakage index. Particle grading evolution was often used to define the breakage index [2,3]. Investigations have indicated that particle breakage index is correlated to plastic-dissipation energy and formulated as a hyperbolic function of plastic work [5].
Besides the constitutive frameworks of traditional elastoplasticity [7], generalised plasticity [8] and critical state soil mechanics [9] have been often combined to construct the constitutive models of gravelly soils. In this group of models, as an important state parameter, particle breakage index has been incorporated into the equation of critical state line [3,5,6]. Such mathematical treatments can describe the translation effects of particle breakage on the critical state line of gravelly soils [5]. On the other hand, generalised plasticity is a type of simple constitutive framework, due to without consideration on the complex failure surfaces of geomaterials [8]. Thus, a number of generalised plastic models have been developed for gravelly soils based on the critical state concept [5,10–12]. These models considering particle breakage could well capture the main mechanical behaviours of gravelly soils, including stress-dependent volumetric dilatancy and nonlinear strength and deformation.
However, most of these models have not made clear expositions on the variations of void ratio during volume changing process. As we all know, current void ratio of a soil mass closely relates to and evolves with the volume deformation. By identifying the current, maximum and minimum void ratio values, the relative density state of soil mass could be estimated. As for gravelly soils, relative density state (dense or loose sates relative to critical state) decides whether they exhibit volume dilatation or contraction behaviours [12]. Considering the relationship between void ratio and relative density state, the evolution of void ratio should be included in the constitutive descriptions. In this way, the changing process of relative density state synchronous with the variation of volume deformation can be captured precisely. Therefore, besides particle breakage, it is reasonable to take the evolution of void ratio into account to build the constitutive models for gravelly soils. In this respect, there are some research attempts of considering evolution of void ratio in the constitutive models of granular soils [6,13].
In this study, an evolution equation of void ratio was incorporated into a generalised plastic model that was established within the framework of critical state soil mechanics. In the model, current void ratio and particle breakage index were regard as two state-dependent variables updating with the variation of volumetric strain and shifting the critical state line, respectively. The model was used to simulate the mechanical responses of four types of gravelly soils during triaxial tests. By analysing the simulation results, constitutive modelling effectiveness of considering evolution of void ratio and particle breakage was evaluated.
2 Constitutive Modelling Description
2.1 Generalised Plasticity Framework
In this study, generalised plasticity framework firstly proposed by Pastor and Zienkiewicz [8] was used to build the constitutive model for gravelly soils. In a generalised plasticity model, incremental stress-strain relationship is expressed as follows:
where
where
2.2 Elastic Behaviour
Nakai [14] provided the following Eqs 3, 4 to describe the elastic and plastic volumetric strains of sands under isotropic consolidation.
where
Using Eq. 3 and Poisson’s ratio
2.3 Critical State Considering Particle Breakage
As for gravelly soils, particle breakage remarkably changes the critical void state. This phenomenon was observed in triaxial tests [15,16]. In this study, a sigmoid function suggested by Liu et al. [3] was adopted to define the critical state line (CSL) influenced by particle breakage. That is:
where
where
2.4 Evolution of Void Ratio
In soil mechanics, it is always assumed that the volume of solid phase
The second formula in Eq. 9 is a differential equation. It has a solution expressed as follows:
In Eq. 10, the parameter
The current void ratio
where the state variable
2.5 Nonlinear Strength and Dilatancy Behaviours
Gravelly soils generally exhibit significant nonlinear strength behaviours. A power function is widely used to describe the nonlinear strength behaviours of geomaterials [3,19]:
where
In Eq. 12,
The dilatation stress ratio
where
The dilatation coefficient
where
2.6 Plastic Flow and Loading Direction
In the
As the nonassociated flow rule is assumed, the plastic loading direction
where
2.7 Plastic Modulus
Under the isotropic compression condition, there is
Additionally, the plastic volumetric strain increment can be determined by differentiating Eq. 4, that is:
Combination Eqs 19, 20 leads to the formula of plastic modulus
Eq. 21 is only suitable for the isotropic compression condition. Inspired by Chen et al. [10], a formulation of plastic modulus
3 Model Calibration and Simulations
This constitutive model has 15 material constants and can be classified into six groups. They can be determined using triaxial compression tests.
3.1 Calibration of Model Constants
3.1.1 Compression and Elastic Constants
Material constants
Additionally, using the elastic constants:
3.1.2 Initial void Ratio
Initial void ratio
where
3.1.3 Critical state Constants
The critical state constants
3.1.4 Strength constants
The strength constants:
3.1.5 Dilatation constants
Using the test data of plastic volumetric and shear strains,
Using the test data at the dilatation point, the dilatation stress ratio
3.1.6 Particle breakage Parameters
Using Eq. 8, the plastic dissipated energy
If
3.2 Performance of the Proposed Model
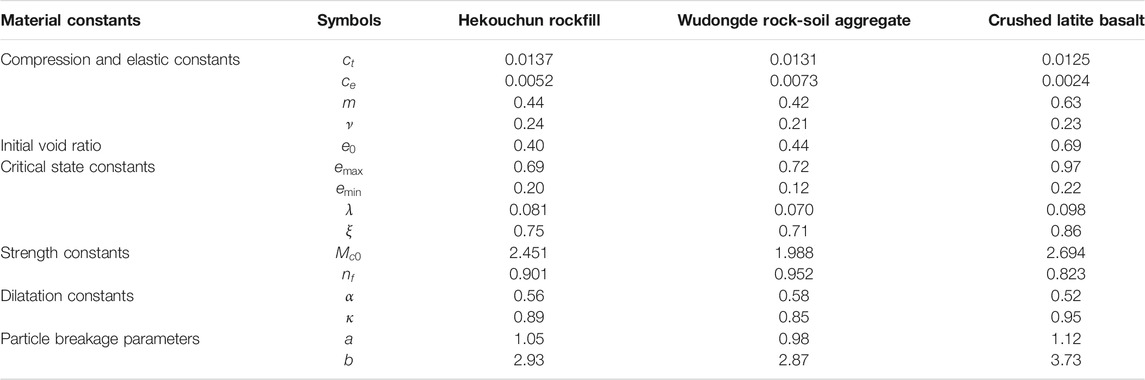
The proposed model was used to simulate the mechanical behaviours of four gravelly soils: Hekouchun rockfill [21], Wudongde rock-soil aggregate [22] and crushed latite basalt [23]. The material constants of the gravelly soils are given in Table 1. The test data and simulation results are shown in Figures 1–3. In these figures, the scatter symbols and curves represent the test data and modelling results, respectively.
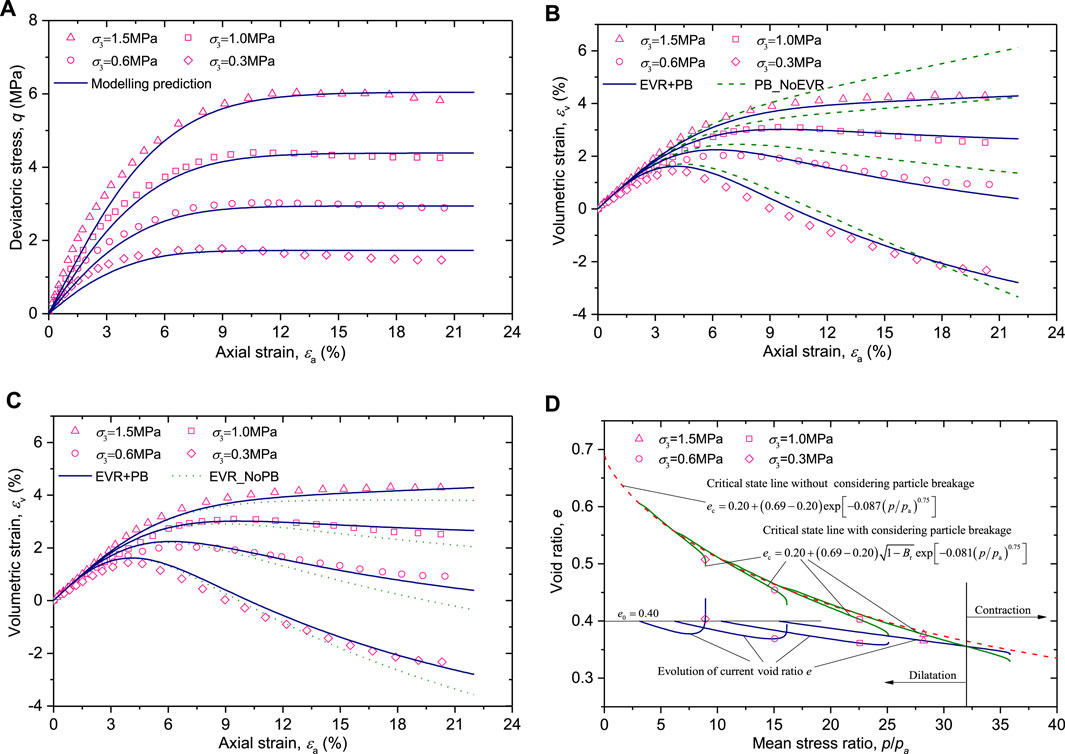
FIGURE 1. Model predations and experimental results of the Hekouchun rockfill (test data were from [21]).
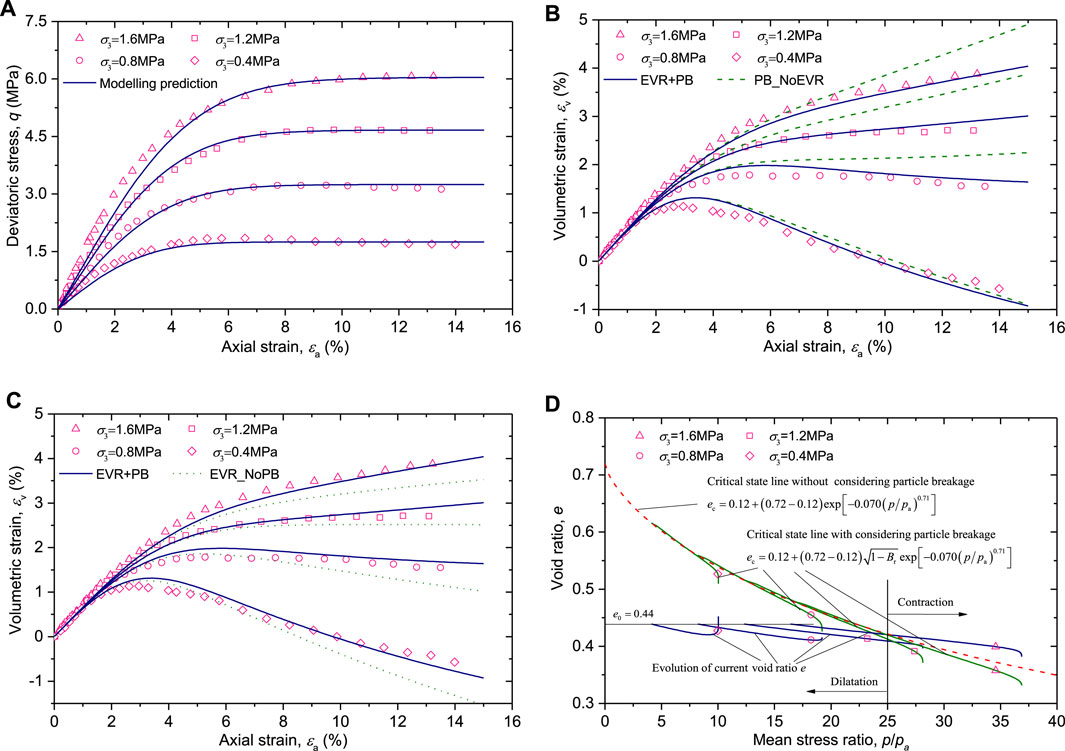
FIGURE 2. Model predations and experimental results of the Wudongde rock-soil aggregate (test data were from [22]).
FIGURE 3. Model predations and experimental results of the crushed basalt (test data were from [23]).
Two factors: particle breakage and evolution of void ratio were taken into account to formulate the constitutive model. To observe their influences on the modelling effectiveness, three computing conditions were comparatively analysed. They are termed as:
A “EVR + PB”, which represent that the modelling predictions consider the compound effects of evolution of void ratio and particle breakage.
B “PB_NoEVR”, which represent that the modelling predictions only consider the effect of particle breakage.
C “EVR_NoPB”, which represent that the modelling predictions only consider the evolution of void ratio.
In the model, the shapes of numerical modelling
3.2.1 Hekouchun rockfill
Hekouchun rockfill material was a type of dolomitic limestone, which would be adopted to construct the Hekouchun reservoir dam. Cai et al. [21] conducted a series of large-scale consolidated and drained triaxial shear tests on Hekouchun rockfill material with an initial relative density
As seen from Figure 1 in both stress-strain and volume deformation responses, there is a good agreement between the test data and modelling predictions. Figure 1A shows that the model is capable of capturing the deformation and strength behaviours of Hekouchun rockfill material over a range of confining pressures from 0.3 to 1.5 MPa. Figures 1B,C show the testing volumetric strains and modelling results predicted by EVR + PB, PB_NoEVR and EVR_NoPB. It is found that, on the whole, EVR + PB achieves better simulations, but PB_NoEVR and EVR_NoPB overestimates and under-predicts the volumetric contraction strains, respectively.
The evolution curves of current and critical-state void ratios modelled by EVR + PB are shown in Figure 1D. The ideal CSL without considering particle breakage is plotted using a red dash curve. It is found that the realistic CSLs are influenced by particle breakage and gradually depart from the ideal CSL with the increase of mean stress. When the confining pressure increases, the volume-contraction behaviour of Hekouchun rockfill material becomes more prominent. The evolution rule of current void ratio is consistent with the volume changing rules.
3.2.2 Wudongde rock-Soil Aggregate
Wudongde rock-soil aggregate was a type of natural gravelly soil, sampled from an ancient landslide mass, which was located downstream of the Wudongde Hydropower Dam on the Jinsha River, southwest China. Huang et al. [22] conducted large-scale triaxial tests on the Wudongde rock-soil aggregate under the confining pressures of 0.4, 0.8, 1.2, and 1.6 MPa. The material constants are listed in Table 1 and the modelling results are compared with test data in Figure 2.
Figure 2A shows that the modelling stress-strain relations exhibit good agreements in accordance with the test data. Figures 2B,C show that EVR + PB provides more accurate modelling predictions. PB_NoEVR overestimates volume contraction strains. EVR_NoPB tends to over-predict the volume-dilatation behaviour. In Figure 2D, it is found that EVR + PB modelling curves of current and critical-state void ratios have an intersection point at
3.2.3 Crushed latite Basalt
Salim and Indraratna [23] used a series of confining pressures: 0.05, 0.1, 0.2, and 0.3 MPa to conduct large-scale triaxial tests on a type of crushed latite basalt. Although the confining pressures were relatively lower, the volumetric strains had still undergone a transition from dilatation to contraction. Table 1 lists the material constants of the crushed latite basalt. Figure 3 shows the test data and modelling predictions.
Figure 3A indicates that the model is capable of reproducing the stress-strain relations of the crushed latite basalt. The testing and modelling volumetric strains are compared in Figures 3B,C. Under the confining pressures of 0.05 and 0.1 MPa, EVR + PB, PB_NoEVR and EVR_NoPB achieve relatively better simulations for the volume-dilatation behaviour. With an increase of confining pressure, PB_NoEVR predicts larger volumetric contraction strains. This phenomenon may be related to that PB_NoEVR overestimates the gap between the current void ratio and the CSL. Figure 3D shows the EVR + PB modelling curves of current and critical-state void ratios. Upward-bending evolutions of current void ratios indicates that volume-dilatation responses occur under the confining pressures of 0.05, 0.1, and 0.2 MPa. Under the confining pressure of 0.3 MPa, when the mean stress ratio
4 Conclusions
In this study, a generalised plastic model considering evolution of void ratio and particle breakage was developed for gravelly soils. The model was used to simulate the mechanical behaviours of four gravelly soils. By comparing three computing conditions: EVR + PB, PB_NoEVR, and EVR_NoPB, the effects of void ratio evolution and particle breakage on the modelling predictions were analysed. Following conclusions can be summarised:
1. Because the evolution of void ratio and particle breakage are not considered in the constitutive descriptions of stiffness and strength behaviours, the three computing conditions: EVR + PB, PB_NoEVR, and EVR_NoPB predict almost the same relations between deviatoric stress and axial strain.
2. Under the PB_NoEVR computing condition, current void ratio is constant. In this condition, the proposed model overestimates the volume-contraction strains. The higher the confining pressure, PB_NoEVR will more greatly overestimate the volume-contraction strains.
3. Under the EVR_NoPB computing condition, the ideal CSL is used and current void ratio evolves with the variation of volumetric strain. Overall, EVR_NoPB underestimates the volume-contraction strains and overestimates volume-dilatation strains.
4. In general, the model considering EVR + PB achieves relatively better simulation results for the volume dilatation/contraction responses of gravelly soils. It is reasonable for us to believe that the constitutive model considering EVR + PB could better reflect the volume deformation and failure mechanism of gravelly soils.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author Contributions
Conception and design of study was mainly contributed by RW. Numerical simulations was mainly contributed by JZ, YL. Drafting the manuscript was mainly contributed by JZ.
Funding
The work presented in this paper were financially supported by Open Funds at the Key Laboratory of Geological Hazards on Three Gorges Reservoir Area (China Three Gorges University), Ministry of Education (Grant Nos. 2015KDZ16 and 2015KDZ15).
Conflict of Interest
YL is employed by Sinosteel Ma’anshan Institute of Mining Research Co., Ltd.
The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Xiao Y, Liu H, Zhang W, Liu H, Yin F, Wang Y. Testing and Modeling of Rockfill Materials: A Review. J Rock Mech Geotechnical Eng (2016) 8:415–22. doi:10.1016/j.jrmge.2015.09.009
2. Hardin BO. Crushing of Soil Particles. J Geotechnical Eng (1985) 111:1177–92. doi:10.1061/(asce)0733-9410(1985)111:10(1177)
3. Liu M, Zhang Y, Zhu H. 3D Elastoplastic Model for Crushable Soils with Explicit Formulation of Particle Crushing. J Eng Mech (2017) 143:04017140. doi:10.1061/(asce)em.1943-7889.0001361
4. Christophe D. A Constitutive Model for Granular Materials Considering Grain Breakage. Sci China Technol Sci (2011) 54:2188–96.
5. Liu H, Zou D. Associated Generalized Plasticity Framework for Modeling Gravelly Soils Considering Particle Breakage. J Eng Mech (2013) 139:606–15. doi:10.1061/(asce)em.1943-7889.0000513
6. Saberi M, Annan C-D, Konrad J-M. Constitutive Modeling of Gravelly Soil-Structure Interface Considering Particle Breakage. J Eng Mech (2017) 143:04017044. doi:10.1061/(asce)em.1943-7889.0001246
7. Sukkarak R, Pramthawee P, Jongpradist P. A Modified Elasto-Plastic Model with Double Yield Surfaces and Considering Particle Breakage for the Settlement Analysis of High Rockfill Dams. KSCE J Civil Eng (2017) 21:1–12. doi:10.1007/s12205-016-0867-9
8. Pastor M, Zienkiewicz OC, Chan AHC. Generalized Plasticity and the Modelling of Soil Behaviour. Int J Numer Anal Methods Geomech (1990) 14:151–90. doi:10.1002/nag.1610140302
9. Roscoe KH, Schofield AN, Wroth CP. On the Yielding of Soils. Géotechnique (2008) 8:22–53. doi:10.1680/geot.1958.8.1.22
10. Chen S-s., Fu Z-z., Han H-q., Peng C. An Elastoplastic Model for Rockfill Materials Considering Particle Breakage. Chin J Geotechnical Eng (2011) 33:1489–95.
11. Guo W-l., Zhu J-g., Peng W-m. Study on Dilatancy Equation and Generalized Plastic Constitutive Model for Coarse-Grained Soil. Chin J Geotechnical Eng (2017) 32:1–7.
12. Liu MC, Gao YF. Constitutive Modeling of Coarse-Grained Materials Incorporating the Effect of Particle Breakage on Critical State Behavior in a Framework of Generalized Plasticity. Int J Geomechanics (2016) 17:04016113. doi:10.1061/(ASCE)GM.1943-5622.0000759
13. Bauer E, Fu Z, Liu S. Hypoplastic Constitutive Modeling of Wetting Deformation of Weathered Rockfill Materials. Front Archit Civ Eng China (2010) 4:78–91. doi:10.1007/s11709-010-0011-8
14. Nakai T. An Isotropic Hardening Elastoplastic Model for Sand Considering the Stress Path Dependency in Three-Dimensional Stresses. Soils and Foundations (1989) 29:119–37. doi:10.3208/sandf1972.29.119
15. Bandini V, Coop MR. The Influence of Particle Breakage on the Location of the Critical State Line of Sands. Soils and Foundations (2011) 51:591–600. doi:10.3208/sandf.51.591
16. Ghafghazi M, Shuttle DA, Dejong JT. Particle Breakage and the Critical State of Sand. Soils and Foundations (2014) 54:451–61. doi:10.1016/j.sandf.2014.04.016
17. Lade PV, Yamamuro JA, Bopp PA. Significance of Particle Crushing in Granular Materials. J Geotechnical Eng (1996) 122:309–16. doi:10.1061/(asce)0733-9410(1996)122:4(309)
18. Been K, Jefferies MG. A State Parameter for Sands. Géotechnique (1985) 35:99–112. doi:10.1680/geot.1985.35.2.99
19. Yao Y-P, Yamamoto H, Wang N-D. Constitutive Model Considering Sand Crushing. Soils and Foundations (2008) 48:603–8. doi:10.3208/sandf.48.603
20. Dafalias YF, Manzari MT. Simple Plasticity Sand Model Accounting for Fabric Change Effects. J Eng Mech (2004) 130:622–34. doi:10.1061/(asce)0733-9399(2004)130:6(622)
21. Cai Z-y., Li X-m., Han L, Guan Y-f. Critical State of Rockfill Materials Considering Particle Gradation and Breakage. Chin J Geotechnical Eng (2016) 38:1357–64.
22. Huang S, Ding X, Zhang Y, Cheng W. Triaxial Test and Mechanical Analysis of Rock-Soil Aggregate Sampled from Natural Sliding Mass. Adv Mater Sci Eng (20152015) 2015:1–14. doi:10.1155/2015/238095
Keywords: gravelly soil, volume-dilatation/contraction, evolution of void ratio, particle breakage, constitutive model
Citation: Zhang J, Li Y and Wang R (2021) A Generalised Plastic Model for Gravelly Soils Considering Evolution of Void Ratio and Particle Breakage. Front. Phys. 9:767821. doi: 10.3389/fphy.2021.767821
Received: 31 August 2021; Accepted: 13 October 2021;
Published: 02 November 2021.
Edited by:
Chun Zhu, Hohai University, ChinaReviewed by:
Huang Qiang, Ningbo University, ChinaXiaohu Zhang, Guizhou University of Engineering Science, China
Copyright © 2021 Zhang, Li and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Rubin Wang, cmJ3YW5nX2hodUBmb3htYWlsLmNvbQ==
 Jiuchang Zhang
Jiuchang Zhang Yue Li
Yue Li Rubin Wang
Rubin Wang