Abstract
We consider a harmonically trapped rotating spin-1 Bose–Einstein condensate with SU(3) spin–orbit coupling subject to a gradient magnetic field. The effects of SU(3) spin–orbit coupling, rotation, and gradient magnetic field on the ground-state structure of the system are investigated in detail. Our results show that the interplay among SU(3) spin–orbit coupling, rotation, and gradient magnetic field can result in a variety of ground states, such as a vortex ring and clover-type structure. The numerical results agree well with our variational analysis results.
1 Introduction
Spin–orbit coupling (SOC) plays an important role in a variety of physics branches. The realization of SOC in neutral atomic gases has attracted major attention both theoretically and experimentally [1–10]. Previous works have shown that the SOC can induce a variety of topological defects, such as skyrmions and half-quantum vortices and solitons, which are useful for the design and exploration of new functional materials [11–18]. Besides the ground-state structure, the dynamic properties of the system are significantly altered in the presence of SOC due to the close relationship between the spin and motional degrees of freedom in the topological excitations [19–24].
With the development of low-temperature technology, various types of SOC, such as Rashba, Dresselhaus, Weyl, and spin–orbit angular momentum, can be realized in experiments [1, 4, 25, 26]. However, most of previous studies of SOC have focused on the type of SU(2), where the internal states are coupled to their momenta via the SU(2) Pauli matrices. Only few works consider the SU(3) SOC, where the spin operators are spanned by the Gell-Mann matrices, which is more effective in describing the internal couplings among three-component condensates, such as a spin-1 Bose–Einstein condensate (BEC). Recently, Han and his co-authors have considered a homogenous SU(3) SO-coupled Bose gas and obtained the double-quantum spin vortices [27]. On the base of their pioneering research work, Li and Chen have studied the SU(3) SO-coupled BEC confined in a harmonic plus quartic trap [28]. Very recently, the ground states of a harmonically trapped spin-1 BEC with SU(3) BEC affected by the external rotation are investigated in [29], where a clover-type ground-state structure is discovered.
Nowadays, the gradient magnetic field has attracted more and more attention. More specifically, it is found that a variety of topological defects, such as a magnetic monopole and quantum knot, and even the artificial SOC can be realized by controlling the gradient magnetic field [30–34]. Li and his co-authors have investigated the ground state of three-component BEC in the gradient magnetic field and obtained the central Mermin–Ho vortex, magnetic monopole, and symmetry vortex lattices [35, 36]. They have also investigated the ground state of SU(2) SO-coupled BEC in the magnetic field and found that the skyrmion chain can induced by the isotropic SU(2) SOC [37]. As far as we know, there is little study on an SU(3) SO-coupled BEC subject to both rotation and gradient magnetic field, which is we attempt to do. In this work, we consider an SU(3) SO-coupled rotating BEC subject to a gradient magnetic field and show that the system has a rich variety of ground states. Here, we want to note that, in real experiments, it is difficult to realize a rotating BEC with fixed SOC [38–40]. To do so, we can rotate the lasers creating SOC for an isotropic trap or rotate both the lasers creating SOC and an anisotropic trap, which leads to an effective time-independent Hamiltonian, Heff = H − ΩLz, describing the system in a rotating frame of Ref. [41].
The rest of this paper is organized as follows. In Section 2, we formulate the theoretical model describing an SU(3) SO-coupled BEC subject to both rotation and gradient magnetic field and briefly introduce the numerical method. The numerical results and its corresponding theoretical analysis through the variational approach are presented in Section 3. Finally, in Section 4, the main results of the work are summarized.
2 Model and Method
To begin with, we consider a quasi-two-dimensional (Q2D) spin-1 BEC with SU(3) SOC [27], which is confined in a controllable magnetic field [36]. Under the mean-field approximation, the Hamiltonian of such a system can be written as [42–44]where with r = (x, y) denotes the spinor order parameters of the spin-1 BEC with normalization ∫Ψ+Ψd2r = N. M is the atomic mass, n = ∑mnm with nm = |ψm(r)|2, and m = 0, ±1 is defined as the condensate density. The Q2D geometry can be realized by imposing a strong harmonic potential along the axial direction with ωz ≫ ω⊥. In this case, the external trapping potential can be written as , with ω⊥ being the radial trapping frequencies. For the interaction terms, the coupling parameters are given by and , where a0,2 are two-body s-wave scattering lengths for total spins 0 and 2, respectively. Lz = − iℏ(x∂y − y∂x) is the z-component of the angular momentum, and Ω is the angular frequency of the external rotation. The vector of spin-1 matrices is defined by , wherein Fx, Fy, and Fz are the 3 × 3 Pauli spin-1 matrices.
The SU(3) SOC considered in the present work can be written as νso = κλ ⋅ p, where κ is the strength of SU(3) SOC and represents the momentum in the Q2D space. is expressed in terms of λx = λ(1) + λ(4) + λ(6) and λy = λ(2) − λ(5) + λ(7), with λ(i)(i = 1, 2, …8) being the Gell-Mann matrices. In this case, the generators of the SU(3) group can be written as [45]
Note that the SU(3) SOC in the Hamiltonian involves all the pairwise couplings between three states. This is distinct from the SU(2) case, where the state of ψ1(r) and ψ−1(r) cannot be coupled directly. In real experiments, the Hamiltonian with SU(3) SOC can be realized using a similar method of Raman dressing as in the SU(2) case, where three laser beams with different polarizations and frequencies, intersecting at an angle of 2π/3, are used for the Raman coupling [27]. The external magnetic field is given by , where the condition B1 = B is the magnetic field gradient in the 2D plane, and we focus on the case of axial bias field B2 = 0. The Lande factor , and μB is the Bohr magneton. The ground state and dynamics of the system can be described by the following dimensionless coupled Gross–Pitaevskii equations:where the length and time units are chosen as and and the normalized wave functions , satisfying the condition . The contact interaction parameters are scaled by Ω = Ω/ω⊥, κ = κ/(ℏω⊥l⊥), B = BgFμBl⊥/(ℏω⊥), and . The ground state of the system can be obtained by using the standard imaginary-time propagation combined with the finite difference methods [46–48]. In our numerical simulations, we prepare with different initial states and then propagate the wave functions in imaginary time to make sure that we proceed to a sufficiently large number of time steps, which guarantees that we have reached a steady state.
3 Results and Discussions
In what follows, we will perform a detailed numerical study of the effects of system parameters on the ground-state structure. The richness of the present system lies in the large number of free parameters, which include the spin-dependent and spin-independent contact interactions, SU(3) SOC, rotation, and gradient field. To highlight the effects of the SOC, rotation, and gradient field, we focus on the antiferromagnetic condensate with c2 > 0 and fix the contact coupling parameters c0 = 100 and c2 = 3.
We first consider the system without SOC and fix the rotation frequency as Ω = 0.7. The typical density and phase distributions of such a system are shown in Figure 1 for different gradient magnetic fields, where only component 1 is shown as the other two components show similar behavior. In the absence of both gradient field (B = 0) and SU(3) SOC (κ = 0), the system is located at the center of the external harmonic potential, and no other lumps are formed. In this case, discrete vortices are formed due to the external rotation, but no vortex lattice can be formed due to the small contact interactions, as shown in Figure 1A. In the presence of a gradient magnetic field, the density distribution of the system shows a ring structure, and the size of center hole increases with the strength of the gradient magnetic field, as shown in Figures 1B,C for B = 1 and B = 2, respectively. In these cases, a vortex ring is formed along the ring direction (see Figure 1F for the phase distribution of Figure 1C), and the number of vortex also increases with the gradient magnetic field. Furthermore, if we increase the strength of gradient magnetic to B = 3 (see Figure 1D), most of vortices begin to move into the central hole, and the vortex ring is gradually destroyed. Upon increasing the gradient field to B = 4, all the vortices move to the central hole and form a giant vortex at the center of the trapping potential. In this case, no visible vortex remains, as shown in Figure 1E. Comparing Figures 1A–E, it is found that the radius of the ring increases with the gradient magnetic field.
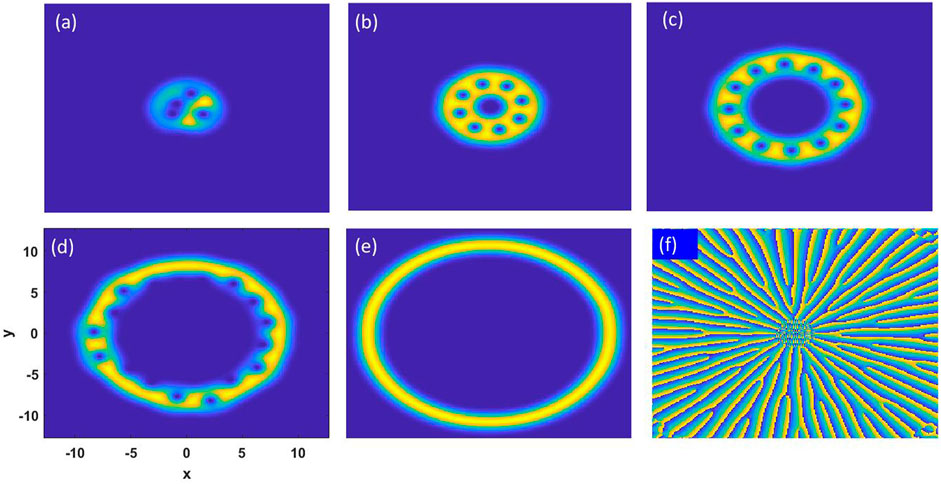
FIGURE 1
Typical ground-state structures of a rotating BEC as a function of the gradient magnetic field in the absence of SU(3) spin–orbit coupling. (A)–(E) Density distributions of component 1 for different gradient magnetic fields: (A)B = 0, (B)B = 1, (C)B = 2, (D)B = 3, and (E)B = 4. (F) The corresponding phase distribution of (C). Other parameters are fixed as c0 = 100, c2 = 3, Ω = 0.7, and κ = 0, and the scale of each figure is [−12.8,12.8] in units of .
Now, we turn our attention to the combined effects of SU(3) SOC and gradient magnetic on the ground-state structure of the system and thus set Ω = 0. Figure 2 shows the typical density and phase distributions of the system for the varying SU(3) SOC and gradient magnetic field. Previous studies on the SU(3) SOC Bose gases have shown that the triangular lattice structure is energy favorable for both homogeneous and confined systems [27, 29]. In the present system, we find a similar triangular lattice structure in the absence of the gradient magnetic field (B = 0), as shown in Figure 2A. In the presence of a gradient magnetic field, it is found that, with the increasing strength of the gradient magnetic field, the triangular lattice structure is gradually destroyed. In addition, the system evolves into three parts in space and eventually into a clover-type structure, as shown in Figures 2B–D for B = 1, 2, 3, respectively. Here, we want to note that a similar clover-type structure has been previously discovered in an SU(3) SO-coupled Bose gas with rotation [29]. However, the clover-type structure found in the present work is induced by the combined effects of both SU(3) SOC and a gradient magnetic field, which give us another way to realize the clover-type structure in a non-rotating system. It is interesting to observe that the distance among such three space parts of the clover-type structure is unchanged if we increase the strength of SU(3) SOC but fix the strength of the gradient magnetic field, as shown in Figures 2D,E for B = 3, κ = 3 and B = 3, κ = 5, respectively. If we look at the phase distribution of the clover-type structure, as shown in Figure 2F for Figure 2D, it is easy to find that the local lump is in the plane wave phase, which is consistent with our previous results on the SU(3) SO-coupled system [27].
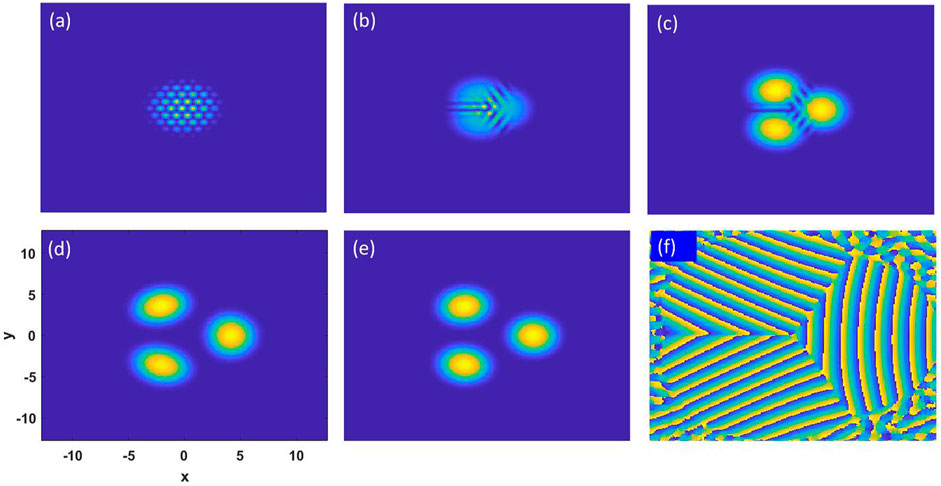
FIGURE 2
Typical ground-state structures of an SU(3) spin–orbit-coupled BEC as a function of SU(3) spin–orbit coupling and gradient magnetic field in the absence of rotation. (A)–(D) Density distributions of component 1 for fixed SU(3) spin–orbit coupling κ = 3 and for different gradient magnetic fields: (A)B = 0, (B)B = 1, (C)B = 2, and (D)B = 3. (E) Density distribution of the system for B = 3 and κ = 5. (F) The corresponding phase distribution of (D). Other parameters are fixed as c0 = 100, c2 = 3, and Ω = 0, and the scale of each figure is [-12.8,12.8] in units of .
Finally, we move to the combined effects of SU(3) SOC, rotation, and the gradient magnetic field on the ground-state structure of the system. To highlight the effect of SU(3) SOC, we further fix Ω = 0.7. Figure 3 shows the typical ground-state structures of a rotating BEC as a function of the SU(3) SOC and gradient magnetic field. In the absence of SU(3) SOC, the system shows a ring structure with a vortex ring (see Figure 3A for B = 2 and κ = 0), which is consistent with that reported in Figure 1C. In the presence of SU(3) SOC, it is found that the annular structure is destroyed even for a small SU(3) SOC, as shown in Figure 3B for κ = 0.5 and B = 2, where two asymmetry lumps with visible vortices are formed. Further increasing the strength of SU(3) SOC, this tendency is becoming more and more obvious, and eventually, the system evolves into a single lump, as shown in Figures 3C,D, and F (the corresponding phase distribution of (Figure 3D)) for κ = 1 and κ = 2, respectively. This is different from the phase diagram in [38], where the density distributions show some symmetry and the center of mass of the system is still around the center of the trap (which also can be seen from their momentum distributions). For the present case, the symmetry of the system is further broken and the center of mass of the system deviates from the center of the trap. Actually, such difference can be understood by the fact that the SU(3) SO-coupled system has three discrete minima in the single-particle energy spectrum, and the number and weight of such three minima are selected for different strengths of SOC. Similar to the former case, it is interesting to observe that the distance between the lump and the center of trapping potential increases with the gradient magnetic field (see Figure 3E for B = 1 and κ = 2). Here, we want to note that we have also calculated other rotation frequencies, and the results show similar behavior.
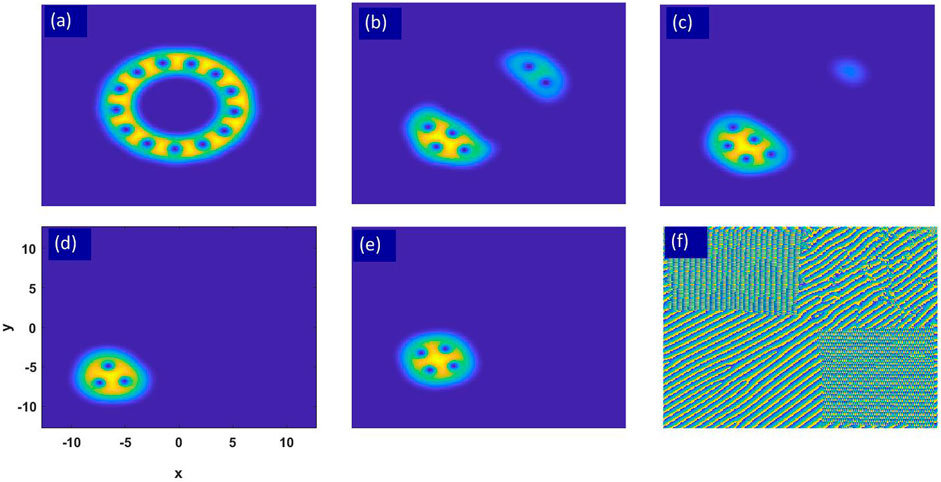
FIGURE 3
Typical ground-state structures of a rotating BEC as a function of the SU(3) spin–orbit coupling and gradient magnetic field. (A)–(D) Density distributions of component 1 for a fixed gradient magnetic field B = 2 and for different SU(3) spin–orbit coupling: (A)κ = 0, (B)κ = 0.5, (C)κ = 1, and (D)κ = 2. (E) Density distribution of the system for κ = 2 and B = 1. (F) The corresponding phase distribution of (D). Other parameters are fixed as c0 = 100, c2 = 3, and Ω = 0.7, and the scale of each figure is [−12.8,12.8] in units of .
To give a clearer understanding of the above results, we employ the variational method and analytically calculate the possible ground state. We begin with the single-particle energy spectrum of the system, which can be obtained by diagonalizing the kinetic energy and SOC terms. It is found that there exist three discrete minima residing on the vertices of an equilateral triangle in the momentum space. As discussed in [27], a threefold-degenerate plane wave ground state is selected as the ground state for a ferromagnetic condensate with SU(3) SOC, while three discrete minima with unequal (equal) weights are selected for the antiferromagnetic case. Consequently, the variational wave function can be written as Ψ = Ψ1 + Ψ2 + Ψ3, wherewhere Ψ1, Ψ2, and Ψ3 are the wave functions corresponding to the three minima of the single-particle spectrum, ( −2κ, 0), , and . Substituting these ansatzes into Equation 1, we can calculate the energy for each minimum in the momentum space as follows:
It is found that the minimum energies are equal to . Consequently, there also exist three points in real space, that is, , , and . In this case, particles can condense at such three real space points, and the three lumps locate at the x-axis, the second quadrant and the third quadrant. In addition, we find that these positions are only related to the gradient magnetic field B and show independence with SU(3) SOC κ. All the results are consistent with those reported in Figure 2. When the rotation is included, we have
In this case, the second equation has the minimum energy . Therefore, all particles condense at a single real space point (), and the distance between the lump and the center of trapping potential increases with the gradient magnetic field B, which are consistent with those reported in Figure 3.
4 Conclusion
We have investigated the ground-state structure of a harmonically trapped rotating spin-1 BEC with SU(3) SOC subject to a gradient magnetic field. In the absence of SU(3) SOC, the system shows an annular structure, where a vortex ring is formed. In the absence of rotation, it is found that the clover-type structure discovered in the previous work can also be induced by the combined effects of SU(3) SOC and gradient magnetic field, and their distance shows sole dependence on the gradient magnetic field. When the rotation is included, we found that only one lump is formed in the three quadrants, and the distance between the lump and the center of trapping potential increases with the gradient magnetic field. Finally, we have employed the variational method and analytically calculated the possible ground state, which agrees well with our numerical simulations.
Statements
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work was supported by the National Natural Science Foundation of China under Grant Nos. 12075163, 12175129, 11775253, 12175027, and 11875010; the Dazhou Science and Technology Bureau under Grant No. 2019CYR0001; and the Natural Science Foundation of Chongqing under Grant No. cstc2019jcyj-msxmX0217.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
LinY-JJiménez-GarcíaKSpielmanIB. Spin-orbit-coupled Bose-Einstein Condensates. Nature (2011) 471:83–6. 10.1038/nature09887
2.
WangPYuZQFuZMiaoJHuangLChaiSet alSpin-orbit Coupled Degenerate Fermi Gases. Phys Rev Lett (2012) 109:095301. 10.1103/PhysRevLett.109.095301
3.
CheukLWSommerATHadzibabicZYefsahTBakrWSZwierleinMW. Spin-Injection Spectroscopy of a Spin-Orbit Coupled Fermi Gas. Phys Rev Lett (2012) 109:095302. 10.1103/PhysRevLett.109.095302
4.
HuangLMengZWangPPengPZhangS-LChenLet alExperimental Realization of Two-Dimensional Synthetic Spin-Orbit Coupling in Ultracold Fermi Gases. Nat Phys (2016) 12:540–4. 10.1038/nphys3672
5.
WuZZhangLSunWXuX-TWangB-ZJiS-Cet alRealization of Two-Dimensional Spin-Orbit Coupling for Bose-Einstein Condensates. Science (2016) 354:83–8. 10.1126/science.aaf6689
6.
KolkowitzSBromleySLBothwellTWallMLMartiGEKollerAPet alSpin-orbit-coupled Fermions in an Optical Lattice Clock. Nature (2017) 542:66–70. 10.1038/nature20811
7.
LiJ-RLeeJHuangWBurcheskySShteynasBTopFÇet alA Stripe Phase with Supersolid Properties in Spin-Orbit-Coupled Bose-Einstein Condensates. Nature (2017) 543:91–4. 10.1038/nature21431
8.
GalitskiVSpielmanIB. Spin-orbit Coupling in Quantum Gases. Nature (2013) 494:49–54. 10.1038/nature11841
9.
ZhaiH. Spin-orbit Coupled Quantum Gases. Int J Mod Phys B (2012) 26:1230001. 10.1142/s0217979212300010
10.
ZhaiH. Degenerate Quantum Gases with Spin-Orbit Coupling: A Review. Rep Prog Phys (2015) 78:026001. 10.1088/0034-4885/78/2/026001
11.
WuCMondragon-SchemIZhouXF. Unconventional Bose-Einstein Conensations from Spin-Orbit Coupling. Chin Phys Lett (2011) 108:010402. 10.1088/0256-307x/28/9/097102
12.
HuHRamachandhranBPuHLiuXJ. Spin-orbit Coupled Weakly Interacting Bose-Einstein Condensates in Harmonic Traps. Phys Rev Lett (2012) 108:010402. 10.1103/PhysRevLett.108.010402
13.
WangCGaoCJianC-MZhaiH. Spin-orbit Coupled Spinor Bose-Einstein Condensates. Phys Rev Lett (2010) 105:160403. 10.1103/physrevlett.105.160403
14.
HoT-LZhangS. Bose-Einstein Condensates with Spin-Orbit Interaction. Phys Rev Lett (2011) 107:150403. 10.1103/physrevlett.107.150403
15.
FungTPoonJLiuXJ. Quantum Spin Dynamics in a Spin-Orbit-Coupled Bose-Einstein Condensate. Phys Rev A (2016) 93:063420. 10.1103/physreva.93.063420
16.
HuHRamachandhranBPuHLiuXJDrummondPDHuH. Spin-orbit Coupled Weakly Interacting Bose-Einstein Condensates in Harmonic Traps. Phys Rev Lett (2012) 108:010402. 10.1103/PhysRevLett.108.010402
17.
KatoMZhangXFSasakiDSaitoH. Twisted Spin Vortices in a Spin-1 Bose-Einstein Condensate with Rashba Spin-Orbit Coupling and Dipole-Dipole Interaction. Phys Rev A (2016) 94:043633. 10.1103/physreva.94.043633
18.
LiuYHolderTYanB. Chirality-Induced Giant Unidirectional Magnetoresistance in Twisted Bilayer Graphene. The Innovation (2021) 2:100085. 10.1016/j.xinn.2021.100085
19.
HanWJuzeliūnasGZhangWLiuWM. Supersolid with Nontrivial Topological Spin Textures in Spin-Orbit-Coupled Bose Gases. Phys Rev A (2015) 91:013607. 10.1103/physreva.91.013607
20.
ZhangXFKatoMHanWZhangSGSaitoH. Spin-orbit-coupled Bose-Einstein Condensates Held under a Toroidal Trap. Phys Rev A (2017) 95:033620. 10.1103/physreva.95.033620
21.
WenLSunQWangHQJiACLiuWM. Ground State of Spin-1Bose-Einstein Condensates with Spin-Orbit Coupling in Zeeman Field. Phys Rev A (2012) 86:043602. 10.1103/physreva.86.043602
22.
WenLSunQChenYWangDSHuJChenHet alMotion of Solitons in One-Dimensional Spin-Orbit-Coupled Bose-Einstein Condensates. Phys Rev A (2016) 94:061602. 10.1103/physreva.94.061602
23.
SunQWenLLiuWMJuzeliūnasGJiAC. Tunneling-assisted Spin-Orbit Coupling in Bilayer Bose-Einstein Condensates. Phys Rev A (2015) 91:033619. 10.1103/physreva.91.033619
24.
SakaguchiHLiBMalomedBA. Creation of Two-Dimensional Composite Solitons in Spin-Orbit-Coupled Self-Attractive Bose-Einstein Condensates in Free Space. Phys Rev E Stat Nonlin Soft Matter Phys (2014) 89:032920. 10.1103/PhysRevE.89.032920
25.
AndersonBMJuzeliūnasGGalitskiVMSpielmanIB. Synthetic 3D Spin-Orbit Coupling. Phys Rev Lett (2012) 108:235301. 10.1103/physrevlett.108.235301
26.
ChenH-RLinK-YChenP-KChiuN-CWangJ-BChenC-Aet alSpin-Orbital-Angular-Momentum Coupled Bose-Einstein Condensates. Phys Rev Lett (2018) 121:113204. 10.1103/physrevlett.121.113204
27.
HanWZhangXFSongSWSaitoHZhangWLiuWMet alDouble-quantum Spin Vortices in SU(3) Spin-Orbit-Coupled Bose Gases. Phys Rev A (2016) 94:033629. 10.1103/physreva.94.033629
28.
LiCHQuCNiffeneggerRJWangSJHeMBlasingDBet alSpin Current Generation and Relaxation in a Quenched Spin-Orbit-Coupled Bose-Einstein Condensate. Nat Commun (2019) 10:375–02. 10.1038/s41467-018-08119-4
29.
PengPLiG-QWangB-HCaoZ-Z. Exotic Ground States in a SU(3) Spin-Orbit Coupled Spin-1 Bose-Einstein Condensate under Rotation. Chaos, Solitons & Fractals (2020) 141:110332. 10.1016/j.chaos.2020.110332
30.
AndersonBMSpielmanIBJuzeliūnasG. Magnetically Generated Spin-Orbit Coupling for Ultracold Atoms. Phys Rev Lett (2013) 111:125301. 10.1103/physrevlett.111.125301
31.
XuZFYouLUedaM. Atomic Spin-Orbit Coupling Syntheized with Magnetic-Field-Gradient Pulses. Phys Rev A (2013) 87:063634. 10.1103/physreva.87.063634
32.
AidelsburgerMAtalaMLohseMBarreiroJTBarreiroBBlochI. Realization of the Hofstadter Hamiltonian with Ultracold Atoms in Optical Lattices. Phys Rev Lett (2013) 111:185301. 10.1103/physrevlett.111.185301
33.
KennedyCJSiviloglouGAMiyakeHBurtonWCKetterleW. Spin-orbit Coupling and Quantum Spin Hall Effect for Neutral Atoms without Spin Flips. Phys Rev Lett (2013) 111:225301. 10.1103/physrevlett.111.225301
34.
RayMWRuokokoskiEKandelSMöttönenMHallDS. Observation of Dirac Monopoles in a Synthetic Magnetic Field. Nature (2014) 505:657–60. 10.1038/nature12954
35.
LiJYuYMZhuangLLiuWM. Dirac Monopoles with a Polar-Core Vortex Induced by Spin-Orbit Coupling in Spinor Bose-Einstein Condensates. Phys Rev A (2017) 95:043633. 10.1103/physreva.95.043633
36.
Liu Jing-SiJSLi JiJLiu Wu-MingWM. Ground State of a Rotating Bose-Einstein Condensate with In-Plane Quadrupole Field. wlxb (2017) 66:130305. 10.7498/aps.66.130305
37.
Li JiJLiu Wu-MingWM. Ground State of Spin-Orbit Coupled Rotating Two-Component Bose-Einstein Condensate in Gradient Magnetic Field. wlxb (2018) 67:110302. 10.7498/aps.67.20180539
38.
RadicJSedrakyanTASpielmanIBGalitskiV. Vortices in Spin-Orbit-Coupled Bose-Einstein Condensates. Phys Rev A (2011) 84:063604. 10.1103/physreva.84.063604
39.
ZhouXFZhouJWuCJ. Vortex Structures of Rotating Spin-Orbit-Coupled Bose-Einstein Condensates. Phys Rev A (2011) 84:063624. 10.1103/physreva.84.063624
40.
XuX-QHanJH. Spin-Orbit Coupled Bose-Einstein Condensate under Rotation. Phys Rev Lett (2011) 107:200401. 10.1103/physrevlett.107.200401
41.
LiuCFJuzeliūnasGLiuWM. Spin-orbit Coupling Manipulating Composite Topological Spin Textures in Atomic-Molecular Bose-Einstein Condensates. Phys Rev A (2017) 95:023624. 10.1103/physreva.95.023624
42.
LiuCFLiuWM. Spin-orbit-coupling-induced Half-Skyrmion Excitations in Rotating and Rapidly Quenched Spin-1 Bose-Einstein Condensates. Phys Rev A (2012) 86:033602. 10.1103/physreva.86.033602
43.
JustinLMagnusOBRuostekoskiJ. Energetically Stable Singular Vortex Cores in an Atomic Spin-1 Bose-Einstein Condensate. Phys Rev A (2012) 86:013613. 10.1103/physreva.86.013613
44.
JiACLiuWMSongJLZhouF. Dynamical Creation of Fractionalized Vortices and Vortex Lattices. Phys Rev Lett (2008) 101:010402. 10.1103/PhysRevLett.101.010402
45.
ArfkenGBWebberHJHrrisFE. Mathematical Methods for Physicists. 7th ed.. New York: Academic Press (2000).
46.
BaoWZDuQ. Computing the Ground State Solution of Bose-Einstein Condensates by Normalized Gradient Flow. SIAM J SCI Comput (2014) 25:1674. 10.1137/s1064827503422956
47.
ZhangXFDongRFLiuTLiuWMZhangSG. Spin-orbit-coupled Bose-Einstein Condensates Confined in Concentrically Coupled Annular Traps. Phys Rev A (2012) 86:063628. 10.1103/physreva.86.063628
48.
ChenS-LWangL-XWenLDaiC-QLiuJ-KZhangX-F. Stripe-on-plane-wave Phase of a Binary Dipolar Bose Gases with Soft-Core Long-Range Interactions. Optik (2021) 247:167932. 10.1016/j.ijleo.2021.167932
Summary
Keywords
Bose–Einstein condensate, SU(3) spin–orbit coupling, gradient magnetic field, rotation, GP equation
Citation
Chen G-P, Tu P, Qiao C-B, Zhu J-X, Jia Q and Zhang X-F (2021) SU(3) Spin–Orbit Coupled Rotating Bose–Einstein Condensate Subject to a Gradient Magnetic Field. Front. Phys. 9:768799. doi: 10.3389/fphy.2021.768799
Received
01 September 2021
Accepted
29 September 2021
Published
02 November 2021
Volume
9 - 2021
Edited by
Zhaoxin Liang, Zhejiang Normal University, China
Reviewed by
Qing Sun, Capital Normal University, China
Wei Yi, University of Science and Technology of China, China
Xiang-Fa Zhou, University of Science and Technology of China, China
Updates
Copyright
© 2021 Chen, Tu, Qiao, Zhu, Jia and Zhang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Guang-Ping Chen, chengp205@126.com; Xiao-Fei Zhang, xfzhang_physics@163.com
This article was submitted to Optics and Photonics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.