Self-Focusing Property of Partially Coherent Beam With Non-Uniform Correlation Structure in Non-Linear Media

Coherence in a light beam has the potential to serve as a degree of freedom for manipulating the beam. In this work, the self-focusing property of a partially coherent beam with a non-uniform correlation structure propagating in a non-linear medium is investigated. The analysis of the evolution of beam width reveals that the coherence structure plays a vital role in the self-focusing formation. A threshold condition for the coherence radius is proposed for the first time, and the relation of self-focusing length and initial coherence radius is studied numerically and analytically. It is shown that a feasible approach for manipulating the self-focusing length by adjusting the initial coherence radius is achieved.

Introduction

Spatial coherence is a crucial intrinsic characteristic of light. Optical coherence is now the subject of a well-developed theory [1]; the laser beam with decreased spatial coherence has been analyzed in depth, and it has been labeled as the partially coherent beam (PCB) [2]. By adjusting the spatial coherence of PCBs, novel properties can be exhibited that play a significant role in the light–matter interaction and have attracted the attention of researchers [1, 3]. In the past few decades, intense interest has been focused on the design of different types of PCBs and the interaction between PCBs and various media. To date, many PCBs with uniform or non-uniform correlation structures have been introduced [4], and their propagation properties in turbulence and uniaxial crystal media have been studied [5, 6]. Although these works have been extensive and might seem to be complete, the investigations have not exhausted all possibilities. The non-linear effect can significantly affect the essence of PCB propagation; in practical terms, the Kerr effect strongly exists when an intense laser beam is present in non-linear media.

There are several approaches to describe the propagation of PCBs in a non-linear medium, for example, the coherent density approach [7], multimode decomposition [8], the geometric optics approach [9], and the mutual coherence function [1]. At present, the Gaussian–Schell source model (GSM) of a partially coherent beam propagating in a non-linear medium is frequently used [10–14]. With a spatially variant correlation function proposed by Gori et al. [15], PCBs with a non-uniform correlation structure not only exhibit self-focusing and self-shifting properties [16–19] but also produce lower scintillation in turbulence [20, 21] than that of GSM beams. The self-focusing property of non-uniformly correlated PCBs (NUC-PCBs) may spark extensive interest owing to their wide application in many fields, such as laser filamentation [10], lightening control [22], high-power atmospheric propagation [23], optical micromanipulation [24], optical communications [25], and optical coherence encryption [26]. Thus, the investigation of the self-focusing property of NUC-PCBs has potential application prospects.

Spatial coherence is regarded as a significant element of a laser beam, and it is vital to achieve the manipulation of self-focusing domain, especially for the control of filamentation one. Until now, the well-known methods for controlling the filamentation domain are as follows: modulating the laser pulse power [27], adjusting the divergence angle of initial laser [28], launching negatively chirped ultrashort pulses [29], and double-lens setup [23]. It is worth mentioning that the input peak intensity is the easiest quantity to change and control precisely [30]; however, the laser power is still limited in the practical scene. If the spatial coherence can be used to control the self-focusing length, it may provide an alternative route to realize the manipulation of filamentation domain. It not only fills in the gap of spatial coherence to control the length of self-focusing but also proposes a feasible solution to obtain the long-range filament propagation. Therefore, it is time to explore an avenue for achieving the manipulation of self-focusing length by adjusting the coherence.

In this work, the self-focusing property of an NUC-PCB propagating in a non-linear medium is investigated. Combining with the non-linear Schrödinger (NLS) equation and mutual coherence function, an analytical expression for beam width is derived. By analyzing the evolution of beam width, the result illustrates that the coherence structure is a key element for self-focusing formation. Furthermore, with the first proposal of the threshold condition of coherence radius, the analytical formula of self-focusing length is obtained. More importantly, it is found that a feasible approach for manipulating the self-focusing length by adjusting the initial coherence radius is realized. These new findings may provide a theoretical and numerical basis in optical communication, optical encryption, optical micro-fabrication, and related areas.

Theory

The propagation dynamics of laser beams in a Kerr medium is described by the NLS equation. Under the slowly varying amplitude approximation, the NLS equation for a two-dimensional quasi-monochromatic partially coherent beam is [10]

$\text{i}\frac{\partial \mathbf{E}}{\partial z}+\frac{\beta }{2}{\nabla }^2\mathbf{E}+\frac{n_{2}k}{n_0}\langle \mathbf{E}{\mathbf{E}}^{\ast }\rangle \mathbf{E}=0,(1)$

where $\text{E}=\text{E}\left(\text{r},z\right)$ is the amplitude of the electric field, $\beta$ is the diffraction or second-order dispersion coefficient, ${\nabla }^2={\partial }^2/\partial x^2+{\partial }^2/\partial y^2$ is the transverse Laplacian, $n_0$ $\left(n_2\right)$ is the linear (non-linear) refractive index, $k=2\pi /\lambda$ is the wavenumber related to the wavelength, $\langle •\rangle$ denotes the statistical ensemble average, and $\ast$ is the conjugation operator.

Using a PCB as the laser source, Eq. 1 is unable to correctly describe the propagation evolution in a non-linear medium. Spatial coherence refers to the correlation of complex fields at the same time but at different transverse points ${\text{r}}_1$ and ${\text{r}}_2$. To clarify and emphasize the influence of spatial coherence, the temporal coherence will not be involved here. If Eq. 1 is applied to $\text{E}\left({\text{r}}_1,z\right)$ and multiplied through by ${\text{E}}^{\ast }\left({\text{r}}_2,z\right)$, followed by subtracting a similar expression, which is the equation applied to ${\text{E}}^{\ast }\left({\text{r}}_2,z\right)$ and multiplied through by $\text{E}\left({\text{r}}_1,z\right)$, and the statistical ensemble averaging the resulting expression [10, 12], one obtains

$\begin{array}{l}\mathrm{i}\frac{\partial \langle \mathbf{E}\left({\mathbf{r}}_1\right){\mathbf{E}}^{\ast }\left({\mathbf{r}}_2\right)\rangle }{\partial z}+\frac{\beta }{2}\left({\nabla }_1^2-{\nabla }_2^2\right)\langle \mathbf{E}\left({\mathbf{r}}_1\right){\mathbf{E}}^{\ast }\left({\mathbf{r}}_2\right)\rangle \\ +\frac{n_{2}k}{n_0}\left[{\left|\mathbf{E}\left({\mathbf{r}}_2\right)\right|}^2-{\left|\mathbf{E}\left({\mathbf{r}}_1\right)\right|}^2\right]\langle \mathbf{E}\left({\mathbf{r}}_1\right){\mathbf{E}}^{\ast }\left({\mathbf{r}}_2\right)\rangle =0.\end{array}(2)$

Mutual coherence function, i.e., $\mathbf{W}\left({\mathbf{r}}_i,{\mathbf{r}}_j\right)=\langle \mathbf{E}\left({\mathbf{r}}_i\right){\mathbf{E}}^{\ast }\left({\mathbf{r}}_j\right)\rangle \left(i,j=\mathrm{1,2}\right)$, is a common method to solve PCBs in propagation media [1, 31–34]. Equation 2 can be converted to [10, 12–14]

$\begin{array}{l}\text{i}\frac{\partial \mathbf{W}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)}{\partial z}+\frac{\beta }{2}\left({\nabla }_1^2-{\nabla }_2^2\right)\mathbf{W}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)\\ +\frac{n_{2}k}{n_0}\left[\mathbf{W}\left({\mathbf{r}}_2,{\mathbf{r}}_2\right)-\mathbf{W}\left({\mathbf{r}}_1,{\mathbf{r}}_1\right)\right]\mathbf{W}\left({\mathbf{r}}_1,{\mathbf{r}}_2\right)=0.\end{array}(3)$

Considering the PCB with non-uniform correlation function, i.e., assuming Gaussian weight and kernel functions in the spatial domain, the mutual coherence function at the source plane is [17, 18]

$\begin{array}{l}\mathbf{W}\left({\mathbf{r}}_1,{\mathbf{r}}_2,0\right)=\exp \left[-\left({\mathbf{r}}_1^2+{\mathbf{r}}_2^2\right)/2w_0^2\right]\\ \times \exp \left\{-{\left[{\left({\mathbf{r}}_2-{\mathbf{r}}_0\right)}^2-{\left({\mathbf{r}}_1-{\mathbf{r}}_0\right)}^2\right]}^2/{\sigma }_0^4\right\},\end{array}(4)$

with the initial coherence radius ${\sigma }_0$ and the maximum intensity being in the region centered at ${\mathbf{r}}_0$.

By setting $\mathbf{u}=\left({\mathbf{r}}_1+{\mathbf{r}}_2\right)/2$ and $\mathbf{v}={\mathbf{r}}_1-{\mathbf{r}}_2$ in Eq. 4, we obtain from Eq. 3

$\left\{\frac{\partial }{\partial z}-\text{i}\beta {\nabla }_u{\nabla }_v+\frac{2\mathrm{i}{n}_2\mathrm{k}\mathbf{uv}}{n_0{w}_0^2}\right\}\mathbf{W}\left(\mathbf{u},\mathbf{v},z\right)=0,(5)$

where

$\mathbf{W}\left(\mathbf{u},\mathbf{v},z\right)=I_z\exp \left(-{\mathbf{u}}^2/w_z^2-{\mathbf{v}}^2/w_z^2-4{\mathbf{u}}^2{\mathbf{v}}^2/{\sigma }_z^2+\text{i}\mathbf{u}\mathbf{v}{\phi }_z\right).$

Inserting initial conditions (beam width $w_{z=0}=w_0$, coherence radius ${\sigma }_{z=0}={\sigma }_0$, phase ${\phi }_{z=0}=0$, and intensity $I_{z=0}=1$) into Eq. 5, a set of coupled equations for these quantities is obtained:

$\frac{\mathrm{d}{w}_z}{\mathrm{d}z}=\beta {\phi }_z{w}_z,(6)$

$\frac{\mathrm{d}{\sigma }_z}{\mathrm{d}z}=\beta {\phi }_z{\sigma }_z,(7)$

$\frac{\mathrm{d}{\phi }_z}{\mathrm{d}z}=\beta /w_z^4-\beta {\phi }_z^2-16\beta /{\sigma }_z^4-2n_{2}k/n_0{w}_z^2,(8)$

$\frac{\mathrm{d}{I}_z}{\mathrm{d}z}=-\beta {\phi }_z{I}_z.(9)$

Combining Eqs. 6, 8, the dynamics of beam width of an NUC-PCB is

$\frac{{\mathrm{d}}^2{w}_z}{\mathrm{d}{z}^2}=\frac{{\beta }^2\left(1-{\gamma }^2\right)}{w_z^3}-\frac{2\beta n_{2}k}{n_0{w}_z},(10)$

with the boundary condition ${\left(\mathrm{d}{w}_z/\mathrm{d}z\right)|}_{z=0}=0$; Equation 10 can then be formulated as

${\left(\frac{\mathrm{d}{w}_z}{\mathrm{d}z}\right)}^2+{\beta }^2\left(1-{\gamma }^2\right)\left(\frac{1}{w_z^2}-\frac{1}{w_0^2}\right)+\frac{4\beta n_{2}k}{n_0}\ln \left(\frac{w_z}{w_0}\right)=0.(11)$

To ensure the NUC-PCB with a minimum beam width (without collapse), the first and second derivatives of beam width should satisfy the following requirements: $\mathrm{d}{w}_z/\mathrm{d}z=0$ and ${\mathrm{d}}^2{w}_z/\mathrm{d}{z}^2>0$, i.e.,

$\{\begin{array}{l}{\beta }^2\left(1-{\gamma }^2\right)\left(\frac{1}{w_z^2}-\frac{1}{w_0^2}\right)+\frac{4\beta n_{2}k}{n_0}\ln \left(\frac{w_z}{w_0}\right)=0,\\ \frac{{\beta }^2\left(1-{\gamma }^2\right)}{2w_0^2}-\frac{\beta n_{2}k}{n_0}>0.\end{array}(12)$

Based on Eq. 12, the critical coherence radius for the formation of self-focusing is given by

$\frac{1}{{\sigma }_{cr}^4}=\frac{1}{16w_0^4}-\frac{n_{2}k}{8\beta n_0{w}_0^2}.(13)$

Here, the initial coherence radius should be considered as ${\sigma }_0<{\sigma }_{cr}$.

With boundary conditions $w_{z=0}=w_0$ and ${\left(\mathrm{d}{w}_z/\mathrm{d}z\right)|}_{z=0}=0$, an analytical expression for beam width is obtained:

$w_z^2=w_0^2+\frac{{\beta }^2\left(1-{\gamma }^2\right)z^2}{w_0^2}-\frac{2\beta n_{2}k\left(1+2\alpha \right)z^2}{n_0}.(14)$

Physically, the evolution of beam width is determined by a competition for two main factors: 1) spreading induced by free-space diffraction and 2) self-focusing caused by the non-uniform correlation structure and non-linearity of the medium. Here, the parameters are recorded as $\gamma =4w_0^2/{\sigma }_0^2=4w_z^2/{\sigma }_z^2$, $\alpha =\ln \left({\sigma }_z/{\sigma }_0\right)$, and the focusing case with $n_2>0$ is considered.

When the critical coherence radius is satisfied, the self-focusing length can be expressed as

$z_f=\frac{\left({\sigma }_0^2/{\sigma }_{cr}^2-1\right)}{\sqrt{{\beta }^2\left(1-{\gamma }^2\right)/w_0^4-2\beta n_{2}k\left[1+2\ln \left({\sigma }_0/{\sigma }_{cr}\right)\right]/n_0{w}_0^2}},(15)$

where a variable substitution is used, due to the common range of variables ${\sigma }_z/{\sigma }_0\in \left(\mathrm{0,1}\right]$ and ${\sigma }_0/{\sigma }_{cr}\in \left(\mathrm{0,1}\right]$.

Numerical Calculations and Analysis

Using the fast Fourier transform split-step method [35], the initial parameters are chosen as follows: wavelength $\lambda =0.8$ µm, initial beam width $w_0=0.8$ mm, Rayleigh length for PCBs $z_R=k{w}_0{\sigma }_0/2$[12], coefficient $\beta =1/n_{0}k$, propagation length $z=0.6z_R$, linear refractive index of the medium $n_0=1$, transverse size $20w_0$, grid number $N=512$, and step number $M=2000$.

The self-focusing length for the NUC-PCB in the linear and non-linear media is investigated numerically, where the non-linear refractive index is $n_2=3\times {10}^{-21}$ m²/W, the critical coherence radius for self-focusing is satisfied with ${\sigma }_{cr}=2w_0$, and the initial coherence radius is ${\sigma }_0=0.25{\sigma }_{cr}$. Due to the existence of non-linearity, the self-focusing length in a linear medium (Figure 1A, i.e., $z=0.1056z_R$) is shorter than that in a non-linear medium (Figure 1B, i.e., $z=0.1935z_R$), and the peak intensity for the linear case is lower than that of the non-linear one (Figure 1D). It shows that the property of propagation medium can affect the self-focusing length, and in a medium with $n_2>0$, that length can be extended. Besides, the propagation property for the GSM is mentioned; there is no self-focusing phenomenon seen in Figure 1C because the peak intensity is located at the source plane (blue curve in Figure 1D). It may be predicted that the non-uniform coherence structure plays a vital role in the formation of self-focusing.

FIGURE 1

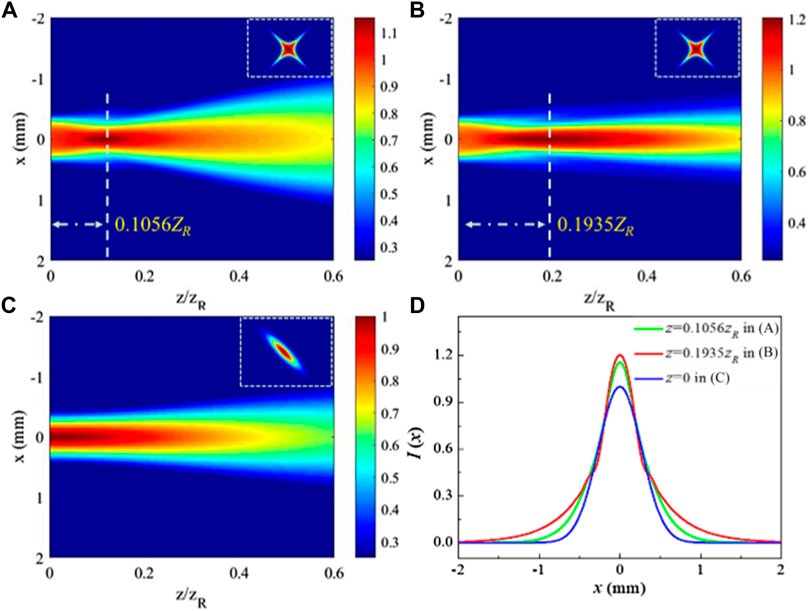
FIGURE 1. Propagation evolution of three cases: (A) NUC-PCB in a linear medium, (B) NUC-PCB in a non-linear medium, and (C) GSM beam in a non-linear medium, where (D) shows the corresponding intensity distribution at the locations of maximum intensity in (A–C). The insets represent the mutual coherence function (or cross-spectral density) at the source plane.

For the analytical expression of beam width (i.e., Eq. 14), it is obvious that the propagation dynamics are determined by a balance of three elements, i.e., diffraction (or dispersion), coherence structure of beam, and property of propagation medium. Similarly, the beam width for the GSM beam is derived as $w_G^2=w_0^2+{\beta }^2\left(1+\gamma \right)z^2/w_0^2-2\beta n_{2}k\left(1+2\alpha \right)z^2/n_0$. The critical coherence radius is $1/{\sigma }_G^2=n_{2}k/2n_0\beta -1/4w_0^2$, which shows that there is no real root in the GSM case, i.e., there is no beam focusing. For the same non-linear refractive index, the GSM beam spreads (magenta curve in Figure 2), while the NUC-PCB is focused (green curve in Figure 2). For NUC-PCBs, a higher non-linear refractive index causes a more obvious beam focusing (red curve in Figure 2). It illustrates that the formation of self-focusing is more affected by the non-uniform correlation structure than by the non-linearity of the medium. The numerical and analytical analysis indicates that the coherence structure is the core element for the self-focusing formation. Besides, with the initial coherence radius increased, the beam spreading of GSM becomes significant, and the self-focusing effect for NUC-PCBs is gradually reduced.

FIGURE 2

FIGURE 2. Dependence of the beam width on the initial coherence radius.

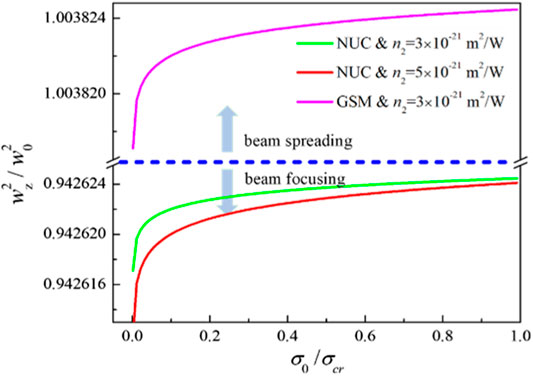
Based on the analysis of the beam width’s dependence on the coherence structure, it appears that the initial coherence radius can be regarded as a degree of freedom for manipulating the self-focusing length. To verify this hypothesis, the numerical and analytical methods were successively used. In the numerical calculation, the initial coherence radii are selected as follows: ${\sigma }_0=0.2{\sigma }_{cr}$, $0.4{\sigma }_{cr}$, $0.6{\sigma }_{cr}$, and $0.8{\sigma }_{cr}$; the non-linear refractive index is $n_2=3\times {10}^{-23}$ m²/W. Figure 3 shows that the corresponding self-focusing lengths are approximately $0.085z_R$, $0.1596z_R$, $0.2052z_R$, and $0.2064z_R$, respectively. With the aid of numerical results, the initial coherence radius can change the self-focusing length to some extent, but the specific relation is not clarified. Therefore, the analytical relation of the self-focusing length and initial coherence radius was studied. Based on Eq. 15, the relative self-focusing length $z_f/z_R$ is investigated. It is shown that the dependence of the relative self-focusing length on the initial coherence radius is not monotonic, and the maximum of the relative self-focusing length is located at ${\sigma }_0=0.71{\sigma }_{cr}$. It is found that the relative self-focusing length can be continuously controlled by varying the initial coherence radius; thus, the conclusion that the initial coherence radius may be regarded as a degree of freedom for manipulating the self-focusing length is established. In addition, by a modestly sized change in parameters such as the initial beam width and wavelength, the self-focusing length may be tunable in the range from microns to kilometers, and it is even possible to realize controllability from the micro to macro domains. It is worth mentioning that the correctness of the analytical expression is verified by comparing numerical and analytical results, and the results show that two methods have a good agreement with each other, as shown in Figure 4 (i.e., magenta dots).

FIGURE 3

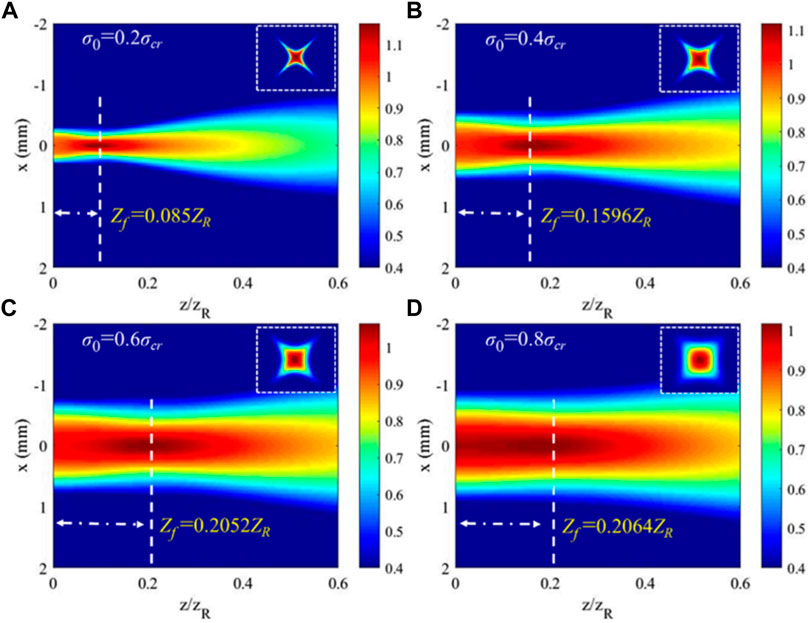
FIGURE 3. Self-focusing length with various initial coherence radii: (A) ${\sigma }_0=0.2{\sigma }_{cr}$, (B) ${\sigma }_0=0.4{\sigma }_{cr}$, (C) ${\sigma }_0=0.6{\sigma }_{cr}$, and (D) ${\sigma }_0=0.8{\sigma }_{cr}$, where the insets represent the mutual coherence function (or cross-spectral density) at the source plane.

FIGURE 4

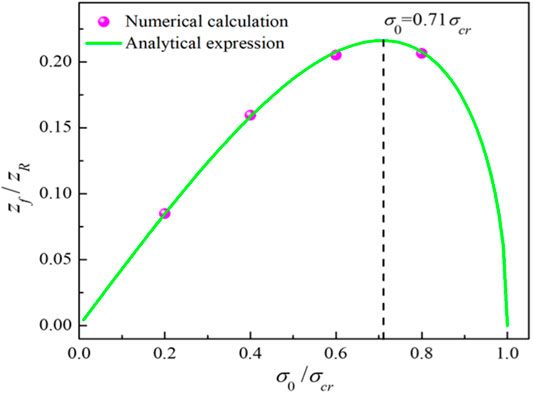
FIGURE 4. Dependence of the relative self-focusing length on the initial coherence radius. The magenta dots correspond to the cases in Figure 3.

Conclusion and Discussions

In summary, the self-focusing property of a partially coherent beam with a non-uniform correlation structure propagating in a non-linear medium was investigated using numerical and analytical methods. It is found that the non-uniform correlation structure plays a core role in the self-focusing formation. Furthermore, with the threshold condition of initial coherence radius proposed for the first time, the analytical formula for the self-focusing length is obtained. The result shows that the relation of relative self-focusing length and initial coherence radius is not monotonic, and it can be continuously controlled by changing the initial coherence radius. More significantly, a feasible approach for manipulating the self-focusing length by adjusting the initial coherence radius has been realized. These findings may have potential applications in optical communication, optical encryption, all-optical signal processing, and related areas. For example, it is known that the polarization [36–38] and orbital angular momentum [39] can be used as a carrier basis of signals for optical communication links. Herein, spatial coherence is regarded as the degree of freedom of a light beam as well, and it may provide another dimension for data-coding. In addition, the self-focusing length can be manipulated by varying the initial coherence radius of NUC-PCBs, benefiting for a controllable high-power laser atmospheric propagation for moving targets.

Data Availability Statement

The original contributions presented in the study are included in the article, and further inquiries can be directed to the corresponding authors.

Author Contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

We acknowledge the National Key Research and Development Project of China (2019YFA0705000), National Natural Science Foundation of China (91750201, 11974218, 11804234, 11903062, 12192254, and 11904087), Innovation Group of Jinan (2018GXRC010), and Local Science and Technology Development Project of the Central Government (YDZX20203700001766). We appreciate the valuable comments from reviewers.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Mandel L, Wolf E. Optical Coherence and Quantum Optics. Cambridge, UK: Cambridge University Press (1995).

Google Scholar

2. Cai Y, Chen Y, Yu J, Liu X, Liu L. Generation of Partially Coherent Beams. Prog Opt (2017) 62:157–223. doi:10.1016/bs.po.2016.11.001

CrossRef Full Text | Google Scholar

3. Chen Y, Norrman A, Ponomarenko SA, Friberg AT. Optical Coherence and Electromagnetic Surface Waves. Prog Opt (2020) 65:105–72. doi:10.1016/bs.po.2019.11.001

CrossRef Full Text | Google Scholar

4. Cai Y, Chen Y, Wang F. Generation and Propagation of Partially Coherent Beams with Nonconventional Correlation Functions: a Review [Invited]. J Opt Soc Am A (2014) 31(9):2083–96. doi:10.1364/josaa.31.002083

CrossRef Full Text | Google Scholar

5. Gbur G. Partially Coherent Beam Propagation in Atmospheric Turbulence [Invited]. J Opt Soc Am A (2014) 31(9):2038–45. doi:10.1364/josaa.31.002038

CrossRef Full Text | Google Scholar

6. Lin R, Chen M, Liu Y, Zhang H, Gbur G, Cai Y, et al. Measuring Refractive Indices of a Uniaxial crystal by Structured Light with Non-uniform Correlation. Opt Lett (2021) 46(10):2268–71. doi:10.1364/ol.424259

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Christodoulides DN, Coskun TH, Mitchell M, Segev M. Theory of Incoherent Self-Focusing in Biased Photorefractive Media. Phys Rev Lett (1997) 78:646–9. doi:10.1103/physrevlett.78.646

CrossRef Full Text | Google Scholar

8. Christodoulides DN, Coskun TH, Mitchell M, Segev M. Multimode Incoherent Spatial Solitons in Logarithmically Saturable Nonlinear Media. Phys Rev Lett (1998) 80:2310–3. doi:10.1103/physrevlett.80.2310

CrossRef Full Text | Google Scholar

9. Snyder AW, Mitchell DJ. Big Incoherent Solitons. Phys Rev Lett (1998) 80:1422–4. doi:10.1103/physrevlett.80.1422

CrossRef Full Text | Google Scholar

10. Królikowski W, Edmundson D, Bang O. Unified Model for Partially Coherent Solitons in Logarithmically Nonlinear media. Phys Rev E (2000) 61:3122–6. doi:10.1103/physreve.61.3122

CrossRef Full Text | Google Scholar

11. Mendonça JT, Tsintsadze NL. Analog of the Wigner-Moyal Equation for the Electromagnetic Field. Phys Rev E (2000) 62:4276–82. doi:10.1103/physreve.62.4276

CrossRef Full Text | Google Scholar

12. Nayyar VP. Propagation of Partially Coherent Gaussian Schell-Model Sources in Nonlinear media. J Opt Soc Am B (1997) 14(9):2248–53. doi:10.1364/josab.14.002248

CrossRef Full Text | Google Scholar

13. Wang H, Ji X-L, Zhang H, Li X-Q, Deng Y. Propagation Formulae and Characteristics of Partially Coherent Laser Beams in Nonlinear media. Opt Lett (2019) 44(4):743–6. doi:10.1364/ol.44.000743

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang H, Ji X-L, Deng Y, Li X-Q, Yu H. Theory of the Quasi-Steady-State Self-Focusing of Partially Coherent Light Pulses in Nonlinear media. Opt Lett (2020) 45(3):710–3. doi:10.1364/ol.379902

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Gori F, Santarsiero M. Devising Genuine Spatial Correlation Functions. Opt Lett (2007) 32(24):3531–3. doi:10.1364/ol.32.003531

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Lajunen H, Saastamoinen T. Propagation Characteristics of Partially Coherent Beams with Spatially Varying Correlations. Opt Lett (2011) 36(20):4104–6. doi:10.1364/ol.36.004104

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Tong Z, Korotkova O. Nonuniformly Correlated Light Beams in Uniformly Correlated media. Opt Lett (2012) 37(15):3240–2. doi:10.1364/ol.37.003240

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Lajunen H, Saastamoinen T. Non-uniformly Correlated Partially Coherent Pulses. Opt Express (2013) 21(1):190–5. doi:10.1364/oe.21.000190

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Yu J, Cai Y, Gbur G. Rectangular Hermite Non-uniformly Correlated Beams and its Propagation Properties. Opt Express (2018) 26(21):27894–906. doi:10.1364/oe.26.027894

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Yu J, Wang F, Liu L, Cai Y, Gbur G. Propagation Properties of Hermite Non-uniformly Correlated Beams in Turbulence. Opt Express (2018) 26(13):16333–43. doi:10.1364/oe.26.016333

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Gu Y, Gbur G. Scintillation of Nonuniformly Correlated Beams in Atmospheric Turbulence. Opt Lett (2013) 38(9):1395–7. doi:10.1364/ol.38.001395

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Houard A, D’Amico C, Liu Y, Andre YB, Franco M, Prade B, et al. High Current Permanent Discharges in Air Induced by Femtosecond Laser Filamentation. Appl Phys Lett (2007) 90:171501. doi:10.1063/1.2734396

CrossRef Full Text | Google Scholar

23. Fibich G, Sivan Y, Ehrlich Y, Louzon E, Fraenkel M, Eisenmann S, et al. Control of the Collapse Distance in Atmospheric Propagation. Opt Express (2006) 14(12):4946–57. doi:10.1364/oe.14.004946

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Zhao C, Cai Y, Lu X, Eyyuboğlu HT. Radiation Force of Coherent and Partially Coherent Flat-Topped Beams on a Rayleigh Particle. Opt Express (2009) 17(3):1753–65. doi:10.1364/oe.17.001753

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Yu J, Zhu X, Lin S, Wang F, Gbur G, Cai Y. Vector Partially Coherent Beams with Prescribed Non-uniform Correlation Structure. Opt Lett (2020) 45(13):3824–7. doi:10.1364/ol.397316

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Peng D, Huang Z, Liu Y, Chen Y, Wang F, Ponomarenko SA, et al. Optical Coherence Encryption with Structured Random Light. PhotoniX (2021) 2(1):6. doi:10.1186/s43074-021-00027-z

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Houard A, Franco M, Prade B, Durécu A, Lombard L, Bourdon P, et al. Femtosecond Filamentation in Turbulent Air. Phys Rev A (2008) 78:033804. doi:10.1103/physreva.78.033804

CrossRef Full Text | Google Scholar

28. Jin Z, Zhang J, Xu MH, Lu X, Li YT, Wang ZH, et al. Control of Filamentation Induced by Femtosecond Laser Pulses Propagating in Air. Opt Express (2005) 13(25):10424–30. doi:10.1364/opex.13.010424

PubMed Abstract | CrossRef Full Text | Google Scholar

29. Sprangle P, Peñano JRB, Hafizi B. Propagation of Intense Short Laser Pulses in the Atmosphere. Phys Rev E Stat Nonlin Soft Matter Phys (2002) 66:046418. doi:10.1103/PhysRevE.66.046418

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Buryak A, Trapani PD, Skryabin DV, Trillo S. Optical Solitons Due to Quadratic Nonlinearities: from Basic Physics to Futuristic Applications. Phys Rep (2002) 370(2):63–235. doi:10.1016/s0370-1573(02)00196-5

CrossRef Full Text | Google Scholar

31. Wolf E. A Macroscopic Theory of Interference and Diffraction of Light from Finite Sources II. Fields with a Spectral Range of Arbitrary Width. Proc Roy Soc (1955) A230:246.

Google Scholar

32. Born M, Wolf E. Principles of Optics. New York: Pergamon Press (1959).

Google Scholar

33. Wolf E. Introduction to the Theory of Coherence and Polarization of Light. Cambridge, UK: Cambridge University Press (2007).

Google Scholar

34. Andrews LC, Phillips RL. Laser Beam Propagation through Random Media. Bellingham: SPIE Press (2005).

Google Scholar

35. Hermansson B, Yevick D, Friberg AT. Optical Coherence Calculations with the Split-step Fast Fourier Transform Method. Appl Opt (1986) 25(16):2645–7. doi:10.1364/ao.25.002645

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Andrews MR, Mitra PP, deCarvalho R. Tripling the Capacity of Wireless Communications Using Electromagnetic Polarization. Nature (2001) 409(6818):316–8. doi:10.1038/35053015

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Turpin A, Loiko Y, Kalkandjiev TK, Mompart J. Free-space Optical Polarization Demultiplexing and Multiplexing by Means of Conical Refraction. Opt Lett (2012) 37(20):4197–9. doi:10.1364/ol.37.004197

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Lu L, Wang Z, Cai Y. Propagation Properties of Phase-Locked Radially-Polarized Vector fields Array in Turbulent Atmosphere. Opt Express (2021) 29(11):16833–44. doi:10.1364/oe.427003

PubMed Abstract | CrossRef Full Text | Google Scholar

39. Zou L, Gu X, Wang L. High-dimensional Free-Space Optical Communications Based on Orbital Angular Momentum Coding. Opt Commun (2010) 410:333–7. doi:10.1016/j.optcom.2017.10.035

CrossRef Full Text | Google Scholar