Time and Space Resolved First Order Optical Interference Between Distinguishable Photon Paths

Interference between different photons occurs and has been observed under diverse experimental conditions. A necessary condition in order to obtain interference fringes is the existence of at least two possible paths and unknown which-path information. If the photon beams have different frequencies, stability of the sources and fast spatially distributed detectors are required in order to detect the time displaced interference fringes. First order optical interference between two truly independent CW laser sources is observed. In contrast with the standard quantum criterion, interference is observed although the photon beams are distinguishable and, from quantum measurements, the path is unequivocally known for each photon beam. Segments of the continuous wave wavetrains are selected with an acousto-optic modulator. Temporal and spatial interference are integrated in a single combined phenomenon via streak camera detection. The displacement of the fringes in the time versus space interferograms evince the trajectories of the labeled photons. These results suggest that in non-degenerate frequency schemes, the ontology has to be refined and the which-path criterion must be precisely formulated. On the one hand, if the query refers to the frequency labeled photons, the path of each red or blue photon is known, whereas on the other hand, if the query is performed in terms of the detected photons, the path is unknown.

1 Introduction

The two manifestations of first order interference between two wave-fields are 1) spatial interference fringes and 2) temporal interference or beating. The beams in optical spatial interference setups are usually derived from the same source but traveling along separate paths. In contrast, temporal interference is commonly achieved with different sources having different frequencies. Early experiments in the laser era demonstrated the temporal [1] and spatial [2] interference of independent sources. The position-momentum uncertainty provided an explanation of these results without having to renounce to the Dirac statement that ’Interference between different photons never occur’ [3]. However, later experiments where the photon source statistics were carefully controlled, showed ineluctably that independent photons can interfere [4]. Interference fringes in the visible region of the spectrum with two different frequencies have also been observed [5, 6]. For a constant frequency difference, a single laser source is commonly used. The frequency of one beam can then be shifted with an acousto optic modulator [7] or by selecting different frequencies from a spatially chirped femtosecond pulsed source [8]. If separate lasers are used, the frequency difference varies from shot to shot and so does the fringe pattern [9]. The fringes in most of these experiments with different frequencies have been observed using a streak camera and more recently, with a modulated CMOS camera [10].

First order interference comes from the correlations between the fields whereas second order interference arises from correlations between the fields’ intensities. These correlations can be described with continuum field theory (CFT) or quantum field theory (QFT). The archetypal Young’s two slit interference experiment displays identical first order interference patterns when produced by short exposure with a intense light source or by a long exposure with feeble light. However, the ontology in the two theories is rather different. CFT requires a stable amplitude and phase correlation between the two interfering fields during the detector integration time [11]. In contrast, QFT asserts that interference takes place only when the path of the photons is unknown [12]. Recall that the two theories do produce measurable differences in second order interference experiments [13]. Many theoretical predictions and experimental verifications without classical analogue, favor the quantum nature of electromagnetic fields.

The present experimental results are at odds with the standard formulation of the quantum which path problem: “A measurement which shows whether the photon passed through A or through B perturbs the state of the photon to such an extent that no interference fringes are detected. Thus, either we know which slit the photon passed through, or we observe interference fringes. We cannot achieve both goals: the two possibilities are incompatible ([14], p.22).” Many authors consider that the which path information problem is an example of Bohr’s principle of complementarity, where the interference/which-way duality is a manifestation of the wave/particle mutually exclusive concepts [15]. However, Bohr’s idea of complementarity is a much broader principle dealing with observation and the definition of quantum states [16, 17]. As we shall presently show, interference with which-path certainty is possible in non-degenerate frequency schemes if the statement is made in terms of the frequency labeled photons but without reference to a detected photon. However, the path of a detected photon in the interference region, cannot be traced back. This latter, more precise assertion, is consistent with the prevailing quantum viewpoint. Our observations are consistent with Heisenberg’s uncertainty principle and Busch measurement/disturbance theorem. They are also consistent with Englert, which way detector inequality. However, they compromise certain versions of Bohr’s complementary principle.

2 Experimental Considerations and Setup

Two photon beams were generated from two independent Nd:YAG lasers code named cheb and oxeb ¹. These continuous wave (CW), monomode lasers (AOTK 532Q) have a coherence time greater than 300 ns [18]. The operation of each laser does not rely in any way on the working of the other laser, nor are they synchronized. The temperature of each of them was monitored and controlled independently. Temperature was measured with a 100 Ω platinum resistance and controlled with a Peltier module external to the cavity but attached to its base. A temperature controller (Stanford Research SRC10) provided the electronic feedback to maintain a stable temperature within 0.01°C. The wavelengths of the two lasers, measured with an spectrometer (Spex1704 with 0.01 nm resolution), were temperature tuned so that their frequencies were sufficiently close to be resolved by a streak camera (Optronis SC-10). At sweep speeds of 10 ns/mm with the TSU-12–10 unit, fringes are comfortably observed in the streak camera for frequency differences below 1 GHz. The two laser beams were steered with mirrors into a TeO₂ acousto optic modulator (AOM) (10/10 ns, 10–90% rise/fall time for a 55 μm beam-waist). The general setup is shown in Figure 1. Preliminary results were reported at a PIERS conference [19]. Beam splitters were avoided (except for alignment purposes, prior to operation), so that a two slit wavefront division interferometer is emulated throughout the trajectories. The expanded collimated beams were overlapped and detected with the streak camera. The beams collimation was adjusted with the aid of a shear interferometer. A streak camera is an optical version of an electronic oscilloscope; at the entrance slit light impinges on a photocathode placed on the inner part of a vacuum tube. The photo-electrons emitted by the photocathode (8 mm × 2 mm) are accelerated and swept in the perpendicular direction to its long axis, in this way a two dimensional image is produced. Each photoelectron eventually impacts a multichannel plate (MCP) and is cascaded so that the bunch of electrons produces a bright point as it reaches a phosphor screen. The MCP amplification voltage is adjusted so that the intensity of the spot is adequately detected by a CCD camera. At low intensity levels, the streak camera operates in a spatially resolved photon counting mode. If at some spots more than one photon is detected, this information is encoded onto a level of gray, typically not more than 50 events per 0.7 ns as can be seen from Figure 6B. In the streak camera images, the abscissa corresponds to the time axis whereas the ordinate is a transverse spatial coordinate. The density of bright spots is proportional to the photon density in the two dimensional time and space coordinates. Streak images cannot be accumulated in this experiment because the frequency and relative phase between the two lasers vary stochastically in time from sweep to sweep. For this reason, the fringe pattern was recorded in single exposures with a time duration of the order of the coherence time. Low repetition rates between 1 and 3 Hz had to be used to acquire and save the digital images in real time. The streak camera detector performs an integration both in space and time,

${⟨I\left(t,y\right)⟩}_{\delta t,\delta x,\delta y}=\frac{1}{\delta t\delta x\delta y}{\int }_y^{y+\delta y}{\int }_x^{x+\delta x}{\int }_t^{t+\delta t}I\left(\tau ,\xi ,\eta \right)d\tau d\xi d\eta ,$

where $I\left(\tau ,\xi ,\eta \right)$ is the light intensity incident on the photocathode as a function of time and the transverse dimensions. $I\left(t,y\right)$ is the intensity at the CCD screen as a function of the “coarse grain” time and one spatial direction. In the transverse dimensions, the x direction is limited to x = ±7.5 μm using a δx = 15 μm entrance slit. In the y direction, the position detection range is 15 mm with δy = 70 μm resolution. The temporal sweep is performed in the x direction with 0.34% resolution of the full sweep time. The resolution of the apparatus is given by the instrumental integration δt, δx, δy together with the image amplification and digitization bins (Anima-PX/25, 19.5 × 14.9 mm², 12 bit A/D CCD 1392 × 1024). The quantum efficiency (QE) of the low noise photocathode is 10.37% at 532 nm with dark noise of 100 e⁻/cm²s (Photek ST-LNS20). The temporal resolution at the phosphor screen placed after the image intensifier is 66 μm.

FIGURE 1

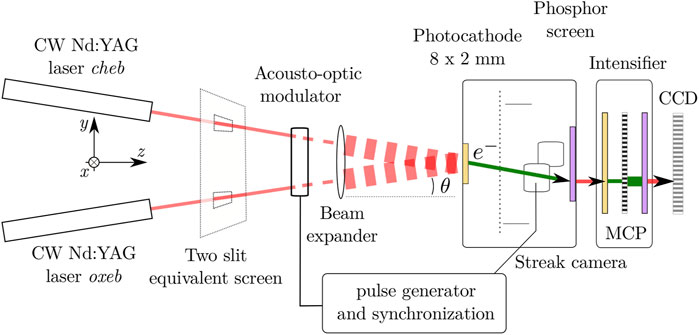
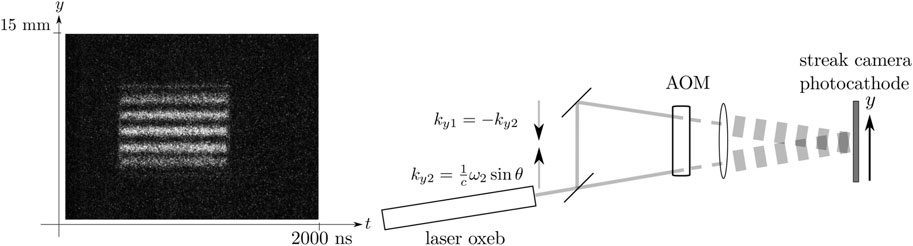
FIGURE 1. Schematic diagram of the experimental arrangement. The setup is equivalent to a Young’s two slit experiment but each ’slit’ is illuminated by an independent laser. The slits can be conceived to be placed at any plane between the sources and the photocathode detector before the beams overlap. (Optical beams drawn in red, electron beams within the streak camera drawn in green.)

FIGURE 6

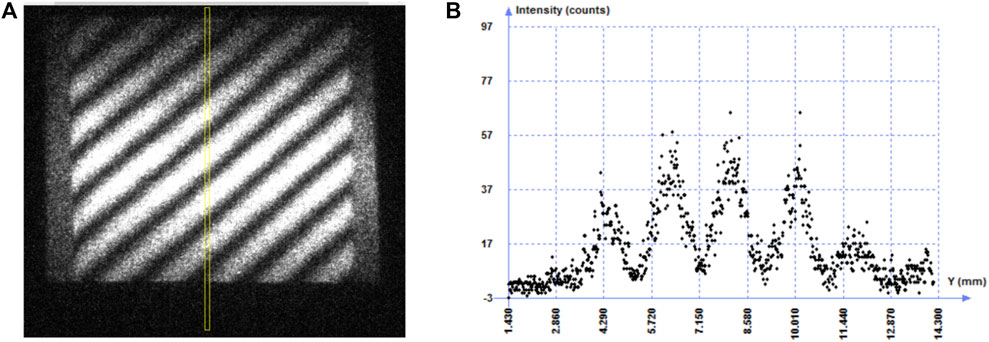
FIGURE 6. Region of interferogram shown in Figure 4, limited to small range in t but the whole range in y. (A) Rectangle width is 0.7 ns (width is over sized in image for clarity), height encompasses the entire y range; (B) Plot of spatial profile averaged over △t = 0.7 ns (Optoanalyze v3.71).

The AOM input angle was aligned with the oxeb laser beam. In our experiments, delay generator pulses with 120, 300 and 700 ns width were used. The AOM first order deflection angle is 25 mrad with a diffraction frequency shift of 210 MHz. The oxeb laser beam was diffracted in first order (210 MHz) whereas the cheb beam was operated in second order (2 × 210 MHz). There was thus a 210 MHz frequency difference that posed no problem because it was compensated by the laser’s temperature tuning. Half wave retardation plates were used at the output of each laser to adjust the polarization plane in order to improve fringe visibility. A typical ≈ 100 ns output pulse is shown in Figure 2A. The cheb beam is a bit mismatched due to a 25 mrad oblique incidence in a displaced region of the acoustic wave within the crystal. This inclination produces a pulse delay and a pulse front tilt as may be seen in Figure 2C. This sweep mode neatly exhibits three regions, two to the left and right in Figure 2B, where only one of the pulses is present and the central area where both pulses overlap in time and interference is observed.

FIGURE 2

FIGURE 2. Streak camera images. The abscissa represents time at 10 ns/mm sweep rate with δt = 1 ns temporal resolution. The ordinate depicts the beams transverse distance in the y direction. (A) 97 ns pulse from laser code named oxeb.; (B) Interferogram when both laser pulses are present; (C) 95 ns pulse from laser code named cheb.

In a conventional single source Young’s experiment, the two slits separate the wavefront into two distinct wave-fronts. Here, the waves emanate from two different truly independent sources. The physical setup can be conceived as each source illuminating a slit. The plane where the slits are placed is any arbitrary plane between the sources and the region where the beams begin to overlap just before interfering at the detection plane. Moreover, each slit could be placed at different planes, reminiscent of second order interference patterns produced by non-local objects [20].

2.1 Photon Labeling

The two beams are collimated and thereafter incident on the streak camera photocathode at an angle of 0.14 mrad between them in order to have comfortably resolved interference fringe maxima separated by 1.88 mm at the detection plane. Cartesian coordinates are set with z normal to the detector surface and the fields are linearly polarized in the x direction. The two waves propagate in the $\left(y,z\right)$ plane, paraxially to the z direction at a small but opposite angle θ in the y axis. The wave vector of the field coming from the laser code named cheb is

${\mathbf{k}}_1={\mathbf{k}}_{y1}+{\mathbf{k}}_{z1}=-k_1\sin \theta {\widehat{\mathbf{e}}}_y+k_1\cos \theta {\widehat{\mathbf{e}}}_z,$

and the wave-field coming from the laser code named oxeb is

${\mathbf{k}}_2={\mathbf{k}}_{y2}+{\mathbf{k}}_{z2}=k_2\sin \theta {\widehat{\mathbf{e}}}_y+k_2\cos \theta {\widehat{\mathbf{e}}}_z,$

where the wave vector magnitudes are $\left|{\mathbf{k}}_1\right|=k_1=\frac{{\omega }_1}{c}$ and $\left|{\mathbf{k}}_2\right|=k_2=\frac{{\omega }_2}{c}$ and ${\widehat{\mathbf{e}}}_y,{\widehat{\mathbf{e}}}_z$ are unit vectors in the y and z directions. The y axis positive direction was set in the same direction of k_y2, that is, the photons coming from the oxeb laser have positive momentum, $\hslash {\mathbf{k}}_{y2}=\hslash \left|{\mathbf{k}}_{y2}\right|{\widehat{\mathbf{e}}}_y$ at the detector plane (The y axis positive direction could have been set in the opposite sense. Either convention applied consistently yields the same results). In addition to their linear momentum, the photons are also labeled by their frequency. Since each laser source has its own oscillation frequency, the wave-field coming from the oxeb laser with ℏk_y2 momentum projection, has frequency ω₂ and the wave-field coming from the cheb laser with ℏk_y1 momentum projection, has frequency ω₁. The wave vector projection in the transverse y direction and the corresponding frequency are highly correlated. This so-called photon’s labeling is similar to the temporal and spatial labeling terminology in HOM second order interferometers [21]. However, the frequency of each laser is not known a priori, due to the fluctuations (albeit tiny) in the two lasers. As we shall presently see, it is only when a set of quantum tests is performed that the relative frequencies of the two lasers can be inferred.

2.2 QFT Description

In quantum field theory, the standard representation of two quantized complex electric field operators with linear polarization is ${\widehat{E}}_1^{\left(+\right)}\left(\mathbf{r}\right)=i{\mathcal{E}}_1^{\left(1\right)}\exp \left(i{\mathbf{k}}_1\cdot \mathbf{r}\right){\widehat{a}}_1$ and ${\widehat{E}}_2^{\left(+\right)}\left(\mathbf{r}\right)=i{\mathcal{E}}_2^{\left(1\right)}\exp \left(i{\mathbf{k}}_2\cdot \mathbf{r}\right){\widehat{a}}_2$, where ${\mathcal{E}}_1^{\left(1\right)},{\mathcal{E}}_2^{\left(1\right)}$ are the one-photon amplitudes and ${\widehat{a}}_1,{\widehat{a}}_2$ are the annihilation operators for modes 1 and 2, respectively. The fields coming from each monomode laser are adequately represented by single mode coherent states $\left|{\alpha }_1\right.⟩$ and $\left|{\alpha }_2\right.⟩$ [22]. These quasi-classical states are eigenstates of the annihilation operators ${\widehat{a}}_1\left|{\alpha }_1\right.⟩={\alpha }_1\left|{\alpha }_1\right.⟩$ and ${\widehat{a}}_2\left|{\alpha }_2\right.⟩={\alpha }_2\left|{\alpha }_2\right.⟩$ with eigenvalues α₁, α₂. Since the two fields are completely independent, their superposition is a two mode factorizable state, $\left|{\psi }_{\mathrm{1,2}-qc}\left(t\right)\right.⟩=\left|{\alpha }_1\exp \left(-i{\omega }_{1}t\right)\right.⟩\left|{\alpha }_2\exp \left(-i{\omega }_{2}t\right)\right.⟩$. These states allow for the factorization of the first order coherence function [23]. The quantum photo detection probability is $w\left(\mathbf{r},t\right)=s\left.⟨{\psi }_{\mathrm{1,2}-qc}\left(t\right)\right|{\widehat{E}}^{\left(-\right)}\left(\mathbf{r}\right){\widehat{E}}^{\left(+\right)}\left(\mathbf{r}\right)\left|{\psi }_{\mathrm{1,2}-qc}\left(t\right)\right.⟩$, where s is the sensitivity of the detector and the operator ${\widehat{E}}^{\left(-\right)}\left(\mathbf{r}\right)$ is the Hermitian conjugate of the positive frequency part of the electric field operator ${\widehat{E}}^{\left(+\right)}\left(\mathbf{r}\right)$. This expression evaluates to

$\begin{array}{l}\hfill w\left(\mathbf{r},t\right)=s{\left({\mathcal{E}}_1^{\left(1\right)}{\mathcal{E}}_2^{\left(1\right)}\right)}^2\\ \hfill \left({\left|{\alpha }_1\right|}^2+{\left|{\alpha }_2\right|}^2+{\alpha }_1^{\ast }{\alpha }_2\exp \left[i\left(\left({\mathbf{k}}_2-{\mathbf{k}}_1\right)\cdot \mathbf{r}-\left({\omega }_2-{\omega }_1\right)t+{\phi }_2-{\phi }_1\right)\right]+c.c.\right),\end{array}(1)$

where φ₁, φ₂ are independent stochastic functions with coherence times τ₁, τ₂ due to the laser cavities instabilities. Recall that in this experiment, the coherence time of each laser is somewhere above 300 ns.

The spatially dependent interference argument of the exponential function is $\left({\mathbf{k}}_2-{\mathbf{k}}_1\right)\cdot \mathbf{r}=2\bar{k}\sin \theta y+△k\cos \theta z$, where $2\bar{k}=k_1+k_2$, △k = k₂ − k₁. The fields superposition is observed at a detector placed at the z = z₀ plane, thus the term △k cos θ z₀, only adds a constant phase shift. The phase as a function of the transverse distance y and time is

$\varphi =2\bar{k}\sin \theta y+△k\cos \theta z_0-△\omega t+△\phi ,(2)$

where △ω = ω₂ − ω₁ and △φ = φ₂ − φ₁. When the two frequencies are different, the constant phase surfaces evolve in both, time and space. In contrast, wave-fronts in frequency degenerate setups entail spatial coordinates alone. The velocity of an equal phase plane, provided that △φ varies slowly in time and space, is

$\frac{dy}{dt}=\frac{△\omega }{2\bar{k}\sin \theta }.(3)$

The fringes are therefore displaced in time with a slope $\frac{dy}{dt}$, whose sign is determined by the value of △ω.

3 Experimental Results

Each point in the streak camera image represents a quantum test of whether a photon arrived at position y of the streak camera photocathode at a given time t. A streak camera image consists of two sets of quantum tests, one in the spatial domain and another in the temporal domain. In the y ordinate direction, electrons in the photocathode long axis act as a set of spatially distributed detectors. For each y position, there is another set of different consecutive quantum tests that probe the dynamical evolution of the quantum system ([24], p.33, p.237). This set is depicted in the abscissas time axis. A photoelectron is emitted with 10.37% quantum efficiency at the streak camera photocathode, if a photon is present at $\left(y,t\right)$ where the two photon beams overlap. These events are amplified by the MCP and recorded in the 1024 × 1392 = 1.425 × 10⁶ detectors at the CCD. Thus, each streak camera interferogram involves 10⁶ quantum tests (order of magnitude). The interferograms in Figures 3, 4 were registered at 50 ns/mm sweep speed with 3.4 ns temporal resolution. The transverse spatial range is 15 mm with 70 μ resolution. The 655 ns segments obtained with the AOM modulator, where the two CW lasers temporally overlap, exhibit high contrast interference fringes with visibility above 70% as shown in the figures before mentioned.

FIGURE 3

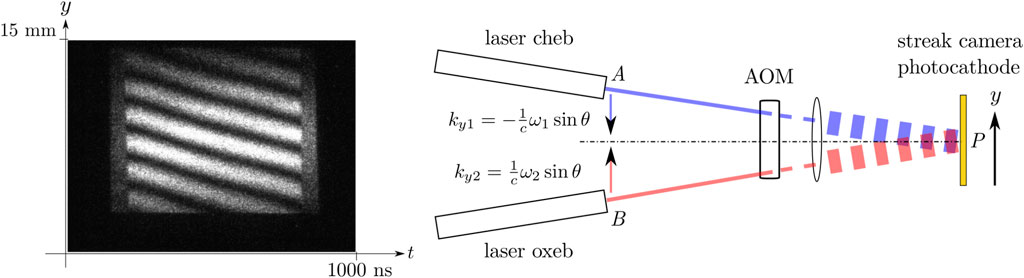
FIGURE 3. The steak camera image (left) shows negative slope interference fringes. Therefore, the oxeb laser emitted lower frequency photons that followed the path $\overline{BP}$. The higher frequency photons from the cheb laser followed the path $\overline{AP}$.

FIGURE 4

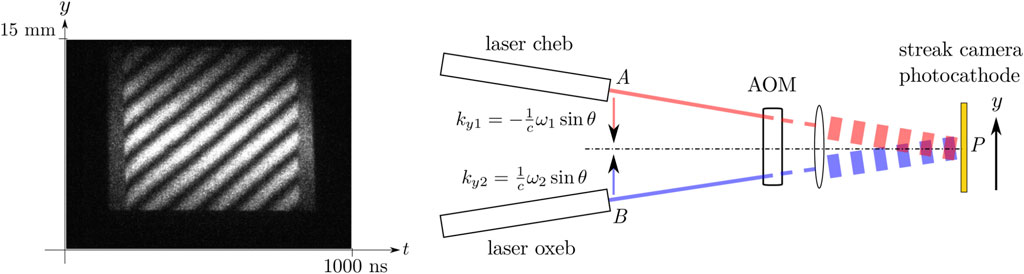
FIGURE 4. Positive slope interference fringes, the oxeb laser emitted higher frequency photons than the cheb laser. Photons from the oxeb laser followed the lower path $\overline{BP}$ whereas photons from the cheb laser followed the upper path $\overline{AP}$.

The interferogram shown in Figure 3 exhibits fringes with negative slope. From Eq. 3, if the slope of the equal phase lines is negative, the frequency difference △ω is negative and thus ω₂ < ω₁. Therefore, in this particular exposure, the oxeb laser emitted photons with lower energy ℏω₂, drawn in red in Figure 3. Each of the photons comprising this beam have positive linear momentum projection ℏk_y2 in the y direction. These red photons ineluctably followed the path $\overline{BP}$, where B is the position of the beam at the laser oxeb output and P is a point in the streak camera photocathode screen. The converse is true for the photons that constitute the cheb laser beam. These higher energy photons drawn in blue in Figure 3, have negative linear momentum projection $-\hslash \left|{\mathbf{k}}_{y1}\right|{\widehat{\mathbf{e}}}_y$ in the y direction at the detector plane. They followed the path $\overline{AP}$, where A is the position of the beam at the cheb laser output. From the time-space interferogram, it is of course possible to evaluate the frequency difference △ω = − 19.4 MHz, although the specific value is irrelevant for the present discussion. Notice that the diagram drawn on the right hand side of Figure 3 is obtained from the 10⁶ quantum tests. It is the spatial and temporal distribution of these quantum tests that allow us to figure out the path that the blue or red photons followed.

Although the lasers were carefully stabilized, tiny frequency fluctuations produce quantitative and qualitative differences in the interference patterns. The interferogram shown in Figure 4, was acquired merely 1014 ms after the previous interferogram shown in Figure 3. The lasers’ frequency drifted so that the slope changed sign from one scan to the next. This was of course not always the case for subsequent exposures, spatial frequency and slope varied stochastically from frame to frame. For a positive slope, the frequency difference △ω is positive and then ω₂ > ω₁. Therefore, in this exposure, the oxeb laser emitted photons with higher energy ℏω₂, drawn in blue in Figure 4. Each of these higher energy photons necessarily followed the path $\overline{BP}$ in this case. The photons emitted by the cheb laser beam now have lower energy and followed the path $\overline{AP}$. In this interferogram, △ω = 54.9 MHz. Summing up the two previous results: The fringes are displaced, as a function of time, in the same direction of the transverse momentum projection of the photons with higher energy. It should be stressed that the detected photons are neither blue nor red but photons with information from both sources given by the quantum photo detection probability stated in Eq. 1.

In the interferogram of Figure 4, if there were some red photons that had positive momentum but came from the lower slit and some blue ones had negative momentum but came from the upper slit, their interference would produce fringes with a negative slope. However, the interferogram in Figure 4 does not exhibit even the faintest fringes with negative slope, thus this possibility is ruled out. Therefore, we must conclude that in either case (ω₂ > ω₁ or ω₂ < ω₁), the trajectory of the photons is well defined, yet a high contrast interference pattern is observed!

In contrast, consider the case where the frequencies are equal. This degenerate frequency condition is easier to achieve experimentally using the same laser source but it could actually be accomplished with two laser sources with the appropriate stability and bandwidth or a frame where the two lasers have the same frequency within the exposure time. In this degenerate frequency case, interference fringes have zero slope and the pattern is constant in time as shown in Figure 5. Strictly speaking, there is no need of a streak camera. There is no frequency labeling of the photons and it is not possible to deduce which path they followed. Nonetheless, there is still a momentum labeling but, due to the position-momentum uncertainty, the sources are unresolved at the detector [25].

FIGURE 5

FIGURE 5. Zero slope interference fringes. Photons are no longer frequency distinguished.

4 Evaluation of Quantum Uncertainties

In order to establish the path of the photons, it is sufficient to measure whether the fringes displacement is positive or negative. Nevertheless, it is reassuring to confirm that the actual numerical values of the measurements do not violate an uncertainty relationship, nor are they buried below the quantum noise.

The number of photons Φ^ph per unit time is given by the power Φ over the energy per photon ℏω_ℓ. The power of each laser is 50 mW but losses due to off optimal temperature operation and beam steering reduces the power roughly by a factor of 5. For a 10 mW average power with angular frequency ω_ℓ = 3.54 × 10¹⁵Hz, the average number of photons per nanosecond is ${\mathrm{\Phi }}^{\text{ph}}=\frac{\mathrm{\Phi }}{\hslash {\omega }_{\ell }}=2.68\times 10^7\mathrm{p}\mathrm{h}\mathrm{o}\mathrm{t}\mathrm{o}\mathrm{n}\mathrm{s}\cdot {\mathrm{n}\mathrm{s}}^{-1}$. The δx = 15 μ horizontal entrance slit reduces the power by a factor of approximately 10⁻³ and the QE of the photodetector by 1.037 × 10⁻¹. The average number of photons detected per nanosecond is then Φ^ph = 2.68 × 10³photons ns⁻¹. The standard deviation in the number of photons is thus $\sqrt{⟨N_{\ell }⟩}=\sqrt{{\mathrm{\Phi }}^{\text{ph}}}=\sqrt{2.68\times 10^3}=51.7$. The phase uncertainty in the standard quantum limit (SQL) [26] in one nanosecond is then approximately

$△{\varphi }_{\text{SQL}}=\frac{1}{2\sqrt{⟨N_{\ell }⟩}}=9.66\times 10^{-3}\approx 10^{-2}\mathrm{r}\mathrm{a}\mathrm{d}\mathrm{i}\mathrm{a}\mathrm{n}\mathrm{s}.(4)$

This value of the SQL establishes the minimum achievable uncertainty in the phase of each photon beam at the detector. On the other hand, let us assess the measurement error in the interference pattern produced by the two sources. From Figure 6, the distance between maxima is △y_max = 1.88 ± 0.023 mm. The main error coming from the instrumental resolution in the y direction. The spatial resolution between maxima located 1.88 mm apart, due to the sources phase uncertainty △ϕ_SQL per nanosecond is 3 μm. The spatial frequency measurement uncertainty due to the interference of the two photon beams is thus about 8 times larger than the SQL of each laser source.

The fringes observed in the various interferograms presented in the paper follow straight lines, thus their slope is constant as predicted by Eq. 3. Figure 7, reproduces the positive slope interference fringes, (where the oxeb laser emits higher frequency photons than the cheb laser) together with a straight line fit. Therefore the lasers relative phase fluctuation △φ must be constant (or at most linear in time) during the ≈ 603 ns where there is temporal overlap of the two beams. Frequency fluctuations are thus smaller than the long term average △ν = 3 MHz laser bandwidth in the μs timescale. For short detection times, the laser cavity fluctuations are ’frozen’ and the lasers bandwidth approaches the Schawlow-Townes quantum limit, $△{\nu }_{laser}=\frac{4\pi \hslash \omega }{{\tau }_{cav}^{2}P}$ [27]. For these Nd:YAG monomode laser systems, the quantum limit bandwidth is of the order of a few kHz.

FIGURE 7

FIGURE 7. Straight line superimposed on the interference fringes shown in Figure 4.

The existence of an energy-time uncertainty relation in quantum mechanics has been subject to much debate [28, 29]. Due to the lack of a self-adjoint time operator, there is formally no quantum uncertainty relationship of time with any other dynamical variable [30], in particular an uncertainty relationship with energy or linear momentum. Nonetheless, time and frequency are, of course, Fourier transform conjugate variables subject to the inequality, $\delta t\delta \omega \ge \frac{1}{2}$ for Gaussian pulses based on the mean square deviation ([31], p.623). For example, the beat frequency (△ω = 54.9 MHz) in the interferogram shown in Figure 7, is obtained from the measurement during the beam’s temporal overlap of δt = 603 ns. The frequency resolution is thus at most, $\delta \omega \ge 1/\left(2\delta t\right)=0.83$ MHz. In quantum parlance, photons in different modes are distinguishable if the detection time is longer than the inverse of the modes frequency separation. Photons in modes separated by △ω = 54.9 MHz are distinguishable if they are detected in times longer than 1/△ω ≈ 18 ns. This time is considerably larger than the photolelectric response time [32] and the uncertainty in the time axis for a single temporal event. Nonetheless, the detection is performed in successive time measurements over a time span larger than 603 ns.

In the limit of macroscopic fields and small quantum fluctuations, the photon number N_ℓ and phase ϕ_ℓ fluctuations (ℓ = 1, 2), look like complementary variables in the usual sense of quantum mechanics $△N_{\ell }△{\varphi }_{\ell }\ge \frac{1}{2}$ [22]. For minimum uncertainty states and in particular for coherent states, the equality is fulfilled because fluctuations are proportional to the square root of the average number of particles in a Poisson distribution,

$△{\varphi }_{\ell }=\frac{1}{2\sqrt{⟨N_{\ell }⟩}}.(5)$

The time-space interferograms shown here nicely depict the trend of this behavior. For a few scattered dots, $⟨N_{\ell }⟩$ is small and constant phase lines are difficult to establish. However, as the number of events (dots) increase, the equal-phase lines become better delineated and the uncertainty in their slope is thus reduced. The number of detected events N_ℓ can be varied, either by attenuation of the sources or by evaluation of a limited portion of the interferometric frame. In the latter case, if the slope is evaluated from a partial region of the image, the number of dots is smaller and the uncertainty in the phase and therefore in the fringes slope, becomes larger.

5 Experimental Rationale

Many which-path experiments have been tried out: “A succession of suggestions for more and more ingenious experiments has failed to provide any method for simultaneous fringe and path observations”[33]. So called welcher weg experiments were even proposed by eminent physicists, Einstein and Feynman amongst them ([34], Sec.1.1.3). However, even in the thought experiments, monitoring the path introduces an uncertainty that disrupts the interference pattern. The less disruptive probes implemented so far involve weak measurements that provide fuzzy quantum information [35, 36]. We shall say more about this approach in the following lines. Our setup, was designed to study the dynamics of decoherence, it was not intended to undertake a which-path problem; The before mentioned facts being enough to deter almost anyone from doing so. Nonetheless, we should also mention that previous interference experiments with photons of different energy were already indicative of a well known frequency going to a specific slit [37, 38].

Why then does this experiment succeed in the measurement of path knowledge without destroying the interference pattern? From our understanding, there are three reasons:

1. The path information is obtained from measurements at the interference detection plane.

a. The trajectory is in no way perturbed since the path detection is not performed in mid trajectory but at the end plane where the fringes are observed. The Englert inequality establishes that for a given fringe visibility there is an upper bound on the amount of information that can be stored in a which-way detector (WWD) [39]. Englert inequality is derived assuming that the WWD’s are placed somewhere in the way between the two alternative trajectories before the photon beams overlap. Here, the photocathode plays the role of the WWD’s; However, it is placed at the interference plane where the beams overlap but not before.

b. Recall that no information can be obtained without disturbing a quantum system [40]. In the present experiment, photons are destroyed when detected at the streak camera photo-cathode where information is extracted, thus Busch theorem is not violated. Our measurement is not a weak measurement. On the contrary, each of the 10⁶ quantum tests of a given frame, destroy the photons involved in each test. The system is destroyed, that is completely disturbed, by the measurement.

2. The fringes slope in the time-space coordinates is the decisive parameter in order to establish the photons path.

a. It is necessary to accumulate a sufficiently large number of photons in order to produce a fringe pattern. Whether this pattern is obtained by intense or attenuated beam exposures does not alter the statistics of the laser light and are thus entirely equivalent [4]. It does not make sense to ask whether a single photon produces a fringe pattern. At least two dots are needed to draw a line, and if the position uncertainty of the photons (dots) is large, many dots are required to draw a line with some confidence. Nonetheless, the collection of measurements gives information about each trial even to the point of stating that “Each photon then interferes only with itself” ([41], p.9). In an analogous fashion, the trajectory of the photons is revealed here from the measurement of a large number of events. Nonetheless, information about the trajectory of each photon is obtained.

b. Successive time measurements of the fringe pattern are recorded. This scheme follows the rationale of quantum measurements distributed in time where the path-integral formulation is particularly well suited to describe time dependent experiments [42]. Feynman’s rules for combining probability amplitudes depend on whether intermediate states are measured [43]. In the present experiment no intermediate state is measured. Nonetheless, information about intermediate states is obtained from measurements at a succession of final states.

3. Photons need to be frequency labeled.

As a rule, photons need to be doubly labeled with tags that are not conjugate variables. In this experiment, labels are “photon linear momentum projection in the y axis” and “photon energy” or quantities derived thereof. Thus determination of one of them does not obstruct the determination of the other. One label, in this case its frequency, distinguishes the type of photon; while the other, describes its momentum that ultimately establishes the path that it followed.

Regarding point 2a, it could be argued that only the average behavior of the system is being probed. However, this is not the case. In the prevailing Copenhagen view of quantum mechanics, or its modern quantum Bayesian version, the theory is intrinsically probabilistic. A prediction can only be related to observation in an statistical way given by Born’s rule. The larger the number of measured events, the sharper the measured property (within the uncertainty principle if complementary variables are involved). From the measurement of a large number of independent events, it is possible to infer certain properties of each event. The fundamental reason being that events independence imply that each event is not altered in any way by the other events.

The uncertainty principle has been stated as “Any determination of the alternative taken by a process capable of following more than one alternative destroys the interference between alternatives” ([44], 1−2, p.9). This assertion by Feynman and coauthors is certainly compromised by the present results. However, they do not contradict the uncertainty principle. Heisenberg’s uncertainty principle is, strictly speaking, related to the uncertainty between conjugate variables, that is, operators that do not commute [24]. In Section 4, we have shown that the present experimental results are in full accordance with quantum uncertainties.

6 Ontology and Discussion

6.1 Which Way Query

In order to clarify the delicate conceptual difference of the which path query, let us pose two questions that are seemingly the same but have different answers:

• Do the experimental results reveal which path each photon followed?

The answer is YES. Let the outcome of the 10⁶ quantum tests be positive slope fringes. Then, in the experimental layout that has been presented, each red photon came through A and each blue photon came through B. The path that each photon followed is known, yet, an interference pattern is observed. The interference pattern is built up by the accumulation single photon events. The certainty of the assertion depends on the visibility of the interference fringes, and these in turn, depend on the number of quantum events (and of course, the appropriate experimental arrangement with truly independent but stable enough sources).

• Do the experimental results reveal which path did a detected photon (a white speck on the screen) followed?

The answer is NO. When we refer to “this” photon that impinged on the screen, it is not known whether it is a red or a blue photon or even a redblue photon. In order to specify which way it followed, the color must be known but we only detect a white speck regardless of the photon frequency. Thus interference is observed but the detected photon path is unknown.

The subtle but fundamental difference between these two queries is that the former question does not involve the category of the detected entity. In contrast, the detected entity is at the core of the latter question.

6.2 Detected Photons

A closely related but different question is the nature of the detected photons. Before embarking onto it, we should be aware of the tacit assumption that photons are considered to exist as an indivisible lump of electromagnetic energy or at least provide the best description we have so far of the EM fields. To some extent, this is a matter, as Prof. Penrose puts it, of quantum faith [45]. A faith not exempt of support and vast evidence considering the overwhelming success of quantum field theory. For this reason, the alternatives mentioned here below do not admit the possibility of a detector (say an atom) absorbing part of one photon and part of another photon, for this would destroy the photon concept altogether.

Two alternatives are envisaged regarding the nature of each detected photon:

1) Detected photons are either blue or red. One possibility is to consider that a detected photon is either blue or red but its frequency cannot be known if interference occurs. An asset of this approach is that the entities “red photon” or “blue photon” retain their identity. Thus, the photon concept remains a good concept, in the sense of good quantum numbers. However, this view has the major problem that there is then no superposition of the disturbances, but it is superposition that produces the interference phenomenon. A thought experiment has been proposed before, involving frequency sensitive photo detectors with different predictions for the expected outcome ([37], App. A). It has also been stressed that superposition actually takes place only in the presence of charges that respond to the superimposed fields [46].

2) Detected photons bear information of both frequencies (mainstream view). The other possibility is to consider that a detected photon within the interference region has information on both laser fields as expounded by Paul ([47], p.221). In the present experiment, it must bear information of both frequencies according to the superposition described in Subsection 2.2. The difficulty with this view is that a photon cannot give part of it to another photon because it would then loose its entity. Somehow, it has to give information to the other photon while retaining its photon identity. Photons cannot be conceived like classical particles. What is more, photons cannot even be conceived like other quantum material particles because, in general, there is no mathematical object that represents a photon wavefunction [48]. The photon notion arises naturally in number states as the elementary energy unit ℏω. Number states are eigenstates of the Hamiltonian but their phase is random. In order to observe first order interference, a well defined phase, up to uncertainty limitations, is required. Single mode coherent states exhibit a well defined phase but are not eigenstates of the Hamiltonian. Their energy is not well defined due to the uncertainty in photon number but, being single mode states, the energy per photon is fixed. As mentioned by Paul ([47], p.221), in the detection process, “an energy packet hν is taken from the superposition field to which both lasers contribute equally, and hence it is only natural that this photon bears information on both laser fields.”

6.3 Final Remark

According to the present results, the which way assertion should be refined in order to have an unambiguous meaning: The path that each photon followed, in a non-degenerate frequency scheme, whether red or blue, can be known without destroying the interference pattern. In this formulation of the statement, the slit that each photon passed through is known, but it is not known to which detected spot it corresponds. Another, equally correct formulation is that, within the interference region, the path of a detected photon cannot be traced back. That is, if interference occurs, it is not possible to assert the path followed by a photon detected on the screen.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

MF-G conceived and performed the experiment. MF-G wrote the manuscript, CG-G revised the text. CG-G collaborated in the setup and maintained the stringent conditions needed to stabilize the two CW lasers.

Funding

Part of the equipment used in these experiments was funded by CONACYT, projects CB2005-51345-F-24696 and CB2010-151137-F.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Tseltal variant of Mayan language for numbers two → cheb and three → oxeb

References

1. Javan A, Ballik EA, Bond WL. Frequency Characteristics of a Continuous-Wave He-Ne Optical Maser. J Opt Soc Am (1962) 52:96–8. doi:10.1364/JOSA.52.000096

CrossRef Full Text | Google Scholar

2. Magyar G, Mandel L. Interference Fringes Produced by Superposition of Two Independent Maser Light Beams. Nature (1963) 198:255–6. doi:10.1038/198255a0

CrossRef Full Text | Google Scholar

3. Pfleegor RL, Mandel L. Interference of Independent Photon Beams. Phys Rev (1967) 159:1084–8. doi:10.1103/physrev.159.1084

CrossRef Full Text | Google Scholar

4. Kaltenbaek R, Blauensteiner B, Żukowski M, Aspelmeyer M, Zeilinger A. Experimental Interference of Independent Photons. Phys Rev Lett (2006) 96:240502. doi:10.1103/PhysRevLett.96.240502

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Bratescu GG, Tudor T. On the Coherence of Disturbances of Different Frequencies. J Opt (1981) 12:59–64. doi:10.1088/0150-536x/12/1/005

CrossRef Full Text | Google Scholar

6. Lee D-I, Roychoudhuri C. Measuring Properties of Superposed Light Beams Carrying Different Frequencies. Opt Express (2003) 11:944–51. doi:10.1364/OE.11.000944

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Davis LM. Interference between Resolvable Wavelengths with Single-Photon-Resolved Detection. Phys Rev Lett (1988) 60:1258–61. doi:10.1103/PhysRevLett.60.1258

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Saveliev IG, Sanz M, Garcia N. Time-resolved Young$rquot$s Interference and Decoherence. J Opt B: Quan Semiclass. Opt. (2002) 4:S477–S481. doi:10.1088/1464-4266/4/4/343

CrossRef Full Text | Google Scholar

9. Louradour F, Reynaud F, Colombeau B, Froehly C. Interference Fringes between Two Separate Lasers. Am J Phys (1993) 61:242–5. doi:10.1119/1.17298

CrossRef Full Text | Google Scholar

10. Patel R, Achamfuo-Yeboah S, Light R, Clark M. Widefield Two Laser Interferometry. Opt Express (2014) 22:27094–101. doi:10.1364/OE.22.027094

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Marathay AS. Elements of Optical Coherence Theory. New York: Wiley (1982).

Google Scholar

12. Eichmann U, Bergquist JC, Bollinger JJ, Gilligan JM, Itano WM, Wineland DJ, et al. Young's Interference experiment with Light Scattered from Two Atoms. Phys Rev Lett (1993) 70:2359–62. doi:10.1103/physrevlett.70.2359

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Riedmatten Hd., Marcikic I, Tittel W, Zbinden H, Gisin N. Quantum Interference with Photon Pairs Created in Spatially Separated Sources. Phys Rev A (2003) 67:022301. doi:10.1103/PhysRevA.67.022301

CrossRef Full Text | Google Scholar

14. Esposito G, Marmo G, Miele G, Sudarshan G. Advanced Concepts in Quantum Mechanics. Cambridge, United Kingdom: CUP (2014).

Google Scholar

15. Jacques V, Wu E, Grosshans F, Treussart F, Grangier P, Aspect A, et al. Delayed-choice Test of Quantum Complementarity with Interfering Single Photons. Phys Rev Lett (2008) 100:220402. doi:10.1103/PhysRevLett.100.220402

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Katsumori M. Niels Bohr’s Complementarity. Dordrecht: Springer (2011).

Google Scholar

17. Plotnitsky A. Niels Bohr and Complementarity. New York: Springer (2013).

Google Scholar

18. Fernández-Guasti M, Palafox H, Chandrasekar R. Coherence and Frequency Spectrum of a Nd:YAG Laser - Generation and Observation Devices. In: Optics and Photonics 2011. San Diego: SPIE (2011). p. 81211E–1–10. vol. 8121 of The nature of light: What are photons? IV. doi:10.1117/12.893194

CrossRef Full Text | Google Scholar

19. Fernández-Guasti M, García-Guerrero C. Optical Interference between Distinguishable Photon Paths. In: 2019 PhotonIcs Electromagnetics Research Symposium - Spring (PIERS-Spring). Rome: IEEE Xplore (2020). p. 3634–42.

Google Scholar

20. Vidal I, Caetano DP, Fonseca EJS, Hickmann JM. Observation of Interference Pattern in the Intensity Correlation of a Non-local Object Using a Hanbury Brown and Twiss-type experiment. Europhys Lett (2008) 82:34004. doi:10.1209/0295-5075/82/34004

CrossRef Full Text | Google Scholar

21. Lee PSK, van Exter MP. Spatial Labeling in a Two-Photon Interferometer. Phys Rev A (2006) 73:063827. doi:10.1103/PhysRevA.73.063827

CrossRef Full Text | Google Scholar

22. Grynberg G, Aspect A, Fabre C. Introduction to Quantum Optics. New York: CUP (2010).

Google Scholar

23. Glauber R. Quantum Theory of Optical Coherence. Heppenheim: WILEY-VCH Verlag (2007).

Google Scholar

24. Peres A. Quantum Theory: Concepts and Methods. Boston: Kluwer Academic (2002). vol. 72 of Fundamental Theories of Physics.

Google Scholar

25. Mandel L. Photon Interference and Correlation Effects Produced by Independent Quantum Sources. Phys Rev A (1983) 28:929–43. doi:10.1103/PhysRevA.28.929

CrossRef Full Text | Google Scholar

26. Clerk AA, Devoret MH, Girvin SM, Marquardt F, Schoelkopf RJ. Introduction to Quantum Noise, Measurement, and Amplification. Rev Mod Phys (2010) 82:1155–208. doi:10.1103/RevModPhys.82.1155

CrossRef Full Text | Google Scholar

27. Schawlow AL, Townes CH. Infrared and Optical Masers. Phys Rev (1958) 112:1940–9. doi:10.1103/physrev.112.1940

CrossRef Full Text | Google Scholar

28. Busch P. On the Energy-Time Uncertainty Relation. Part I: Dynamical Time and Time Indeterminacy. Found Phys (1990) 20:1–32. doi:10.1007/BF00732932

CrossRef Full Text | Google Scholar

29. Miyadera T. Energy-time Uncertainty Relations in Quantum Measurements. Found Phys (2016) 46:1522–50. doi:10.1007/s10701-016-0027-6

CrossRef Full Text | Google Scholar

30. Aharonov Y, Bohm D. Time in the Quantum Theory and the Uncertainty Relation for Time and Energy. Phys Rev (1961) 122:1649–58. doi:10.1103/physrev.122.1649

CrossRef Full Text | Google Scholar

31. Diels JC, Rudolph W. Ultrashort Laser Pulse Phenomena: Fundamentals, Techniques, and Applications on a Femtosecond Time Scale. 2nd ed. Amsterdam: Academic Press, Elsevier Science Publishers (2006).

Google Scholar

32. Liu J, Zhou Y, Zheng H, Chen H, Li F-l., Xu Z. Two-photon Interference with Non-identical Photons. Opt Commun (2015) 354:79–83. doi:10.1016/j.optcom.2015.05.072

CrossRef Full Text | Google Scholar

33. Roychoudhuri C, Roy R. The Nature of Light: What Is a Photon? Boca Raton: Taylor and Francis (2003). p. S1–S35. Optics and Photonics News.

Google Scholar

34. Ficek Z, Swain S. Quantum Interference and Coherence: Theory and Experiments. New York: Springer (2005).

Google Scholar

35. Aharonov Y, Albert DZ, Vaidman L. How the Result of a Measurement of a Component of the Spin of a Spin-1/2particle Can Turn Out to Be 100. Phys Rev Lett (1988) 60:1351–4. doi:10.1103/PhysRevLett.60.1351

PubMed Abstract | CrossRef Full Text | Google Scholar

36. Kocsis S, Braverman B, Ravets S, Stevens MJ, Mirin RP, Shalm LK, et al. Observing the Average Trajectories of Single Photons in a Two-Slit Interferometer. Science (2011) 332:1170–3. doi:10.1126/science.1202218

PubMed Abstract | CrossRef Full Text | Google Scholar

37. Garcia N, Saveliev IG, Sharonov M. Time-resolved Diffraction and Interference: Young's Interference with Photons of Different Energy as Revealed by Time Resolution. Philos Trans A Math Phys Eng Sci (2002) 360:1039–59. doi:10.1098/rsta.2001.0980

PubMed Abstract | CrossRef Full Text | Google Scholar

38. Grave de Peralta L. Phenomenological Quantum Description of the Ultrafast Response of Arrayed Waveguide Gratings. J Appl Phys (2010) 108:103110. doi:10.1063/1.3512860

CrossRef Full Text | Google Scholar

39. Englert B-G. Fringe Visibility and Which-Way Information: An Inequality. Phys Rev Lett (1996) 77:2154–7. doi:10.1103/PhysRevLett.77.2154

PubMed Abstract | CrossRef Full Text | Google Scholar

40. Myrvold WC, Christian J. Quantum Reality, Relativistic Causality, and Closing the Epistemic Circle. Netherlands: Springer (2009).

Google Scholar

41. Dirac PAM. The Principles of Quantum Mechanics. 4th ed. Oxford: OUP (1978).

Google Scholar

42. Caves CM. Quantum Mechanics of Measurements Distributed in Time. A Path-Integral Formulation. Phys Rev D (1986) 33:1643–65. doi:10.1103/PhysRevD.33.1643

CrossRef Full Text | Google Scholar

43. Feynman RP. Space-time Approach to Non-relativistic Quantum Mechanics. Rev Mod Phys (1948) 20. doi:10.1103/revmodphys.20.367

CrossRef Full Text | Google Scholar

44. Feynman R, Hibbs A, Styer D. Quantum Mechanics and Path Integrals. New York: Dover Books on Physics (Dover Publications) (2010).

Google Scholar

45. Penrose R. Fashion, Faith and Fantasy. Woodstock: Princeton Univ. Press (2016).

Google Scholar

46. Roychoudhuri C. Causal Physics: Photons by Non-interactions of Waves. Boca Raton: CRC Press, Taylor and Francis (2017).

Google Scholar

47. Paul H. Interference between Independent Photons. Rev Mod Phys (1986) 58:209–31. doi:10.1103/RevModPhys.58.209

CrossRef Full Text | Google Scholar

48. Scully MO, Zubairy MS. Quantum Optics. Cambridge: CUP (2001).

Google Scholar