Numerical Simulations of Temporary Plugging-Refracturing Processes in a Conglomerate Reservoir Under Various In-Situ Stress Difference Conditions

In this study, a numerical model of the conglomerate reservoir is established using ABAQUS. Cohesive elements are embedded into the numerical model to simulate the hydraulic fracturing behaviours of the conglomerate reservoir. The cohesive elements split by the high-pressure liquid flow are identified by tracing the crack propagation. A USDFLD (user-defined field variable) subroutine is used to increase the liquid flow’s dynamic viscosity in these cracked cohesive elements. Using this method, ABAQUS successfully simulates the temporary plugging-refracturing processes in the conglomerate reservoir under four in-situ stress states. This study found that with the increase of the horizontal in-situ stress difference, the pore pressure at the fluid injection point increased correspondingly. Under the conditions of higher horizontal in-situ stress differences, more complex branch fractures were generated in the conglomerate reservoir.

Introduction

The temporary plugging-refracturing technology achieves the purpose of increasing oil and gas production by injecting high-pressure fluid flow into the oil or gas reservoir to generate tension fractures [1-2]. Simulating the complex branched fractures in the oil and gas reservoirs has always been a challenge in temporary plugging-refracturing technology [1, 3].

Many numerical methods are used to simulate the hydraulic fracturing problem of rock mass [1]. Some scholars use the discrete element method (DEM) [4–6]. This method can better simulate the fracture network of rock masses. Thus, it has good adaptability to model the hydraulic fracturing of a rock mass. Other scholars use the finite element method (FEM) [7] and extended finite element methods (XFEM) [3, 8] to simulate the hydraulic fracturing process in rock masses. However, XFEM is not very effective in simulating the mechanical behaviour of rock masses with a large number of cross-cracks. The introduction of the cohesive element is a good supplement to the FEM for simulating the discontinuous deformation and failure of materials [3]. Some researchers have validated that this method (cohesive element-based FEM) has good adaptability in modelling hydraulic fracturing of complex fractured rock masses [9-11].

Based on previous studies, this paper takes conglomerate reservoirs as the research object and establishes a numerical model using ABAQUS. Then, in this numerical model, the cohesive elements considering seepage-stress coupling behaviors are embedded to simulate the hydraulic fracturing of a conglomerate reservoir. Then, a USDFLD subroutine is coded to simulate the temporary plugging process in the conglomerate reservoir. Finally, the temporary plugging-refracturing processes in conglomerate reservoirs under various in-situ stress differences are numerically simulated.

Methods

Cohesive Element-Based FEM

The cohesive element was first applied to the bond crack model in ductile materials such as metals [12, 13]. The simulation of jointed rock mass based on FEM is shown in Figures 1A,B. Combining the principle of conservation of energy, the weak solution form of FEM considering the adhesion is described as follows:

$\begin{array}{l}\text{δ}{W}^{\text{ext}}=\text{δ}{W}^{\mathrm{int}}+\text{δ}{W}^{\text{coh}}\\ \text{δ}{W}^{\text{int}}={\displaystyle {\int }_{\mathrm{\Omega }}{\nabla }^s\text{δ}u:\sigma \text{d}\mathrm{\Omega }}\\ \text{δ}{W}^{\text{ext}}={\displaystyle {\int }_{\mathrm{\Omega }}\text{δ}u\cdot b\text{d}\mathrm{\Omega }}+{\displaystyle {\int }_{{\mathrm{\Gamma }}_t}\text{δ}u\cdot \overline{t}\text{d}{\mathrm{\Gamma }}_t}\\ \text{δ}{W}^{\text{coh}}={\displaystyle {\int }_{{\mathrm{\Gamma }}_d}\text{δ}u\cdot t^c\text{d}{\mathrm{\Gamma }}_d}\end{array}(1)$

where, $u$ denotes the displacement jump in a cohesive element.

FIGURE 1

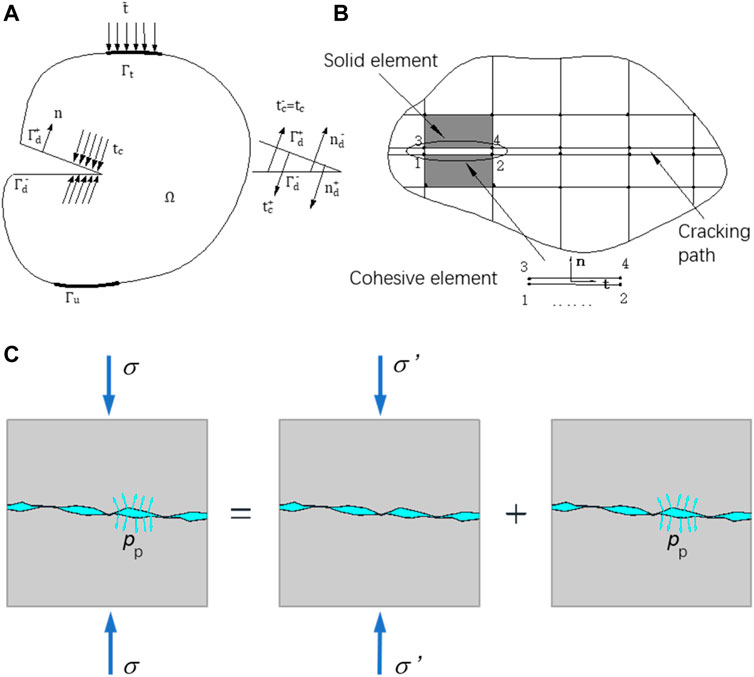
FIGURE 1. (A) Schematic diagram of cohesive element simulating cracking of rock material; (B) Schematic diagram of joint crack propagation simulated by cohesive element; (C) Schematic diagram of stress seepage coupling of joints and fissures.

The displacement field of the cohesive element can be controlled by the relative displacement of the upper and lower surfaces, and the following expression is established:

$\begin{array}{l}{u}^{+}=N^{\mathrm{int}}{u}^{+},u^{-}=N^{\mathrm{int}}{u}^{-}\\ u\left(x\right)=u^{+}-u^{-}=N^{\mathrm{int}}\left(u^{+}-u^{-}\right)\end{array}(2)$

where, $u^{+}$ and $u^{-}$ represent the nodal displacements on the upper and lower surfaces, respectively. $N^{\mathrm{int}}$ represents the shape function, which is the same as that of the face element.

Combine the relationship between the displacement field of the solid element and the node displacement. We have

$u=N_{\text{I}}{u}_{\text{I}}\text{,}\text{δ}u=N_{\text{I}}\text{δ}{u}_{\text{I}}(3)$

where, $N_{\text{I}}$ and $u_{\text{I}}$ are the shape function and node displacement, respectively.

By combining the displacement expression of the solid element and the cohesive element, the following governing equation is established based on the weak solution form of the finite element:

$\begin{array}{l}{f}^{\text{ext}}=f^{\mathrm{int}}+f^{\text{coh}}\\ f^{\text{ext}}={\displaystyle {\int }_{{\mathrm{\Omega }}_e}{B}^T\sigma \text{d}{\mathrm{\Omega }}_e}\\ f^{\mathrm{int}}={\displaystyle {\int }_{{\mathrm{\Omega }}_e}{N}^{T}b\text{d}{\mathrm{\Omega }}_e}+{\displaystyle {\int }_{{\mathrm{\Gamma }}_t^e}{N}^T\overline{t}\text{d}{\mathrm{\Gamma }}_t^e}\\ f_{ie,+}^{\text{coh}}={\displaystyle {\int }_{{\mathrm{\Gamma }}_d^e}{N}^T\overline{t}\text{d}{\mathrm{\Gamma }}_d^e},f_{ie,-}^{\text{coh}}=-{\displaystyle {\int }_{{\mathrm{\Gamma }}_d^e}{N}^T\overline{t}\text{d}{\mathrm{\Gamma }}_d^e}\end{array}(4)$

where, $f^{\text{ext}}$, $f^{\mathrm{int}}$ and $f^{\text{coh}}$ are the vectors of external force, internal force and cohesion force, respectively. $b$ represents the body force. $\overline{t}$ is the surface force.

Combined with the stress-strain relationship of solid element and the traction separation law of cohesive element, a complete finite element solution process using the cohesive element can be established as follows:

1) Loop at the ith cohesive element under the specified loading step.

2) Obtain the node code ‘inodes’ of the ith cohesive element.

3) Obtain the degrees of freedom of the upper and lower surfaces of the ith cohesive element: idofsA and idofsB.

4) Obtain the node displacement of the upper and lower surfaces of the ith cohesive element: $u^{+}$ and $u^{-}$.

5) Compute the traction displacement of the ith cohesive element.

6) Loop each Gaussian integral point by conducting the following procedure.

  1) Calculate the traction displacement on the jth integral point.

#x02003; 2) Convert to local coordinate system.

#x02003; 3) Based on the traction-separation constitutive relationship, compute the bond force.

#x02003; 4) Convert the local bond force into the bond force in the global coordinate.

#x02003; 5) Calculate and update the uniform stiffness matrix of the traction-separation criterion.

7) The cohesive element’s node force and stiffness matrix are assembled into the global system to obtain the stiffness matrix and node force.

Constitutive Model for Cohesive Element

In ABAQUS, the mechanical behaviours of cohesive element are generally described using a bilinear traction-separation model [14]. In this model, the linear-growth stage before the peak-strengths describes the interfacial elastic behavior of cohesive element. It can be described by the following formula:

$\left\{\begin{array}{c}{\sigma }_{\text{n}}\\ {\tau }_{\text{s}}\end{array}\right\}=\left[\begin{array}{cc}{E}_{\text{nn}}& E_{\text{ns}}\\ E_{\text{sn}}& E_{\text{ss}}\end{array}\right]\left\{\begin{array}{c}{\epsilon }_{\text{n}}\\ {\epsilon }_{\text{s}}\end{array}\right\}=\frac{1}{T_0}\left[\begin{array}{cc}{E}_{\text{nn}}& E_{\text{ns}}\\ E_{\text{sn}}& E_{\text{ss}}\end{array}\right]\left\{\begin{array}{c}{\delta }_{\text{n}}\\ {\delta }_{\text{s}}\end{array}\right\}(5)$

where ${\sigma }_{\text{n}}$ and ${\tau }_{\text{s}}$ are the nominal traction stress components applied on the interface of the cohesive element in a 2D problem. ${\epsilon }_{\text{n}}$ and ${\epsilon }_{\text{s}}$ are the two components of the nominal strains, respectively. ${\delta }_{\text{n}}$ and ${\delta }_{\text{s}}$ are corresponding separations. $T_0$ denotes the original thickness of the cohesive element. $E_{\text{nn}}$, $E_{\text{ss}}$, $E_{\text{ns}}$ and $E_{\text{sn}}$ are the material constants. When the interaction between shear and normal stress is not considered, $E_{\text{ns}}$ and $E_{\text{sn}}$ are equal to zeros.

When the nominal traction stress reach the maximum values (peak-strengths) ${\sigma }_{\text{n0}}$ and ${\tau }_{\text{s0}}$, it is regarded that the cohesive element damage initiates, which can be described using the following nominal stress criterion:

$\max \left\{\frac{\langle {\sigma }_{\text{n}}\rangle }{{\sigma }_{\text{n0}}},\frac{\langle {\tau }_{\text{s}}\rangle }{{\tau }_{\text{s0}}}\right\}=1(6)$

where $\langle \rangle$ is the Macaulay bracket. It has $\langle {\sigma }_{\text{n}}\rangle ={\sigma }_{\text{n}}$, when ${\sigma }_{\text{n}}\ge 0$ (tension), and $\langle {\sigma }_{\text{n}}\rangle =0$, when ${\sigma }_{\text{n}}<0$ (compression).

When the above damage criterion is satisfied, the nominal traction stress decreases linearly, and enters the post-peak linear softening stage. A scalar damage variable $D$ (evolve from 0 to 1) is used to describe the degradation of cohesive element in the following equation.

${\sigma }_{\text{n}}=\left(1-D\right){\overline{\sigma }}_{\text{n}},{\tau }_{\text{s}}=\left(1-D\right){\overline{\tau }}_{\text{s}}(7)$

The stress components ${\overline{\sigma }}_{\text{n}}$ and ${\overline{\tau }}_{\text{s}}$ are predicted using the traction-separation model for the current strains without damage. The effective displacement is defined as ${\delta }_{\text{m}}=\sqrt{{\langle {\delta }_{\text{n}}\rangle }^2+{\delta }_s^2}$ to describe the damage evolution under the combination of normal and shear deformation.

For the linear softening, the damage evolution can be expressed as follows:

$D=\frac{{\delta }_{\text{m}}^{\text{f}}\left({\delta }_{\text{m}}^{\max }-{\delta }_{\text{m}}^0\right)}{{\delta }_{\text{m}}^{\max }\left({\delta }_{\text{m}}^{\text{f}}-{\delta }_{\text{m}}^0\right)}(8)$

where ${\delta }_{\text{m}}^0$ and ${\delta }_{\text{m}}^{\text{f}}$ represent the effective displacement at damage initiation and complete failure, respectively. ${\delta }_{\text{m}}^{\max }$ is the maximum value of the effective displacement attained during the loading history.

At the current nominal stress-strain state, the geometry area below the stress-strain curve is the normal and shear fracture energy, which can be denoted using $G_{\text{n}}$ and $G_{\text{s}}$, respectively. Thus, the fracture energy on the mode mix can be expressed using a power-law fracture criterion, as follows:

$G_{\text{n}}^{\text{C}}+\left(G_{\text{s}}^{\text{C}}-G_{\text{n}}^{\text{C}}\right){\left\{\frac{G_{\text{s}}}{G_{\text{n}}}\right\}}^{\eta }=G^C(9)$

Where $G_{\text{n}}^{\text{C}}$, $G_{\text{s}}^{\text{C}}$ and $\eta$ are the material constants for describing fracture behaviors.

Cohesive Element Modeling Seepage-Stress Coupling Problem

The water flow in the fractured rock mass is a typical seepage-stress coupling problem (Figure 1C). This problem is mainly manifested in three aspects.

1) The pore pressure in the fractures affects the strength and deformation of the rock mass, especially the normal deformation of the fracture. The effective stress principle can be expressed as:

$\sigma =\sigma \mathrm{\prime }+\alpha p_{\text{p}}(10)$

where, $\sigma$, ${\sigma }^{\prime }$ and $p_{\text{p}}$ are the total stress, effective stress and pore pressure, respectively. $\alpha$ is the effective stress coefficient.

2) Joint void $u_{\text{m}}$ can be defined as the average distance between different fracture surfaces. Hydraulic gap width $u_{\text{h}}$ is used to calculate the fluid velocity in the fractures. The relationship between hydraulic gap width $u_{\text{h}}$ and deformation is defined as follows:

$u_{\text{h}}=f{u}_{\text{m}}=u_{\text{h0}}+f\mathrm{\Delta }{u}_{\text{m}}(11)$

where, unknown variables $u_{\text{h0}}$ and $f$ can be obtained by linear data-fitting.

3) Introducing the Darcy seepage formula in the cohesive element can simulate the seepage-stress coupling behaviour of rock mass. The fracture width $d$ and hydrodynamic viscosity $\mu$ affect the tangential permeability $k_{\text{t}}$, satisfying the following equation.

$k_{\text{t}}=\frac{d^3}{12\mu }(12)$

Models

Geological Model of Conglomerate Reservoir

The deep conglomerate reservoir is a kind of heterogeneous sedimentary rock. In terms of its geological structure, it is composed of conglomerate particles and filler matrices. When studying its material mechanical and seepage behavior, the heterogeneity of conglomerate reservoir can be simplified as a two-phase material in which conglomerate particles of different sizes are randomly embedded into the filler matrix.

Figure 2A show the plane geological model of conglomerate reservoir. It is a square area with a side length of 6000 mm. There is an initial crack extending horizontally in the middle of the left side. This initial crack penetrates the surrounding rock and extends to 200 mm in the core area of the conglomerate reservoir. The crack is used to simulate the fluid conveyance channel of hydraulic fracturing.

FIGURE 2

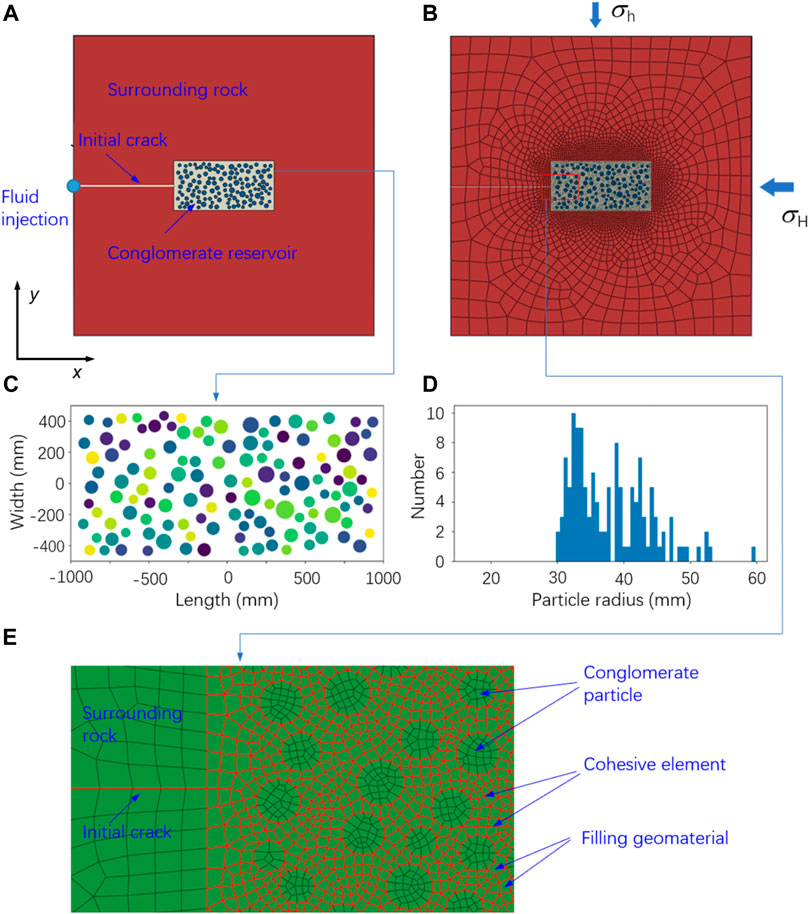
FIGURE 2. (A) Plane geological model; (B) Plane numerical model; (C) Aggregate distribution of conglomerate reservoir in the core area; (D) Statistical distribution of the aggregate size of the conglomerate reservoir in the core area; (E) An enlarged picture showing the meshes of conglomerate particles and filling geomaterial, as well as the cohesive elements embedded into the filling geomaterial.

The model size of the core stratum of the conglomerate reservoir is set to a square area of 2000 mm long and 1000 mm wide. Conglomerate aggregates are randomly generated in this area, as shown in Figure 2C. There are 129 round particles used for filling the core area. Their radius of the generated aggregates is in a range of 30–60 mm. The particle content is 30% in volume.

In the geological model of the conglomerate reservoir shown in Figure 2C, these aggregates are divided into six groups using different colors according to size. Figure 2D performs a statistical analysis on the geometric dimensions of the generated 129 aggregates. It can be seen that most conglomerate particles are concentrated in the size range of 30–45 mm.

Numerical Model of Conglomerate Reservoir

The problem concerned in this study is simplified to a plane strain problem to be solved using ABAQUS. The first-order linear plane strain quadrilateral element is used to mesh the geological model. Then, a numerical model is obtained, as shown in Figure 2B. The numerical model has 8,895 plane strain quadrilateral elements and 8,927 nodes.

This study uses the cohesive element to simulate the conglomerate reservoir’s discontinuous deformation and failure under hydraulic fracturing loads. We consider that the conglomerate aggregates do not fail and the hydraulic fracturing cracks only occur inside the filler. Therefore, the cohesive elements are only embedded within the plane strain elements of the filler of the conglomerate reservoir. Figure 2E shows the numerical calculation model after embedding the cohesive elements. This new model has a total of 9,226 cohesive elements.

Loads and Boundary Conditions

The model’s left side is the symmetrical plane, which is an impervious boundary. The midpoint of the initial fracture on the left side is the fluid injection point (Figure 2A). In calculation, the mechanical boundary condition at this point is the pore pressure of hydraulic fracturing. The nodal displacements in the x-axis and y-axis directions of the four edges around the model are constrained.

All of the nodes in the model are set as constant pore pressure conditions. The initial pore pressure of these nodes is set to 0 MPa, and the initial void ratio is set as $e_0=0.1$ for the rock mass in the whole model. The hydraulic fracturing pore pressure value at the fluid injection point is set as 100 MPa.

As shown in Figure 2B, the horizontal minor principal in-situ stress ${\sigma }_{\text{h}}=10\text{MPa}$ is applied vertically on the whole model, the horizontal major principal stress ${\sigma }_{\text{H}}$ is applied horizontally, and the principal stress ${\sigma }_{\text{z}}={\sigma }_{\text{h}}$ is applied in the z-axis direction. To study the influence of in-situ stress difference ($\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}$), four stress states are set up, which are $\Delta \sigma =$ 4, 8, 12 and 16 MPa, respectively.

Mechanical Parameters

In this numerical model, four types of geomaterials are involved: surrounding rocks, conglomerate aggregates, fillers, and cohesive interfaces around the aggregates. The material parameters used in the numerical simulations are given in Table 1.

TABLE 1

TABLE 1. Mechanical parameters of the geomaterials used in the numerical simulations.

Implementation of Temporary Plugging Simulation

The numerical modeling of the temporary plugging treatment in the rock mass is difficult in FEM simulations. In order to realize this modeling in ABAQUS, an available method is by reading the crack propagation data of the cohesive elements and increasing the fluid’s dynamic viscosity in these positions.

In actual execution, the coordinates of the crack tips in the cohesive elements at the temporary plugging moment can be recorded. Then, a USDFLD subroutine (user-defined field variable) is called by ABAQUS to increase the liquid flow’s dynamic viscosity in these cohesive elements in the subsequent calculations. Thereby, an increase in the fluid’s resistance passing through these cohesive elements would force the initiation and propagation of new branch fractures in other locations with lower resistance.

The calculation time lasts to 21 s, divided into two stages. 1) During the period of t = 0–1 s, the pore pressure increases sharply at the fluid injection point from 0 to 10 MPa. 2) During the period of t = 1–8 s, the increased pore pressure leads to the first splitting crack propagation at the tip of the fracture. 3) Starting from t = 8 s, at the forefront of the formed hydraulic fractures, temporary plugging is conducted by changing the value of dynamic viscosity of the fluid at the cracking cohesive elements. The blocking length is set to 100 mm.

Modelling Results and Analysis

Fracturing Characteristics

Figure 3 shows the expansion and distribution of the fractures induced by temporary pugging-refracturing in the conglomerate reservoir under four in-situ stress differences. It can be seen that the fractures caused by hydraulic fracturing in the conglomerate reservoir propagate along the initial fracture and the direction of the major principal in-situ stress.

FIGURE 3

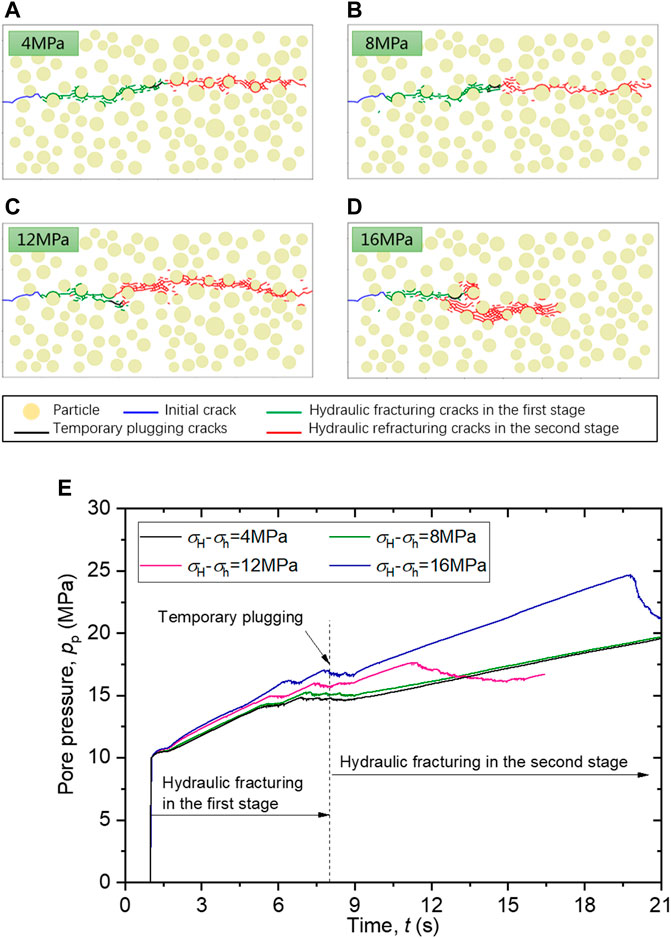
FIGURE 3. (A,B,C,D) Fracture evolution characteristics of temporary plugging-refracturing under different in-situ stress differences; (E) Pore pressure history curve at injection point under different horizontal stress difference.

When the in-situ stress difference is relatively smaller, that is $\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}=4\text{MPa}$ and 8 MPa (Figures 3A,B), it is that, after the temporary plugging, the hydraulic fractures are easy to break through the temporary plugging position and continue to expand. Under the condition of these two in-situ stress differences, the overall propagation direction of hydraulic fractures is slightly upward to the right than the horizontal direction.

Figures 3C,D shows the expansion and distribution of the fractures in the conglomerate reservoir under higher horizontal stress difference conditions, i.e., $\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}=12\text{MPa}$ and 16 MPa. It is observed that, after temporary blocking, the injected fluid is difficult to break the temporary blocking position, but generates new branch fracturing regions. In the calculation time range of 21 s, as $\Delta \sigma =12\text{MPa}$, the secondary refracturing cracks extend to the core region of the right end conglomerate reservoir boundary. Around the main crack, more short and small branch cracks sprouted. Compared to $\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}=4\text{MPa}$ and 8 MPa, when $\Delta \sigma =12\text{MPa}$, the secondary refracturing crack belt is much wider (Figure 3C).

It is observed from Figure 3D that, when $\Delta \sigma =16\text{MPa}$, when secondary refracturing cracks do not extend to the rightmost boundary of the conglomerate reservoir. Due to the influence of the distribution of conglomerate aggregates and the in-situ stress difference, the secondary refracturing crack belt generally expands from the lower side of the horizontal direction to the lower right under the condition of $\Delta \sigma =16\text{MPa}$. A large number of branch cracks are formed around the main crack.

Evolution of Pore Pressure

Figure 3E shows the pore pressure changes with time at the fluid injection point. In general, with the increase of the major principal in-situ stress ${\sigma }_{\text{H}}$, the pore pressure at the fluid injection point used to produce hydraulic fracturing increases, too. In the 0–1 s stage, the pore water pressure at the fluid injection point increased sharply to 10 MPa. In this stage, there is almost no difference in pore pressure at the fluid injection point under the four different in-situ stress conditions. In the 1–6 s stage, the pore pressure increases linearly with time at the fluid injection point. The greater the in-situ stress difference, the higher the pore pressure growth rate at the fluid injection point.

When time exceeds 6 s, the pore pressures at the fluid injection point enter relatively flat plateaus under the four in-situ stress conditions. The conglomerate reservoir was hydraulically fractured at these flat plateaus of the pore pressures. Because of the initiation and propagation of the fractures, the fracture volumes increase, making it difficult for the pore pressure at the fluid injection point to increase continuously.

When time = 8 s, the cracks produced by the first hydraulic fracturing are temporarily blocked. After the temporary plugging treatment, for the case of $\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}=4\text{MPa}$ and 8 MPa, the pore pressure at the fluid injection point hardly increased significantly. It shows not many branch fractures under these two conditions in the conglomerate reservoir. However, the pumped fluid breaks through the plugging point and continues to expand forward, as shown in Figures 3A,B. When time exceeds 9 s, the pore pressure at the fluid injection point increases linearly.

In the case of $\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}=12\text{MPa}$, during the 9–11 s period, the pore pressure at the injection point increases linearly with time. In the 11–15 s period, the pore pressure decreases linearly with time. It can be determined that during this period, the conglomerate reservoir is refractured again by hydraulic forces, forming secondary fractures. Because the newly formed cracks increase the crack volumes, resulting in the unloading of pore pressure. Comparing Figure 3C with Figures 3A,B, it can be seen that more secondary branch fractures occur under the condition of $\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}=12\text{MPa}$. The occurrence of many secondary branch hydraulic fracturing cracks is associated with the reduction of pore pressure at the fluid injection point at this stage.

For the case of $\Delta \sigma ={\sigma }_{\text{H}}-{\sigma }_{\text{h}}=16\text{MPa}$ (Figure 3D), during the 8–9 s period, the pore pressure at the injection point decreases slightly during the fluctuating process. During the 9–20 s period, the pore pressure at the fluid injection point increases linearly to 24.68 MPa with time at a faster rate. When the time exceeds 20 s, the pore pressure at the injection point decreases sharply. This indicates that at this moment, due to the continuous pumping and pressurization of high-pressure fluid, a large number of hydraulic fractures are rapidly formed in the conglomerate reservoir.

Conclusions

In this study, ABAQUS is used to numerically simulate the temporary plugging-refracturing process in the conglomerate reservoir under four in-situ stress states. The following conclusions can be summarised:

1) In FEM analysis, the cohesive element can effectively simulate the discontinuous deformation and failure of the rock mass. Furthermore, the cohesive element containing the constitutive relationship of Darcy seepage is capable of simulating the seepage-stress coupling behaviour of the fractured rock mass.

2) In this study, by reading the data of crack propagation, the cracked cohesive elements are identified. A USDFLD subroutine is used to increase the dynamic viscosity of the liquid flow in these cracked cohesive elements. The numerical simulation of plugging treatment is successfully realized.

3) While under higher horizontal in-situ stress difference, it is easier to generate new branch fractures to bypass the temporary plugging position. With the increase of in-situ stress difference, the more complex the branch fractures and the higher the pore pressure used for hydraulic fracturing the conglomerate reservoir.

4) During temporary plugging-refracturing process, pore pressure distribution and fracture propagation can be observed. By analyzing the pore pressure-time history curve of the fluid injection point, the hydraulic fracturing events in the conglomerate reservoir can be judged.

5) The numerical simulation results obtained in this study are relatively intuitive, but the model of the conglomerate reservoir is somewhat different from the actual geological condition. When the actual engineering geological conditions are clear and there are accurate calculation parameters, the work carried out in this research can provide effective and reasonable suggestions for the actual petroleum engineering.

Data Availability Statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author Contributions

Numerical simulations were contributed by JC and JZ. Programming the USDFLD subroutine was mainly contributed by QZ. Drafting the manuscript was contributed by JC and JZ.

Funding

This research was financially supported by the Open Research Fund of Key Laboratory of Construction and Safety of Water Engineering of the Ministry of Water Resources, China Institute of Water Resources and Hydropower Research (Grant No. 202101) and by National Natural Science Foundation of China (Grant No. 12062026).

Conflict of Interest

JC is employed by Sany Heavy Industry Co. Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Bakhshi E, Golsanami N, Chen L. Numerical Modeling and Lattice Method for Characterizing Hydraulic Fracture Propagation: A Review of the Numerical, Experimental, and Field Studies. Arch Computat Methods Eng (2021) 28:3329–60. doi:10.1007/s11831-020-09501-6

CrossRef Full Text | Google Scholar

2. Zhang R, Hou B, Tan P, Muhadasi Y, Fu W, Dong X, et al. Hydraulic Fracture Propagation Behavior and Diversion Characteristic in Shale Formation by Temporary Plugging Fracturing. J Pet Sci Eng (2020) 190:107063. doi:10.1016/j.petrol.2020.107063

CrossRef Full Text | Google Scholar

3. Wang B, Zhou F, Wang D, Liang T, Yuan L, Hu J. Numerical Simulation on Near-Wellbore Temporary Plugging and Diverting during Refracturing Using XFEM-Based CZM. J Nat Gas Sci Eng (2018) 55:368–81. doi:10.1016/j.jngse.2018.05.009

CrossRef Full Text | Google Scholar

4. Chen W, Konietzky H, Liu C, Tan X. Hydraulic Fracturing Simulation for Heterogeneous Granite by Discrete Element Method. Comput Geotechnics (2018) 95:1–15. doi:10.1016/j.compgeo.2017.11.016

CrossRef Full Text | Google Scholar

5. Nagel NB, Sanchez-Nagel MA, Zhang F, Garcia X, Lee B. Coupled Numerical Evaluations of the Geomechanical Interactions Between a Hydraulic Fracture Stimulation and a Natural Fracture System in Shale Formations. Rock Mech Rock Eng (2013) 46:581–609. doi:10.1007/s00603-013-0391-x

CrossRef Full Text | Google Scholar

6. Zou Y, Zhang S, Ma X, Zhou T, Zeng B. Numerical Investigation of Hydraulic Fracture Network Propagation in Naturally Fractured Shale Formations. J Struct Geology (2016) 84:1–13. doi:10.1016/j.jsg.2016.01.004

CrossRef Full Text | Google Scholar

7. Deng J, Yang Q, Liu Y, Liu Y, Zhang G. 3D Finite Element Modeling of Directional Hydraulic Fracturing Based on Deformation Reinforcement Theory. Comput Geotechnics (2018) 94:118–33. doi:10.1016/j.compgeo.2017.09.002

CrossRef Full Text | Google Scholar

8. Dong Y, Tian W, Li P, Zeng B, Lu D. Numerical Investigation of Complex Hydraulic Fracture Network in Naturally Fractured Reservoirs Based on the XFEM. J Nat Gas Sci Eng (2021) 96:104272. doi:10.1016/j.jngse.2021.104272

CrossRef Full Text | Google Scholar

9. Cai X, Liu W, Shen X, Gao Y. Flow-coupled Cohesive Interface Framework for Simulating Heterogeneous Crack Morphology and Resolving Numerical Divergence in Hydraulic Fracture. Extreme Mech Lett (2021) 45:101281. doi:10.1016/j.eml.2021.101281

CrossRef Full Text | Google Scholar

10. Li J, Dong S, Hua W, Li X, Guo T. Numerical Simulation of Temporarily Plugging Staged Fracturing (TPSF) Based on Cohesive Zone Method. Comput Geotechnics (2020) 121:103453. doi:10.1016/j.compgeo.2020.103453

CrossRef Full Text | Google Scholar

11. Nguyen VP, Lian H, Rabczuk T, Bordas S. Modelling Hydraulic Fractures in Porous media Using Flow Cohesive Interface Elements. Eng Geology (2017) 225:68–82. doi:10.1016/j.enggeo.2017.04.010

CrossRef Full Text | Google Scholar

12. Barenblatt GI. The Formation of Equilibrium Cracks during Brittle Fracture. General Ideas and Hypotheses. Axially-Symmetric Cracks. J Appl Mathematics Mech (1959) 23:622–36. doi:10.1016/0021-8928(59)90157-1

CrossRef Full Text | Google Scholar

13. Dugdale DS. Yielding of Steel Sheets Containing Slits. J Mech Phys Sol (1960) 8:100–4. doi:10.1016/0022-5096(60)90013-2

CrossRef Full Text | Google Scholar

14. Abaqus UM. Abaqus Analysis User's Guide (2012). Version 6.14. Rhode Island: Dassault Systemes Simulia Corp.

Google Scholar