- 1School of Public Health, Chongqing Medical University, Chongqing, China
- 2School of Information and Software Engineering, University of Electronic Science and Technology of China, Chengdu, China
- 3Yangtze Delta Region Institute of University of Electronic Science and Technology of China, Huzhou, China
Higher-order networks can be used to describe the interaction of multiple entities in real-world collective behaviors such as dining, conference attendance, and public transportation use. Collective behavior is often one of the main reasons for “super-spreading events” during epidemics. How to propose effective immunization strategies is a Frontier research topic in network science and public health. To the best of our knowledge, there is a lack of systematic research on immunization strategies for epidemics on higher-order networks. We use synthetic networks and real-world networks as underlying structures to construct simplicial complexes to describe higher-order interaction networks, including pairwise and group interactions, and then propose a simplicial irreversible epidemic spreading model (i.e., simplicial Susceptible-Infected-Removed model). The temporal evolution process of nodes in different states in the system is described by extending the Microscopic Markov Chain Approach. Based on the node degree index and betweenness index, immunization strategies are proposed on the higher-order networks. Through theoretical analysis and numerical simulations, we discuss the effects of different higher-order infection rates, immunization ratios, and immunization strategies on the simplicial irreversible epidemic spread. Under some specific parameter configurations, we observe continuous growth, discontinuous growth, reduction of outbreak threshold, etc.
1 Introduction
With the rapid expansion of computer science and data science in recent years, the research on the spread of network epidemics has entered a golden era, garnering significant interest from academics in mathematics, physics, and public health [1–3].
Complex network theory provides a good framework for studying the structure and dynamics of complex interactive systems, can effectively demonstrate the essential characteristics of real-world social systems, demonstrates excellent mathematical performance, and is capable of performing rigorous mathematical calculations [4–7]. In 2001, Pastor-Satorras et al. [8] utilized complex networks to study for the first time the dynamic spread process of computer viruses. This new epidemiological framework ushered in the era of complex network epidemic spread dynamics and received a great deal of scholarly interest domestically and internationally. Since then, complex network-based epidemiological spread research has been the dominant approach in the field of epidemiological spread research [9–12]. However, the majority of past research has focused on the spread process of epidemics on complex networks in order to provide quantitative analysis for policy-making in the field of public health.
The Susceptible-Infected-Removed (SIR) model is one of the classic models of epidemic spread. It is frequently applied to epidemics with irreversible spread processes, such as chickenpox, measles, whooping cough, etc. After the treatment of such epidemics, patients can develop lifelong immunity, which is prevalent in the actual world [13]. Nesteruk [14] predicted the coronavirus epidemic in South Korea using the SIR model. Guo et al. [15] investigated the impact of discontinuous treatment strategies on the spread dynamics of SIR epidemics.
The majority of previous studies on network epidemic spread dynamics are based on simple networks (i.e., classical complex networks), but an increasing number of studies have demonstrated that higher-order network structures have a substantial effect on the epidemic spread process [16–18]. For instance, Althouse et al. [19] discovered that the collective behavior in higher-order networks is the primary cause of “super spreading events” during the Covid-19. Higher-order networks can be used to describe the interaction of multiple entities in real-world collective behaviors such as dining, conference attendance, and public transportation use. Numerous attempts have been made by scientists to describe networks with both pairwise and higher-order interactions. Newman et al. [20] attempted to use a bipartite graph to describe, and other researchers attempted to use clique expansion and the threshold model to describe [21–24], but neither method produced satisfactory results. To better characterize higher-order network structures, scientists propose simplicial complex, which describe higher-order interactions by sets of interactions as opposed to pairs of edges [25–27]. A simplicial complex Z is consisted of several simplexes, and if a simplex θ is contained within Z, then all the sub-simplexes σ ⊂ θ of simplex θ are also included in Z [28,29].
The purpose of studying the pathogenesis and spread rules of epidemics is to control the wanton spread of epidemics, so as to reduce or avoid the harm caused by them. The spread of epidemics depends to a large extent on the structure of population contact networks. The strategy of how to screen out some key points for immunization based on network information (local or global), so as to suppress the large-scale spread of epidemics is called immunization strategy. Immunization is a crucial topic in the field of epidemiology and has been investigated for a variety of epidemiological models in complex networks [30–34].
Pastor-Satorras et al. [35] were the pioneers in investigating immunization strategies in uniform and scale-free networks. For a uniform network, the nodes are roughly equivalent, so they proposed a simple and effective immunization strategy, random immunization, in which each node in the network has the same probability of being immune, and disease cannot continue to spread in the network when the immunization ratio exceeds a certain critical value. For a scale-free network with an uneven degree distribution of nodes, the random immunization strategy is currently invalid. They proposed a another effective immunization strategy, target immunization, which involves selecting the network nodes with the higher degree for immunization [36]. Target immunization needs to obtain the global information of the network, and it is often difficult to obtain the global information of the real population exposure network, which severely limits the practical application of this method. By randomly selecting a certain proportion of nodes as auxiliary nodes and then randomly selecting a neighboring node for immunization for each auxiliary node, a new immunization strategy known as acquaintance immunization was proposed by Cohen et al. [30]. The acquaintance immunization strategy does not require global network information and is simple to implement, but its immune effect is not the best. Gallos et al. [37] enhanced the acquaintance immunization strategy, which is to randomly select a certain proportion of individuals and then, for each individual, select the individual whose degree in the neighbor node is greater than its own or greater than a given threshold as the final immune object. The structure of the contact network often determines the efficacy of the immunization strategy. Bridge nodes are the two end nodes that connect the edges of different modules in a network; bridge nodes do not necessarily have a high degree value, so the degree-based target immunization strategy or the acquaintance immunization strategy may fail [38]. Considering that bridge nodes often have high betweenness, Freeman [39] proposed another effective immunization strategy, betweenness immunization, that is, selecting nodes with larger network betweenness values for immunization. In addition, Newman [40] proposed a random walk-based node-centricity immunization strategy, Salathe et al. [41] proposed the Community-Bridge-Find algorithm, and a novel utility model of vaccination game was formulated by Jin et al. [42], etc.
The development of higher-order networks has aroused great interest in the research community. Jhun [43] investigated the spread of epidemics on hypergraphs and proposed an immunization strategy for hyperedges with high simultaneous infection rate (SIP), i.e., the probability that all nodes in a hyperedge are in the infected state, which is derived from individual-based mean-field theory. To the best of our knowledge, there is a scarcity of systematic study on epidemiological immunization strategies on higher-order networks.
The main contributions of this paper are as follows: 1) We characterize higher-order networks by constructing simplicial complex and present a simplicial model for the spread of irreversible epidemic on simplicial complex. 2) On the basis of this model, we validate and compare the performance of traditional random immunization, target immunization, and betweenness immunization strategies, and we investigate the impact of higher-order network structures on their immune effects.
This paper is structured as follows: In Section 2, we describe how to construct simplicial complex using synthetic (heterogeneous network) and real-world networks, and then we present a simplicial irreversible epidemic spread model on the simplicial complex. Next, we perform numerical simulations in Section 3 to investigate the influence of higher-order network topologies on the spread process and the immune effects of various immunization strategies. In addition, we introduce the theoretical model framework in Section 4 and derive the temporal evolution equations of individuals in different states in the network. Conclusions are drawn and discussed in Section 5.
2 Model description
In this paper, a simplicial complex is constructed to characterize higher-order networks containing both pairwise interactions (i.e., 1-simplex) and higher-order interactions (e.g., 2-simplex), and a simplicial irreversible epidemic spread model is proposed on it. Next, we first introduce the basic concepts of simplicial complex, and then describe how to build simplicial complex with synthetic and real-world networks as the underlying network structures. Finally, to describe the spread dynamics of irreversible epidemics and explore the impact of higher-order network structure on the immune effect of different immunization strategies, a new spread model is proposed on the higher-order network based on the simplicial complex.
2.1 Simplicial complex
A simplicial complex Z is specified by two parameters (N, M), where N is the set of nodes and M is the set of simplexes constituting Z. A m-simplex θ ⊂ Z is made up of a filled clique of a set of m + 1 nodes (i.e., θ = [n0, n1, … nm]), which defines a (m + 1)-body interaction. Specifically, a m-simplex describes the simultaneous interaction between m + 1 nodes, where a 0-simplex designates an separate node without any interaction (e.g [n0], [n1],… [nm]), a 1-simplex illustrates the pairwise interaction between two nodes (e.g [n0, n1], [n0, nm]), a 2-simplex describes three nodes connected pairwisely by edges and form a ‘full’ triangle (e.g., [n0, n1, nm]), and so on, as shown in Figure 1A. A simplicial complex Z consisted of a set of nodes is a set of simplexes, matching the following requirements: If a simplex θ ⊂ Z, then any simplex σ composed of subsets of simplex θ are also included in Z, e.g., a 2-simplicial complex Z is a collection of 0-, 1- and 2-simplexes.
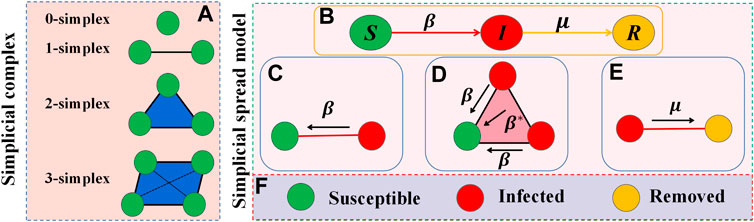
FIGURE 1. Illustration of the model description. The composition of the simplicial complex is shown in (A). (B) Depicts the classic SIR model. Epidemic infection and recovery processes are shown in (C–E). The “full” triangle denotes the 2-simplex structure, while the green, red, and yellow circles indicate susceptible, infected, and removed individuals, respectively, as shown in (F).
2.2 Synthetic simplicial complex
We build a simplicial complex with heterogeneous network and real-world network as the underlying network structure, respectively. The Random Simplicial Complex (RSC) model permits the formation of simplicial complex with a specified average degree [29], we initially employed this model to construct synthetic simplicial complex. Using the RSC model to generate a K-simplicial complex requires K + 1 parameters, which are N vertices and K probabilities
2.3 Real-world simplicial complex
Using a publicly available dataset that depict face-to-face interactions between individuals collected by the SocioPatterns Collaboration [44], we then design a real-world simplicial complex. We use data collected from two real social scenarios: a conference (SFHH) and a workplace (InVS15). Every 20 seconds, face-to-face interaction data is gathered for each scenario. We begin by aggregating the data using a sliding time window with a period of Δt = 5 min, then search for 2- and 3-cliques in each window and weight them according to the frequency with which they occur. Then, 20% of the most frequent simplexes are preserved and aggregated to produce the 2-simplicial complex. The size of each real simplicial complex is 403 and 214, with the average degree of 2-simplexes κ* = 9.4, 5.8 and the average degree of 2-simplicial complex κ = 26.6, 20.8.
2.4 Simplicial spread model
Peer effects and reinforcement effects are extremely prevalent in social contagion, from which emerge higher-order network interactions. With this in mind, we propose an epidemic spread model on the simplicial complex, assuming that the spread of the disease conforms to the Susceptible-Infected-Removed (SIR) model. There are three possible states for a node in the network: Susceptible state S, infected state I and removed state R, as shown in Figure 1B. The spread of the epidemic is controlled by two parameters β and β*. Initially, a proportion ρ0 of nodes are infected. If a node o is in S state, an infected neighbor p can infect it via their pairwise interaction (o, p) with rate β, as shown in Figure 1C. Node o can also get infection from node p and q via a 2-simplex (o, p, q) with rate β*, where both node p and q are in the infected state, and this event can be seen as a synergistic reinforcing effect, as shown in Figure 1D. In addition, infected nodes can recover to the removed state with rate μ, as shown in Figure 1E. Individuals who reverted to the R state are immune to future infections.
3 Numerical simulation
Taking into account the varying average degrees of 1-simplexes and 2-simplexes across networks, we combine k⋆, k*, β, β*, and μ into a single infection rate parameter. Specifically, there are λ = βk⋆/μ and λ* = β*k*/μ. λ and λ* denote the 1-simplex infection rate and 2-simplex infection rate, respectively. Next, based on the simplicial complex constructed from heterogeneous network and real-world networks, we investigate the effect of higher-order interactions on the process of irreversible epidemic spread and the immune effects of various immunization strategies. We stipulate that every node joining the network chooses M = 4 vertices to connect links, up until the network size N reaches 500, when building simplicial complex based on heterogeneous network. Set k⋆ = 20 and k* = 6 to change the connection probability p1 and p2. Finally, the average degree of the network κ is determined to be 20.
In this study, epidemic spread from initial infection seed density of ρ0 = 0.02, and we set the recovery rate μ = 0.02. The final infection density ρ* in the figure represents the density of nodes in the R state in the network when the spread process reaches the ultimate state. The symbols in the figures represent the average results of 200 numerical simulations, and the solid lines represent the theoretical results calculated from Eq. 9. Due to a shortcoming intrinsic to the theoretical approach, the results of theory and simulation cannot match precisely. We employed the Microscopic Markov Chain Approach, which assumes that the probability of two neighbors infecting the same individual is independent and disregards the dynamical correlations between the states of nodes. Higher-order interactions serve to exacerbate these dynamical correlations, making it difficult for theory to represent the simulation process in its entirety. The observable phenomena in the figures is primarily demonstrated by theoretical results in our explanation.
3.1 The effect of 2-simplex infection rates
To study the effect of higher-order interactions on the irreversible epidemic spread process, we investigate the epidemic final infection density ρ* as a function of the 1-simplex infection rate λ on synthetic and real-world simplicial complex, as shown in Figure 2. This figure displays both continuous and discontinuous growth. In addition, the 2-simplex infection rate exerts varying degrees of effect on the spread process in different ranges of 1-simplex infection rate. As depicted by the red solid lines and circles in the figure, we first conduct theoretical analysis and numerical simulations on the heterogeneous network. As illustrated in Figures 2A,B,C, when the 2-simplex infection rate is relatively low, the growth of ρ* with λ is always continuous. As depicted in Figure 2D, when the 2-simplex infection rate is high, there is a discontinuous increase in the growth of ρ* with λ. In particular, as demonstrated by Figure 2D, when λ* = 12 and 0 < λ < 0.5, the growth of ρ* with λ is continuous. When 0.5 < λ < 1, growth of ρ* with λ goes from continuous to discontinuous as λ increases. We also find that as λ* increases, the outbreak threshold of the epidemic decreases, as shown in Figures 2A–D. For instance, when λ* = 0.5, λ needs to increase to around 3 for the epidemic to break out, as shown in Figure 2A. When λ* = 12, λ only has to increase to about 1 for the outbreak of the epidemic, as shown in Figure 2D.
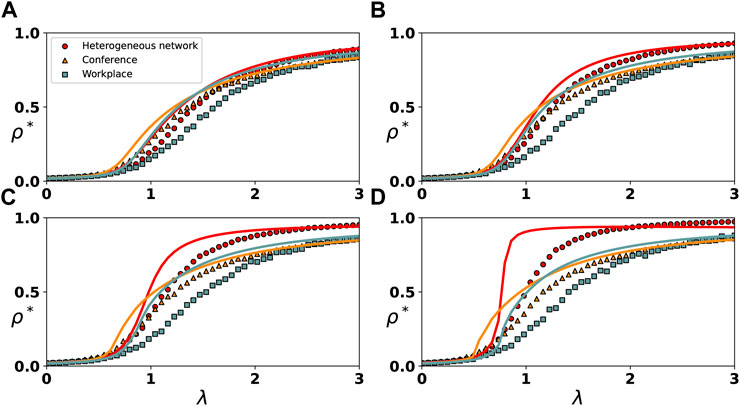
FIGURE 2. Evolution of the final infection density ρ* with λ under varying rates of 2-simplex. The spread of the epidemic on the heterogeneous network and two real-world networks are represented by circles, triangles and squares, respectively. For the spread on the heterogeneous network, we set λ* = 0.5 in (A), λ* = 3.5 in (B), λ* = 6.5 in (C) and λ* = 12 in (D). For the spread on the real-world networks, we set λ* = 0.5 in (A), λ* = 1.5 in (B), λ* = 2.5 in (C) and λ* = 4.5 in (D).
In addition, we find that the 2-simplex infection rate exerts varying degrees of effect on the spread process of the epidemic in different ranges of λ. When the 1-simplex infection rate is small (e.g., λ = 0.5), the increase in the 2-simplex infection rate has almost no effect on the spread process, as shown in Figures 2A–D. When 0.5 < λ < 1.5, the 2-simplex infection rate has the greatest impact on the spread process, which causes the growth of ρ* with λ to gradually become discontinuous with the increase of λ*, as shown in Figures 2A–D. When 1.5 < λ < 3, the 2-simplex infection rate has less of an impact on the spread process, as shown in Figures 2A–D.
Next, we repeat the same investigation on real-world simplicial complex constructed from a conference and workplace, respectively, and observe similar phenomena as on synthetic simplicial complex. Due to the small size and complex structure of real-world networks, a high 2-simplex infection rate leads to large error fluctuations in the simulation results. On the real-world networks, we reduce the 2-simplex infection rate, so no obvious discontinuous growth is observed.
3.2 The effect of immunization strategies
Then, we investigate the impact of higher-order interactions on epidemic spread under various immunization strategies. Based on the node degree index and betweenness index, we categorize network nodes. First, we select 10% of the nodes at random for immunization, which is the random immunization strategy (Random). Select 10% of the nodes with the greatest degree, the smallest degree, the greatest betweenness, and the smallest betweenness for immunization, i.e., the maximum degree strategy (Degree _ max), the minimum degree strategy (Degree _ min), the maximum betweenness strategy (Betweenness _ max), and the minimum betweenness strategy (Betweenness _ min). Figure 3 shows the evolution of ρ* with λ under different immunization strategies and 2-simplex infection rates.
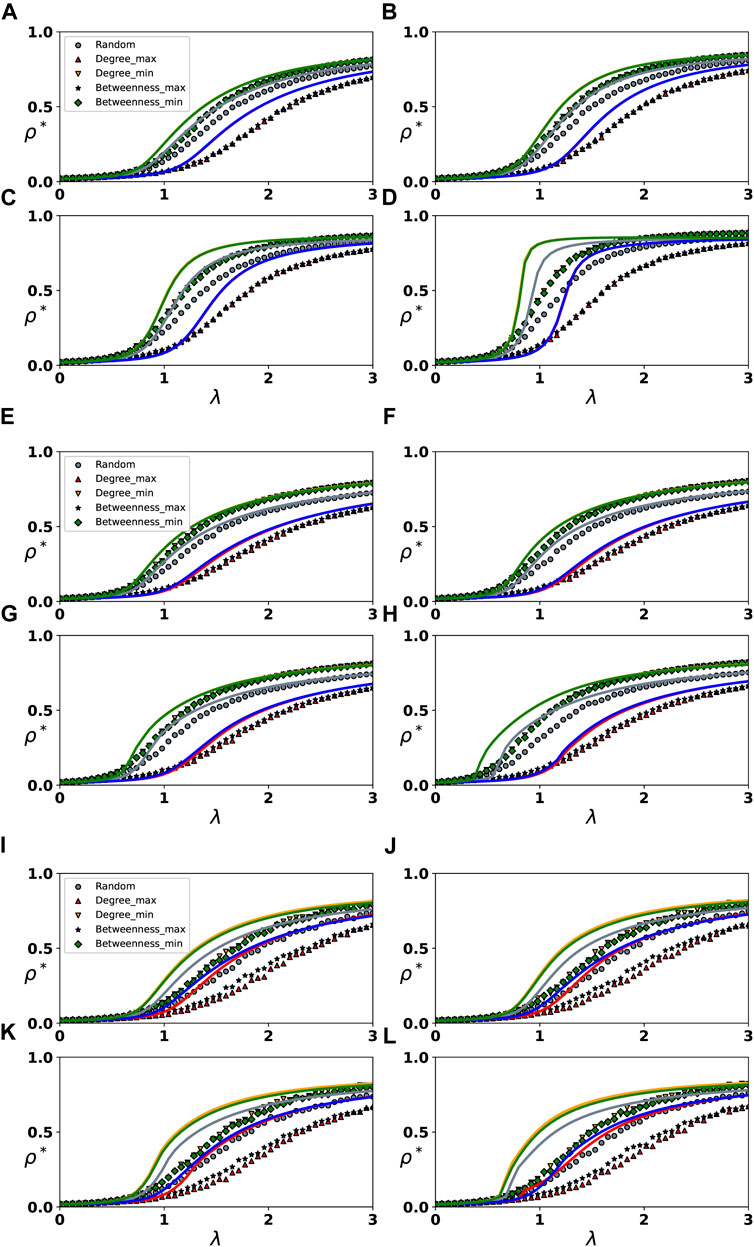
FIGURE 3. Evolution of the final infection density ρ* with λ under varying 2-complex infection rates and immunization strategies. Subgraphs (A–D), (E–H) and (I–L) represent the spread of epidemics on the synthetic network and two real-world networks, respectively. Different colors and symbols have been used to depict different immunization strategies. For the spread on the heterogeneous network, we set λ* = 0.5 in (A), λ* = 3.5 in (B), λ* = 6.5 in (C) and λ* = 12 in (D). For the spread on the real-world networks, we set λ* = 0.5 in (E) and (I), λ* = 1.5 in (F) and (J), λ* = 2.5 in (G) and (K), λ* = 4.5 in (H) and (L).
We first perform theoretical analysis and numerical simulations on the heterogeneous network, as shown in Figures 3A–D. We find that the immunization strategy based on node degree has the same immune effect as the betweenness immunization strategy. When selecting the node with the highest degree and betweenness for immunization, the effect is definitely superior to when selecting the node with the lowest degree and betweenness for immunization, however the effect of the random immunization strategy is intermediate. Furthermore, in some special parameter scenarios, we observe similar phenomena to those in Figure 2. When the node with the smallest degree or betweenness of 10% is selected for immunization, the increase in the 2-simplex infection rate has a significant impact on the spread of the epidemic. When the 2-simplex rate is large enough, there is an obvious discontinuous growth in the growth of ρ* with λ, as shown by the green and yellow lines in Figures 3A–D. When 10% of nodes are randomly selected for immunization, the effect of the increase in the 2-simplex rate on the spread of the epidemic is diminished, and the growth of ρ* with λ gradually becomes discontinuous, as illustrated by the gray lines in Figures 3A–D. When the node with the largest degree and betweenness of 10% is selected for immunization, the increase in 2-simplex infection rate has no discernible effect on the spread of the epidemic, and the growth process of ρ* with λ is always continuous, as depicted by the red and blue lines in Figures 3A–D. Regardless of the immunization strategy, an increase in the 2-simplex infection rate leads to a reduction in the outbreak threshold of the epidemic. Similar to the phenomenon depicted in Figure 2, the increase in the infection rate of the 2-simplex has varying degrees of impact on the spread process of the epidemic in various λ ranges. Furthermore, when λ is small (e.g., λ = 0.5), the epidemic cannot break out under either immunization strategy. When 2 < λ < 3, λ* = 12, the epidemic spread under different immunization strategies has the same spread size. In other words, when both the 1-simplex rate and the 2-simplex rate are large and 10% of the nodes are selected for immunization, alternative immunization strategies have the same effect, as shown in Figure 3D.
Likewise, we conduct research on two real-world networks, a conference and workplace, and observe similar phenomena. However, as shown in Figures 3H,L, when the infection rates of 1-simplex and 2-simplex are both large, the spread size of epidemics under various immunization strategies varies, which may be related to the ratio of immunized nodes and the network structure. Furthermore, since we set the 2-simplex infection rate relatively small on real-world networks, we do not observe obvious discontinuous growth.
3.3 The effect of immunization ratios
Finally, to further investigate the effect of different immunization strategies on the spread of the epidemic on higher-order networks, we examine the effect of different immunization strategies on the spread size of the epidemic under different 2-simplex infection rates and different immunization ratios on the simplex complex constructed based on the heterogeneous network. Figure 4 depicts the evolution of final infection density ρ* as a function of immune ratio g and 1-simplex infection rate λ for various 2-simplex infection rates λ*. We first investigate the case of random immunization strategy, as shown in Figures 4A–D. We discover that when g is small (about less than 0.3), the increase of λ* will cause the growth of ρ* to become discontinuous with the increase of λ, hence decreasing the outbreak threshold. When both g and λ* are small, the interval between different colors is large, and the growth of final infection density with λ is continuous, as shown in Figures 4A–C. When g is small and λ* is large, brown is squeezed toward blue, and the interval between different colors becomes smaller. At this time, the growth of final infection density with λ is discontinuous, and a slight change in λ can lead to the outbreak of the epidemic. When g exceeds around 0.3, the increase of λ* has little effect on the increase of ρ* with λ. In addition, we discover that the epidemic cannot spread when g is approximately 0.8 or when λ is small (approximately less than 0.5).
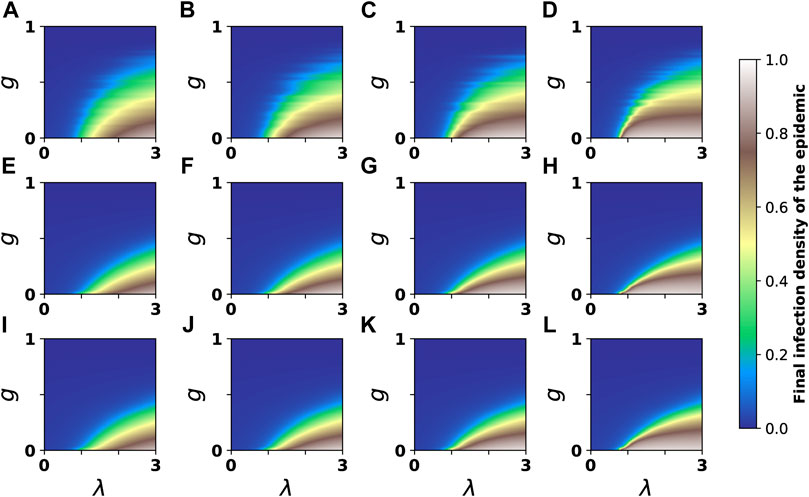
FIGURE 4. Evolution of the final infection density with λ and g under varying 2-simplex infection rates. g represents the ratio of immune nodes. Colors indicate theoretical results for final infection density. Four subgraphs (A–D) at the top represent random immunization strategy, four subgraphs (E–H) in the middle represent the maximum degree immunization strategy, and four subgraphs (I–L) at the bottom represent the maximum betweenness immunization strategy. From the left to the right, λ* corresponds to 0.5, 3.5, 6.5 and 12.
Next, we discuss the case of the maximum degree strategy and the maximum betweenness strategy, as demonstrated in Figures 4E–L. Similar phenomena are observed as with the random immunization strategy. When g is relatively small, the increase of λ* will cause the process of ρ* to grow discontinuously with λ, as shown in Figure 4H. When g is relatively large, an increase in λ* will have little effect on the process of increasing ρ* with λ, as shown in Figures 4E–H. Compared with the random immunization strategy, the g required to fully sustain the epidemic outbreak with the maximum degree immunization strategy is smaller, about 0.5. When g is small (about 0.1) and both λ* and λ are large, different immunization strategies have the same immune effect and have less impact on the spread size of the epidemic, as shown in Figures 4D,H,L when λ* = 12 and λ = 3. In addition, the maximum degree immunization strategy and the maximum betweenness immunization strategy have the same immune effect.
4 Theoretical method
To the best of our knowledge, existing studies mostly use Mean-Field theory to study the dynamics of epidemic spread on higher-order networks. This method regards the individuals in the network as equivalent nodes, which ignores the heterogeneity between individuals, cannot fully reflect the complete structural information of the contact network, and cannot track the evolution of individual nodes. In order to more accurately describe the irreversible epidemic spread process on higher-order networks and track the state evolution of each node in the network, we use the Microscopic Markov Chain Approach to construct the theoretical model [45–47].
As mentioned in Section 2, our model contains a total of N nodes, each node has three possible existence states (S, I, R) at any time. The spread process can be performed by 1-simplex or 2-simplex. We use
The left side of Eq. 1 represents the probability that a node i in the system is in the S state at time t + 1, the right side represents the probability that a node i is in the S state at time t and is not infected and immune. ℏi(t) and
For Eq. 4, the right side represents the probability that an S state node i is not infected by its I state neighbor node m through 1-simplex at time t, τi represents the set of neighbor nodes connected by node i through 1-simplex. For Eq. 5, the right side represents the probability that an S state node i is not infected by its two I state neighbors m and n through a 2-simplex at time t, and Δi represents the set of neighbor nodes connected by node i through 2-simplex.
When N is large enough, we define ρT(t) to represent the proportion of individuals who are in state T at time t in the system, which can be approximated as the average of the probability that individuals are in state T,
Correspondingly, the proportion of nodes in the S, I and R state in the system at time t can be expressed as:
When t → ∞, the system reaches the final state, we denote ρ(t → ∞) as ρ, at this time, ρI = 0.
5 Conclusion
In this work, we construct simplicial complex to represent higher-order networks and propose a simplicial irreversible epidemic spread model (SIR) on it. On the basis of the degree index and betweenness index of nodes, we compare and analyze the impacts of five different immunization strategies on the spread of the epidemic using this model. We first construct simplicial complex containing both pairwise interactions and higher-order interactions on synthetic networks and real-world networks. By extending the Microscopic Markov Chain theoretical analysis model, the temporal evolution equations of nodes in three distinct states are then determined. Finally, the effects of 1-simplex infection rate, 2-simplex infection rate, and different immunization strategies on the epidemic spread process are examined by numerical simulations.
We first investigate the effect of different 2-simplex infection rates on the process of epidemic spread in the absence of immunization strategies. We discover that when λ* is relatively small, the growth of ρ* with λ is always continuous. When λ* is relatively large, there is a discontinuous growth of ρ* along with the growth of λ. As λ* increases, the outbreak threshold of the epidemic decreases. In addition, we discover that the 2-simplex infection rate exerts variable degrees of effect on the spread process of the epidemic in different ranges of λ.
Then we discuss the impact of higher-order interactions on the spread of the epidemic under five different immunization strategies with a fixed immunization ratio of 10%. We find that the immunization strategy based on the node degree index has the same immune effect as the one based on the node betweenness index. Selecting the node with the largest degree and betweenness for immunization has the best effect, followed by the random immunization strategy, and finally the immunization strategy with the smallest degree and betweenness. When nodes with a ratio of 10% are selected for immunization, the increase in 2-simplex infection rate has a significant impact on the spread of epidemics under the degree and betweenness minimum immunization strategy, resulting in discontinuous growth in the system. The impact on the epidemic spread under the random immunization strategy is weakened, and there is no significant impact on the epidemic spread under the degree and betweenness maximum immunization strategy. Regardless of the immunization strategy, an increase in the 2-simplex infection rate leads to a reduction in the outbreak threshold of the epidemic.
Finally, we examine the evolution of the final infection density with the immunization ratio and the 1-simplex infection rate for various 2-simplex infection rates. We find that when the immunization ratio and 2-simplex infection rate are both small, the growth of the final infection density is always continuous with 1-simplex infection rate. When the ratio of immune is small and the infection rate of 2-simplex is large, there will be a discontinuous growth in the growth of final infection density with the 1-simplex infection rate. Compared with the random immunization strategy, the ratio of immunization required to fully sustain the outbreak of the epidemic is smaller when the degree and betweenness maximum immunization strategies are adopted. When the immunization ratio is small and both the 2-simplex and 1-simplex infection rate are large, different immunization strategies have the same immune effect and have less impact on the spread size of the epidemic.
In summary, this paper investigates the effects of different immunization strategies, 2-simplex and 1-simplex infection rates on the spread of the irreversible epidemic on higher-order networks. This research has certain practical significance for epidemic prevention and control. For example, in the early stage of an outbreak, when vaccines are lacking, it is more effective to immunize a large number of exposed persons than to randomly choose individuals for immunization. This work has limitations as well. Our conclusions are primarily supported by theoretical analysis. However, due to the inherent limits of the theoretical method, our theoretical results do not precisely correspond to the simulation results. How to develop a more accurate theoretical method to simulate the spread process is a direction worthy of consideration.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
WL wrote the original draft of this opinion manuscript. BP, SS and WW provided feedback on the manuscript. LN and YZ edited the final manuscript. All authors approved for the final version of the manuscript.
Funding
This research was supported by the Social Science Foundation of Chongqing (No. 2021PY53), National Natural Science Foundation of China (No. 61903266), Natural Science Foundation of Chongqing (No. cstc2021jcyj-msxmX0132), Natural Science Foundation of Yuzhong District, Chongqing (No.20210117), Science and Technology Research Program of Chongqing Municipal Education Commission (No. KJQN202200429).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Zhang R-x., Jin Z, Li S-p. Epidemic spreading with time delay on complex networks. Acta Math Appl Sin Engl Ser (2016) 32:319–26. doi:10.1007/s10255-016-0554-1
2. Qu J, Tang M, Liu Y, Guan S. Identifying influential spreaders in reversible process. Chaos, Solitons & Fractals (2020) 140:110197. doi:10.1016/j.chaos.2020.110197
3. Malik HAM, Abid F, Wahiddin MR, Waqas A. Modeling of internal and external factors affecting a complex dengue network. Chaos, Solitons & Fractals (2021) 144:110694. doi:10.1016/j.chaos.2021.110694
4. Albert R, Barabási A-L. Statistical mechanics of complex networks. Rev Mod Phys (2002) 74:47–97. doi:10.1103/revmodphys.74.47
5. Newman ME. The structure and function of complex networks. SIAM Rev Soc Ind Appl Math (2003) 45:167–256. doi:10.1137/s003614450342480
6. Salfenmoser L, Obermayer K. Nonlinear optimal control of a mean-field model of neural population dynamics. Front Comput Neurosci (2022) 90:931121. doi:10.3389/fncom.2022.931121
7. Chen P, Guo X, Jiao Z, Liang S, Li L, Yan J, et al. Effects of individual heterogeneity and multi-type information on the coupled awareness-epidemic dynamics in multiplex networks. Front Phys (2022) 689. doi:10.3389/fphy.2022.964883
8. Pastor-Satorras R, Vespignani A. Epidemic spreading in scale-free networks. Phys Rev Lett (2001) 86:3200–3. doi:10.1103/physrevlett.86.3200
9. Liu Z, Hu B. Epidemic spreading in community networks. Europhys Lett (2005) 72:315–21. doi:10.1209/epl/i2004-10550-5
10. Saumell-Mendiola A, Serrano MÁ, Boguná M. Epidemic spreading on interconnected networks. Phys Rev E (2012) 86:026106. doi:10.1103/physreve.86.026106
11. Stegehuis C, Van Der Hofstad R, Van Leeuwaarden JS. Epidemic spreading on complex networks with community structures. Sci Rep (2016) 6:29748–7. doi:10.1038/srep29748
12. Qu J-Y, Tang M, Liu Y, Guan S-G. The relative importance of structure and dynamics on node influence in reversible spreading processes. Front Phys (Beijing) (2021) 16:51503–10. doi:10.1007/s11467-021-1082-9
13. Pastor-Satorras R, Castellano C, Van Mieghem P, Vespignani A. Epidemic processes in complex networks. Rev Mod Phys (2015) 87:925–79. doi:10.1103/revmodphys.87.925
14. Nesteruk I. Estimations of the coronavirus epidemic dynamics in South Korea with the use of sir model. ResearchGate (2020). Preprint.
15. Guo Z, Huang L, Zou X. Impact of discontinuous treatments on disease dynamics in an sir epidemic model. Math Biosci Eng (2012) 9:97–110. doi:10.3934/mbe.2012.9.97
16. Battiston F, Cencetti G, Iacopini I, Latora V, Lucas M, Patania A, et al. Networks beyond pairwise interactions: Structure and dynamics. Phys Rep (2020) 874:1–92. doi:10.1016/j.physrep.2020.05.004
17. Li W, Xue X, Pan L, Lin T, Wang W. Competing spreading dynamics in simplicial complex. Appl Maths Comput (2022) 412:126595. doi:10.1016/j.amc.2021.126595
18. Wang W, Li W, Lin T, Wu T, Pan L, Liu Y. Generalized k-core percolation on higher-order dependent networks. Appl Maths Comput (2022) 420:126793. doi:10.1016/j.amc.2021.126793
19. Althouse BM, Wenger EA, Miller JC, Scarpino SV, Allard A, Hébert-Dufresne L, et al. Superspreading events in the transmission dynamics of sars-cov-2: Opportunities for interventions and control. Plos Biol (2020) 18:e3000897. doi:10.1371/journal.pbio.3000897
20. Newman ME, Strogatz SH, Watts DJ. Random graphs with arbitrary degree distributions and their applications. Phys Rev E (2001) 64:026118. doi:10.1103/physreve.64.026118
21. Palla G, Derényi I, Farkas I, Vicsek T. Uncovering the overlapping community structure of complex networks in nature and society. nature (2005) 435:814–8. doi:10.1038/nature03607
22. Kahle M. Topology of random clique complexes. Discrete Math (2009) 309:1658–71. doi:10.1016/j.disc.2008.02.037
23. Czaplicka A, Toral R, San Miguel M. Competition of simple and complex adoption on interdependent networks. Phys Rev E (2016) 94:062301. doi:10.1103/physreve.94.062301
24. Sizemore AE, Giusti C, Kahn A, Vettel JM, Betzel RF, Bassett DS. Cliques and cavities in the human connectome. J Comput Neurosci (2018) 44:115–45. doi:10.1007/s10827-017-0672-6
25. Perc M. Does strong heterogeneity promote cooperation by group interactions? New J Phys (2011) 13:123027. doi:10.1088/1367-2630/13/12/123027
26. Millán AP, Torres JJ, Bianconi G. Synchronization in network geometries with finite spectral dimension. Phys Rev E (2019) 99:022307. doi:10.1103/physreve.99.022307
27. Skardal PS, Arenas A. Abrupt desynchronization and extensive multistability in globally coupled oscillator simplexes. Phys Rev Lett (2019) 122:248301. doi:10.1103/physrevlett.122.248301
28. Kee KF, Sparks L, Struppa DC, Mannucci M. Social groups, social media, and higher dimensional social structures: A simplicial model of social aggregation for computational communication research. Commun Q (2013) 61:35–58. doi:10.1080/01463373.2012.719566
29. Iacopini I, Petri G, Barrat A, Latora V. Simplicial models of social contagion. Nat Commun (2019) 10:2485–9. doi:10.1038/s41467-019-10431-6
30. Cohen R, Havlin S, Ben-Avraham D. Efficient immunization strategies for computer networks and populations. Phys Rev Lett (2003) 91:247901. doi:10.1103/physrevlett.91.247901
31. Chen Y, Paul G, Havlin S, Liljeros F, Stanley HE. Finding a better immunization strategy. Phys Rev Lett (2008) 101:058701. doi:10.1103/physrevlett.101.058701
32. Matamalas JT, Arenas A, Gómez S. Effective approach to epidemic containment using link equations in complex networks. Sci Adv (2018) 4:eaau4212. eaau4212. doi:10.1126/sciadv.aau4212
33. Costa GS, Ferreira SC. Nonmassive immunization to contain spreading on complex networks. Phys Rev E (2020) 101:022311. doi:10.1103/physreve.101.022311
34. Shim E. Optimal allocation of the limited Covid-19 vaccine supply in South Korea. J Clin Med (2021) 10:591. doi:10.3390/jcm10040591
35. Pastor-Satorras R, Vespignani A. Immunization of complex networks. Phys Rev E (2002) 65:036104. doi:10.1103/physreve.65.036104
36. Pastor-Satorras R, Vespignani A. Handbook of graphs and networks. Berlin: Wiley VCH (2003). Epidemics and immunization in scale-free networks.
37. Gallos LK, Liljeros F, Argyrakis P, Bunde A, Havlin S. Improving immunization strategies. Phys Rev E (2007) 75:045104. doi:10.1103/physreve.75.045104
38. Morris M, Podhisita C, Wawer MJ, Handcock MS. Bridge populations in the spread of hiv/aids in Thailand. AIDS (London, England) (1996) 10:1265–71. doi:10.1097/00002030-199609000-00013
39. Freeman LC. Centrality in social networks conceptual clarification. Social networks (1978) 1:215–39. doi:10.1016/0378-8733(78)90021-7
40. Newman ME. A measure of betweenness centrality based on random walks. Soc networks (2005) 27:39–54. doi:10.1016/j.socnet.2004.11.009
41. Salathé M, Jones JH. Dynamics and control of diseases in networks with community structure. Plos Comput Biol (2010) 6:e1000736. doi:10.1371/journal.pcbi.1000736
42. Jin X, An T, Wang J, Cui G, Zhao J. Impact of strategy conformity on vaccination behaviors. Front Phys (2022) 735. doi:10.3389/fphy.2022.972457
43. Jhun B. Effective epidemic containment strategy in hypergraphs. Phys Rev Res (2021) 3:033282. doi:10.1103/physrevresearch.3.033282
44.SocioPatterns. Featured: Infectious sociopatterns poster (2008). Available at: http://www.sociopatterns.org/[Accessed on September 10, 2021].
45. Gómez S, Arenas A, Borge-Holthoefer J, Meloni S, Moreno Y. Discrete-time Markov chain approach to contact-based disease spreading in complex networks. Europhys Lett (2010) 89:38009. doi:10.1209/0295-5075/89/38009
46. Granell C, Gómez S, Arenas A. Dynamical interplay between awareness and epidemic spreading in multiplex networks. Phys Rev Lett (2013) 111:128701. doi:10.1103/physrevlett.111.128701
Keywords: immunization strategy, simplicial irreversible epidemic, simplicial complex, higher-order network, epidemic spread
Citation: Li W, Ni L, Zhang Y, Su S, Peng B and Wang W (2022) Immunization strategies for simplicial irreversible epidemic on simplicial complex. Front. Phys. 10:1018844. doi: 10.3389/fphy.2022.1018844
Received: 14 August 2022; Accepted: 12 September 2022;
Published: 29 September 2022.
Edited by:
Xiyun Zhang, Jinan University, ChinaReviewed by:
Min Lin, Sichuan Normal University, ChinaZhidan Zhao, Shantou University, China
Jiaxing Shang, Chongqing University, China
Copyright © 2022 Li, Ni, Zhang, Su, Peng and Wang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Bin Peng, cGVuZ2JpbkBjcW11LmVkdS5jbg==; Wei Wang, d3d6cWJ4QGhvdG1haWwuY29t, d3d6cWJjQGNxbXUuZWR1LmNu
 Wenjie Li1
Wenjie Li1 Linghao Ni
Linghao Ni Bin Peng
Bin Peng Wei Wang
Wei Wang