Traversable Finslerian wormholes supported by phantom energy

1 Introduction

Two distinct spacetimes are possible to be connected through a shortcut, which arises due to the hypothetical topological behavior of spacetime, popularly known as “wormhole”. It is interesting to note that in their work Fuller and Wheeler [1], first coined the term wormhole and provided due credit to Weyl [2] for the fundamental idea of the possibility of non-simply connected spacetime. However, according to few researchers, the study of the wormhole was actually initiated by Flamm [3]. Later an important study by Einstein and Rosen revealed the wormhole geometry popularly known as the Einstein-Rosen bridge where they investigated the non-singular coordinate patches of the Reissner-Nordström and the Schwarzschild solutions. Clearly, these two fundamental ideas of wormholes are completely different from each other. The wormholes, which are offspring of the eternal black hole solution, are not suitable for transferring information, and they are actually non-traversable in their nature. On the other hand, the idea of a wormhole due to the non-simply connected nature of spacetime as endorsed by Weyl predicts the presence of electromagnetic field lines without a source, which actually possible to be used as a classical communication channel.

With the proposal of the idea of a wormhole, researchers showed great curiosity about whether it is possible to construct a sustainable wormhole, the topological tunnel of space, and whether will it be consistent with the laws of physics. In 1962 in his seminal work Wheeler [4] predicted the Reissner-Nordström and Kerr wormhole geometries in the form of quantum foam at the Planck scale. In the further study by Hawking [7] these wormholes have been featured as “Euclidean wormholes” which are not traversable. With the suitable choice of topology this wormhole geometry which is described by the Schwarzschild metric [4], contains the horizon and it is impossible to traverse through them as its throat squeezes very quickly [5]. Hence, it is obvious to consider the presence of non-zero stress and energy to support the configuration of the wormhole throat [6]. This endorses the presence of the material near the throat that must have a radial tension greater than its mass-energy density which property has not been seen so far in any material. In their detailed study, Morris et al. [8] successfully explained static and spherically symmetric traversable wormholes which support the presence of such exotic matter that violates the energy conditions. Immediately questions arise such as i) Is it admissible by quantum field theory to consider such type of stress-energy tensor to maintain a two-way traversable wormhole? ii) Whether is it possible to form a wormhole that arises due to the non-simply connected nature of spacetime as it is not the usual case of spatial sections of the wormhole? These questions should be answered as the laws of physics must be consistent with the physics of traversable wormholes. In fact, a traversable wormhole may act like a “time machine”, which in that case may violate the causality [9].

In their studies, different researchers have confirmed that it is necessary to consider exotic matter around the throat of the static wormhole configurations, which also guarantees the violation of the null energy condition (NEC). Although an important letter by Visser et al. [10] reveals that though it is essential to violate averaged null energy condition (ANEC), but it is enough to have the presence of ANEC-violating matter infinitesimally small. It is worth mentioning that the solutions of the static configuration of wormholes are studied in literature [10–16] must be consistent with some property to be traversable. However, to understand the extensive delineation of the physical aspects of wormholes, we suggest readers to study different wormhole configurations such as rotating wormholes [17, 18], dynamical wormholes [19, 20], wormholes with a cosmological constant Λ [21, 22], etc. Matters violating the energy conditions can be categorized by the equation of state parameter ω = p/ρ. The strong energy condition demands ω ≥ −1/3 for normal fluids and becomes exotic fluids (dark energy) if ω < − 1/3. The cosmological constant corresponds to ω = −1, phantom ω < − 1 and quintessence −1 < ω < − 1/3. Since opening the throat of a wormhole requires the violation of null energy condition, i.e. ρ+p < 0 demands ω < − 1, the throat can be open either by phantom energy or cosmological constant. Many authors presented wormhole solutions supported by exotic matters in GR and modified gravity [23–27].

Investigation of the different properties of spacetime in more generalized theories of gravity has attracted much attention among scientists in recent days. Interestingly, most of the articles are concerned with the geometrical aspect of the field equation. Also, recent observational evidence has triggered the search for a more generalized form of gravitational theory compared to general relativity (GR). In fact, with the advancements of quantum gravity research, many investigations came up with the idea that GR is actually embedded in some more generalized form of the gravity field. Besides the astrophysical significance, there are many possible applications of spacetime in ADS/CFT correspondence, string theory, induced gravity, and de Sitter gauge theory [28, 29].

Importantly based on the following reasons, it is suitable to choose Finsler geometry over GR are given by i) the geometry is dependent on the dynamics as well as the position of the system, and no quadratic restrictions are required to bound the length element in Finsler geometry [30]. The measurement of time between two events that appeared to an observer is actually the same as the distance between two events that occurred in the world line of the same observer. ii) The measurement depends on the tangent bundle of a homogeneous function which results that the arcs depending on length as well as velocity. iii) Also, one can easily resolve by considering $F(x,y)=\sqrt{g_{\mu \nu }{y}^{\mu }{y}^{\nu }}$ in Riemannian manifold $\left(M,g_{\mu \nu }(x)\right)$ the present Finsler space which is quadratic in terms of y^θ and y^ϕ. In fact, the covariant derivative of the Riemannian space is possible to be used in this present case as it is a semi-definite Finsler space. Hence, the Bianchi identity in this Finsler space is the same as found in the Riemannian space. The gravitational field equations are found as the present Finsler space reduces into the Riemannian space.

A detailed study of Einstein’s gravity in the framework of Finslerian geometry is found in the literature [31–34]. Also, in several recent articles [35–42] researchers have studied anisotropy of the Universe and the violation of Lorentzian invariance in Finsler geometry. Further, in the framework of Finsler geometry Minguzzi [43] has studied the singularity theorem and the Raychaudhuri equation. In their important study, Stavrinos and Alexious [44] have studied scalar-tensor theory and the generalized form of Raychaudhuri equation in the Finsler-Rander spacetime. Aazami and Javaloyes [45] have studied Penrose’s singularity theorem in Finslerian geometry. Rahaman et al. [46] and Chowdhuri et al. [47] have presented an important study on the compact stars model in Finsler spacetime. On the other hand, the investigation made by Li [48] provides the eigenfunction of the Finslerian Laplacian operator and also features Finslerian Reissner-Nordström solution for vacuum. Li and Chang [49] also presented the exact vacuum solution in Finsler spacetime. Other traversable wormholes are also presented by many authors in various modified gravity theories [50, 51]. $\ddot{O}$vgün and Sakalli presented a thin shell wormhole solution using Visser cut and paste technique [52], gravitino and vector particles as Hawking radiation from the traversable Lorentzian wormholes [53, 54], the deflection angle of light by wormholes [55]. A model of cosmic springs in Finslerian geometries was also presented by Lake [56].

2 Finslerian geometry and wormhole field equations

The Finslerian geometry is constructed from Finsler structure F which is defined as [57]

$\left(x,\mu y\right)=\mu F\left(x,y\right)\forall \mu >0.(1)$

Here x ∈ M represents position and y = dx/dt, the velocity. The metric describing Finslerian geometry is given as [58]

$g_{\mu \nu }\equiv \frac{\partial }{\partial y^{\mu }}\frac{\partial }{\partial y^{\nu }}\left(\frac{1}{2}{F}^2\right).(2)$

The geodesic equation in the Finsler manifold is expressed as [58]

$\frac{d^2{x}^{\mu }}{d{\tau }^2}+2G^{\mu }=0,(3)$

where G^μ is called the geodesic spray coefficients defined as [58]

$G^{\mu }=\frac{1}{4}{g}^{\mu \nu }\left(\frac{{\partial }^2{F}^2}{\partial x^{\lambda }\partial y^{\nu }}{y}^{\lambda }-\frac{\partial F^2}{\partial x^{\nu }}\right).(4)$

The Ricci scalar in Finsler geometry is written as [58]

$\mathcal{R}\equiv R_{\mu }^{\mu }=\frac{1}{F^2}\left(2\frac{\partial G^{\mu }}{\partial x^{\mu }}-y^{\lambda }\frac{{\partial }^2{G}^{\mu }}{\partial x^{\lambda }\partial y^{\mu }}\right.\left.+2G^{\lambda }\frac{{\partial }^2{G}^{\mu }}{\partial x^{\lambda }\partial y^{\mu }}-\frac{\partial G^{\mu }}{\partial y^{\lambda }}\frac{\partial G^{\lambda }}{\partial y^{\mu }}\right)(5)$

$R_{\nu }^{\mu }=\frac{1}{F^2}{R}_{\lambda \nu \rho }^{\mu }{y}^{\lambda }{y}^{\rho }.(6)$

Here $R_{\lambda \nu \rho }^{\mu }$ depends on connection and $R_{\nu }^{\mu }$ depends only on the Finsler structure F.

Due to Birkhoff’s theorem, it is well-known that most of static vacuum solutions are reducible to the Schwarzschild’s form, hence we will assume the Finsler structure in the similar form

$F^2=B\left(r\right)y^t{y}^t-A\left(r\right)y^r{y}^r-r^2{\bar{F}}^2\left(\theta ,\varphi ,y^{\theta },y^{\varphi }\right).(7)$

The Finsler metric is given below

$g_{\mu \nu }=\mathrm{diag}\left(B,-A,-r^2{\bar{g}}_{ij}\right),(8)$

$g^{\mu \nu }=\mathrm{diag}\left(B^{-1},-A^{-1},-r^2{\bar{g}}^{ij}\right),(9)$

Where ${\bar{g}}^{ij}$ are derived from ${\bar{F}}^2$ and (θ, ϕ) ≡ (i, j). The components of the geodesic spray coefficient become

$G^t=\frac{B^{\prime }}{2B}{y}^t{y}^r,(10)$

$G^r=\frac{A^{\prime }}{4A}{y}^r{y}^r+\frac{B^{\prime }}{4A}{y}^t{y}^t-\frac{r}{2A}{\bar{F}}^2,(11)$

$G^{\theta }=\frac{1}{r}{y}^{\theta }{y}^r+{\bar{G}}^{\theta },(12)$

$G^{\varphi }=\frac{1}{r}{y}^{\varphi }{y}^r+{\bar{G}}^{\varphi },(13)$

Where the prime represents differentiation with respect to r and the $\bar{G}$ is the geodesic spray coefficients derived by $\bar{F}$. Substituting (Eq. 10)-(Eq. 13) to (Eq. 5) we the expression of Ricci scalar as

$F^2\mathcal{R}=\left[\frac{B^{″}}{2A}-\frac{B^{\prime }}{4A}\left(\frac{A^{\prime }}{A}+\frac{B^{\prime }}{B}\right)+\frac{B^{\prime }}{rA}\right]y^t{y}^t+\left[-\frac{B^{″}}{2B}+\frac{B^{\prime }}{4B}\left(\frac{A^{\prime }}{A}+\frac{B^{\prime }}{B}\right)+\frac{A^{\prime }}{rA}\right]y^r{y}^r+\left[\bar{\mathcal{R}}-\frac{1}{A}+\frac{r}{2A}\left(\frac{A^{\prime }}{A}-\frac{B^{\prime }}{B}\right)\right]{\bar{F}}^2,(14)$

where $\bar{\mathcal{R}}$ denotes the Ricci scalar correspond to $\bar{F}$.

Akbar-Zadeh [59] first introduced the notion of Ricci tensor in the Finsler geometry as

${\mathcal{R}}_{\mu \nu }=\frac{{\partial }^2}{\partial y^{\mu }\partial y^{\nu }}\left(\frac{1}{2}{F}^2\mathcal{R}\right).(15)$

The scalar curvature in the Finsler geometry is defined as $S=g^{\mu \nu }{\mathcal{R}}_{\mu \nu }$. Now the modified Einstein’s tensor is given by (See Appendix A)

$G_{\mu \nu }\equiv {\mathcal{R}}_{\mu \nu }-\frac{1}{2}{g}_{\mu \nu }S.(16)$

The covariant conservation of G_μν in Finsler geometry i.e., $G_{\nu ;\mu }^{\mu }=0$ was proved by Chang and Li [37].

Now we can write the components of Einstein’s tensor in Finsler geometry as

$G_t^t=\frac{A^{\prime }}{r{A}^2}-\frac{1}{r^{2}A}+\frac{\lambda }{r^2},(17)$

$G_r^r=-\frac{B^{\prime }}{rAB}-\frac{1}{r^{2}A}+\frac{\lambda }{r^2},(18)$

$G_{\theta }^{\theta }=G_{\varphi }^{\varphi }=-\frac{B^{″}}{2AB}-\frac{B^{\prime }}{2rAB}+\frac{A^{\prime }}{2r{A}^2}+\frac{B^{\prime }}{4AB}\left(\frac{A^{\prime }}{A}+\frac{B^{\prime }}{B}\right).(19)$

Finally, we can write the field equations in Finsler spacetime as

$G_{\nu }^{\mu }=8{\pi }_F{T}_{\nu }^{\mu },(20)$

with $T_{\nu }^{\mu }$ is the energy-momentum tensor and 4π_F is expressing the volume of $\bar{F}$ in the field equation.

Assuming a matter distribution with anisotropic pressure, the form of the energy-momentum tensor can be written as

$T_{\xi }^{\mu }=\rho v^{\mu }{v}_{\xi }+p_r{\chi }_{\xi }{\chi }^{\mu }+p_t\left(v^{\mu }{v}_{\xi }-{\chi }_{\xi }{\chi }^{\mu }+g_{\xi }^{\mu }\right),(21)$

where v^μv_μ = −χ^μχ_μ = 1, p_r and p_t denote radial and transverse pressures, respectively. ρ is the density of the fluid distribution, v^μ is the four velocity, and χ^μ is the unit space-like vector in the radial direction.

By using the energy-momentum tensor in (Eq. 21) along with the field Eq. 20 we get.

$8{\pi }_F\rho =\frac{A^{\prime }}{2A^2}-\frac{1}{r^{2}A}+\frac{\lambda }{r^2},(22)$

$8{\pi }_F{p}_r=\frac{B^{\prime }}{rAB}+\frac{1}{r^{2}A}-\frac{\lambda }{r^2},(23)$

$8{\pi }_F{p}_t=\frac{B^{″}}{2AB}+\frac{B^{\prime }}{2rAB}-\frac{A^{\prime }}{2r{A}^2}-\frac{B^{\prime }}{4AB}\left(\frac{A^{\prime }}{A}+\frac{B^{\prime }}{B}\right),(24)$

With λ, the constant flag curvature. Now the Finsler form of the Morris-Thorne [6] wormhole geometry can be written as

$F^2=-e^{2f\left(r\right)}{y}^t{y}^t+\frac{y^r{y}^r}{1-\frac{b}{r}}+r^2{\bar{F}}^2\left(\theta ,\varphi ,y^{\theta },y^{\varphi }\right),(25)$

where yⁱ = di/dτ. And the 2-surface ${\bar{F}}^2$ is taken as

${\bar{F}}^2=y^{\theta }{y}^{\theta }+f\left(\theta ,\varphi \right)y^{\varphi }{y}^{\varphi }(26)$

with the corresponding metric ${\bar{g}}_{ij}=\text{diag}(1,f(\theta ,\varphi ))$. To get vanishing off-diagonal components of $F^2\mathcal{R}$ in (Eq. 14) the function f (θ, ϕ) = f(θ) and one of the possible choice that preserves the spherical symmetry is $f(\theta )={\sin }^2(\sqrt{\lambda }\theta )$. Hence, the final form of the Finsler-Morris-Thorne wormhole geometry can be written as

$F^2=-e^{2f\left(r\right)}{y}^t{y}^t+\frac{y^r{y}^r}{1-\frac{b}{r}}+r^2\left(y^{\theta }{y}^{\theta }+{\sin }^2\left(\sqrt{\lambda }\theta \right)y^{\varphi }{y}^{\varphi }\right)(27)$

The Finslerian field (Eq. 22, Eq. 24) reduce to

$8{\pi }_F\rho =\frac{b^{\prime }+\lambda -1}{r^2},(28)$

$8{\pi }_F{p}_r=\left(1-\frac{b}{r}\right)\left(\frac{2f^{\prime }}{r}+\frac{1}{r^2}\right)-\frac{\lambda }{r^2},(29)$

$8{\pi }_F{p}_t=\left[1-\frac{b}{r}\right]\left[f^{″}+\frac{f^{\prime }}{r}+f^{\prime 2}\right]-\left[\frac{b^{\prime }}{r}-\frac{b}{r^2}\right]\left[\frac{f^{\prime }}{2}+\frac{1}{2r}\right].(30)$

Here, b(r) and f(r) are shape-function and redshift functions respectively. To solve the above field equations, we need extra information to integrate further. To solve the above field equations we will adopt few techniques i.e., assuming specific equation of state, well-known wormhole shape function and redshift function or assuming p_r & p_t relationship.

3 Finslerian wormholes with linear equation of state

In these cases, we will assume a linear equation of state of the form p_r = ωρ along with a specific choice of shape functions.

3.1 Model I: $b(r)=a{\left(r/a\right)}^n$

Considering this shape function along with the linear EoS, the field equations can be integrated to yield the red-shift function as

$f\left(r\right)=A+\frac{1}{2\left(n-1\right)}\log \left(r\right)\left\{n\left(\lambda \omega +\lambda -1\right)+1\right\}-\left\{\lambda \left(\omega +1\right)+\left(n-1\right)\omega \right\}\log \left\{r-a{\left(\frac{r}{a}\right)}^n\right\}.(31)$

Here A is the constant of integration. Therefore, the density and pressure take the forms

$8{\pi }_F\rho =\frac{n{\left(r/a\right)}^{n-1}+\lambda -1}{r^2},(32)$

$8{\pi }_F{p}_r=\frac{\omega }{r^2}\left[n{\left(\frac{r}{a}\right)}^{n-1}+\lambda -1\right],(33)$

$\begin{array}{c}8{\pi }_F{p}_t=\frac{1}{4r^3\left[r-a{\left(r/a\right)}^n\right]}\left[a^{2}n\left\{n{\omega }^2-\left(n-3\right)\omega +1\right\}{\left(\frac{r}{a}\right)}^{2n}+ar{\left(\frac{r}{a}\right)}^n\left\{\left(\lambda -1\right)\left(\omega +1\right)\right.\right.\hfill \\ +\left.\left.2n^2\omega +n\left(2\lambda {\omega }^2+3\lambda \omega +\lambda -2{\omega }^2-5\omega -1\right)\right\}+{\left(\lambda -1\right)}^2{r}^2{\left(\omega +1\right)}^2\right].\hfill \end{array}(34)$

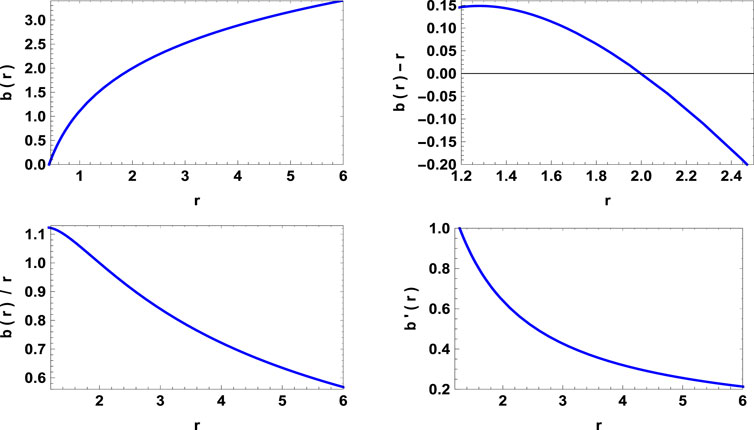
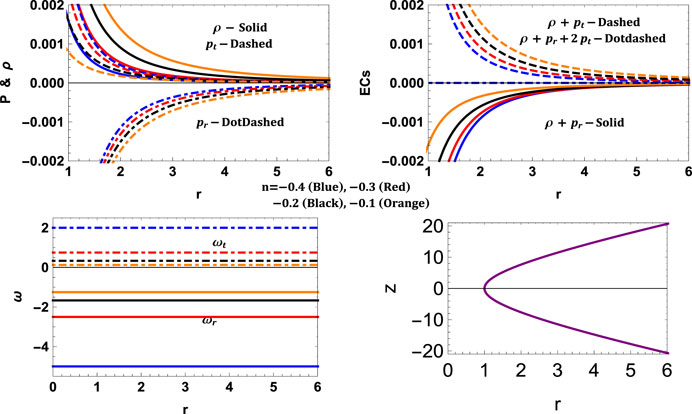
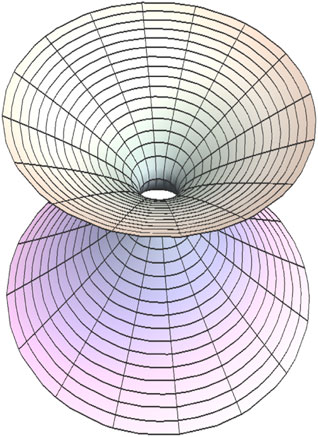
The rest of the quantities can be calculated from the above physical quantities. The quantity a is the throat radius of the wormhole. The variations of all these parameters can be shown in Figures 1, 2. Now we can see that the throat is at a = 5 and is asymptotically flat. Now, since NEC is violated, i.e. ρ+p_r < 0, the throat is supported by exotic matter or precisely by phantom energy (ω < − 1). The revolution of the embedded surface can be seen in Figure 3.

FIGURE 1

FIGURE 1. Variation of b, b−2, b/r and b′(r) for model I with a = 3, λ = 1.2, ω = −2 and n = 0.4.

FIGURE 2

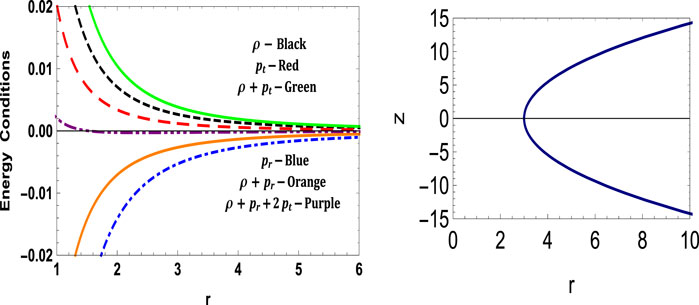
FIGURE 2. Variation of energy conditions and embedding diagram for the model I with a = 3, λ = 1.2, ω = −2 and n = 0.4.

FIGURE 3

FIGURE 3. Surface revolution of embedding diagram for model I.

3.2 Model II: $b(r)=a^{3}c\log \left(a/r\right)+a$

For this shape function in the linear EoS, the field equations lead to

$f^{\prime }\left(r\right)=\frac{a^{3}c\log \left(\frac{a}{r}\right)-a^{3}c\omega +a+r\left(\lambda -1\right)\left(\omega +1\right)}{2r\left(r-a^{3}c\log \left(\frac{a}{r}\right)-a\right)},(35)$

which is not exactly integrable, however, one can always find the related physical quantities as they are dependent only on their derivatives. Here the physical parameters take the form

$8{\pi }_F\rho =\frac{\lambda r-a^{3}c-r}{r^3},(36)$

$8{\pi }_F{p}_r=\frac{\omega \left(\lambda r-a^{3}c-r\right)}{r^3},(37)$

$\begin{array}{c}8{\pi }_F{p}_t=\frac{1}{4r^3\left(r-a^{3}c\log \left(\frac{a}{r}\right)-a\right)}\left[a^6{c}^2\omega \left(\omega +1\right)-a^4\left(3c\omega +c\right)-a^{3}cr\left(2\lambda {\omega }^2+3\lambda \omega +\lambda -2{\omega }^2\right.-\left.5\omega -1\right)\right.\hfill \\ \left.-,a^3,c,\log ,\left(\frac{a}{r}\right),\left[a^3\left(3c\omega +c\right)-r\left(\lambda -1\right)\left(\omega +1\right)\right],+,a,r,\left(\lambda -1\right),\left(\omega +1\right),+,{\left(\lambda -1\right)}^2,r^2,{\left(\omega +1\right)}^2\right].\hfill \end{array}(38)$

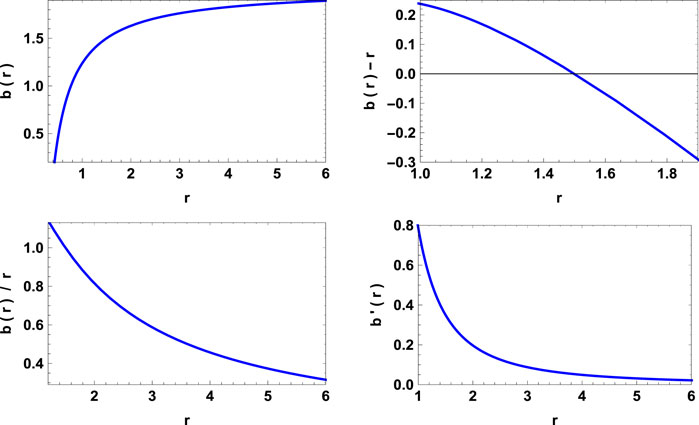
Now the energy conditions etc., can be calculated using the above expressions. Further, the variations of these physical parameters can be seen in Figures 4, 5. The throat radius is found to be 2 km and is opened by phantom energy.

FIGURE 4

FIGURE 4. Variation of b, b−2, b/r and b′(r) for model II with a = 2, λ = 1.2, ω = −2, c = −0.16.

FIGURE 5

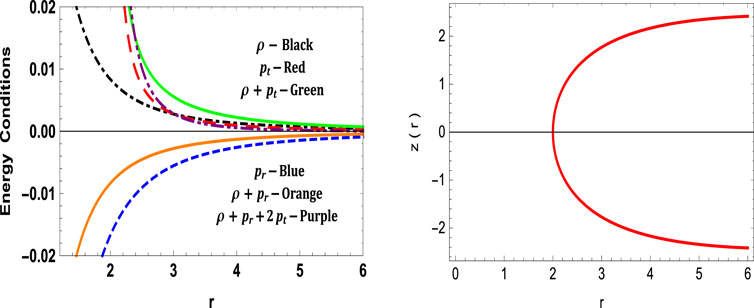
FIGURE 5. Variation of energy conditions and embedding surface for model II with a = 2, λ = 1.2, ω = −2, c = −0.16.

3.3 Model III: $b(r)=ac\left(1-a/r\right)+a$

The solution, in this case, is found to be

$f\left(r\right)=D+\left[-\log \left(r-a\right)\left[\left(c-1\right)\omega +\lambda \left(\omega +1\right)\right]+\left[c\left(\lambda \omega +\lambda -\omega \right)+\omega \right]\log \left(r-ac\right)+\left(c-1\right)\left(\omega -1\right)\log \left(r\right)\right].(39)$

Further, the physical quantities are found to be

$8{\pi }_F\rho =\frac{a^{2}c/r^2+\lambda -1}{r^2},(40)$

$8{\pi }_F{p}_r=\frac{\omega \left(a^{2}c/r^2+\lambda -1\right)}{r^2},(41)$

$\begin{array}{ll}\hfill 8{\pi }_F{p}_t& =\frac{1}{4r^4\left(a-r\right)\left(ac-r\right)}\left[a^4{c}^2\left({\omega }^2-4\omega -1\right)+a^{3}cr\left(c+1\right)\left(5\omega +1\right)+2a^{2}c{r}^2\omega \right.\hfill \\ \hfill & \times \left.\left(\lambda \omega +\lambda -\omega -3\right)+a\left(c+1\right)\left(\lambda -1\right)r^3\left(\omega +1\right)+{\left(\lambda -1\right)}^2{r}^4{\left(\omega +1\right)}^2\right].\hfill \end{array}(42)$

The variations of these physical quantities are given in Figures 6, 7. Here also, the NEC is violated, and therefore the WH throat is supported by the exotic matter which is found to be phantom energy. The revolution of the embedded surface can be seen in Figure 8.

FIGURE 6

FIGURE 6. Variation of b, b−2, b/r and b′(r) for model III with a = 1.5, λ = 1.2, ω = −2, c = 0.35.

FIGURE 7

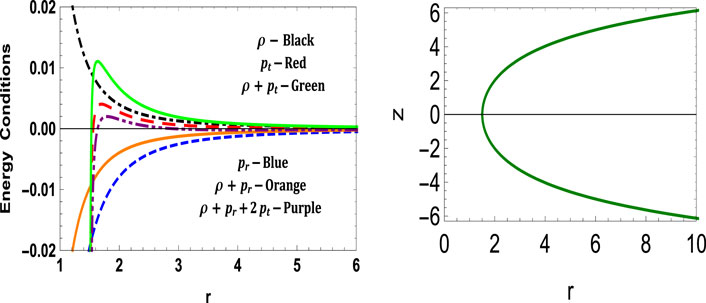
FIGURE 7. Variation of energy conditions and embedding surface for model III with a = 1.5, λ = 1.2, ω = −2, c = 0.35.

FIGURE 8

FIGURE 8. Surface revolution of embedding diagram for model III.

4 Finslerian wormholes with p_t = np_r

Unlike the first method we have adopted above, we would like to extend our investigation by assuming a linear relationship between the tangential and radial pressure as p_t = np_r, where n can be treated as an anisotropic parameter. To solve the field equations, further we ansatz different forms of f(r).

4.1 Model IV: f(r) = c

For the initial assumptions p_t = np_r and f(r) = c, the resulting solution is

$b=r\left(H{r}^{2n}-\lambda +1\right),(43)$

with H as the constant of integration. Here one can clearly see that this solution is not asymptotically flat since ${\lim }_{r\to \infty }[b(r)/r]\nrightarrow 0$. To make it asymptotically flat we must match it with exterior Schwarzschild spacetime. The matching equation can be written as

$e^{2f\left(R\right)}=1-\frac{2\mathcal{M}}{R}=1-\frac{b\left(R\right)}{R},(44)$

where R is the surface when the two spacetimes meet. Using (Eq. 44), we get

$b\left(R\right)=R\left(H{R}^{2n}-\lambda +1\right)=2\mathcal{M}(45)$

$R=2\mathcal{M}{\left(1-e^{2c}\right)}^{-1},(46)$

Which leads to a constraint on the constants H and c as

$c=\ln {\left\{\lambda -H{\left[2\mathcal{M}{\left(1-e^{2c}\right)}^{-1}\right]}^{2n}\right\}}^{1/2}.(47)$

Now the density, pressures, and energy conditions are given by

$8{\pi }_F\rho =\frac{H{r}^{2n}+2Hn{r}^{2n}}{r^2},(48)$

$8{\pi }_F{p}_r=-H{r}^{2n-2},(49)$

$8{\pi }_F{p}_t=-Hn{r}^{2n-2},(50)$

$8{\pi }_F\left(\rho +p_r\right)=2Hn{r}^{2n-2},(51)$

$8{\pi }_F\left(\rho +p_t\right)=H\left(n+1\right)r^{2n-2},(52)$

$8{\pi }_F\left(\rho +p_r+2p_t\right)=0.(53)$

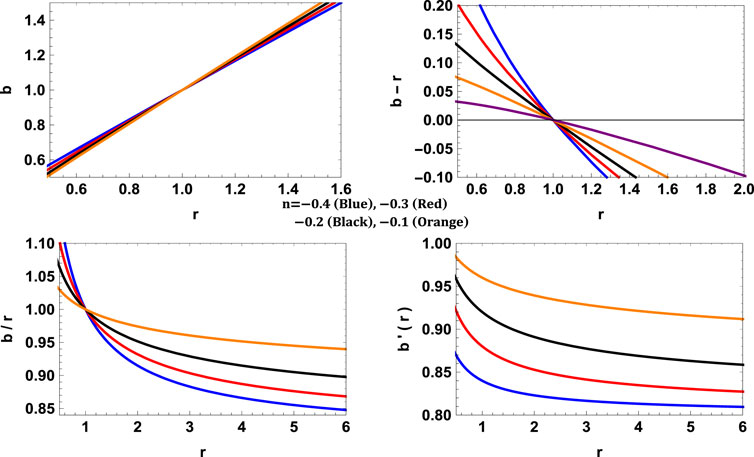
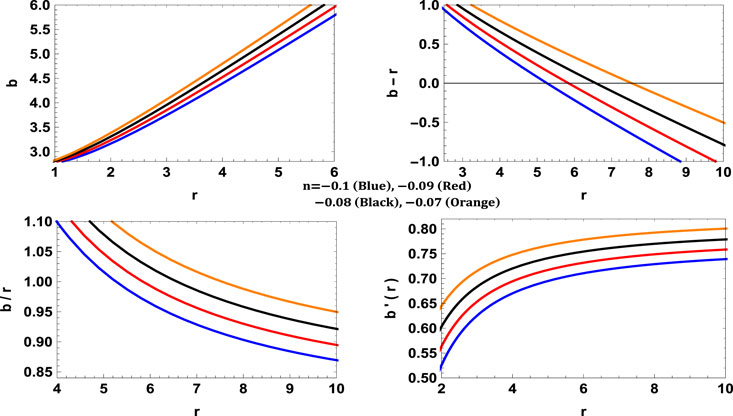
The variations of b(r), b′(r) and b(r) − r is given in Figure 9. The variations of p_r, p_t, and energy density can be seen in Figure 10. Here we can see that the throat radii are the same for all the EoS parameters ω = −4.98, − 2.5, − 1.66, − 1.24. Again, the NEC is violated, and the corresponding EoS parameter ω_r = p_r/ρ is less than −1 thereby, the WH is supported by phantom energy. The surface revolution of the embedded surface is shown in Figure 11.

FIGURE 9

FIGURE 9. Variation of b, b−2, b/r and b′(r) for model IV with H = 0.2, λ = 0.2.

FIGURE 10

FIGURE 10. Variation of energy conditions and embedding surface for model IV with H = 0.2, λ = 0.2.

FIGURE 11

FIGURE 11. Surface revolution of embedding diagram for model IV.

4.2 Model V: $f(r)=\log \left(r/\gamma \right)$

For this redshift function, one can find the solution as

$b\left(r\right)=M{r}^{3n}+\frac{\left(\lambda -3\right)nr+r}{1-3n},(54)$

where M is the constant of integration. Again, this solution is not asymptotically flat due to ${\lim }_{r\to \infty }[b(r)/r]\nrightarrow 0$, so we have to match this interior spacetime with exterior Schwarzschild spacetime. Further, using (Eq. 44) we get

$R=\frac{3^{2/3}{\gamma }^2+\sqrt[3]{3}{a}_1^{2/3}}{3a_1^{1/3}}(55)$

$b\left(R\right)=2\mathcal{M}=R\left[M{R}^{3n-1}+\frac{\left(\lambda -3\right)n+1}{1-3n}\right].(56)$

These above equations lead to a constraint given as

$2\mathcal{M}=\frac{3^{2/3}{\gamma }^2+\sqrt[3]{3}{a}_1^{2/3}}{3a_1^{1/3}}\left[M{\left(\frac{3^{2/3}{\gamma }^2+\sqrt[3]{3}{a}_1^{2/3}}{3a_1^{1/3}}\right)}^{3n-1}+\frac{\left(\lambda -3\right)n+1}{1-3n}\right],(57)$

where,

$a_1=\sqrt{81{\gamma }^4{\mathcal{M}}^2-3{\gamma }^6}-9{\gamma }^2\mathcal{M}.(58)$

Now the density and pressure take form

$8{\pi }_F\rho =\frac{\lambda +3Mn{r}^{3n-1}+\frac{\left(\lambda -3\right)n+1}{1-3n}-1}{r^2},(59)$

$8{\pi }_F{p}_r=\frac{1}{r^3}\left(\frac{\lambda r}{3n-1}-3M{r}^{3n}\right),(60)$

$8{\pi }_F{p}_t=\frac{n}{r^3}\left(\frac{\lambda r}{3n-1}-3M{r}^{3n}\right),(61)$

And the energy conditions take the very simple forms

$\rho +p_r=\frac{3M\left(3n^2-4n+1\right)r^{3n}+2\lambda nr}{8{\pi }_F\left(3n-1\right)r^3},(62)$

$\rho +p_t=\frac{\lambda }{8{\pi }_F{r}^2},(63)$

$\rho +p_r+2p_t=\frac{4\lambda nr-3M\left(3n^2+2n-1\right)r^{3n}}{8{\pi }_F\left(3n-1\right)r^3}.(64)$

The variations of pressure, density, energy conditions, etc. are shown in Figures 12, 13. Here one can observe that the throat radius depends on the parameter n for which the r_th is smaller for n = −1 and larger for n = −0.07. Further, EoS parameter ω also increases when n increases leading to more exotic matter and thereby wider throat radius. Further, the violation of NEC and ω_r = p_r/ρ < − 1 shows that the matter is exotic (phantom energy).

FIGURE 12

FIGURE 12. Variation of b, b−2, b/r and b′(r) for model V with λ = 3, γ = 1.5, M = 2.

FIGURE 13

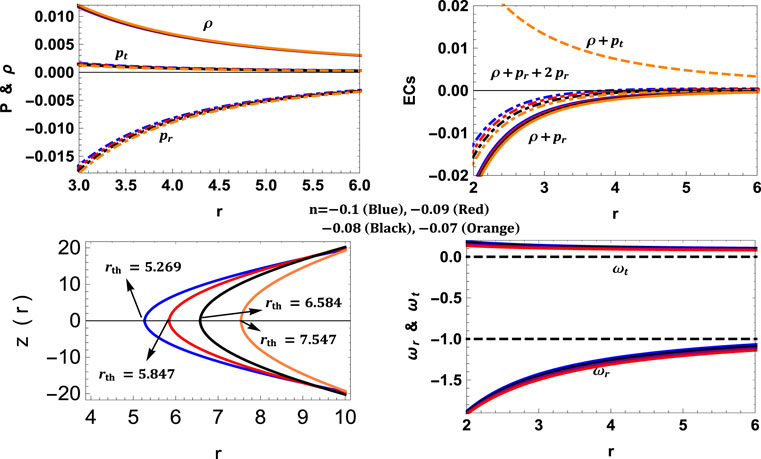
FIGURE 13. Variation of energy conditions and embedding surface for model V with λ = 3, γ = 1.5, M = 2.

5 Finslerian wormholes with specific density profile and a linear EoS (model VI)

To find the third category of solutions, we will assume a specific density profile with a linear equation of state of the form

$\rho =c{\left(\frac{a}{r}\right)}^{\alpha },p_r=\omega \rho .(65)$

From the first relation with the field equation, we get

$b\left(r\right)=\frac{c{r}^3}{3-\alpha }{\left(\frac{a}{r}\right)}^{\alpha }+F-\lambda r+r,(66)$

where F is the constant of integration. Since the expression of the shape function doesn’t include ω, its throat will not be affected by EoS parameter. And the linear EoS with the density profile after using the field equations and the above b(r), we can find f′(r) as

$f^{\prime }\left(r\right)=\frac{c{r}^3\left[\left(\alpha -3\right)\omega -1\right]{\left(\frac{a}{r}\right)}^{\alpha }+\left(\alpha -3\right)F}{2r\left(c{r}^3{\left[\frac{a}{r}\right)}^{\alpha }-\left(\alpha -3\right)F+\left(\alpha -3\right)\lambda r\right]}.(67)$

Which is not exactly integrable. Although, one can find the physical parameters as

$8{\pi }_F\rho =\frac{1}{r^2}\left[\frac{3c{r}^2{\left(a/r\right)}^{\alpha }}{3-\alpha }-\frac{a\alpha cr{\left(a/r\right)}^{\alpha -1}}{3-\alpha }\right],(68)$

$8{\pi }_F{p}_r=c\omega {\left(\frac{a}{r}\right)}^{\alpha },(69)$

$8{\pi }_F{p}_t=\frac{c{\left(a/r\right)}^{\alpha }}{4\left[c{r}^3{\left(\frac{a}{r}\right)}^{\alpha }-\left(\alpha -3\right)F+\left(\alpha -3\right)\lambda r\right]}c{r}^3\left(\alpha \left(\omega -1\right)\omega -3{\omega }^2-1\right){\left(\frac{a}{r}\right)}^{\alpha }+\left(\alpha -3\right)F\left[\left(2\alpha -3\right)\omega +1\right]-2\left({\alpha }^2-5\alpha +6\right)\lambda r\omega .(70)$

Figure 14 shows the behavior of the shape function and its related parameters. The trends of pressures, density and energy conditions are given in Figure 15, which shows that the NEC is again violated. The nature of the exotic matter can be known if we see the EoS parameter ω_r = p_r/ρ. Here ω = −1.5, i.e. less than −1, so again the exotic matter is phantom energy. The r_th depends on the parameter α, smaller values of α yields narrower throats and vice versa.

FIGURE 14

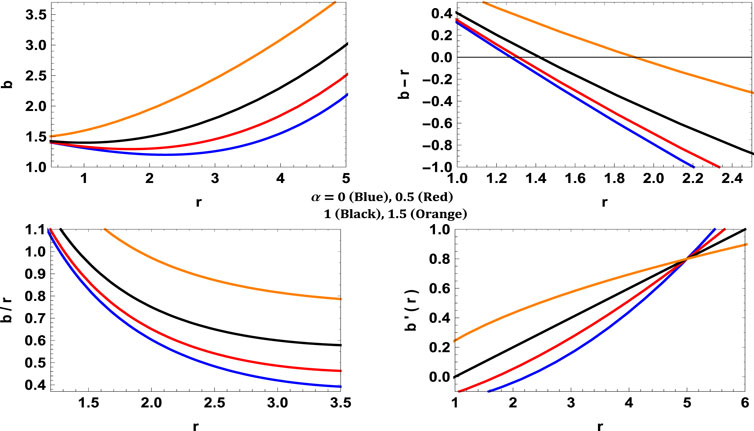
FIGURE 14. Variation of b, b−2, b/r and b′(r) for model VI with c = 0.04, λ = 1.2, F = 1.5, a = 5, ω = −1.5.

FIGURE 15

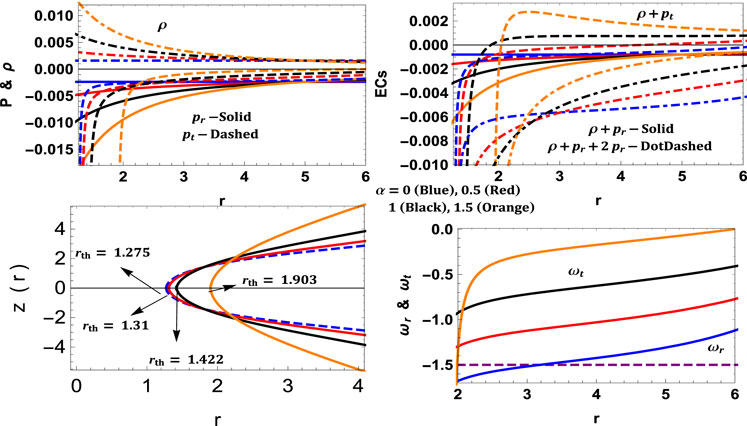
FIGURE 15. Variation of energy conditions and embedding surface for model VI with c = 0.04, λ = 1.2, F = 1.5, a = 5, ω = −1.5.

6 Construction of embedding diagrams

Considering a constant time slice i.e., y^t = 0 and in the 2-dimensional Finsler space ${\bar{F}}^2$ if one chooses $\theta =(\pi /2\sqrt{\lambda })$ (hence y^θ = dθ/dτ = 0), then [Eq. 27] reduces to

$F^2=\frac{y^r{y}^r}{1-b/r}+r^2{y}^{\varphi }{y}^{\varphi }.(71)$

If this Eq. 71 reduces to a 3-D cylindrical coordinate of the form

$F^2=y^z{y}^z+y^r{y}^r+r^2{y}^{\varphi }{y}^{\varphi },(72)$

than by comparing (Eq. 71) and (Eq. 72), the form of z(r) can be found as

$\begin{array}{ccc}\hfill \frac{y^r{y}^r}{1-b/r}& =\hfill & y^z{y}^z+y^r{y}^r\text{or}\frac{1}{1-b/r}=\frac{y^z{y}^z}{y^r{y}^r}+1={\left(\frac{dz/d\tau }{dr/d\tau }\right)}^2+1\hfill \\ \hfill & \Rightarrow \hfill & {\left(\frac{dz}{dr}\right)}^2+1={\left(1-\frac{b}{r}\right)}^{-1}.\hfill \end{array}(73)$

On simplifying (Eq. 73) we get

$\frac{dz}{dr}=\pm \frac{1}{\sqrt{r/b\left(r\right)-1}}\text{or}z\left(r\right)=\pm \int \frac{dr}{\sqrt{r/b\left(r\right)-1}}.(74)$

For model I, Eq. 74 is not integrable for the general case, however integrable for a given value of n. Further, for model II i.e., $b(r)=a^{3}c\log \left(a/r\right)+a$ the embedding surface is not integrable exactly, thereby we used numerical integration to generate it. For model III the embedding surface can be integrated exactly and is given by

$z\left(r\right)=\frac{2ar}{\sqrt{r-a}\sqrt{r-ac}}\sqrt{\frac{\left(r-a\right)\left(r-ac\right)}{r^2}}\left[\left(c+1\right)\log \left(\sqrt{r-ac}+\sqrt{r-a}\right)-\sqrt{c}{\tanh }^{-1}\left(\frac{\sqrt{c}\sqrt{r-a}}{\sqrt{r-ac}}\right)\right].$

In a similar fashion, the embedding surface for model IV is found to be

$z\left(r\right)=\frac{r}{\left(n+1\right)\sqrt{\lambda -H{r}^{2n}}}\left[\left(1-\lambda n+n\right){\sqrt{1-\frac{H{r}^{2n}}{\lambda }}}_2{F}_1\left(\frac{1}{2},\frac{1}{2n};1+\frac{1}{2n};\frac{H{r}^{2n}}{\lambda }\right)+H{r}^{2n}-\lambda \right].(75)$

Again, due to the non-integrability of Eq. 74 for model V and VI, we have used numerical integration to generate the 2-D embedding surface.

7 Results and discussions

In this work, we have presented six new wormhole (WH) solutions in Finslerian geometry. The first three models assumed a linear EoS along with specific forms of the shape function. The next two solutions were found by considering a linear relation between p_r and p_t through a constant parameter n. To close the system of equations, we have assumed two different redshift functions. Here the throat radius of WH IV depends on the redshift function only, however for the WH V, the r_th depends on the anisotropic parameter n, i.e., more anisotropy makes the throat narrower and vice versa. Finally, the last solution was obtained via a linear EoS and a specific form of the density profile. In this case, the throat radius depends on density-related α parameter, more the density larger is the r_th.

Next, we have determined all the embedded surfaces for each WHs in 3D Euclidean space assuming an instant of time t = constant and $\theta =(\pi /2\sqrt{\lambda })$. Models I, III, and IV only have exactly integrable embedding surfaces where we have also found their surface revolutions. The rest of the three WHs i.e., Models II, V, and VI were integrated numerically to generate the embedded surfaces. It is found that all these WH models are supported by exotic matter as the NEC is violated. The exact nature of these exotic matters can be found by analyzing the EoS parameter. All these cases yield ω = ω_r = p_r/ρ < − 1 implying that the matter is simply phantom energy. It is also found that WHs III and IV were asymptotically non-flat i.e., ${\lim }_{r\to \infty }[b/r]\nrightarrow 0$. This problem has been resolved by matching the interior spacetime with the Schwarzschild vacuum. Further, it is also to be noted that Models I, II, III, and VI can have ω = −1 (cosmological constant) with the flare-out conditions i.e., b (r_th) = r_th & b′(r_th) < 1 and b(r) < r for r > r_th still holds. Overall, these new WH solutions might represent traversable wormholes.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

KNS conceptualized the manuscript including mathematical calculations, graph plotting, result analysis, and interpretations, FR did mathematical calculations and the resulting analysis, DD did the writing of the manuscript and interpretation of the results, SM did the editing, literature survey and the resulting analysis.

Acknowledgments

KNS and FR are thankful to the authorities of the Inter-University Centre for Astronomy and Astrophysics, Pune, India for providing the research facilities.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Fuller RW, Wheeler JA. Causality and multiply connected space-time. Phys Rev (1962) 128:919–29. doi:10.1103/physrev.128.919

CrossRef Full Text | Google Scholar

2. Weyl H. Feld und materie. Ann Phys (1921) 65:541–63. doi:10.1002/andp.19213701405

CrossRef Full Text | Google Scholar

3. Flamm L. Beiträge zur einsteinschen gravitationstheorie. Phys Z (1916) 17:448.

Google Scholar

4. Wheeler JA. Geometrodynamics. New York: Academic (1962).

Google Scholar

5. Misner CW, Thorne KS, Wheeler JA. San Francisco: Gravitation, Freeman (1973).

6. Morris MS, Thorne KS. Wormholes in spacetime and their use for interstellar travel: A tool for teaching general relativity. Am J Phys (1988) 56:395–412. doi:10.1119/1.15620

CrossRef Full Text | Google Scholar

7. Hawking SW. Wormholes in spacetime. Phys Rev D (1988) 37:904–10. doi:10.1103/physrevd.37.904

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Morris MS, Thorne KS, Yurtsever U. Wormholes, time machines, and the weak energy condition. Phys Rev Lett (1988) 61:1446–9. doi:10.1103/physrevlett.61.1446

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Frolov VP, Novikov ID. Physical effects in wormholes and time machines. Phys Rev D (1990) 42:1057–65. doi:10.1103/physrevd.42.1057

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Visser M, Kar S, Dadhich N. Traversable wormholes with arbitrarily small energy condition violations. Phys Rev Lett (2003) 90:201102. doi:10.1103/physrevlett.90.201102

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Hochberg D, Visser M. Geometric structure of the generic static traversable wormhole throat. Phys Rev D (1997) 56:4745–55. doi:10.1103/physrevd.56.4745

CrossRef Full Text | Google Scholar

12. Ida D, Hayward SA. How much negative energy does a wormhole need?. Phys Lett A (1999) 260:175–81. doi:10.1016/s0375-9601(99)00518-6

CrossRef Full Text | Google Scholar

13. Fewster CJ, Roman TA. On wormholes with arbitrarily small quantities of exotic matter. Phys Rev D (2005) 72:044023. doi:10.1103/physrevd.72.044023

CrossRef Full Text | Google Scholar

14. Kuhfittig PKF. More on wormholes supported by small amounts of exotic matter. Phys Rev D (2006) 73:084014. doi:10.1103/physrevd.73.084014

CrossRef Full Text | Google Scholar

15. Rahaman F, Kalam M, Sarker M, Gayen K. A theoretical construction of wormhole supported by phantom energy. Phys Lett B (2006) 633:161–3. doi:10.1016/j.physletb.2005.11.080

CrossRef Full Text | Google Scholar

16. Jamil M, Kuhfittig PKF, Rahaman F, Rakib SA. Wormholes supported by polytropic phantom energy. Eur Phys J C (2010) 67:513–20. doi:10.1140/epjc/s10052-010-1325-3

CrossRef Full Text | Google Scholar

17. Teo E. Rotating traversable wormholes. Phys Rev D (1998) 58:024014. doi:10.1103/physrevd.58.024014

CrossRef Full Text | Google Scholar

18. Kuhfittig PKF. Axially symmetric rotating traversable wormholes. Phys Rev D (2003) 67:064015. doi:10.1103/physrevd.67.064015

CrossRef Full Text | Google Scholar

19. Hochberg D, Visser M. Dynamic wormholes, antitrapped surfaces, and energy conditions. Phys Rev D (1998) 58:044021. doi:10.1103/physrevd.58.044021

CrossRef Full Text | Google Scholar

20. Hayward SA. Dynamic wormholes. Int J Mod Phys D (1999) 8:373–82. doi:10.1142/s0218271899000286

CrossRef Full Text | Google Scholar

21. Lemos JPS, Lobo FSN, de Oliveira SQ. Morris-Thorne wormholes with a cosmological constant. Phys Rev D (2003) 68:064004. doi:10.1103/physrevd.68.064004

CrossRef Full Text | Google Scholar

22. Rahaman F, Kalam M, Sarker M, Ghosh A, Raychaudhuri B. Wormhole with varying cosmological constant. Gen Relativ Gravit (2007) 39:145–51. doi:10.1007/s10714-006-0380-4

CrossRef Full Text | Google Scholar

23. Wang D, Meng X-H. Traversable geometric dark energy wormholes constrained by astrophysical observations. Eur Phys J C (2016) 76:484. doi:10.1140/epjc/s10052-016-4321-4

CrossRef Full Text | Google Scholar

24. Lobo FSN. Stability of phantom wormholes. Phys Rev D (2005) 71:124022. doi:10.1103/physrevd.71.124022

CrossRef Full Text | Google Scholar

25. Banerjee A, Singh KN, Jasim M, Rahaman F. Conformally symmetric traversable wormholes in f(R, T) gravity. Ann Phys (2020) 422:168295. doi:10.1016/j.aop.2020.168295

CrossRef Full Text | Google Scholar

26. Singh KN, Banerjee A, Rahaman F, Jasim MK. Conformally symmetric traversable wormholes in modified teleparallel gravity Phys Rev D (2020) 101:084012. doi:10.1103/PhysRevD.101.084012

CrossRef Full Text | Google Scholar

27. Rahaman F, Sarkar S, Singh KN, Pant N. Generating functions of wormholes. Mod Phys Lett A (2019) 34:1950010. doi:10.1142/s021773231950010x

CrossRef Full Text | Google Scholar

28. Banados M, Bautier K, Coussaert O, Henneaux M, Ortiz M. Anti–de Sitter–CFT correspondence in three-dimensional supergravity. Phys Rev D (1998) 58:085020. doi:10.1103/physrevd.58.085020

CrossRef Full Text | Google Scholar

29. Cvetič M, Nojiri S, Odintsov SD. Cosmological anti–de Sitter space-times and time-dependent AdS/CFT correspondence. Phys Rev D (2004) 69:023513. doi:10.1103/physrevd.69.023513

CrossRef Full Text | Google Scholar

30. Bao D, Chern SS, Shen Z. An introduction to riemann-finsler geometry, graduate texts in mathematics. New York: Springer (2000).

Google Scholar

31. Rutz SF. A Finsler generalisation of Einstein's vacuum field equations. Gen Relat Gravit (1993) 25:1139–58. doi:10.1007/bf00763757

CrossRef Full Text | Google Scholar

32. Vacaru S, Stavrinos P, Gaburov E, Gonta D. Clifford and Riemann–Finsler structures in geometric mechanics and gravity. Buchares: Geometry Balkan Press (2005).

Google Scholar

33. Pfeifer C, Wohlfarth MNR. Finsler geometric extension of Einstein gravity. Phys Rev D (2012) 85:064009. doi:10.1103/physrevd.85.064009

CrossRef Full Text | Google Scholar

34. Rahaman F, Paul N, Banerjee A, De SS, Ray S, Usmani AA. The Finslerian wormhole models. Eur Phys J C (2016) 76:246. doi:10.1140/epjc/s10052-016-4066-0

CrossRef Full Text | Google Scholar

35. Girelli F, Liberati S, Sindoni L. Planck-scale modified dispersion relations and Finsler geometry. Phys Rev D (2007) 75:064015. doi:10.1103/physrevd.75.064015

CrossRef Full Text | Google Scholar

36. Gibbons GW, Gomis J, Pope CN. General very special relativity is Finsler geometry. Phys Rev D (2007) 76:081701. doi:10.1103/physrevd.76.081701

CrossRef Full Text | Google Scholar

37. Chang Z, Li X. Lorentz invariance violation and symmetry in Randers–Finsler spaces. Phys Lett B (2008) 663:103–6. doi:10.1016/j.physletb.2008.03.045

CrossRef Full Text | Google Scholar

38. Kostelecky VA. Riemann–Finsler geometry and Lorentz-violating kinematics. Phys Lett B (2011) 701:137. doi:10.1016/j.physletb.2011.05.041

CrossRef Full Text | Google Scholar

39. Kostelecky VA, Russell N, Tsoc R. Bipartite Riemann–Finsler geometry and Lorentz violation. Phys Lett B (2012) 716:470. doi:10.1016/j.physletb.2012.09.002

CrossRef Full Text | Google Scholar

40. Kouretsis AP, Stathakopoulos M, Stavrinos PC. General very special relativity in Finsler cosmology. Phys Rev D (2009) 79:104011. doi:10.1103/physrevd.79.104011

CrossRef Full Text | Google Scholar

41. Kouretsis AP, Stathakopoulos M, Stavrinos PC. Imperfect fluids, Lorentz violations, and Finsler cosmology. Phys Rev D (2010) 82:064035. doi:10.1103/physrevd.82.064035

CrossRef Full Text | Google Scholar

42. Li X, Lin HN, Wang S, Chang Z. Anisotropic inflation in the Finsler spacetime. Eur Phys J C (2015) 75:260. doi:10.1140/epjc/s10052-015-3468-8

CrossRef Full Text | Google Scholar

43. Minguzzi E. Raychaudhuri equation and singularity theorems in Finsler spacetimes. Class Quan Grav (2015) 32:185008. doi:10.1088/0264-9381/32/18/185008

CrossRef Full Text | Google Scholar

44. Stavrinos PC, Alexiou M. Raychaudhuri equation in the Finsler–Randers space-time and generalized scalar-tensor theories. Int J Geom Methods Mod Phys (2018) 15:1850039. doi:10.1142/s0219887818500391

CrossRef Full Text | Google Scholar

45. Aazami AB, Javaloyes MA. Penrose’s singularity theorem in a Finsler spacetime. Class Quan Grav (2016) 33:025003. doi:10.1088/0264-9381/33/2/025003

CrossRef Full Text | Google Scholar

46. Rahaman F, Paul N, De SS, Ray S, Jafry MAK. The Finslerian compact star model. Eur Phys J C (2015) 75:564. doi:10.1140/epjc/s10052-015-3797-7

CrossRef Full Text | Google Scholar

47. Chowdhury SR. Hawking emission of charged particles from an electrically charged spherical black hole with scalar hair. Eur Phys J C (2019) 79:928. doi:10.1140/epjc/s10052-019-7452-6

CrossRef Full Text | Google Scholar

48. Li X. Special finslerian generalization of the reissner-nordström spacetime. Phys Rev D (2018) 98:084030. doi:10.1103/physrevd.98.084030

CrossRef Full Text | Google Scholar

49. Li X, Chang Z. Exact solution of vacuum field equation in Finsler spacetime. Phys Rev D (2014) 90:064049. doi:10.1103/physrevd.90.064049

CrossRef Full Text | Google Scholar

50. Övgün A, Jusufi K, Sakallı İ. Exact traversable wormhole solution in bumblebee gravity. Phys Rev D (2019) 99:024042. doi:10.1103/physrevd.99.024042

CrossRef Full Text | Google Scholar

51. Vacaru SI. Springer Proc Math Stat (2013) 439–43.

52. Övgün A, Sakalli I. A particular thin-shell wormhole. Theor Math Phys (2017) 190:120–9. doi:10.1134/s004057791701010x

CrossRef Full Text | Google Scholar

53. Sakalli I, Ovgun A. Gravitinos tunneling from traversable Lorentzian wormholes. Astrophys Space Sci (2015) 359:32. doi:10.1007/s10509-015-2482-5

CrossRef Full Text | Google Scholar

54. Sakalli I, Övgün A. Tunnelling of vector particles from Lorentzian wormholes in 3+1 dimensions. Eur Phys J Plus (2015) 130:110. doi:10.1140/epjp/i2015-15110-9

CrossRef Full Text | Google Scholar

55. Jusufi K, Övgün A, Banerjee A, Sakallı İ. Gravitational lensing by wormholes supported by electromagnetic, scalar, and quantum effects. Eur Phys J Plus (2019) 134:428. doi:10.1140/epjp/i2019-12792-9

CrossRef Full Text | Google Scholar

56. Lake MJ. Modelling cosmic springs with finsler and generalised finsler geometries. Symmetry (2022) 14:2166. doi:10.3390/sym14102166

CrossRef Full Text | Google Scholar

57. Caxathodory C. Variationsrechnung und partielle Differenialgleiehungenerster Ordnung. Leipzig: Teubner Press (1935).

Google Scholar

58. Bao D, Chern SS, Shen Z. An introduction to riemann–finsler geometry. New York: Springer (2000).

Google Scholar

59. Akbar-Zadeh H. Sur les espaces de Finsler à courbures sectionnelles constantes. Acad R Belg Bull Cl Sci (1988) 74:281.

CrossRef Full Text | Google Scholar