Universal quantum obfuscation for quantum non-linear functions

1 Introduction

The development of quantum cryptography has borne witness to a variety of distinguished quantum theories, such as quantum one-time pad [1], quantum money [2], and quantum homomorphic encryption [3]. Currently, quantum key distribution Sibson et al. [4] and quantum secure direct quantum communication [5] are the two major forces of secure communication. In addition, quantum incompatibility [6] and perfect NOT and conjugate transformations [7] also provide the capability of hiding information in a set of states. However, efficient compilers applied in quantum cryptosystems may lead to the reverse engineering of quantum circuits. Quantum obfuscation is a developing branch of quantum cryptography. It can hide or encrypt the functionality of quantum circuits and quantum functions to prevent the decompilation of quantum circuits and can thus improve the security of encryption. It is essentially an infant topic and requires more basic research studies and applications.

Quantum obfuscation stems from the concept of classical obfuscation and at first refers to code obfuscation in software engineering [8]. In 2001, Barak et al. [9] initiated the first negative result of classical obfuscation that it is impossible to achieve virtual black-box (VBB) obfuscation. They considered indistinguishability obfuscation to avoid the impossibility of black-box obfuscation. In 2013, Garg et al. [10] constructed indistinguishability obfuscation and functional encryption that support all circuits of polynomial size. Subsequently, a significant number of applications [11–17] were gradually presented. The security of classical obfuscation was threatened with the advent of quantum computing which can destroy the hardness of logarithms. It is natural to consider using quantum obfuscation to encrypt circuits or functions against quantum adversaries. In 2016, Alagic and Fefferman [18] initiated the definition of quantum black-box obfuscation and quantum indistinguishability obfuscation. They then suggested some related applications, including quantum-secure one-way functions, quantum private-key encryption, and quantum public-key encryption. Their work promoted the research on quantum obfuscation significantly. Subsequently, there are quite a number of applications of quantum obfuscation such as quantum homomorphic encryption [19], quantum symmetric and asymmetric encryption [20,21], and quantum zero-knowledge [22].

However, there are few constructions of quantum obfuscation for some types of quantum functions. Quantum non-linear function plays a significant role in constructing quantum circuits, and its correlation with quantum obfuscation still needs exploration. The first idea of utilizing quantum obfuscation to construct public-key encryption was initiated succinctly by Alagic and Fefferman [18] as an application of efficient black-box obfuscators. It is enlightening to consider the relationship between quantum obfuscation and quantum asymmetric encryption, which can be intensively applied in quantum digital signature [23], quantum secure network [24], quantum experiment [25], and quantum key distribution [26]. In this work, we propose a construction of quantum obfuscation for quantum non-linear functions and give the concrete circuits of obfuscation for two specific quantum non-linear functions. Moreover, we propose a quantum asymmetric encryption scheme based on the obfuscation and verify its correctness and security. Our work formally demonstrates the implementation and application of quantum obfuscation. We hope that the work will be constructive in the area of quantum obfuscation.

The main contributions of our work are as follows:

(1) Construction of universal quantum obfuscation for quantum non-linear functions. The quantum obfuscation based on quantum teleportation is universal to quantum non-linear functions. The functionality of quantum functions can be represented as a quantum state |a⟩ to be obfuscated. We provide a valid application of quantum obfuscation to some specific quantum non-linear functions, including the quantum power function and quantum point function.

(2) Application in quantum asymmetric encryption based on quantum obfuscation. We clarify the construction of the public-key quantum encryption by means of the quantum obfuscation we design. We show that the scheme embodies the essential link between quantum obfuscation and quantum asymmetric encryption and provide a rigorous analysis of its correctness and IND-security.

This paper is structured as follows: first, the work introduces preliminaries, including basic quantum operation, quantum teleportation, and quantum obfuscation. Second, it focuses on the construction of quantum obfuscation for quantum non-linear functions. Then, quantum obfuscation is applied to some specific quantum functions, including the quantum power function and quantum point function. Finally, this paper presents the IND-secure quantum asymmetric encryption based on quantum obfuscation.

2 Preliminaries

2.1 Basic quantum operation

2.1.1 Pauli matrix

The Pauli matrix refers to four frequently used matrices which are of 2 × 2 size and own their names, respectively. Eq. 1 shows these matrices and their symbols. Sometimes, we omit matrix I and regard matrices X, Y, and Z as the Pauli matrix.

${\sigma }_I=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill \end{array}\right],{\sigma }_X=\left[\begin{array}{cc}\hfill 0\hfill & \hfill 1\hfill \\ \hfill 1\hfill & \hfill 0\hfill \end{array}\right],{\sigma }_Y=\left[\begin{array}{cc}\hfill 0\hfill & \hfill -i\hfill \\ \hfill i\hfill & \hfill 0\hfill \end{array}\right],{\sigma }_Z=\left[\begin{array}{cc}\hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill -1\hfill \end{array}\right].(1)$

2.1.2 Quantum measurement

Quantum measurement is the main way to observe the internal situation of a quantum system. The state of the system will collapse to a state when the measurement is completed. Quantum measurement is an irreversible operation which transforms quantum information into classical information. If quantum measurement was reversible, it would never reveal any information on quantum states.

Quantum measurement is described by a set of operations of measurement M_m, where m represents any possible measurement results for the subsystems measured. The measurement operation M_m satisfies the completeness equation.

$\sum \underset{m}{\overset{†}{M}}{M}_m=I.(2)$

The possible measurement result of a quantum system of the state |ψ⟩ can be expressed as $p=⟨\psi |M_m^{†}{M}_m|\psi ⟩$, which holds for all |ψ⟩. After the measurement of a quantum system is finished, its state converts to be $\frac{M_m|\psi \rangle }{\sqrt{⟨\psi |M_m^{†}{M}_m|\psi ⟩}}$.

2.2 Quantum teleportation

Quantum teleportation is a quantum communication branch theory proposed by Bennett et al. [27]. It is used to transfer quantum states between the sender Alice and the receiver Bob without direct connection of a quantum communication channel. Alice and Bob share an EPR (Einstein–Podolsky–Rosen) pair to form a quantum entanglement channel, $|{\beta }_{00}\rangle =\frac{1}{\sqrt{2}}(|00\rangle +|11\rangle )$.

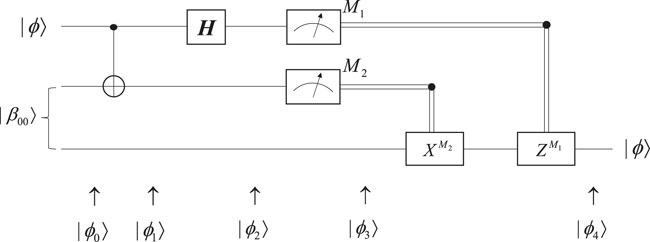
The circuit in Figure 1 gives an accurate description of quantum teleportation. The state ready to be teleported is |ϕ⟩ = α|0⟩ + β|1⟩, where α and β donate unknown amplitudes, and the input state is |ϕ₀⟩.

$|{\varphi }_0\rangle =|\varphi \rangle |{\beta }_{00}\rangle =\frac{1}{\sqrt{2}}\left[\alpha |0\rangle \left(|00\rangle +|11\rangle \right)+\beta |1\rangle \left(|00\rangle +|11\rangle \right)\right].(3)$

FIGURE 1

FIGURE 1. Quantum teleportation circuit of a qubit.

In (3), we define that the first two qubits belong to Alice, while the third qubit belongs to Bob. The second qubit of Alice and the qubit of Bob are derived from the same EPR pair. Alice sends her qubit to a CNOT gate to get the state |ϕ₁⟩.

$|{\varphi }_1\rangle =\frac{1}{\sqrt{2}}\left[\alpha |0\rangle \left(|00\rangle +|11\rangle \right)+\beta |1\rangle \left(|10\rangle +|01\rangle \right)\right].(4)$

Then, Alice has the first qubit implemented by a Hadamard gate to get the state |ϕ₂⟩.

$|{\varphi }_2\rangle ={\left(\frac{1}{\sqrt{2}}\right)}^2\left[\alpha \left(|0\rangle +|1\rangle \right)\left(|00\rangle +|11\rangle \right)+\beta \left(|0\rangle -|1\rangle \right)\left(|10\rangle +|01\rangle \right)\right].(5)$

After regrouping these items, the state can be rewritten as follows:

$|{\varphi }_3\rangle ={\left(\frac{1}{\sqrt{2}}\right)}^2\left[|00\rangle \left(\alpha |0\rangle +\beta |1\rangle \right)+|01\rangle \left(\alpha |1\rangle +\beta |0\rangle \right)+|10\rangle \left(\alpha |0\rangle -\beta |1\rangle \right)+|11\rangle \left(\alpha |1\rangle -\beta |0\rangle \right)\right].(6)$

As listed in Table 1, Alice may obtain four measurement results and send them to Bob via the classical channel. Bob needs to perform the transformation of $Z^{M_1}{X}^{M_2}$ to the qubit received.

TABLE 1

TABLE 1. Relationship of measurement results, collapsed states, and unitary operations.

2.3 Quantum obfuscation

Quantum obfuscation is derived from classical obfuscation and was first proposed by Alagic et al.[18].

Definition 1: A black-box quantum obfuscator is a quantum algorithm O and a QPT (quantum polynomial time) interpreter δ such that whenever C is an n-qubit quantum circuit, the output of O is an m-qubit state O(C), satisfying the following three conditions:

1. Polynomial expansion:

$m=poly\left(n\right).(7)$

Here, m means the scale of quantum algorithm.

2. Functional equivalence: For any possible qubit ρ,

${‖\delta \left(O\left(C\right)\otimes \rho \right)-U_C\rho U_C^{†}‖}_{tr}\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right).(8)$

Here, O is the quantum obfuscator, δ is the quantum interpreter, and U_C represents the quantum circuit.

3. Virtual black-box: For any QPT adversary A who has output of obfuscation, there exists S which can simulate A’s behavior by virtual black-box access to the circuit C,

$\left|\mathrm{Pr}\left[A\left(O\left(C\right)\right)=1\right]-\mathrm{Pr}\left[S^{U_C}\left(\left|0^n\right.⟩\right)=1\right]\right|\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right).(9)$

Here, A means QPT adversary and S means quantum simulator.

Definition 2: A quantum point function U_α,β with a general output is

$U_{\alpha ,\beta }:|x,0^n\rangle \mapsto |x,P_{\alpha ,\beta }\left(x\right)\rangle .(10)$

Here, α ∈ {0.1}ⁿ, β ∈ {0.1}ⁿ\0ⁿ, and P_α,β is a classical point function with a multi-bit output working as

$P_{\alpha ,\beta }\left(x\right)=\left\{\begin{array}{cc}\beta \hfill & \mathrm{i}\mathrm{f}x=\alpha \hfill \\ 0^n\hfill & \mathrm{o}\mathrm{t}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{w}\mathrm{i}\mathrm{s}\mathrm{e}\hfill \end{array}\right..(11)$

By means of constructive proof, Shang et al.[22] demonstrated the obfuscatability of the quantum point function with a general output.

3 Quantum obfuscation for quantum non-linear functions

In this section, we introduce quantum obfuscation based on quantum teleportation to obfuscate quantum non-linear functions. Quantum non-linear functions are derived from classical non-linear functions, which mean the non-linear relationship between the independent variable and dependent variable. The property of quantum functions can be extracted to a quantum state or some quantum states which we name as parameter states. Here, we obfuscate one quantum state for example.

3.1 Construction of quantum obfuscation

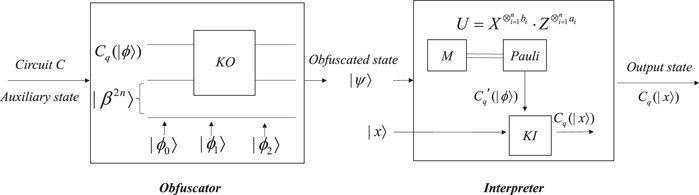
For quantum obfuscation based on quantum teleportation, an obfuscator is used to obfuscate a quantum function and output an obfuscated state, while an interpreter can transform the obfuscated state back to its original state.

The parameter of the quantum function is expressed as an m-qubit state C_q (|ϕ⟩). C_q (|ϕ⟩) is extracted from the n-qubit circuit C of the quantum non-linear function. It can be obtained by inputting an auxiliary state into the circuit of the quantum function. For example, we get the parameter |a⟩ of the quantum exponential function |y⟩ = |a⟩^|x⟩ with |x⟩ = |0⟩ input. So, C_q (|ϕ⟩) is another representation of the function’s functionality.

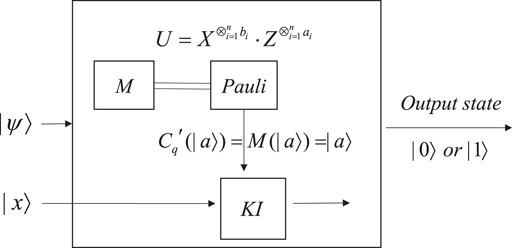
The state |ψ⟩ is measured so that we can get a classical bit string. According to the classical bit string measured, we use the corresponding Pauli matrix to restore the quantum state $C_q^{\prime }(|\varphi \rangle )$. Both C_q (|ϕ⟩) and $C_q^{\prime }(|\varphi \rangle )$ represent the functionality of the quantum function. We input a quantum state |x⟩ into the interpreter. With the input quantum state |x⟩ and the circuit C restored from the function’s parameter C_q (|ϕ⟩), we obtain the output value C_q (|x⟩). In this way, we achieve the objective of quantum obfuscation, which utilizes the functionality of the quantum functions to calculate some values without divulging any information about it.

Theorem 1: Quantum non-linear functions are obfuscatable by means of quantum teleportation. It satisfies the three conditions of quantum obfuscation.

Proof 1: To prove the correctness of quantum obfuscation based on quantum teleportation, we prove its polynomial expansion, functional equivalence, and virtual black-box property as follows.

For the quantum polynomial functions of quantum non-linear functions, the input size and output size of the quantum obfuscator are certainly of polynomial size. While for other quantum non-linear functions, the state C_q (|ϕ⟩) is transformed into an obfuscated state |ψ⟩ with a Bell state through quantum teleportation. Obviously, the obfuscator O computes H(C_q (|ϕ⟩) ⊕|β⟩) and generates |ψ⟩, which is also of polynomial size. Supposing C_q (|ϕ⟩) = |ϕ₀⟩, the output of O, i.e., the obfuscation of C, is

$O\left(C\right)=H|{\varphi }_0\oplus \beta \rangle .(12)$

Here, C is an n-qubit quantum circuit, β is a variable according to the size of C, and ϕ₀ is m-qubit. The total size of the output of the quantum obfuscator O is m + n.

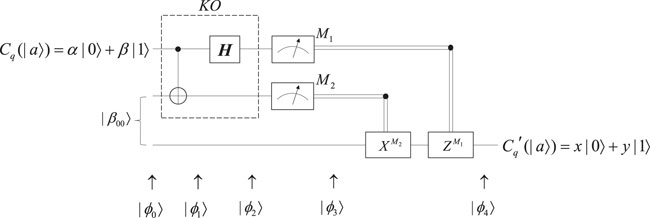
In the obfuscator, the state C_q (|ϕ⟩) is obfuscated by the kernel operation KO. In the interpreter (taking one-qubit C_q (|ϕ⟩) as an example), the first two qubits of the obfuscated quantum state |ψ⟩ are measured into a classical bit string so that we can perform the operation of the Pauli matrix to get the state $C_q^{\prime }(|\varphi \rangle )$. According to the principle of quantum teleportation, we know $C_q^{\prime }(|\varphi \rangle )$ is equal to C_q (|ϕ⟩), and they both present the functionality of the quantum function to be obfuscated. Then, we implement the kernel operation KI equivalent to the functionality of the quantum function on the input state |x⟩ to get C_q (|x⟩). Thus, the interpreter makes $C_q^{\prime }(|\varphi \rangle )$ correspond to the function correctly with the probability 1. For specific quantum non-linear functions, the construction of the interpreter and its property are elaborated in Section 4.

The size of O(C) is m + n. So, the polynomial expansion property holds when m = ploy(n). Through the aforementioned explanation and the overall construction of δ in Figure 2 (Figures 5, 6 for specific quantum functions), the functionality equivalence property is demonstrated. Since the oracle is truly random to any adversary, the obfuscation O(C) leaks no information about C_q (|ϕ⟩). Therefore, quantum non-linear functions are obfuscatable.

FIGURE 2

FIGURE 2. Overall construction of quantum obfuscation for quantum non-linear functions.

3.2 Universality of quantum obfuscation

Quantum obfuscation based on quantum teleportation is universal to quantum non-linear functions. The specific explanation is as follows.

Theorem 2: Quantum obfuscation based on quantum teleportation is universal to quantum non-linear functions whose parameter can be represented as a quantum state |a⟩. That is,

$|x,O\left(C\right)\rangle \mapsto |x,a\rangle .(13)$

Proof 2: For quantum non-linear functions, we can transform its parameter into a corresponding quantum state and input it into a quantum obfuscator. KO operation in the obfuscator contains a set of quantum gates. It depends on what the input quantum state of the parameter is. If we input a single-qubit state, KO operation can be presented as the circuit shown in Figure 3. If we input a multi-qubit state, the circuit can be altered by other forms of quantum gates. According to the function we want to obfuscate, we can design KI operation in the interpreter to restore its functionality. Significantly, for KI operation, we just present the idea of constructing the interpreter for quantum non-linear functions, so the basic circuit of KI operation cannot be described as a unified form but adaptive to the types of the functions to be obfuscated. Hence, we achieve the universality of quantum obfuscation based on quantum teleportation.

FIGURE 3

FIGURE 3. Obfuscation for quantum non-linear functions.

For example, if we want to obfuscate the quantum point function in Definition 2.3 to determine whether the input quantum state is equal to |a⟩, we can obfuscate its parameter |a⟩. In the same way, if we would like to obfuscate a quantum power function |y⟩ = |x⟩^|a⟩, we can obfuscate |a⟩. The exact KO operation of quantum teleportation in the obfuscator in Figure 3 depends on whether the parameter is a single-qubit state or multi-qubit state. To utilize the functionality of the original function, we just need to design the corresponding KI operation of the interpreter. Through the aforementioned proof, these functions are obfuscatable and satisfy the three properties of quantum obfuscation.

4 Application of quantum obfuscation to quantum power function and quantum point function

Quantum obfuscation based on quantum teleportation is universal to various types of quantum non-linear functions. The universal phase of quantum obfuscation is listed in Table 2. The obfuscator keeps the functionality secret, while the interpreter is designed to interpret the functionality to implement it in the input state. Figure 4 shows the construction of the interpreter of quantum non-linear functions. In this section, we take two quantum non-linear functions that have only one single parameter as examples. One is a quantum point function which is an easy form of quantum non-linear functions to implement the functionality of judgment. The other is a quantum power function which is the component of quantum polynomial functions.

TABLE 2

TABLE 2. Universal steps of quantum obfuscation.

FIGURE 4

FIGURE 4. Interpreter of quantum non-linear functions.

4.1 Quantum power function obfuscation

A quantum power function is derived from the classical power function. In the classical case, a power function is defined as

$y=x^a.(14)$

According to the theory of quantum computation, any classical function f can be implemented by a quantum circuit. To implement such a function, a quantum circuit maps the input register and target register |x, b⟩ to |x, b ⊕ f(x)⟩. On this premise, we now define a quantum power function.

Definition 3: A quantum power function U_a is defined as

$U_a:|x,y\rangle \mapsto |x,y\oplus P_a\left(x\right)\rangle .(15)$

Here, a ∈ {0, 1} and P_a is a function working expressed as

$|P_a\left(x\right)\rangle =|{x\rangle }^{|a\rangle }=\left\{\begin{array}{cc}|1\rangle \hfill & \mathrm{i}\mathrm{f}a=|0\rangle \hfill \\ |x\rangle \hfill & \mathrm{i}\mathrm{f}a=|1\rangle \hfill \end{array}\right..(16)$

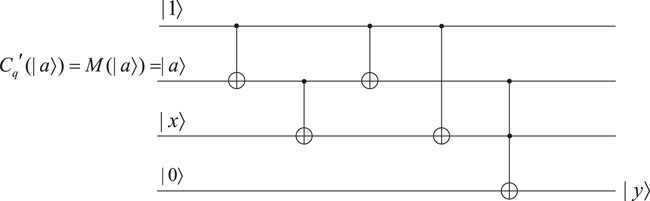
The parameter of the quantum power function is represented as |a⟩. We then obfuscate it by quantum teleportation to get an obfuscated state |ψ⟩ which is one of the possible states α|0⟩ + β|1⟩, α|0⟩ − β|1⟩, α|1⟩ + β|0⟩, or α|1⟩ − β|0⟩. For every qubit, we measure its first two qubits to get a classical bit string. According to the classical bit string obtained, we perform the corresponding Pauli matrix to restore each qubit making up the state M(|a⟩). Hence, we know what exactly |a⟩ is. Apparently, with the superposition state α|0⟩ + β|1⟩ input, we can give the overall construction of the quantum power function interpreter as shown in Figure 5. The ‘OR’ operation can be achieved by NAND relation. Thus, we reach the goal of outputting |1⟩ when |a⟩ = |0⟩ and outputting |x⟩ when |a⟩ = |1⟩, which satisfies the functionality of a quantum power function.

FIGURE 5

FIGURE 5. Equivalent circuit of quantum power function in KI operation of the interpreter.

4.2 Quantum point function obfuscation

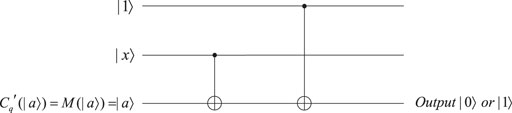
The concept of quantum point function is presented in Definition 2.3. We transform the property of a point function into a single-qubit quantum state |a⟩. Then, for every qubit, we measure its first two qubits to get a classical bit string. According to the classical bit string obtained, the corresponding Pauli matrix is performed to restore each qubit, and the result is represented as the quantum state M(|a⟩). Here, M(|a⟩) = |a⟩ holds. In this way, we design the quantum circuit as shown in Figure 6, which presents an implementable way to determine the equivalence of two quantum states to represent a quantum point function. We use it to judge whether |x⟩ is equal to |a⟩ or not and finally output |0⟩ or |1⟩.

FIGURE 6

FIGURE 6. Equivalent circuit of single-qubit point function in KI operation of the interpreter.

5 Quantum asymmetric encryption scheme based on obfuscation

In this section, we construct a quantum asymmetric encryption scheme based on quantum obfuscation for quantum non-linear functions. We prove the IND-security of the obfuscation scheme according to the VBB property of quantum obfuscation.

5.1 Scheme

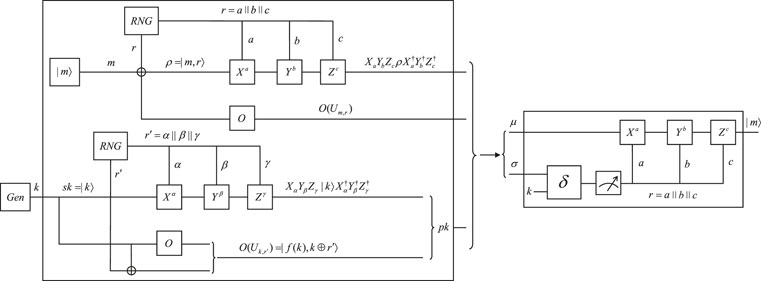
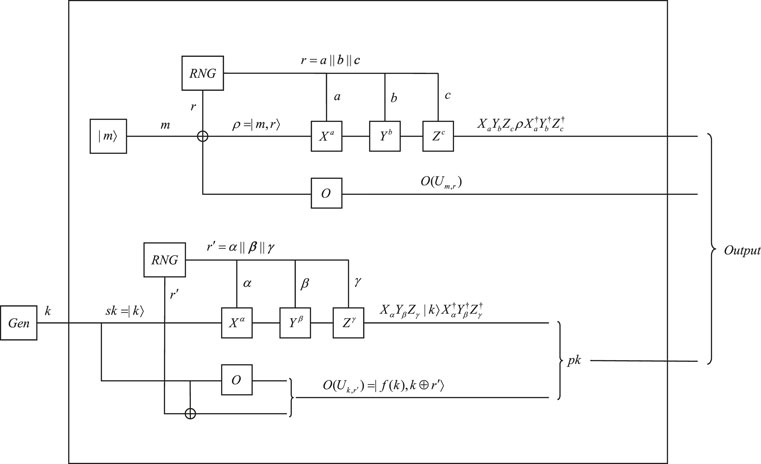
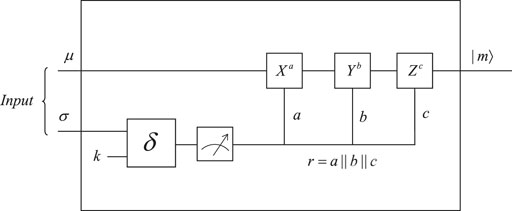
Let O be a quantum obfuscator for quantum non-linear functions and U_k,r be a quantum non-linear function. A quantum asymmetric encryption scheme based on quantum obfuscation is shown in Figure 7 (consisting of Figures 8, 9) and can be described as the following algorithms:

FIGURE 7

FIGURE 7. Quantum encryption scheme.

FIGURE 8

FIGURE 8. Quantum circuit of encryption.

FIGURE 9

FIGURE 9. Quantum circuit of decryption.

5.1.1 Key generation

Output sk = |k⟩, k ∈ {0,1}ⁿ and $pk=X_{\alpha }{Y}_{\beta }{Z}_{\gamma }|k\rangle Z_{\gamma }^{†}{Y}_{\beta }^{†}{X}_{\alpha }^{†}\otimes O(U_{k,r^{\prime }})$, where sk is the secret key generated randomly from the uniform key space {0,1}ⁿ. Thus, the public key $pk={\mathrm{E}\mathrm{n}\mathrm{c}}_{sk}^{\prime }={\mathrm{E}\mathrm{n}\mathrm{c}}_k^{\prime }=X_{\alpha }{Y}_{\beta }{Z}_{\gamma }|k\rangle Z_{\gamma }^{†}{Y}_{\beta }^{†}{X}_{\alpha }^{†}\otimes O(U_{k,r^{\prime }})$, where r′ is chosen from {0,1}³ⁿ randomly and α, β, and γ are the first, second, and last n bits of r′, respectively. Here, the quantum obfuscation is implemented to achieve the goal of generating the public key of the quantum asymmetric encryption scheme.

5.1.2 Encryption

Output ${\mathrm{E}\mathrm{n}\mathrm{c}}_{pk}(\rho )=pk(|m,r\rangle )=[X_{\alpha }{Y}_{\beta }{Z}_{\gamma }|k\rangle Z_{\gamma }^{†}{Y}_{\beta }^{†}{X}_{\alpha }^{†}\otimes O(U_{k,r^{\prime }})]\otimes [X_a{Y}_b{Z}_c(|r\rangle ⟨r|\otimes |m⟩)Z_c^{†}{Y}_b^{†}{X}_a^{†}]$, where |m⟩ refers to the information to be encrypted, r ∈ {0,1}ⁿ, and a, b, and c represent the first, second, and last n bits of the random bit r, respectively. Enc_pk(ρ) means utilizing the public key pk to encrypt the integration of random qubit |r⟩ and the message |m⟩.

5.1.3 Decryption

Output Dec_sk (μ ⊗ σ) = δ(σ ⊗|k⟩⟨k|⊗ μ), where σ is the measurement result of O(U_k,r′) and μ is the measurement result of $X_a{Y}_b{Z}_c(|r\rangle ⟨r|\otimes |m⟩)Z_c^{†}{Y}_b^{†}{X}_a^{†}$.

5.2 Theoretical analysis

5.2.1 Correctness

To demonstrate the correctness of the obfuscation scheme for quantum non-linear functions, we suppose the information |m, r⟩ is to be encrypted; thus, we have

$\begin{array}{c}{\mathrm{D}\mathrm{e}\mathrm{c}}_{sk}\left({\mathrm{E}\mathrm{n}\mathrm{c}}_{pk}\left(|m,r\rangle \right)\right)\hfill \\ =\mathrm{Tr}\left(\delta \left(\sigma \otimes |k\rangle \langle k|\otimes \mu \right)\right)\hfill \\ =\mathrm{Tr}\left(O\left(U_{k,r^{\prime }}\right)\otimes |k\rangle ⟨k|\otimes X_a{Y}_b{Z}_c|m,0^n⟩Z_c^{†}{Y}_b^{†}{X}_a^{†}\right)\hfill \\ =\mathrm{Tr}\left(U_{k,r^{\prime }}\left(|k\rangle ⟨k|\otimes X_a{Y}_b{Z}_c|m,0^n⟩Z_c^{†}{Y}_b^{†}{X}_a^{†}\right)U_{k,r^{\prime }}^{†}\right)\hfill \\ =\mathrm{Tr}\left(|k\rangle ⟨k|\otimes U_{m,r}|m,0^n⟩U_{m,r}^{†}\right)\hfill \\ =\mathrm{Tr}\left(|k\rangle ⟨k|\otimes |m,0^n⟩\right)\hfill \\ =\rho .\hfill \end{array}(17)$

According to the properties of quantum obfuscation and density operator, we explain the correctness of the aforementioned quantum asymmetric encryption scheme. We calculate the trace of the quantum state to obtain the value ρ, which is the system density operator of the quantum state |m, r⟩. Here, ρ = ∑_ip_i|m_i, r⟩⟨m_i, r| holds. In this way, the quantum state |m, r⟩ is presented by ρ, and the information to be encrypted is restored. Thus, we prove the correctness of the quantum asymmetric encryption scheme.

5.2.2 Security

The quantum asymmetric encryption scheme based on quantum obfuscation for quantum non-linear functions satisfies IND-security, which can be described as follows.

Theorem 3: If there exists a secure quantum one-way trapdoor function and quantum black-box obfuscation, then the quantum asymmetric encryption scheme based on obfuscation for quantum non-linear functions satisfies indistinguishability chosen-plaintext attack (IND-CPA) security.

Proof 3: A quantum polynomial time interpreter δ with only black-box access to Enc_sk can be used to simulate the access of any QPT adversary A and simulator S. Here, for any QPT adversary, A = (Γ, Δ), $w={(P_u\rho P_u^{†}\otimes I)}_{{\rho }_{\mathrm{\Gamma }}}$, $v=(P_u\rho P_u^{†}\otimes I)(|0\rangle \langle 0|\otimes \rho )$, and P_u represents the unitary matrix transformation of X_aY_bZ_c. So, there is

$\begin{array}{c}\left|\mathrm{Pr}\right\{\mathrm{\Delta }{\left[{\mathrm{E}\mathrm{n}\mathrm{c}}_{pk}\otimes I\right]}_{{\rho }_{\text{T}}}=1\}-\mathrm{Pr}\{\mathrm{\Delta }\left[\left({\mathrm{E}\mathrm{n}\mathrm{c}}_{pk}\otimes I\right)\left(|0\rangle \langle 0|\otimes \rho \right)\right]=1\left\}\right|\hfill \\ =\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left[w\otimes O\left(U_{k,r^{\prime }}\right)\right]=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left[v\otimes O\left(U_{k,r^{\prime }}\right)\right]=1\right\}\right|\hfill \\ =\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left[w,O\left(U_{k,r^{\prime }}\right)\right]=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left[v,O\left(U_{k,r^{\prime }}\right)\right]=1\right\}\right|.\hfill \end{array}(18)$

After decomposing the aforementioned formula with the probability theory,

$\begin{array}{c}\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left[w,O\left(U_{k,r^{\prime }}\right)\right]=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left[v,O\left(U_{k,r^{\prime }}\right)\right]=1\right\}\right|\hfill \\ \le {\sum }_{p\left(r^{\prime }\right)}\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left[w,p\left(\rho \right)\right]=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left[v,p\left(\rho \right)\right]=1\right\}\right|\hfill \\ \cdot \mathrm{Pr}\left\{{\mathrm{\Delta }}^{\prime }\left(O\left(U_{k,r^{\prime }}\right)\right)=p\left(\rho \right)\right\}.\hfill \end{array}(19)$

According to the properties of virtual black-box, there is

$|\mathrm{Pr}\left[\mathrm{\Delta }\left(O\left(U_{k,r^{\prime }}\right)\right)=1\right]-\mathrm{Pr}\left[S^{U_{k,r^{\prime }}}\left(0^n\right)=1\right]|\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right).(20)$

Under the quantum accessible random oracle model, if the simulator S successfully accesses the quantum non-linear function U_k,r′, there is p(ρ) = ρ; if not, there is p(ρ) = 0.

$\begin{array}{c}{\sum }_{p\left(\rho \right)}\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left[w,p\left(\rho \right)\right]=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left[v,p\left(\rho \right)\right]=1\right\}\right|\cdot \mathrm{Pr}\left\{{\mathrm{\Delta }}^{\prime }\left(O\left(U_{k,r^{\prime }}\right)\right)=p\left(\rho \right)\right\}\hfill \\ \le {\sum }_{p\left(\rho \right)}\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left[w,p\left(\rho \right)\right]=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left[v,p\left(\rho \right)\right]=1\right\}\right|\cdot \left|\mathrm{Pr}\left[S^{U_{k,r^{\prime }}}\left(0^n\right)=p\left(\rho \right)\right]+\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)\right|\hfill \\ =\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left(w,\rho \right)=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left(v,\rho \right)=1\right\}\right|\cdot \left|\mathrm{Pr}\left[S^{U_{k,r^{\prime }}}\left(0^n\right)=\rho \right]+\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)\right|\hfill \\ +\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left(w,0\right)=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left(v,0\right)=1\right\}\right|\cdot \left|\mathrm{Pr}\left[S^{U_{k,r^{\prime }}}\left(0^n\right)=0\right]+\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)\right|.\hfill \end{array}(21)$

As $\mathrm{Pr}[S^{U_{k,r^{\prime }}}(0^n)=\rho ]\le \frac{1}{2}\mathrm{p}\mathrm{o}\mathrm{l}\mathrm{y}(n)\le \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}(n)$, there is

$\begin{array}{c}|\mathrm{Pr}\left\{\mathrm{\Delta }\left(w,0\right)=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left(v,0\right)=1\right\}|\hfill \\ =\left|\mathrm{Pr}\right\{\mathrm{\Delta }{\left(P_u\rho P_u^{†}\otimes I\right)}_{{\rho }_{\mathrm{\Gamma }}}=1\}-\mathrm{Pr}\left\{\left(P_u\rho P_u^{†}\otimes I\right)\left(|0\rangle \langle 0|\otimes \rho \right)=1\right\}|.\hfill \end{array}(22)$

The aforementioned error can be ignored, so

$\begin{array}{c}|\mathrm{Pr}\left\{\mathrm{\Delta }{\left[\mathrm{E}\mathrm{n}{\mathrm{c}}_{pk}\otimes I\right]}_{{\rho }_{\mathrm{\Gamma }}}=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left[\left(\mathrm{E}\mathrm{n}{\mathrm{c}}_{pk}\otimes I\right)\left(|0\rangle \langle 0|\otimes \rho \right)\right]=1\right\}|\hfill \\ \le \left|\mathrm{Pr}\left\{\mathrm{\Delta }\left(w,\rho \right)=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left(v,\rho \right)=1\right\}\right|\cdot \left|\mathrm{Pr}\left[S^{U_{k,r^{\prime }}}\left(0^n\right)=\rho \right]+\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)\right|\hfill \\ +\left|\mathrm{Pr}\left\{\mathrm{\Delta }\left(w,0\right)=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left(v,0\right)=1\right\}\right|\cdot \left|\mathrm{Pr}\left[S^{U_{k,r^{\prime }}}\left(0^n\right)=0\right]+\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)\right|\hfill \\ \le \left|\mathrm{Pr}\left\{\mathrm{\Delta }\left(w,\rho \right)=1\right\}-\mathrm{Pr}\left\{\mathrm{\Delta }\left(v,\rho \right)=1\right\}\right|\cdot \mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)+\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)\cdot \left|\mathrm{Pr}\left[S^{U_{k,r^{\prime }}}\left(0^n\right)=0\right]+\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right)\right|\hfill \\ =\mathrm{n}\mathrm{e}\mathrm{g}\mathrm{l}\left(n\right).\hfill \end{array}(23)$

In conclusion, the asymmetric encryption scheme of quantum obfuscation satisfies IND-security.

5.3 Simulation results

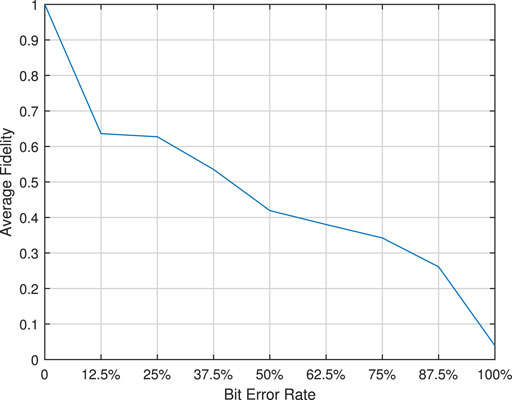
In this section, we use the quantum computing simulation tool QLib [28] to simulate the quantum asymmetric encryption scheme mentioned previously and prove the correctness of the scheme. The simulation results of average fidelity and bit error rate are shown in Figure 10.

FIGURE 10

FIGURE 10. Average fidelity—bit error rate curve for eight-qubit keys.

We simulate the circumstance of using different secret keys of 8 bits to decrypt ciphertext and draw the following curve with average fidelity. For example, supposing the quantum plaintext to be transmitted |m⟩ = [0.93614, − 0.14736 + 0.31925i], random number r = 111, r′ = 000, and secret key sk = 11100010, then we have pk = 10000111, X_aY_bZ_c|m⟩X_aY_bZ_c = [0.35161, 0.39234 + 0.84996i], the obfuscated result O = [0, 0, − 0.93299, 0, 0, 0, 0.3599, 0], and ciphertext c = [0, 0, − 0.32805, 0, 0, 0, −36605 − 79301i, 0]. If the correct secret key sk = 11100010 is used to decrypt the ciphertext, we can obtain the original quantum plaintext |m′⟩ = [0.93614, − 0.14736 + 0.31925i] with fidelity F = 1. When the wrong secret key sk’ = 01101000 is used, the fidelity is as low as 0.2759, and we cannot get the original quantum plaintext information. As the length of the erroneous bits of the secret key increases, the fidelity of the information decrypted with the wrong secret key decreases further.

5.4 Further discussion

Although the problem of applying quantum obfuscation to the quantum encryption scheme is solved, the real difficulty exists in the construction of the quantum circuits in the interpreter to restore the functionality of quantum functions. In the construction of the quantum interpreter of a quantum power function, Definition 4.1 is achieved by the quantum circuit which uses |1⟩ and the XOR gate to reverse the quantum state |a⟩. In this way, when |a⟩ = |0⟩, |x⟩^|a⟩ = |1⟩ is output from the circuit. When |a⟩ = |1⟩, the quantum state |0⟩ is obtained after reversal. The final result is |x⟩ by operating the XOR gate on |0⟩ and |x⟩. Now, the key to the problem comes to the output of the whole interpreter. The OR result of the outputs under two cases should be output, but there is no quantum OR gate. Because just the functionality of the quantum power function needs to be achieved, the NAND gate constructed by the XOR gate will be used to achieve the functionality of the quantum OR gate in the future implementation.

6 Conclusion

The construction and application of quantum obfuscation are significant to the development of the quantum computing theory. In this work, we proposed quantum obfuscation for quantum non-linear functions and applied it to quantum power functions. In addition, the correctness and security of the quantum asymmetric encryption scheme are also demonstrated in this work. The obfuscation illuminated the connection between quantum obfuscation and quantum teleportation. In particular, this work just suggested the idea of designing quantum obfuscation for quantum non-linear functions, so the structure of the quantum obfuscator and interpreter is variable according to the specific properties of quantum non-linear functions to be obfuscated. In addition, the applications of obfuscation to other types of circuits remain open and will be explored in our further work.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

CP proposed quantum obfuscation for quantum non-linear functions and constructed circuits of the quantum obfuscator and quantum interpreter. CP and TS demonstrated the correctness and security of the quantum asymmetric encryption scheme. CP and YZ analyzed the simulation results. All authors reviewed the manuscript.

Funding

This project was supported by the National Natural Science Foundation of China (Nos 61971021 and 61571024), the Aeronautical Science Foundation of China (No. 2018ZC51016), and the National Key Research and Development Program of China (No. 2016YFC1000307).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Ambainis A, Mosca M, Tapp A, De Wolf R. Private quantum channels. In: Proceedings 41st Annual Symposium on Foundations of Computer Science; 12-14 November 2000; Redondo Beach (2000).

Google Scholar

2. Scott A, Edward F, David G, Avinatan H, Jonathan K, Lutomirski A. Quantum money. Commun ACM (2012) 55:84–92. doi:10.1145/2240236.2240258

CrossRef Full Text | Google Scholar

3. Broadbent A, Jeffery S. Quantum homomorphic encryption for circuits of low t-gate complexity. Lecture Notes Comp Sci (2015) 9216:609–29. doi:10.1007/978-3-662-48000-7_30

CrossRef Full Text | Google Scholar

4. Sibson P, Erven C, Godfrey M, Miki S, Yamashita T, Fujiwara M, et al. Chip-based quantum key distribution. Nat Commun (2017) 8:13984. doi:10.1038/ncomms13984

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Zhang H, Sun Z, Qi R, Yin L, Long G-L, Lu J. Realization of quantum secure direct communication over 100 km fiber with time-bin and phase quantum states. Light: Sci Appl (2022) 11:83. doi:10.1038/s41377-022-00769-w

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Zhang X, Qu R, Chang Z, Quan Q, Gao H, Li F, et al. A geometrical framework for quantum incompatibility resources. AAPPS Bull (2022) 32:17. doi:10.1007/s43673-022-00047-2

CrossRef Full Text | Google Scholar

7. Yan F, Gao T. Perfect not and conjugate transformations. AAPPS Bull (2022) 32:7. doi:10.1007/s43673-022-00038-3

CrossRef Full Text | Google Scholar

8. Hada S. Zero-knowledge and code obfuscation. In: T Okamoto, editor. Advances in cryptology — asiacrypt 2000. Germany: Springer (2000). p. 443–57. doi:10.1007/3-540-44448-3_34

CrossRef Full Text | Google Scholar

9. Barak B, Goldreich O, Impagliazzo R, Rudich S, Sahai A, Vadhan S, et al. On the (im)possibility of obfuscating programs. In: J Kilian, editor. Advances in cryptology — crypto 2001. Berlin, Heidelberg: Springer Berlin Heidelberg (2001). p. 1–18. doi:10.1007/3-540-44647-8_1

CrossRef Full Text | Google Scholar

10. Garg S, Gentry C, Halevi S, Raykova M, Sahai A, Waters B. Candidate indistinguishability obfuscation and functional encryption for all circuits. In: 2013 IEEE 54th Annual Symposium on Foundations of Computer Science; 26-29 October 2013; Berkeley, CA, USA (2013).

CrossRef Full Text | Google Scholar

11. Sahai A, Waters B. How to use indistinguishability obfuscation: Deniable encryption, and more. SIAM J Comput (2021) 50:857–908. doi:10.1137/15M1030108

CrossRef Full Text | Google Scholar

12. Barak B, Garg S, Kalai YT, Paneth O, Sahai A. Protecting obfuscation against algebraic attacks. Lecture Notes Comp Sci (including subseries Lecture Notes Artif Intelligence Lecture Notes Bioinformatics) (2014) 8441:221–38. doi:10.1007/978-3-642-55220-5_13

CrossRef Full Text | Google Scholar

13. Bitansky N, Canetti R, Cohn H, Goldwasser S, Kalai YT, Paneth O, et al. The impossibility of obfuscation with auxiliary input or a universal simulator. Lecture Notes Comp Sci (including subseries Lecture Notes Artif Intelligence Lecture Notes Bioinformatics) (2014) 8617:71–89. doi:10.1007/978-3-662-44381-1_5

CrossRef Full Text | Google Scholar

14. Boneh D, Zhandry M. Multiparty key exchange, efficient traitor tracing, and more from indistinguishability obfuscation. Algorithmica (2017) 79:1233–85. doi:10.1007/s00453-016-0242-8

CrossRef Full Text | Google Scholar

15. Brakerski Z, Rothblum GN. Virtual black-box obfuscation for all circuits via generic graded encoding. Lecture Notes Comp Sci (including subseries Lecture Notes Artif Intelligence Lecture Notes Bioinformatics) (2014) 8349:1–25. doi:10.1007/978-3-642-54242-8_1

CrossRef Full Text | Google Scholar

16. Garg S, Gentry C, Halevi S, Wichs D. On the implausibility of differing-inputs obfuscation and extractable witness encryption with auxiliary input. Algorithmica (2017) 79:1353–73. doi:10.1007/s00453-017-0276-6

CrossRef Full Text | Google Scholar

17. Hohenberger S, Sahai A, Waters B. Replacing a random oracle: Full domain hash from indistinguishability obfuscation. Lecture Notes Comp Sci (including subseries Lecture Notes Artif Intelligence Lecture Notes Bioinformatics) (2014) 8441:201–20. doi:10.1007/978-3-642-55220-5_12

CrossRef Full Text | Google Scholar

18. Alagic G, Fefferman B (2016). On quantum obfuscation. ArXiv abs/1602.

Google Scholar

19. Zhang Y-J, Shang T, Liu J-W, Wu W. Quantum homomorphic encryption based on quantum obfuscation. 2020 Int Wireless Commun Mobile Comput IWCMC (2020) 2020:2010–5. doi:10.1109/IWCMC48107.2020.9148407

CrossRef Full Text | Google Scholar

20. Chen R, Shang T, Liu J. Ind-secure quantum symmetric encryption based on point obfuscation. Quan Inf Process (2019) 18:161. doi:10.1007/s11128-019-2280-z

CrossRef Full Text | Google Scholar

21. Pan C, Shang T, Liu J. Computational science. In: Quantum asymmetric encryption based on quantum point obfuscation Lecture Notes in Computer Science (including subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 12747 LNCS; June 16–18, 2021; Krakow, Poland (2021).

Google Scholar

22. Shang T, Chen R-y.-l., Liu J-w. On the obfuscatability of quantum point functions. Quan Inf Process (2019) 18:55. doi:10.1007/s11128-019-2172-2

CrossRef Full Text | Google Scholar

23. Yin H-L, Fu Y, Chen Z-B. Practical quantum digital signature. Phys Rev A (2016) 93:032316. doi:10.1103/PhysRevA.93.032316

CrossRef Full Text | Google Scholar

24. Yin H-L, Fu Y, Li C-L, Weng C-X, Li B-H, Gu J, et al. Experimental quantum secure network with digital signatures and encryption. Natl Sci Rev (2022). doi:10.1093/nsr/nwac228

CrossRef Full Text | Google Scholar

25. Zhou M-G, Cao X-Y, Lu Y-S, Wang Y, Bao Y, Jia Z-Y, et al. Experimental quantum advantage with quantum coupon collector. Research (2022) 2022:1–11. doi:10.34133/2022/9798679

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Xie Y-M, Lu Y-S, Weng C-X, Cao X-Y, Jia Z-Y, Bao Y, et al. Breaking the rate-loss bound of quantum key distribution with asynchronous two-photon interference. PRX Quan (2022) 3:020315. doi:10.1103/prxquantum.3.020315

CrossRef Full Text | Google Scholar

27. Bennett CH, Brassard G, Crepeau C, Jozsa R, Peres A, Wootters WK. Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels. Phys Rev Lett (1993) 70:1895–9. doi:10.1103/PhysRevLett.70.1895

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Machnes S (2007). QLib - a matlab package for quantum information theory calculations with applications. arXiv e-prints, arXiv:0708.0478.

Google Scholar