Reconstruction of the interplanetary magnetic field from the magnetosheath data: A steady-state approach

In the steady-state picture, the magnetic field can be formulated by a curl-free potential field in the magnetosheath region, and the sheath field is uniquely and linearly determined by the upstream field and the transformation matrix which contains the effect of field cancellation making the magnetospheric cavity. The curl-free sheath model can be used to reconstruct the upstream field for a given magnetic field data set in the magnetosheath region. The applicability and the limits are theoretically evaluated such that the reconstruction works reasonably as far as the sheath sampling position is not close to the magnetopause, and that the upstream field can be estimated within an error ranging from 10 to 40 percent, depending on the region of sampling.

1 Introduction

After the deceleration of the solar wind plasma at the bow shock, the plasma is deflected and streams around the planetary magnetosphere within the so-called magnetosheath region. This region exhibits various types of wave activities as well as turbulent fluctuations and serves as a direct interface between the solar wind plasma and the magnetospheric plasma [1]. However, the large-scale structures of the sheath region are mainly determined by the mean fields, such as the steady-state magnetic field and the steady-state flow velocity. Different approaches have been introduced for modeling the large-scale structures of the magnetosheath. For example, Spreiter et al. [2] revealed in their seminal paper the large-scale sheath structure with a compression on the dayside and an expanding, re-acceleration region in the flank region. Nabert et al. [3] solved the set of MHD (magnetohydrodynamic) equations self-consistently and semi-analytically to determine the magnetic field and flow velocity in the sheath region theoretically.

The problem of analytically expressing the sheath field was elegantly solved by Kobel and Flückiger [4] by considering the sheath region as current-free such that the sheath field is given as a superposition of the upstream field with the cancelling field that forms the magnetospheric cavity. The sheath field can thus uniquely be determined by solving the Laplace equation under the condition of the current-flowing boundaries at the bow shock and the magnetopause. The sheath field is then expressed as a linear transformation of the upstream field. This property enables the estimation of the upstream magnetic field directly from the sheath-field sampled at a single measurement point.

Here we revisit the model of Kobel and Flückiger [4] (hereafter, KF model), and point out the usefulness of the potential field treatment in the sheath and reconstruct the upstream field using the sheath data. The magnetic mapping property from the upstream to the downstream fields in the KF model has largely been overlooked in the space plasma physics studies. Our study is presented as a concept paper here, which is yet to be expanded into a proof-of-concept paper at the next stage. Nevertheless, our analytical and numerical calculation strongly supports the idea of developing an algorithm of upstream field reconstruction as an analysis tool. Immediate applications include observational cases in which only the sheath field is available and not the upstream one, such as 1) when studying the near-Earth space plasma by revisiting the data before the advent of long-term solar wind monitors (such as DSCOVR and Geotail) and 2) when working on the Mercury magnetosphere studies with the BepiColombo mission (with the Mio spacecraft orbiting around Mercury at an apo-herm of about 6 planet radii, [5]).

2 Curl-free magnetosheath model

The steady-state magnetosheath field is uniquely determined by the upstream field. The sheath field is obtained as a solution of the Laplace equation under the assumption that the magnetosheath is curl-free (which justifies the use of potential field theory). As discussed by Kobel and Flückiger [4], this assumption is only valid, if the steady state magnetic field changes slowly inside the magnetosheath region compared to the boundary regions. In this case, the sheath field is a superposition of the upstream field permeating the sheath and the cancelling field caused by the magnetopause current (such that the field does not permeate into the magnetosphere). The expression of the sheath field is given analytically for the parabolic shape of the bow shock and magnetopause [4] as

${\mathit{B}}^{(\mathrm{s}\mathrm{h})}=\frac{C}{R_{\text{mp}}}{\mathit{B}}^{(\mathrm{s}\mathrm{w})}+C{\mathit{B}}^{(\mathrm{c}\mathrm{c})}.(1)$

Here, B^(sh) denotes the sheath field, B^(sw) the solar wind field, and B^(cc) the cancelling field. The coefficient C is determined by the stand-off distance to the bow shock (R_bs) and that to the magnetopause (R_mp) under the boundary condition of parabolically-shaped bow shock and magnetopause as

$C=\frac{R_{\text{mp}}\left(2R_{\text{bs}}-R_{\text{mp}}\right)}{2\left(R_{\text{bs}}-R_{\text{mp}}\right)}.(2)$

The solar wind field B^(sw) is treated as given in the forward modeling. The cancelling field is obtained by solving the Laplace equation for the scalar potential under the boundary condition of the bow shock and magnetopause. The solution of the Laplace equation is represented as a Fourier-Bessel series, i.e., the solution is expanded into a Fourier series in the azimuthal directions around the symmetry axis (i.e., the solar wind direction intersecting the magnetic dipole of the planet), and is further expanded into a series of Bessel functions. For the parabolic boundaries, the Bessel expansion becomes truncated at the first order, and the cancelling field is analytically (also algebraically) expressed as

$B_x^{(\mathrm{c}\mathrm{c})}=-\frac{1}{d\left(d+x-x_{\text{f}}\right)}\left[\frac{1}{2}\left(d+x-x_{\text{f}}\right)B_x^{(\mathrm{s}\mathrm{w})}+y{B}_y^{(\mathrm{s}\mathrm{w})}+z{B}_z^{(\mathrm{s}\mathrm{w})}\right](3)$

$B_y^{(\mathrm{c}\mathrm{c})}=-\frac{1}{d\left(d+x-x_{\text{f}}\right)}\left[\frac{y}{2}{B}_x^{(\mathrm{s}\mathrm{w})}-\left(d-\frac{y^2}{d+x-x_{\text{f}}}\right)B_y^{(\mathrm{s}\mathrm{w})}-\frac{yz}{d+x-x_{\text{f}}}{B}_z^{(\mathrm{s}\mathrm{w})}\right](4)$

$B_z^{(\mathrm{c}\mathrm{c})}=\frac{1}{d\left(d+x-x_{\text{f}}\right)}\left[\frac{z}{2}{B}_x^{(\mathrm{s}\mathrm{w})}+\frac{yz}{d+x-x_{\text{f}}}{B}_y^{(\mathrm{s}\mathrm{w})}+\left(d-\frac{z^2}{d+x-x_{\text{f}}}\right)B_z^{(\mathrm{s}\mathrm{w})}\right](5)$

Here, our coordinate system is constructed by the sunward direction (as the x axis) and a further reference direction to determine the y and z direction. For example, one may choose the ecliptic north direction as the z direction in the spirit of the GSE coordinate system. We use the notation introduced by Soucek and Escoubet [6] such that the focal point of the bow shock and magnetopause is located at x_f along the x axis (hence the coordinates are r_f = (x_f, 0, 0) in our coordinate system), and the radial distance to the focal point is given by d = |r − r_f|. The magnetic field components are converted from the coordinate system in the KF model into the GSE coordinate system, e.g., that used in the paper by Soucek and Escoubet [6] by the following rule: $B_z^{(\mathrm{k}\mathrm{f})}\to B_x^{(\mathrm{g}\mathrm{s}\mathrm{e})}$, $B_x^{(\mathrm{k}\mathrm{f})}\to B_z^{(\mathrm{g}\mathrm{s}\mathrm{e})}$, and $B_y^{(\mathrm{k}\mathrm{f})}\to -B_y^{(\mathrm{g}\mathrm{s}\mathrm{e})}$.

The cancelling field is linearly proportional (in the vectorial sense) to the solar wind field, and Eq. 1 can be formulated using a transformation matrix T as

${\mathit{B}}^{(\mathrm{s}\mathrm{h})}=\mathbf{T}{\mathit{B}}^{(\mathrm{s}\mathrm{w})}(6)$

with

$\mathbf{T}=\frac{C}{R_{\text{mp}}}\mathrm{diag}\left(\mathrm{1,1,1}\right)+\frac{C}{d\left(d+x-x_{\text{f}}\right)}\left(\begin{array}{ccc}\hfill -\frac{1}{2}\left(d+x-x_{\text{f}}\right)\hfill & \hfill -y\hfill & \hfill -z\hfill \\ \hfill -\frac{y}{2}\hfill & \hfill \left(d-\frac{y^2}{d+x-x_{\text{f}}}\right)\hfill & \hfill \frac{yz}{d+x-x_{\text{f}}}\hfill \\ \hfill \frac{z}{2}\hfill & \hfill \frac{yz}{d+x-x_{\text{f}}}\hfill & \hfill d-\frac{z^2}{d+x-x_{\text{f}}}\hfill \end{array}\right),(7)$

where diag (1, 1, 1) is the 3-by-3 unit matrix.

As an example, the magnetic field lines within the magnetosheath calculated via Eq. 6 are illustrated in Figure 1 for the case of B^(sw) = −B₀ e_x as well as B^(sw) = −B₀ e_y, where B₀ is an arbitrary amplitude of the upstream field and e_x and e_y are the corresponding unit vectors of the x- and y-axis in the GSE coordinate system. The geometry is adapted to the terrestrial case (R_E = 6,371 km), where R_mp = 9 R_E and R_bs = 12.5 R_E [4]. The magnetic field lines clearly and smoothly bend around the magnetosphere and are tangential to the magnetopause.

FIGURE 1

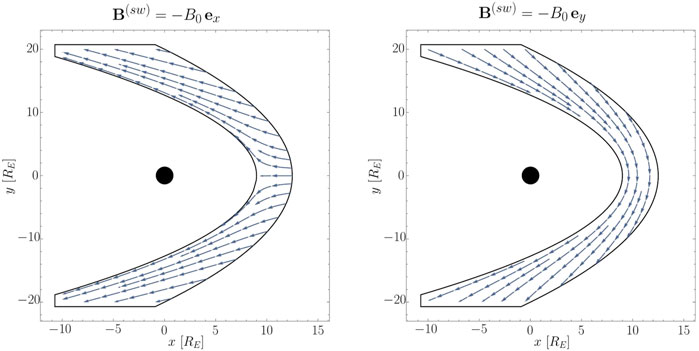
FIGURE 1. Field lines in the magnetosheath in the x-y plane for the case of B^(sw) = −B₀ e_x as well as B^(sw) = −B₀ e_y.

3 Upstream field estimation

Eq. 6 can potentially be inverted such that the upstream magnetic field B^(sw) is estimated from the inverse transformation matrix T⁻¹ and the sheath field B^(sh) as

${\mathit{B}}^{(\mathrm{s}\mathrm{w})}={\mathbf{T}}^{-1}{\mathit{B}}^{(\mathrm{s}\mathrm{h})}.(8)$

This approach would particularly be helpful in the planetary missions because the spacecraft may encounter the planetary sheath region along its trajectory but not always the solar wind. An example is BepiColombo Mio [5] which has an apo-herm of about 6 planetary radii. Depending on the observation time or season, there are time slots in which the spacecraft stays mostly in the magnetosphere and magnetosheath, and not in the solar wind. It should be noted that the bow shock and magnetopause are modeled as parabolically shaped and that the standoff distances R_bs and R_mp must be known a priori or from the data when inverting the transformation matrix. Furthermore, the shape of the boundaries needs to be (approximately) parabolic with known focal points.

3.1 Invertibility of the transformation matrix

Estimating the upstream field from magnetic field measurements within the magnetosheath, requires the existence of the matrix T⁻¹ (Eq. 8). Therefore, the question arises whether the transformation matrix is regular within the whole sheath region. For a first discussion we evaluate the matrix T along the stagnation line where y = 0 = z. From the definition of d it follows that d = x − x_f so that

$\mathbf{T}=\frac{C}{R_{\text{mp}}}\mathrm{diag}\left(\mathrm{1,1,1}\right)$

$+\frac{C}{2{\left(x-x_{\text{f}}\right)}^2}\left(\begin{array}{ccc}\hfill -\left(x-x_{\text{f}}\right)\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill x-x_{\text{f}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill x-x_{\text{f}}\hfill \end{array}\right)(9)$

$=\frac{C}{R_{\text{mp}}}\mathrm{diag}\left(\mathrm{1,1,1}\right)$

$+\frac{C}{2\left(x-x_{\text{f}}\right)}\left(\begin{array}{ccc}\hfill -1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right)(10)$

$=C\left(\begin{array}{ccc}\hfill \frac{1}{R_{\text{mp}}}-\frac{1}{2\left(x-x_{\text{f}}\right)}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{1}{R_{\text{mp}}}+\frac{1}{2\left(x-x_{\text{f}}\right)}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill \frac{1}{R_{\text{mp}}}+\frac{1}{2\left(x-x_{\text{f}}\right)}\hfill \end{array}\right).(11)$

The determinant results in

$\det \left(\mathbf{T}\right)=C^3\left(\frac{1}{R_{\text{mp}}}-\frac{1}{2\left(x-x_{\text{f}}\right)}\right){\left(\frac{1}{R_{\text{mp}}}+\frac{1}{2\left(x-x_{\text{f}}\right)}\right)}^2(12)$

and vanishes in the case of

$2\left(x-x_{\text{f}}\right)=R_{\text{mp}}(13)$

or equivalently

$x-x_{\text{f}}=\frac{R_{\text{mp}}}{2}.(14)$

Using $x_{\text{f}}=\frac{R_{\text{mp}}}{2}$ [6], shows that the matrix becomes singular at the magnetopause

$x=R_{\text{mp}}.(15)$

Figure 2 displays the determinant of the matrix T in the x-y plane within the sheath region. The matrix is regular within the whole sheath and the determinant reaches its maximum value directly at the bow shock. The determinant decreases towards the magnetosphere and vanishes at the magnetopause where the matrix becomes singular. This behaviour can be understood as follows: The model requires the sheath field to be tangential at the magnetopause. Therefore, different upstream field orientations cannot be discerned from each other at the magnetopause. In the remaining regions of the sheath the upstream field can be properly estimated by making use of Eq. 8.

FIGURE 2

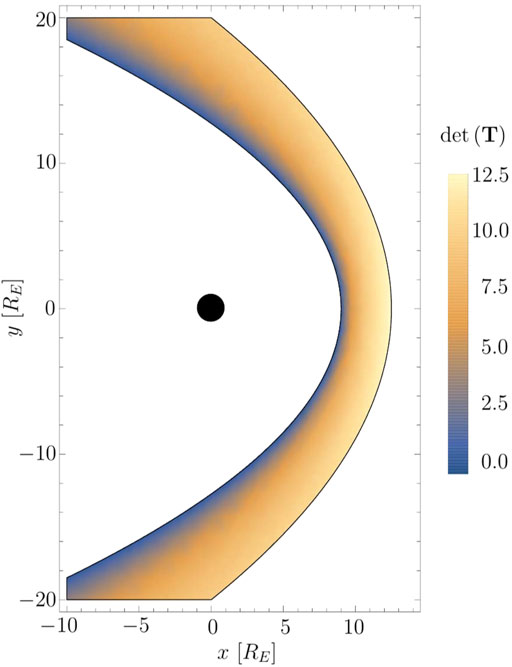
FIGURE 2. Determinant of the matrix T in the x-y plane. The matrix becomes singular at the magnetopause.

3.2 Accuracy of upstream field estimation

In the practical application of the method to magnetosheath in situ data, the quality of the upstream field estimation is affected by measurement errors. The goal is to classify regions within the magnetosheath that are preferable for estimating the upstream field. We use a test scenario and model the sheath field B^(sh) via Eq. 6 for B^(sw) = −B₀ e_x. Afterwards, each resulting component of the sheath field is disturbed by one random error with a maximum value of 10% of the background field B₀ resulting in the field ${\tilde{\mathit{B}}}^{(\mathrm{s}\mathrm{h})}$ (i.e., the error of each component lies in the range [ − 0.1 B₀, 0.1 B₀]). Finally, the upstream field ${\tilde{\mathit{B}}}^{(\mathrm{s}\mathrm{w})}$ is estimated via

${\tilde{\mathit{B}}}^{(\mathrm{s}\mathrm{w})}={\mathbf{T}}^{-1}{\tilde{\mathit{B}}}^{(\mathrm{s}\mathrm{h})}.(16)$

Figure 3 displays the errors of the amplitude $|\delta {\mathit{B}}^{(\mathrm{s}\mathrm{w})}|=|{\tilde{\mathit{B}}}^{(\mathrm{s}\mathrm{w})}-{\mathit{B}}^{(\mathrm{s}\mathrm{w})}|$ and of the components $\delta {\mathit{B}}_i^{(\mathrm{s}\mathrm{w})}={\tilde{\mathit{B}}}_i^{(\mathrm{s}\mathrm{w})}-{\mathit{B}}_i^{(\mathrm{s}\mathrm{w})}$ for i = x, y, z normalized to the background field B₀ in the x-y-plane. As the boundary shapes are assumed to be rotationally symmetric, the same picture arises within the x-z-plane.

FIGURE 3

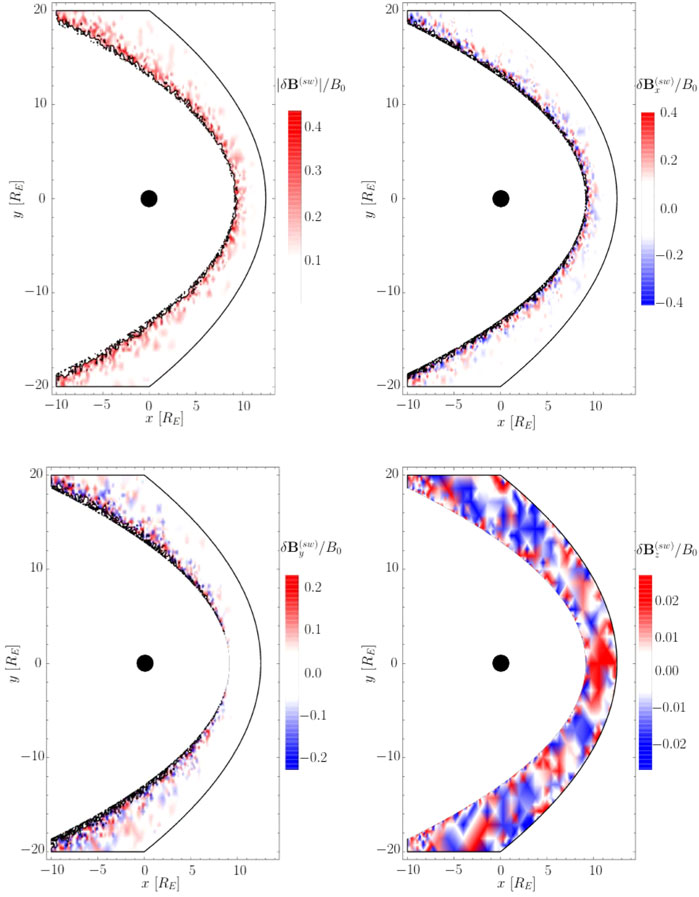
FIGURE 3. Relative error of the reconstructed amplitude and the components of the upstream field resulting from disturbed measurements.

The relative error of the amplitude follows the structure of the determinant of the matrix T (Figure 2) and reaches its maximum value of about 40% in the vicinity of the magnetopause. The error of the amplitude is mainly controlled by the x and y components that show errors of about 20–40%. The error of the z component is smallest with values of the order of 1%. A similar structure arises in the case of B^(sw) = −B₀ e_y. Therefore, the field can be most accurately determined in the plane perpendicular to the plane where the field bends around the magnetosphere. It should be noted that the estimation error solely depends on the distance to the magnetopause. Thus, the field can also be estimated adequately in the far tail regions.

As discussed at the beginning of the section, the standoff distances R_bs and R_mp must be known a priori or estimated from the data when calculating the upstream field. To analyze the effect of defectively determined standoff distances, we assume values of R_mp = 9.1 R_E and R_bs = 12.6 R_E, which are about 1% larger than the true values of R_mp = 9 R_E and R_bs = 12.5 R_E. The defectively determined distances result in a disturbed transformation matrix $\tilde{\mathbf{T}}$. The sheath field is again calculated using Eq. 6 with B^(sw) = −B₀ e_x and the field estimation is performed via

${\tilde{\mathit{B}}}^{(\mathrm{s}\mathrm{w})}={\tilde{\mathbf{T}}}^{-1}{\mathit{B}}^{(\mathrm{s}\mathrm{h})}.(17)$

The resulting estimation error of the amplitude $|\delta {\mathit{B}}^{(\mathrm{s}\mathrm{w})}|=|{\tilde{\mathit{B}}}^{(\mathrm{s}\mathrm{w})}-{\mathit{B}}^{(\mathrm{s}\mathrm{w})}|$ is displayed in Figure 4. The error again increases towards the magnetopause with a maximum value of about 15%.

FIGURE 4

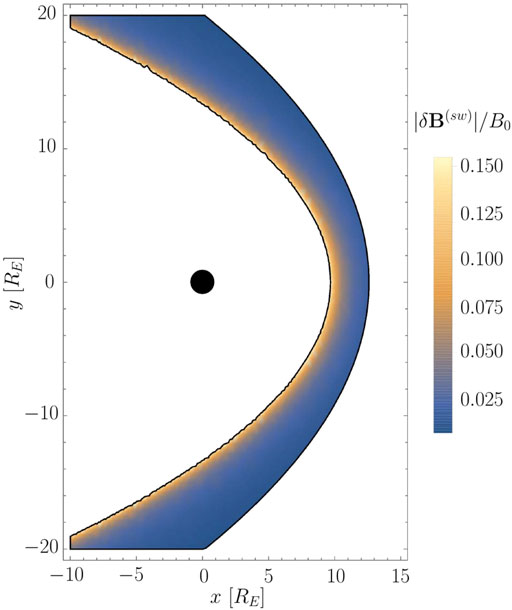
FIGURE 4. Relative error of the reconstructed amplitude of the upstream field resulting from defectively determined standoff distances R_mp and R_bs.

Furthermore, defectively determined measurement positions of the spacecraft can cause estimation errors of the upstream field.

4 Summary and outlook

The KF model [4] enables the analytical modelling of the magnetic field within the magnetosheath for a given upstream field. As the sheath field results from a linear transformation of the upstream field, the model can also be used for estimating the upstream field from magnetosheath measurements acquired at a single measurement point. It turns out that the upstream field can be properly estimated within the whole magnetosheath region except for the magnetopause, where the sheath field is bend around the magnetosphere and lies tangential to the magnetopause for all upstream field orientations.

In the practial application, the accuracy of the estimation is affected by measurement errors and defectively determined standoff distances. Using a test scenario, we find that the estimation error decreases with increasing distance to the magnetopause. Therefore, data far away from the magnetopause are preferable to guarantee an accurate upstream field reconstruction.

The presented inversion procedure opens the door for a wide range of practical applications. For example, the model can be applied to the BepiColombo Mio data to estimate the upstream field in the vicinity of Mercury [5]. It should be noted that the model is based on the evaluation of magnetic field data in current-free regions. Regarding the different scales of the magnetospheres of planet Earth and planet Mercury it might be useful to extend the modelling by making use of the toroidal-poloidal decomposition, also known as the Mie representation [7], which enables the evaluation of magnetic field data in current-carrying regions. Especially, the model should be tested against simulated magnetic field data to evaluate the quality of the results conducted by the model. Regarding the different shape models of planetary magnetospheres (e.g., [8, 9]) and bow shocks (e.g., [10, 11]), the model can also be extended to different geometries by making use of curvilinear coordinates. Furthermore, this enables us to analyze the robustness of different boundary models and model parameters (e.g., magnetopause flaring, non-confocal boundary shapes, magnetosheath thickness) towards the magnetic field estimation and the error propagation, especially when data from far-tail regions are evaluated.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Acknowledgments

The authors are grateful for stimulating discussions and helpful suggestions by Uwe Motschmann. We acknowledge support by the German Research Foundation and the Open Access Publication Funds of the Technische Universität Braunschweig.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Narita Y, Plaschke F, Vörös Z. The magnetosheath, space physics and aeronomy collection volume 2: Magnetospheres in the solar system. Geophys Monogr (2021) 259:137–52. doi:10.1002/9781119815624.ch9

CrossRef Full Text | Google Scholar

2. Spreiter JR, Summers AL, Alksne AY. Hydromagnetic flow around the magnetosphere. Planet Space Sci (1966) 14:223–53. doi:10.1016/0032-0633(66)90124-3

CrossRef Full Text | Google Scholar

3. Nabert C, Glassmeier K-H, Plaschke F. A new method for solving the MHD equations in the magnetosheath. Ann Geophys (2013) 31:419–37. doi:10.5194/angeo-31-419-2013

CrossRef Full Text | Google Scholar

4. Kobel E, Flückiger EO. A model of the steady state magnetic field in the magnetosheath. J Geophys Res (1994) 99:23617–22. doi:10.1029/94JA01778

CrossRef Full Text | Google Scholar

5. Benkhoff J, Murakami G, Baumjohann W, Besse S, Bunce E, Casale M, et al. BepiColombo - mission overview and science goals. Space Sci Rev (2021) 217:90. doi:10.1007/s11214-021-00861-4

CrossRef Full Text | Google Scholar

6. Soucek J, Escoubet CP. Predictive model of magnetosheath plasma flow and its validation against Cluster and THEMIS data. Ann Geophys (2012) 30:973–82. doi:10.5194/angeo-30-973-2012

CrossRef Full Text | Google Scholar

7. Toepfer S, Narita Y, Glassmeier KH, Heyner D, Kolhey P, Motschmann U, et al. The Mie representation for Mercury’s magnetic field. Earth Planets Space (2021) 73:65. doi:10.1186/s40623-021-01386-4

CrossRef Full Text | Google Scholar

8. Shue JH, Chao JK, Fu HC, Russell CT, Song P, Khurana KK, et al. A new functional form to study the solar wind control of the magnetopause size and shape. J Geophys Res (1997) 102:9497–511. doi:10.1029/97JA00196

CrossRef Full Text | Google Scholar

9. Zhong J, Wan WX, Slavin JA, Wei Y, Lin RL, Chai LH, et al. Mercury’s three-dimensional asymmetric magnetopause. J Geophys Res Space Phys (2015) 120:7658–71. doi:10.1002/2015JA021425

CrossRef Full Text | Google Scholar

10. Slavin JA, Holzer RE. Solar wind flow about the terrestrial planets 1. Modeling bow shock position and shape. J Geophys Res (1981) 86:11401–18. doi:10.1029/JA086iA13p11401

CrossRef Full Text | Google Scholar

11. Farris MH, Petrinec SM, Russell CT. The thickness of the magnetosheath: Constraints on the polytropic index. Geophys Res Lett (1991) 18:1821–4. doi:10.1029/91GL02090

CrossRef Full Text | Google Scholar