- 1Early Warning Academy, Wuhan, China
- 2Department of Physics, National University of Defense Technology, Changsha, China
To investigate plasma density during the Breit–Wheeler positron generation, a comparative study of four plasma targets is performed via the PIC (particle-in-cell) code EPOCH. When an ultra-intense laser (
1 Introduction
As a result of the quick development of laser technology, a peak intensity of
According to creation mechanisms, laser-induced positron generation includes two ways: an indirect way and a direct way [8]. In the indirect way, high-energy electrons are obtained via the laser–plasma interaction first. Then, these electrons are shot into a second-class target to produce positrons. For example, the trident process and the BH (Bethe–Heitler) process belong to the indirect way [9]. The indirect way always requires a thick, solid target for transition [10], and the required laser intensity can be afforded by current large laser facilities. When an ultra-short (∼1 ps) and ultra-intense (
In this work, taking an ultra-intense laser irradiating foam-like plasmas into account, the influence of plasma density on the BW positron generation is studied. Laser intensity is also discussed in the optimized plasmas. Results show that the increasing density plasma favors positron generation and acceleration, and increasing the incident laser intensity is still an effective way to enhance positron generation. This work will promote the investigation of the laser-induced positron source and its further applications.
2 Methods and model
When a laser pulse propagates in under-dense plasmas, a plasma density that matched the laser pulse favors electron acceleration. Taking the bubble regime, for example, a bubble is formed only when the normalized laser amplitude
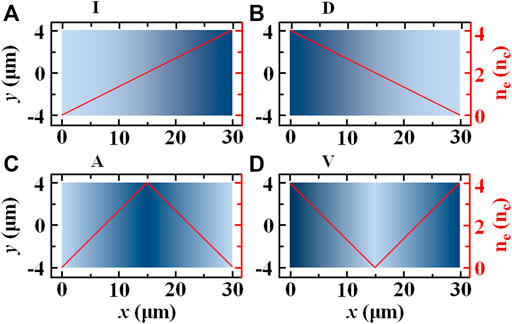
FIGURE 1. Schematics of four types of plasmas: type I is linearly increasing density plasmas (A); type D is linearly decreasing density plasmas (B); type A is first increasing and then decreasing density plasmas (C); and type V is first decreasing and then increasing density plasmas (D).
3 Results and discussion
As the laser is ultra-intense and ultra-short and foam-like plasmas are employed, the multi-photon BW process dominates positron generation in the laser–plasma interaction. When the laser propagates in plasmas, electrons are accelerated to radiate high-energy gamma photons. These photons further interact with laser photons, resulting in positron generation. Figure 2A shows the evolution of positron yield in four types of plasmas. It can be seen from the figure that the positron yield gradually reaches its maximum in A- and D-type plasmas. Even though the positron yield is small at first, it increases quickly and keeps increasing in I-and V-type plasmas. In the I-type plasmas, whose density increases linearly, the positron yield is the highest among these four plasma targets. At
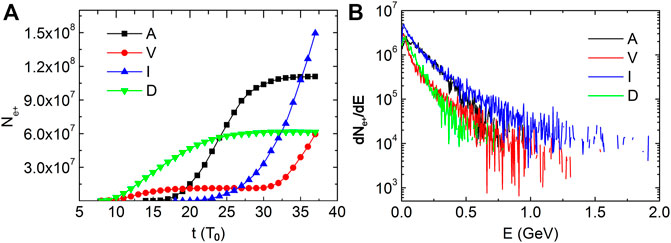
FIGURE 2. Evolutions of the positron yield (A) and spectra of positrons (B) at
When the laser propagates in increasing density plasmas, on the one hand, the under-dense plasmas favor electron acceleration. High-energy electrons are obtained, and they propagate along with the laser pulse. On the other hand, when plasmas get denser, partial laser is reflected [18]. It is to be noted that gamma photon radiation is controlled by
Figure 2B shows the spectra of positrons at
For more details, the energy density distributions of gamma photons and the location of the laser pulse are provided in Figure 3. It can be seen from the figure that high-energy density gamma photons are well focused in the I-type plasmas when compared with those in the other plasmas. Also, these high-energy density gamma photons are distributed in the center of the laser pulse, where the laser field is the strongest. In the positron generation-controlling parameter, higher
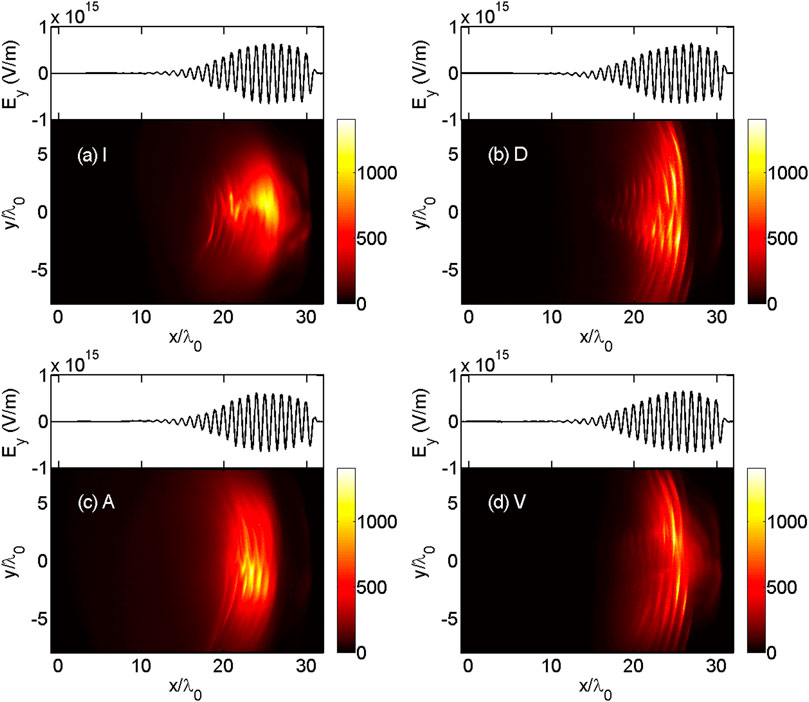
FIGURE 3. Energy density (
Laser intensity plays an important role in electron acceleration, photon radiation, and positron generation. Taking the positron generation process into account, laser intensity even induces different mechanisms. Provided that the Schwinger field is realized, the vacuum will break down to generate electron–positron pairs. However, that field is too strong to be realized in a laboratory. Researchers are concerned with the feasibility of experiments in state-of-the-art laser facilities. In the following, simulations of different intensity lasers irradiating plasmas are performed. The normalized laser amplitude
Figure 4 provides simulation results for different intensity lasers irradiating the I-type plasma target at
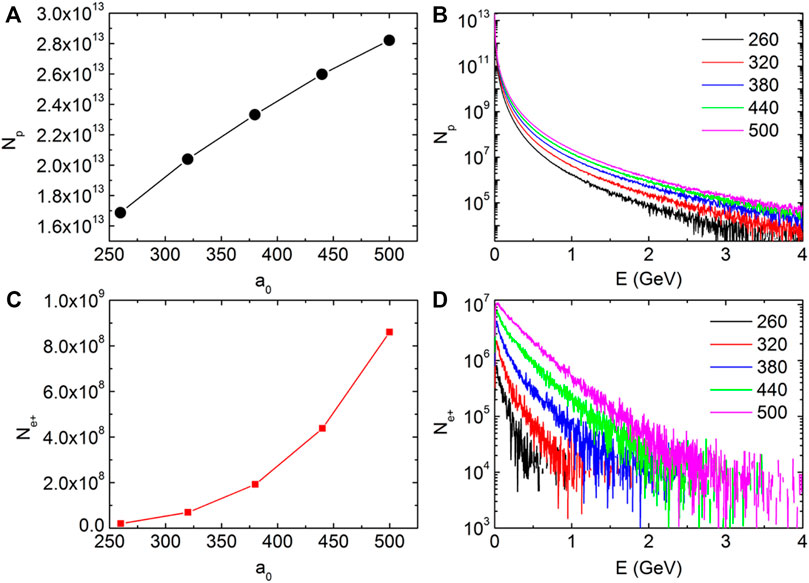
FIGURE 4. Photon yield (A) and positron yield (C) as a function of the normalized laser amplitude; spectra of photons (B) and positrons (D) at
4 Conclusion
In conclusion, a comparative study of four plasma targets in the BW process for positron generation is performed. It is found that increasing density plasmas favor high-flux and high-density positron generation. When an ultra-intense laser irradiates increasing density plasmas, under-dense plasmas will contribute to electron acceleration, and dense plasmas will reflect the laser in order to collide with high-energy electrons. The Compton back-scattering is enhanced as a result of the collision, followed by the enhancement of positron generation. When different intensity lasers irradiate increasing density plasmas, it is found that increasing the normalized laser amplitude induces exponential growth of positron yield. High-flux and high-density positrons are generated even with lower laser intensities. This investigation provides a feasible basis for obtaining positrons experimentally via the BW process.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
All authors took part actively in carrying out all simulations, in the analysis of results, and in the writing of the article. In particular, W-QD, T-YL, and XW prepared the proposal for simulations. H-BJ, T-PY, and J-XL contributed to the analysis of simulation results. J-XL and TG prepared the manuscript.
Funding
This work was financially supported by the National Natural Science Foundation (Grant Nos 11805278 and 11875319), the Youth Promotion Project of Early Warning Academy, the Science and Technology Innovation Program of Hunan Province (Grant No. 2020RC4020), and the Fok Ying-Tong Education Foundation (Grant No. 161007).
Acknowledgments
The authors wish to thank the Centre for Fusion, Space, and Astrophysics at the University of Warwick for allowing the usage of EPOCH.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Turcu I., Shen B., Neely D., Sarri G., Tanaka K. A., Mckenna P., et al. Quantum electrodynamics experiments with colliding petawatt laser pulses. High Power Laser Sci.Eng. (2019) 7(1):e10. doi:10.1017/hpl.2018.66
2. Chen H., Wilks S., Meyerhofer D., Bonlie J., Chen C., Chen S., et al. Relativistic quasimonoenergetic positron jets from intense laser-solid interactions. Phys Rev Lett (2010) 105:015003. doi:10.1103/physrevlett.105.015003
3. Jiang J., Wu Y. C., Liu X. B., Wang R. S., Nagai Y., Inoue K., et al. Microstructural evolution of RPV steels under proton and ion irradiation studied by positron annihilation spectroscopy. J Nucl Mater (2015) 458:326–34. doi:10.1016/j.jnucmat.2014.12.113
4. Yu T. P., Hu L. X., Yin Y., Shao F. Q., Zhuo H. B., Ma Y. Y., et al. Bright tunable femtosecond x-ray emission from laser irradiated micro-droplets. Appl Phys Lett (2014) 105:114101. doi:10.1063/1.4895928
5. Ruffini R., Vereshchagin G., Xue S. Electron-positron pairs in physics and astrophysics: From heavy nuclei to black holes. Phys Rep (2010) 487:1–140. doi:10.1016/j.physrep.2009.10.004
6. Müller C., Keitel C. H. Antimatter: Abundant positron production. Nat Photon (2009) 3:245–6. doi:10.1038/nphoton.2009.56
7. Chen H., Wilks S. C., Bonlie J. D., Liang E. P., Myatt J., Price D. F., et al. Relativistic positron creation using ultraintense short pulse lasers. Phys Rev Lett (2009) 102:105001. doi:10.1103/physrevlett.102.105001
8. Yan Y., Zhang B., Wu Y., Dong K., Yao Z., Gu Y. Comparison of direct and indirect positron-generation by an ultra-intense femtosecond laser. Phys Plasmas (2013) 20:103114. doi:10.1063/1.4826219
9. Sarri G., Schumaker W., Di Piazza A., Vargas M., Dromey B., Dieckmann M. E., et al. Table-top laser-based source of femtosecond, collimated, ultrarelativistic positron beams. Phys Rev Lett (2013) 110:255002. doi:10.1103/physrevlett.110.255002
10. Breit G., Wheeler J. A. Collision of two light quanta. Phys Rev (1934) 46:1087–91. doi:10.1103/physrev.46.1087
11. Yan Y., Dong K., Wu Y., Zhang B., Yao Z., Gu Y. Numerical simulation study of positron production by intense laser-accelerated electrons. Phys Plasmas (2013) 20:103106. doi:10.1063/1.4824107
12. Burke D. L., Field R. C., Horton-Smith G., Spencer J. E., Walz D., Berridge S. C., et al. Positron production in multiphoton light-by-light scattering. Phys Rev Lett (1997) 79:1626–9. doi:10.1103/physrevlett.79.1626
13. Liu J. X., Ma Y. Y., Zhao J., Yu T. P., Yang X. H., Gan L. F., et al. High-flux low-divergence positron beam generation from ultra-intense laser irradiated a tapered hollow target. Phys Plasmas (2015) 22:103102. doi:10.1063/1.4932997
14. Jirka M., Klimo O., Bulanov S. V., Esirkepov T. Z., Gelfer E., Bulanov S. S., et al. Electron dynamics andγande−e+production by colliding laser pulses. Phys Rev E (2016) 93:023207. doi:10.1103/physreve.93.023207
15. Ridgers C. P., Brady C. S., Duclous R., Kirk J., Bennett K., Arber T., et al. Dense electron-positron plasmas and bursts of gamma-rays from laser-generated quantum electrodynamic plasmas. Phys Plasmas (2013) 20:056701. doi:10.1063/1.4801513
16. Yu J. Q., Lu H. Y., Takahashi T., Hu R. H., Yan X. Q., Ma W., et al. Creation of electron-positron pairs in photon-photon collisions driven by 10-PW laser pulses. Phys Rev Lett (2019) 122:014802. doi:10.1103/physrevlett.122.014802
17. Zhu X-L., Yu T-P., Sheng Z-M., Yin Y., Turcu I. C. E., Pukhov A. Dense GeV electron–positron pairs generated by lasers in near-critical-density plasmas. Nat Commun (2016) 7:13686. doi:10.1038/ncomms13686
18. Jian-Xun L., Yan-Yun M., Tong-Pu Y., Jun Z., Xiao-Hu Y., Long-Fei G., et al. Enhanced electron–positron pair production by ultra intense laser irradiating a compound target. Plasma Phys Control Fusion (2016) 58:125007. doi:10.1088/0741-3335/58/12/125007
19. Jian-Xun L., Yan-Yun M., Tong-Pu Y., Jun Z., Xiao-Hu Y., De-Bin Z., et al. Dense pair plasma generation by two laser pulses colliding in a cylinder channel. Chin Phys B (2017) 26:035202. doi:10.1088/1674-1056/26/3/035202
20. Liu J. X., Zhao Y., Wang X. P., Quan J. Z., Yu T. P., Zhang G. B., et al. High-flux positrons generation via two counter-propagating laser pulses irradiating near-critical-density plasmas. Phys Plasmas (2018) 25:103106. doi:10.1063/1.5043627
21. Lu W., Tzoufras M., Joshi C., Tsung F. S., Mori W. B., Vieira J., et al. Generating multi-GeV electron bunches using single stage laser wakefield acceleration in a 3D nonlinear regime. Phys Rev Spec Top Acc Beams (2017) 10:061301. doi:10.1103/physrevstab.10.061301
22. Lu W., Huang C., Zhou M., Mori W. B., Katsouleas T. Nonlinear theory for relativistic plasma wakefields in the blowout regime. Phys Rev Lett (2006) 96:165002. doi:10.1103/physrevlett.96.165002
23. Gahn C., Tsakiris G., Pretzler G., Witte K., Thirolf P., Habs D., et al. Generation of MeV electrons and positrons with femtosecond pulses from a table-top laser system. Phys Plasmas (2002) 9:987–99. doi:10.1063/1.1446879
24. Arber T. D., Arber T. D., Bennett K., Bennett K., Brady C. S., Brady C. S., et al. Contemporary particle-in-cell approach to laser-plasma modelling. Plasma Phys Control Fusion (2015) 57:113001. doi:10.1088/0741-3335/57/11/113001
25. Ridgers C. P., Brady C. S., Duclous R., Kirk J., Bennett K., Arber T., et al. Dense electron-positron plasmas and ultraintenseγrays from laser-irradiated solids. Phys Rev Lett (2012) 108:165006. doi:10.1103/physrevlett.108.165006
Keywords: Compton back-scattering, ultra-intense laser pulse, laser–plasma interaction, electron–positron pair, gamma-ray emission
Citation: Liu J-X, Gao T, Wang X, Jin H-B, Deng W-Q, Liu T-Y and Yu T-P (2023) High-flux positron generation via the ultra-intense laser irradiating density-modulated plasmas. Front. Phys. 10:1052654. doi: 10.3389/fphy.2022.1052654
Received: 24 September 2022; Accepted: 14 December 2022;
Published: 04 January 2023.
Edited by:
Zi-Yu Chen, Sichuan University, ChinaReviewed by:
Yan-Fei Li, Xi’an Jiaotong University, ChinaYanqing Deng, Shanghai Jiao Tong University, China
Copyright © 2023 Liu, Gao, Wang, Jin, Deng, Liu and Yu. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Tong-Pu Yu, dG9uZ3B1QG51ZHQuZWR1LmNu
 Jian-Xun Liu
Jian-Xun Liu Ting Gao1
Ting Gao1 Tong-Pu Yu
Tong-Pu Yu