A robust self-referenced 2D nyquist ghost correction for different MRI-biomarker measurements based on multi-band interleaved EPI

Purpose: To enable 2D Nyquist ghost correction for multi-band interleaved echo-planar imaging (EPI) without reference scan.

Methods: 2D phase errors between positive and negative echo were directly measured from the multi-band interleaved EPI data acquired with alternating readout polarity, and then corrected by using multiplexed sensitivity encoding (MUSE) framework. The proposed method was tested on brain data acquired with and without multi-band imaging under different multi-shot factors (4, 8, and 16). In addition, the 2D phase corrections for the interleaved EPI data acquired with 2D zoomed-FOV, 2D reduced-FOV, or 3D multi-band imaging were also performed with the proposed method. The performance of our proposed method was assessed with single-to-noise ratio (SNR) and ghost-to-signal ratio (GSR), and then compared with an iterative 2D phase correction method. The g-factor penalty of the proposed 2D Nyquist ghost correction method associated with 2D phase error was also evaluated. The feasibility of the proposed method was evaluated in diffusion MRI and multi-echo fMRI where quantitative biomarkers with high quality are desired.

Results: The proposed method successfully suppressed the ghost artifacts for the multi-shot interleaved EPI data acquired with different multi-shot factors, 2D and 3D multi-band acquisitions, zoomed-FOV, or reduced-FOV. Compared with the iterative method, our proposed method showed lower GSR and comparable SNR performance. Through g-factor penalty simulation, the proposed method showed less than 9% of overall SNR loss associated with a maximum y-linear phase error of $\pi$. The residual aliasing artifact was effectively eliminated in the quantitative biomarkers (ADC, FA and dynamic T2*) when applying the proposed method in diffusion imaging and multi-echo fMRI.

Conclusion: The proposed method can perform robust 2D Nyquist ghost correction for multi-band multi-shot interleaved EPI without reference scan, and thus can be a generalized 2D ghost correction method for multi-shot interleaved EPI based acquisitions and applications.

Introduction

Two-dimensional single-shot echo planar imaging (2D-ssEPI) is one of the fastest magnetic resonance imaging (MRI) techniques, and most preferred for diffusion MRI (dMRI) and functional MRI (fMRI) data acquisitions [1, 2]. In the past two decades, many clinical applications and neuroscience research have been proposed based on different MRI-biomarker measurements using dMRI and fMRI, such as the fractional anisotropy of white matter fiber [3] or the brain activation during specific tasks [4]. In addition, the apparent diffusion coefficient (ADC) measured by dMRI can also provide complementary diagnostic information for classifying the tissue types [5, 6] and therefore the measurement of this important biomarker has been integrated into different routine MRI exam protocols.

However, the measurements of dMRI-biomarkers and fMRI-biomarkers rely on the use of 2D-ssEPI technique for data acquisition, and 2D-ssEPI suffers from Nyquist ghost artifact caused by the gradient delay associated with alternating readout polarity [7]. It is because the 2D-ssEPI always uses the upper hardware limit of gradient coils, such as maximum slew rate and continuous fast switching, leading to prominent eddy current effect. This gradient delay usually leads to the misalignment between positive and negative echoes during MRI data sampling [8], resulting in Nyquist ghost artifact in the reconstructed images (as shown in Figure 1). Thus, to make 2D-ssEPI feasible for dMRI and fMRI data acquisitions, there is a need to reduce Nyquist ghost to insignificant level. A recent study showed that the insufficient suppression of Nyquist ghost artifact can resemble brain lesion during the measurement of dMRI-biomarkers [9]. In addition, 2D-ssEPI is also prone to insufficient geometric fidelity due to its intrinsic susceptibility to magnetic field inhomogeneity [10]. Although 2D-ssEPI shows low image quality and suffers from different EPI-related artifacts, its high acquisition efficiency makes the measurement of different MRI-biomarkers feasible in routine MRI exams (e.g., whole volume coverage with 2D slices acquired in a few seconds). It is because the measurement of MRI-biomarkers often requires multiple volume data with different encoding or dynamic scans with sufficient temporal resolution.

FIGURE 1

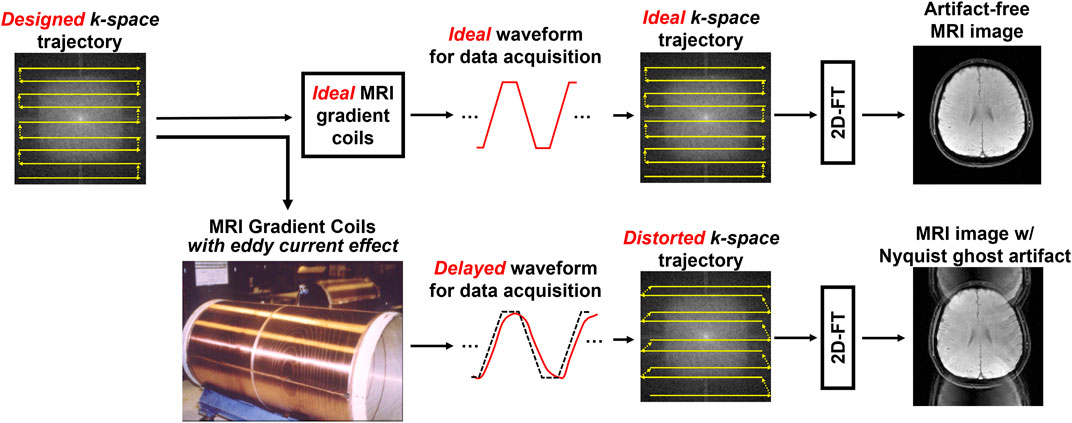
FIGURE 1. The demonstration of the cause of Nyquist ghost artifact in two-dimensional single-shot echo planar imaging (2D-ssEPI). The ideal gradient waveform for data sampling can produce an artifact-free MRI image with rapid back and forth traversal trajectory in k-space (upper). However, the hardware imperfection, such as eddy current effect of gradient coil, can lead to delayed gradient waveform, resulting in distorted k-space trajectory (lower). The misalignments of k-space lines cause the Nyquist ghosting artifact.

Since 2D-ssEPI is crucial for successful measurements of different MRI-biomarkers, numerous techniques have been proposed to improve the quality of 2D-ssEPI. Some of them have even become the commercialized pulse sequences on clinical MRI scanners for being used in routine MRI exam. For instance, 2D EPI can be combined with multi-shot acquisition (e.g., multi-shot interleaved EPI with multiplexed sensitivity encoding (MUSE) [11], readout segmented EPI [12], image reconstruction using image-space sampling functions (IRIS) [13], reduced field-of-view (FOV) with 2D spatially-selective radiofrequency (2D-RF) excitation [14] or multi-band imaging [15–17], for improving its geometric fidelity, spatial resolution and scan efficiency. In addition, combination of three-dimensional (3D) acquisition and multi-shot interleaved EPI can also enable ultra-high-resolution diffusion MRI at submillimeter voxel [8]. However, the Nyquist ghost correction for removing the artifact associated with the gradient coil delay still relies on a 1D reference scan based method existing in clinical MRI scanners [7]. Although 1D phase correction is often effective in removing Nyquist ghost for straight plane acquisition [18, 19], 2D phase correction is desired to achieve better suppression of Nyquist ghost, especially for the EPI acquisition with oblique plane [20]. Therefore, 2D reference scan methods have been proposed to estimate the 2D phase error between positive and negative echoes [20, 21]. Despite better efficacy of ghost correction, the inaccurate estimation of the 2D phase error around image edges and overfitting of background phase may cause residual artifacts after performing 2D phase correction for Nyquist ghost removal [20–22]. Moreover, the 2D reference scan sometimes requires longer acquisition time than 1D reference scan for collecting sufficient data. In the view of this shortcoming of 2D phase correction, the phase cycled reconstruction (PCR) has been proposed to iteratively derive the 2D phase error map without the need of any reference data [22]. However, it is time-consuming for estimating the non-linear phase error along the phase encoding direction through iteration and may not be preferable for the biomarker estimation in dynamic imaging (e.g. dynamic T2* quantification in fMRI) in practice.

Recently, several low-rank based methods have been proposed to perform 2D phase correction for fully-sampled or under-sampled EPI data, without reference data or extra scan [23, 24]. The application of low-rank matrix completion problem in Nyquist ghost removal has been extended to eliminate the Nyquist ghost present in multi-band EPI data, such as virtual coil simultaneous autocalibrating and k-space estimation (SAKE) method [25]. Despite the robustness in Nyquist ghost removal, the virtual coil SAKE requires the single-band EPI reference data for estimating the slice-dependent phase error.

In this study, we aimed to enable a robust self-referenced 2D Nyquist ghost correction method for multi-band multi-shot EPI acquisition that can be generalized to different applications, with higher number of shots (i.e., 16 shots) and less computational burden. To achieve this goal, first, alternating readout polarity was applied for the data acquisition of multi-band multi-shot interleaved EPI that only requires minimal modification for all clinical MRI scanners. Second, the k-space segments were divided into two under-sampled datasets with opposite readout polarity. Afterward, the 2D phase errors were extracted from two under-sampled datasets using MUSE, which was originally developed for eliminating inter-shot phase variations present in multi-shot diffusion data [11]. Finally, the image with Nyquist ghost removal was reconstructed from fully-sampled data using MUSE with 2D phase errors taken into account. The proposed method was tested on different MRI-biomarker measurements based on interleaved EPI acquisition.

Materials and methods

Data sampling

In conventional interleaved EPI, the polarity of readout gradient train remains same for all interleaves, as shown as in Figure 2A (left panel). Similar to single-shot EPI, the k-space data of 2N-shot interleaved EPI can be separated into two datasets acquired with either positive or negative echoes. Note that 2N describes that the number of shots for the interleaved EPI acquisition will be a multiple of 2. Subsequently, each separate dataset can be further split into 2N subsets of k-space data with the same under-sampling factor (R) of 4N (Figure 2B), and then reconstructed a fully-sampled image for measuring the 2D phase error. However, the reconstruction of under-sampled data may fail when the number of interleaves (i.e., 8 or 16 shots) increases. It is because N consecutive k-lines are missing for every N k-line in the separate dataset that can lead to lack of image energy around k-space center. To address this issue, alternating readout polarity is adopted to achieve a nearly uniform sampling of k-space between positive and negative echoes for interleaved EPI acquisition (right panel of Figures 2A,C).

FIGURE 2

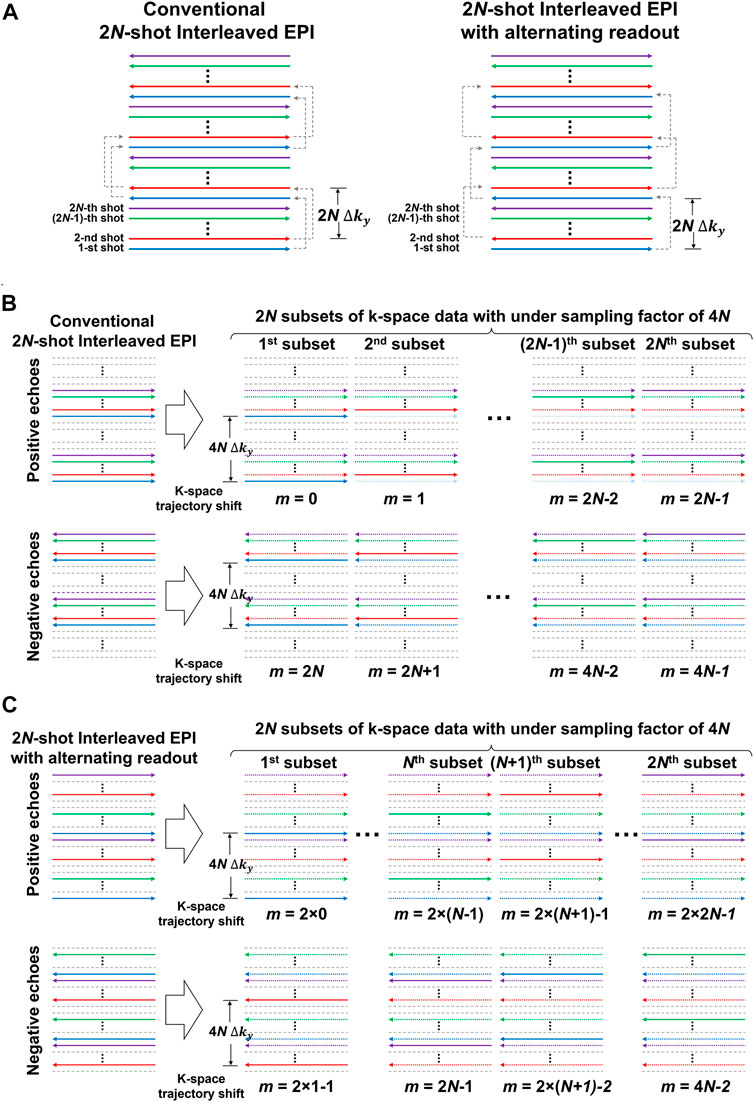
FIGURE 2. (A) The k-space trajectories of conventional multi-shot interleaved EPI (left) and multi-shot interleaved EPI with alternating readout (right). (B) k-space data of 2N-shot interleaved EPI can be separated into two datasets acquired with either positive or negative echoes according to the readout polarity. Each separate dataset can be further split into 2N subsets of k-space data with same under-sampling factor (R) as 4N, and then reconstructed to a fully-sampled image for measuring 2D phase error of Nyquist ghost. However, when the number of interleaves increases, the reconstruction of under-sampled data may fail for the separate dataset containing either positive or negative echoes. It is because N consecutive k-lines are missing for every N k-line in the separate dataset that can lead to lack of image energy around k-space center. (C) Alternating readout polarity during the acquisition of interleaves is adopted to achieve a nearly uniform sampling of k-space between positive and negative echoes, thereby improving the conditioning when reconstructing under-sampled data. For (A–C), the trajectories with the same color represent the data acquired from the same shot.

2D phase error estimation

The two separate datasets of 2N-shot interleaved EPI acquired with alternating readout each consist of 2N subsets of k-space data with identical under-sampling factor of 4N (Figure 2C) but at different shifts (m) of k-space trajectory along phase encoding (k_y), resulting in a point-spread-function (PSF) for each subset of k-space data as below:

$PSF\left(x,y\right)={\displaystyle \sum }_{n=-4N/2}^{4N/2-1}\delta \left(x,y-n\frac{FO{V}_y}{4N}\right)e^{\frac{i2\pi \cdot n\cdot m}{4N}}(1)$

For a 2D imaging object $o\left(x,y\right)$ acquired from a γ-channel coil $C_{\gamma }\left(x,y\right)$ with above sampling trajectory of each subset of k-space data, the aliased image $I_{\gamma }\left(x,y\right)$ directly Fourier-transformed from γ-th channel is given by:

$\begin{array}{ll}\hfill I_{\gamma }\left(x,y\right)& =PSF\left(x,y\right)\ast \left[C_{\gamma }\left(x,y\right)\cdot o\left(x,y\right)\right]={\displaystyle \sum }_{n=-4N/2}^{4N/2-1}\left[\left(C_{\gamma }\left(x,y-n\frac{FO{V}_y}{4N}\right)e^{\frac{i2\pi \cdot n\cdot m}{4N}}\right)\cdot o\left(x,y-n\frac{FO{V}_y}{4N}\right)\right]\hfill \\ \hfill & ={\displaystyle \sum }_{n=-4N/2}^{4N/2-1}\left[{\stackrel{\sim }{C}}_{\gamma }\left(4N,n,m\right)\cdot o\left(x,y-n\frac{FO{V}_y}{4N}\right)\right]\hfill \end{array}(2)$

where ${\stackrel{\sim }{C}}_{\gamma }\left(4N,n,m\right)$ is the effective coil sensitivity profile incorporated with an addition phase term (i.e., $e^{\frac{i2\pi \cdot n\cdot m}{4N}}$) caused by k-space trajectory shift (m). According to Eq. 2, the multi-channel aliased images generated from kth subset of multi-channel k-space data with either positive echoes $\left({\mathbf{I}}_{\mathbf{p},k}\right.$) or negative $\left({\mathbf{I}}_{\mathbf{n},k}\right.$) echoes can be concatenated into a single matrix as below:

$\left[\begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{p},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{p},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},2\mathbf{N}}\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=0\right)\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2\left(N-1\right)\right)\end{array}\\ \begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=2N+1\right)\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2\cdot 2N-1\right)\end{array}\end{array}\right]{\mathbf{O}}_{\mathbf{p}}(3)$

and

$\left[\begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{n},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{n},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},2\mathbf{N}}\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=1\right)\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2N-1\right)\end{array}\\ \begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=2N\right)\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=4N-2\right)\end{array}\end{array}\right]{\mathbf{O}}_{\mathbf{n}}(4)$

where $o_p\left(x,y\right)$ in Eq. 3 and $o_n\left(x,y\right)$ in Eq. 4 are the imaging object $o\left(x,y\right)$ fully-sampled with only positive and negative echoes in k-space with additional 2D phase errors ${\Psi }_p\left(x,y\right)$ and ${\Psi }_n\left(x,y\right)$, respectively. Eqs 3, 4 are also the short matrix forms of MUSE reconstruction with an effective under-sampling factor of 2. By solving Eqs 3, 4, the fully-sampled images for positive echoes $o_p\left(x,y\right)$ and negative echoes $o_n\left(x,y\right)$ are respectively used to measure the 2D phase errors ${\Psi }_p\left(x,y\right)$ and ${\Psi }_n\left(x,y\right)$. Afterward, the phase maps are smoothed by using a total variation filter for reducing the noise.

2D phase correction for 2N-shot interleaved EPI

Although the magnitudes of reconstructed images $o_p\left(x,y\right)$ and $o_n\left(x,y\right)$ can be directly averaged together to generate an image without Nyquist ghost, the undesired noise amplification due to reconstruction of under-sampling data (i.e, least-square inversion of Eqs 3, 4) may remain in the averaged image. To improve SNR performance, the estimated 2D phase errors ${\Psi }_p\left(x,y\right)$ and ${\Psi }_n\left(x,y\right)$ can be incorporated into Eqs 3, 4, and therefore all aliased images from positive and negative echoes (i.e., ${\mathbf{I}}_{\mathbf{p},k}$ and ${\mathbf{I}}_{\mathbf{n},k}$) can be concatenated to form a MUSE framework with full data sampling and 4N k-space segments as below:

$\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{p},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{p},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},2\mathbf{N}}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{n},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{n},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},2\mathbf{N}}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=0\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2\left(N-1\right)\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\end{array}\\ \begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=2N+1\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2\cdot 2N-1\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=1\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2N-1\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\end{array}\\ \begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=2N\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=4N-2\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\end{array}\end{array}\end{array}\right]\mathbf{O}(5)$

where $\otimes$ is the Kronecker product operator. Finally, the fully-sampled image $o\left(x,y\right)$ without Nyquist ghost can be obtained by solving Eq. 5.

2D phase correction for multi-band 2N-shot interleaved EPI

The estimation of 2D phase errors for interleaved EPI with multi-band imaging can be achieved by extending Eqs 3, 4 to form a multi-band MUSE framework [15, 16]. The below equations show an example of 2D phase error estimation for a 2-band 2N-shot interleaved EPI acquisition with alternating readout:

$\left[\begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{p},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{p},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},2\mathbf{N}}\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{l}\begin{array}{l}{\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=0\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=2\left(N-1\right)\right)\end{array}\\ \begin{array}{c}{\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=2N+1\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=2\cdot 2N-1\right)\end{array}\end{array}& \begin{array}{c}\begin{array}{c}{\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=0\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=2\left(N-1\right)\right)\end{array}\\ \begin{array}{c}{\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=2N+1\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=2\cdot 2N-1\right)\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{\mathbf{O}}_{1\mathbf{p}}\\ {\mathbf{O}}_{2\mathbf{p}}\end{array}\right](6)$

and

$\left[\begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{n},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{n},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},2\mathbf{N}}\end{array}\end{array}\right]=\left[\begin{array}{cc}\begin{array}{c}\begin{array}{c}{\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=1\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=2N-1\right)\end{array}\\ \begin{array}{c}{\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=2N\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_1\left(4N,m=4N-2\right)\end{array}\end{array}& \begin{array}{c}\begin{array}{c}{\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=1\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=2N-1\right)\end{array}\\ \begin{array}{c}{\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=2N\right)\\ ⋮\\ {\stackrel{\sim }{\mathbf{C}}}_2\left(4N,m=4N-2\right)\end{array}\end{array}\end{array}\right]\left[\begin{array}{c}{\mathbf{O}}_{1\mathbf{n}}\\ {\mathbf{O}}_{2\mathbf{n}}\end{array}\right](7)$

where $o_1\left(x,y\right)$ and $o_2\left(x,y\right)$ are the fully-sampled images at two different slice locations with corresponding coil sensitivity profiles as $C_1\left(x,y\right)$ and $C_2\left(x,y\right)$, respectively. By solving Eqs 6, 7, four 2D phase error maps can be estimated for the image data acquired with positive echo (${\Psi }_{1p}\left(x,y\right)$ and ${\Psi }_{2p}\left(x,y\right)$) and negative echoes (${\Psi }_{1n}\left(x,y\right)$ and ${\Psi }_{2n}\left(x,y\right)$) from two different slice locations. Similar to single-band case, the separation of two overlapped slices with Nyquist ghost correction can be simultaneously achieved by incorporating 2D phase error maps into Eqs 6, 7 and then reconstructed with multi-band MUSE framework [15, 16].

Inter-shot phase correction for diffusion MRI

For diffusion MRI, the inter-shot phase variations need to be considered and there is an assumption that the inter-shot phase variations are negligible when the diffusion gradient is off (i.e., acquisition of T2-weighted image with b-value = 0 s/mm²). Then both phase errors (${\mathbf{\Psi }}_{\mathbf{p}}$ and ${\mathbf{\Psi }}_{\mathbf{n}}$) resulting in EPI Nyquist ghosting and inter-shot phase variations (${\mathit{\theta }}_{\mathit{s}}$) can be corrected with the following steps: Firstly, the phase errors (${\mathbf{\Psi }}_{\mathbf{p}}$ and ${\mathbf{\Psi }}_{\mathbf{n}}$) caused by the misalignments between positive and negative echoes are estimated from the T2-weighted image (b-value = 0 s/mm²). Subsequently, the phase errors derived from T2-weighted image are incorporated into the SENSE reconstruction for each individual segment (i.e., segment acquired from the same shot) using Eq. 5, and the segment-specific phase inconsistencies are calculated from the reconstructed images. Finally, the phase errors resulting in Nyquist ghosting and the inter-shot phase variations are incorporated into the standard MUSE to reconstruct the image from all k-space segments using Eq. 8 below:

$\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{p},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{p},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{p},2\mathbf{N}}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}{\mathbf{I}}_{\mathbf{n},1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},\mathbf{N}}\end{array}\\ \begin{array}{c}{\mathbf{I}}_{\mathbf{n},\mathbf{N}+1}\\ ⋮\\ {\mathbf{I}}_{\mathbf{n},2\mathbf{N}}\end{array}\end{array}\end{array}\right]=\left[\begin{array}{c}\begin{array}{c}\begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=0\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\otimes {\mathit{\theta }}_1\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2\left(N-1\right)\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\otimes {\mathit{\theta }}_{\mathit{N}}\end{array}\\ \begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=2N+1\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\otimes {\mathit{\theta }}_{\mathit{N}+1}\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2\cdot 2N-1\right)\otimes {\mathbf{\Psi }}_{\mathbf{p}}\otimes {\mathbf{\theta }}_{2\mathit{N}}\end{array}\end{array}\\ \begin{array}{c}\begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=1\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\otimes {\mathbf{\theta }}_1\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=2N-1\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\otimes {\mathbf{\theta }}_{\mathit{N}}\end{array}\\ \begin{array}{c}\stackrel{\sim }{\mathbf{C}}\left(4N,m=2N\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\otimes {\mathbf{\theta }}_{\mathit{N}+1}\\ ⋮\\ \stackrel{\sim }{\mathbf{C}}\left(4N,m=4N-2\right)\otimes {\mathbf{\Psi }}_{\mathbf{n}}\otimes {\mathbf{\theta }}_{2\mathit{N}}\end{array}\end{array}\end{array}\right]\mathbf{O}(8)$

Where ${\mathit{\theta }}_{\mathit{s}}$ represent the inter-shot phase variations, the subscript $s$ denotes the sth shot for the data acquisition of sth k-space segment (i.e., s ranging from 1 to 2N).

Influence of 2D phase error

It can be seen from Eq. 5 that the 2D phase errors of positive and negative echoes can contribute to encoding power because they are included in the encoding matrix. The 2D phase correction with MUSE framework is a line-by-line reconstruction process. Therefore, the x component of 2D phase error acts as a constant phase coefficient across all aliased pixels, and only the y-component of 2D phase error can alter the encoding power. The reconstruction performance of the proposed method was evaluated by quantifying g-factor penalty, and the 2D linear phase profile was considered as the representative 2D phase error associated with oblique EPI acquisition. A multi-channel image acquired from a cylindrical water phantom with nearly tight FOV was used for estimating the 1/g-factor maps under different simulated y-linear phase errors from 0 to π with an increment of 0.1π (corresponding to the relative $k_y$ shifts between positive and negative echoes from 0 to 0.5 $\Delta k_y$). A region-of-interest (ROI) covering the entire area of the phantom was used to measure the 1/g-factor for different y-linear phase errors, and then compared with box plots. The g-factor simulation was designed to estimate the impact of phase errors on the g-factor penalty when using the proposed k-space sampling pattern and MUSE reconstruction for the Nyquist ghost correction. The linear phase error was applied in image space, and then the image was transformed to k-space using 2D inverse Fourier transform. The positive and negative echoes were respectively selected from the original data and the data with simulated linear phase error according to the proposed sampling trajectory. In this case, the phase error ($\varphi$) was incorporated into the reconstruction matrix of MUSE (S), and the g-factor map was calculated pixel-by-pixel using the following formula [26]:

$g_{\rho }=\sqrt{{\left[{\left(S^H{\mathrm{\Psi }}^{-1}S\right)}^{-1}\right]}_{\rho ,\rho }{\left(S^H{\mathrm{\Psi }}^{-1}S\right)}_{\rho ,\rho }}(9)$

and

$S_{\gamma ,\rho }=C_{\gamma ,\rho }\cdot {\varphi }_{\rho }(10)$

Where the superscript H indicates the transposed complex conjugate, $\Psi$ is the receiver noise matrix. $S_{\gamma ,\rho }$ is the element of the encoding matrix S. The subscripts $\gamma ,\rho$ count the coils and super-imposed pixels. $C_{\gamma ,\rho }$ is the spatial sensitivity of γ-th coil at the position of pixel $\rho$. ${\varphi }_{\rho }$ denotes the phase term at the position of pixel $\rho$.

In vivo MRI experiments

The data were acquired from two healthy volunteers. One volunteer underwent the scan using a 1.5T MRI (HDxt, GE Healthcare, Waukesha, United States ) with an 8-channel head coil, while another using a 3.0T MRI (Achieva, Philips Healthcare, Best, Netherlands) with a 32-channel head coil. All subjects were requested to keep their heads with an in-plane rotation (about 20°) during the entire scan. The oblique axial plane was prescribed for all data acquisitions, and it was rotated along the slice-selection axis to align the centerline of FOV with the midline of the brain.

Two-dimensional conventional interleaved EPI and interleaved EPI with alternating readout were used to acquire 4-shot, 8-shot, and 16-shot gradient-echo EPI (GE-EPI) data with either single-band or 2-band acquisition. The imaging parameters included the following: TE/TR = 24/2000 ms; matrix size = 128 × 128; FOV = 240 × 240 mm²; slice thickness = 5 mm; number of slices = 20. In addition, the 2D-RF excitation was combined with either conventional 4-shot interleaved EPI or 4-shot interleaved EPI with alternating readout to acquire 2D zoomed (matrix size = 96 × 96; FOV = 140 × 140 mm²) and 2D reduced-FOV (matrix size = 128 × 48; FOV = 240 × 60 mm²) EPI data. In addition, a 3D 2-band 8-shot interleaved EPI with alternating readout was combined with CAIPIRINHA [16, 27] to acquire 3D multi-band EPI data with following imaging parameters: in-plane matrix = 128 × 128; FOV = 240 × 240 mm²; slab thickness = 12 mm; number of kz = 12.

2D self-referenced nyquist ghost correction for diffusion MRI

Two sets of DWI/DTI data were acquired from a healthy subject using a 2D 4-shot interleaved EPI sequence with or without alternating readout polarity. The data were collected with in-plane rotation using a 12-channel coil head coil on a 1.5T GE scanner (Artist, GE Healthcare), with the following parameters: FOV = 24 cm, matrix size = 192 $\times$ 192, b = 1000 s/mm² with 3 orthogonal diffusion directions for DWI and 11 diffusion directions for DTI, number of slices = 20, slice thickness = 5 mm, TR/TE = 4,000/78 ms, number of overscans for partial Fourier = 16. The ADC and fractional anisotropy (FA) maps were respectively calculated from DWI and DTI data for quantitative evaluation.

2D self-referenced nyquist ghost correction for multi-echo fMRI

The feasibility of the proposed 2D Nyquist ghost correction for dynamic quantitative imaging was also tested for a 2D multi-echo fMRI acquisition [28] which aimed to obtain dynamic T2* quantification in a resting-state fMRI experiment using 4-shot EPI with two different image resolutions. The data were acquired from a healthy volunteer using a 48-channel phase-array head receiver coil on a 3T GE scanner (Signa, GE healthcare). The imaging parameters were as follows for routine and high-resolution acquisition: TR = 2000 ms, matrix size = 64 × 64/96 × 96, number of slices = 24/27, FOV = 24.3/24.0 cm, slice thickness = 3.8/3.5 mm, voxel size = 3.8 × 3.8×3.8/2.5 × 2.5 × 3.5 mm³, number of echoes = 4, TE₁ = 10.1/13.2 ms, delta TE = 8.2/14.5 ms. The total number of volumes for each dataset is 80. The first and last volumes were discarded to ensure magnetization stabilization. For each TR, the image was generated from the data acquired at different TEs using T2*-weighted echo combination method [29]. Signal-to-fluctuation-noise ratio (SFNR) was calculated using the signal image and the temporal fluctuation noise image for the evaluation of temporal stability [30].

Nyquist ghost correction and quantitative evaluation

The proposed self-reference 2D Nyquist ghost correction method was performed for all data acquired using either conventional interleaved EPI or interleaved EPI with alternating readout. For the 3D multi-band EPI data, the 2D phase errors were estimated from the central kz plane (i.e., kz = 0), and subsequently corrected for each kz plane data with simultaneous separation of two overlapped slices. In addition, an iterative reference-free 2D phase correction method, namely PCR [22], was also applied to the data acquired with 2D single-band conventional interleaved EPI for comparing the performance of 2D Nyquist ghost correction. The SNR and ghost-to-signal ratio (GSR) were measured from 10 representative slices of 2D single-band data produced by either conventional interleaved EPI with PCR or interleaved EPI with alternating readout and MUSE reconstruction. SNR was calculated from the ratio of the mean signal of white matter to the standard deviation of background signal. GSR was calculated from the ratio of the mean signal of background ghost to the mean signal of brain center. The ROI selection for ghost and noise measurements is the same as that mentioned in (22) for each slice. The significant differences of SNR and GSR measurements were assessed with two-sample t test, and the p-value less than 0.05 were considered statistically significant.

Results

Figure 3A shows six representative 1/g-factor maps corresponding to relative 0 to 0.5 $\Delta k_y$ shifts (with increment of 0.05 $\Delta k_y$) between positive and negative echoes for the reconstruction performance of proposed 2D Nyquist ghost correction method. Figure 3B shows the box plot of 1/g-factors measured from an ROI covering entire area of the phantom for different y-linear phase errors (from 0 to π with an increment of 0.1π). The higher g-factor penalty is associated with the increase of the $\Delta k_y$ shifts.

FIGURE 3

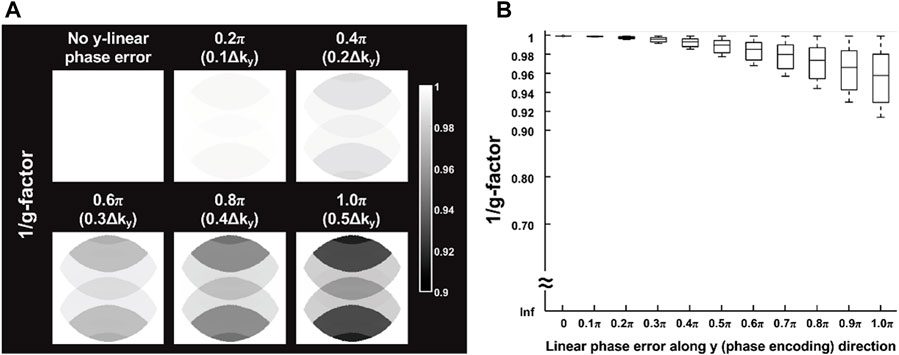
FIGURE 3. (A) Simulation results of six representative 1/g-factor maps corresponding to relative 0 to 0.5 $\Delta k_y$ shifts (with increment of 0.05 $\Delta k_y$) between positive and negative echoes for the reconstruction performance of proposed 2D Nyquist ghost correction method. (B) The box plot of the measured 1/g-factor maps from an ROI covering entire area of the phantom for different linear phase errors along PE direction (from 0 to π with an increment of 0.1π). The worst case reveals a mean SNR loss less than 5% and maximum SNR loss less than 10% for certain pixels. Nevertheless, the y-linear phase error is often less than π (e.g., 0.5π maximum) and the overall SNR loss is less than 3% for the proposed correction method. Without the presence of y-linear phase error, the proposed correction method will not cause any SNR loss and it is still robust for correcting the phase error along x (Figure 3A). Therefore, the proposed method can be an alternative for enabling self-referenced 2D Nyquist ghost correction with only negligible loss of SNR associated with its reconstruction algorithm.

Figure 4 shows 2D single-band multi-shot GE-EPI images produced from conventional interleaved EPI with PCR, conventional interleaved EPI with MUSE, and interleaved EPI with alternating readout and MUSE. When the number of shots exceeded four for conventional interleaved EPI, the 2D phase errors could not be measured and corrected with MUSE (Figure 4B). With the implementation of reconstruction program using Matlab, the data processing time of a single slice for PCR and our proposed method is 22.5 s and 3.1 s, respectively.

FIGURE 4

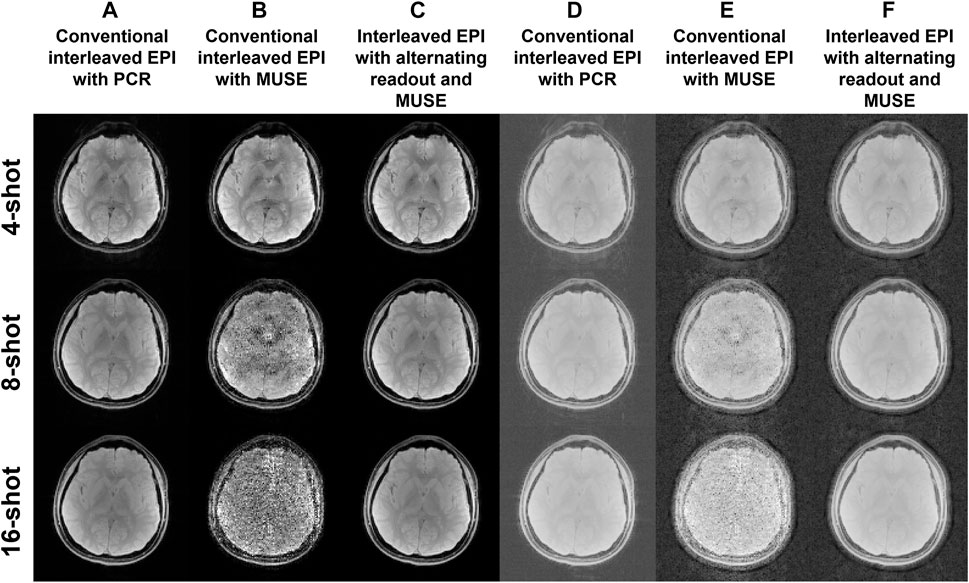
FIGURE 4. Two-dimensional single-band multi-shot GE-EPI images produced from (A) conventional interleaved EPI with PCR, (B) conventional interleaved EPI with MUSE reconstruction, and (C) interleaved EPI with alternating readout and MUSE reconstruction. (D–F) The reconstructed images corresponding to (A–C) are scaled with a factor of power of 0.2 for showing the background signal intensity.

Figures 5A,B show the bar plots of SNR and GSR measurements from 2D single-band multi-shot GE-EPI images produced from conventional interleaved EPI with PCR, and interleaved EPI with alternating readout and MUSE. Compared to conventional interleaved EPI with PCR, the proposed method shows comparable SNR performance (statistically insignificant) and significantly lower GSR (all p-values <0.05).

FIGURE 5

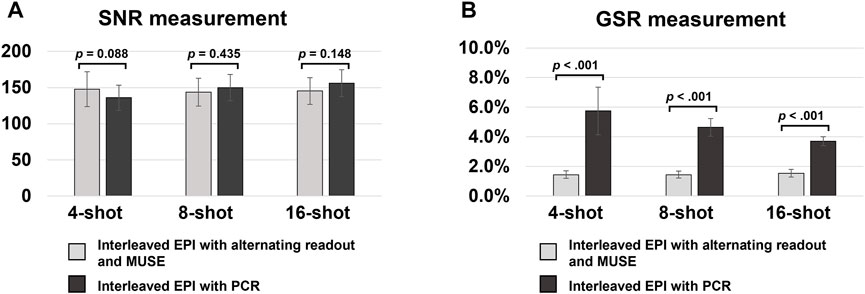
FIGURE 5. (A,B) show the bar plots of SNR and GSR measurements from 2D single-band multi-shot GE-EPI images produced from conventional interleaved EPI with PCR, and interleaved EPI with alternating readout and MUSE reconstruction. Compared to conventional interleaved EPI with PCR, the proposed method shows comparable SNR performance (statistically insignificant) and significantly lower GSR (all p-value <0.05). It demonstrated that the proposed method can effectively suppress the Nyquist ghost artifact for single-band multi-shot GE-EPI with higher number of shots (i.e., 8 or 16 shots).

Figure 6 shows 2D multi-band multi-shot GE-EPI images produced from MUSE reconstruction of the data acquired using either conventional interleaved EPI (Figure 6A) or interleaved EPI with alternating readout (Figure 6B). Only interleaved EPI with alternating readout and MUSE successfully performed 2D Nyquist ghost correction for the 2-band GE-EPI acquired with different number of shots (i.e., 4, 8, and 16 shots).

FIGURE 6

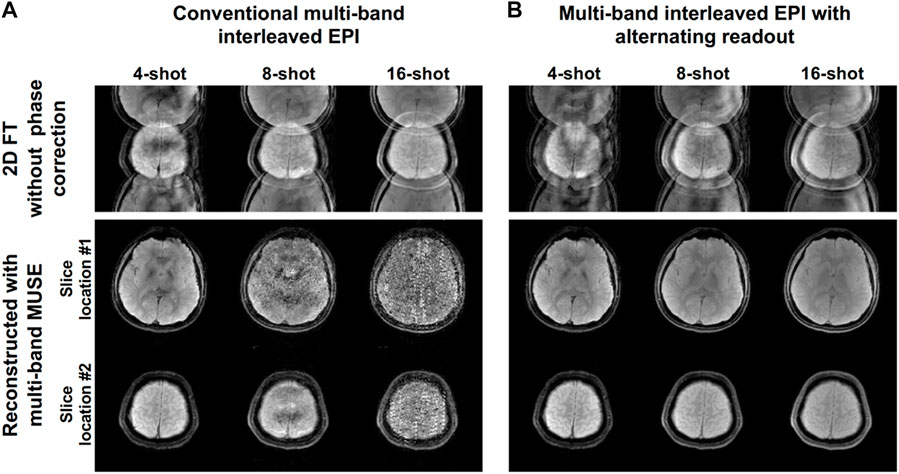
FIGURE 6. Two-dimensional multi-band multi-shot GE-EPI images produced from MUSE reconstruction of the data acquired using either (A) conventional interleaved EPI or (B) interleaved EPI with alternating readout. Only interleaved EPI with alternating readout and MUSE reconstruction successfully performed 2D Nyquist ghost correction for the 2-band GE-EPI acquired with different number of shots (i.e., 4, 8, and 16 shots). This experiment demonstrated that the proposed method can simultaneously perform data reconstruction of multi-band multi-shot GE-EPI (i.e., separation of two overlapped slices) and 2D Nyquist ghost correction with considering slice-dependent phase errors.

Figures 7A,B show zoomed EPI and reduced-FOV EPI images produced from MUSE reconstruction of the data acquired using either conventional 4-shot interleaved EPI or 4-shot interleaved EPI with alternating readout. Compared to the conventional 4-shot interleaved EPI, the alternating readout in 4-shot interleaved EPI makes the proposed correction method robust for 2D Nyquist correction in the data acquired with tight FOV. Figure 7C shows a 3D multi-band EPI dataset acquired using 3D 2-band 8-shot interleaved EPI with alternating readout and multi-band MUSE. The encoded slices from two different excited slab locations were successfully separated with simultaneous 2D Nyquist ghost correction.

FIGURE 7

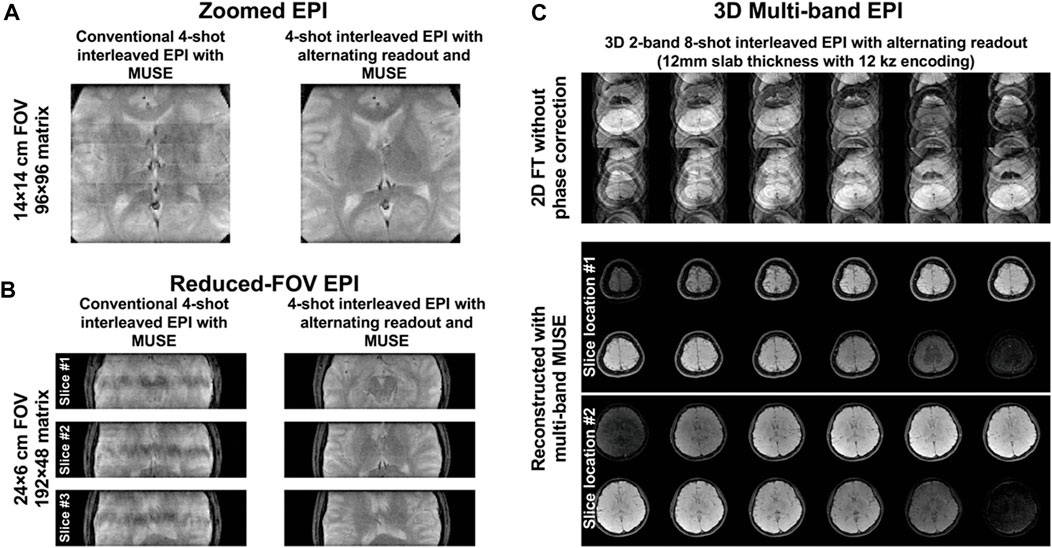
FIGURE 7. (A) Zoomed EPI and (B) reduced-FOV EPI images produced from MUSE reconstruction of the data acquired using either conventional 4-shot interleaved EPI or 4-shot interleaved EPI with alternating readout. The proposed method with alternating readout can successfully perform 2D Nyquist ghost correction for the data acquired with very tight FOV. (C) 3D multi-band EPI dataset acquired using 3D 2-band 8-shot interleaved EPI with alternating readout and reconstructed with multi-band MUSE framework. The encoded slices from two different excited slab locations were successfully separated with simultaneous 2D Nyquist ghost correction. It demonstrated that the proposed method can also be extended to deal with the Nyquist ghost artifacts present in 3D multi-band multi-shot EPI, proving its potential in generalization.

Figure 8 shows the comparison results between the conventional interleaved EPI with PCR and the proposed method where the alternating readout polarity and MUSE-based Nyquist ghost correction are combined. The proposed method can effectively remove the Nyquist ghost and provide the T2-weighted images as well as DW images with superior image quality. The ADC map and FA map calculated from the images obtained by our proposed method are free from the residual aliasing artifact compared to PCR.

FIGURE 8

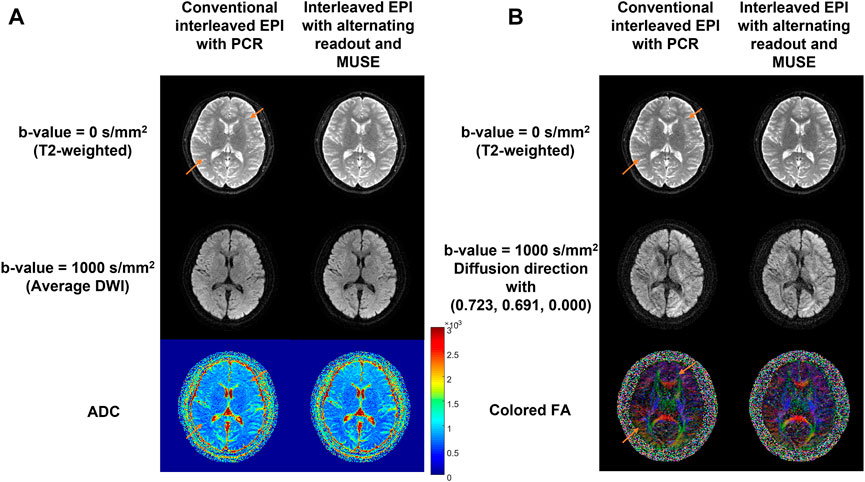
FIGURE 8. Comparison between the conventional 4-shot interleaved EPI with PCR and the proposed method in diffusion imaging. Left panel (A) shows the DWI results and right panel (B) shows the DTI results. The reconstructed T2-weighted images (top row), average DW images (A)/DW images with a representative diffusion direction (B) at b-value = 1000 s/mm² (middle row) and ADC (A) /FA (B) maps (bottom row) from two reconstruction methods are shown. The residual aliasing artifacts are marked using orange arrows. This in-vivo test demonstrated that the proposed method can completely eliminate the residual Nyquist ghost artifact, and therefore enable high-quality mapping of MRI biomarkers using multi-shot interleaved EPI.

Figures 9A,B respectively show the T2* maps at a single time point of multi-echo 4-shot fMRI data, and the SFNR maps of a representative slice with the average SFNR value at the bottom, for two different spatial resolutions. At the resolution of 64 $\times$ 64, the SFNR value is 53.5 using PCR for Nyquist ghost correction, while the proposed 2D Nyquist ghost correction can achieve a higher SFNR of 109.7. At the resolution of 96 $\times$ 96, the SFNR increase is up to 91.7% using the proposed method (65.2) for 2D Nyquist ghost correction compared to PCR (34.0).

FIGURE 9

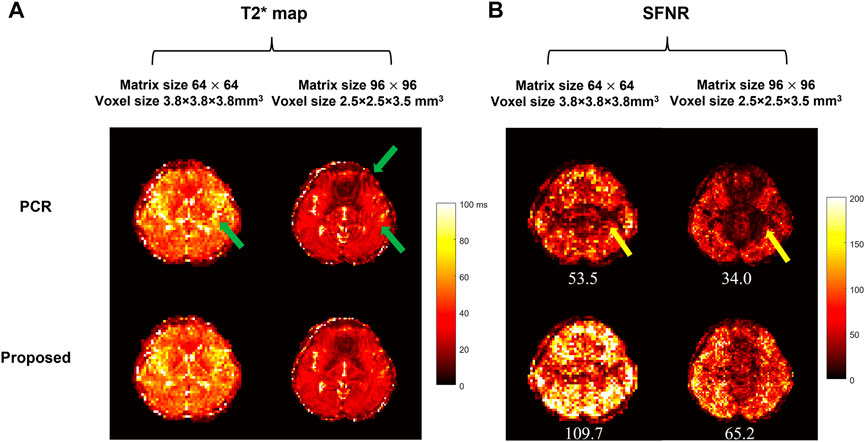
FIGURE 9. Comparison between the conventional interleaved EPI with PCR and the proposed method in multi-echo 4-shot fMRI with two resolutions (64 × 64/96 × 96) and voxel sizes (3.8 × 3.8 × 3.8/2.5 × 2.5 × 3.5 mm³). (A) shows the dynamic T2* maps and (B) shows the SFNR maps of a representative image. The average SFNR value is shown at the bottom of each corresponding SFNR map. The residual aliasing artifact resulting from insufficient suppression of Nyquist ghost are marked in the dynamic T2* map [green arrows in (A)] and SFNR map [yellow arrows in (B)] respectively. The proposed method can enable dynamic Nyquist ghost correction for time-series fMRI data without the need of additional internal reference scan. The improved stability of time-course fMRI signal can allow to better detect the small signal change (e.g., 5%–7% signal change [34]) due to brain activation.

Discussion and conclusion

A robust and generalized self-referenced 2D Nyquist ghost correction method has been proposed for multi-shot EPI in this study to obtain more reliable MRI biomarker measurements from images with reduced Nyquist ghost artifacts. The MUSE reconstruction was originally proposed for eliminating the inter-shot phase variations between different k-space segments of diffusion-weighted interleaved EPI. Combining interleaved EPI with alternating readout and MUSE reconstruction extends the MUSE framework to eliminate the phase errors between positive and negative readouts that can successfully enable self-referenced 2D Nyquist ghost correction for interleaved EPI acquisition with either single-band or multi-band imaging. The proposed correction method is capable of correcting non-linear phase errors and slice-dependent phase errors because of the direct estimation of 2D phase errors from the imaging data. Even when high number of shots was used for interleaved EPI acquisition (i.e., 16 shots), the proposed correction method could still effectively eliminate the Nyquist ghost and perform image reconstruction for both single-band and multi-band acquisition (Figure 4C, Figure 6B), rendering the robustness in Nyquist ghost correction for different number of shots. It is because the use of alternating readout in interleaved EPI acquisition can provide a nearly uniform distribution of k-space sampling between positive and negative echoes (Figure 2C), and therefore improve the conditioning for measuring 2D phase errors from the under-sampled data. In contrast, while proposed correction method was still feasible in conventional interleaved EPI with lower number of shots (i.e., ≤4 shots), the increased number of shots led to failure of Nyquist ghost correction due to unsuccessful measurement of 2D phase errors (Figure 4B, Figure 6A). Furthermore, the proposed correction method can be applied for correcting the 2D Nyquist ghost present in 3D multi-band interleaved EPI data acquired with alternating readout and multi-band MUSE framework (Figure 7C). For 3D multi-band diffusion-weighted interleaved EPI acquired with alternating readout, the inter-shot phase variations (${\theta }_s$) shown in Eq. 8 can also be incorporated into multi-band MUSE framework.

Correcting Nyquist ghost artifacts in Zoomed EPI and Reduced-FOV EPI are challenging for PCR method because the tight FOV does not provide sufficient background region for searching the correction parameters during the iteration [22]. A correction method based on double-FOV reference scan has been reported to enable 2D Nyquist ghost correction for single-shot EPI with tight FOV. Our in-vivo experiment demonstrates that the 2D Nyquist ghost correction for the data acquired with tight FOV is feasible by using a 4-shot interleaved EPI with alternating readout and MUSE reconstruction (Figures 7A,B). Although proposed correction method successfully eliminated the Nyquist ghost for conventional 4-shot interleaved EPI with regular FOV (Figure 4B), it could not accurately measure the 2D phase errors from the data acquired with tight FOV due to worse conditioning (Figures 7A,B). Hence, employing alternating readout in multi-shot interleaved makes the proposed correction method robust for 2D Nyquist correction in the data acquired with tight FOV.

The quantitative assessment of the proposed self-reference 2D Nyquist ghost correction method shows significantly better suppression of background ghost (Figure 5B), and comparable SNR performance to conventional interleaved EPI with PCR (Figure 5A). Although there is no statistical difference in the comparison of SNR performance, the variations of SNR measurement can be observed across different number of shots between proposed method and PCR. One possible underlying cause is that the regional SNR measurement might only reflect the SNR performance of a particular ROI, rather than an overall assessment. Thus, the g-factor penalty associated with y-linear phase error was also assessed for proposed Nyquist correction method by considering a maximum y-linear phase error of π (corresponding to 0.5 $∆k_y$ shift between positive and negative echoes). The worst case reveals a mean SNR loss less than 5% and maximum SNR loss less than 10% for certain pixels (Figure 3). Nevertheless, the y-linear phase error is often less than π (e.g., 0.5π maximum) and the overall SNR loss is less than 3% for the proposed correction method (Figure 3B). Without the presence of y-linear phase error, the proposed correction method will not cause any SNR loss and it is still robust for correcting the phase error along x (Figure 3A).

The preliminary results show the feasibility of the proposed 2D self-reference Nyquist ghost correction method for different MRI-biomarker measurements using DWI, DTI or multi-echo fMRI. As shown in Figure 8, the insufficient suppression of Nyquist ghost degraded the image quality and thus provided the ADC map and colored FA map with residual aliasing artifacts, which may resemble brain lesions in patient cases as reported in a previous study [9]. In our previous study, the effective removal of 2D phase errors can improve the fidelity of ADC estimation in the patient cohort [9]. Hence, the proposed method shows superior performance in ghost correction compared to PCR and may provide more reliable quantitative diffusion measurements for diagnosis in clinical practice. For multi-echo fMRI application, the influence of residual aliasing artifacts can be effectively eliminated in dynamic T2* maps (Figure 9A) and the improved SFNR can be achieved by our proposed method (Figure 9B), demonstrating the robustness of the proposed method for Nyquist ghosting related to time-varying gradient delays in a long acquisition [31]. It has been reported that the increased residual Nyquist ghosting caused by subject movement, gradient heating, or the use of oblique planes [20, 32] may lead to false-positive activation in fMRI maps [18]. In a previous study, the dynamic slice-specific Nyquist ghosting correction in multi-band EPI is beneficial to BOLD activation maps [33]. Thus, our proposed method can enable dynamic Nyquist ghost correction for time-series data even using the oblique planes for acquisition and obtain reliable BOLD activation maps from improved stability of time-course fMRI signal with eliminated Nyquist ghosting. In addition, our proposed method has an advantage over the existing ghost artifact correction method [22] in terms of time efficiency, with no additional calibration data and less computational complexity. Therefore, the proposed method is an effective and generalized method for 2D Nyquist ghost correction and helpful to obtain more reliable MRI biomarkers (e.g., ADC, FA, and dynamic T2* maps).

There were two limitations in this study for the proposed correction method. First, the eddy current effect induced by gradient switching is assumed to remain the same across the acquisition of different shots and two different readout polarities. Thus, the application of proposed correction method for the time-series data acquisition with higher number of shots (e.g., 8 or 16 shots) may need to be further investigated its performance. Second, the sample size for SNR and GSR measurements is relatively small and the statistical results may not precisely reflect the performance of the proposed method in terms of SNR or artifact reduction. A larger cohort of patients is needed for further evaluating the reliability of MRI biomarker measurements benefiting from the effective artifact reduction of the proposed method.

In conclusion, the proposed correction method can perform robust 2D Nyquist ghost correction for multi-band interleaved EPI without the needs of reference scan and iterative calculation, as well as be a generalized 2D ghost correction method for different interleaved EPI based acquisitions and applications.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving human participants were reviewed and approved by Hong Kong Hospital Authority. The patients/participants provided their written informed consent to participate in this study.

Author contributions

All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Funding

The work was supported in part by the Research Grant Council (RGC) of Hong Kong (GRF 17121517, GRF 17106820, GRF 17125321, and ECS 24213522).

Conflict of interest

QC was empolyed by Philips Healthcare.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Baliyan V., Das C. J., Sharma R., Gupta A. K. Diffusion weighted imaging: Technique and applications. World J Radiol (2016) 8(9):785–98. doi:10.4329/wjr.v8.i9.785

PubMed Abstract | CrossRef Full Text | Google Scholar

2. Glover G. H. Overview of functional magnetic resonance imaging. Neurosurg Clin N Am (2011) 22(2):133–9. vii. doi:10.1016/j.nec.2010.11.001

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Dong Q., Welsh R. C., Chenevert T. L., Carlos R. C., Maly-Sundgren P., Gomez-Hassan D. M., et al. Clinical applications of diffusion tensor imaging. J Magn Reson Imaging (2004) 19(1):6–18. doi:10.1002/jmri.10424

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Biswal B., Zerrin Yetkin F., Haughton V. M., Hyde J. S. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn Reson Med (1995) 34(4):537–41. doi:10.1002/mrm.1910340409

PubMed Abstract | CrossRef Full Text | Google Scholar

5. Sener R. Diffusion MRI: Apparent diffusion coefficient (ADC) values in the normal brain and a classification of brain disorders based on ADC values. Comput Med Imaging graphics (2001) 25(4):299–326. doi:10.1016/s0895-6111(00)00083-5

PubMed Abstract | CrossRef Full Text | Google Scholar

6. Tsushima Y., Takahashi-Taketomi A., Endo K. Magnetic resonance (MR) differential diagnosis of breast tumors using apparent diffusion coefficient (ADC) on 1.5-T. J Magn Reson Imaging (2009) 30(2):249–55. doi:10.1002/jmri.21854

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Bruder H., Fischer H., Reinfelder H. E., Schmitt F. Image reconstruction for echo planar imaging with nonequidistant k-space sampling. Magn Reson Med (1992) 23(2):311–23. doi:10.1002/mrm.1910230211

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Chang H. C., Sundman M., Petit L., Guhaniyogi S., Chu M. L., Petty C., et al. Human brain diffusion tensor imaging at submillimeter isotropic resolution on a 3Tesla clinical MRI scanner. Neuroimage (2015) 118:667–75. doi:10.1016/j.neuroimage.2015.06.016

PubMed Abstract | CrossRef Full Text | Google Scholar

9. Liu X., Hui E. S., Chang H. C. Elimination of residual aliasing artifact that resembles brain lesion on multi-oblique diffusion-weighted echo-planar imaging with parallel imaging using virtual coil acquisition. J Magn Reson Imaging (2020) 51(5):1442–53. doi:10.1002/jmri.26966

PubMed Abstract | CrossRef Full Text | Google Scholar

10. Hennel F., Buehrer M., von Deuster C., Seuven A., Pruessmann K. P. SENSE reconstruction for multiband EPI including slice-dependent N/2 ghost correction. Magn Reson Med (2016) 76(3):873–9. doi:10.1002/mrm.25915

PubMed Abstract | CrossRef Full Text | Google Scholar

11. Chen N. K., Guidon A., Chang H. C., Song A. W. A robust multi-shot scan strategy for high-resolution diffusion weighted MRI enabled by multiplexed sensitivity-encoding (MUSE). Neuroimage (2013) 72:41–7. doi:10.1016/j.neuroimage.2013.01.038

PubMed Abstract | CrossRef Full Text | Google Scholar

12. Holdsworth S. J., Skare S., Newbould R. D., Guzmann R., Blevins N. H., Bammer R. Readout-segmented EPI for rapid high resolution diffusion imaging at 3T. Eur J Radiol (2008) 65(1):36–46. doi:10.1016/j.ejrad.2007.09.016

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Jeong H. K., Gore J. C., Anderson A. W. High-resolution human diffusion tensor imaging using 2-D navigated multishot SENSE EPI at 7 T. Magn Reson Med (2013) 69(3):793–802. doi:10.1002/mrm.24320

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Saritas E. U., Cunningham C. H., Lee J. H., Han E. T., Nishimura D. G. DWI of the spinal cord with reduced FOV single-shot EPI. Magn Reson Med (2008) 60(2):468–73. doi:10.1002/mrm.21640

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Chang H. C., Gaur P., Chou Y. H., Chu M. L., Chen N. K. Interleaved EPI based fMRI improved by multiplexed sensitivity encoding (MUSE) and simultaneous multi-band imaging. PLoS One (2014) 9(12):e116378. doi:10.1371/journal.pone.0116378

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Chang H. C., Guhaniyogi S., Chen N. K. Interleaved diffusion-weighted improved by adaptive partial-Fourier and multiband multiplexed sensitivity-encoding reconstruction. Magn Reson Med (2015) 73(5):1872–84. doi:10.1002/mrm.25318

PubMed Abstract | CrossRef Full Text | Google Scholar

17. Feinberg D. A., Setsompop K. Ultra-fast MRI of the human brain with simultaneous multi-slice imaging. J Magn Reson (2013) 229:90–100. doi:10.1016/j.jmr.2013.02.002

PubMed Abstract | CrossRef Full Text | Google Scholar

18. van der Zwaag W., Marques J. P., Lei H., Just N., Kober T., Gruetter R. Minimization of Nyquist ghosting for echo-planar imaging at ultra-high fields based on a "negative readout gradient" strategy. J Magn Reson Imaging (2009) 30(5):1171–8. doi:10.1002/jmri.21951

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Ahn C. B., Cho Z. H. A new phase correction method in NMR imaging based on autocorrelation and histogram analysis. IEEE Trans Med Imaging (1987) 6(1):32–6. doi:10.1109/tmi.1987.4307795

PubMed Abstract | CrossRef Full Text | Google Scholar

20. Chen N. K., Wyrwicz A. M. Removal of EPI Nyquist ghost artifacts with two-dimensional phase correction. Magn Reson Med (2004) 51(6):1247–53. doi:10.1002/mrm.20097

PubMed Abstract | CrossRef Full Text | Google Scholar

21. Xu D., King K. F., Zur Y., Hinks R. S. Robust 2D phase correction for echo planar imaging under a tight field-of-view. Magn Reson Med (2010) 64(6):1800–13. doi:10.1002/mrm.22577

PubMed Abstract | CrossRef Full Text | Google Scholar

22. Chen N. K., Avram A. V., Song A. W. Two-dimensional phase cycled reconstruction for inherent correction of echo-planar imaging Nyquist artifacts. Magn Reson Med (2011) 66(4):1057–66. doi:10.1002/mrm.22896

PubMed Abstract | CrossRef Full Text | Google Scholar

23. Lee J., Jin K. H., Ye J. C. Reference-free single-pass EPI Nyquist ghost correction using annihilating filter-based low rank Hankel matrix (ALOHA). Magn Reson Med (2016) 76(6):1775–89. doi:10.1002/mrm.26077

PubMed Abstract | CrossRef Full Text | Google Scholar

24. Lobos R. A., Javed A., Nayak K. S., Hoge W. S., Haldar J. P. Robust autocalibrated loraks for epi ghost correction. Proc IEEE Int Symp Biomed Imaging (2018) 2018:663–6. doi:10.1109/ISBI.2018.8363661

PubMed Abstract | CrossRef Full Text | Google Scholar

25. Lyu M., Barth M., Xie V. B., Liu Y., Ma X., Feng Y., et al. Robust SENSE reconstruction of simultaneous multislice EPI with low-rank enhanced coil sensitivity calibration and slice-dependent 2D Nyquist ghost correction. Magn Reson Med (2018) 80(4):1376–90. doi:10.1002/mrm.27120

PubMed Abstract | CrossRef Full Text | Google Scholar

26. Pruessmann K. P., Weiger M., Scheidegger M. B., Boesiger P. Sense: Sensitivity encoding for fast MRI. Magn Reson Med (1999) 42(5):952–62. doi:10.1002/(sici)1522-2594(199911)42:5<952:aid-mrm16>3.0.co;2-s

PubMed Abstract | CrossRef Full Text | Google Scholar

27. Breuer F. A., Blaimer M., Heidemann R. M., Mueller M. F., Griswold M. A., Jakob P. M. Controlled aliasing in parallel imaging results in higher acceleration (CAIPIRINHA) for multi-slice imaging. Magn Reson Med (2005) 53(3):684–91. doi:10.1002/mrm.20401

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Chen S., Chu M-L., Chan Q., Chen N-K, Juan C-J, Liang L., Chang H-C. Multi-echo multi-segment EPI based fMRI using sliding-window acquisition and multiplexed sensitivity encoding (MUSE). In: Proceedings of the 28th Annual Meeting & Exhibition of the International Society for Magnetic Resonance in Medicine (ISMRM) was a virtual conference, August 8–14, 2020. Concord, CA: International Society for Magnetic Resonance in Medicine (ISMRM) (2020).

Google Scholar

29. Posse S., Wiese S., Gembris D., Mathiak K., Kessler C., Grosse-Ruyken M. L., et al. Enhancement of BOLD-contrast sensitivity by single-shot multi-echo functional MR imaging. Magn Reson Med (1999) 42(1):87–97. doi:10.1002/(sici)1522-2594(199907)42:1<87:aid-mrm13>3.0.co;2-o

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Friedman L., Glover G. H. Report on a multicenter fMRI quality assurance protocol. J Magn Reson Imaging (2006) 23(6):827–39. doi:10.1002/jmri.20583

PubMed Abstract | CrossRef Full Text | Google Scholar

31. Hey S., Koonen J., Chen Z., Jvd B. Potential impact of time-varying gradient delays in the EPI train on nyquist ghost correction. In: International Society for Magnetic Resonance in Medicine (ISMRM); 20-26 April 2013; Utah, USA (2013).

Google Scholar

32. Zaitsev M., Akin B., LeVan P., Knowles B. R. Prospective motion correction in functional MRI. Neuroimage (2017) 154:33–42. doi:10.1016/j.neuroimage.2016.11.014

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Yarach U., Tung Y. H., Setsompop K., Chatnuntawech I., Yakupov R., Godenschweger F, et al. Dynamic 2D self-phase-map Nyquist ghost correction for simultaneous multi-slice echo planar imaging. Magn Reson Med (2018) 80(4):1577–87. doi:10.1002/mrm.27123

PubMed Abstract | CrossRef Full Text | Google Scholar

34. van der Zwaag W., Francis S., Head K., Peters A., Gowland P., Morris P., et al. fMRI at 1.5, 3 and 7 T: characterising BOLD signal changes. Neuroimage (2009) 47(4):1425–34. doi:10.1016/j.neuroimage.2009.05.015

PubMed Abstract | CrossRef Full Text | Google Scholar