- School of Science, East China Jiaotong University, Nanchang, China
In this paper, we study the finite-time synchronization problem of a Kuramoto-oscillator network with a pacemaker. By constructing a cyber-physical system (CPS), the finite-time phase agreement and frequency synchronization of the network are explored for identical and non-identical oscillators, respectively. According to the Lyapunov stability analysis, sufficient conditions are deduced for ensuring the phase agreement and frequency synchronization for arbitrary initial phases and/or frequencies under distributed strategies. Furthermore, the upper bound estimations of convergence time are obtained accordingly, which is related to the initial phases and/or frequencies of oscillators. Finally, numerical examples are presented to verify the effectiveness of the theoretical results.
1 Introduction
Synchronization of complex networks has been extensively investigated by researchers due to its numerous practical applications. As one of the most celebrated periodic-oscillator models, Kuramoto model [1] and its variations have been widely used for explaining various synchronization phenomena, and they have attracted considerable attention from researchers in diverse fields ranging from biology [2, 3], mathematics [4], physics [5, 6] and engineering [7–10]. In the past decade, many progresses concerning on the synchronization of Kuramoto-oscillator networks have been made by researchers in the control community [10–20], where synchronization criteria with respect to constraints on coupling strengths and initial phases have been developed. For example, in [10], the relationship between the algebraic connectivity of a connected Kuramoto-oscillator network and critical coupling was revealed. In [11], Chopra and Spong showed that initial relative phases should be confined to π/2 and a critical coupling strength should be satisfied, which guaranteed the frequency synchronization of an all-to-all connected Kuramoto network.
In [14, 15, 17, 20], researchers have taken the pacemaker (i.e. the so-called leader) into consideration, where synchronization criteria were related to not only the constraint on coupling strengths and initial phases, but also the selection of direct controlled oscillators. Since the interactions between oscillators are usually in the sinusoidal form of phase differences, the theoretical results mentioned above were based on the requirements of initial phases, and only local stability analyses were provided. Based on the framework of cyber-physical systems [21, 22], distributed linear controllers have been adopted to synchronize Kuramoto-oscillator networks in [23, 24], where the derived stability conditions were independent of the initial phases such that the global synchronization was achieved. In [24], sufficient criteria were established for the Kuramoto-oscillator network with a pacemaker under distributed linear control.
The results aforementioned merely focused on the asymptotical synchronization, which indicated that synchronization was realized when t → ∞. Recently, in [18, 19, 25–27], more researchers have focused on the finite-time synchronization of Kuramoto-oscillator networks, which is also of significance in practical applications. For example, power girds need to get rid of local power failures as soon as possible in order to avoid the cascading failure. In [27], Wu and Li investigated the finite-time and fixed-time synchronization of Kuramoto-oscillator networks by employing a novel multiplex control. However, the finite-time synchronization of Kuramoto-oscillator network in present of a pacemaker has not been investigated so far.
Inspired by the above literatures, it is worth investigating the finite-time synchronization of Kuramoto-oscillator network with a pacemaker. In this paper, we aim to explore finite-time synchronization criteria of such network by adopting distributed schemes based on CPS. The main contributions of this paper are summarized as follows: Firstly, effective criteria are established to deal with finite-time phase agreement and frequency synchronization for Kuramoto-oscillator network with a pacemaker, and the upper bound of synchronization time is also provided; Secondly, synchronization can be achieved for arbitrary initial phases, which only influence the upper bound of synchronization time; Finally, the requirement on the connectivity of physical system is relaxed, even if it is an unconnected network.
The remainder of this paper is organized as follows. In Section 2, the framework of CPS is constructed, which consists of the physical Kuramoto-oscillator network system and the cyber (controlling) system. Furthermore, two definitions and some necessary mathematical preliminaries are encompassed in Section 2. Finite-time phase agreement in an identical Kuramoto-oscillator network and frequency synchronization in a non-identical Kuramoto-oscillator network cover the heart body of Section 3 and Section 4, respectively. Section 5 presents the numerical simulation results, and Section 6 concludes the whole paper.
2 Model and preliminaries
In the framework of CPS, a Kuramoto-oscillator network consisting of N oscillators with control input u i can be described as
where
Assume that there is a pacemaker with dynamics
where θ 0 and ω 0 are the phase and natural frequency of the pacemaker, respectively.
In this paper, we concern phase agreement and frequency synchronization with respect to the pacemaker in finite time.
Definition 1. Network Eq. 1 with control input u i achieves (pacemaker-based) finite-time phase agreement, if there exists a settling time T > 0 depending on the initial states θ i (0) (i ∈ {0}⋃I), such that
and θ i − θ 0 ≡ 0 for t ≥ T.
Definition 2. Network Eq. 1 with control input u
i
achieves (pacemaker-based) finite-time frequency synchronization, if there exists a settling time T > 0 depending on the initial states
and
Lemma 1. [28] For an undirected graph
Lemma 2. [29] Consider the system of differential equation
where
If in addition
3 Finite-time phase agreement for identical Kuramoto oscillators
In this section, we first concentrate on the case of oscillators with identical natural frequency, i.e., ω i = ω 0, ∀i ∈ I. Thus, network Eq. 1 with control input u i becomes
For achieving finite-time phase agreement, a distributed control strategy is constructed as
where
By transforming θ i into ξ i , network Eq. 5 with distributed control strategy Eq. 6 becomes
Theorem 1. Network Eq. 1 with identical oscillator under distributed control strategy Eq. 6 achieves finite-time phase agreement with the settling time bounded by
if
where f
min = min{f
1, …, f
N
},
Proof 1. Consider the following Lyapunov functional candidate
The derivation of V 1 along trajectories Eq. 7 gives
According to < href="statement-Lemma_1">Lemma 1 and the fact
And,
Combining Eqs. 10–12, Eq. 9 yields
If
By < href="statement-Lemma_2">Lemma 2 and < href="statement-Definition_1">Definition 1 , network Eq. 1 with identical oscillator under distributed control strategy Eq. 6 achieves finite-time phase agreement with the settling time bounded by
This completes the proof.
Remark 1.
According to (8), we find that the upper bound of synchronization time is proportionate to initial state ‖ξ(0)‖, and is inversely proportional to f
min
. According to < href="statement-Theorem_1">Theorem 1
, it is sufficient to achieve finite-time phase agreement if
4 Finite-time frequency synchroniztion for non-identical Kuramoto oscillators
Now we further concentrate on the case of oscillators with non-identical natural frequencies, i.e., there exists some i ∈ I such that ω i ≠ ω 0. For achieving finite-time frequency synchronization, a distributed control strategy u i is designed as
where
Theorem 2. Network Eq. 1 with non-identical oscillators under distributed control strategy Eq. 13 achieves frequency synchronization with the settling time bounded by
if
where
Proof 2. By taking the derivation of Eq. 1 , we obtain
Consider the following Lyapunov functional candidate
The derivation of V 2 along trajectories Eq. 15 gives
According to < href="statement-Lemma_1">Lemma 1 and the fact
And,
Combining Eqs. 17–19, Eq. 16 yields
If
By < href="statement-Lemma_2">Lemma 2 and < href="statement-Definition_2">Definition 2 , network Eq. 1 with non-identical oscillators under distributed control strategy Eq. 13 achieves finite-time frequency synchronization with the settling time bounded by
This completes the proof.
Remark 2.
According to Eq. 14
, we find that the upper bound of synchronization time is proportionate to initial state
5 Numerical simulation
In this section, we assume networks associated with adjacency matrices A and B as shown in Figures 1A,B, respectively.
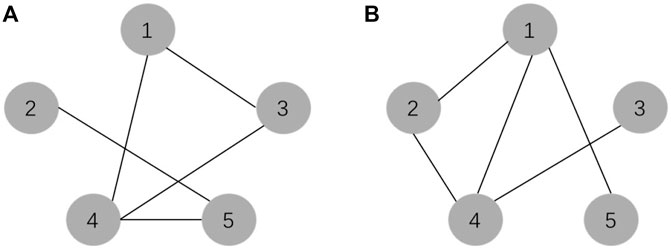
FIGURE 1. (A) Network associated with adjacency matrix A. (B) Network associated with adjacency matrix B.
We first verify < href="statement-Theorem_1">Theorem 1. Obviously,
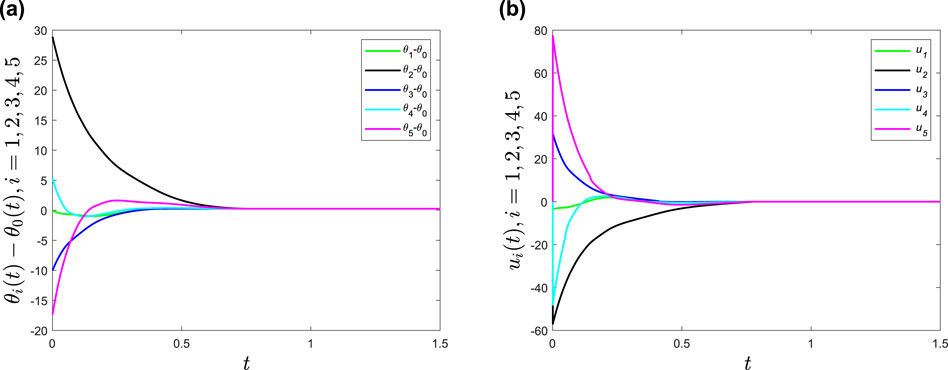
FIGURE 2. (A) Time evolutions of phase differences θ i − θ 0 (i = 1, 2, 3, 4, 5) under distributed control strategy Eq. 6. (B) Time evolutions of the distributed control strategy Eq. 6.
Secondly, we verify < href="statement-Theorem_2">Theorem 2. Obviously,
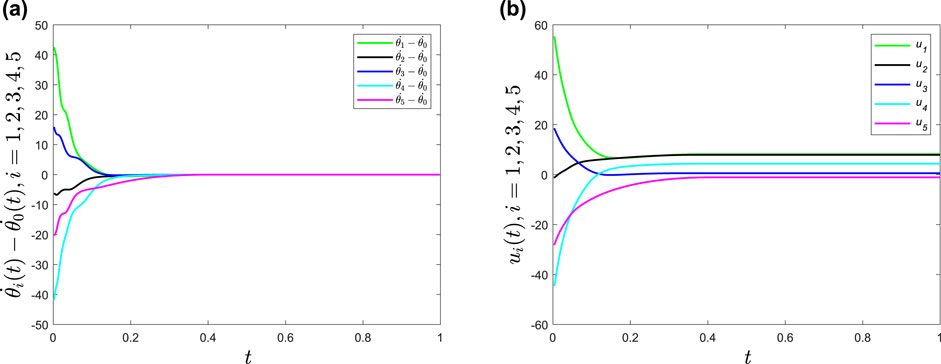
FIGURE 3. (A) Time evolutions of frequencies differences
Finally, we move to see the influence of parameter α on synchronization time. In the simulations, we set α = 0.1, 0.3, 0.5, 0.7, 0.9. In Figure 4, it is showed that the synchronization time decreases as α grows.
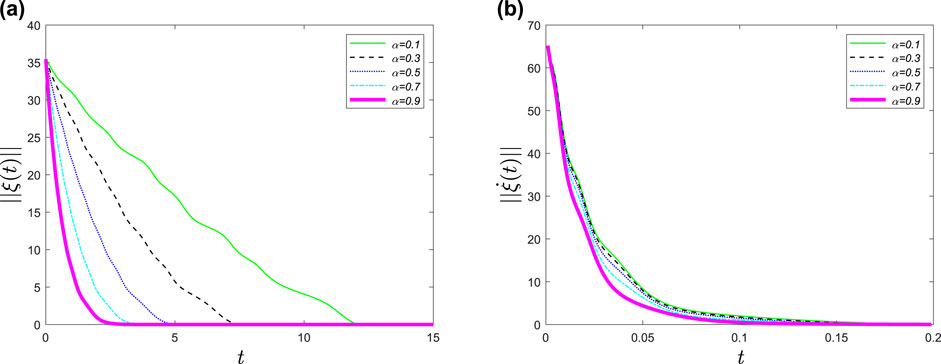
FIGURE 4. (A) Time evolutions of ‖ξ(t)‖ under the distributed control strategy Eq. 6 with respect to different parameters α = 0.1, 0.3, 0.5, 0.7, 0.9. (B) Time evolutions of
6 Conclusion
In this paper, the problems of finite-time phase agreement and frequency synchronization of Kuramoto-oscillator networks with a pacemaker have been investigated. Two distributed control strategies, based on the CPS, have been designed to drive the Kuramoto-oscillator networks. In the light of finite-time stability theory, the sufficient criteria have been derived for guaranteeing the phase agreement and frequency synchronization of identical and non-identical Kuramoto-oscillator networks with a pacemaker. At the same time, the upper bounds estimation of convergence time of Kuramoto-oscillator networks have been given accordingly. Numerical examples have validated the effectiveness of the derived theoretical results.
However, the convergence time estimations of this paper are heavily related to initial phases and/or frequencies of oscillators. Therefore, it is urgent to explore the fixed-time synchronization of Kuramoto model with a pacemaker in the future.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.
Author contributions
All authors listed have made a substantial, direct, and intellectual contribution to the work and approved it for publication.
Funding
This work is supported by National Natural Science Foundation of China (Grant No. 61903142), the Science and Technology Project of Jiangxi Education Department (Grant No. GJJ180356).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
2. Liu C, Weaver DR, Strogatz SH, Reppert SM. Cellular construction of a circadian clock: period determination in the suprachiasmatic nuclei. Cell (1997) 91:855–60. doi:10.1016/s0092-8674(00)80473-0
3. Chen C, Liu S, Shi X-Q, Chaté H, Wu YL. Weak synchronization and large-scale collective oscillation in dense bacterial suspensions. Nature (2017) 542:210–4. doi:10.1038/nature20817
4. Kim J-H, Park J-H. Exponential synchronization of Kuramoto oscillators using spatially local coupling. Physica D: Nonlinear Phenomena (2014) 277:40–7. doi:10.1016/j.physd.2014.03.006
5. Wiesenfeld K, Colet P, Strogatz SH. Frequency locking in josephson arrays: connection with the Kuramoto model. Phys Rev E (1998) 57:1563–9. doi:10.1103/physreve.57.1563
6. Daido H. Quasientrainment and slow relaxation in a population of oscillators with random and frustrated interactions. Phys Rev Lett (1992) 68:1073–6. doi:10.1103/physrevlett.68.1073
7. Sun W, Lü JH, Yu XH, Chen Y, Chen SH. Cooperation of multiagent systems with mismatch parameters: a viewpoint of power systems. IEEE Trans Circuits Syst (2016) 63:693–7. doi:10.1109/tcsii.2016.2530178
8. Seyboth GS, Wu JB, Qin JH, Yu CB, Allgöwer F. Collective circular motion of unicycle type vehicles with non-identical constant velocities. IEEE Trans Control Netw Syst (2014) 1:167–76. doi:10.1109/tcns.2014.2316995
9. Sepulchre R, Paley DA, Leonard NE. Stabilization of planar collective motion: all-to-all communication. IEEE Trans Automat Contr (2007) 52:811–24. doi:10.1109/tac.2007.898077
10. Dörfler F, Bullo F. Synchronization in complex networks of phase oscillators: a survey. Automatica (2014) 50:1539–64. doi:10.1016/j.automatica.2014.04.012
11. Chopra N, Spong MW. On exponential synchronization of Kuramoto oscillators. IEEE Trans Automat Contr (2009) 54:353–7. doi:10.1109/tac.2008.2007884
12. Ha S-Y, Li ZC, Xue XP. Formation of phase-locked states in a population of locally interacting Kuramoto oscillators. J Differential Equations (2013) 255:3053–70. doi:10.1016/j.jde.2013.07.013
13. Li HQ, Chen G, Liao XF, Huang TW. Attraction region seeking for power grids. IEEE Trans Circuits Syst (2017) 64:201–5. doi:10.1109/tcsii.2016.2561410
14. Li X, Rao PC. Synchronizing a weighted and weakly-connected Kuramoto oscillator digraph with a pacemaker. IEEE Trans Circuits Syst (2015) 62:899–905. doi:10.1109/tcsi.2014.2382193
15. Rao PC, Li X, Ogorzalek MJ. Stability of synchronous solutions in a directed Kuramoto-Oscillator network with a pacemaker. IEEE Trans Circuits Syst (2017) 64:1222–6. doi:10.1109/tcsii.2017.2679216
16. Jadbabaie A, Motee N, Barahona M. On the stability of the Kuramoto model of coupled nonlinear oscillators. Proc Amer Control Conf (2004) 5.
17. Tong DB, Rao PC, Chen QY, Ogorzalek MJ, Li X. Exponential synchronization and phase locking of a multilayer Kuramoto-oscillator system with a pacemaker. Neurocomputing (2018) 308:129–37. doi:10.1016/j.neucom.2018.04.067
18. Wu J, Liu MQ, Wang XF, Ma R-R. Achieving fixed-time synchronization of the Kuramoto model via improving control techniques. J Korean Phys Soc (2021) 79:998–1006. doi:10.1007/s40042-021-00302-z
19. Wu J, Li X. Global stochastic synchronization of Kuramoto-oscillator networks with distributed control. IEEE Trans Cybern (2021) 51:5825–35. doi:10.1109/tcyb.2019.2959854
20. Wang YQ, Doyle FJ. Exponential synchronization rate of Kuramoto oscillators in the presence of a pacemaker. IEEE Trans Automat Contr (2013) 58:989–94. doi:10.1109/tac.2012.2215772
21. Derler P, Lee EA, Vincentelli AS. Modeling cyber-physical systems. Proc IEEE (2012) 100:13–28. doi:10.1109/jproc.2011.2160929
22. Lee EA. Computing foundations and practice for cyber-physical systems: a preliminary report. California: University of California (2007).
23. Zhang W-Y, Yang C, Guan Z-H, Liu Z-W, Chi M, Zheng G-L. Bounded synchronization of coupled Kuramoto oscillators with phase lags via distributed impulsive control. Neurocomputing (2016) 218:216–22. doi:10.1016/j.neucom.2016.08.054
24. Rao PC, Li X. Pacemaker-based global synchronization of Kuramoto oscillators via distributed control. IEEE Trans Circuits Syst (2018) 65:1768–72. doi:10.1109/tcsii.2017.2763184
25. Dong J-G, Xue XP. Finite-time synchronization of Kuramoto-type oscillators. Nonlinear Anal Real World Appl (2015) 26:133–49. doi:10.1016/j.nonrwa.2015.05.006
26. Zhang XX, Sun ZY, Yu CB. Finite-time synchronization of networked Kuramoto-like oscillators. In: Proceedings of Australian Control Conference; 3-4 Nov; Newcastle (2016).
27. Wu J, Li X. Finite-time and fixed-time synchronization of kuramoto-oscillator network with multiplex control. IEEE Trans Control Netw Syst (2019) 6:863–73. doi:10.1109/tcns.2018.2880299
28. Olfati-Saber R, Murray RM. Consensus problems in networks of agents with switching topology and time-delays. IEEE Trans Automat Contr (2004) 49:1520–33. doi:10.1109/tac.2004.834113
Keywords: finite-time, synchronization, Kuramoto-oscillator, pacemaker, cyber-physical system (CPS)
Citation: Rao P and Guo X (2022) Finite-time synchronization of Kuramoto-oscillator networks with a pacemaker based on cyber-physical system. Front. Phys. 10:1077045. doi: 10.3389/fphy.2022.1077045
Received: 22 October 2022; Accepted: 09 November 2022;
Published: 24 November 2022.
Edited by:
Jianbo Wang, Southwest Petroleum University, ChinaReviewed by:
Zhao-Long Hu, Zhejiang Normal University, ChinaRongzhong Yu, Jiujiang University, China
Copyright © 2022 Rao and Guo. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pengchun Rao, cGNyYW9AZWNqdHUuZWR1LmNu
 Pengchun Rao
Pengchun Rao Xiufeng Guo
Xiufeng Guo