On the Pareto Type III Distribution

1 Introduction

Zipf’s Law [1], and Pareto Laws in general [2], have been assumed, since a relative long time, as reliable descriptions of the distributional properties of variables characterizing different social and natural phenomena (see Newman [3], the critical review in Kleiber and Kotz [4] and references therein). The application is the domain of economics are many, ranging from portfolio theory to economic growth [5,6]. These Laws are usually assumed valid when sufficiently large realizations of the variable of interest are considered, that is for the upper tail of the associated distributions. If a random variable X follows the Pareto Law with tail index a, the associated survival function possesses a power-like asymptotic behavior, 1 − F(x) ∼ x^−a, so that its n-th moment E[Xⁿ], for sufficiently large values of n, it is not defined. This property is particularly relevant when small values of the tail parameter are considered. For instance, when a ≤ 2, the variance (n = 2) is already absent. Contrary to the Pareto hypothesis, however, the empirical evidence often suggests finite values for the central moments, also when heavy-tail distributed variables are considered. Sometimes this can be understood with the presence of a natural upper bound which limits the largest attainable value of a given variable. Indeed in several cases it has been reported that a truncated Pareto provides a better fit to the data (Burroughs and Tebbens, 2001) than a pure power Law. In this paper I introduce a new three parameter version of the two parameter family of distributions originally proposed in Pareto [7]. The added parameter is a “dispersion” parameter which explicitly accounts for the typical scale of the underlying random variable, thus reducing the negative effect of the latter on the estimation of the power and exponential coefficients reported in Creedy [8]. Since the shape of the distribution is essentially the same of the orignal two parameter family proposed by Pareto, following Kleiber and Kotz [4] I retain the name of Pareto Type III distribution. The exponential dumping in the upper tail makes this distribution particularly suitable in describing all those samples which display power behavior for intermediate values and a more than power-like decrease in probability above a certain threshold or for particularly large observations (c.f. the examples in Burroughs and Tebbens [9]).

2 The Pareto Type III Distribution

Consider the three parameter family of distributions

$F\left(x\right)=1-{\left(\frac{x}{s}+1\right)}^{-a}{e}^{-b\frac{x}{s}},x\ge 0,(1)$

where s > 0 is a scale parameter, a > 0 the power coefficient and b ≥ 0 the exponential coefficient. The upper-tail of the distribution is characterized by a power-like behavior dumped by an exponential factor. When the exponential coefficient is set to zero, b = 0, the previous distribution reduces to a Pareto Type II distribution [4], which is asymptotically equivalent to the original Pareto distribution. The effect of the values of the exponential coefficient b on the overall shape of the distribution can be see in Figure 1, where the logarithm of the survival function log(1 − F(x)) is reported. For x/s ≪ 1 (left panel), when b is large the exponential factor becomes leading and the survival function decreases linearly. At the same time, when x/s ≫ 1 (right panel) an increase in b introduces a deviation (on the log-log graph) from the straight line characteristic of the Pareto power like behavior. With respect to the original formulation of Pareto and some later works, the functional expression proposed in Eq. 1 contains the additional scale parameter s. The addition of the scale parameter does not change the general properties of the distribution. In fact, it can be simplified away by a simple redefinition of the random variable. However, it might be useful in application, when the typical scale of the variable under study is not clear and has to be derived from data. The density associated to Eq. 1 reads

$f\left(x\right)=\frac{1}{s}{\left(\frac{x}{s}+1\right)}^{-a}{e}^{-b\frac{x}{s}}\left(b+\frac{a}{x/s+1}\right).(2)$

FIGURE 1

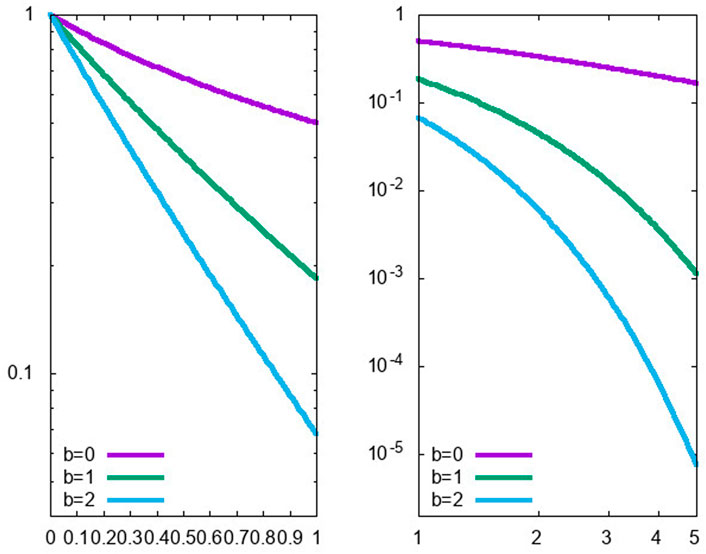
FIGURE 1. Lower (left) and upper (right) tail of the survival function of the Pareto III distribution for a = 1, s = 1 and different values of the exponential coefficient b. The case b = 0 corresponds to the Zipf’s law log(1 − F(x)) ∼ x⁻¹.

The density f(x) is strictly decreasing, thus the Pareto III distribution is unimodal with mode in x = 0.

2.1 Characteristic Function and Moments

Following Abramowitz and Stegun [10] (equation 6.5.20, p. 262)) define

${\alpha }_n\left(x\right)={\int }_1^{+\infty }dt{e}^{-xt}{t}^n=x^{-n-1}\mathrm{\Gamma }\left(n+1,x\right),(3)$

where Γ(n, x) stands for the incomplete gamma function

$\mathrm{\Gamma }\left(n,x\right)={\int }_x^{+\infty }dt{e}^{-t}{t}^{n-1}.$

Using the properties of Γ(n, x), it is immediate to obtain the following recurrence relation

${\alpha }_n\left(x\right)=\frac{e^{-x}}{x}+\frac{n}{x}{\alpha }_{n-1}\left(x\right).(4)$

Using this relation it is easy to show the following

Theorem 2.1. If the random variable X is distributed according to Eq. 1, its characteristic function ϕ(k) = E[e^ikX] reads

$\varphi \left(k\right)=1+iks{e}^{-iks+b}{\alpha }_{-a}\left(b-iks\right).(5)$

Proof. By definition one has

$\varphi \left(k\right)={\int }_0^{+\infty }dx{e}^{ikx}\frac{1}{s}{\left(\frac{x}{s}+1\right)}^{-a}{e}^{-b\frac{x}{s}}\left(b+\frac{a}{x/s+1}\right)$

which, after the change of variable z = x/s + 1, reduces to

$\varphi \left(k\right)={\int }_1^{+\infty }dz{z}^{-a}{e}^{-\left(b-iks\right)z}\left(b+\frac{a}{z}\right).$

Using Eq. 3 this can be rewritten as

$\varphi \left(k\right)=e^{-iks+b}\left(b{\alpha }_{-a}\left(b-iks\right)+a{\alpha }_{-a-1}\left(b-iks\right)\right),$

which using (Eq. 4) reduces to (Eq. 5).

In principle, all the moments of Eq. 1 can be obtained from the characteristic function (Eq. 5). For instance, one immediately has that the mean m₁ is

$m_1={\left.\left(-i\right)\frac{d}{dk}\varphi \left(k\right)\right|}_{k=0}=s{e}^b{\alpha }_{-a}\left(b\right).(6)$

A more practical expression can be obtained for higher moments.

Theorem 2.2. The moments m_n = E[Xⁿ], where X is distributed according to Eq. 1, admit the following representation:

$m_n=s^n{e}^b{b}^a\sum _{h=0}^n\left(\genfrac{}{}{0.0pt}{}{n}{h}\right){\left(-1\right)}^{n-h}\frac{h}{b^h}\mathrm{\Gamma }\left(h-a,b\right).(7)$

Proof. By definition of the n-th moment and using z = x/s + 1 one has

$m_n=s^n{e}^b{\int }_1^{+\infty }dz{\left(z-1\right)}^n{z}^{-a}{e}^{-bz}\left(b+\frac{a}{z}\right).$

Taking the binomial expansion of (z − 1)ⁿ and using Eq. 3, it becomes

$m_n=s^n{e}^b\sum _{h=0}^n\left(\genfrac{}{}{0.0pt}{}{n}{h}\right)\left(b{\alpha }_{h-a}\left(b\right)+a{\alpha }_{h-a-1}\left(b\right)\right),$

which given Eq. 4 and the definition of the α function in terms of incomplete gamma function, reduces to Eq. 7.

2.2 Inverse Distribution Function

The distribution function in Eq. 1 is defined over [0, + ∞) and has image in [0, 1). In this Section 1 derive its inverse, the quantile function Q(q). Consider the real function g(x) = x e^x. Since it is continuous and strictly increasing for x ≥−1, it admits a continuous inverse W(y) defined for y ≥−1/e, that satisfies the equations

$W\left(y\right)e^{W\left(y\right)}=y,\text{\hspace{0.17em}and\hspace{0.17em}}W\left(x{e}^x\right)=x,(8)$

for any y ≥−1/e and x ≥−1. The function W(y) corresponds to the real branch of the Lambert function (c.f. Jeffrey et al. [11]).

Theorem 2.3. The inverse distribution function Q of Eq. 1 reads

$Q\left(q\right)=s\frac{a}{b}W\left(\frac{b}{a}{e}^{\frac{b}{a}}{\left(1-q\right)}^{-1/a}\right)-s,(9)$

where W(x) is the real branch of the Lambert function.

Proof. Let q ∈ [0, + ∞). We are interested in the value of x that satisfy F(x) = q. Considering the expression in Eq. 1 this reduces to the equation

${\left(\frac{x}{s}+1\right)}^{-a}{e}^{-b\frac{x}{s}}=1-q.$

The expression can be rewritten in terms of z = (x/s + 1) b/a. After some manipulations one gets

$z{e}^z=\frac{b}{a}{e}^{\frac{b}{a}}{\left(1-q\right)}^{-1/a}.$

The right hand side is non-negative, thus from Eq. 8 it is

$z=W\left(\frac{b}{a}{e}^{\frac{b}{a}}{\left(1-q\right)}^{-1/a}\right),$

whence the assertion.

When q ∈ [0, + ∞), the argument of the function W in Eq. 9 is positive, so that the above expression is well defined. From Eq. 8, it follows that Q(0) = s a/b W(b/a exp(b/a)) − s = 0, as expected. The quantile function Eq. 9 can be used to generate i.i.d. pseudo-random variables extracted from a Pareto Type III distribution: generate a set of independent realizations {q_i} uniformly distributed in [0, 1) and apply the inverse distribution function Q to each realization to obtain a set {Q(q_i)} of independent variates distributed according to Eq. 1. Another application of the quantile function, common in exploratory data analysis, is the construction of q-q plots to investigate the agreement of data to the theoretical model.

3 Firms Size Distribution

The upper tail exponential cut-off which characterizes the Pareto Type III distribution can prove extremely useful in obtaining better and more reliable descriptions of empirical data. I illustrate this claim with an example based on the size distribution of business firms. The Pareto III distribution will be used to describe the upper tail of the Empirical Distribution Function (EDF) of annual revenues of the largest worldwide companies. This choice seems particularly fit, as it was precisely the problem of finding a reliable statistical description of the distribution of wealth which originally prompted the work of Pareto. I consider the Fortune 500 database, published each year by the Fortune magazine, which collects the revenues of the largest 500 firms in the world. Using Maximum Likelihood (ML) estimation (c.f. Hill [12] and for details Bottazzi et al. [13]) I fit the Pareto Type III distribution defined in Eq. 1 to the EDF upper tail, using subpopulations of different sizes. The analytic nature of the distribution and density functions, Eqs 1, 2, guarantee an asymptotic optimal performance of the ML approach. For comparison, I also fit a Pareto Type I distribution defined as

$F\left(x\right)=1-{\left(\frac{x}{s}\right)}^{-a}.(10)$

The Pareto Type I is the distribution traditionally applied to the description of the upper tail of wealth or income distribution (see for instance Castaldi and Milakovic [14] and references therein). Results are reported in Figure 2: the power-like decay of the Pareto I distribution shows up as a straight line in the log-log plot (left panel) while the exponential cut-off of the Pareto III distribution appears as a convex shape. As can be seen, the latter is remarkably less sensitive to the size of the considered sample and much more adapted to empirical observations. The estimate values for the tail index $\widehat{a}$ and the exponential correction $\widehat{b}$ are reported in Table 1.

FIGURE 2

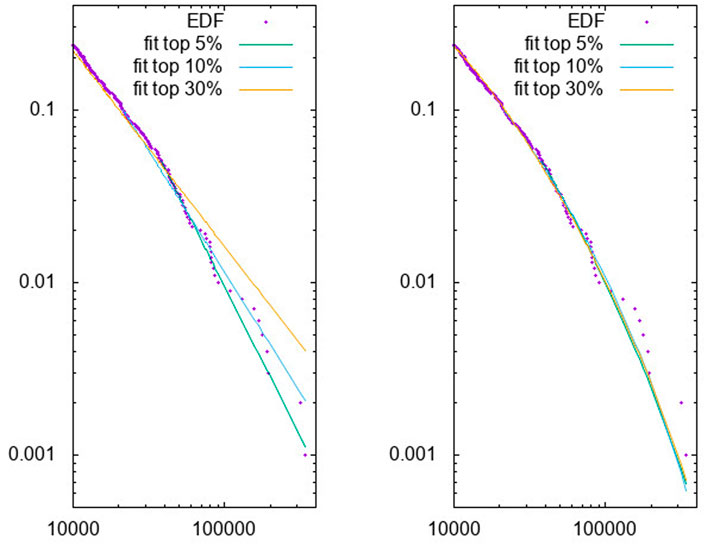
FIGURE 2. Distribution of the largest worldwide firms in 2006 according to Fortune 500 (revenues in millions of dollar). The maximum likelihood estimation of the upper tail obtained using 5%,10% and 30% of the available data is plotted for the Pareto Type I (left) and Pareto Type III (right) distribution.

TABLE 1

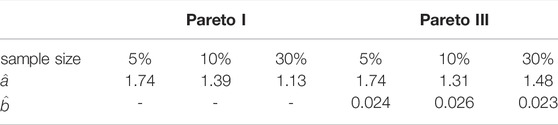
TABLE 1. Estimated coefficients for Pareto Type I and III on Fortune 500 data using different upper tail fractions of observations.

4 Conclusion

The Pareto Type III distribution, originally proposed by Pareto in 1896 as one of the possible statistical characterization of the distributional properties of the wealth in the Grand Duchy of Oldenburg, has never received much attention. However, its exponential asymptotic shape assures the existence of all central moments. Due to its relative simplicity and analytical tractability, it can be successfully used as an alternative candidate to probe for the presence of “deviation” from the power-like behavior of the upper tail of empirical distributions. The use of an exponentially dumped power behaviour could help in shading some new light on the difficulty of statistically differentiate between a power-like or a stretched exponential behavior [15]. As shown in Gabaix [16], the assumption of a power-like behavior of the size distribution of individual firms has important implications for the observed dynamics at the aggregate, macroeconomic, level. Thus, investigating the validity and extent of the Paretian assumption acquires a new relevance and the particular distribution analyzed in these notes might help in this investigation.

Data Availability Statement

Publicly available datasets were analyzed in this study. This data can be found here: http://cafim.santannapisa.it/∼giulio/other/Fortune500/index.html.

Author Contributions

The author confirms being the sole contributor of this work and has approved it for publication.

Funding

Support from the Scuola Superiore Sant’Anna (grant E6006GB) and from the EU (Contract No 12410 (NEST)) is gratefully acknowledged.

Conflict of Interest

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

I would like to thank Herman Rubin for his suggestion of using Lambert function to express the Pareto Type III inverse distribution function. I also thank Federico Tamagni and Angelo Secchi for a number of helpful comments.

References

1. Zipf GK. Human Behaviour and the Principle of Least-Effort. Cambridge MA: Addison-Wesley (1949).

Google Scholar

2. Pareto V. Cours D’économie Politique. Lousanne: Ed. Rouge (1987).

Google Scholar

3. Newman M. Power Laws, Pareto Distributions and Zipf's Law. Contemp Phys (2005) 46:323–51. doi:10.1080/00107510500052444

CrossRef Full Text | Google Scholar

4. Kleiber C, Kotz S. Statistical Size Distributions in Economics and Actuarial Sciences. New York: Wiley and Sons Statistics (2003).

Google Scholar

5. de Wit G. Firm Size Distributions. Int J Ind Organ (2005) 23:423–50. doi:10.1016/j.ijindorg.2005.01.012

CrossRef Full Text | Google Scholar

6. Gabaix X. Power Laws in Economics and Finance. Annu Rev Econ (2009) 1:255–94. doi:10.1146/annurev.economics.050708.142940

CrossRef Full Text | Google Scholar

7. Pareto V. Sur la Courve de la rèpartition de la richesse, Universitè de Lousanne. English traslation. Revista di Politica Economica (1986) 87:647–700.

Google Scholar

8. Creedy J. Notes and Memoranda Pareto and the Distribution of Income*. Rev Income Wealth (1977) 23:405–11. doi:10.1111/j.1475-4991.1977.tb00026.x

CrossRef Full Text | Google Scholar

9. Burroughs SM, Tebbens SF. Upper-truncated Power Law Distributions. Fractals (2001) 09:209–22. doi:10.1142/s0218348x01000658

CrossRef Full Text | Google Scholar

10. Abramowitz M, Stegun IA. Handbook of Mathematical Functions. New York: Dover (1964).

Google Scholar

11. Jeffrey DJ, Hare DEG, Corless RM. Unwinding the Branches of the Lambert W Function. Math Scientist (1996) 21:1–7.

Google Scholar

12. Hill BM. A Simple General Approach to Inference about the Tail of a Distribution. Ann Stat (1975) 3:1163–74. doi:10.1214/aos/1176343247

CrossRef Full Text | Google Scholar

13. Bottazzi G, Pirino D, Tamagni F. Zipf Law and the Firm Size Distribution: a Critical Discussion of Popular Estimators. J Evol Econ (2015) 25:585–610. doi:10.1007/s00191-015-0395-7

CrossRef Full Text | Google Scholar

14. Castaldi C, Milaković M. Turnover Activity in Wealth Portfolios. J Econ Behav Organ (2007) 63(3):537–52. doi:10.1016/j.jebo.2005.06.008

CrossRef Full Text | Google Scholar

15. Clauset A, Shalizi CR, Newman MEJ. Power-Law Distributions in Empirical Data. SIAM Rev (2009) 51(4):661–703. doi:10.1137/070710111

CrossRef Full Text | Google Scholar

16. Gabaix x. The Granular Origins of Aggregate Fluctuations. Econometrica (2011) 79:733–72.

Google Scholar