Critical Scaling of Entropy and Thermal Drude Weight in Anisotropic Heisenberg Antiferromagnets: A Thermodynamic Quest for Quantum Criticality

Introduction

A quantum phase transition (QPT) takes place at zero temperature, as a result of the quantum fluctuations arising from Heisenberg uncertainty relation [1]. Usually, it manifests that the ground state of a quantum system changes upon tuning an external nonthermal parameter such as pressure or magnetic field to a critical value, which is marked by a quantum critical point (QCP) for a continuous transition. The QC fluctuations will result in an exotic behavior in stark contrast to the conventional gapped or gapless low-lying excitations of materials. Near the QCP, a QC regime emerges at finite temperatures in an extended parameter space attributed to the interplay between quantum and thermal fluctuations [2]. This intriguing region is featured by the absence of energy scales other than temperature as well as the corresponding critical properties of quantum correlations or thermodynamic quantities, which culminate into scaling characteristic and universality [3–6]. In this regard, one-dimensional (1D) quantum spin systems offer field tunability for probing QPT and critical phenomena. A variety of magnetic compounds have been regarded as the 1D antiferromagnetic (AF) Heisenberg chain model [3–9], whose ground state resides in a Tomonaga–Luttinger liquid (TLL) characterized by spinon quasiparticles with gapless elementary excitations [10, 11]. However, the magnetic anisotropy (∆) would make a significant impact on its properties. For ∆ > 1, it turns into an Ising-type model, which is realized in experiment for CoNb₂O₆ and BaCo₂V₂O₈ [12–14]. A transverse field induces an Ising QPT with gapless quantum criticality and self-duality of QCP [15]. Differently, for ∆ < 1, it becomes an XY-type spin chain, the experimental realization of which is Cs₂CoCl₄ [16, 17], whose ground state lies in a TLL state. In a longitude magnetic field, it induces a QPT without self-duality of QCP. Herein, we focus on the AF Heisenberg chain for the anisotropy ∆ ≤ 1, whose ground state still resides in a TLL. Up to the critical field B_c = J (1+∆)/gμ_B, a QPT occurs from TLL to a spin polarized ferromagnetic (FM) state with an excitation gap opened up by the field [14].

As we know, the magnetic entropy shows anomaly close to the QCP, where two ground states compete with each other and it does not determine which state to be reside in [18]. Besides, the thermal Drude weight Dth is a good indicator signaling gapped (D_th = 0) or gapless (D_th>0) low-lying excitations [19]. In fact, due to that the absolute zero temperature cannot be attained experimentally, the field-induced quantum criticality has been intensively investigated by using the field dependence of magnetization measurement to determine the kink at finite temperature [3, 6, 9, 13, 16], which becomes rounded such that the QCP cannot be measured exactly. The nature of quantum fluctuations near the QCP remains enigmatic. Thus, it is urgent need to provide a new clue to capture QCP for diagnosing QPT at finite temperatures such that the QC scaling becomes rather important, which is one of the cornerstone concepts in modern physics and plays a key role in understanding quantum criticality, namely, the QPT. Near QCP, the physical quantities such as magnetization, magnetic susceptibility, and specific heat are featured by a set of critical exponents and scaling functions [3, 4]. Note that the critical behavior of entropy should be the same as the specific heat. However, whether the thermal Drude weight can be done critical scaling analysis instead of magnetization (ineffective in Ising model) or not? What critical scaling forms to feature quantum criticality? Although several thermodynamic quantities were carried out to do critical scaling analysis for detecting the QPT, it is still challenging to measure the thermal Drude weight as an effective detector of quantum criticality.

To fully assess the universality of quantum criticality, we will demonstrate the scaling behavior of entropy and thermal Drude weight divided by temperature to extract the critical exponents and capture the QCP. On the one hand, such scaling is a direct consequence of the scaled temperature to a certain universal power multiplied by the field that collapse onto a single curve for the plot against a scaling transformation for thermodynamic quantity. On the other hand, as the magnetic field is scaled to a certain universal power multiplied by temperature, the data points of scaling transformation for thermodynamic quantity will fall on two independent branches. In the forthcoming section, we present the model Hamiltonian and Green’s function theory. In Results and Discussion, the renormalized quantum phase diagram and phase crossover behavior are explored, and the field dependence of magnetization for different anisotropies has been tested, which are compared to the experimental observations; the QC scaling behavior is analyzed and discussed. Finally, a conclusion is drawn in Conclusion.

Model Hamiltonian and Method

The 1D anisotropic Heisenberg AF chain in an external magnetic field is governed by the Hamiltonian [6, 14, 16, 20],

$H=J{\displaystyle \sum _l\left[S_l^x{S}_{l+1}^x+S_l^y{S}_{l+1}^y+\mathrm{\Delta }{S}_l^z{S}_{l+1}^z\right]}-g{\mu }_{B}B{\displaystyle \sum _l{S}_l^z},(1)$

where J > 0 denotes the AF coupling and ∆ represents the anisotropy. Hereafter, we define the reduced magnetic field $h=g{\mu }_{B}B$ (Zeeman energy). By performing Jordan–Wigner (JW) transformation [21],

$S_j^z=c_j^{+}{c}_j-1/2,S_j^y=2i{S}_j^x{S}_j^z,S_j^x=\frac{1}{2}{\displaystyle \prod _{i<j}\left(1-2c_i^{+}{c}_i\right)}\left(c_j^{+}+c_j\right),(2)$

the Hamiltonian (1) becomes

$H=J{\displaystyle \sum _l\left[\frac{1}{2}\left(c_l^{+}{c}_{l+1}+H.c.\right)+\mathrm{\Delta }\left(c_l^{+}{c}_l-\frac{1}{2}\right)\left(c_{l+1}^{+}{c}_{l+1}-\frac{1}{2}\right)\right]}-h{\displaystyle \sum _l\left(c_l^{+}{c}_l-\frac{1}{2}\right),}(3)$

where the operator $c_l^{+}\left(c_l\right)$ creates (annihilates) a spinless fermion at site l, which describes a system of interacting spinless fermions in a magnetic field.

The method that we employ is the two-time Green’s function theory. The retarded Green’s function for JW fermions is defined as [22]

$G_{ij}\left(t-t\mathrm{\prime }\right)=<<c_i\left(t\right);c_j^{+}\left(t\mathrm{\prime }\right)>>=-i\theta \left(t-t\mathrm{\prime }\right)<c_i{c}_j^{+}+c_j^{+}{c}_i>,(4)$

where the subscripts i and j label lattice sites. After the time Fourier transformation, the Green’s function is put into the equation of motion,

$\omega \ll c_i;c_j^{+}\gg =<{\left[c_i,c_j^{+}\right]}_{+}>+\ll \left[c_i,H\right];c_j^{+}\gg .(5)$

It is clearly shown that a rigorous calculation is not available as a result of the Ising interacting quartic terms. For the high-order Green’s function $\ll \left[c_i,H\right];c_j^{+}\gg$, doing the equation of motion analogous to Eq. 4, it will generate higher-order Green’s function appearing on the right hand, resulting in an infinite set of coupled equations. In terms of Wick’s theorem, we adopt the decoupling scheme for the four-operator Green’s function [23]

$\ll c_i^{+}{c}_i{c}_j;c_j^{+}\gg \approx <c_i^{+}{c}_i>\ll c_j;c_j^{+}\gg -<c_i^{+}{c}_j>\ll c_i;c_j^{+}\gg .(6)$

For further Fourier transformation into k-space, the Green’s function can be expressed as

$G_{ij}=\frac{1}{N}{\displaystyle \sum _{k}g\left(k\right)}{e}^{ik\cdot \left(i-j\right)}.(7)$

The integral of the wavevector k extends over the first Brillouin zone. Thus, the momentum space Green’s function $g\left(k,\omega \right)$ can be described as a function of wavevector k and the elementary excitation spectrum $\omega =\omega \left(k\right)$. According to the standard spectral theorem, the correlation function of the product of fermion operators can be calculated through the corresponding Green’s function

$<c_j^{+}{c}_i>=\frac{i}{2\pi N}{\displaystyle \sum _k{e}^{ik\cdot \left(i-j\right)}}{\displaystyle \int \frac{d\omega }{e^{\beta \omega }+1}}\left[g\left(k,\omega +i{0}^{+}\right)-g\left(k,\omega -i{0}^{+}\right)\right],(8)$

where $\beta =1/k_{B}T$, $k_B$ is the Boltzman’s constant, and T is the absolute temperature. Thus, it gives rise to a set of self-consistent integral equations of correlation function that can be solved numerically. In calculation, an initial value of correlation functions is put into Eq. 7 to produce resultant values, the iteration of which continues until convergence is reached.

Then, the average magnetization M per site, specific heat, and thermal entropy are defined as

$M=\frac{1}{N}{\displaystyle \sum _l{S}_l^z}=\frac{1}{N}{\displaystyle \sum _l\left(c_l^{+}{c}_l-\frac{1}{2}\right),}(9)$

$C_V=\frac{dE}{dT}=\frac{d\langle H\rangle }{dT},S={\displaystyle {\int }_0^T\frac{C_V}{T^{\prime }}}dT\mathrm{\prime }.(10)$

Hence, the isothermal magnetic entropy change is expressed as [24]

$\mathrm{\Delta }S=S\left(T,h\right)-S\left(T,0\right)={{\displaystyle {\int }_0^h\left(\frac{\partial M}{\partial T}\right)}}_{h}dh.(11)$

In addition, within the Kubo linear response theory, the zero-frequency weight of the thermal conductivity is called thermal Drude weight D_th, which is defined as [25–29]

$D_{th}=\frac{\pi {\beta }^2}{ZN}{\displaystyle \sum _{\begin{array}{l}n,m\\ E_n=E_m\end{array}}{e}^{-\beta E_n}}{\left|\langle n|j_{th}|m\rangle \right|}^2,(12)$

with $j_{th}=J^2{\displaystyle \sum _l{\stackrel{\rightharpoonup }{S}}_l}\cdot \left({\stackrel{\rightharpoonup }{S}}_{l+1}\times {\stackrel{\rightharpoonup }{S}}_{l+2}\right)$ being the energy current. D_th = 0 and D_th > 0 denote the thermal insulator and ideal thermal conductor, respectively [19]. Namely, D_th = 0 or D_th > 0 reflects the gapped or gapless low-lying excitations.

Results and Discussion

In what follows, k_B = ħ = 1 and J = 1 is set as an energy unit; hereafter, all other parameters are scaled by it. At first sight, without loss of generality, the field dependence of magnetization at low temperatures is calculated for different anisotropies and done a comparison to the experimental results. For Δ = 0.25, the system is an XY-like antiferromagnet with gapless TLL. The magnetization increases gradually as the field ascends and reaches its saturation at B_c = J (1 + ∆)/gμ_B = 2.07T for J = 0.23 meV and g = 2.4, as shown in Figure 1A, which is in accordance with the experimental observation value B_c = 2.1T on compound Cs₂CoCl₄ [16]. Nonetheless, it becomes an isotropic case with Δ = 1, for which a series of compounds have been identified as candidates in experiment [6–9]. For example, a copper-containing coordination polymer CuPzN (a good realization of a spin-1/2 AF chain) [6], whose magnetization is fitted by J = 10.6 K and g = 2.27 at low temperatures in Figure 1B, manifests a relatively sharp kink around B_c = 13.9T, close to the experimental, Bethe–Ansatz and QTM results. Beyond B_c, the magnetization reaches the saturation value 1.135 μ_B per Cu²⁺, in excellent agreement with 1.15 μ_B obtained from the experimental observation [3]. As the temperature ascends, the sharp critical signatures broaden systematically due to the enhanced thermal fluctuations. As it is well known, the absolute zero temperature cannot be attained experimentally such that the critical field cannot be measured exactly. How to feature the universality of quantum criticality and phase crossover with gapped or gapless low-lying excitations? How to capture the exact critical field at finite temperature to diagnose the QPT? In addition to the abovementioned magnetization characterization, on the one hand, the magnetic entropy is a good quantity to characterize the quantum criticality by its maximum value at the lowest temperature because two quantum phases compete with each other at the QCP, where it is not determined which ground state to be resided in. Herein, the magnetic field is renormalized by the anisotropy λ = h/(1 + ∆). Figure 1C presents the ∆-λ phase diagram by the contour plot of entropy. It is clearly shown that the renormalized critical field λ_c = 1.0 associated with a sharp peak of entropy separates the TLL and FM phases for any anisotropy. At finite temperature, the different states are featured by the magnetic entropy change in Figure 1D, in which the inverse magnetocaloric effect (IMCE) (−∆S < 0) predominates in TLL at low temperature for λ < λ_c, while only conventional magnetocaloric effect (CMCE) (−∆S > 0) persists in FM state beyond λ_c. Furthermore, it has been pointed out that |ΔS| follows a power–law dependence of the field: |ΔS|∼λⁿ with $n=\frac{d\ln \left|\Delta S\right|}{d\ln \lambda }$ the local exponent, which is available for both IMCE and CMCE [30, 31]. Figure 1E shows n∼2 power–law curve that is performed by the same slope of linear ln|ΔS | versus lnλ plots for different temperatures (see the inset in Figure 1E), which is demonstrated in the AF materials La_1-xGa_xMnO₃ with IMCE experimentally rather than the FM one showing CMCE with n dependent of temperature and magnetic field [30, 31]. On the other hand, the thermal Drude weight is a good signature of gapped or gapless low-lying excitation, as shown in Figure 1F. It manifests finite values in the TLL signaling gapless behavior, which drops to zero at λ_c = 1.0, denoting the gapped low-lying excitation in FM state. Meanwhile, its QC scaling will provide a new clue to detect QPT. Similar to the performance of magnetization, nearby but below the critical field, one can find that

$D_{th}/T\propto {\left({\lambda }_c-\lambda \right)}^{1/\delta },(13)$

demonstrated by the linear double logarithm with δ = 2.009 (see the inset in Figure 1F), which agrees well with the experimental value 1.98 obtained from the critical scaling of magnetization on CuPzN [3].

FIGURE 1

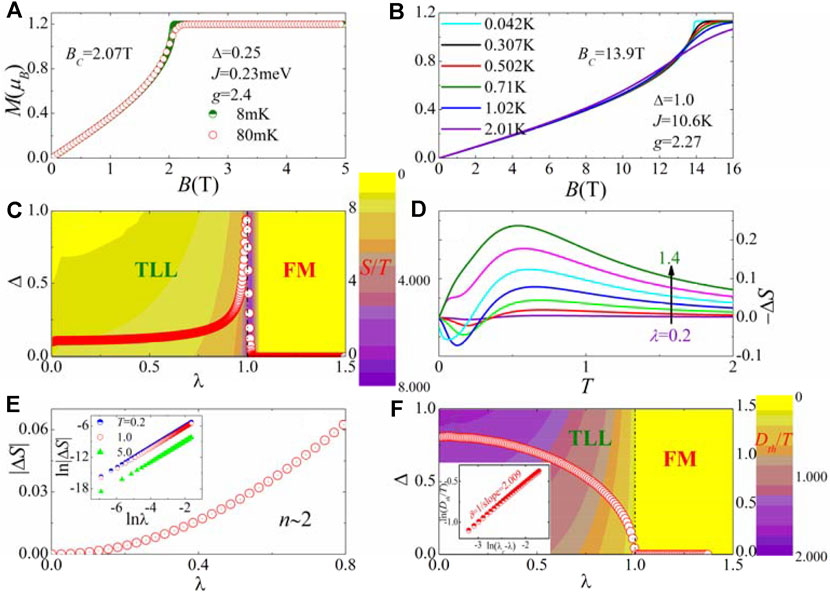
FIGURE 1. At low temperatures, the field dependence of magnetization for ∆ = 0.25 in (A) (J, g) = (0.23 meV, 2.4) and for ∆ = 1.0 in (B) (J, g) = (10.6 K, 2.27). (C) The renormalized quantum phase diagram by the contour plot of entropy at T = 0.005 with Tomonaga–Luttinger liquid (TLL) and spin polarized ferromagnetic (FM) phase being unveiled. For ∆ = 0.25, (D) the temperature dependence of magnetic entropy change under different fields. (E) The field dependence of magnetic entropy change; the inset is its log-log scale under different temperatures. (F) The thermal Drude weight landscape of renormalized quantum phase diagram; the inset is its scaling around the quantum critical point.

However, at finite temperatures, the QPT disappears, and it only shows a phase crossover behavior. Proceeding the same way as that observed in Sr₃Ru₂O₇ [18], the field derivative of the entropy divided by temperature is employed to characterize the landscape of temperature–field phase diagram, as shown in Figure 2A. A peak-valley structure marks two crossover temperatures fanning out a QC regime, which constitute two branches of the phase crossover boundaries. In the QC regime, it is well known that the correlation length ξ diverges as $\xi \propto |\lambda -{\lambda }_c{|}^{-v}$, whereas the correlation time τ_c diverges as ${\tau }_c\propto {\xi }^z\propto |\lambda -{\lambda }_c{|}^{-zv}$ [1], and the energy gap E_g is inversely proportional to the correlation length $E_g\propto {\xi }^{-z}\propto |\lambda -{\lambda }_c{|}^{zv}$ [32, 33], wherein v and z are defined as the correlation length and dynamic critical exponents, respectively. It presents a linear relation of crossover temperature $T^{\ast }\propto |\lambda -{\lambda }_c{|}^{zv}$ with zv = 1. From the high-temperature extrapolation to zero temperature, the T-linear relations intersect at a point located on the field axis, so that one can get the QCP λ_c = 1.0. It is worth noting that, at λ_c, the dispersion presents $\omega {|}_{\lambda ={\lambda }_c}\propto |k-k_c{|}^z$ with the dynamic critical exponent z = 2 for d = 1 [33, 34]. Thus, one can obtain ν = 1/2. It is different from the TLL low-energy property that satisfies a linear dispersion relation $\omega ={\upsilon }_s\left|k\right|$ (υ_s the sound velocity) with ν = 1 and z = 1 [4, 32]. Under different fields, the temperature dependence of entropy behaves differently. At high temperature, the entropy approaches its saturation value ln (2S + 1) = ln2, as shown in Figure 2B. Upon cooling down to zero temperature, one can find that the entropy displays a T-linear relation, implying a gapless behavior, while it decays exponentially $S\propto e^{-E_g/k_{B}T}$, suggesting the gapped low-lying excitation with the gap E_g manifested by the linear lnS-1/T curve, the negative slope of which is equal to $E_g=\lambda -{\lambda }_c$ (see the inset in Figure 2B). However, at λ_c, it is incurved. After a transformation, S/T diverges as T→0, as shown in Figure 2C, which indicates a power–law temperature dependence

$S/T\propto T^{-\alpha },(14)$

with α = 0.497 demonstrated by the slope of linear lnS/T–lnT curve in the inset, which turns out to be a T^1/2 behavior of the entropy. In fact, one can obtain α = 1/2 from the scaling relation α = 2-(d + z)/z with dynamic exponent z = 2 and spatial dimension d = 1 [3, 4, 34].

FIGURE 2

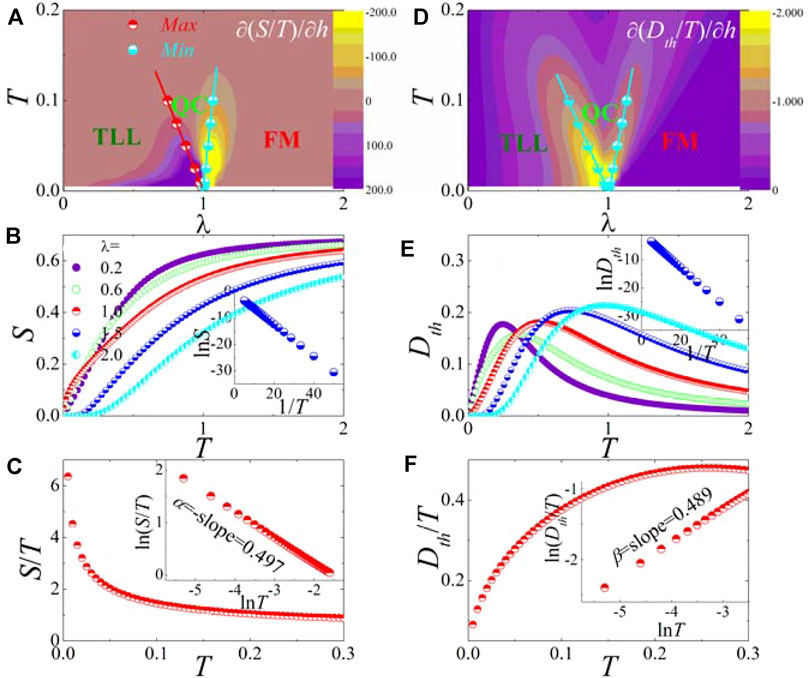
FIGURE 2. Temperature–field phase diagram based on the contour plot of the field derivative of (A) entropy and (D) thermal Drude weight divided by temperature, fanning out a quantum critical (QC) regime. The temperature dependence of (B) entropy and (E) thermal Drude weight under different fields; the insets are the logarithm as a function of 1/T, revealing the spin excitation gap by the magnitude of slope. (C) S/T and (F) Dth/T as a function of temperature at the critical field; the insets are the corresponding double logarithm plot, unveiling the critical exponents.

For a comparison, the field derivative of thermal Drude weight divided by temperature is also employed to characterize the landscape of temperature–field phase diagram, as shown in Figure 2D, which shows the similar behavior as the entropy plotted in Figure 2A. A double-valley structure marks two crossover temperatures fanning out a QC regime, which also feature the phase crossover boundaries. Under different fields, the thermal Drude weight as a function of temperature behaves differently, as shown in Figure 2E. As T→0, one can find that the thermal Drude weight displays a T-linear relation for λ < λ_c, implying a gapless behavior, while it is exponentially activated: $D_{th}\propto e^{-E_g/k_{B}T}$ for λ > λ_c, suggesting the gapped low-lying excitation with the gap E_g manifested by the slope of linear lnD_th against 1/T curve in the inset of Figure 2E. However, at λ_c, it is necked out. After a transformation, D_th/T is incurved, as shown in Figure 2F, which implies a power–law temperature dependence

$D_{th}/T\propto T^{\beta },(15)$

with β = 0.489 demonstrated by the slope of linear lnD_th/T–lnT curve in the inset of Figure 2F, which turns out to be a T^3/2 behavior of the thermal Drude weight [28].

Thus, one can find that α+β(1+δ) = 1.968 fulfills the Essam–Fisher relation [35]

$\alpha +\beta \left(1+\delta \right)=2.(16)$

In addition, we propose some scaling hypothesis equations to confirm the reliability and self-consistency of the obtained critical exponents. From the above analysis, it is clearly shown that the critical exponents δ and β describe the field and temperature dependence of thermal Drude weight $D_{th}\left(T\to 0,{\lambda }_c-\lambda \right)/T\propto {\left({\lambda }_c-\lambda \right)}^{1/\delta }$ and $D_{th}\left(\lambda ={\lambda }_c,T\right)/T\propto T^{\beta }$, respectively, whereas α features the temperature dependence of entropy $S\left(\lambda ={\lambda }_c,T\right)/T\propto T^{-\alpha }$. Although three critical exponents are found, indeed, only two are mutually independent as a result of the Essam–Fisher relation, so that one can select arbitrary two exponents as scaling checking benchmark. In general, β and δ are selected to testify the critical scaling laws. Herein, two scaling hypothesis checking manners are adopted. One is the magnetic field rescaled, i.e., the magnetic field multiplied by a scaled temperature. The entropy hypothesis equation on the temperature scaling is assumed as

$S\left(\lambda -{\lambda }_c,T\right)/T=T^{-\alpha }\Re \left(\left(\lambda -{\lambda }_c\right)/T^{\beta \delta }\right)(17)$

with $\Re \left(x\right)$ being a scaling function. At λ = λ_c, it allows one to get the critical exponent β from $S\left(\lambda ={\lambda }_c,T\right)/T=T^{-\alpha }\Re \left(0\right)$. In Figure 3A, the scaling transformation of isothermal entropy collapses into a universal curve, indicating the critical exponents consistent with the scaling hypothesis. We further give the critical scaling behavior of thermal Drude weight as

$D_{th}\left(\lambda -{\lambda }_c,T\right)/T\propto T^{\beta }\mathrm{\Phi }\left(\left(\lambda -{\lambda }_c\right)/T^{\beta \delta }\right)(18)$

with $\Phi \left(x\right)$ being a scaling function, which allows an unequivocal determination of β from the critical field thermal Drude weight $D_{th}\left(\lambda ={\lambda }_c,T\right)/T\propto T^{\beta }\mathrm{\Phi }\left(0\right)$. The scaling transformation also collapses onto a universal curve, as shown in Figure 3B.

FIGURE 3

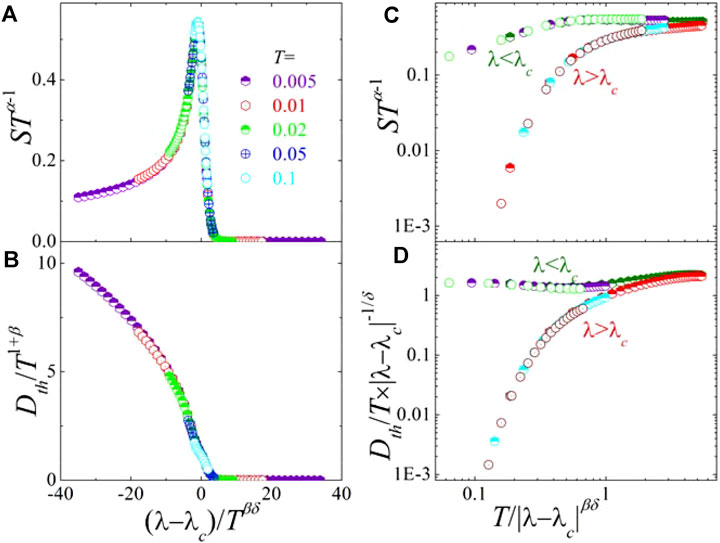
FIGURE 3. Scaling transformation of (A) entropy and (B) thermal Drude weight as a function of rescaled field at different temperatures, while they are plotted as a function of rescaled temperature around the critical field in (C) and (D), respectively. All the data points collapse onto a universal curve or two independent branches, indicating the self-consistency and reliability of the obtained critical exponents.

The other is the temperature rescaled, i.e., the temperature multiplied by a scaled magnetic field. Differently, in the asymptotic QC region, the thermal Drude weight equation is proposed as

$D_{th}\left(T,\lambda -{\lambda }_c\right)/T=|\lambda -{\lambda }_c{|}^{1/\delta }f\left(T/{\left|\lambda -{\lambda }_c\right|}^{\beta \delta }\right),(19)$

in which f(x) is a regular function that behaves differently for λ < λ_c and λ > λ_c, respectively. Thus, as T→0, it allows an unambiguous determination of the critical exponent δ from the thermal Drude weight $D_{th}\left(T\to 0,\lambda -{\lambda }_c\right)/T=|\lambda -{\lambda }_c{|}^{1/\delta }f\left(0\right)$, which is explicitly demonstrated in the inset of Figure 1F. Nevertheless, at finite temperature, the transformation of D_th/T×|λ-λ_c|^−1/δ versus T/|λ-λ_c|^βδ will form two universal curves for λ < λ_c and λ > λ_c, respectively. Figure 3D shows the double logarithm scale of thermal Drude weight around λ_c, wherein all the data points fall on two independent branches. Proceeding the same way, the data of scaling transformation for entropy around λ_c as a function of T/|λ-λ_c|^βδ plotted in Figure 3C also fall on two independent branches, which explicitly confirm the self-consistency of the critical exponents. Therefore, it is clearly shown that the normalized variables obey the scaling hypothesis equations, which not only testify the quantum criticality but also verify the reliability and self-consistency of the obtained critical exponents that meet the critical scaling law.

Conclusion

In conclusion, the QPT and low-temperature properties of 1D spin-1/2 anisotropic Heisenberg AF chains are investigated by means of Green’s function theory. For different anisotropies, the field dependence of magnetization is calculated at low temperatures, which are in good agreement with the experimental results. We further renormalize the quantum phase diagram by the anisotropy that manifests a gapless TLL transition into gapped FM state at h_c = 1 + ∆, which is demonstrated by the drops to zero from a finite value of thermal Drude weight. At low temperature, two crossover temperatures fan out a QC regime and capture the QCP from linear high-temperature extrapolation to zero temperature. The T-linear dependence of entropy and thermal Drude weight signals the gapless low-lying excitation in TLL, while it decays exponentially upon cooling down to zero temperature, suggesting the gapped behavior in FM state. At the QCP, it takes on a T^1/2 or T^3/2 behavior. Furthermore, we demonstrate the QC scaling via analyzing the entropy and thermal Drude weight around QCP to extract the critical exponents (α, δ, and β) that fulfill the Essamm–Fisher relation α+β(1+δ) = 2, which provides a novel thermodynamic means to detect QPT for experiment. Meanwhile, scaling hypothesis equations with two scaling transformation manners are proposed to check the scaling analysis. One is the plot against the rescaled magnetic field, for which all the data points collapse onto a universal single curve, whereas the other is the rescaled temperature such that the data points fall on two independent branches, indicating the self-consistency and reliability of the obtained critical exponents, which provide an explicit physical picture for understanding QC phenomena at finite temperatures.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

LD conceived the work and wrote the manuscript. YZ performed some theoretical calculation results. All the authors participated in the discussion and interpretation of the results.

Funding

This work was supported by the Natural Science Foundation of Chongqing (cstc2021jcyj-msxmX0878) and the Youth Project of Scientific and Technological Research Program of Chongqing Education Commission (KJQN202101210).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Vojta M. Quantum Phase Transitions. Rep Prog Phys (2003) 66:2069–110. doi:10.1088/0034-4885/66/12/r01

CrossRef Full Text | Google Scholar

2. Frérot I, Roscilde T. Reconstructing the Quantum Critical Fan of Strongly Correlated Systems Using Quantum Correlations. Nat Commun (2019) 10:577. doi:10.1038/s41467-019-08324-9

PubMed Abstract | CrossRef Full Text | Google Scholar

3. Kono Y, Sakakibara T, Aoyama CP, Hotta C, Turnbull MM, Landee CP, et al. Field-induced Quantum Criticality and Universal Temperature Dependence of the Magnetization of a Spin-1/2 Heisenberg Chain. Phys Rev Lett (2015) 114:037202. doi:10.1103/physrevlett.114.037202

PubMed Abstract | CrossRef Full Text | Google Scholar

4. Jeong M, Rønnow HM. Quantum Critical Scaling for a Heisenberg Spin-12chain Around Saturation. Phys Rev B (2015) 92:180409(R). doi:10.1103/physrevb.92.180409

CrossRef Full Text | Google Scholar

5. Hoch MJR. Magnon-induced Nuclear Relaxation in the Quantum Critical Region of a Heisenberg Linear Chain. Phys Rev B (2017) 96:024444. doi:10.1103/physrevb.96.024444

CrossRef Full Text | Google Scholar

6. Breunig O, Garst M, Klümper A, Rohrkamp J, Turnbull MM, Lorenz T. Quantum Criticality in the Spin-1/2 Heisenberg Chain System Copper Pyrazine Dinitrate. Sci Adv (2017) 3:eaao3773. doi:10.1126/sciadv.aao3773

PubMed Abstract | CrossRef Full Text | Google Scholar

7. Wolf B, Tsui Y, Jaiswal-Nagar D, Tutsch U, Honecker A, Removic-Langer K, et al. Magnetocaloric Effect and Magnetic Cooling Near a Field-Induced Quantum-Critical point. Proc Natl Acad Sci (2011) 108:6862–6. doi:10.1073/pnas.1017047108

CrossRef Full Text | Google Scholar

8. Blanc N, Trinh J, Dong L, Bai X, Aczel AA, Mourigal M, et al. Quantum Criticality Among Entangled Spin Chains. Nat Phys (2018) 14:273–6. doi:10.1038/s41567-017-0010-y

CrossRef Full Text | Google Scholar

9. Chakraborty T, Singh H, Chaudhuri D, Jeevan HS, Gegenwart P, Mitra C. Investigation of Thermodynamic Properties of Cu(NH 3 ) 4 SO 4 ·H 2 O, a Heisenberg Spin Chain Compound. J Magnetism Magn Mater (2017) 439:101–6. doi:10.1016/j.jmmm.2017.05.020

CrossRef Full Text | Google Scholar

10. Zaliznyak IA. A Glimpse of a Luttinger Liquid. Nat Mater (2005) 4:273–5. doi:10.1038/nmat1358

PubMed Abstract | CrossRef Full Text | Google Scholar

11. He F, Jiang Y, Yu Y-C, Lin H-Q, Guan X-W. Quantum Criticality of Spinons. Phys Rev B (2017) 96(R):220401. doi:10.1103/physrevb.96.220401

CrossRef Full Text | Google Scholar

12. Liang T, Koohpayeh SM, Krizan JW, McQueen TM, Cava RJ, Ong NP. Heat Capacity Peak at the Quantum Critical point of the Transverse Ising Magnet CoNb2O6. Nat Commun (2015) 6:7611. doi:10.1038/ncomms8611

PubMed Abstract | CrossRef Full Text | Google Scholar

13. Wang Z, Lorenz T, Gorbunov DI, Cong PT, Kohama Y, Niesen S, et al. Quantum Criticality of an Ising-like Spin- 1/2 Antiferromagnetic Chain in a Transverse Magnetic Field. Phys Rev Lett (2018) 120:207205. doi:10.1103/physrevlett.120.207205

PubMed Abstract | CrossRef Full Text | Google Scholar

14. Wang Z, Schmidt M, Loidl A, Wu JD, Zou HY, Yang W, et al. Quantum Critical Dynamics of a Heisenberg-Ising Chain in a Longitudinal Field: Many-Body Strings versus Fractional Excitations. Phys Rev Lett (2019) 123:067202. doi:10.1103/physrevlett.123.067202

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Zhang L. Universal Thermodynamic Signature of Self-Dual Quantum Critical Points. Phys Rev Lett (2019) 123:230601. doi:10.1103/physrevlett.123.230601

PubMed Abstract | CrossRef Full Text | Google Scholar

16. Kenzelmann M, Coldea R, Tennant DA, Visser D, Hofmann M, Smeibidl P, et al. Order-to-disorder Transition in theXY-like Quantum magnetCs2CoCl4induced by Noncommuting Applied fields. Phys Rev B (2002) 65:144432. doi:10.1103/physrevb.65.144432

CrossRef Full Text | Google Scholar

17. Breunig O, Garst M, Sela E, Buldmann B, Becker P, Bohatý L, et al. Spin-12XXZChain SystemCs2CoCl4in a Transverse Magnetic Field. Phys Rev Lett (2013) 111:187202. doi:10.1103/physrevlett.111.187202

PubMed Abstract | CrossRef Full Text | Google Scholar

18. Rost AW, Perry RS, Mercure J-F, Mackenzie AP, Grigera SA. Entropy Landscape of Phase Formation Associated with Quantum Criticality in Sr 3 Ru 2 O 7. Science (2009) 325:1360–3. doi:10.1126/science.1176627

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Sologubenko AV, Lorenz T, Ott HR, Freimuth A. Thermal Conductivity via Magnetic Excitations in Spin-Chain Materials. J Low Temp Phys (2007) 147:387–403. doi:10.1007/s10909-007-9317-x

CrossRef Full Text | Google Scholar

20. Takahashi M, Suzuki M. One-Dimensional Anisotropic Heisenberg Model at Finite Temperatures. Prog Theor Phys (1972) 48:2187–209. doi:10.1143/ptp.48.2187

CrossRef Full Text | Google Scholar

21. Jordan P, Wigner E. Über das Paulische Äquivalenzverbot. Z Physik (1928) 47:631–51. doi:10.1007/bf01331938

CrossRef Full Text | Google Scholar

22. Fröbrich P, Kuntz PJ. Many-body Green's Function Theory of Heisenberg Films. Phys Rep (2006) 432:223. doi:10.1016/j.physrep.2006.07.002

CrossRef Full Text | Google Scholar

23. de Lima JP, Gonçalves LL. The XY Model on the One-Dimensional Superlattice: Static Properties. J Mag Mag Mater (1999) 206:135–48. doi:10.1016/s0304-8853(99)00446-1

CrossRef Full Text | Google Scholar

24. Franco V, Blázquez JS, Ipus JJ, Law JY, Moreno-Ramírez LM, Conde A. Magnetocaloric Effect: From Materials Research to Refrigeration Devices. Prog Mater Sci (2018) 93:112–232. doi:10.1016/j.pmatsci.2017.10.005

CrossRef Full Text | Google Scholar

25. Heidrich-Meisner F, Honecker A, Cabra DC, Brenig W. Thermal Conductivity of Anisotropic and Frustrated Spin-12chains. Phys Rev B (2002) 66(R):140406. doi:10.1103/physrevb.66.140406

CrossRef Full Text | Google Scholar

26. Orignac E, Chitra R, Citro R. Thermal Transport in One-Dimensional Spin gap Systems. Phys Rev B (2003) 67:134426. doi:10.1103/physrevb.67.134426

CrossRef Full Text | Google Scholar

27. Zotos X. High Temperature Thermal Conductivity of Two-Leg Spin- 1/2 Ladders, Phys Rev Lett (2004) 92:067202. doi:10.1103/physrevlett.92.067202

PubMed Abstract | CrossRef Full Text | Google Scholar

28. Heidrich-Meisner F, Honecker A, Brenig W. Thermal Transport of theXXZchain in a Magnetic Field. Phys Rev B (2005) 71:184415. doi:10.1103/physrevb.71.184415

CrossRef Full Text | Google Scholar

29. Hess C, ElHaes H, Waske A, Büchner B, Sekar C, Krabbes G, et al. Linear Temperature Dependence of the Magnetic Heat Conductivity in CaCu2O₃. Phys Rev Lett (2007) 98:027201. doi:10.1103/physrevlett.98.027201

PubMed Abstract | CrossRef Full Text | Google Scholar

30. Biswas A, Chandra S, Samanta T, Ghosh B, Datta S, Phan MH, et al. Universality in the Entropy Change for the Inverse Magnetocaloric Effect. Phys Rev B (2013) 87:134420. doi:10.1103/physrevb.87.134420

CrossRef Full Text | Google Scholar

31. Biswas A, Chandra S, Samanta T, Phan MH, Das I, Srikanth H. The Universal Behavior of Inverse Magnetocaloric Effect in Antiferromagnetic Materials. J Appl Phys (2013) 113:17A902. doi:10.1063/1.4793768

CrossRef Full Text | Google Scholar

32. Yang B, Chen Y-Y, Zheng Y-G, Sun H, Dai H-N, Guan X-W, et al. Quantum Criticality and the Tomonaga-Luttinger Liquid in One-Dimensional Bose Gases. Phys Rev Lett (2017) 119:165701. doi:10.1103/physrevlett.119.165701

PubMed Abstract | CrossRef Full Text | Google Scholar

33. Adelhardt P, Koziol JA, Schellenberger A, Schmidt KP. Quantum Criticality and Excitations of a Long-Range Anisotropic XY Chain in a Transverse Field. Phys Rev B (2020) 102:174424. doi:10.1103/physrevb.102.174424

CrossRef Full Text | Google Scholar

34. Blosser D, Bhartiya VK, Voneshen DJ, Zheludev A. z=2 Quantum Critical Dynamics in a Spin Ladder. Phys Rev Lett (2018) 121:247201. doi:10.1103/physrevlett.121.247201

PubMed Abstract | CrossRef Full Text | Google Scholar

35. Essam JW, Fisher ME. Padé Approximant Studies of the Lattice Gas and Ising Ferromagnet below the Critical Point. J Chem Phys (1963) 38:802–12. doi:10.1063/1.1733766

CrossRef Full Text | Google Scholar