Abstract
Unlike their cuprate counterparts, the undoped nickelates are weak insulators without long-range antiferromagnetic order. Identifying the origin of this insulating behavior, found on both sides of the superconducting dome, is potentially a crucial step in the development of a coherent understanding of nickelate superconductivity. In this work, we study the normal-state resistivity of infinite-layer nickelates using high magnetic fields to suppress the superconductivity and examine the impact of disorder and doping on its overall temperature (T) dependence. In superconducting samples, the resistivity of Nd- and La-based nickelates continues to exhibit weakly insulating behavior with a magnitude and functional form similar to that found in underdoped electron-doped cuprates. We find a systematic evolution of the insulating behavior as a function of nominal hole doping across different rare-earth families, suggesting a pivotal role for strong electron interactions, and uncover a correlation between the suppression of the resistivity upturn and the robustness of the superconductivity. By contrast, we find very little correlation between the level of disorder and the magnitude and onset temperature of the resistivity upturn. Combining these experimental observations with previous Hall effect measurements on these two nickelate families, we consider various possible origins for this correlated insulator behavior and its evolution across their respective phase diagrams.
Introduction
The recent discovery of superconductivity in the infinite-layer nickelates (ILN) [1–4] represents the culmination of a three-decade-long search to successfully dope the 3d9 (Ni1+) configuration in a square planar geometry as a means of replicating the structural and orbital motif found in high-Tc cuprates. Unlike the cuprates, whose parent ground state is a Mott insulator with long-range antiferromagnetic (AFM) order, the undoped ILN were found to be metallic at elevated temperatures with a crossover to a weakly insulating state below approximately 100 K, at which the resistivity starts to develop a moderate upturn. While static AFM order has thus far remained undetected in the nickelates, recent resonant x-ray scattering [5] and nuclear magnetic resonance (NMR) experiments [6, 7] reported signatures consistent with fluctuating AFM paramagnon excitations. Other NMR studies, however, claimed an absence of magnetic order in the nickelates [8]. The occurrence of weakly insulating behavior at a high hole doping level, beyond the range within which superconductivity is realized, further contrasts with the correlated but nonetheless metallic ground state found in highly overdoped cuprates [9]. Numerous theoretical calculations [10–22] have indeed pointed out that the 5d (and possibly 4f) band of the rare-earth (RE) elements contributes a finite density of states at the Fermi level, highlighting a fundamental difference between the two 3d9 oxides. The sizeable negative Hall coefficient [1, 3] and the finite spectral weight at the Fermi level [23] experimentally found in undoped nickelates appear to corroborate this picture.
Despite the recent progress in understanding the low-energy electronic structure of superconducting nickelates, an understanding of the anomalous insulating behavior that is ubiquitously found in ILN is lacking. Here, we present a systematic study of the normal-state transport of two doped families of ILN—the Nd- and La-based systems—by employing high magnetic fields up to 35 T to fully suppress the superconductivity. The effect of varying the rare-earth (RE) element on the functional form of the insulating resistivity, as well as the impact of (hole) doping and disorder level on the transport characteristics are also investigated. By taking into account the evolution of the Hall coefficient in both systems, we arrive at a number of salient points with regards to the origin of the insulating behavior: 1) The resistive upturns at low doping are likely to be due to a partial gapping of the states derived from the RE ions. 2) Hole doping x is much more effective in suppressing the resistivity upturn than a decrease in disorder (as inferred from the residual resistivity ratio). 3) The upturns, though notably weaker in the superconducting samples, nevertheless persist into the superconducting regime, and show a different functional form depending on the choice of RE. 4) In this region of the phase diagram, the insulating behavior is more likely to be associated with the correlated 3d states on the Ni. 5) The field dependence of the magnetoresistance in superconducting samples appears to rule out localization or the Kondo effect as the origin of the resistive upturns. 6) The RE dependence on the functional form of the low-T resistivity, as well as its overall magnitude, are more reminiscent of that seen in electron-doped cuprates than in hole-doped cuprates. 7) Finally, we find that Tc in the nickelates is sensitive to the level of disorder, suggesting that superconductivity in the ILN is unconventional in nature.
Materials and Methods
La1−xSrxNiO2 and PrNiO2 thin films were grown by pulsed laser technique described in [3, 24], respectively. Electrical resistivity was measured with a four-point configuration using the ac lock-in technique, with an alternating current I = 10 μA applied within the ab-plane at a frequency between 13 and 30 Hz. Static magnetic fields up to 35 T, applied parallel to the crystalline c-axis, were generated using a Bitter magnet at the High Field Magnet Laboratory in Nijmegen, the Netherlands.
Results and Discussion
Figure 1 shows the T-dependent in-plane resistivity ρab(T) of a set of undoped RENiO2 films (RE = La, Pr, Nd). Several key features of its normal-state resistivity are revealed in these plots. Firstly, for all films, ρab(T) undergoes a resistivity minimum (ρmin) at T = Tmin that delineates the metallic regime from the insulating-like regime at lower temperatures. Secondly, the absolute values of ρab show significant variation between samples, with the newer generation exhibiting lower absolute resistivities as well as a reduced level of disorder, as inferred from the higher ρ300K/ρmin ratios. As ρ300K/ρmin increases, Tmin shifts to lower values, suggesting that disorder plays some role in the insulating behavior, at least in the parent compound(s). (The resistivity of LaNiO2 from an early report [25] was found to be an exceptionally low yet its ρ300K/ρmin ratio is the lowest among all samples investigated, the origin of which is yet unclear). Thirdly, in the high-T metallic regime for PrNiO2 and NdNiO2, the slope dρab/dT is found to be very similar despite a large variation in their absolute values. This suggests that the excess disorder, while increasing the impurity scattering rate (and the magnitude of ρab), does not significantly affect the intrinsic metallic resistivity. Fourthly, the functional form of the resistive upturn over the accessible temperature range depends on the choice of RE. In LaNiO2, for example, ρab(T) initially follows a log(1/T) behavior for T < Tmin but then tends towards a constant value below 10 K. In contrast, ρab(T) in PrNiO2 and NdNiO2ρab(T) ∝ log(1/T) down to the lowest measured temperatures. Whether or not ρab(T) in (Pr, Nd)NiO2 saturates below ≈2 K, however, remains to be seen.
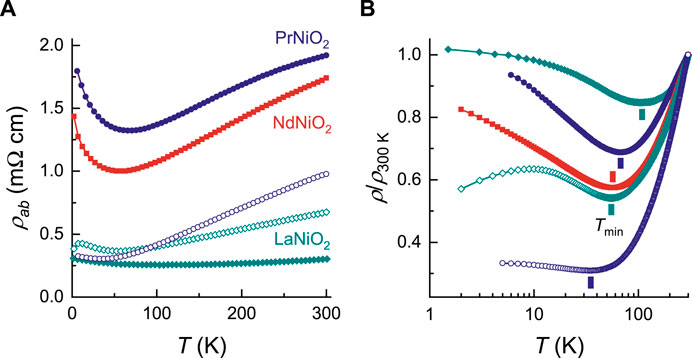
FIGURE 1
In-plane resistivity versus temperature ρab(T) for undoped infinite-layer nickelates with selected rare earth elements. (A) Data from a previous generation of samples of PrNiO2 [2], NdNiO2 [28], and LaNiO2 [25] are shown in solid points; data from a new generation of samples of LaNiO2 [3] and PrNiO2 (this work) in open points. (B) Normalized resistivity ρ(T)/ρ300 K in linear-log scale with the same color code as in (A). Vertical bars indicate Tmin, the temperature at which ρab shows a minimum.
An emerging picture for the electronic structure of undoped ILN, based on recent spectroscopic studies and realistic theoretical calculations with electron interaction taken into account [15, 16, 23, 26, 27], indicates that its Fermi surface comprises a small electron pocket with a dominant character of the RE 5d band (which hybridizes with the Ni 3 band). The Ni 3 band, on the other hand, is split into the upper and lower Hubbard bands and thus does not directly contribute to the Fermi level. The Hall coefficient RH(T) in both LaNiO2 and NdNiO2 is found to be negative [3, 28], consistent with the notion that the 3d states on the Ni sites are Mott localized and that the longitudinal and Hall conductivities are dominated by the electron pocket derived from the RE 5d states. Hence, it is these states that must be responsible for the resistive upturns in the parent compounds. Secondly, in both systems, Tmin is found to mark the onset of a marked increase in RH(T), possibly indicating some form of gap opening below Tmin. Thirdly, the fact that ρab(T) appears to saturate eventually, at least in LaNiO2 (and possibly in PrNiO2 too), implies that this gapping is only partial and that a finite density of states remains on the electron pocket(s) whose low-T ground state is ultimately metallic.
According to the conventional Drude transport model, the electrical conductivity σ is given bywhere i denotes the distinct channel of conducting carriers, e is the elementary charge, and (μ, τ, m*) denote the associated mobility, relaxation time, and effective mass, respectively. Consequently, ρ = 1/(neμ) = RH/μ for a single-band metal, where is the Hall coefficient. From Eq. 1, it can be seen that a reduction of conductivity (i.e. a metal-insulator transition) can be caused by a reduction of n (loss of carrier) or τ (increased scattering rate), an increase in m* (effective mass enhancement), or a combination of these factors. For simplicity, here we estimate the carrier mobility using the measured RH, known as the Hall mobility μH = RH/ρ for undoped LaNiO2 and NdNiO2, for which the single-band picture is most likely to apply. As shown in Figure 2, both LaNiO2 and NdNiO2 show a relatively unchanged μH above Tmin, below which μH increases moderately. Crucially, the increase in μH below Tmin indicates that the increase in ρ below Tmin is not related to a reduction of mobility (i.e. a change in τ/m*), but is most likely caused by a reduction in n. The minimization of RH at low T as x approaches 0.20, at which Tmin and ρ0 − ρmin are most suppressed (see Figure 4) further supports this scenario. Possible candidates responsible for the loss of carriers below Tmin include the emergence of a secondary order parameter (e.g. magnetic, charge, or stripe order), the opening of a pseudogap that partially depletes the density of states at the Fermi level [29], or a transfer of spectral weight to higher energy [30, 31].
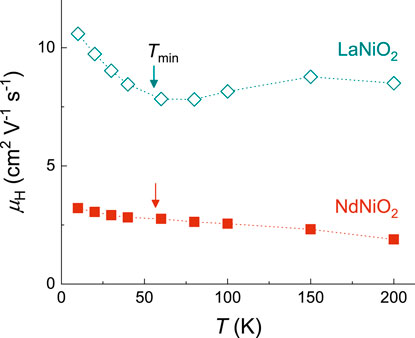
FIGURE 2
Hall mobility μH of undoped LaNiO2 and NdNiO2. μH is estimated using μH = RH/ρ with the Hall coefficient data RH reported in [3, 28] and ρ as shown in Figure 1. The locations of Tmin are marked by vertical arrows.
With hole-doping, the situation evolves in a systematic fashion. In Nd1−xSrxNiO2, we revealed previously by destroying superconductivity with a large magnetic field, that the resistivity upturn, though persisting throughout the doping range of superconductivity, is progressively suppressed, essentially vanishing as x approaches the edge of the superconducting dome xc ≈ 0.225 [32]. Here, we examine the evolution of the low-T resistivity in La1−xSrxNiO2 in the field-induced normal state for 0.15 0.20, i.e. across much of the superconducting doping range [3]. A contrasting behavior manifests in the functional form of ρab(T) below Tc, as shown in Figure 3. Similar to the undoped compound, ρab(T) in the field-induced normal state of superconducting La1−xSrxNiO2 exhibits an initial log(1/T)-behavior followed by a leveling off as T → 0. The magnitude of the resistive upturn decreases as x increases from 0.15 to 0.18, after which it again increases at x = 0.20.
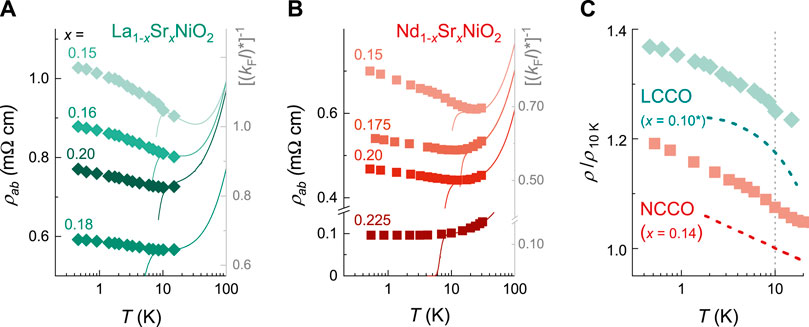
FIGURE 3
Normal-state resistivity of superconducting nickelates at low temperatures. (A)ρab(T) of La1−xSrxNiO2 and (B) Nd1−xSrxNiO2 [32] thin films with 0.15 0.20 measured at zero applied magnetic field (lines) and at 35 T (solid points). Magnetic field is applied along the crystalline c-axis. Right axis shows the estimates of assuming a two-dimensional free electron model (see main text for details). (C) Comparison of resistivity normalized by its 10 K value in the field-induced normal state, ρ/ρ10 K, for selected hole-doped nickelates (x = 0.15) and electron-doped cuprates below optimal dopings as specified. LCCO: representative rhoab(T) La2−xCexCuO4 measured at μ0H = 10 T [38]. NCCO: representative rhoab(T) Nd2−xCexCuO4 measured at μ0H = 14 T [37]. Note that the temperature axes are shown in log-scale and a vertical shift is applied to (C) for clarity. For LCCO, a rescaling factor of 0.50 is applied to the change in ρ/ρ10 K, which does not affect the functional form of ρ(T).
The overall magnitude of the resistive upturn, on the order of 10% between 0.5 K and Tmin, is considerably smaller than that observed in the underdoped hole-doped cuprates (≳ 100%) [33, 34, 35] but is comparable with that reported in the electron-doped cuprates RE2−xCexCuO4 below optimal doping [36–38]. A direct comparison of the low-T resistivities in the ILN and RE2−xCexCuO4 is shown in Figure 3C. Intriguingly, the functional form of the low-T resistivity in RE2−xCexCuO4 also depends on the RE elements in a similar manner to what is seen in the ILN. For La2−xCexCuO4 (LCCO, x = 0.08) ρab(T) appears to saturate below 4 K, while for Nd2−xCexCuO4 (NCCO, x = 0.14), ρab(T) ∝ log(1/T) down to the lowest measured temperature. This close alignment to the experimental situation in the n-doped cuprates is curious, but may simply be a consequence of the way in which carriers are doped into each system. In the cuprates, doped holes sit preferentially on the O sites while doped electrons reside on the Cu sites [39]. In the ILN, it is thought that the carriers are also introduced directly into the 3 orbital on the Ni sites [40]. At the same time, the similarities found in the low-T ρab(T) behavior of the ILN (for which no long-range AFM order exists at half-filling) and the n-doped cuprates suggests that the resistive upturns in the latter are not necessarily caused by short-range spin correlations, as is believed to be the case for the p-doped cuprates.
The evolution of RH(T) with doping in both ILN families is qualitatively the same, with a gradual reduction in the overall magnitude of RH culminating in a crossover from negative to positive RH(0) (the Hall coefficient in the low-T limit) around optimal doping [1, 3]. In any two-band metallic system, the sign of RH(0) reflects the sign of the most mobile carriers. Hence, the observed sign change signals a delocalization of the 3d hole states on the Ni sites with hole-doping until eventually, they become the most mobile carriers in each system. Nevertheless, the fact that ρab(T) continues to exhibit a logarithmic divergence (at least in Nd1−xSrxNiO2) implies that these carriers are also prone to some form of localization, however weak. (Note that RH(T) exhibits no upturns within the superconducting doping range, and so it is unlikely that the resistive upturns here are due to partial gapping).
It was noted early on that the insulator-to-metal crossover in the cuprates occurs at a threshold value of kFℓ > 10 for both the hole- [35] and electron-doped [36] compounds, far higher than the usual criterion kFℓ ≈ 1. Assuming that the suppression of the resistive upturn in Nd0.775Sr0.225NiO2 reflects a metallic ground state and using the two-dimensional free electron model [35]:where d is the c-axis lattice spacing, kF is the Fermi wavevector, and l is the electronic mean free path, we find a threshold kFl ≈ 2 − 10 for low-T metallicity in the ILN. We note, however, that the assumption of a single-band, 2D Fermi surface is likely not valid for the entire series of hole-doped nickelates (due to the expected presence of a 3D electron pocket derived from the 5d band of RE elements); therefore the estimates of kFl here should be interpreted with caution.
Several proposals have been put forward to explain the anomalous upturn in the normal-state resistivity in the nickelates [31, 41, 42]. Two well-known mechanisms to produce a logarithmically diverging resistivity at low T are weak localization due to disorder [43, 44] and Kondo scatterings due to magnetic impurities [14, 45]. In both circumstances, however, a strong negative magnetic-field dependence of the insulating resistivity is expected, which is not observed in the nickelates. Moreover, a monotonic suppression of the insulating behavior with decreasing residual resistivity, expected for a localization-driven origin, is not seen (Figure 4) while the re-entrant insulating behavior found at high dopings also cannot be naturally explained by a Kondo-like mechanism.
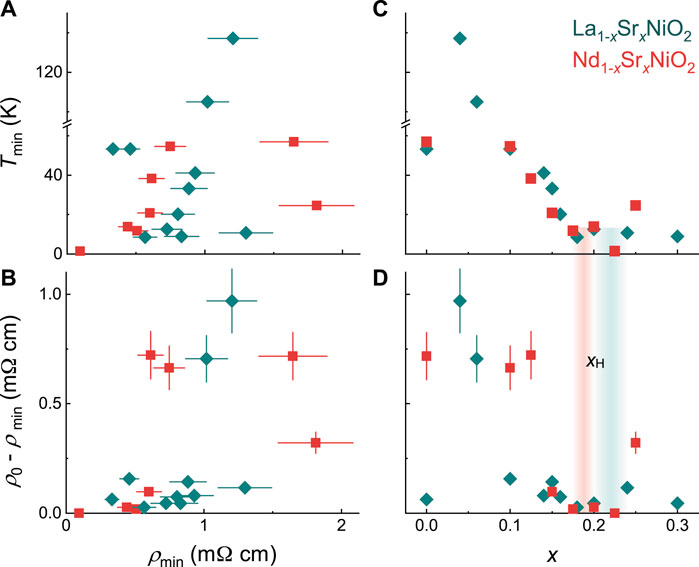
FIGURE 4
Effect of disorder and hole doping on the insulating characteristics. (A) Onset temperature of the resistive upturn (Tmin) and (B) its absolute magnitude (ρ0 − ρmin) versus the normal-state resistivity at its minimum (ρmin) for La1−xSrxNiO2 (diamonds) and Nd1−xSrxNiO2 (squares). (C)Tmin and (D)ρ0 − ρmin versus the hole doping x given by the nominal Sr level. Color shades indicate the doping levels xH at which the Hall coefficients change sign at low temperatures (10 K) [3, 28]. Error bars of 15% due to geometric uncertainties are applied to the resistivity data.
In order to gain further insights into the origin of the resistive upturns, we have examined the impact of disorder and doping on the insulating characteristics in the ILN, namely the onset temperature (Tmin) and the size of the resistivity upturn (ρ(T → 0) − ρ(Tmin), denoted as ρ0 − ρmin), as shown in Figure 4. We find no clear correlations between Tmin and ρmin (Figure 4A) nor between ρ0 − ρmin and ρmin (Figure 4B), for both Nd1−xSrxNiO2 and La1−xSrxNiO2. Meanwhile, Tmin and ρ0 − ρmin both appear to collapse near x = 0.20 (Figures 4C,D), though deviations from the overall trends are visible both at zero doping and at the highest dopings. Notably, while Tmin and ρ0 − ρmin are gradually suppressed with improved sample quality (Figure 1B), varying x is seen as much more effective in suppressing the insulating behavior, suggesting that it is sensitive to carrier screenings and primarily driven by electron correlation effects. A number of non-Fermi-liquid models have been proposed to explain the anomalous insulating behavior seen in underdoped cuprates, including those based on the marginal Fermi liquid [46], the 2D Luttinger liquid [47] and the polaronic Bose liquid [48] model. The relevance of these more exotic models to the ILN, whose distinction from the (hole-doped) cuprates has become increasingly established, remains to be examined.
Lastly, we examine the impact of disorder on the critical temperature of superconducting nickelates. Figure 5 shows a compilation of Nd0.8Sr0.2NiO2 resistivity data reported to date [1, 28, 32, 49–53]. A large difference in the absolute values of ρab is found, with ρab(300 K) ranging from ∼ 0.1–6.75 mΩ cm for nominally the same samples. Meanwhile, the agreement in the normalized resistivity ρ/ρ300 K is much better across different reports, as shown in Figure 5B, with a good overlap found in 6 out of 9 traces. This suggests the discrepancy in the absolute resistivities arises from geometric uncertainties. Importantly, we find that Tc depends strongly on the residual resistivity ratio, defined as ρ300 K/ρ20 K, with Tc increasing from ≈5 K to over 12.5 K as ρ300 K/ρ20 K increases. Such a strong dependence of Tc with respect to the level of disorder points to an unconventional nature of the superconductivity in the nickelates, and hints at a possible further increase in Tc with improved sample quality.
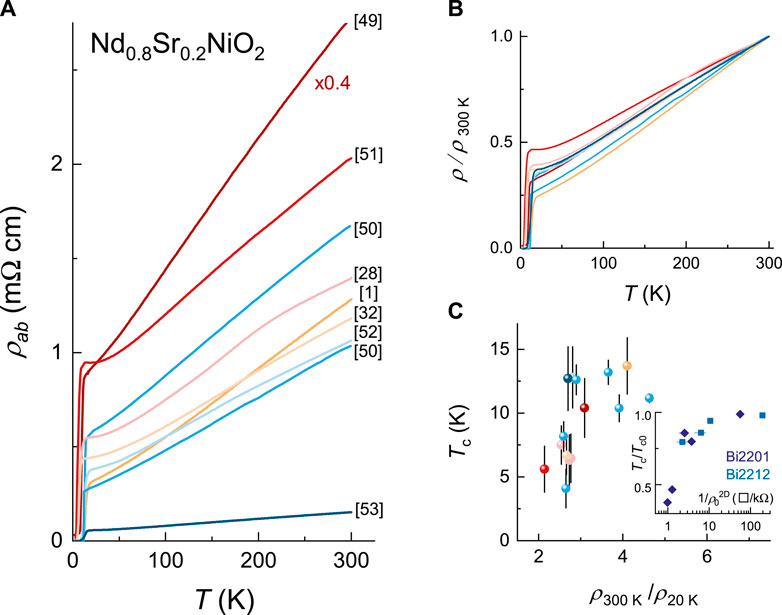
FIGURE 5
Impact of disorder on the critical temperature Tc of Nd0.8Sr0.2NiO2. (A) A compilation of representative resistivity data on Nd0.8Sr0.2NiO2 films reported in [1, 28, 32, 49–53]. Data reported in [49] is rescaled by a factor of 0.4 for clarity. (B) Normalized resistivity ρ/ρ300 K of data shown in (A). (C)Tc versus residual resistivity ratio ρ300 K/ρ20 K. Tc is defined as the midpoint of the resistive superconducting transition and the error bars reflect the 10–90% transition width. The same color code is applied to all panels. Inset: The impact of disorder on Tc of Bi-based cuprates. For both Bi2(Sr, La)2CuO6+δ (Bi2201) and Bi2Sr2CaCu2O8+δ (Bi2212), Tc is found to be strongly reduced from the optimized value Tc0 with an increase in residual resistivity per CuO2 plane (, similar to that found in Nd0.8Sr0.2NiO2. Data reproduced from [54].
Conclusion
In summary, by suppressing superconductivity with high magnetic fields, we find the unusual resistivity upturn in the undoped infinite-layer nickelates persists into the superconducting regime and appears to be maximally suppressed near x = 0.20 in both La- and Nd-based systems. The resilience of the resistivity upturn against magnetic fields rules out localization and Kondo effect as its origin, and points to a partial gapping of the states with dominant RE 5d character as its cause at low doping as supported by Hall mobility analysis. In the superconducting doping range, the resistive upturn is found to be highly reminiscent in both its functional form and its overall magnitude to that found in electron-doped cuprates, which suggests the insulating behaviour is associated with the correlated Ni 3d states. While disorder has only a minor impact on the insulating behavior, the robustness of superconductivity is strongly affected by the level of disorder, pointing towards the unconventional nature of nickelate superconductivity.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
YTH, HYH and NEH conceived the experiments. MO, BW, SH, KL, and DL grew and prepared the thin-film samples. YTH, MB, CD, and SW performed the resistivity measurements. YTH and NEH analyzed the data and wrote the manuscript with contribution from all authors.
Funding
This work was supported by the Netherlands Organisation for Scientific Research (NWO) grant No. 16METL01 “Strange Metals” and the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (Grant Agreement No. 835279-Catch-22). The work at SLAC/Stanford is supported by the US Department of Energy, Office of Basic Energy Sciences, Division of Materials Sciences and Engineering, under contract number DE-AC02-76SF00515; and the Gordon and Betty Moore Foundations Emergent Phenomena in Quantum Systems Initiative through grant number GBMF9072 (synthesis equipment).
Acknowledgments
We acknowledge the support of the HFML-RU/NWO, a member of the European Magnetic Field Laboratory (EMFL).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
LiDLeeKWangBYOsadaMCrossleySLeeHRet alSuperconductivity in an Infinite-Layer Nickelate. Nature (2019) 572:624–7. 10.1038/s41586-019-1496-5
2.
OsadaMWangBYGoodgeBHLeeKYoonHSakumaKet alA Superconducting Praseodymium Nickelate with Infinite Layer Structure. Nano Lett (2020) 20:5735–40. 10.1021/acs.nanolett.0c01392
3.
OsadaMWangBYGoodgeBHHarveySPLeeKLiDet alNickelate Superconductivity without Rare‐Earth Magnetism: (La,Sr)NiO2. Adv Mater (2021) 33:2104083. 10.1002/adma.202104083
4.
ZengSWLiCJChowLECaoYZhangZTTangCSet alSuperconductivity in Infinite-Layer Lanthanide Nickelates (2021). preprints, arXiv:2105.13492.
5.
LuHRossiMNagAOsadaMLiDFLeeKet alMagnetic Excitations in Infinite-Layer Nickelates. Science (2021) 373:213–6. 10.1126/science.abd7726
6.
CuiYLiCLiQZhuXHuZYangY-f.et alNMR Evidence of Antiferromagnetic Spin Fluctuations in Nd 0.85Sr0.15 NiO2. Chin Phys. Lett. (2021) 38:067401. 10.1088/0256-307x/38/6/067401
7.
LinHGawrylukDJKleinYMHuangfuSPomjakushinaEvon RohrFet alUniversal Spin-Glass Behavior in Bulk La NiO2, PrNiO2, and NdNiO2. Preprints (2021). arXiv:2104.14324.
8.
ZhaoDZhouYBFuYWangLZhouXFChengHet alIntrinsic Spin Susceptibility and Pseudogaplike Behavior in Infinite-Layer LaNiO2. Phys Rev Lett (2021) 126:197001. 10.1103/physrevlett.126.197001
9.
NakamaeSBehniaKMangkorntongNNoharaMTakagiHYatesSJCet alElectronic Ground State of Heavily Overdoped nonsuperconducting La2−xSrx CuO4. Phys Rev B (2003) 68:100502. 10.1103/physrevb.68.100502
10.
LeeK-WPickettWE. Infinite-layer LaNiO2: Ni1+ is not Cu2+. Phys Rev B (2004) 70:165109. 10.1103/physrevb.70.165109
11.
NomuraYHirayamaMTadanoTYoshimotoYNakamuraKAritaR. Formation of a Two-Dimensional Single-Component Correlated Electron System and Band Engineering in the Nickelate Superconductor Nd NiO2. Phys Rev B (2019) 100:205138. 10.1103/physrevb.100.205138
12.
BotanaASNormanMR. Similarities and Differences between LaNiO2 and CaCuO2 and Implications for Superconductivity. Phys Rev X (2020) 10:011024. 10.1103/physrevx.10.011024
13.
WuXDi SanteDSchwemmerTHankeWHwangHYRaghuSet alRobust-wave Superconductivity of Infinite-Layer Nickelates. Phys Rev B (2020) 101:060504. 10.1103/physrevb.101.060504
14.
ZhangYHVishwanathA. Type-II T − J Model in Superconducting Nickelate Nd1−xSrxNiO2. Phys Rev Res (2020) 2:023112. 10.1103/physrevresearch.2.023112
15.
LechermannF. Late Transition Metal Oxides with Infinite-Layer Structure: Nickelates versus Cuprates. Phys Rev B (2020) 101:081110. 10.1103/physrevb.101.081110
16.
BeenELeeWSHwangHYCuiYZaanenJDevereauxTet alElectronic Structure Trends across the Rare-Earth Series in Superconducting Infinite-Layer Nickelates. Phys Rev X (2021) 11:011050. 10.1103/physrevx.11.011050
17.
KarpJBotanaASNormanMRParkHZinglMMillisA. Many-body Electronic Structure of NdNiO2 and CaCuO2. Phys Rev X (2020) 10:021061. 10.1103/physrevx.10.021061
18.
SakakibaraHUsuiHSuzukiKKotaniTAokiHKurokiK. Model Construction and a Possibility of Cupratelike Pairing in a New D9 Nickelate Superconductor (Nd, Sr)NiO2. Phys Rev Lett (2020) 125:077003. 10.1103/physrevlett.125.077003
19.
AdhikaryPBandyopadhyaySDasTDasguptaISaha-DasguptaT. Orbital-selective Superconductivity in a Two-Band Model of Infinite-Layer Nickelates. Phys Rev B (2020) 102:100501. 10.1103/physrevb.102.100501
20.
WangYKangCJMiaoHKotliarG. Hund’s Metal Physics: From SrNiO2 to LaNiO2. Phys Rev B (2020) 102:16118. 10.1103/physrevb.102.161118
21.
LiuZXuCCaoCZhuWWangZFYangJ. Doping Dependence of Electronic Structure of Infinite-Layer NdNiO2. Phys Rev B (2021) 103:045103. 10.1103/physrevb.103.045103
22.
HigashiKWinderMKunesJHarikiA. Core-level X-ray Spectroscopy of Infinite-Layer Nickelate: LDA + DMFT Study. Phys Rev X (2021) 11:041009. 10.1103/physrevx.11.041009
23.
ChenZOsadaMLiDBeenEMChenSDHashimotoMet alElectronic Structure of Superconducting Nickelates Probed by Resonant Photoemission Spectroscopy (2021). preprints, arXiv:2106.03963.
24.
OsadaMWangBYLeeKLiDHwangHY. Phase Diagram of Infinite Layer Praseodymium Nickelate Pr1−xSrx NiO2 Thin Films. Phys Rev Mater (2020) 4:121801. (R). 10.1103/physrevmaterials.4.121801
25.
IkedaAKrockenbergerYIrieHNaitoMYamamotoH. Direct Observation of Infinite NiO2planes in LaNiO2 films. Appl Phys Express (2016) 9:061101. 10.7567/apex.9.061101
26.
HeptingMLiDJiaCJLuHParisETsengYet alElectronic Structure of the Parent Compound of Superconducting Infinite-Layer Nickelates. Nat Mater (2020) 19:381–5. 10.1038/s41563-019-0585-z
27.
GoodgeBHLiDLeeKOsadaMWangBYSawatzkyGAet alDoping Evolution of the Mott-Hubbard Landscape in Infinite-Layer Nickelates. Proc Natl Acad Sci USA (2021) 118:e2007683118. 10.1073/pnas.2007683118
28.
LiDWangBYLeeKHarveySPOsadaMGoodgeBHet alSuperconducting Dome in Nd1−xSrxNiO2 Infinite Layer Films. Phys Rev Lett (2020) 125:027001. 10.1103/physrevlett.125.027001
29.
LaliberteFTabisWBadouxSVignolleBDestrazDMomonoNet alOrigin of the Metal-To-Insulator Crossover in Cuprate Superconductors. preprints (2016). arXiv:1606.04491.
30.
HusseyNETakenakaKTakagiH. Universality of the Mott-Ioffe-Regel Limit in Metals. Philos Mag (2004) 84:2847–64. 10.1080/14786430410001716944
31.
SinghN. A Road-Map of Nickelate Superconductivity (2019). preprints, arXiv:1909.07688.
32.
HsuY-TWangBYBerbenMLiDLeeKDuffyCet alInsulator-to-metal Crossover Near the Edge of the Superconducting Dome in Nd1−xSrx NiO2. Phys Rev Res (2021) 3:L042015. 10.1103/physrevresearch.3.l042015
33.
AndoYBoebingerGSPassnerAKimuraTKishioK. Logarithmic Divergence of Both In-Plane and Out-Of-Plane Normal-State Resistivities of Super conducting La2−xSrx CuO4 in the Zero-Temperature Limit. Phys Rev Lett (1995) 75:4662–5. 10.1103/physrevlett.75.4662
34.
BoebingerGSAndoYPassnerAKimuraTOkuyaMShimoyamaJet alInsulator-to-Metal Crossover in the Normal State of La2−xSrx CuO4 Near Optimum Doping. Phys Rev Lett (1996) 77:5417–20. 10.1103/physrevlett.77.5417
35.
OnoSAndoYMurayamaTBalakirevFFBettsJBBoebingerGS. Metal-to-Insulator Crossover in the Low-Temperature Normal State of Bi2 Sr2−xLax CuO6+δ. Phys Rev Lett (2000) 85:638–41. 10.1103/physrevlett.85.638
36.
FournierPMohantyPMaiserEDarzensSVenkatesanTLobbCJet alInsulator-Metal Crossover Near Optimal Doping in Pr2−xCex CuO4: Anomalous Normal-State Low Temperature Resistivity. Phys Rev Lett (1998) 81:4720–3. 10.1103/physrevlett.81.4720
37.
LiSYMoWQChenXHXiongYMWangCHLuoXGet alLow-temperature Transport Properties of Nd2−xCex CuO4+δ: Metal-Insulator Crossover in the Overdoped Regime. Phys Rev B (2002) 65:224515. 10.1103/physrevb.65.224515
38.
SarkarTMandalPRHigginsJSZhaoYYuHJinKet alFermi Surface Reconstruction and Anomalous Low-Temperature Resistivity in Electron-Doped La2−xCex CuO4. Phys Rev B (2017) 96:155449. 10.1103/physrevb.96.155449
39.
ArmitageNPFournierPGreeneRL. Progress and Perspectives on Electron-Doped Cuprates. Rev Mod Phys (2010) 82:2421–87. 10.1103/revmodphys.82.2421
40.
BotanaASKwan-Woo LeeKWNormanMRPardoVPickettWE. Low Valence Nickelates: Launching the Nickel Age of Superconductivity. preprints (2021) 10. arXiv:2111.01296.
41.
ZhangGMYangYFZhangFC. Self-doped Mott Insulator for Parent Compound of Nickelate Superconductors. Phys Rev B (2020) 101:020501. 10.1103/physrevb.101.020501
42.
WangZZhangG-MYangY-f.ZhangF-C. Distinct Pairing Symmetries of Superconductivity in Infinite-Layer Nickelates. Phys Rev B (2020) 102:220501. 10.1103/physrevb.102.220501
43.
Rullier-AlbenqueFAlloulHTourbotRProustC. Disorder and Transport in Cuprates: Weak Localization and Magnetic Contributions. Phys Rev Lett (2001) 87:157001. 10.1103/physrevlett.87.157001
44.
Rullier-AlbenqueFAlloulHBalakirevFProustC. Disorder, Metal-Insulator Crossover and Phase Diagram in High-T C Cuprates. Europhys Lett (2008) 81:37008. 10.1209/0295-5075/81/37008
45.
DaganYBarrMCFisherWMBeckRDhakalTBiswasAet alOrigin of the Anomalous Low Temperature Upturn in the Resistivity of the Electron-Doped Cuprate Superconductors. Phys Rev Lett (2005) 94:057005. 10.1103/PhysRevLett.94.057005
46.
KotliarGAbrahamsERuckensteinAEVarmaCMLittlewoodPBSchmitt-RinkS. Long-wavelength Behavior, Impurity Scattering and Magnetic Excitations in a Marginal Fermi Liquid. Europhys Lett (1991) 15:655–60. 10.1209/0295-5075/15/6/016
47.
AndersonPWRamakrishnanTVStrongSClarkeDG. Coherence and Localization in 2D Luttinger Liquids. Phys Rev Lett (1996) 77:4241–4. 10.1103/physrevlett.77.4241
48.
AlexandrovAS. Logarithmic normal State Resistivity of High-Tc Cuprates. Phys Lett A (1997) 236:132–6. 10.1016/s0375-9601(97)00714-7
49.
ZengSTangCSYinXLiCLiMHuangZet alPhase Diagram and Superconducting Dome of Infinite-Layer Nd1xSrxNiO2 Thin Films. Phys Rev Lett (2020) 125:147003. 10.1103/physrevlett.125.147003
50.
ZengSWYinXMLiCJTangCSHanKHuangZet alObservation of Perfect Diamagnetism and Interfacial Effect on the Electronic Structures in Nd0.8Sr0.2NiO2 Superconducting Infinite Layers (2021). arXiv:2104.14195
51.
GaoQZhaoYZhouX-JZhuZ. Preparation of Superconducting Thin Films of Infinite-Layer Nickelate Nd0.8Sr0.2NiO2. Chin Phys. Lett. (2021) 38:077401. 10.1088/0256-307x/38/7/077401
52.
XiangYLiQLiYYangHNieYWenH-H. Physical Properties Revealed by Transport Measurements for Superconducting Nd0.8Sr0.2NiO2 Thin Films. Chin Phys. Lett. (2021) 38:047401. 10.1088/0256-307x/38/4/047401
53.
LiYSunWYangJCaiXGuoWGuZet alImpact of Cation Stoichiometry on the Crystalline Structure and Superconductivity in Nickelates. Front Phys (2021) 9:719534. 10.3389/fphy.2021.719534
54.
HobouHIshidaSFujitaKIshkadoMKojimaKMEisakiHet alEnhancement of Superconducting Critical Temperature in Bi2Sr2CaCu2O8+δ by Controlling Disorder outside CuO2 Planes. Phys Rev B (2009) 79:064507. 10.1103/physrevb.79.064507
Summary
Keywords
superconductivity, nickelates, charge transport, metal-insulator crossover, high magnetic fields
Citation
Hsu Y-T, Osada M, Wang BY, Berben M, Duffy C, Harvey SP, Lee K, Li D, Wiedmann S, Hwang HY and Hussey NE (2022) Correlated Insulating Behavior in Infinite-Layer Nickelates. Front. Phys. 10:846639. doi: 10.3389/fphy.2022.846639
Received
31 December 2021
Accepted
11 February 2022
Published
24 March 2022
Volume
10 - 2022
Edited by
Veerpal Singh Awana, National Physical Laboratory (CSIR), India
Reviewed by
Jie Yuan, Institute of Physics (CAS), China
Atsushi Fujimori, Waseda University, Japan
Updates
Copyright
© 2022 Hsu, Osada, Wang, Berben, Duffy, Harvey, Lee, Li, Wiedmann, Hwang and Hussey.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Y.-T. Hsu, yute.hsu@ru.nl
This article was submitted to Condensed Matter Physics, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.