Abstract
Entangled photons are promising candidates for a variety of novel spectroscopic applications. In this paper, we simulate two-photon absorption (TPA) of entangled photons in a molecular ensemble with inhomogeneous broadening. We compare our results with a homogeneously broadened case and comment on the consequences for the possible quantum enhancement of TPA cross sections. We find that, while there are differences in the TPA cross section, this difference always remains small and of the order unity. We further consider the impact of the polarization degrees of freedom and carry out the orientational average of a model system Hamiltonian. We find that certain molecular geometries can give rise to a substantial polarization dependence of the entangled TPA rate. This effect can increase the TPA cross section by up to a factor of five.
1 Introduction
Entangled photons have been identified as promising new tools for spectroscopic or imaging applications [1–7]. Their strong quantum correlations could circumvent certain classical Fourier uncertainties and thus enhance the sensing capabilities of optical measurements [8–16]. The detection of quantum correlations could also provide new spectroscopic information [17–25], and the use of quantum light in interferometric setups promises additional control knobs to analyze spectroscopic information [26–29] as well as access to out-of-time correlations [30]. The main driving force behind this development of entangled photon spectroscopy, however, is the linear scaling of nonlinear optical signals such as the two-photon absorption (TPA) rate with the incident photon flux [31–34], which could enable measurements on photosensitive samples at reduced photon numbers. This linear scaling has been observed conclusively in atomic samples [33, 35, 36]. Similar experiments in molecular samples, however, have resulted in widely differing estimates for the entangled two-photon absorption (ETPA) cross section σe [37–47]. The reported values range from σe ∼ 10–17 cm2 [37] or 10–21 cm2 [43] to cm2 [46, 47].
In theoretical work, recent analyses predict a very small enhancement of the ETPA cross section due to spectral entanglement [48, 49]. The key assumption in these publications is that molecular resonances are broadened much more strongly than their atomic counterparts. As a consequence, spectral quantum correlations cannot enhance the absorption probability in the same way as in atomic samples. This would imply that the large absorption cross sections mentioned above cannot be explained by ETPA, and have to be attributed to other processes that remain to be clarified. In contrast, another study by Kan et al. alleges that ETPA takes place into final states with much weaker broadening [50], such that large enhancements due to quantum correlations become possible. Here we investigate whether these two scenarios can give rise to vastly different absorption cross sections. In particular, we consider ETPA in an ensemble of inhomogeneously broadened molecules, where sharp absorption resonances are distributed randomly within a certain frequency distribution (see Figure 2). This enables us to interpolate between these two scenarios mentioned above. We will investigate whether strongly enhanced absorption in a subset of molecules that can be excited resonantly can overcompensate the reduced absorption probabilities in the remaining molecules.
In addition, we will scrutinize the impact of the polarization degrees of freedom on the ETPA cross section. By carrying out an orientational average of the molecular dipoles, we will explore how the relative orientation of the two dipoles affects the ETPA process. A recent study [43] detected no discernible dependence on the photon polarization. Here we show that this is true only for certain molecular dipole orientations.
2 The Model
We consider the interaction of broadband entangled photons with matter. For a quantum light field propagating in a fixed spatial direction (without loss of generality, we here consider the z-direction), the electric field operator in the interaction picture with respect to the field Hamiltonian reads [51]with the positive frequency componentand E(−) its hermitian conjugate. Here, ϵ0 denotes the vacuum permittivity, and A0 is the quantization area perpendicular to the propagation direction of the field. The photon annihilation and creation operators obey the usual permutation relations . The polarization vector distinguishes horizontal or vertical polarization. In the second line, we define the scalar fields Eν. In the following, we will consider a sample, which is placed at the origin of our coordinate system and set z = 0.
We will investigate the ETPA probability of a multilevel system with ground state g, an off-resonant intermediate states e, and a final state f. This is shown in Figure 1. The probability to excite the final state f can be derived with perturbation theory with respect to the light-matter interaction Hamiltonian, which reads within the rotating-wave approximation for a sample placed at the origin of our coordinate system
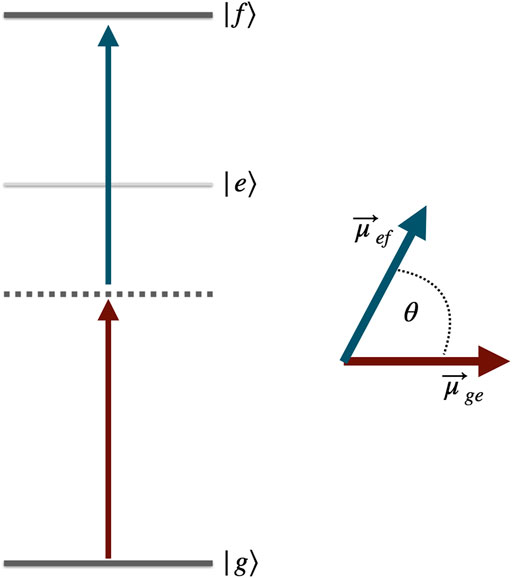
FIGURE 1
Level scheme and dipole orientation considered in this paper: We consider two-photon excitation from the ground state |g⟩ to the final state |f⟩. The intermediate state |e⟩ is far-off-resonant from the carrier frequencies of the two photons. The dipoles between ground and intermediate state, , and between intermediate and final state, , form a relative angle θ.
Here, V(−)(t) denotes the negative frequency component of the dipole operator, i.e. it creates a molecular excitation, and we have dropped the spatial dependence of the operators. A detailed account for the derivation of the ETPA probability can be found, e.g., in [49, 52]. Here, we only present the final result which, neglecting the polarization degrees of freedom at first, readswith the classical TPA cross section given by
Here, we have defined the transition frequency to the final state of the molecule, ωfg, as well as the inverse lifetime γfg. The intermediate state transition frequency is denoted ωeg, and dge and def are the dipole matrix elements connecting ground and intermediate, or intermediate and final states, respectively. In Eq. 5, we also included the so-called entanglement area A0, which could be a function of the entanglement of the two-photon state [44]. Here, we will not consider this effect and treat A0 as a constant. We further introduced the four-point correlation function of the field in the numerator of the second line of Eq. 5. It is evaluated with respect to the initial state of the light field, which we will specify later in Section 2.3. In writing Eq. 5, we require the intermediate states to be far off-resonant from the entangled photons’ centre frequency ω0. If this condition is violated the intermediate state resonances cannot be taken out of the frequency integrations and need to be considered separately [2]. In this resonant regime, which will not be considered here, we could already show how quantum correlations can enhance the absorption probability [53–55].
2.1 Inhomogeneous Broadening
Two-photon transitions in the presence of inhomogeneous broadening were already discussed in [56]. Here we model it by assuming that the resonance of the final state ωfg is distributed around a central value with a Gaussian distribution with width σD, i.e.
The TPA probability is then given by the average with respect to this ensemble,where PTPA (ωfg) is given by Eq. 5 at frequency ωfg. This situation is illustrated is Figure 2, where we plot the two-photon resonance in Eq. 5, i.e., vs. the detuning . In an inhomogeneously broadened ensemble, the broad resonance is in fact composed of the incoherent mixture of much more narrow resonances of the ensemble constituents. We note that the role of the Lorentzian width γfg changes between the homogeneously and inhomogeneously broadened samples. In the former case, Eq. 5, γfg denotes the width that one would measure in a spectroscopic experiment. In the latter case, it is the narrow linewidth of an individual molecule, but experiments would detect the much broader distribution described by Eq. 8. To distinguish the two situations, we will call the Lorentzian width in the inhomogeneously broadened sample the intrinsic width of the resonance, γinh in the following. In contrast, we will call it the homogeneous width γhom in the homogeneously broadened case.
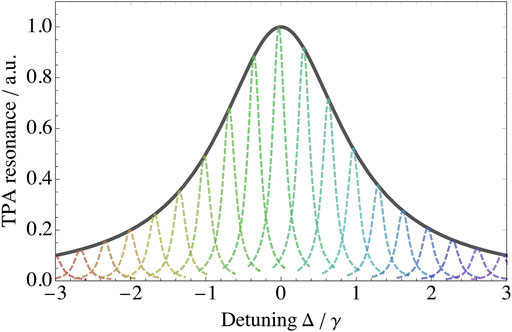
FIGURE 2
Inhomogeneously broadened two-photon absorption resonance, , vs. the detuning . The gray solid line corresponds to an homogenously broadened ensemble, whereas the small dashed Lorentzians indicate an inhomogeneously broadened ensemble which creates the same broad absorption feature.
2.2 Orientational Average
We next discuss how to carry out an orientational average of the molecular absorption. To this end, the dipole elements in Eq. 5 have to be treated as vectors, i.e. . More specifically, we consider dipole vectors in the molecular reference frame,
We further take the polarization of the light fields into account, see Equation 2. We then generalize Eq. 5 towhere the TPA tensor is given by
Here, we denote ⟨…,⟩ens the orientational average which accounts for the random orientation of the molecules in the sample with respect to the lab frame. To evaluate this average, we have to transform from the lab frame into the molecular frame. This orientational average was first carried out in [57]. The application to nonlinear spectroscopy can be found, e.g., in [58]. The result is that we can straightforwardly relate the dipole elements in the lab frame with the corresponding dipole vectors in the molecular frame using the transformationwhere the indices αi = x, y, z label the components of the dipole operator in the molecular frame. The transformation tensor is given by
2.3 The Field Correlation Function
We finally have to evaluate the field correlation function in Eqs 5, 11, respectively. For an initial two-photon state, which we will denote |ψ⟩, this function factorizes as
Here, we have inserted an identity in between and . For a two-photon state, the only non-vanishing contribution stems from the vacuum. In our discussion of the inhomogeneous broadening, where we do not account for the polarization degree of freedom, we simply drop the indices νi. With the entangled field propagating along the z-direction, see Eq. 2, we consider the horizontal polarization to be along the x-direction and the vertical polarization along the y-direction. In the third line, we defined the function Ψν,ν′(ω, ω′) = ⟨ 0|aν(ω)aν′(ω′)|ψ⟩, which is often called the two-photon wavefunction. Its absolute square is referred to as the joint spectral intensity. As explained in detail in [52], in the situation described by Eq. 5 where the intermediate states are far off-resonant and can be subsumed into σ(2), the marginal of the two-photon wavefunction along the anti-diagonal is what is relevant for the TPA process, and we can write Eq. 5 aswhere the marginal is given by
We further defined the detuning Δ = ωfg − 2ω0. In the homogeneously broadened case, we simply set this to zero (i.e. we assume that the entangled pair is resonant with the transition), but in the inhomogeneous case, this detuning will be weighted by the ensemble’s frequency distribution (7) below. In this paper, we will focus on bi-Gaussian two-photon wavefunctions, i.e. we writewhere σN is the spectral width of the individual photon wavepackets and σB is the width of the sum frequency ω + ω′. Please note the factor in front of the wavefunction, which accounts for the fact that in the case of indistinguishable photons we have the normalization ⟨ψ|ψ⟩ = 2∫dω∫dω′|Ψ(ω, ω′)|2/(2π)2 = 1. In a strongly entangled state, we will typically have σN ≫ σB. This regime is dominated by strong frequency anti-correlations between the entangled photons, as well as strong correlations in their respective arrival times [2]. We further write the full two-photon wavefunction aswhere we consider specifically the two cases
Please not that the factor is included in Eq. 20 to ensure normalization with respect to the frequency wavefunction (18). In the first two cases, f1 and f2, the two-photon state is not polarization entangled, as Eq. 18 is symmetric with respect to the exchange of its frequency arguments. In the latter case, the state is polarization entangled. We note that, as pointed out in [52], within the current model the molecular response is symmetric with respect to the exchange of the frequency arguments in Eq. 15, because any photon can excite either the g → e or the e → f transition. Consequently, even if the initial two-photon frequency wavefunction Ψ(ω, ω′) is not symmetric (as is the case, e.g., for type-II downconversion), the correlation function (15) selects the symmetric superposition . As a consequence, a photonic singlet state of the form will not give rise to a TPA signal within the current model due to the destructive interference between the two terms. This situation would change, for instance, in the presence of near-resonant intermediate states or any other process that breaks the abovementioned symmetry between the g → e and e → f transitions.
3 Results
3.1 Inhomogeneous Broadening
We now compare how inhomogeneously broadened ensembles can affect the two-photon absorption probability. In this part of our investigation, we will neglect the polarization degrees of freedom at first. For simplicity, we divide the ETPA probability, Eq. 5, by its constant prefactor . For each combination of intrinsic linewidth γinh and inhomogeneous broadening σD, we calculate the full width at half maximum of the f-state distribution as shown in Figure 3A. We also calculate the ETPA probability from Eq. 8. As shown in Figure 3B, its behaviour inversely follows the broadening of the f-state in the sense that a broader f-distribution in panel (a) results in a reduced ETPA probability. There is however a noticeable asymmetry between the two plots. The ETPA probability appears to be reduced more rapidly with increasing intrinsic linewidth γinh compared to an increase of the inhomogeneous broadening σD. This behaviour could be a consequence of the photonic entanglement and in the following we investigate it more closely.
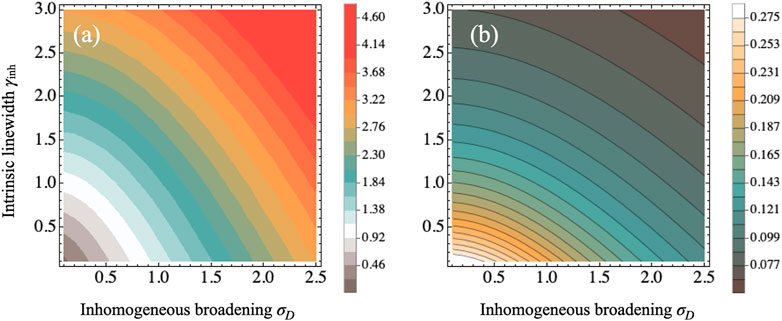
FIGURE 3
(A) Full width half maximum of the f-state resonance as a function of the intrinsic linewidth γinh and the inhomogeneous broadening σD. (B) ETPA probability according to Eq. 8 in units of as a function of the intrinsic linewidth γinh and the inhomogeneous broadening σD. We use an frequency-anticorrelated, entangled state with σN = 1 and σB = 1.
To compare ETPA in homogeneously and inhomogeneously broadened ensembles, we define the ratio between the absorption probability in an inhomogeneously broadened sample, Eq. 8, and in a homogeneously broadened sample, Eq. 5,where we use as homogeneous broadening γhom the width of the f-state distribution, which we determined in Figure 3A. We note, however, that the convolution of an intrinsic Lorentzian broadening with a Gaussian as in Eq. 8 gives rise to a Voigt line profile. This is markedly different from the Lorentzian resonance of the homogeneous case. As a consequence, one should keep in mind that the ratio (23) compares two slightly different situations.
We plot the ratio (23) in Figure 4 as a function of both γinh and σD for three different two-photon states. In Figure 4A, the entangled photons show very strong frequency anti-correlations, in panel (b) they are separable, and in panel (c) the show strong positive frequency correlations. We see that, even though there are notable differences between these cases, the general trend is identical. The ratio of the two excitation probabilities can be enhanced, and the effect increases with increasing inhomogeneous broadening σD and with decreasing intrinsic linewidth γinh. This effect is stronger when the exciting photon pair is entangled with strong frequency anti-correlations as in panel (a). In contrast, positive frequency correlations which are nevertheless associated with an entangled wave function, have the opposite effect and reduce this enhancement.
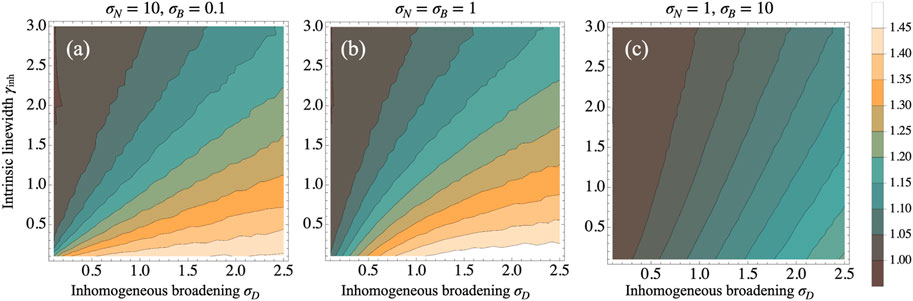
FIGURE 4
Ratio of the absorption probability (23) between ETPA in an inhomogeneously broadened sample and in a homogeneously broadened sample with the same linewidth broadening is plotted for three different input states vs. the intrinsic linewidth and the inhomogeneous broadening. As indicated above the contour plots, the parameters are chosen as (A)σN = 10 and σB = 0.1, i.e. a two-photon state featuring strong frequency anti-correlations, (B)σN = σB = 1, i.e. almost separable photon pairs, and (C)σN = 1 and σB = 10, i.e. a state featuring strong positive frequency correlations.
Still we also find that this enhancement saturates to increasing inhomogeneity of the distribution. This is shown in Figure 5 for different entanglement strengths. The broadening at which the saturation is reached depends strongly on the degree of entanglement. However, the ratio rrel always remains of order unity, as the enhanced resonant excitation probability is balanced by an increase in the number of molecules which can not be excited resonantly and thus become dark. Therefore, inhomogeneous broadening cannot account for the enormous disparity in the reported ETPA cross sections in the literature.
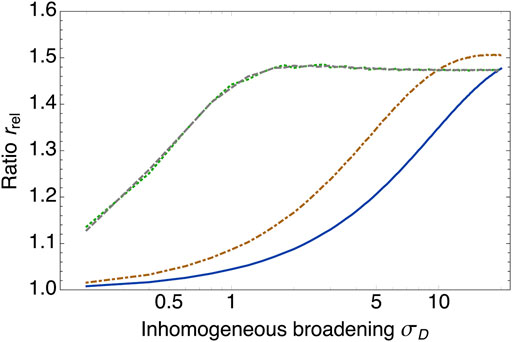
FIGURE 5
Ratio rrel, Eq. 23, is plotted vs. the inhomogeneous broadening σD and entangled states with σB = 20, σN = 1 (solid, blue), σB = 10, σN = 1 (dot-dashed, red), σN = σB = 1 (dotted, green), and σB = 1, σN = 10 (dashed, gray). The intrinsic broadening is fixed at γinh = 0.1.
3.2 Orientational Average
With our choice of the Gaussian two-photon wavefunction (18), which is symmetric with respect to its frequency arguments, we can separate the orientational average from the frequency integrations. Thus, using the definition of our molecular dipoles (10), their transformation to the laboratory frame in Eqs. 13, 14, we can carry out the index summations ν1, … , ν4 and α1, … , α4. Note that this orientational average will always reduce the ETPA rate, since the dipole vectors in Eqs. 11 are chosen normalized. As a consequence, their orientationally averaged overlap with any polarization mode will be smaller than unity.
For the polarization state (20), we obtain
Here, denotes the isotropic result where the vectorial nature of the dipoles and the photons has been neglected. Likewise, we obtain from Eq. 21and for the entangled polarization state (22), we arrive at
These results are shown in Figure 6. The separable states, Eqs 24, 25, show a weaker dependence on the dipole angle compared to the entangled state (26). The latter shows the largest dependence at an angle ϕ = 0, i.e. for a symmetric superposition state, where it also takes its maximal value. This is consistent with our discussion in Section 2.3, where we pointed out that the molecular response projects onto a symmetric superposition. Hence, such a state is optimal for the ETPA cross section. Conversely, the entangled state shows the smallest variation at ϕ = π/2 (not shown), where it coincides with the product state (25).
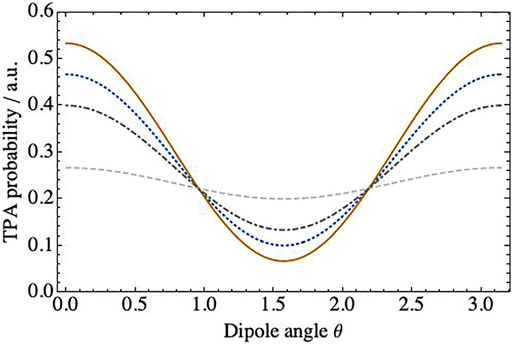
FIGURE 6
Polarization dependence of ETPA probability on the angle between the molecular dipoles according to Eq. 10. The gray, dashed line depicts the dependence (24) which is created by the input state (20). The black, dot-dashed line is given by Eq. 25, created by the state (21). The polarization dependence (26), which is created by the state (22), is shown as a solid, yellow line for ϕ = 0, and as a blue, dotted line for ϕ = π/3.
The polarization dependence of ETPA in rhodamine 6G molecules was carefully examined in [43], and no discernable dependence on the interphoton polarization angle was reported. This can be recounciled with our simulations provided the dipole angle is around θ ≃ π/3 or 2π/3. Indeed, as we see in Figure 6, in such a case the polarization state should not affect the ETPA probability regardless of the polarization state of the light. This appears broadly consistent with measurements in [59], where an angle of around 40° was reported, thus implying a rather weak ETPA polarization dependence. A further possibility, which we have not discussed here, would be the interference between different excitation pathways. Such a situation could wash out the strong polarization dependence observed here for a single excitation pathway.
4 Conclusion
In summary, we have extended the existing theory of entangled two-photon absorption to describe excitation in inhomogeneously broadened molecular ensembles, and to investigate the influence of the polarization degrees of freedom on ETPA.
In our investigation of inhomogeneously broadened samples, we showed that ETPA can be enhanced compared to homogeneously broadened samples. However, this enhancement always remains relatively small, of order unity. It cannot explain the several orders of magnitudes in difference among the various measured ETPA cross sections in the literature. The presence of near-resonant intermediate states could change this conclusion. As shown in [53–55], optimized entangled states of light can substantially enhance the ETPA probability. It remains an open question, however, how these conclusions would be affected by inhomogeneous broadening. Furthermore, entangled states with large spectral tails in their single-photon spectrum also affect the present conclusion. As shown in the context of virtual state spectroscopy [60], these large frequency tails render the key assumption in the current theoretical model - that intermediate states are far detuned from the photonic states (see Eq. 5) - problematic and further emphasize the need for the investigation of near-resonant intermediate states in ETPA.
In our simulation of the orientationally averaged absorption of polarization entangled photon pairs, we showed that polarization entanglement can have a substantial influence on the ETPA absorption probability. It can increase or reduce the absorption probability by as much as a factor of five, provided the molecular dipoles are aligned in parallel or perpendicular. These findings rely on a single excitation pathway, i.e. a single intermediate molecular state. In case there are several, competing excitation pathways, the pronounced angular dependence of the ETPA rate could be washed out by the mixing of these pathways. Furthermore, it is one of the consequences of the employed theoretical model, as observed already by Landes et al. in [60], that the molecular response projects the entangled photon wavefunction onto a symmetrized superposition. As a consequence, the present model predicts a vanishing ETPA probability for a photonic singlet state due to destructive interference. This effect could be tested experimentally, e.g., in atomic ETPA measurements. It could further provide an experimental test in molecular ETPA experiments to gauge the strength of single-photon losses, which should not be suppressed by destructive interference.
Statements
Data availability statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
The author acknowledges support from the Cluster of Excellence “Advanced Imaging of Matter” of the Deutsche Forschungsgemeinschaft (DFG) - EXC 2056 - project ID 390 715 994.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
DorfmanKESchlawinFMukamelSNonlinear Optical Signals and Spectroscopy with Quantum Light. Rev Mod Phys (2016) 88:045008. 10.1103/RevModPhys.88.045008
2.
SchlawinFEntangled Photon Spectroscopy. J Phys B: Mol Opt Phys (2017) 50:203001. 10.1088/1361-6455/aa8a7a
3.
SchlawinFDorfmanKEMukamelSEntangled Two-Photon Absorption Spectroscopy. Acc Chem Res (2018) 51:2207–14. 10.1021/acs.accounts.8b00173
4.
Gilaberte BassetMSetzpfandtFSteinlechnerFBeckertEPertschTGräfeMPerspectives for Applications of Quantum Imaging. Laser Photon Rev (2019) 13:1900097. 10.1002/lpor.201900097
5.
SzokeSLiuHHickamBPHeMCushingSKEntangled Light-Matter Interactions and Spectroscopy. J Mater Chem C (2020) 8:10732–41. 10.1039/D0TC02300K
6.
MukamelSFreybergerMSchleichWBelliniMZavattaALeuchsGet alRoadmap on Quantum Light Spectroscopy. J Phys B: At Mol Opt Phys (2020) 53:072002. 10.1088/1361-6455/ab69a8
7.
MaY-ZDoughtyBNonlinear Optical Microscopy with Ultralow Quantum Light. The J Phys Chem A (2021) 125:8765–76. 10.1021/acs.jpca.1c06797
8.
SchlawinFDorfmanKEFingerhutBPMukamelSSuppression of Population Transport and Control of Exciton Distributions by Entangled Photons. Nat Commun (2013) 4:1782. 10.1038/ncomms2802
9.
RaymerMGMarcusAHWidomJRVitulloDLPEntangled Photon-Pair Two-Dimensional Fluorescence Spectroscopy (Epp-2dfs). The J Phys Chem B (2013) 117:15559–75. 10.1021/jp405829n
10.
LeverFRamelowSGührMEffects of Time-Energy Correlation Strength in Molecular Entangled Photon Spectroscopy. Phys Rev A (2019) 100:053844. 10.1103/PhysRevA.100.053844
11.
DebnathARubioAEntangled Photon Assisted Multidimensional Nonlinear Optics of Exciton–Polaritons. J Appl Phys (2020) 128:113102. 10.1063/5.0012754
12.
IshizakiAProbing Excited-State Dynamics with Quantum Entangled Photons: Correspondence to Coherent Multidimensional Spectroscopy. J Chem Phys (2020) 153:051102. 10.1063/5.0015432
13.
OkaHEntangled Two-Photon Absorption Spectroscopy for Optically Forbidden Transition Detection. J Chem Phys (2020) 152:044106. 10.1063/1.5138691
14.
FujihashiYIshizakiAAchieving Two-Dimensional Optical Spectroscopy with Temporal and Spectral Resolution Using Quantum Entangled Three Photons. J Chem Phys (2021) 155:044101. 10.1063/5.0056808
15.
ChenFMukamelSVibrational Hyper-Raman Molecular Spectroscopy with Entangled Photons. ACS Photon (2021) 8:2722–7. 10.1021/acsphotonics.1c00777
16.
CutipaPChekhovaMVBright Squeezed Vacuum for Two-Photon Spectroscopy: Simultaneously High Resolution in Time and Frequency, Space and Wavevector. Opt. Lett. (2022) 47:465. 10.1364/OL.448352
17.
SchlawinFDorfmanKEMukamelSPump-probe Spectroscopy Using Quantum Light with Two-Photon Coincidence Detection. Phys Rev A (2016) 93:023807. 10.1103/PhysRevA.93.023807
18.
LiHPiryatinskiAJerkeJKandadaARSSilvaCBittnerERProbing Dynamical Symmetry Breaking Using Quantum-Entangled Photons. Quan Sci Technology (2017) 3:015003. 10.1088/2058-9565/aa93b6
19.
ZhangZSaurabhPDorfmanKEDebnathAMukamelSMonitoring Polariton Dynamics in the Lhcii Photosynthetic Antenna in a Microcavity by Two-Photon Coincidence Counting. J Chem Phys (2018) 148:074302. 10.1063/1.5004432
20.
LiHPiryatinskiASrimath KandadaARSilvaCBittnerERPhoton Entanglement Entropy as a Probe of many-body Correlations and Fluctuations. J Chem Phys (2019) 150:184106. 10.1063/1.5083613
21.
Sánchez MuñozCSchlawinFPhoton Correlation Spectroscopy as a Witness for Quantum Coherence. Phys Rev Lett (2020) 124:203601. 10.1103/PhysRevLett.124.203601
22.
GuBMukamelSManipulating Two-Photon-Absorption of Cavity Polaritons by Entangled Light. J Phys Chem Lett (2020) 11:8177–82. 10.1021/acs.jpclett.0c02282
23.
SchlawinFDorfmanKEMukamelSDetection of Photon Statistics and Multimode Field Correlations by Raman Processes. J Chem Phys (2021) 154:104116. 10.1063/5.0039759
24.
YangZSaurabhPSchlawinFMukamelSDorfmanKEMultidimensional Four-Wave-Mixing Spectroscopy with Squeezed Light. Appl Phys Lett (2020) 116:244001. 10.1063/5.0009575
25.
DorfmanKLiuSLouYWeiTJingJSchlawinFet alMultidimensional Four-Wave Mixing Signals Detected by Quantum Squeezed Light. Proc Natl Acad Sci (2021) 118. 10.1073/pnas.2105601118
26.
YeLMukamelSInterferometric Two-Photon-Absorption Spectroscopy with Three Entangled Photons. Appl Phys Lett (2020) 116:174003. 10.1063/5.0004617
27.
EshunAGuBVarnavskiOAsbanSDorfmanKEMukamelSet alInvestigations of Molecular Optical Properties Using Quantum Light and Hong–Ou–Mandel Interferometry. J Am Chem Soc (2021) 143:9070–81. 10.1021/jacs.1c02514
28.
AsbanSMukamelSDistinguishability and “Which Pathway”information in Multidimensional Interferometric Spectroscopy with a Single Entangled Photon-Pair. Sci Adv (2021) 7:eabj4566. 10.1126/sciadv.abj4566
29.
DorfmanKEAsbanSGuBMukamelSHong-ou-mandel Interferometry and Spectroscopy Using Entangled Photons. Commun Phys (2021) 4:49. 10.1038/s42005-021-00542-2
30.
AsbanSDorfmanKEMukamelSInterferometric Spectroscopy with Quantum Light: Revealing Out-Of-Time-Ordering Correlators. J Chem Phys (2021) 154:210901. 10.1063/5.0047776
31.
Gea-BanaclocheJTwo-photon Absorption of Nonclassical Light. Phys Rev Lett (1989) 62:1603–6. 10.1103/PhysRevLett.62.1603
32.
JavanainenJGouldPLLinear Intensity Dependence of a Two-Photon Transition Rate. Phys Rev A (1990) 41:5088–91. 10.1103/PhysRevA.41.5088
33.
GeorgiadesNPPolzikESEdamatsuKKimbleHJParkinsASNonclassical Excitation for Atoms in a Squeezed Vacuum. Phys Rev Lett (1995) 75:3426–9. 10.1103/PhysRevLett.75.3426
34.
GeorgiadesNPPolzikESKimbleHJAtoms as Nonlinear Mixers for Detection of Quantum Correlations at Ultrahigh Frequencies. Phys Rev A (1997) 55:R1605–R1608. 10.1103/PhysRevA.55.R1605
35.
DayanBPe’erAFriesemAASilberbergYTwo Photon Absorption and Coherent Control with Broadband Down-Converted Light. Phys Rev Lett (2004) 93:023005. 10.1103/PhysRevLett.93.023005
36.
DayanBPe’erAFriesemAASilberbergYNonlinear Interactions with an Ultrahigh Flux of Broadband Entangled Photons. Phys Rev Lett (2005) 94:043602. 10.1103/PhysRevLett.94.043602
37.
LeeD-IGoodsonTEntangled Photon Absorption in an Organic Porphyrin Dendrimer. J Phys Chem B (2006) 110:25582–5. 10.1021/jp066767g
38.
GuzmanARHarphamMRSüzerOHaleyMMGoodsonTGSpatial Control of Entangled Two-Photon Absorption with Organic Chromophores. J Am Chem Soc (2010) 132:7840–1. 10.1021/ja1016816
39.
UptonLHarphamMSuzerORichterMMukamelSGoodsonTOptically Excited Entangled States in Organic Molecules Illuminate the Dark. J Phys Chem Lett (2013) 4:2046–52. 10.1021/jz400851d
40.
Villabona-MonsalveJPCalderón-LosadaONuñez PortelaMValenciaAEntangled Two Photon Absorption Cross Section on the 808 Nm Region for the Common Dyes Zinc Tetraphenylporphyrin and Rhodamine B. J Phys Chem A (2017) 121:7869–75. 10.1021/acs.jpca.7b06450
41.
Villabona-MonsalveJPVarnavskiOPalfeyBAGoodsonTTwo-photon Excitation of Flavins and Flavoproteins with Classical and Quantum Light. J Am Chem Soc (2018) 140:14562–6. 10.1021/jacs.8b08515
42.
LiTLiFAltuzarraCClassenAAgarwalGSSqueezed Light Induced Two-Photon Absorption Fluorescence of Fluorescein Biomarkers. Appl Phys Lett (2020) 116:254001. 10.1063/5.0010909
43.
TabakaevDMontagneseMHaackGBonacinaLWolfJ-PZbindenHet alEnergy-time-entangled Two-Photon Molecular Absorption. Phys Rev A (2021) 103:033701. 10.1103/PhysRevA.103.033701
44.
BurdickRKSchatzGCGoodsonTEnhancing Entangled Two-Photon Absorption for Picosecond Quantum Spectroscopy. J Am Chem Soc (2021) 143:16930–4. 10.1021/jacs.1c09728
45.
LerchSStefanovAExperimental Requirements for Entangled Two-Photon Spectroscopy. J Chem Phys (2021) 155:064201. 10.1063/5.0050657
46.
LandesTAllgaierMMerkoucheSSmithBJMarcusAHRaymerMGExperimental Feasibility of Molecular Two-Photon Absorption with Isolated Time-Frequency-Entangled Photon Pairs. Phys Rev Res (2021) 3:033154. 10.1103/PhysRevResearch.3.033154
47.
ParzuchowskiKMMikhaylovAMazurekMDWilsonRNLumDJGerritsTet alSetting Bounds on Entangled Two-Photon Absorption Cross Sections in Common Fluorophores. Phys Rev Appl (2021) 15:044012. 10.1103/PhysRevApplied.15.044012
48.
LandesTRaymerMGAllgaierMMerkoucheSSmithBJMarcusAHQuantifying the Enhancement of Two-Photon Absorption Due to Spectral-Temporal Entanglement. Opt Express (2021) 29:20022–33. 10.1364/OE.422544
49.
RaymerMGLandesTAllgaierMMerkoucheSSmithBJMarcusAHHow Large Is the Quantum Enhancement of Two-Photon Absorption by Time-Frequency Entanglement of Photon Pairs?Optica (2021) 8:757–8. 10.1364/OPTICA.426674
50.
KangGNasiri AvanakiKMosqueraMABurdickRKVillabona-MonsalveJPGoodsonTet alEfficient Modeling of Organic Chromophores for Entangled Two-Photon Absorption. J Am Chem Soc (2020) 142:10446–58. 10.1021/jacs.0c02808
51.
LoudonRThe Quantum Theory of Light. Oxford, UK: Oxford science publications (1979) Clarendon Press.
52.
RaymerMGLandesTMarcusAHEntangled Two-Photon Absorption by Atoms and Molecules: A Quantum Optics Tutorial. J Chem Phys (2021) 155:081501. 10.1063/5.0049338
53.
SchlawinFBuchleitnerATheory of Coherent Control with Quantum Light. New J Phys (2017) 19:013009. 10.1088/1367-2630/aa55ec
54.
CarnioEGBuchleitnerASchlawinFOptimization of Selective Two-Photon Absorption in Cavity Polaritons. J Chem Phys (2021) 154:214114. 10.1063/5.0049863
55.
CarnioEGBuchleitnerASchlawinFHow to Optimize the Absorption of Two Entangled Photons. Scipost Phys Core (2021) 4:28. 10.21468/SciPostPhysCore.4.4.028
56.
Ben-ReuvenAJortnerJKleinLMukamelSCollision Broadening in Two-Photon Spectroscopy. Phys Rev A (1976) 13:1402–10. 10.1103/PhysRevA.13.1402
57.
AndrewsDLThirunamachandranTOn Three-Dimensional Rotational Averages. J Chem Phys (1977) 67:5026–33. 10.1063/1.434725
58.
AbramaviciusDMukamelSCoherent Third-Order Spectroscopic Probes of Molecular Chirality. J Chem Phys (2005) 122:134305. 10.1063/1.1869495
59.
KauertMStollerPCFrenzMRičkaJAbsolute Measurement of Molecular Two-Photon Absorption Cross-Sections Using a Fluorescence Saturation Technique. Opt Express (2006) 14:8434–47. 10.1364/OE.14.008434
60.
de J León-MontielRSvozilíkJSalazar-SerranoLJTorresJPRole of the Spectral Shape of Quantum Correlations in Two-Photon Virtual-State Spectroscopy. New J Phys (2013) 15:053023. 10.1088/1367-2630/15/5/053023
Summary
Keywords
entangled photons, two-photon absorption, quantum correlations, inhomogeneous broadening, polarization entanglement
Citation
Schlawin F (2022) Polarization-Entangled Two-Photon Absorption in Inhomogeneously Broadened Ensembles. Front. Phys. 10:848624. doi: 10.3389/fphy.2022.848624
Received
04 January 2022
Accepted
28 January 2022
Published
14 March 2022
Volume
10 - 2022
Edited by
Roberto de J. León-Montiel, National Autonomous University of Mexico, Mexico
Reviewed by
Jiri Svozilik, Palacký University Olomouc, Czechia
Mike Mazurek, National Institute of Standards and Technology (NIST), United States
Updates
Copyright
© 2022 Schlawin.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Frank Schlawin, frank.schlawin@mpsd.mpg.de
This article was submitted to Quantum Engineering and Technology, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.