Abstract
Unextendible product basis (UPB), a set of incomplete orthonormal product states whose complementary space has no product state, is very useful for constructing bound entangled states. Naturally, instead of considering the set of product states, Bravyi and Smolin considered the set of maximally entangled states. They introduced the concept of unextendible maximally entangled basis (UMEB), a set of incomplete orthonormal maximally entangled states whose complementary space contains no maximally entangled state [Phys. Rev. A 84, 042,306 (2011)]. An entangled state whose nonzero Schmidt coefficients are all equal to is called a special entangled state of “type k”. In this paper, we introduce a concept named special unextendible entangled basis of “type k” which generalizes both UPB and UMEB. A special unextendible entangled basis of “type k” (SUEBk) is a set of incomplete orthonormal special entangled states of “type k” whose complementary space has no special entangled state of “type k”. We present an efficient method to construct sets of SUEBk. The main strategy here is to decompose the whole space into two subspaces such that the rank of each element in one subspace can be easily upper bounded by k while the other one can be generated by two kinds of the special entangled states of “type k”. This method is very effective when k = pm ≥ 3 where p is a prime number. For these cases, we can obtain sets of SUEBk with continuous integer cardinality when the local dimensions are large.
1 Introduction
Quantum entanglement [1] is an important resource for many quantum information processing, such as quantum teleportation [2, 3] and quantum key distribution [4, 5]. Therefore, it is fundamental to characterize quantum entanglement in quantum information. Bound entangled (BE) states [6, 7] are a special entanglement in nature: non-zero amount of free entanglement is needed to create them but no free entanglement can be distilled from such states under local operations and classical communication.
Unextendible product basis (UPB) [8, 9], a set of incomplete orthonormal product states whose complementary space has no product state, has been shown to be useful for constructing bound entangled states and displaying quantum nonlocality without entanglement [10–12].
As anology of the UPB, Bravyi and Smolin introduced the concept of unextendible maximally entangled basis (UMEB) [13], a set of orthonormal maximally entangled states in consisting of fewer than d2 vectors which has no additional maximally entangled vector orthogonal to all of them. The UMEBs can be used to construct examples of states for which entanglement of assistance (EoA) is strictly smaller than the asymptotic EoA, and can be also used to find quantum channels that are unital but not convex mixtures of unitary operations [13]. There they proved that no UMEB exists in two qubits system and presented examples of UMEBs in and . Since then, the UMEB was further studied by several researchers [14–21]. Lots of the works paid attention to the UMEBs for general quantum systems . The cardinality of the constructed UMEBs are always multiples of d or d′.
Guo et al. extended these two concepts to the states with fixed Schmidt numbers and studied the complete basis [22] and the unextendible ones [23]. There they introduced the notion of special entangled states of type k: an entangled state whose nonzero Schmidt coefficients are all equal to . Then a special unextendible entangled basis of type k (SUEBk) is a set of orthonormal special entangled states of type k in consisting of fewer than dd’ vectors which has no additional special entangled state of type k orthogonal to all of them. Quite recently, there are several results related to this subject [24, 25]. Similar to the UMEBs, the cardinality of most of the known SUEBk’s are multiples of k. Therefore, it is interesting to ask whether there is SUEBk with other cardinality. Based on the technique used in [26], we try to address this question in this work.
The remaining of this article is organized as follows. In Section 2, we first introduce the concept of special unextendible entangled basis and its equivalent form in matrix settings. In Section 3, we present our main idea to construct the SUEBk. In Section 4 and Section 5, based on the combinatoric concept: weighing matrices, we give two constructions of SUEBk whose cardinality varying in a consecutive integer set. Finally, we draw the conclusions and put forward some interesting questions in the last section.
2 Preliminaries
Let [n] denote the set {1, 2, … , n}. Let , be Hilbert spaces of dimension d and d′ respectively. It is well known that any bipartite pure state in has a Schmidt decomposition. That is, any unit vector |ϕ⟩ in can be written aswhere λi > 0 and are orthonormal states of system A (resp. B). The number k is known as the Schmidt number of |ϕ⟩ and we denote it by Sr(ϕ). The set is called the nonzero Schmidt coefficients of |ϕ⟩. If all these λis are equal to , we call |ϕ⟩ a special entangled state of type k (2 ≤ k ≤ d).
Definition 1
(See [
22])
.A set of states(1 ≤
n≤
dd’ − 1)
inis called a special unextendible entangled basis of typek(SUEB
k)
if.
(i) ⟨ϕi|ϕj⟩ = δij, i, j ∈ [n];
(ii) For anyi ∈ [n], the state |ϕi⟩ is a special entangled state of typek;
(iii) If ⟨ϕi|ϕ⟩ = 0 for alli ∈ [n], then |ϕ⟩ can not be a special entangled state of typek.
We call the
d×
d′ matrix
the corresponding matrix representation of |
ϕ⟩. This correspondence satisfies the following key properties related to SUEB
k(1) Inner product preserving:
(2) The Schmidt number corresponds to the matrix rank: Sr (|ϕ⟩) = rank (Mϕ);
(3) The nonzero Schmidt coefficients correspond to the nonzero singular values.
Definition 2
.
(i) ⟨Mi, Mj⟩ = δij, i, j ∈ [n];
(ii) The nonzero singular values ofMiare all equal tofor eachi ∈ [n];
(iii) If ⟨Mi, M⟩ = 0 for alli ∈ [n], then some nonzero singular value ofMdo not equal to.
3 Strategy for Constructing SUSVBk
Observation 1It is usually not easy to calculate the singular values of an arbitrary matrix. However, if there are only k nonzero elements in M (say ) and these elements happen to be in different rows and columns, then there are exactly k nonzero singular values of M and they are just . For example, let M be the matrix defined bywhere . Then the nonzero singular values of M are , , , , .
Observation 2If there are exactly k nonzero singular values of a matrix, then the rank of that matrix is k. Therefore, the condition rank(M) < k implies that M cannot be a matrix with k nonzero singular values.With the two observations above, our strategy for constructing an n-members SUSVBk can be roughly described by two steps (note that this is only a sufficient condition, not a necessary and sufficient condition). Firstly, we construct a set of n-members of orthonormal matrices such that there are exactly k nonzero elements in Mi whose modules are all and these elements happen to be in different rows and columns. Secondly, we need to show that the rank of any matrix in the complementary space of (define as ) is less than k.Let d, d′ be integers such that 2 ≤ d ≤ d′. We define the coordinate set to beNow we define an order for the set . Equivalently, we can define a bijection:Then we call an ordered set (See Figure 1 for an example). We can also define an order for the case d′ ≤ d by .Let (i1, j1), (i2, j2) be two different coordinates in . It is easy to check that if i1 = i2 or j1 = j2, then . Therefore, any d − 1 consecutive coordinates in under the order is coordinately different. That is, these d − 1 coordinates must come from different rows and different columns.Let . Then P inherit an order from that of (An order here means a bijective map from P to [#P] where #P denotes the number of elements in the set P). In fact, as , there is an unique map πP from the set to [#P] which preserves the order of the numbers. First, list P1, P2, … , PN ∈ P such that for 1 ≤ i < j ≤ N. Then . Then we define (that is, the composition of and πP) to be the order of P inherit from that of . For example, let . Then the πP from the set to [3] = {1, 2, 3} is just defined by: πP (6) = 1, πP (10) = 2, πP (44) = 3. Therefore, the order of P inherited from that of is exactly the map: .In order to step forward, we first state the following observation which is helpful for determine the orthogonality of matrices. Let and denote the order of P inherit from the l denotes the number of elements in P. As we have defined an order for the set , it induces an order relation on its subset P. For any vector , we define a d × d′ matrixwhere Ei,j denote the d × d′ matrix whose (i, j) coordinate is 1 and zero elsewhere.
FIGURE 1
This is a picture of the order on the coordinate set . For examples, , and .
Lemma 1
Let
be nonempty sets and
v,
wbe vectors of dimensions
#P1and
#P2respectively. Then we have the following statements:
(1) IfP1 ∩ P2 = ∅, then we have
(2) IfP1 = P2andv, ware orthogonal to each other, then we also have
Proof
Denote
and
the orders of
P1and
P2inherit from the
respectively.
(a) As
we have
The last equality holds as the condition
P1∩
P2= ∅ implies
δikδjl= 0.
(b) For the second part, we have the following equalities:
4 Constructions of SUEBk
In the following, we try to construct a set of matrices consisting of matrices of the form T1. While its complementary space is the set of matrices of the form T2.
We start our construction by a simple example.
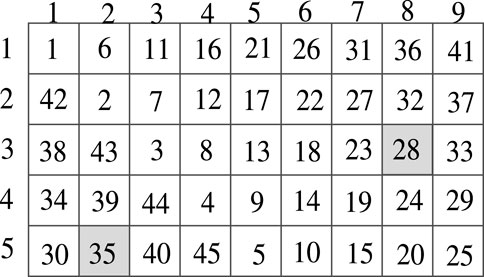
Example 1There exists a SUEB3inwhose cardinality is 41.Proof. As 41 = 6 × 7–1, we define to be the set with 41 elements which is obtained from by deleting {(7, 1) (7, 2), (7, 3) (7, 4), (7, 5) (7, 6), (7, 7), (6, 1)}. We can define an order for the set . In fact, the is chosen to be the order of inherited from that of (See Figure 2A for an intuitive view). Any five consecutive elements of under the order come from different rows and columns. Firstly, we have the following identitySince there are 41 elements in the set , by the decomposition (12), we can divide the set into (7 + 5) sets: seven sets of short states (denote by Si, 1 ≤ i ≤ 7) of cardinality 3 and five sets of long states (denote by Lj, 1 ≤ j ≤ 5) of cardinality 4. In fact, we can divide into these 12 sets through its order . That is,where denotes the inverse map of the bijection . See Figure 2B for an intuitive view of the set Si, Lj. Setwhere . We can easily check that and Now set vx to be the xth row of H3 (x = 1, 2, 3) and wy to be the yth row of O4 (y = 1, 2, 3, 4). So and . So we can construct the following 7 × 3 + 5 × 4 = 41 matrices:Let be the set of the above matrices. Note that the elements of each Si or Lj are coordinately different. Hence by Observation 1, the states corresponding to the above 41 matrices are special entangled states of type 3. Since , v1, v2, v3 are pairwise orthogonal. Similarly, as , w1, w2, w3, w4 are also pairwise orthogonal. And the 12 sets above are pairwise disjoint. Therefore, by Lemma 1, the 41 matrices above are pairwise orthogonal. Let V be the linear space spanned by the matrices in . Therefore, dim V = 41 as orthogonal elements are always linearly independent. Denote dim V⊥ the set of all elements in that are orthogonal to every elements in V. By the definition of at the beginning of the proof, each matrix in is orthogonal to V. Hence, . Aswe have dim V⊥ = 8. Note that the dimension of is just 8. Both and V⊥ are Hilbert space of dimensional 8. By the inclusion , we must have . One should note that the rank of any nonzero matrix in is less than 2. Such a matrix cannot correspond to a special entangled state of type 3. Therefore, the set of states corresponding to the matrices is a SUEB3.One can find that the H3 and O4 play an important role in the proof of the Example 1. We give their generalizations by the following matrix and the weighing matrix in Definition 3. There always exists some complex Hadamard matrix of order d. For example,where . In fact, this is the Fourier d-dimensional matrix (discrete Fourier transform). The matrix Hd satisfies
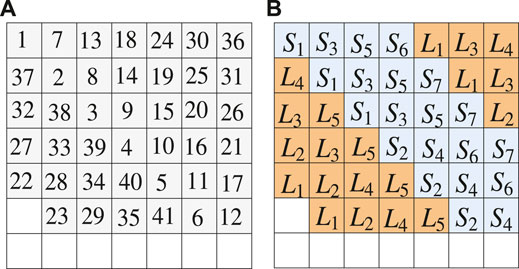
FIGURE 2
(A) shows the order of subset of . While the (B) shows the distribution of the short and long states through this order.
Definition 3(See [27]). A generalized weighing matrix is a square a × a matrix A all of whose non-zero entries are nth roots of unity such that AA† = kIa. It follows that is a unitary matrix so that A†A = kIa and every row and column of A has exactly k nonzero entries. k is called the weight and n is called the order of A. We denote W (n, k, 1) the set of all weight k and order a generalized weighing matrix whose nonzero entries being nth root.One can find the following lemma via theorem 2.1.1 on the book “The Diophantine Frobenius Problem” [28]. The related problem is also known as Frobenius coin problem or coin problem.
Lemma 2([28]). Let a, b be positive integers and coprime. Then for every integer N ≥ (a − 1) (b − 1), there are non-negative integers x, y such that N = xa + yb.Now we give one of the main result of this paper.
Let k be a positive integer. Suppose there exist such that W (m, k, a) and W (n, k, b) are nonempty and gcd (a, b) = 1. If d, d′ are integers such that d ≥ max{a, b} + k and d′ ≥ max{a, b} + 1, then for any integer N ∈ [(d − k + 1)d′, dd’ − 1], there exists a SUEBk in whose cardinality is exactly N.
Proof. Without loss of generality, we suppose a < b and A ∈ W (m, k, a), B ∈ W (n, k, b). Any integer N ∈ [(d − k + 1)d′, dd’ − 1] can be written uniquely as N = d′q + r where (d − k + 1) ≤ q ≤ d − 1 and r is an integer with 0 ≤ r < d′. Then we have a coordinate set with order . Notice that any q consecutive elements of under the order are coordinately different. Denote to be the set by deleting the elements {(q + 1, i)|1 ≤ i ≤ d′ − r} from . The subset inherit an order from that of . As for any 1 ≤ i ≠ j ≤ d′, any q − 1 consecutive elements of under the order are coordinately different. Since q − 1 ≥ d − k ≥ max{a, b}, any a or b consecutive elements of under the order come from different rows and columns. As N ≥ qd’ > (a − 1) × (b − 1), by Lemma 2, there exist nonnegative integers s, t such that
Since there are N elements in the set , by the decomposition (19), we can divide the set into (s + t) sets: s sets (denote by Si, 1 ≤ i ≤ s) of cardinality a and t sets (denote by Lj, 1 ≤ j ≤ t) of cardinality b. In fact, we can divide into these s + t sets through its order . That is,
Now let vx be the xth row of (1 ≤ x ≤ 1) and wy be the yth row of (1 ≤ y ≤ b). So and . Then we can construct the following s × a + t × b = N matrices:
Let be the set of the above matrices. Note that the (s + t) sets S1, … , Ss, L1⋯, Lt are pairwise disjoint. And the rows of A (resp. B) are orthogonal to each other as AA† = kIa (resp. BB† = kIb). By Lemma 1, the above sa + tb matrices are orthogonal to each other. By construction, all the sets S1… , Ss, L1, … , Lt are all coordinately different. Using this fact and the definition of generalized weighing matrices, the states corresponding to these matrices are all special entangled states of type k (see Observation 1). Set V be the linear subspace of generated by . Note that each matrix in is orthogonal to V. And the dimension of is just dd’ − N. Therefore, . One should note that the rank of any matrix in is less than k. That is to say, any state orthogonal to the states corresponding to has Schmidt rank at most (k − 1). Such state cannot be a special entangled state of type k. Therefore, the set of states corresponding to the matrices is a SUEBk.
Noticing that Hk ∈ W (k, k, k) for all integer k ≥ 2. Therefore, by Theorem 1, we arrive at the following corollary.
Corollary 1Let k be an integer such that W (n, k, k + 1) is nonempty for some integer n. Then there exists some SUEBk with cardinality varying from (d − k + 1)d′ to dd’ − 1 in whenever d ≥ 2k + 1 and d′ ≥ k + 2.In the following, we list a result about the weighing matrices proved by Gerald Berman.
Lemma 3(See [27]). If p, t, r and n are positive integers such that p is prime, n|r (n ≥ 2) and r|(pm − 1). Then there exists a generalized weighing matrix W (n, p(t−1)m, (ptm − 1)/r).In particular, set t = 2, r = n = pm − 1. If pm > 2, then W (pm − 1, pm, pm + 1) is nonempty. As the set W (pm, pm, pm) is always nonempty, we have the following corollaries.
Corollary 2Letpbe a prime andk = pm > 2 for some positive integerm. Then there exists some SUEBkwith cardinality varying from (d − k + 1)d′ todd’ − 1 inwheneverd ≥ 2k + 1 andd′ ≥ k + 2.
Corollary 3Letp1, … , psbe different primes andwherem1, … , msare positive integers. Iffor eachi = 1, … , s, Then there exists some SUEBkwith cardinality varying from (d − k + 1)d′ todd’ − 1 inwheneverandd ≥ 2k + 1 and.
5 Second Type of SUEBk
In the following, we try to construct a set of matrices consisting of matrices of the following left form. While its complementary space is the set of matrices of the following right form where r + s < k.
We also start our construction from a simple example.
Example 2There exists a SUEB4inwhose cardinality is 54.Proof. As 54 = 7 × 8–2, we can define to be the set with 54 elements which can be obtained by deleting {(6, 8), (7, 8)} from . Notice that any six consecutive elements of under the order come from different rows and columns. Denote as the order of inherited from . As , any five consecutive elements of under the order come from different rows and columns (See Figure 3A for an intuitive view). We have the following identitySince there are 54 elements in the set , by the decomposition (22), we can divide the set into (6 + 6) sets: six sets of short states (denote by Si, 1 ≤ i ≤ 6) of cardinality four and six sets of long states (denote by Lj, 1 ≤ j ≤ 6) of cardinality 5. In fact, we can divide into these 12 sets through its order . That is,See Figure 3B for an intuitive view of the set Si, Lj. SetWe can easily check that Now set vx be the xth row of H4 (x = 1, 2, 3, 4) and wy be the yth row of O5 (y = 1, 2, 3, 4, 5). So and . So we can construct the following 6 × 4 + 6 × 5 = 54 matrices:Let to be the set of the above matrices. Note that the elements of each Si or Lj are coordinately different. Hence by Observation 1, the states corresponding to the above 54 matrices are special entangled states of type 4. Since , v1, v2, v3, v4 are pairwise orthogonal. Similarly, as , w1, w2, w3, w4, w5 are also pairwise orthogonal. And the 12 sets above are pairwise disjoint. Therefore, by Lemma 1, the 54 matrices above are pairwise orthogonal. Set V be the linear subspace of generated by . Each matrix in is orthogonal to V. And the dimension of is just (72–54). Therefore, . One should note that the rank of any matrix in is less than 4. That is to say, any state orthogonal to the states corresponding to has Schmidt rank at most 3. Such state cannot be a special entangled state of type 4. Therefore, the set of states corresponding to the matrices is a SUEB4.
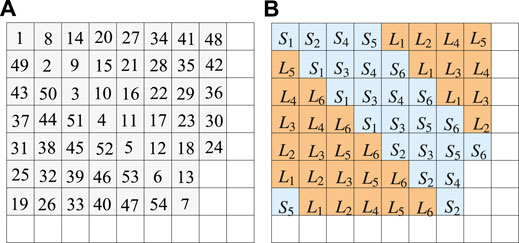
FIGURE 3
(A) shows the order of subset of . While the (B) shows the distribution of the short and long states through this order.
Let k be a positive integer. Suppose there exist such that W (m, k, 1) and W (n, k, b) are nonempty and gcd (a, b) = 1. Let d, d′ be integers. If there are decompositions d = m1 + q, d′ = m2 + r such that m1, m2 ≥ max{a, b} + 2 and 1 ≤ q + r < k. Then for any integer N ∈ [m1m2, dd’ − 1], there exists a SUEBk in whose cardinality is exactly N.
Proof. Without loss of generality, we suppose a < b and A ∈ W (m, k, a), B ∈ W (n, k, b). We separate the interval into q + r pairwise disjoint intervals:
Any integer N ∈ [m1m2, dd’ − 1] lies in one of the above q + r intervals. Without loss of generality, we assume that for some i0 ∈ {0, … , q − 1}. Suppose N = (m1 + i0)m2 + f, with 0 ≤ f ≤ m2 − 1. Denote to be the set by deleting the elements {(m1 + i0 + 1, i)|1 ≤ i ≤ m2 − f} from . Then we have a coordinate set with order . Notice that any max{a, b}+1 consecutive elements of under the order are coordinate different as m1, m2 ≥ max{a, b} + 2. The subset inherit an order from that of . One can find that any a or b consecutive elements of under the order come from different rows and columns. As N ≥ m1m2 > (a − 1) × (b − 1), by Lemma 2, there exist nonnegative integers s, t such that
Since there are N elements in the set , by the decomposition (27), we can divide the set into (s + t) sets: s sets (denote by Si, 1 ≤ i ≤ s) of cardinality a and t sets (denote by Lj, 1 ≤ j ≤ t) of cardinality b. In fact, we can divide into these s + t sets through its order . That is,
Now set vx to be the xth row of (1 ≤ x ≤ 1) and wy to be the yth row of (1 ≤ y ≤ b). So and . Then we can construct the following s × a + t × b = N matrices:
Let to be the set of the above matrices. Note that the (s + t) sets S1, … , Ss, L1⋯, Lt are pairwise disjoint. And the rows of A (resp. B) are orthogonal to each other as AA† = kIa (resp. BB† = kIb). By Lemma 1, the above sa + tb matrices are orthogonal to each other. By construction, all the sets S1… , Ss, L1, … , Lt are all coordinately different. Using this fact and the definition of generalized weighing matrices, the states corresponding to these matrices are all special entangled states of type k (see Observation 1). Set V be the linear subspace of generated by . Each matrix in is orthogonal to V. And the dimension of is just dd’ − N. Therefore, . As r + s < k, so the rank of any matrix in is less than k. That is to say, any state orthogonal to the states corresponding to has Schmidt rank at most (k − 1). Such state cannot be a special entangled state of type k. Therefore, the set of states corresponding to the matrices is a SUEBk.
Remark: Theorem 1 (the first type) can not obtain from Theorem 2 (the second type) by setting r = 0. In fact, in Theorem 2, we assume d, d′ ≥ max{a, b} + 2 while we only assume d′ ≥ max{a, b} + 1 in Theorem 1.
As application, Theorem 2 give us that there is some SUEB4 in whose cardinality being one of the integer in the interval [49, 71], where a = 4, b = 5, m1 = 7, q = 1, m2 = 7, r = 2.
In fact, we may move further than the results showed in Theorem 2. Here we present some examples (See Example 3) which is beyond the scope of Theorem 2. But their proof can be originated from the main idea of the constructions of SUEBk.
Example 3For any integerN ∈ [12, 19], there exists a SUEB3inwhose cardinality is exactlyN(See Figure 4).
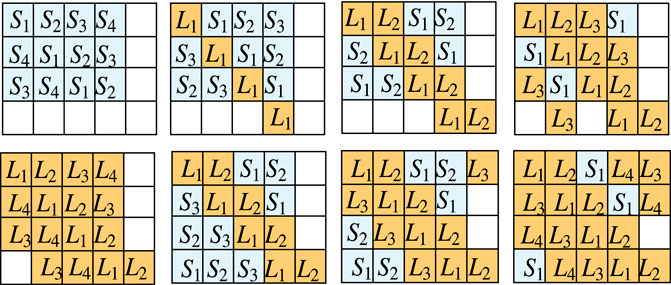
FIGURE 4
This figure shows the distribution of the short states and long states for constructing SUEB3 in with cardinality N varying from 12 to 19.
6 Conclusion and Discussion
We presented a method to construct the special unextendible entangled basis of type k. The main idea here is to decompose the whole space into two subspaces such that the rank of each element in one subspace is easily bounded by k and the other can be generated by two kinds of the special entangled states of type k. We presented two constructions of special unextendible entangled states of type k by relating it to a combinatoric concept which is known as weighing matrices. This method is effective when k = pm ≥ 3.
However, there are lots of unsolved cases. Finding out the largest linear subspace such that it does not contain any special entangled states of type k. This is related to determine the minimal cardinality of possible SUEBk. It is much more interesting to find some other methods that can solve the general existence of SUEBk. Note that the concept of SUEBk is a mathematical generalization of the UPB (k = 1) and the UMEB (k = d). Both UPBs and UMEBs are useful for studying some other problems in quantum information. Therefore, another interesting work is to find out some applications of the SUEBk.
Statements
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.
Author contributions
The author confirms being the sole contributor of this work and has approved it for publication.
Funding
This work is supported by the NSFC with Grant No. 11901084, the Basic and Applied Basic Research Funding Program of Guangdong Province with Grant No. 2019A1515111097, and the Research startup funds of DGUT with Grant No. GC300501-103.
Acknowledgments
The author thank Mao-Sheng Li for helpful discussion.
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
The handling editor LC declared a past co-authorship with the author YLW.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1.
HorodeckiRHorodeckiPHorodeckiMHorodeckiK. Quantum Entanglement. Rev Mod Phys (2009) 81:865–942. 10.1103/revmodphys.81.865
2.
BennettCHBrassardGCrépeauCJozsaRPeresAWoottersWK. Teleporting an Unknown Quantum State via Dual Classical and Einstein-Podolsky-Rosen Channels. Phys Rev Lett (1993) 70:1895–9. 10.1103/physrevlett.70.1895
3.
BouwmeesterDPanJ-WMattleKEiblMWeinfurterHZeilingerA. Experimental Quantum Teleportation. Nature (1997) 390:575–9. 10.1038/37539
4.
BennettCH. Quantum Cryptography Using Any Two Nonorthogonal States. Phys Rev Lett (1992) 68:3121–4. 10.1103/physrevlett.68.3121
5.
GisinNRibordyGTittelWZbindenH. Quantum Cryptography. Rev Mod Phys (2002) 74:145–95. 10.1103/revmodphys.74.145
6.
HorodeckiPLewensteinM. Bound Entanglement and Continuous Variables. Phys Rev Lett (2000) 85:2657–60. 10.1103/physrevlett.85.2657
7.
BrußDPeresA. Construction of Quantum States with Bound Entanglement. Phys Rev A (2000) 61(R):030301. 10.1103/physreva.61.030301
8.
BennettCHDiVincenzoDPMorTShorPWSmolinJATerhalBM. Unextendible Product Bases and Bound Entanglement. Phys Rev Lett (1999) 82:5385–8. 10.1103/physrevlett.82.5385
9.
DiVincenzoDPMorTShorPWSmolinJATerhalBM. Unextendible Product Bases, Uncompletable Product Bases and Bound Entanglement. Commun Math Phys (2003) 238:379–410. 10.1007/s00220-003-0877-6
10.
BennettCHDiVincenzoDPFuchsCAMorTRainsEShorPWet alQuantum Nonlocality without Entanglement. Phys Rev A (1999) 59:1070–91. 10.1103/physreva.59.1070
11.
De RinaldisS. Distinguishability of Complete and Unextendible Product Bases. Phys Rev A (2004) 70:022309. 10.1103/physreva.70.022309
12.
HorodeckiMSenASenUHorodeckiK. Local Indistinguishability: More Nonlocality with Less Entanglement. Phys Rev Lett (2003) 90:047902. 10.1103/PhysRevLett.90.047902
13.
BravyiSSmolinJA. Unextendible Maximally Entangled Bases. Phys Rev A (2011) 84:042306. 10.1103/physreva.84.042306
14.
ChenBFeiS-M. Unextendible Maximally Entangled Bases and Mutually Unbiased Bases. Phys Rev A (2013) 88:034301. 10.1103/physreva.88.034301
15.
LiM-SWangY-LZhengZ-J. Unextendible Maximally Entangled Bases in $\Mathbb{C}^{d}\bigotimes\Mathbb{C}^{d^{\prime}}$. Phys Rev A (2014) 89:062313. 10.1103/PhysRevA.90.034301
16.
WangY-LLiM-SFeiS-M. Unextendible Maximally Entangled Bases in $\Mathbb{C}^{d}\bigotimes\Mathbb{C}^{d}$. Phys Rev A (2014) 90:034301. 10.1103/PhysRevA.89.062313
17.
NanHTaoY-HLiL-SZhangJ. Unextendible Maximally Entangled Bases and Mutually Unbiased Bases in ℂ D ⊗ ℂ d′$\Mathbb{C}^{d}\bigotimes\Mathbb{C}^{d^{\prime}}$. Int J Theor Phys (2015) 54:927–32. 10.1007/s10773-014-2288-1
18.
WangY-LLiM-SFeiS-MZhengZ-J. Connecting Unextendible Maximally Entangled Base with Partial Hadamard Matrices. Quan Inf. Process (2017) 16:84. 10.1007/s11128-017-1537-7
19.
GuoYJiaYLiX. Multipartite Unextendible Entangled Basis. Quan Inf Process (2015) 14:3553–68. 10.1007/s11128-015-1058-1
20.
GuoY. Constructing the Unextendible Maximally Entangled Basis from the Maximally Entangled Basis. Phys Rev A (2016) 94:052302. 10.1103/physreva.94.052302
21.
ZhangG-JTaoY-HHanY-FYongX-LFeiS-M. Unextendible Maximally Entangled Bases in $${\mathbb {C}}^{pd}\otimes {\mathbb {C}}^{qd}$$ C Pd ⊗ C qd$\Mathbb{C}^{qd}\otimes \Mathbb{C}^{qd}$. Quan Inf. Process (2018) 17:318. 10.1007/s11128-018-2094-4
22.
GuoYDuSLiXWuS. Entangled Bases with Fixed Schmidt Number. J Phys A: Math Theor (2015) 48:245301. 10.1088/1751-8113/48/24/245301
23.
GuoYWuS. Unextendible Entangled Bases with Fixed Schmidt Number. Phys Rev A (2014) 90:054303. 10.1103/physreva.90.054303
24.
ShiFZhangXGuoY. Constructions of Unextendible Entangled Bases. Quan Inf. Process (2019) 18:324. 10.1007/s11128-019-2435-y
25.
YongXSongYTaoY. New Constructions of Unextendible Entangled Bases with Fixed Schmidt Number. Quan Inf. Process (2019) 18:337. 10.1007/s11128-019-2451-y
26.
LiM-SWangY-L. Construction of Special Entangled Basis Based on Generalized Weighing Matrices. J Phys A: Math Theor (2019) 52:375303. 10.1088/1751-8121/ab331b
27.
BermanG. Families of Generalized Weighing Matrices. Can J Math (1978) 30:1016–28. 10.4153/cjm-1978-086-8
28.
AlfonsinJR. The Diophantine Frobenius Problem. Oxford: Oxford University Press (2006).
Summary
Keywords
unextendible entangled bases, unextendible product bases, entanglement, schmidt number, schmidt coefficients
Citation
Wang Y-L (2022) Constructions of Unextendible Special Entangled Bases. Front. Phys. 10:884327. doi: 10.3389/fphy.2022.884327
Received
26 February 2022
Accepted
20 April 2022
Published
27 May 2022
Volume
10 - 2022
Edited by
Lin Chen, Beihang University, China
Reviewed by
Yuanhong Tao, Zhejiang University of Science and Technology, China
Zhenhuan Liu, Tsinghua University, China
Hao Dai, Tsinghua University, China
Updates
Copyright
© 2022 Wang.
This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Yan-Ling Wang, wangylmath@yahoo.com
This article was submitted to Quantum Engineering and Technology, a section of the journal Frontiers in Physics
Disclaimer
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article or claim that may be made by its manufacturer is not guaranteed or endorsed by the publisher.