- 1Physics Department, University of California, Santa Barbara, Santa Barbara, CA, United States
- 2Physics Department, Harvard University, Cambridge, MA, United States
Boundary conditions dictate how fluids, including liquid crystals, flow when pumped through a channel. Can boundary conditions also be used to control internally driven active fluids that generate flows spontaneously? By using numerical simulations and stability analysis we explore how parallel surface anchoring of active agents at the boundaries and substrate drag can be used to rectify coherent flow of an active polar fluid in a 2D channel. Upon increasing activity, a succession of dynamical states is obtained, from laminar flow to vortex arrays to eventual turbulence, that are controlled by the interplay between the hydrodynamic screening length and the extrapolation length quantifying the anchoring strength of the orientational order parameter. We highlight the key role of symmetry in both flow and order and show that coherent laminar flow with net throughput is only possible for weak anchoring and intermediate activity. Our work demonstrates the possibility of controlling the nature and properties of active flows in a channel simply by patterning the confining boundaries.
1 Introduction
Active fluids are composed of active entities, such as bacteria [1, 2], biofilaments driven by motor proteins [3, 4] or self-propelled colloids [5, 6], that consume energy to generate their own motion. Such active particles exert dipolar forces on their surroundings, driving self-sustained active flows. The elongated nature of the active units endows the fluid with liquid crystalline degrees of freedom, allowing for the onset of orientational order, with either polar or nematic symmetry [7].
The orientationally ordered state of bulk active fluids is generically unstable at all activities due to the feedback between deformations and flow [8], resulting in spatiotemporal chaotic dynamics at zero Reynolds number that has been referred to as bacterial or active turbulence [9]. Several strategies have been proposed to stabilize laminar flows in active fluids such as the inclusion of substrate friction [10–13] or spatial confinement [14–20], but a systematic treatment unifying these various results has remained elusive.
The dynamics of confined two-dimensional (2D) active fluids also depends on the symmetry of local order, though some features are common. Polar active fluids, such as dense suspensions of swimming bacteria, transition from laminar to undulating and periodic travelling flows upon increasing the channel width, eventually giving place to turbulent dynamics [21–24]. In active nematics, both numerical studies [25–28] and experiments with microtubule-kinesin suspensions [29] with strong anchoring to the channel walls have revealed a transition from laminar to oscillatory flows to a lattice of counter-rotating flow vortices with associated order of disclinations in the nematic texture. Similar flow states and transitions are also reported in other geometries, such as in circular confinement [15, 19, 30]. Recent work has also begun exploring the influence of varying and conflicting anchoring boundary conditions in active nematics in channels [24, 31]. In general the interplay of the geometry of confinement and boundary conditions yields a rich variety of flow states, but coherent flow with a finite throughput in the channel is only achieved by finely tuning activity and other system parameters. Hence, quantifying the conditions that yield specific flow patterns, and especially identifying states of finite throughput is important for controlling bacterial flow through channels and for microfluidic applications of active flows [32–36].
Motivated by the sensitivity of liquid crystals to surface effects and anchoring on the boundary [37], in this paper, we suggest a simple strategy to control channel flows of active fluids by tuning boundary conditions. We consider an incompressible polar active fluid confined to a two-dimensional (2D) channel with friction, and examine the role of parallel surface anchoring in selecting the spontaneously flowing states of the fluid. The model may be appropriate, for instance, to describe the spontaneous flow of a bacterial suspension in a channel. We show that the selection of the flow patterns is controlled by the interplay of two length scales: 1) the hydrodynamic screening length
We find that coherent active flows with finite throughput are only possible when the orientational order parameter is weakly anchored to the channel walls, corresponding to large ℓκ compared to the width W of the channel. In the opposite limit of strong anchoring, the spontaneous flow transition leads instead to a single file of flow vortices evenly spaced along the length of the channel that we refer to as flow vortex lattice. These vortices appear in counter-rotating pairs and their number is determined by the aspect ratio of the channel and the activity. The succession of flow states obtained when activity is increased above the spontaneous flow instability on the way to turbulence are summarized schematically in Figure 1 for both weak and strong homogeneous anchoring. For weak anchoring, the spontaneous flow transition leads to coherent laminar flow and associated splay deformation of the polarization field. At higher activity the system settles into a state of shear banded flow, with bend deformations of the polarization field across the channel. For strong anchoring, in contrast, the spontaneous flow instability first results in a lattice of flow vortices lined up along the channel, with longitudinal bend deformations of the polarization. At higher activity this gives way to the shear banded flow as for weak anchoring, albeit with stronger amplitude of polarization deformations. For all anchoring strengths, the flow eventually becomes chaotic at larger activity (not shown). By considering variable boundary conditions, we unify previous results in a comprehensive phase diagram that crucially combines the well-known active length scale
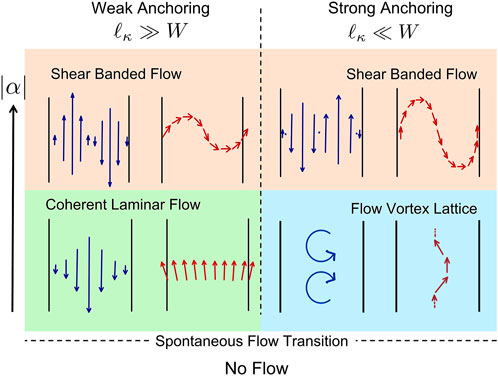
FIGURE 1. Schematic showing the effect of wall anchoring of the polarization on the steady flow states of a polar active fluid in a channel of width W. The blue arrows depict the flow field, v, and the red arrows represent the polarization, p. The extended arrow on the left indicates the direction of increasing activity |α|.
In the rest of the paper, we first introduce the hydrodynamic model and the boundary conditions used in the channel geometry. In section 3 we report results from numerical solutions of the continuum equations and describe the various spontaneous flow states observed with increasing activity. We define and evaluate the mean normalized throughput through the channel to distinguish between coherent and non-coherent flows. In section 4 we present a linear stability analysis of the hydrodynamic model for a rectangular periodic box that qualitatively accounts for the transitions between the various flow states. The results are summarized in a comprehensive phase diagram in terms of activity, hydrodynamic screening and anchoring strength. In Section 5 we discuss the effect of a polar propulsive force in the momentum equation which breaks flow symmetry and destroys the non-flowing ordered state. Finally, we conclude with a discussion of potential experimental realisations and possible extensions of our work.
2 Hydrodynamic model
We consider a two-dimensional active polar fluid on a frictional substrate, as appropriate, for instance, to describe a thin film of a bacterial suspension [40]. At high bacterial concentration, we assume both the suspension density and the bacterial concentration to be constant and describe the dynamics in terms of two fields, the bacterial polarization p that characterizes the local direction of bacterial motility and the flow velocity v of the fluid.
The dynamics of the polarization is governed by
where Dtp = ∂tp + v ⋅∇p + Ω ⋅p is the material derivative that embodies advection and rotation of polarization by flow, with
where a, b > 0 and the bacterial concentration c controls the transition to polar order. Here, we have assumed that a single elastic constant K controls the stiffness to both bend and splay distortions. For simplicity we neglect in Eq. 1 flow alignment terms proportional to v which arise through a lubrication approximation [40]. We have verified that these terms do not qualitatively change our results.
At low Reynolds number the flow is governed by force balance through the Stokes equation,
where the pressure Π is determined by the condition of incompressibility, ∇ ⋅v = 0. Here, Γ is the friction with the substrate. Dissipation is controlled by the interplay of friction and viscosity η, with
Finally, the dipolar forces exerted by the swimmers on the fluid yield an active stress σa [7],
where the activity α0 provides a measure of the strength of active forces, depending, for instance, on bacterial concentration and swimming speed. Its sign depends on whether such forces are extensile (α0 < 0 as for pushers) or contractile (α0 > 0 as for pullers). Here we focus on extensile active forces which are relevant to most bacteria. Note that, other sources of activity such as self-advection are neglected here for simplicity, and their effects are briefly discussed later in Section 5.
We assume that the fluid is confined to a channel of width W and length L, in the geometry shown in Figure 2, with periodic boundary conditions along the y direction. Below we focus on the dynamics of the ordered state with c > c0 and
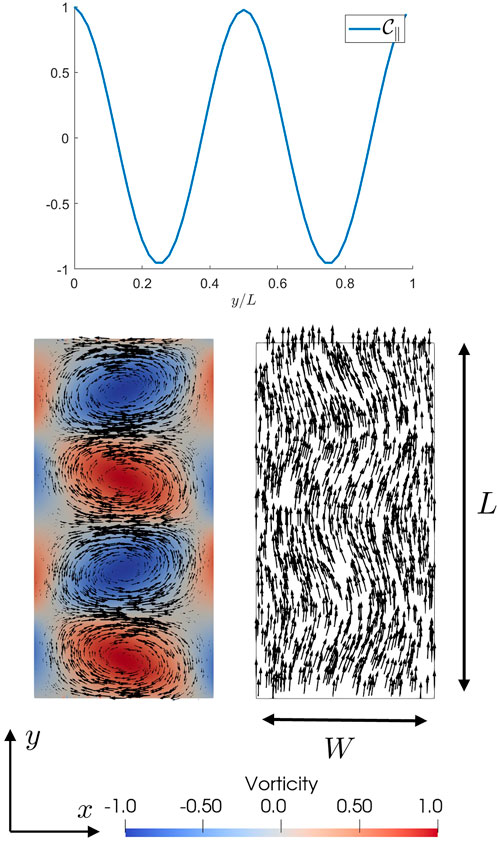
FIGURE 2. The velocity correlation function along the channel, C∥, for the vortex lattice state (ℓη = 0.30, α = −2.00) with strong anchoring (ℓκ = 0.01). The flow profile v (bottom left) and polarization p (bottom right) in the vortex lattice state are plotted at the bottom.
The hydrodynamic equations are solved with the boundary conditions.
Where
The hydrodynamic equations for our model have nematic symmetry, as they are invariant for p → −p. The boundary conditions, however, break the symmetry in polarization by aligning p with the channel walls in
3 Numerical simulations
The hydrodynamic equations are solved numerically using the finite element platform FEniCs [41, 42]. We use the width of the channel, W, as unit of length, the nematic relaxation time, τn = γ/a, as unit of time and the condensation energy a in the polar free energy as a unit of stress. With this choice, the dimensionless activity
In bulk, an extensile active fluid ordered along y, is destabilized at any value of activity by the unbounded growth of bend fluctuations δpx (y, t) of the order parameter [8, 14]. Both substrate friction (Γ) and a finite system size (L along the y direction) generate a finite activity threshold for the onset of spontaneous flow given by [12, 43].
For vanishing friction (Γ → 0), the screening length diverges (ℓη → ∞) and we recover the viscous limit of the finite size activity threshold
As shown below, wall anchoring geometrically frustrates this bulk instability mode and alters the mechanisms and nature of the instability which is now controlled by an interplay of three length scales: the channel width W, the flow screening length ℓη and the extrapolation length ℓκ.
Upon increasing activity, the quiescent state in a channel is destabilized, driving the system through a succession of flowing states. To classify such dynamical states, we examine the velocity correlation function parallel to the channel, defined as
where ⟨⋅⟩r denotes a spatial average over the entire channel domain. The number of oscillations in the correlation function is used to classify the nature of the flow; see Figure 2 for an example of a flow state (the vortex lattice) with the associated correlation function plotted.
While C∥ captures vorticity in flow patterns, states with finite throughput are quantified by evaluating the normalized throughput
where ⟨|v|⟩r is the mean velocity.
3.1 Strong anchoring, ℓκ ≪ W
The flow states obtained for strong anchoring (here ℓκ/W = 0.01) are summarized in the phase diagram of Figure 3B obtained by varying the activity α and the screening length ℓη. Upon increasing activity at fixed ℓη, we first observe a transition from a quiescent ordered state (grey region of Figure 3B) to a flowing state (blue region) with ⟨|v|⟩ ≠ 0. Strong anchoring suppresses pure bend fluctuations. The instability is then controlled by a growing mode that necessarily has both splay and bend components, as discussed in Section 4. This is evident from the polarization profiles displayed in Figure 4B. The resulting flow is a lattice of counter-rotating flow vortices that span the channel width, with zero net throughput. We refer to this state as a “vortex lattice”.
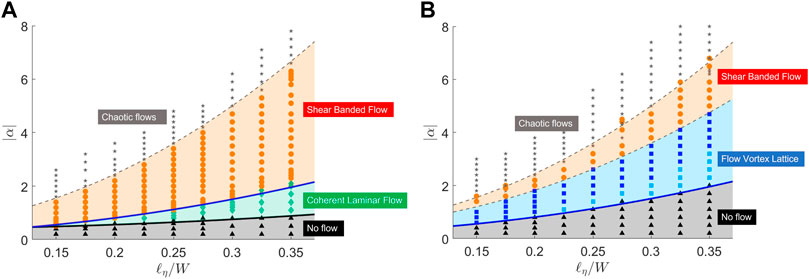
FIGURE 3. These phase diagrams show the various steady flow states in the channel as we change the screening length and the activity at a fixed anchoring strength. The dashed lines are fits to the observed phase boundaries whereas the solid lines correspond to the curves calculated using linear stability analysis in Section 4, with no fitting parameters. The solid blue line in both phase diagrams corresponds to the mixed bend-splay instability αm and the solid black line in (B) corresponds to the splay instability with weak anchoring, αs,w (Eq. 16). (A) Weak Anchoring, ℓκ/W =100. (B) Strong Anchoring, ℓκ/W =0.01.
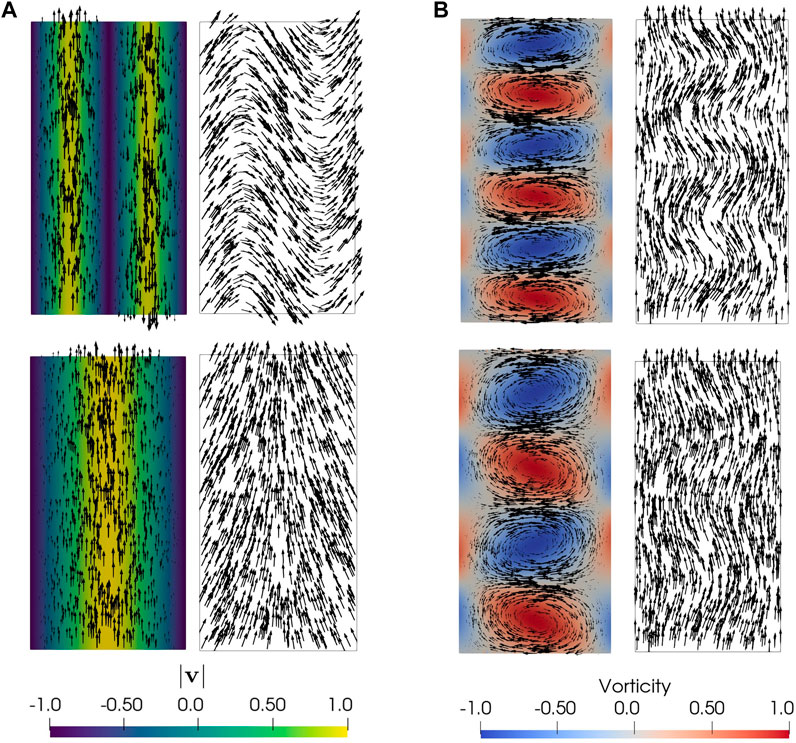
FIGURE 4. Some of the steady states observed in the phase diagrams (ℓη = 0.35) are shown in terms of the flow v (left in each frame) and the polarization p (right). The vorticity and the flow magnitude are colorized to show relative magnitudes and have been scaled by the corresponding maximum/minimum. The arrows represent the vectors for v and p scaled by their magnitudes. ℓκ. (A) Steady States with weak anchoring, ℓκ W =100, and low activity (bottom, α-1.75) and high activity (top, α=-4.00). (B) Steady States with strong anchoring, ℓκ W =0.01, and low activity (bottom, α-2.00) and high activity (top, α =-3.00).
The number n of counter-rotating vortex pairs in the vortex lattice is controlled by the aspect ratio L/W of the channel, together with the topological constraint that the net vorticity must be zero. This can be understood by comparing the energy cost of bend and splay deformations transverse and parallel to the long direction of the channel, with the number of pairs of vortices n ∼ (L/W) (As/Av), where As and Av are the amplitude of the polarization angle in the vortex-lattice and the shear banded flow states (Section 3.3). The minimum number of pairs of counter-rotating vortices is equal to the integer part of the aspect ratio and as we increase activity, additional vortices are added in pairs (light and dark blue points in Figure 3B).
Upon further increasing the activity, we note a transition (blue to orange in Figure 3B) from the ordered vortex lattice to a shear banded flow, with increasing number of shear bands at higher activities. This state is characterized by a bend about the short channel direction, transverse to the original orientation of the polarization field. Here, the flow and polarization are invariant along the channel. Interestingly, the flow transitions to a ‘more ordered state’ on increasing activity.
3.2 Weak anchoring, ℓκ ≫ W
For weak anchoring, and sufficiently large values of ℓη, the steady state corresponds to coherent laminar flow with finite throughput (green region in Figure 3A). But as we increase activity, an ordered vortex lattice similar to that in the strong anchoring limit forms transiently but then leads to a shear banded flow as the long time steady state (Figure 4A).
Notably, the laminar flowing state has non-zero splay but zero bend and can be seen only above a characteristic screening length
Figure 5 shows a phase diagram as a function of activity and extrapolation length, at a fixed screening
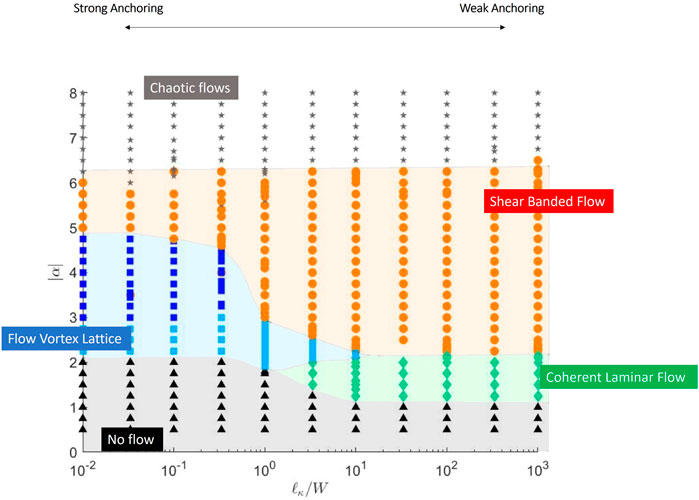
FIGURE 5. Phase diagram as we change the extrapolation length ℓκ at a fixed screening length ℓη = 0.35.
3.3 Lattice of flow vortices
Upon transition from the quiescent to the vortex state, the flow organizes into a single pair of counter-rotating vortices spanning the channel length L and of size of order L/2 (when L = 2W), as illustrated in Figure 4B for α = −2. This is observed in simulations for a large range of ℓη and ℓκ. Upon increasing activity, the number of vortex pairs increases, until eventually the system transitions to shear banded flow. The maximum number n of vortex pairs that can be accommodated in the channel depends of the channel’s aspect ratio. To estimate this number, we examine the elastic energy of channel-spanning bend deformations of the polarization field, described by the angle θ, with
In the shear banded state, the bend deformation is primarily transverse to the channel direction (Figure 6A), corresponding to an angle profile of the form θs ∼ As sin (2πx/W). In the vortex lattice state, away from the walls, bend deformations are primarily along the length of the channel (Figure 6B), corresponding to an angle profile of the form θv ∼ Av sin (2πny/L), where n is the number of counter-rotating vortex pairs. Note that the amplitudes As and Av of the two deformations depend on activity and on the strength of anchoring, and are generally different.
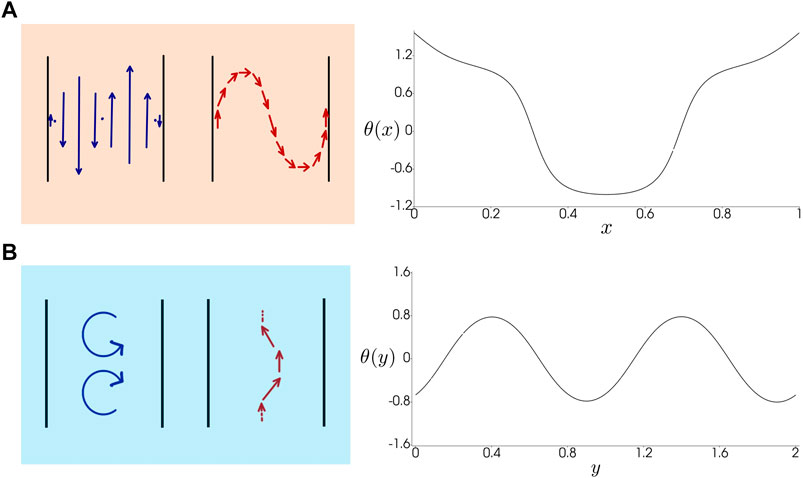
FIGURE 6. Schematic (L = W) for the shear banded and the vortex lattice flows. The line plot shows the angle θ along the polarization p for the two flow states from the numerical simulations (L = 2W) in the case of strong anchoring (ℓκ/W = 0.01, ℓη/W = 0.30). (A) Shear Banded Flow (angular profile is shown for α =-3.80). (B) Flow Vortex Lattice (angular profile is shown for α =-2.00).
The corresponding deformation energies Es and Ev for the shear banded and flow states are then immediately obtained by substituting the respective deformations into (11), with the result
The scaling of the number of vortex pairs with the channel aspect ratio for the lattice of flow vortices is confirmed by numerical simulations in longer channels, as shown in Figure 7, supporting the idea that the channel geometry determines the number of flow vortices.
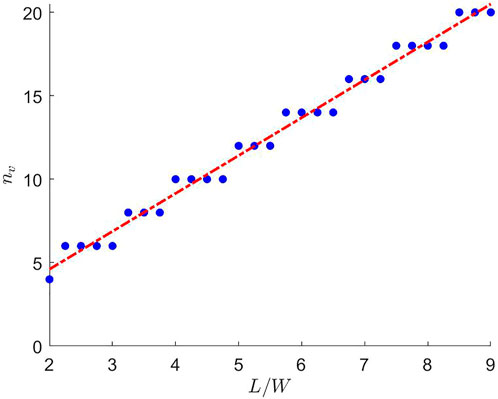
FIGURE 7. Scaling of the number of vortices, nv, in the flow vortex lattice state for strong anchoring as a function of the channel aspect ratio L/W. The blue points correspond to nv observed in numerical simulations (ℓκ = 0.01, ℓη = 0.35, α = −2.30) by increasing L/W in steps of 0.25 from L/W = 2 to L/W = 9. The value of nv increases in steps of 2, corresponding to the addition of a vortex/anti-vortex pair so as to maintain zero net vorticity. The growth is linear, as predicted by the simple scaling argument given in Section 3.3, but with a slope 2.270 ± 0.005 (dashed red line).
In the limit of weak anchoring, we observe transient vortex lattices, but the stable state is always shear banded. We can understand this because in this case the system can easily accommodate bend deformations across the channel, while bend deformations along the channel, which would be required for a vortex state, are energetically more costly.
4 Linear stability analysis
The steady state channel flows summarized in the previous section can be understood using a linear stability analysis of an initial uniformly aligned state with no flow.
First, let us consider the stability of an unconfined active fluid on a frictional substrate. For small activity, the uniform quiescent state with finite polarization
where, q = |q|,
4.1 Bulk
For extensile systems (α0 < 0) of elongated active units (λ > 1), the decay rate given in Eq. 13 can become positive, signalling the instability of the uniformly polarized state. It is known that in a bulk system, defined as one with periodic boundary conditions in all directions, the most unstable modes are bend deformations of the polarization field, corresponding to spatial variations along the direction of order, i.e., qx = 0 and finite qy. The hydrodynamic instability sets in at the longest wavelength, which in a periodic box of size L is 2π/L, yielding an activity threshold
Viscous dissipation enters through the screening length ℓη and shifts the instability to higher values of activity whenever ℓη ∼ L. In other words, viscous dissipation stabilizes the uniform quiescent state. When ℓη ≪ L one recovers the infinite system frictional threshold,
Upon further increasing activity, splay modes, corresponding to qy = 0, also become unstable. This splay instability occurs above a threshold
Note the dependence on the width W of the channel rather than the length L. In a periodic square box (L = W), for elongated flow-aligning swimmers (λ > 1),
The angular dependence of the instability threshold is displayed in the polar plots of Figure 8, where the shaded region corresponds to unstable modes (ν(q) > 0) in the qx − qy plane. It is evident that the fastest growing modes are always along the qx = 0 direction and become unstable for
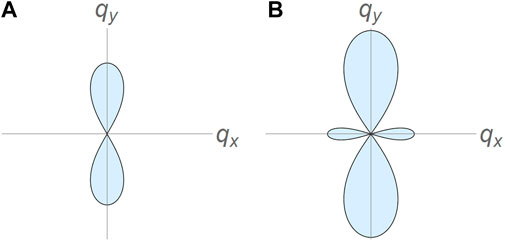
FIGURE 8. The shaded region in the qx-qy plane corresponds to unstable modes (ν > 0) in an extensile active fluid. Beyond the critical activity
4.2 Channel
In a channel geometry, boundary conditions can differentially frustrate bend and splay distortions [31, 44], allowing for distinct modes of spontaneous flow transitions to emerge. As in Ref. [12], we first consider a quasi-1D model that assumes only spatial variations along the direction x of the channel width. This is consistent with the observation that in the channel bend fluctuations (qy ≠ 0) are suppressed either by strong anchoring requiring px = 0 at the boundaries [12, 14] and/or by the condition of no-slip. The instability to spontaneous flow is then controlled by splay fluctuations (qx ≠ 0) and the threshold activity generally depends on the anchoring length, ℓκ. For strong anchoring (ℓκ → 0) the no-slip requirement on the velocity further excludes the possibility of a mode with wavelength 2W. Hence the longest allowed wavelength corresponds to qx = 2π/W and the splay (s) instability threshold for the case of strong anchoring 1) can be estimated as
For weak anchoring (ℓκ → ∞) conversely ∂xpx = 0 at the boundaries, allowing for a cosine wave of wavelength 2W instead that also satisfies no-slip. Hence the splay (s) instability threshold for the case of weak anchoring (w) is estimated as
In the case of weak anchoring, this simple argument provides a good estimate for the transition from the quiescent state to the coherent laminar flow. This is shown in Figure 3A by comparing the expression for
The transition to the vortex lattice can be described as arising from the instability of a mixed bend-splay mode where both qx, qy ≠ 0. To capture this instability, we fix the transverse wave number as
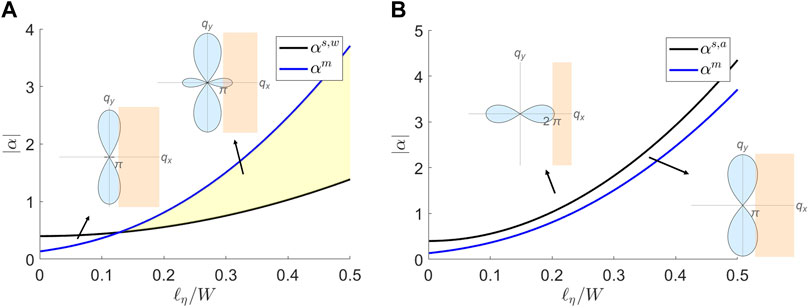
FIGURE 9. Linear instability for splay and the vortex-lattice state in the limits of weak and strong anchoring. In the insets, the orange regions delineate the values of wavector where the instability can occur, as discussed in Section 4.2. The yellow shaded region marks the range of parameters where
5 Role of self propulsion
Throughout the discussion we have described the bacterial fluid using a polar order parameter, p but the model considered has nematic symmetry. In this case the flow arises from spontaneous symmetry breaking of the quiescent state and is entirely determined by deformations of the polarization field. The direction of flow is equally likely to be up or down the channel, with associated “splay-in” and “splay-out” configurations of polarization. In the simulations with finite anchoring this symmetry is broken externally by the boundary conditions on the polarization. The presence of a frictional substrate can, however, allow an additional propulsive force linear in p to be present in force balance [40, 45, 46] which takes the form
This polar active force explicitly breaks the up-down symmetry of the flow. The homogeneous state in bulk is now a uniformly flowing state with v = v0p. As a result, any finite self-propulsion v0 then breaks the flow symmetry and selects the direction of the flowing state. A small self-propulsion provides therefore the minimal forcing required for creating sustained unidirectional channel flows. For small values of v0, corresponding to v0 ≪|α0|/Γℓη, the dipolar active stress dominates over the propulsive force and the structure of the steady state flows is qualitatively unaffected. Above the critical activity for spontaneous flow, we recover coherent laminar flows arising from polarization splay for weak anchoring and flow vortex lattices for strong anchoring, as in the absence of polar self propulsion. The flow lattice, however, acquires a steady drift at speed proportional to v0.
6 Discussion
Using a hydrodynamic model of extensile polar active matter, we have examined the role of confinement and boundary alignment in controlling the spatial and temporal organizations of active flows in a channel. We show that surface anchoring controls the flow structures by selectively frustrating bend or splay distortions in the polarization and that flows with finite throughput can only be obtained with weak surface anchoring. Strong surface anchoring leads to the formation of lattices of flow vortices, with the number of vortices determined by the aspect ratio of the channel, consistent with previous results [25, 26].
Our hydrodynamic model is inherently polar as the anchoring boundary conditions (Eq. 7) imposed at the channel walls break nematic symmetry even in the absence of any polar self propulsion (Section 5). As is evident, the symmetry of the boundary conditions plays a profound role on the selection of flow states. Strong polar anchoring, where the polarization is forced to point in the same direction on both sides of the channel, prevent splay deformation and facilitate bend along the channel walls, resulting in a state of flow vortices (Figure 10, left panel). Strong antipolar anchoring, where the polarization is forced to point in opposite directions on the two sides of the channel, allows bend deformation across the channel, resulting in finite-throughput laminar flow (Figure 10, right panel). We have also examined the case of nematic anchoring where the polarization is forced to orient with the channel wall, but with no preferred direction. This was enforced by requiring
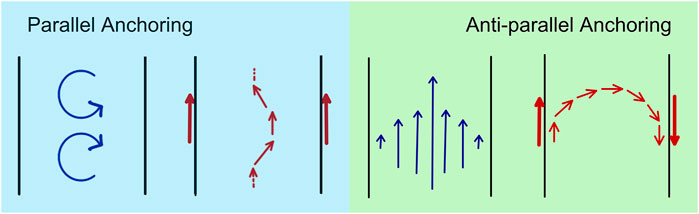
FIGURE 10. The symmetry of the boundary conditions for the polarization controls the steady flow states. Left frame: strong polar anchoring where the polarization is anchored in the same direction on both channel walls suppresses splay deformations and yields bend deformation along the wall with associated flow vortices. Right frame: strong apolar anchoring where the polarization is anchored in opposite directions on the two walls explicitly breaks the nematic symmetry even in the absence of polar self propulsion (v0 = 0) and leads to coherent flow. Both flow states can occur if the boundary conditions are nematic, i.e., agnostic to the direction of the polarization vector.
In this case both flow states depicted in Figure 10 coexist in the phase diagram. Finally, we note that the lattice of flow vortices reported here is distinct from the state of dancing half-integer disclinations found earlier in active nematics confined to channels [47]. Here we consider a polar system, where defect in the polarization texture are +1 and −1 vortices. Such defects are indeed observed in the turbulent state at high activity. The lattice of flow vortices reported here is, however, a defect-free steady state.
Our work quantifies the role surface anchoring in controlling the spatio-temporal structure of confined active flows. This understanding can be useful for the design of active microfluidic devices where channel dimensions and boundary preparation can be independently tuned to control viscous screening and anchoring, respectively.
Recent experiments on microtubule suspensions in 3D and associated numerical studies have demonstrated that coherent flow is only possible for finely tuned geometries [17, 48–50]. Our work suggests that it would be interesting to additionally explore the role of anchoring in these 3D systems where antagonistic boundary conditions on the three walls could result in as of yet unexplored states.
Finally, it would also be interesting to explore the role of surface anchoring on temporal as well as spatial organization of active flows. Recent experiments in dense bacterial suspensions [51] have revealed that viscoelasticity of the suspending medium can drive a circular droplet to self-organize in time-periodic states of vortical flow, consisting of a system-spanning vortex that switches its chirality at a rate controlled by the solvent relaxation time. The vortex state of a circular drops corresponds to unidirectional laminar flow in a channel. As we have seen, the direction of the flow is directly determined by the splay-in or splay-out configuration of the polarization field, which in turn can be controlled with suitable anchoring. This suggest that anchoring may play an important role in controlling temporal as well as spatial organization and that it may be possible to control oscillations between flows of opposite chirality by tuning the boundary conditions. These questions are left for future studies.
Data availability statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author contributions
PG performed the numerical simulations and prepared the figures. All authors contributed to the formulation of the project, the analysis of the model and the writing of the paper.
Funding
This work was directly supported by NSF grant DMR-2041459. SS acknowledges support from the Harvard Society of Fellows. Use was made of computational facilities purchased with funds from the National Science Foundation (CNS-1725797) and administered by the Center for Scientific Computing (CSC). The CSC is supported by the California NanoSystems Institute and the Materials Research Science and Engineering Center (MRSEC; NSF DMR 1720256) at UC Santa Barbara.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Wensink HH, Dunkel J, Heidenreich S, Drescher K, Goldstein RE, Löwen H, et al. Meso-scale turbulence in living fluids. Proc Natl Acad Sci U S A (2012) 109:14308–13. doi:10.1073/pnas.1202032109
2. Zhou S, Sokolov A, Lavrentovich OD, Aranson IS. Living liquid crystals. Proc Natl Acad Sci U S A (2014) 111:1265–70. doi:10.1073/pnas.1321926111
3. Sanchez T, Chen DT, DeCamp SJ, Heymann M, Dogic Z. Spontaneous motion in hierarchically assembled active matter. Nature (2012) 491:431–4. doi:10.1038/nature11591
4. Schaller V, Weber C, Semmrich C, Frey E, Bausch AR. Polar patterns of driven filaments. Nature (2010) 467:73–7. doi:10.1038/nature09312
5. Palacci J, Sacanna S, Steinberg AP, Pine DJ, Chaikin PM. Living crystals of light-activated colloidal surfers. Science (2013) 339:936–40. doi:10.1126/science.1230020
6. Bricard A, Caussin JB, Desreumaux N, Dauchot O, Bartolo D. Emergence of macroscopic directed motion in populations of motile colloids. Nature (2013) 503:95–8. doi:10.1038/nature12673
7. Marchetti MC, Joanny JF, Ramaswamy S, Liverpool TB, Prost J, Rao M, et al. Hydrodynamics of soft active matter. Rev Mod Phys (2013) 85:1143–89. doi:10.1103/revmodphys.85.1143
8. Simha RA, Ramaswamy S. Hydrodynamic fluctuations and instabilities in ordered suspensions of self-propelled particles. Phys Rev Lett (2002) 89:058101. doi:10.1103/physrevlett.89.058101
9. Alert R, Casademunt J, Joanny JF. Active turbulence. Annu Rev Condens Matter Phys (2021) 13:143–70. doi:10.1146/annurev-conmatphys-082321-035957
10. Duclos G, Garcia S, Yevick H, Silberzan P. Perfect nematic order in confined monolayers of spindle-shaped cells. Soft matter (2014) 10:2346–53. doi:10.1039/c3sm52323c
11. Doostmohammadi A, Adamer MF, Thampi SP, Yeomans JM. Stabilization of active matter by flow-vortex lattices and defect ordering. Nat Commun (2016) 7:10557. doi:10.1038/ncomms10557
12. Duclos G, Blanch-Mercader C, Yashunsky V, Salbreux G, Joanny JF, Prost J, et al. Spontaneous shear flow in confined cellular nematics. Nat Phys (2018) 14:728–32. doi:10.1038/s41567-018-0099-7
13. Thijssen K, Khaladj DA, Aghvami SA, Gharbi MA, Fraden S, Yeomans JM, et al. Submersed micropatterned structures control active nematic flow, topology, and concentration. Proc Natl Acad Sci U S A (2021) 118:e2106038118. doi:10.1073/pnas.2106038118
14. Voituriez R, Joanny JF, Prost J. Spontaneous flow transition in active polar gels. Europhys Lett (2005) 70:404–10. doi:10.1209/epl/i2004-10501-2
15. Wioland H, Woodhouse FG, Dunkel J, Kessler JO, Goldstein RE. Confinement stabilizes a bacterial suspension into a spiral vortex. Phys Rev Lett (2013) 110:268102. doi:10.1103/physrevlett.110.268102
16. Lushi E, Wioland H, Goldstein RE. Fluid flows created by swimming bacteria drive self-organization in confined suspensions. Proc Natl Acad Sci U S A (2014) 111:9733–8. doi:10.1073/pnas.1405698111
17. Wu KT, Hishamunda JB, Chen DT, DeCamp SJ, Chang YW, Fernández-Nieves A, et al. Transition from turbulent to coherent flows in confined three-dimensional active fluids. Science (2017) 355:eaal1979. doi:10.1126/science.aal1979
18. Chen S, Gao P, Gao T. Dynamics and structure of an apolar active suspension in an annulus. J Fluid Mech (2018) 835:393–405. doi:10.1017/jfm.2017.759
19. Opathalage A, Norton MM, Juniper MP, Langeslay B, Aghvami SA, Fraden S, et al. Self-organized dynamics and the transition to turbulence of confined active nematics. Proc Natl Acad Sci U S A (2019) 116:4788–97. doi:10.1073/pnas.1816733116
20. You Z, Pearce DJ, Giomi L. Confinement-induced self-organization in growing bacterial colonies. Sci Adv (2021) 7:eabc8685. doi:10.1126/sciadv.abc8685
21. Wioland H, Lushi E, Goldstein RE. Directed collective motion of bacteria under channel confinement. New J Phys (2016) 18:075002. doi:10.1088/1367-2630/18/7/075002
22. Tjhung E, Cates ME, Marenduzzo D. Nonequilibrium steady states in polar active fluids. Soft Matter (2011) 7:7453. doi:10.1039/c1sm05396e
23. Giomi L, Marchetti MC, Liverpool TB. Complex spontaneous flows and concentration banding in active polar films. Phys Rev Lett (2008) 101:198101. doi:10.1103/physrevlett.101.198101
24. Yang X, Wang Q. Role of the active viscosity and self-propelling speed in channel flows of active polar liquid crystals. Soft Matter (2016) 12:1262–78. doi:10.1039/c5sm02115d
25. Chandragiri S, Doostmohammadi A, Yeomans JM, Thampi SP. Active transport in a channel: Stabilisation by flow or thermodynamics. Soft matter (2019) 15:1597–604. doi:10.1039/c8sm02103a
26. Shendruk TN, Doostmohammadi A, Thijssen K, Yeomans JM. Dancing disclinations in confined active nematics. Soft Matter (2017) 13:3853–62. doi:10.1039/c6sm02310j
27. Samui A, Yeomans JM, Thampi SP. Flow transitions and length scales of a channel-confined active nematic. Soft Matter (2021) 17:10640–8. doi:10.1039/d1sm01434j
28. Wagner CG, Norton MM, Park JS, Grover P. Exact coherent structures and phase space geometry of preturbulent 2d active nematic channel flow. Phys Rev Lett (2022) 128:028003. doi:10.1103/physrevlett.128.028003
29. Hardoüin J, Hughes R, Doostmohammadi A, Laurent J, Lopez-Leon T, Yeomans JM, et al. Reconfigurable flows and defect landscape of confined active nematics. Commun Phys (2019) 2:121. doi:10.1038/s42005-019-0221-x
30. Norton MM, Baskaran A, Opathalage A, Langeslay B, Fraden S, Baskaran A, et al. Insensitivity of active nematic liquid crystal dynamics to topological constraints. Phys Rev E (2018) 97:012702. doi:10.1103/physreve.97.012702
31. Rorai C, Toschi F, Pagonabarraga I. Active nematic flows confined in a two-dimensional channel with hybrid alignment at the walls: A unified picture. Phys Rev Fluids (2021) 6:113302. doi:10.1103/physrevfluids.6.113302
32. Poujade M, Grasland-Mongrain E, Hertzog A, Jouanneau J, Chavrier P, Ladoux B, et al. Collective migration of an epithelial monolayer in response to a model wound. Proc Natl Acad Sci U S A (2007) 104:15988–93. doi:10.1073/pnas.0705062104
33. Conrad JC, Poling-Skutvik R. Confined flow: Consequences and implications for bacteria and biofilms. Annu Rev Chem Biomol Eng (2018) 9:175–200. doi:10.1146/annurev-chembioeng-060817-084006
34. Beebe DJ, Mensing GA, Walker GM. Physics and applications of microfluidics in biology. Annu Rev Biomed Eng (2002) 4:261–86. doi:10.1146/annurev.bioeng.4.112601.125916
35. Clark AG, Vignjevic DM. Modes of cancer cell invasion and the role of the microenvironment. Curr Opin Cel Biol (2015) 36:13–22. doi:10.1016/j.ceb.2015.06.004
36. Needleman D, Dogic Z. Active matter at the interface between materials science and cell biology. Nat Rev Mater (2017) 2:17048. doi:10.1038/natrevmats.2017.48
38. Giomi L. Geometry and topology of turbulence in active nematics. Phys Rev X (2015) 5:031003. doi:10.1103/physrevx.5.031003
39. Hemingway EJ, Mishra P, Marchetti MC, Fielding SM. Correlation lengths in hydrodynamic models of active nematics. Soft Matter (2016) 12:7943–52. doi:10.1039/c6sm00812g
40. Maitra A, Srivastava P, Marchetti MC, Ramaswamy S, Lenz M. Swimmer suspensions on substrates: Anomalous stability and long-range order. Phys Rev Lett (2020) 124:028002. doi:10.1103/physrevlett.124.028002
41. Alnæs M, Blechta J, Hake J, Johansson A, Kehlet B, Logg A, et al. The fenics project version 1.5. Archive Numer Softw (2015) 3.
42. Logg A, Mardal KA, Wells G. Automated solution of differential equations by the finite element method: The FEniCS book, vol. 84. Berlin, Germany: Springer Science & Business Media (2012).
43. Thampi SP, Golestanian R, Yeomans JM. Active nematic materials with substrate friction. Phys Rev E (2014) 90:062307. doi:10.1103/physreve.90.062307
44. Green R, Toner J, Vitelli V. Geometry of thresholdless active flow in nematic microfluidics. Phys Rev Fluids (2017) 2:104201. doi:10.1103/physrevfluids.2.104201
45. Brotto T, Caussin JB, Lauga E, Bartolo D. Hydrodynamics of confined active fluids. Phys Rev Lett (2013) 110:038101. doi:10.1103/physrevlett.110.038101
46. Kumar N, Soni H, Ramaswamy S, Sood A. Flocking at a distance in active granular matter. Nat Commun (2014) 5:4688. doi:10.1038/ncomms5688
47. Alert R, Joanny JF, Casademunt J. Universal scaling of active nematic turbulence. Nat Phys (2020) 16:682–8. doi:10.1038/s41567-020-0854-4
48. Chandragiri S, Doostmohammadi A, Yeomans JM, Thampi SP. Flow states and transitions of an active nematic in a three-dimensional channel. Phys Rev Lett (2020) 125:148002. doi:10.1103/physrevlett.125.148002
49. Chandrakar P, Varghese M, Aghvami SA, Baskaran A, Dogic Z, Duclos G, et al. Confinement controls the bend instability of three-dimensional active liquid crystals. Phys Rev Lett (2020) 125:257801. doi:10.1103/physrevlett.125.257801
50. Varghese M, Baskaran A, Hagan MF, Baskaran A. Confinement-induced self-pumping in 3d active fluids. Phys Rev Lett (2020) 125:268003. doi:10.1103/physrevlett.125.268003
Keywords: active matter, polar fluid, confined channels, boundary anchoring, coherent flow
Citation: Gulati P, Shankar S and Marchetti MC (2022) Boundaries control active channel flows. Front. Phys. 10:948415. doi: 10.3389/fphy.2022.948415
Received: 19 May 2022; Accepted: 28 June 2022;
Published: 26 July 2022.
Edited by:
Sujit Datta, Princeton University, United StatesReviewed by:
Ali Najafi, Institute for Advanced Studies in Basic Sciences (IASBS), IranRicard Alert, Max Planck Institute for the Physics of Complex Systems, Germany
Copyright © 2022 Gulati, Shankar and Marchetti. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Paarth Gulati, cGFhcnRoZ3VsYXRpQHBoeXNpY3MudWNzYi5lZHU=
 Paarth Gulati
Paarth Gulati Suraj Shankar
Suraj Shankar M. Cristina Marchetti
M. Cristina Marchetti