On the onset of breathing mode in Hall thrusters and the role of electron mobility fluctuations

Breathing mode is an ionization instability which is observed ubiquitously in the operation of Hall thrusters. It is recognized as a relatively low frequency (10–30 kHz) longitudinal oscillation of the discharge current and the plasma parameters. Although breathing instability is widely studied in the literature, the conditions for its origin are not fully understood. In this work we investigate the mechanisms responsible for the origin of the breathing mode in Hall thrusters by using a numerical model, allowing us to highlight the importance of electron mobility fluctuations for the onset and self-sustenance of the instability. Our one-dimensional, fully fluid model of the thruster channel is calibrated against the measured discharge current signal for a 5 kW-class Hall thruster operating in a condition where breathing mode is fully developed. The corresponding steady, unstable configuration (base state) is numerically computed by applying the Selective Frequency Damping (SFD) method. Then, a series of numerical tests is performed to show the existence of a feedback loop involving fluctuations around the base state of the neutral density, electron mobility, and electric field. We show that oscillations of the electron mobility are mainly caused by variations of the neutral density and are in phase with them; this, in turn, induces oscillations of the electric field, which are in phase opposition. The electric field acts simultaneously on the electron temperature and on the ion dynamics, promoting the depletion and replenishment of neutrals in the chamber.

1 Introduction

Hall thrusters are plasma-based electric propulsion devices for space applications. The cross-field configuration of these devices allows for an efficient (and synergic) ionization and acceleration of the propellant, without space-charge limiting effects that are typical of a configuration based on electrostatic acceleration. However, the strong coupling between the processes of ionization and acceleration is associated with high-amplitude, low frequency (5–30 kHz) discharge current oscillations, the so-called breathing mode. This mode has detrimental effects on the thruster performance and can cause significant coupling issues with the driving electronics. Additional details on the design and operation of Hall thrusters can be found, for instance, in the work of [1].

Several theoretical and experimental research efforts have been dedicated to the investigation of breathing mode. From the experimental point of view, breathing mode is directly diagnosed by sampling at high frequency the thruster discharge current. Measurements performed with intrusive [2–4] and non-intrusive [5–8] diagnostics have shown that breathing oscillations manifest as longitudinal coherent waves propagating in the plasma domain without significant frequency dispersion. From the modelling point of view, investigations were performed by means of zero-dimensional models [9–11] as well as with multidimensional simulations [12]. Zero-dimensional simulations have demonstrated that the origin of the breathing oscillations is associated with the periodic ionization and replenishment cycle of the propellant [10]. However, the proposed mechanisms could not reproduce self-sustained oscillations [13]. One-dimensional fluid models, on the other hand, have shown to be able to simulate the breathing mode. The authors of [13] employed a one dimensional formulation and selectively fixed in time different contributors to the discharge dynamics. Their results, for an uncalibrated case, suggest the importance of the electron temperature oscillations and of the non-linearity in the electron power absorption on the onset of breathing mode. As described in [14], these models can be specifically calibrated using the discharge current signal, in which the breathing mode oscillations are the most distinctive feature, indicative of the thruster operative condition. In the present work, the calibrated model of [14] is used to further investigate the mechanisms responsible for the onset of such self-sustained breathing oscillations in Hall thrusters.

2 Methodology

To describe the thruster discharge we consider an unsteady 1D fluid model [14]. The domain extends along the thruster symmetry axis z, from z = 0 (anode) to z = z_f = 2 L_c, where L_c is the length of the thruster channel. Sensitivity of the results to different choices of the domain length has been verified and it is negligible for the results presented here. The xenon plasma is assumed as quasi-neutral (ions and electrons have equal density n) and involves three species, neutrals, singly-charged ions and electrons. It is assumed that neutrals have a constant axial velocity, ions are unmagnetized and cold, and electrons inertia is neglected, thus relying on a drift-diffusion approximation. Finally, the external magnetic field is assumed to be purely radial, so that the model may not be suited for investigating modern Hall thrusters employing magnetic shielding. The plasma dynamics is described by the following set of equations:

$\frac{\partial n_n}{\partial t}+\frac{\partial }{\partial z}\left(u_n{n}_n\right)=-n{n}_n{k}_I+{\dot{n}}_w,(1)$

$\frac{\partial n}{\partial t}+\frac{\partial }{\partial z}\left(u_{i}n\right)=n{n}_n{k}_I-{\dot{n}}_w,(2)$

$\frac{\partial }{\partial t}\left(n{u}_i\right)+\frac{\partial }{\partial z}\left(n{u}_i^2\right)=-\frac{e}{m_i}n\frac{\partial \mathrm{\Phi }}{\partial z}-u_i{\dot{n}}_w,(3)$

$n{u}_e=-\mu n\left(\frac{1}{en}\frac{\partial p_e}{\partial z}-\frac{\partial \mathrm{\Phi }}{\partial z}\right),(4)$

$\frac{\partial }{\partial t}\left(\frac{3}{2}n{k}_B{T}_e\right)+\frac{\partial }{\partial z}\left(\frac{5}{2}n{k}_B{T}_e{u}_e\right)=\frac{\partial }{\partial z}\left(\frac{5}{2}\frac{\mu }{e}n{k}_B^2{T}_e\frac{\partial T_e}{\partial z}\right)+n{u}_{e}e\frac{\partial \mathrm{\Phi }}{\partial z}-n_{n}nK-nW,(5)$

$u_e=u_i-\frac{J}{en}.(6)$

where n, u and T stand for density, axial velocity and temperature, and k_B is the Boltzmann constant. Subscripts n, i and e indicate neutrals, ions and electrons, respectively. The discharge current density J is computed by integrating Eq. 4 between the anode and the end of the domain. The resulting integral equation contains the applied potential difference ΔV, which is specified in the operating condition. The ionization-rate coefficient k_I and the collisional energy loss coefficient K are computed as a function of the electron internal energy using the LXCat database [15] and the Bolsig+ [16] solver. Bolsig+ is used to parse the cross-section data to compute Maxwellian rates. The terms ${\dot{n}}_w$ and W represent the neutral particles flowing in the domain from the lateral walls due to ion recombination and the electron power loss to the wall, respectively. The cross-field mobility μ is defined as:

$\mu =\frac{{\mu }_0}{1+{\mathrm{\Omega }}^2},(7)$

where μ₀ = e/(ν_e m_e) is the unmagnetized mobility and Ω = ω_e/ν_e is the Hall parameter, ω_e = (eB_r)/m_e being the local cyclotron frequency of electrons and B_r being the external magnetic field intensity. The term ν_e represents the momentum transfer collision frequency and is given by the sum of three contributions:

${\nu }_e={\nu }_c+{\nu }_{ew}+{\nu }_a,(8)$

where ν_ew is the electron-wall collision frequency, proportional to a wall interaction coefficient and the Bohm velocity, and ν_c takes into account collisions between electrons and neutral atoms (elastic, excitation and ionization collisions) and it is given by the product of the neutral density and the relevant reaction rate k_x computed using LXCat and Bolsig+. Coulomb electron-ion (e-i) collision frequency has not been accounted for after having verified that it is always negligible in comparison to ν_e. More specifically, for the investigated case the e-i collision frequency is one order of magnitude lower than ν_c in the ionization and acceleration regions, where the core of the breathing instability is supposed to be localized. The comparison against the experiments of the calibrated model further support this and the other modeling assumptions. However, we underline that in different thrusters the proposed modeling assumptions should be critically reconsidered. Finally, the anomalous collision frequency ν_a is modeled as

${\nu }_a=\beta \frac{e{B}_r}{16m_e}=\frac{\beta }{16}{\omega }_e,(9)$

where β(z), which is time independent, is the same function of the axial position already used in [14]. Several attempts to provide a closure function for the anomalous collision frequency, i.e., to identify a relation between β and the local plasma fields, have been performed (see, for instance [17]), but to date no self-consistent closure function exists. Even if in specific cases different spatial profiles have been adopted (see [18, 19]), the particular choice followed in our model, as shown in [14], leads to reasonable agreement against the experiments for the considered thruster.

For the objectives of the present work it is important to underline that, in our model, the mobility μ depends only on two plasma quantities, the neutrals density and the electron temperature; this aspect is made explicit, when needed for clarity, by writing μ as μ(n_n, T_e). Finally, we assume that the electron population follows an isotropic Maxwellian distribution with temperature T_e. Thus, the electron pressure p_e is related to T_e as follows:

$p_e=n_e{k}_B{T}_e.(10)$

As concerns the boundary conditions, at the inner boundary (z = 0) the neutral density is fixed based on the injected mass flow rate and accounting for the ion recombination at the anode surface. Additionally, ions must enter the anode sheath edge with a velocity greater than or equal to the local sound speed (for the electron-repelling sheath to form), and the electron energy flux is imposed according to the analysis of a sheath in front of a biased electrode. At the outer boundary (z = z_f), instead, we fix T_e = 2eV. For additional details on the adopted boundary conditions and on the finite-volume method used to discretize in space the PDEs of the model refer to [14].

The objective of the present analysis is to investigate the mechanisms at the basis of the self-sustenance of the breathing mode using the model described above. To this purpose a particular configuration is selected in which breathing is evident and well observable. The considered thruster is a 5 kW-class Hall thruster, SITAEL’s HT5k, operating with a conventional magnetic field topology (almost radial magnetic lines at the channel exit) at nearly 2.6 kW, with a discharge voltage of 300 V and a mass flow rate of 8 mg/s. This particular configuration has been investigated experimentally and detailed measurements of the plasma properties are available [2]. Some details on the magnetic topology can be found in [20].

In order to increase the realism of the numerical model, a calibration has been carried out against the discharge current signal available from the experiments, and the resulting estimated properties of the plasma have been compared against the available measurements [14]. More precisely, the neutral velocity, wall interaction coefficient, and anomalous collision frequency profile were progressively varied until the simulated discharge current signal matched as close as possible the measured one in terms of dominant frequency, mean value, and amplitude of the oscillations. The model resulting from the calibration and its accuracy in representing the plasma properties are discussed in details in [14]. We underline that different calibration strategies may be applied, for instance by taking into account local measurements of plasma properties. The one adopted here has the advantage of relying only on a single measurable quantity which is usually available in existing experimental databases. Moreover, although the kind of calibration may affect the resulting model, the core mechanism leading to breathing mode should not be significantly affected because it is by far the dominant dynamical process at play in the selected calibration database. For this reason, in the present work we investigate breathing mode by using the calibrated model of [14].

Since the breathing mode has the characteristics of a self-sustained instability, the first step is to find the steady (unstable) configuration on top of which it develops. This particular configuration, denoted in the following as base configuration, is computed by searching for a steady solution of the calibrated model. This is achieved numerically by applying the Selective Frequency Damping (SFD) method, which is commonly used to find steady solutions in high-dimensional dynamical systems, as for instance in the field of computational fluid dynamics [21, 22]. This technique relies on the application of a proportional feedback control which vanishes on the steady state and makes it stable, so that it can be computed by classical time-advancing methods. In the present case the controller is applied only to the neutral continuity equation, given the importance of neutral density oscillations in the breathing mode dynamics. Equation 1 becomes

$\frac{\partial n_n}{\partial t}+\frac{\partial }{\partial z}\left(u_n{n}_n\right)=-n_e{n}_n{k}_I+{\dot{n}}_w-\chi \left(n_n-{\bar{n}}_n\right),(11)$

where χ ≃ 10⁷ Hz, ${\bar{n}}_n$ is given by

$\frac{\partial {\bar{n}}_n}{\partial t}=\frac{\left(n_n-{\bar{n}}_n\right)}{\mathrm{\Delta }},(12)$

and Δ ≃ 10⁻⁴ s. Equation 12 updates the target solution ${\bar{n}}_n$ (which is not known a priori) at each time step, and must be integrated in time together with the other equations. Free parameters are set following the guidelines presented in the literature and tuned for the specific problem [22]. In general, χ represents the strength of the controller and Δ defines its cutoff frequency, and both need to be tailored for the specific case. Figure 1 reports the discharge current signal of the calibrated model (blue line) together with that obtained applying the SFD (red line) at time t = 0, showing that SFD is effective in damping the oscillations, quickly leading to the base configuration. Figure 1 shows that the discharge current of the base configuration is I ≃ 8.73 A, while it oscillates periodically in the range I ∈ [4.5, 16.4] A when breathing mode is present. Note that the base configuration has already been computed in the literature for different objectives and with different techniques (see for instance [13]).

FIGURE 1

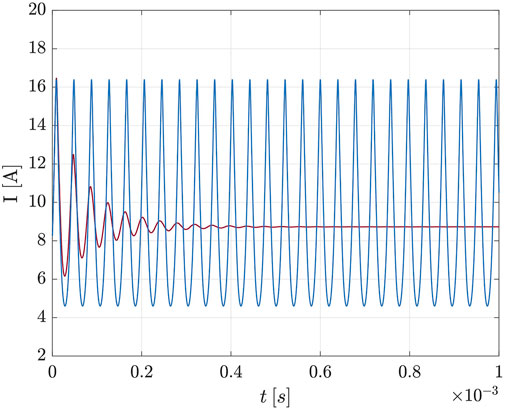
FIGURE 1. Discharge current signal of the calibrated model with (red) and without (blue) the application of the SFD technique.

3 Results

We now investigate the self-sustenance process driving the instability by means of ad-hoc numerical simulations. We start by calculating the base configuration; then, starting from the base configuration, we have verified that the instability spontaneously emerges, leading to an exponential growth of its amplitude. The instability then saturates in the non linear phase finally settling on a periodic limit cycle (Test T1, Figure 2A). This evidence supports the idea that the breathing mode is a linear Hopf-like instability of the base configuration.

FIGURE 2

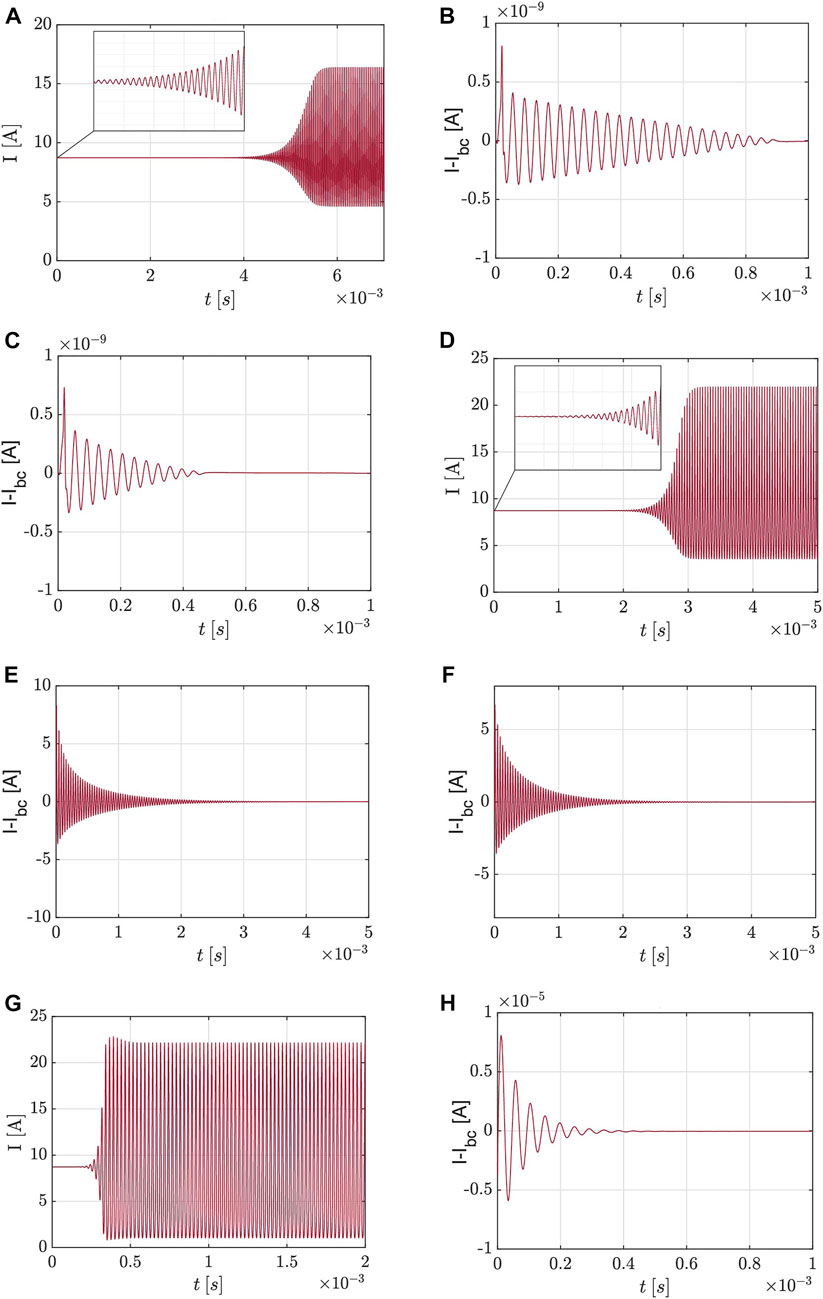
FIGURE 2. Simulated discharge current signal for tests (A) T1, (B) T2, (C) T3 (D) T4 starting from a perturbation of the base configuration and tests (E) T2 and (F) T3 starting from the saturated breathing instability; results from tests T6 and T7 are reported in (G) and (H), respectively.

We now focus on the role of mobility on the self-sustenance mechanism of the breathing mode. The idea that mobility can play a dominant role in the instability originates from the observation that breathing mode can be suppressed, both in experiments [8, 23] and in the present model (not shown here), by increasing the intensity of the magnetic field. Note that in the model, B_r enters only via the mobility μ.

Considering now the calibrated case, a second artificial test (T2) has been carried out by starting from the base configuration with the spatial distribution of μ artificially fixed to the value computed on the base configuration, i.e., μ = μ_bc = μ(n_n,bc, T_e,bc) (where the subscript bc indicates quantities taken in the base configuration). In this way we avoid that μ varies due to plasma fluctuations $n_n^{\prime }(t,z)=n_n(t,z)-n_{n,bc}(z)$ and $T_e^{\prime }(t,z)=T_e(t,z)-T_{e,bc}(z)$. The result is that the instability does not develop and the system stays on the base configuration, as shown in Figure 2B. In order to exclude the possibility to have artificially created a conditional stability region around the base state, the same test has been repeated, still fixing μ = μ_bc, but considering, as initial conditions, fields of the limit cycle (selected at random phase) on which the system settles when the full model is considered and the instability is saturated. In this case the modified system of test T2 shows a damped breathing mode which eventually vanishes, and the system returns to the base configuration (see Figure 2E). As a result, test T2 provides evidence that variations of electron mobility (μ′ = μ − μ_bc) play a fundamental role for the onset and self-sustenance of the breathing mode. This fact has been already observed in [24] where it is shown by 2D simulations that breathing mode oscillations can be induced by modulating spatially the anomalous mobility profile.

Considering that n_n,bc and T_e,bc are fixed quantities, the mobility ${\mu }^{\prime }={\mu }^{\prime }(n_n^{\prime },T_e^{\prime })$ varies in our model with respect to its value at the base configuration only because of the presence of fluctuations of 1) neutral density and 2) electron temperature. Moreover, test T2 shows that if fluctuations μ′ are suppressed the breathing mode disappears. We focus now our attention on fluctuations of μ′ induced separately by $n_n^{\prime }$ and $T_e^{\prime }$ only. To this purpose a third test, T3, is carried out using the following expression for mobility: $\mu ={\mu }_{bc}+{\mu }^{\prime }(0,T_e^{\prime })$ where only variations of μ induced by variations of the electron temperature are considered. As for test T2, the breathing mode does not develop if the simulation is started from the base configuration, as shown in Figure 2C. Furthermore, it disappears when starting the simulation from random points of the limit cycle, as shown in Figure 2F. Thus, test T3 demonstrates that variations of mobility induced by $n_n^{\prime }$ are fundamental for the onset and sustenance of breathing.

A fourth test T4 is carried out by considering only variations of mobility induced by fluctuations of neutral density, $\mu ={\mu }_{bc}+{\mu }^{\prime }(n_n^{\prime },0)$. In this case the breathing mode starts and reaches a self-sustained state for the same set of initial conditions used in the previous tests, as shown in Figure 2D. This and the previous tests indicate that, at least for the configuration under investigation, only fluctuations of mobility due to the variations of the neutral density are necessary for the triggering of the breathing mode. Notice that, in different models/configurations, other mechanisms can be dominating the instability, as for instance in [13, 18].

In order to further investigate this point, a simplified model for μ is derived by fixing T_e = T_e,bc and linearizing its dependence on $n_n^{\prime }$

${\mu }^{\prime }=\underset{\gamma }{\underbrace{\frac{e}{m_e\left({\nu }_{e,bc}^2+{\omega }_e^2\right)}\left[1-\frac{2{\nu }_{e,bc}^2}{\left({\nu }_{e,bc}^2+{\omega }_e^2\right)}\right]k_m}}{n}_n^{\prime }.(13)$

where k_m is the sum of the reaction rates for momentum transfer collisions between electrons and neutrals.

A fifth test, T5, is carried out using $\mu ={\mu }_l={\mu }_{bc}+\gamma n_n^{\prime }$. Results obtained using the same initial conditions as for the previous tests show the development of the breathing mode with typical features quantitatively similar to those obtained when simulating the full system, see Figure 3 in comparison with Figure 2A. Interestingly, we note that by artificially modulating γ it is possible to change the growth rate and the saturation amplitude of the instability, approximately maintaining the same frequency (Figure 3, green and blue lines). This indicates that the linearized mobility μ_l, although very simplified, contains the elements needed to describe quantitatively the breathing mode, confirming two aspects: 1) that linearity in the dependence of μ on n_n is sufficient to trigger breathing and 2) that variations of μ induced by oscillations of T_e play a minor role, both qualitatively and quantitatively on the simulated breathing mode. Thus, the coefficient γ(n_n,bc, T_e,bc) in Eq. 13, which represents a rigidity coefficient relating μ with $n_n^{\prime }$, plays a key role in the breathing instability.

FIGURE 3

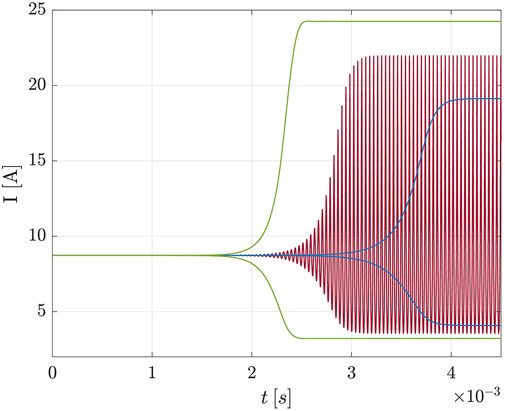
FIGURE 3. Discharge current signal for test T5 (red line); green and blue lines are the envelopes of the discharge current signals obtained by imposing ${\mu }^{\prime }=1.2\gamma n_n^{\prime }$ and ${\mu }^{\prime }=0.8\gamma n_n^{\prime }$, respectively.

With the support of the tests described above, it is now possible to propose a physical interpretation concerning the feedback mechanism that leads to the breathing instability in the investigated case. To this purpose we look at variations around the base configuration and we focus on the region where ionization is concentrated. From Eq. 4 we note first that the electric field $E=-\frac{\partial \mathrm{\Phi }}{\partial z}$ is given by

$E=-\frac{u_e}{\mu }-\frac{1}{e{n}_e}\frac{\partial \left(n_e{k}_B{T}_e\right)}{\partial z}.(14)$

When the neutral density decreases, the same happens for the electron mobility and, through the first term on the right side of Eq. 14, this provides a positive contribution to the electric field. As a matter of fact, during the simulated oscillations, the electric field reaches its peak when the neutral density is at its minimum, and the two quantities oscillate in phase opposition, as depicted in Figure 4A. This phenomenon promotes two parallel effects:

(E1) As concerns T_e, when the neutral density decreases and the electric field increases, the work performed by the electric field on the electron fluid also increases, inducing an increase of electron temperature and, in turn, of ionization rate (see Figure 4B). This creates a positive feedback as it contributes to further decrease the neutral density.

(E2) As concerns the ion dynamics, when replenishment of neutrals begins, the electric field is at its maximum and ions are accelerated towards the exit. As a consequence, during replenishment plasma density decreases and this leads to a decrease of the ionization rate, thus promoting the channel replenishment and creating again a positive feedback on the neutral density.

FIGURE 4

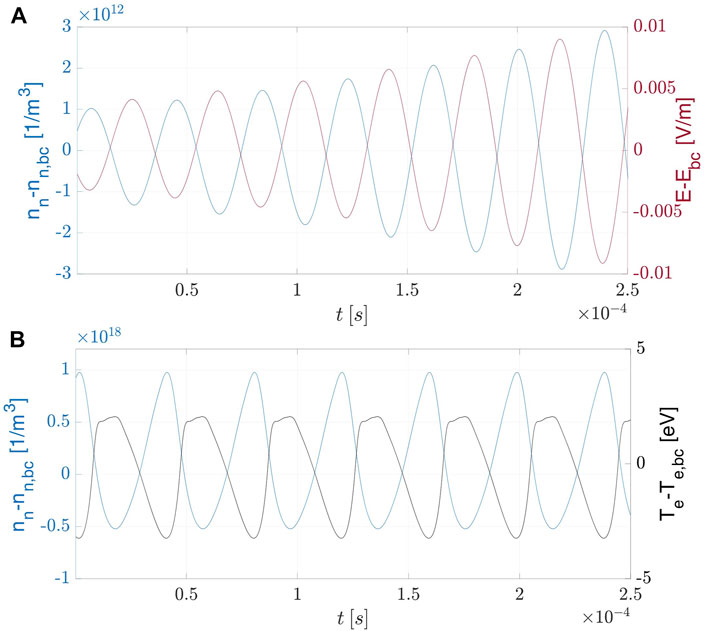
FIGURE 4. Oscillations in time of neutral density (blue) and electric field (red) around their base state values at point z = L_c/2 (A) at incipient instability and (B) of neutral density and temperature (black) on the limit cycle.

The electron temperature fluctuations play an intricate role in the system dynamics, with possible feedback on all species. The performed tests have indicated that their contribution to the variations of mobility are not relevant for the development nor for the sustenance of breathing mode oscillations. Nevertheless, to assess the importance of temperature fluctuations $T_e^{\prime }$ on the whole system, a test (T6) was performed in which mobility was linearized, $\mu ={\mu }_{bc}+\gamma n_n^{\prime }$, and temperature fluctuations were artificially suppressed by eliminating Eq. 5 from the system and replacing it with T_e = T_e,bc. In this case, starting from the same initial conditions used for the previous tests, we find that the system reaches a time-periodic solution, as for breathing mode, and this is shown in see Figure 2G. Scenario E2 is further supported by observing that, for simulations carried out with a fixed ion velocity profile, i.e., u_i = u_i,bc (test T7), oscillations are always damped and no periodic solution can be found, as shown in Figure 2H. We thus conclude that, at least in our specific calibrated case, the most important aspect at the basis of breathing mode is related to the variations of mobility with the neutral density and that the dominating mechanisms for self-sustenance is E2 discussed above. Observe how in [13], for an uncalibrated case, the authors conclude that the breathing mode is triggered by a feedback mechanism akin to the effect E1 discussed above. This suggests that the two described effects, E1 and E2, could be concurring to determine the discharge dynamics and the dominant one, responsible for the onset of the breathing mode, may depend on the specific case under analysis.

4 Conclusion

In this work the mechanisms leading to the onset of breathing mode in Hall thrusters are further investigated numerically and theoretically. A one-dimensional fluid model of the thruster channel is used, which is calibrated and validated against the experimental data available for SITAEL’s HT5K thruster. A crucial element for the proposed analysis is the identification of the base configuration, i.e., the unstable steady configuration of the thruster which undergoes breathing instability, so that breathing can be investigated both during its initial onset and in its final saturated state. Results demonstrate that fluctuations of the electron mobility around its distribution in the base configuration are necessary for the onset of the breathing mode. In particular, a linear dependence between oscillations of neutral density and electron mobility is sufficient for triggering the instability in the proposed model, inducing fluctuations of the electric field in phase opposition. This establishes a positive feedback on the ionization rate via two different mechanisms, one involving the electron energy and one, which is dominant in the case analyzed, involving the ion dynamics. These observations provide a new perspective in the interpretation of the ionization instability at the basis of breathing mode.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

Conceptualization, LL, SC, VG, and TA; methodology, LL, SC, and VG; software, VG, MMS, LL, and SC; analysis, LL, VG, SC, TA, and FC; resources, SC, TA, and FC; writing—original draft preparation, SC, LL, VG, and TA; writing—review and editing, LL, SC, VG, FC, and TA. All authors have read and agreed to the published version of the manuscript.

Funding

The work described in this paper has been funded by the European Union under the H2020 Programme ASPIRE-GA 101004366.

Conflict of interest

Authors VG and TA were employed by the company SITAEL S.p.A.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1. Boeuf J-P. Tutorial: Physics and modeling of Hall thrusters. J Appl Phys (2017) 121:011101. doi:10.1063/1.4972269

CrossRef Full Text | Google Scholar

2. Giannetti V, Saravia MM, Andreussi T. Measurement of the breathing mode oscillations in Hall thruster plasmas with a fast-diving triple Langmuir probe. Phys Plasmas (2020) 27. doi:10.1063/5.0022928

CrossRef Full Text | Google Scholar

3. Lobbia R, Gallimore A. A method of measuring transient plume properties. In: proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit (2008). doi:10.2514/6.2008-4650

CrossRef Full Text | Google Scholar

4. Lobbia RB, Gallimore AD. High-speed dual Langmuir probe. Rev Scientific Instr (2010) 81:073503. doi:10.1063/1.3455201

CrossRef Full Text | Google Scholar

5. Chaplin VH, Lobbia RB, Lopez Ortega A, Mikellides IG, Hofer RR, Polk JE, et al. Time-resolved ion velocity measurements in a high-power Hall thruster using laser-induced fluorescence with transfer function averaging. Appl Phys Lett (2020) 116:234107. doi:10.1063/5.0007161

CrossRef Full Text | Google Scholar

6. Dale ET, Jorns BA. Non-invasive time-resolved measurements of anomalous collision frequency in a Hall thruster. Phys Plasmas (2019) 26:013516. doi:10.1063/1.5077008

CrossRef Full Text | Google Scholar

7. Fabris AL, Young CV, Cappelli MA. Time-resolved laser-induced fluorescence measurement of ion and neutral dynamics in a Hall thruster during ionization oscillations. J Appl Phys (2015) 118:233301. doi:10.1063/1.4937272

CrossRef Full Text | Google Scholar

8. Sekerak MJ, Gallimore AD, Brown DL, Hofer RR, Polk JE. Mode transitions in Hall-effect thrusters induced by variable magnetic field strength. J Propulsion Power (2016) 32:903–17. doi:10.2514/1.B35709

CrossRef Full Text | Google Scholar

9. Dale ET, Jorns BA. Two-zone Hall thruster breathing mode mechanism, Part I: Theory. In: 36th International Electric Propulsion Conference (2019). p. 1.

Google Scholar

10. Fife JM, Martinez-Sanchez M, Szabo J. A numerical study of low-frequency discharge oscillations in Hall thrusters. In: proceedings of the 33rd Joint Propulsion Conference and Exhibit. American Institute of Aeronautics and Astronautics Inc, AIAA (1997). doi:10.2514/6.1997-3052

CrossRef Full Text | Google Scholar

11. Hara K, Sekerak MJ, Boyd ID, Gallimore AD. Perturbation analysis of ionization oscillations in Hall effect thrusters. Phys Plasmas (2014) 21:122103. doi:10.1063/1.4903843

CrossRef Full Text | Google Scholar

12. Hara K. An overview of discharge plasma modeling for Hall effect thrusters. Plasma Sourc Sci Technol (2019) 28:044001. doi:10.1088/1361-6595/ab0f70

CrossRef Full Text | Google Scholar

13. Lafleur T, Chabert P, Bourdon A. The origin of the breathing mode in Hall thrusters and its stabilization. J Appl Phys (2021) 130. doi:10.1063/5.0057095

CrossRef Full Text | Google Scholar

14. Giannetti V, Saravia MM, Leporini L, Camarri S, Andreussi T. Numerical and experimental investigation of longitudinal oscillations in Hall thrusters. Aerospace (2021) 8:148. doi:10.3390/aerospace8060148

CrossRef Full Text | Google Scholar

15. [Dataset] Biagi S. Biagi database (2021). Available from: www.lxcat.net (accessed March 9, 2021).

Google Scholar

16. Hagelaar GJM, Pitchford LC. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models. Plasma Sourc Sci Technol (2005) 14:722–33. doi:10.1088/0963-0252/14/4/011

CrossRef Full Text | Google Scholar

17. Lafleur T, Baalrud SD, Chabert P. Theory for the anomalous electron transport in Hall effect thrusters. II. kinetic model. Phys Plasmas (2016) 23. doi:10.1063/1.4948496

CrossRef Full Text | Google Scholar

18. Hara K, Mikellides IG. Characterization of low frequency ionization oscillations in Hall thrusters using a one-dimensional fluid model. In: 2018 Joint Propulsion Conference. American Institute of Aeronautics and Astronautics (2018). doi:10.2514/6.2018-4904

CrossRef Full Text | Google Scholar

19. Lopez Ortega A, Mikellides IG, Sekerak MJ, Jorns BA. Plasma simulations in 2-d (r-z) geometry for the assessment of pole erosion in a magnetically shielded Hall thruster. J Appl Phys (2019) 125:033302. doi:10.1063/1.5077097

CrossRef Full Text | Google Scholar

20. Andreussi T, Giannetti V, Leporini A, Saravia MM, Andrenucci M. Influence of the magnetic field configuration on the plasma flow in Hall thrusters. Plasma Phys Control Fusion (2018) 60:014015. doi:10.1088/1361-6587/aa8c4d

CrossRef Full Text | Google Scholar

21. Jordi B, Cotter C, Sherwin S. Encapsulated formulation of the selective frequency damping method. Phys Fluids (2014) 26:034101. doi:10.1063/1.4867482

CrossRef Full Text | Google Scholar

22. Åkervik E, Brandt L, Henningson D, Hæpffner J, Marxen O, Schlatter P, et al. Steady solutions of the Navier-Stokes equations by selective frequency damping. Phys Fluids (2006) 18:068102. doi:10.1063/1.2211705

CrossRef Full Text | Google Scholar

23. Giannetti V, Piragino A, Paissoni CA, Ferrato E, Estublier D, Andreussi T, et al. Experimental scaling laws for the discharge oscillations and performance of Hall thrusters. J Appl Phys (2022) 131. doi:10.1063/5.0070945

CrossRef Full Text | Google Scholar

24. Lopez Ortega A, Mikellides IG, Chaplin V. Numerical simulations for the assessment of erosion in the 12.5-kW Hall effect rocket with magnetic shielding (HERMeS). In: proceedings of the 35th International Electric Propulsion Conference. IEPC-2017-154 (2017).

Google Scholar