Characteristics analysis of compact cesium atomic clock with magnetic state selection

This paper introduces a compact magnetic state-selection cesium atomic clock called LIP Cs-3000 and analyses its characteristics. The test results reveal that the ranges of the line width, peak-to-valley ratio and signal-to-noise ratio of Ramsey pattern are 340–410 Hz, 2–13 and 2,000–8,000 respectively. The corresponding distributions of these parameters are derived by using statistical methods. According to these results, some suggestions are put forward for the further development of the clock. It is also pointed out that the most important factor affecting the accuracy of LIP Cs-3000 atomic clock is the uncertainty of cavity phase shift. In addition, the method to estimate the lifetime of a clock has been proposed. In the end, the paper gives some environmental adaptability designs of the clock, which enable the clock to be used in complex environments.

Introduction

The function of a compact cesium atomic clock with magnetic state selection is to realize the definition of SI second in a continuous and reliable manner, providing the user with frequency signals with high stability and accuracy. Thus this kind of clock has been widely used in time keeping, navigation, positioning, communication, and other fields in the world [1–7].

Presently, there are several brands of such atomic clock that can be available on the market. The cesium clock 5071A has specifications with an accuracy of $\pm 5\times {10}^{-13}$ and a stability of $2.7\times {10}^{-14}$ at 100,000 s [8]. OSA 3235B Cesium Clock has a specified accuracy of $\pm 1\times {10}^{-12}$ and a stability of $8.5\times {10}^{-14}$ at 100,000 s [9]. Although these clocks show excellent performance in many applications, the analysis of their characteristics is rarely discussed in the literature. This situation is not conducive to the development of cesium atomic clocks with magnetic state selection.

To solve this problem, the paper introduces a compact magnetic state-selection cesium clock called LIP Cs-3000 which was developed at Lanzhou Institute of Physics in China [10, 11]. The paper adopts statistical methods to obtain the distributions of the line width, signal-to-noise and peak-to-valley ratio of Ramsey pattern. Based on the results, the range of stability of LIP Cs-3000 is calculated and the further development of the clock is suggested. The paper also analyzes various factors affecting accuracy and points out that the most important factor is the uncertainty of cavity phase shift. We expect that this conclusion will help improve the accuracy of the atomic clock in the future. In addition, the paper studies how to estimate the lifetime of LIP Cs-3000 clock and derives that the lifetime of the clock is larger than 5 years. The formula for assessing lifetime can be also used in other brands of cesium atomic clocks. In the end, the paper gives some environmental tests of LIP Cs-3000, which show that the clock can be applied to some complex environments. The contents of this paper not only contribute to the further development of LIP Cs-3000, but also can be applied to other brands of compact cesium atomic clocks to improve performance.

Principle and scheme

LIP Cs-3000 (see Figure 1) uses an identical two-wire magnetic field which realized by Stern-Gerlach magnet to prepare and detect atomic states and Ramsey-separated field excitation to achieve the state transitions [6, 7]. The transition signal is sent to a servo system to tune a voltage controlled crystal oscillator (VCXO).

FIGURE 1

FIGURE 1. LIP Cs-3000 cesium atomic clock. The overall dimension of the LIP Cs-3000 is 435 mm × 133 mm × 500 mm. It is the standard dimension of the 3U case. Thus the LIP Cs-3000 could easily been installed on the standard 19 inch cabinet.

Figure 2A shows a schematic diagram of the cesium atomic clock of LIP Cs-3000. A beam of atoms emerges from the oven at a temperature near 110°C and travels through the state-preparation region (the A magnet in Figure 2A), where the beam is split into two beams of atoms with different atomic states. These states are characterized by two quantum number F and m_F, where F = 3 or 4 and m_F can have integer values between –F and +F (see Figure 2B). Therefore, there are 16 possible states of cesium, but only the transition between the $|\mathrm{4,0}\rangle$ and $|\mathrm{3,0}\rangle$ states is used to define SI second. One of the beams where the atoms are in $F=4$ with $m_F\ne -4$ states is absorbed by getter, but the other where the atoms are in $|F=3,m_F\rangle$ and $|F=4,m_F=-\mathit{4}\rangle$ states is deflected into the Ramsey cavity where the technique of separated oscillating fields is realized. The cavity is bent in a way shown in Figure 2A and the atomic beam enters and leaves the two end sections of the cavity through small holes near the end plates. The atoms in $|F=3,m_F=\mathit{0}\rangle$ state will change their state to $|F=4,m_F=\mathit{0}\rangle$ with probability [12]

$\mathit{P}=\frac{{\mathit{b}}^{\mathbf{2}}{\mathbf{sin}\left(\mathbf{2}\mathit{q}\mathit{t}\right)}^{\mathbf{2}}}{{\mathit{q}}^{\mathbf{2}}}{\left(\mathbf{cos}\left(∆\mathit{T}+\frac{\mathit{\theta }}{\mathbf{2}}\right)-\frac{∆}{\mathit{q}}\mathbf{sin}\left(∆\mathit{T}+\frac{\mathit{\theta }}{\mathbf{2}}\right)\mathbf{tan}\left(\mathit{q}\mathit{t}\right)\right)}^{\mathbf{2}}(1)$

where $∆=\left(\omega -{\omega }_{\mathit{0}}\right)/\mathit{2}$, ${\omega }_0=\mathit{2}\pi v_{\mathit{0}}$, $v_{\mathit{0}}=\mathit{9192631770}$ Hz, ω is the angular microwave excitation frequency, t is the transit time through a cavity end, T is the transit time in the drift region between the cavity ends, θ is the phase angle lead of the microwaves in the second cavity end with respect to that in the first, 2b is the Rabi frequency of the cesium in the microwave magnetic field and $q={\left({∆}^{\mathit{2}}+b^{\mathit{2}}\right)}^{1/2}$. After leaving the Ramsey cavity, the atoms pass through the second two-wire magnetic field (the B magnet in Figure 2A). The two-wire field directs only the atoms in changed state $|F=4,m_F=0\rangle$ to the hot-wire ionizer where the atoms are changed into ions; the other atoms are directed to getter and absorbed. The electron multiplier amplifies the ion flow as an electric current signal which contains the frequency offset of the RF signal that comes from the VCXO. Signal amplifier makes the current signal to the level that the servo system can operate. The servo system calculates the frequency offset of the VCXO and tunes the VCXO to lock to cesium resonance. Then standard output frequencies, such as 5 MHz, and 10 MHz, are derived from the output amplifier and used as reference signals.

FIGURE 2

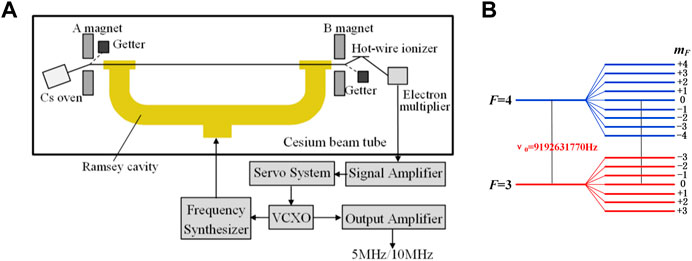
FIGURE 2. Principle of LIP Cs-3000 cesium atomic clock. (A) Schematic of LIP Cs-3000. (B) Cesium ground state sublevels in a magnetic field.

Performance and analysis

Important performance aspects of compact cesium atomic clocks include the stability and accuracy. The stability is the degree to which the atomic clock produces the same value of frequency throughout a specified time interval. The accuracy reflects the degree to which atomic clock output frequency agrees with the value corresponding to the definition of the SI second.

Stability

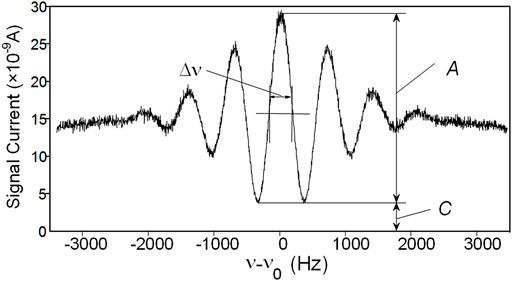
The frequency stability depends on the averaging time and on the Ramsey pattern of the cesium beam tube (CBT) of an atomic clock. The typical curve of Ramsey pattern of LIP Cs-3000 is shown in Figure 3. The curve can be described by three parameters including line width, peak-to-valley ratio and signal-to-noise ratio, which determine the Allan deviation ${\sigma }_f$ according to the formula as follows [13]

${\mathit{\sigma }}_{\mathit{f}}=\mathit{0.55}\sqrt{\frac{\mathit{2}+\mathit{A}/\mathit{C}}{\mathit{1}+\mathit{A}/\mathit{C}}}\frac{∆\mathit{\nu }}{{\mathit{\nu }}_{\mathit{0}}}\frac{\mathit{1}}{\mathit{S}/\mathit{N}}\frac{\mathit{1}}{\sqrt{\mathit{\tau }}}(2)$

where $∆v$ is line width, A is the amplitude of the signal, C is the average valley value of the signal, (A + C)/C is peak-to-valley ratio, S/N is signal-to-noise ratio and τ is the averaging time in seconds.

FIGURE 3

FIGURE 3. The Ramsey pattern of the CBT of LIP Cs-3000 (v₀ = 9192631770 Hz).

The line width $∆v$ is defined as the full width at half maximum of the central fringe. It can be derived from Eq. 1 as follows [14, 15]

$\frac{∆\mathit{\nu }}{{\mathit{\nu }}_{\mathit{0}}}\approx \frac{\mathit{1}}{{{\mathit{t}}_{\mathit{d}}\mathit{\nu }}_{\mathit{0}}}(3)$

where $t_d=L/\langle v\rangle$ is the transit time through the cavity, L is the drift length between microwave interaction regions, $\langle v\rangle =\int v\rho \left(v\right)\mathrm{d}v$, $\rho \left(v\right)$ is the velocity distribution of the signal atoms in changed state $|\mathrm{4,0}\rangle$. Figure 4 shows the velocity distribution of LIP Cs-3000, which derived by Monte Carlo method. Obviously, not every atom in state $|\mathrm{3,0}\rangle$ is selected to finish the transition within CBT. Only the atoms with velocity located in the range from 100 to 200 m/s have a chance to interact with the microwave. According to $\rho \left(v\right)$ given in Figure 4, the line width of the Ramsey pattern for LIP Cs-3000 is less than 400 Hz. Figure 5 shows the line width of over one hundred cesium beam tubes produced in nearly 4 years. The line widths of these tubes meet with the normal distribution with the mean value of 365 Hz and standard deviation of 18 Hz.

FIGURE 4

FIGURE 4. Velocity distribution of the signal atoms in CBT of LIP Cs-3000 clock.

FIGURE 5

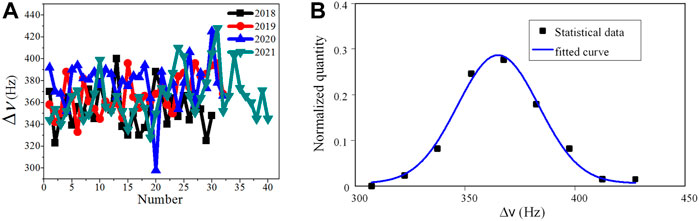
FIGURE 5. The line widths of CBTs. (A) Statistical chart of the line widths of CBTs from 2018 to 2021, and there are about 30 or 40 tubes every year considered. (B) Normal distribution fitting for line width of all tubes.

The peak-to-valley ratios of these clocks lie in the range of 2–13 in Figure 6. It can be seen that the peak-to-valley ratios approximately obey the Burr type XII distribution [16] with shape parameters of 0.8 and 7.0 and a scale parameter of 5.0 respectively. The peak-to-valley ratio of a cesium beam tube reveals the relative position of ionization detector (Hot-wire ionizer in Figure 2A) to the state-selection magnet where cesium atoms pass through. A higher peak-to-valley ratio represents a more accurate position of ionization detector where less cesium atoms without clock transition are collected. This wide distribution implies that the position of ionizer needs more accurate control in the manufacturing process.

FIGURE 6

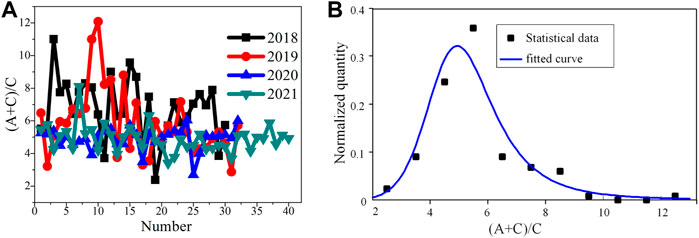
FIGURE 6. The peak-to-valley ratios of CBTs. (A) Statistical chart of the peak-to-valley ratios of CBTs from 2018 to 2021. (B) Burr type XII distribution fitting for the peak-to-valley ratios of all tubes.

The signal-to-noise ratio is the root mean square noise of the signal with 1 Hz bandwidth. Because square wave frequency modulation is employed near the central peak of Ramsey pattern, the signal of CBT is DC signal at each modulation frequency. The signal-to-noise ratio of the DC signal with noise depends on the bandwidth of measurement. The signal is filtered with the 1 Hz low pass filter centered at the frequency 0 Hz. In general, the signal-to-noise ratio increases with the increase of cesium oven temperature. For the convenience of comparison, we fixed the oven temperature at 110°C in the signal-to-noise ratio test of cesium beam tubes. The signal-to-noise ratio lies in 2,000–8,000 shown in Figure 7, which resulting in upmost predicted Allan deviation of less than $5\times {10}^{-12}/1\mathrm{s}$. The signal-to-noise ratio in Figure 7 is also approximately fitted with the Burr type XII distribution with shape parameters of 1.2 and 6.7 and a scale parameter of 4039.5 respectively. It is worth noting that the high signal-to-noise ratio of more than 7,000 can be obtained for the magnetic state-selection CBT. Higher signal-to-noise ratio means better collimation of the atomic beam in CBT. However the proportion of cesium beam tubes with high signal-to-noise ratio is less than 5%. This means that we need to improve the accuracy of beam optical parameters in the manufacturing process of CBT. In particular, considering that the magnetic field is the largest source of atomic beam divergence, we should improve the assembly accuracy of A and B magnets.

FIGURE 7

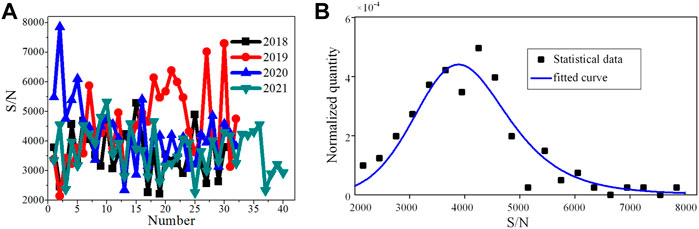
FIGURE 7. The signal-to-noise ratios of the CBTs. (A) Statistical chart of the signal-to-noise ratios of CBTs from 2018 to 2021. (B) Burr type XII distribution fitting for the signal-to-noise ratio of all tubes.

If we take $∆v\approx \mathit{340}\sim \mathit{400}$ Hz, $\left(A+C\right)/C\approx 3.5\sim 10$ and $S/N\approx 2500\sim 6000$ into Eq. 2, we immediately get ${\sigma }_f\approx \mathit{1.1}\times {\mathit{10}}^{-\mathit{11}}\sim \mathit{3.6}\times {\mathit{10}}^{-\mathit{12}}/\sqrt{\tau }$. Figure 8 shows the Allan deviation data of 15 cesium atomic clocks during 15-days continuous measurement at the National Institute of Metrology (NIM) of China. The frequency reference of 10 MHz signal is atomic time scale of NIM. The typical frequency stability of the clock is $5\times {10}^{-12}/1\mathrm{s}$, $3.5\times {10}^{-12}/10\mathrm{s}$, $8.5\times {10}^{-13}/100\mathrm{s}$, $2.7\times {10}^{-13}/1000\mathrm{s}$, $8.5\times {10}^{-14}/10000\mathrm{s}$ and $2.7\times {10}^{-14}/100000\mathrm{s}$. As a supplement, we also give the 5-days stability of LIP Cs-3000 here, which ranges from $9.0\times {10}^{-15}$ to $2.0\times {10}^{-14}$.

FIGURE 8

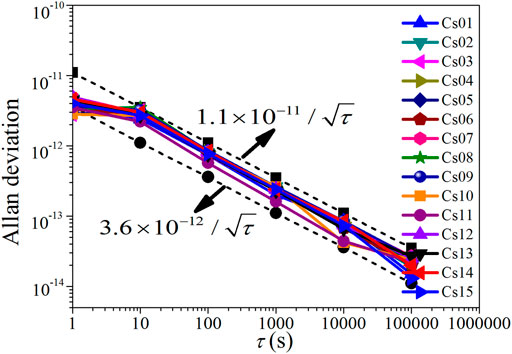
FIGURE 8. The Allan deviation data of LIP Cs-3000 atomic clocks. Csnn–LIP Cs-3000 clocks. The dotted lines are corresponding to $1.1\times {10}^{-11}/\sqrt{\tau }$ and $3.6\times {10}^{-12}/\sqrt{\tau }$.

Accuracy

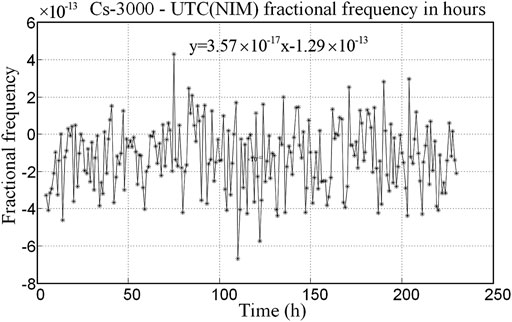
The accuracy of the LIP Cs-3000 clock is within the range of $\pm 3\times {10}^{-13}$. Figure 9 shows the fractional frequency in hours of one of the clock with the accuracy of $-1.29\times {10}^{-13}$ compared with UTC (NIM). There are several factors that influence the accuracy of LIP Cs-3000 clocks. The most important factors include the uncertainty in the derivation of the second-order Zeeman frequency shift, the second-order Doppler effect and the uncertainty in the measurement of the cavity and others.

FIGURE 9

FIGURE 9. The fractional frequency of LIP Cs-3000 cesium atomic clock.

The second-order Zeeman frequency shift is given by [17].

$\mathit{\nu }={\mathit{\nu }}_{\mathit{0}}+\mathbf{427.45}{\mathbf{B}}^{\mathbf{2}},(4)$

where B is the C field and $v_{\mathit{0}}=9192631770$ Hz. If B has an increment dB, then $v$ has an increment $\mathrm{d}v=854.9B\mathrm{d}B$. For LIP Cs-3000 clocks, $B=0.06$G and $\mathrm{d}B/B<1\times {10}^{-4}$. Thus we have $\frac{\mathrm{d}v}{v_{\mathit{0}}}<3.35\times {10}^{-14}$.

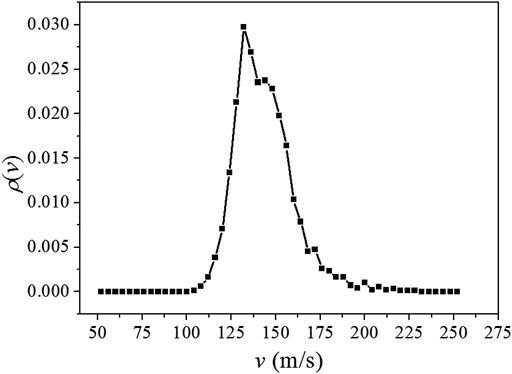
The second-order Doppler effect originates from the time dilation phenomenon of relativity. For an atom of velocity $v$, the fractional frequency shift is given by the equation (17)

$\frac{\mathit{\nu }-{\mathit{\nu }}_{\mathit{0}}}{{\mathit{\nu }}_{\mathbf{0}}}=-\frac{{\mathit{v}}^{\mathit{2}}}{\mathit{2}{\mathit{c}}^{\mathit{2}}},(5)$

where c is the speed of light. Considering the velocities of the atoms are spread according to the distribution $\rho \left(v\right)$ (see Figure 4), so the $v$ in (5) should be displaced by average $v_{avg}$. For LIP Cs-3000, $\mathrm{d}{v}_{avg}/v_{avg}<0.1$, therefore $\frac{\mathrm{d}v}{v_{\mathit{0}}}=-\left(v_{avg}^{\mathit{2}}/c^{\mathit{2}}\right)\left(\mathrm{d}{v}_{avg}/v_{avg}\right)<-1.2\times {10}^{-14}$.

The end-to-end cavity phase shift $\phi$ also introduces a frequency shift as follows [17]

$\mathrm{\delta }\mathrm{v}=-\frac{\phi }{\mathrm{2}\pi T},(6)$

where T is the transit time in the drift region between the cavity ends. The phase shift comes from the energy losses occurring in the cavity wall and in the two terminations and unequal lengths of the two cavity-arms. In general, the relative frequency shift amounts to the level of ${10}^{-13}$ for compact cesium clocks [17, 18]. But the relative frequency variation is difficult to determine from the energy losses, which limit the accuracy to which the phase asymmetry in the Ramsey cavity can be determined. To estimate the relative frequency variation, we had to consider other effects including black body radiation, Bloch-Siegert effect etc. These effects, however, introduce smaller uncertainties than those mentioned above. Table 1 lists the various frequency shifts and the accuracy in the determination of these shifts for LIP Cs-3000. We find that the combined uncertainty of the clock is less than $5\times {10}^{-14}$ if we consider all origin shifts but the cavity phase shift. Considering the accuracy of the clock is ${\pm 3\times 10}^{-13}$, we can conclude that the uncertainty of the cavity distributed phase shift exceeds ${\pm 2\times 10}^{-13}$. Therefore it is easy to find that cavity phase shift is actually the greatest cause of inaccuracy. If we want to improve the accuracy of LIP Cs-3000 further, we must select a higher performance microwave cavity.

TABLE 1

TABLE 1. Summary of frequency shifts and their uncertainties in LIP Cs-3000.

Lifetime evaluation

At present, the lifetime of LIP Cs-3000 cesium atomic clock is almost equal to that of electron multiplier. The multiplier is used to amplify the signal current of about 1 pA to tens or even hundreds of nA. However, this amplification ability will gradually decrease over time [19]. When it reduces to a certain extent, the life of multiplier, that is, the life of cesium clock, will end [20].

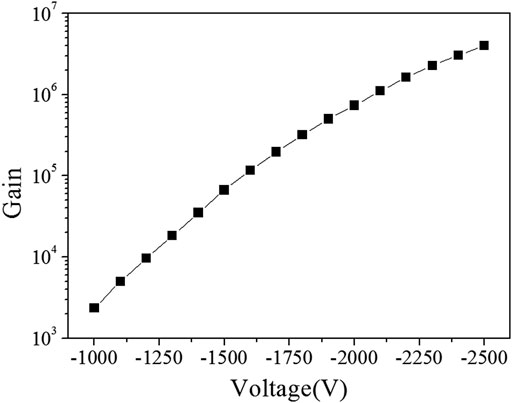
The lifetime of electron multiplier depends on two parameters called gain and decay rate of gain [21, 22]. The higher gain and lower decay rate of gain mean the longer lifetime of a electron multiplier. Gain is a multiple factor by which the electron multiplier amplifies the current signal. One of the characteristics of electron multiplier is that its gain value changes exponentially with the increase of the working voltage. Figure 10 shows the curve of the gain value of the electron multiplier of the LIP Cs-3000 clock changing with operating voltage. We can find from Figure 10 that under the working voltage of −2500 V, the gain value can reach $4\times {10}^6$. Decay rate refers to the average daily decrease of the gain of the electron multiplier. The decay of gain makes signal current of CBT lower and lower and therefore deteriorates the long-term stability of the clock.

FIGURE10

FIGURE10. The curve of the gain value of the electron multiplier changing with operating voltage.

To solve the deterioration problem, the function of automatically regulating the voltage of the electron multiplier is added into the circuit of LIP Cs-3000. When the gain of the multiplier varies, the circuit will changes its voltage accordingly to keep the current stable. Therefore, we can expect that as the gain continues to decrease, the voltage will continue to rise. It should be pointed out that in the initial stage of electron multiplier, one usually observes that the voltage does not increase but decreases (Figure 11). This is because at this stage, the dynode surface of the electron multiplier is covered with a layer of impurities, which will be gradually removed under the bombardment of electrons, so that the gain of the multiplier became higher and higher. This process lasts about 1 month to half a year.

FIGURE11

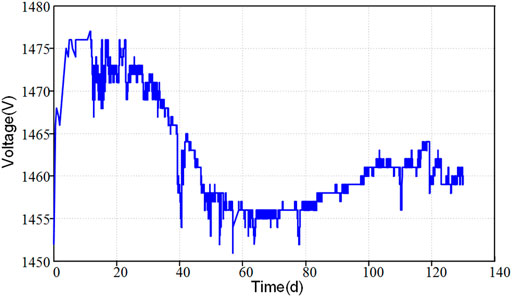
FIGURE11. The curve of the operating voltage of the electron multiplier with time in the early stage.

The added function that introduced to automatically regulate the voltage of the electron multiplier improves the long-term stability of the cesium atomic clock. In addition, it brings another advantage that the lifetime of an electron multiplier can be evaluated. When the cesium atomic clock enters the stable working stage, it can be observed that the voltage increases in a nearly linear form (see Figure 12). Consequently, as long as the daily voltage increase of a multiplier is measured, the lifetime of the multiplier can be calculated according to the following formula approximately

${\mathit{T}}_{\mathit{l}\mathit{i}\mathit{f}\mathit{e}}=\frac{{\mathit{V}}_{\mathit{max}}-{\mathit{V}}_{\mathit{min}}}{∆\mathit{V}}(7)$

where $T_{life}$ represents the lifetime of a multiplier, $V_{\mathit{min}}$ is the starting working voltage of a multiplier, $V_{\mathit{max}}$ is the maximum voltage that the circuit can provide, and $∆V$ represents the daily increase of the voltage.

FIGURE12

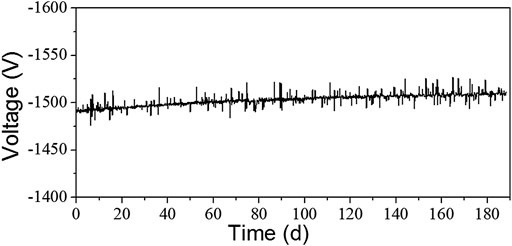
FIGURE12. The curve of the operating voltage of the electron multiplier with time after it enters the stable working stage.

If the initial stage life of the multiplier is considered, the lifetime Eq. 4 will be modified as follows

${\mathit{T}}_{\mathit{l}\mathit{i}\mathit{f}\mathit{e}}={\mathit{T}}_{\mathit{0}}+\frac{{\mathit{V}}_{\mathit{max}}-{\mathit{V}}_{\mathit{min}}}{∆\mathit{V}}(8)$

where $T_{\mathit{0}}$ represents multiplier initial stage life which is in 1 month to half a year. At present, these parameters of the clock are as follows $T_{\mathit{0}}\approx 1\sim 6$ month, $V_{\mathit{min}}\sim -1200$ V, $V_{\mathit{max}}=-2600$ V and $∆V<-0.7$ V/day. According to Eq. 5, the lifetime of the clock can be estimated to be more than 5 years.

Environmental adaptability

In order to meet the requirements for the application of LIP Cs-3000 cesium clock in different environments, we have carried out a series of designs and tests on the environmental adaptability. These works ensure the quality characteristics of the clock in different environments during operation, transportation and storage. Up to now, the designs and tests are mainly related to mechanical vibration environment, thermal environment and electromagnetic field environment.

For the mechanical vibration environment, the finite element analysis method is adopted. The structure of the whole machine is analyzed, the weak area is found and the reinforcement is completed, highly reliable components of beam optics in CBT were designed. On this basis, a random vibration test with road-level was carried out with vibration frequency in the range of 10–500 Hz and the vibration order 1.04 g. As shown in Table 2, there is no significant change in the stability before and after the vibration test.

TABLE 2

TABLE 2. Frequency stability before and after the random vibration test.

A variety of measures have been adopted in the thermal design. Using the thermal imaging technology, it was found that the module with the largest heat sources in a cesium atomic clock is the power supply. Thus the power supply module is installed on the side wall of the case to accelerate heat exchange. In addition, different passages of heat dissipation are designed in the clock. For example, the modules with high power such as microwave source and 1PPS source are also installed on the case wall, and the VCXO is positioned near CBT where temperature variation is relatively smaller. Meanwhile, the clock adopts constant-temperature VCXO with “SC-cut”, which has good temperature characteristics and small temperature coefficient. Therefore the clock can start up and operate normally after low and high temperature storage tests carried out at $-$40°C and +70°C. The temperature coefficient measured in range of $-$20 ∼+55°C is $1.4\times {10}^{-14}$/°C compared with $5.4\times {10}^{-14}$/°C without the design of heat dissipation. The frequency curves under the different temperatures are shown in Figure 13.

FIGURE 13

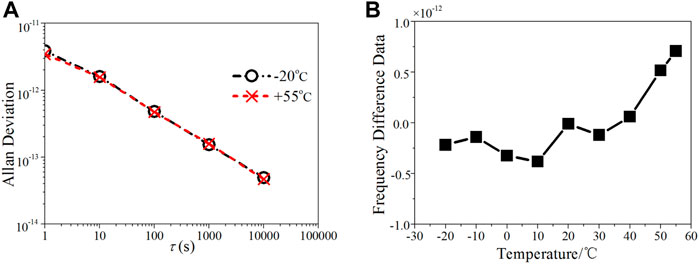
FIGURE 13. The frequency curves under the different working temperatures. (A) Frequency stability. (B) Relative frequency difference at different temperatures.

In terms of electromagnetic field environment, shielding technology is mainly used. By establishing the relation between magnetic sensitivity and permeability of magnetic shield in a cesium clock, a magnetic shield system with high permeability more than 150,000 is designed in CBT. As a result, the total shielding efficiency is greater than $2\times {10}^6$ and the remanence in C field zone is less than 1nT, which can resist the influence of external magnetic field on the uniform of C field. Therefore the magnetic sensitivity of the clock measured by Helmholtz coil at room temperature is less than $2.25\times {10}^{-14}$/G (−2G∼+2G). In addition, each module is shielded by metal screen independently to avoid electromagnetic interference, which made the clocks be passed by some electromagnetic compatibility test items including CE102, CS101, CS114, CS115, Cs116, RE102 and RS103 [23].

Although the clock has passed the above tests, some other tests, such as drop, functional shock and temperature shock, need to be completed in the future. We expect that these new tests will help improve the adaptability of the clocks further and make the clocks be applied to the more complex environments such as vehicles and ships and so on.

Summary

This paper has studied and analyzed the performance of LIP Cs-3000 cesium clocks according to their technical characteristics and test data. The statistical data show that the range of value of line width, peak-to-valley ratio and signal-to-noise ratio of Ramsey pattern are 340–410 Hz, 2–13 and 2,000–8,000 respectively. These values assure that the Allan deviations of the clocks lies in the range of $1.1\times {10}^{-11}\sim 3.6\times {10}^{-12}/\sqrt{\tau }$, which are consistent with the test results (see Figure 8). The statistical data also show that the line widths subject to the normal distribution, while the peak-to-valley ratio and signal-to-noise ratio approximately obey Burr type XII distribution. Their ranges are relatively wide, indicating that the consistency of the manufacture process needs to be improved. In addition, the paper analyzed various factors affecting accuracy and pointed out that LIP Cs-3000 clock has a specified accuracy of $3\times {10}^{-13}$. At the same time, the most important factor affecting accuracy is the uncertainty caused by the cavity phase shift. This means that if we want to improve the accuracy of LIP Cs-3000 further, we must select a higher performance microwave cavity. The paper also studied how to estimate the lifetime of LIP Cs-3000 clock. Considering that lifetime of the clock is almost equal to that of electron multiplier and the multiplier lifetime is related to its voltage variation, we proposed to use the trend of the voltage variation to estimate the clock lifetime. According to this method we obtained that the lifetime of the clock is larger than 5 years. To improve the lifetime further, we need to prepare and adopt such a secondary electron emission film in the multiplier, which is more insensitive to the environment. In the end, the paper introduced some environmental adaptability designs of the clock, which ensure that the temperature coefficient and magnetic sensitivity reach $1.4\times {10}^{-14}$/°C and $2.25\times {10}^{-14}$/G respectively. In order to get a lower temperature coefficient, we need to carry out the optimization of thermal design of the clock.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

JC: conception and idea. JW: testing of CBT. LG: testing of electronic multiplier. JY: testing of environment. PM: testing of circuit. LH: pictures production. ZL: funding acquisition. Data analysis and writing of the paper by JC, JW, LG, JY, and PM.

Funding

National Defense Key Laboratory Stabilization Support Program of China under Grant No. HTKJ2020KL510006. National Natural Science Foundation of China under Grants No. 61971209.

Acknowledgments

The authors thank Professor Wang Yiqiu for his helpful discussions in developing LIP Cs-3000 clocks. The authors also thank the support from National Defense Key Laboratory Stabilization Support Program of China and National Natural Science Foundation of China.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

1.BIPM. BIPM annual report on time activities, volume 15 (2020). Available from: https://www.bipm.org/en/search?p_p_id=search_portlet&p_p_state=normal&p_p_mode=view&_search_portlet_javax.portlet.action=search&_search_portlet_source=BIPM&p_p_lifecycle=0 (Accessed April 24, 2022).

Google Scholar

2. Yuan Hb., Qu LL, Dong SW, Li W, Zhang H. The hydrogen maser and cesium clocks in time keeping at NTSC. In: 2009 Joint Meeting of the European Frequency and Time Forum (EFTF'09) and the IEEE International Frequency Control Symposium (FCS'09) (2009). p. 639–42. doi:10.1109/FREQ.2009.5168261

CrossRef Full Text | Google Scholar

3. Breakiron LA. Kalman filter characterization of cesium clocks and hydrogen masers. In: Proceedings of the 34th Annual Precise Time and Time Interval Systems and Applications Meeting (2002). p. 511–26. Available from: https://www.ion.org/publications/abstract.cfm?articleID=13966 (Accessed August 1, 2022).

Google Scholar

4. Vannicola F, Beard R, White J, Seni K, Largay M, Buisson J. GPS block IIF atomic frequency standard analysis. In: 42nd Annual Precise Time and Time Interval (PTTI) Meeting (2010). p. 181–95. Available from: https://www.ion.org/publications/abstract.cfm?articleID=10732 (Accessed August 1, 2022).

Google Scholar

5. Vannicola F, Beard R, Koch D, Kubik A, Wilson D, White J. GPS block IIF atomic frequency standard analysis. In: Proceedings of the 45th Annual Precise Time and Time Interval Systems and Applications Meeting (2013). p. 244–9. Available from: https://www.ion.org/publications/abstract.cfm?articleID=11597 (Accessed August 1, 2022).

Google Scholar

6. Vanier J, Audoin C. The quantum Physics of atomic frequency standards. New York: Adam Hilger (1989). Available from: http://www.crcpress.com/The-Quantum-Physics-of-Atomic-Frequency-Standards/Vanier-Audoin/p/book/9781420050851 (Accessed August 1, 2022).

Google Scholar

7.Fritz Riehle. Frequency standards: Basics and applications. Weinheim: WILEY-VCH Verlag GmbH (2004). doi:10.1109/MIM.2005.1578626

CrossRef Full Text | Google Scholar

8.Microchip. Microchip (2022). Available from: https://www.microsemi.com/document-portal/doc_download/133269-5071a-datasheet (Accessed August 1, 2022).

Google Scholar

9.Oscilloquartz. Oscilloquartz (2022). Available from: https://www.oscilloquartz.com/en/resources/downloads/data-sheets/osa-3235b-cesium-clock (Accessed August 1, 2022).

Google Scholar

10. Chen J, Ma P, Wang J, Guo L, Liu ZD, Yang J, et al. Progress in commercialization of compact magnetically selected cesium atomic clocks. J Astronautic Metrology Meas (2020) 40(3):12–6. doi:10.12060/j.issn.1000-7202.2020.03.03

CrossRef Full Text | Google Scholar

11. Chen J, Ma P, Wang J, Guo L, Tu JH, Yang W. Test of magnetic-selected cesium atomic clock LIP Cs3000C. J Time Frequency (2018) 41(3):190–3. doi:10.13875/j.issn.1674-0637.2018-03-0190-04

CrossRef Full Text | Google Scholar

12. Cutler LS. Fifty years of commercial caesium clocks. Metrologia (2005) 42(3):90–9. doi:10.1088/0026-1394/42/3/S10

CrossRef Full Text | Google Scholar

13. Wang YQ, Wang QJ, Fu JS, Dong TQ. The theory of frequency standards. Beijing: Science Press (1986). p. 168–73.

Google Scholar

14. Sullivan DB, Bergquist JC, Bollinger JJ, Drullinger RE, Itano WM, Jefferts SR, et al. Primary atomic frequency standards at NIST. J Res Natl Inst Stand Technol (2001) 106(1):47. doi:10.6028/jres.106.004

PubMed Abstract | CrossRef Full Text | Google Scholar

15. Lombardi MA, Heavner TP, Jefferts SR. NIST primary frequency standards and the realization of the SI second. NCSLI Measure (2007) 2(4):74–89. doi:10.1080/19315775.2007.11721402

CrossRef Full Text | Google Scholar

16. Burr IW. Cumulative frequency functions. Ann Math Statist (1942) 13(2):215–32. doi:10.1214/aoms/1177731607

CrossRef Full Text | Google Scholar

17. Vanier J, Audoin C. The classical caesium beam frequency standard: Fifty years later. Metrologia (2005) 42(3):31–42. doi:10.1088/0026-1394/42/3/S05

CrossRef Full Text | Google Scholar

18. Audoin C, Dimarcq N, Giodano V, Viennet J. Physical origin of the frequency shifts in cesium beam frequency standards-related environmental sensitivity. IEEE Trans Ultrason Ferroelectr Freq Control (1992) 39(3):412–21. doi:10.1109/58.143175

PubMed Abstract | CrossRef Full Text | Google Scholar

19. Hirashima M, Miyashiro S. Some factors affecting the decay of secondary electron emission of silver-magnesium alloys. J Phys Soc Jpn (1957) 12(7):770–7. doi:10.1143/JPSJ.12.770

CrossRef Full Text | Google Scholar

20. Brock C, Tolman BW, Taylor RE. End-of-life indicators for nima's high-performance cesium frequency standards. In: Proceedings of the 34th Annual Precise Time and Time Interval Systems and Applications Meeting (2002). p. 117–26. Available from: https://www.ion.org/publications/abstract.cfm?articleID=13932 (Accessed August 1, 2022).

Google Scholar

21. Straka ER. Performance characteristics of cesium beam tube electron multipliers. In: 36th Annual Frequency Control Symposium (1982). p. 230–5. doi:10.1109/FREQ.1982.200575

CrossRef Full Text | Google Scholar

22. Kusters JA, Cutler LS, Powers ED. Long-term experience with cesium beam frequency standards. In: 1999 Joint Meeting EFTF - IEEE IFCS (1999). p. 159–63. doi:10.1109/FREQ.1999.840733

CrossRef Full Text | Google Scholar

23.GJB-151B. Electromagnetic emission and susceptibility requirements and measurements for military equipment and subsystems (2013). p. 12–80. Available from: http://www.bzko.com/std/201059.html (Accessed August 1, 2022).

Google Scholar