- 1School of Electronic Information and Electrical Engineering, Changsha University, Changsha, China
- 2Department of Physics, National University of Defense Technology, Changsha, China
Vortex beams with ultra-high brilliance can greatly enrich the light and matter interaction process and even shed light on the unexpected information in relativistic nonlinear optics. Thus, we propose a scheme for relativistic intense vortex harmonic radiation by use of bi-circular Laguerre–Gaussian lasers irradiating relativistic plasmas. Three-dimensional particle-in-cell simulation results show that the emitted harmonics own controllable spin and orbital angular momentum simultaneously, which can be attributed to the vortex mirror model and the related conservation laws. Meanwhile, the conversion efficiency of harmonic generation can be tuned through adjusting the intensity ratio of the two driving field components.
Introduction
Light waves can carry two distinct forms of angular momenta in the direction of propagation: spin and orbital angular momentum (SAM and OAM). The SAM is manifest as right or left circular polarization of light (
In this paper, we use full three-dimensional particle-in-cell (PIC) simulations to verify the effectiveness of two-color twisted CP laser scheme in the relativistic plasma HHG regime and find that the similar SAM and OAM conservation laws uncovered in laser-gas HHG are applicable to laser-plasma HHG. As a result, intense harmonic radiation with controllable SAM and OAM can be acquired by use of two-color Laguerre–Gaussian (LG) driving pulses irradiating relativistic plasmas. Its underlying mechanism can be attributed to the “vortex oscillating mirror” (VOM) model [2] and the conservation laws of photon’s energy, SAM and OAM. Meanwhile, the vortex mode and conversion efficiency of radiated harmonics can be flexibly tuned. Therefore, this work provides an efficient and practical approach to produce bright, spectral tunable harmonic radiation with designable SAM and OAM, which may own the potential of extending the existing application areas of vortex beams to ultra-high intensity regime and nanometer spatial, sub-femtosecond temporal scales.
Particle-in-cell simulation results
We perform full three-dimensional PIC simulations to investigate the two-color counter-rotating twisted laser scheme with the open-source EPOCH code [24]. The total electric field of the dichromatic twisted pulses can be expressed as:
Where
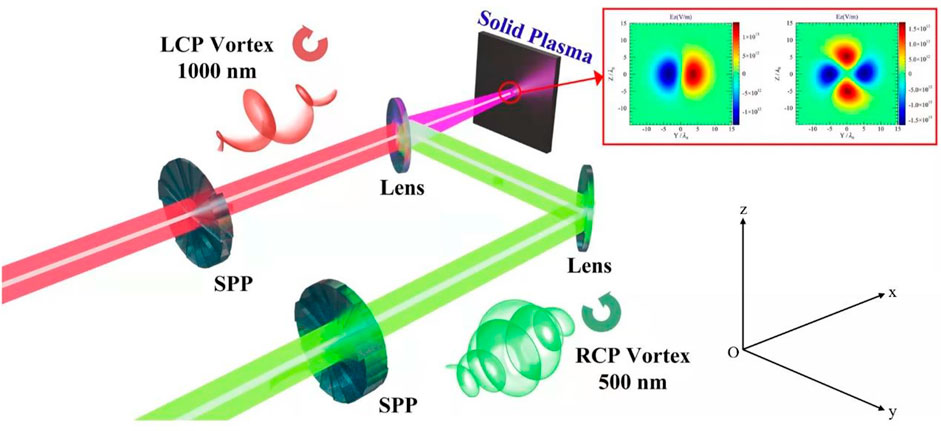
FIGURE 1. The sketch of the two-color counter-rotating LG laser scheme: dichromatic counter-rotating CP twisted laser pulses are spatiotemporally overlapped and normally irradiate the solid target to drive the laser-plasma HHG process (The SPP represent spatial phase plate, the LCP and RCP represent left- and right- CP laser respectively and the inset shows the enlarged view of the vortex modes of the fundamental and second-harmonic driving pulses).
First of all, the spectra feature of produced harmonics including their intensity and ellipticity distribution versus
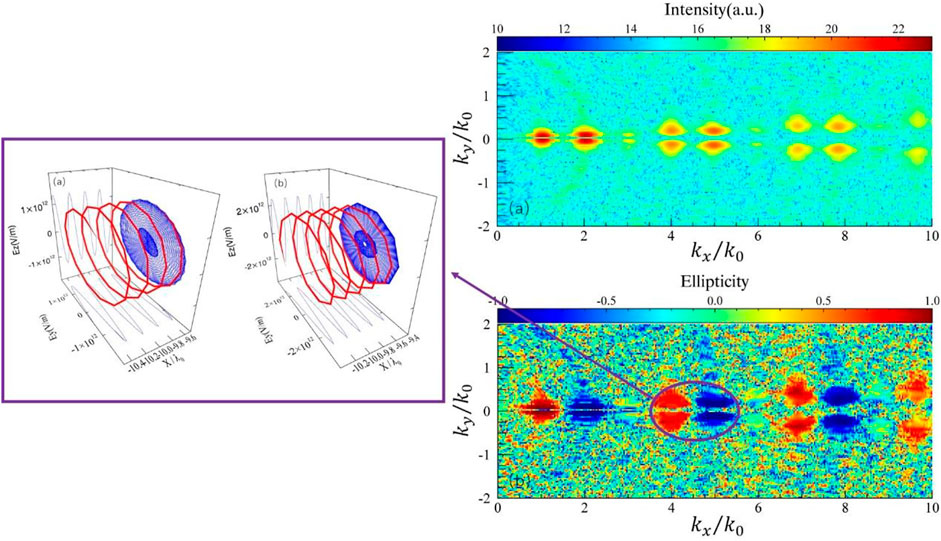
FIGURE 2. (A) The intensity of generated harmonics versus
Moreover, it can be noticed here that only low order harmonics (
In the following, the vortex characteristics of generated harmonics are investigated, which are displayed in Figures 3–5. The six panels of Figure 3 and Figure 4 show the electric field distributions in Z-Y plane at
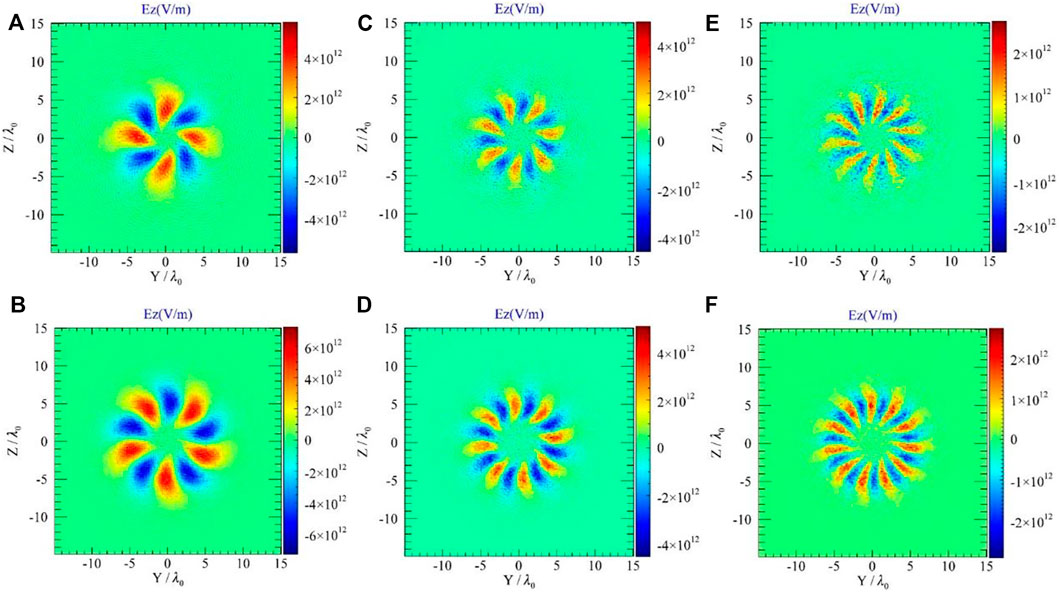
FIGURE 3. The electric field distribution of the (A) fourth, (B) fifth, (C) seventh, (D) eighth, (E) tenth and (F) eleventh harmonics in the Z-Y plane at
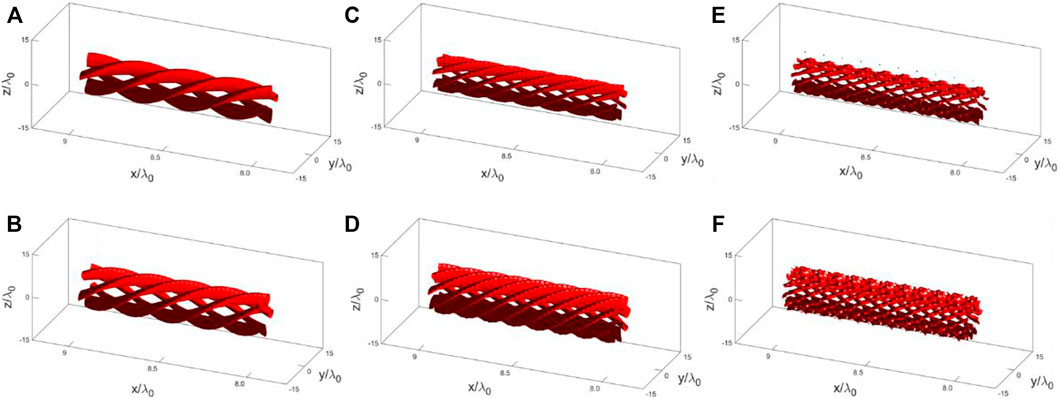
FIGURE 4. The electric field isosurface of the (A) fourth, (B) fifth, (C) seventh, (D) eighth, (E) tenth and (F) eleventh harmonics within a distance of
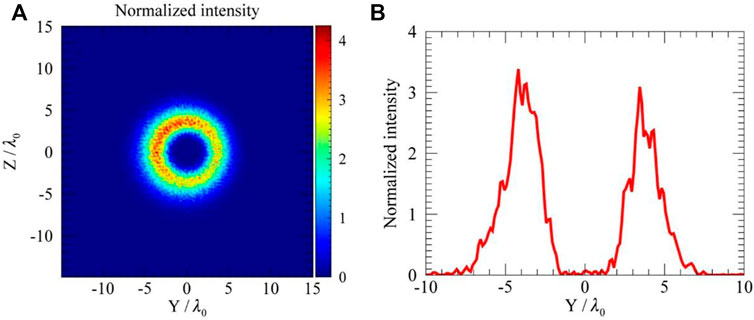
FIGURE 5. (A) The normalized transverse intensity distribution of the fourth harmonic with
Up to now, it has been confirmed that the two-color LG laser-gas HHG scheme is also applicable in relativistic plasma HHG process, and the intensity of produced harmonics can be obviously enhanced.
Theoretical analysis
In this part, the physical mechanism of vortex harmonic radiation will be discussed. For the convenience of theoretical derivation, the expression of two-color counter-rotating twisted laser pulses can be simplified as follows [18]:
where
By squaring the superposed laser electric field
where
The analysis above preliminarily explains the underlying mechanism of HHG through two-color LG laser scheme. However, they are not able to accurately predict the spectra features of produced harmonics (including the allowed harmonic orders, the polarization features and the vortex modes). To predict these, its characteristic selection rules can be acquired based on the conservation laws for energy, parity, SAM and OAM of photos. Considering the HHG process of our scheme in a simple photon-exchange picture, the conservation of energy, SAM and OAM can be expressed as [2, 15]:
In Eqs 5–7,
Discussions
According to the conservation laws for energy, parity, SAM and OAM of photos, it can be easily seen that the vortex modes of emitted harmonics can be tuned just through changing the topological charges of driving pulses. For example, if we set
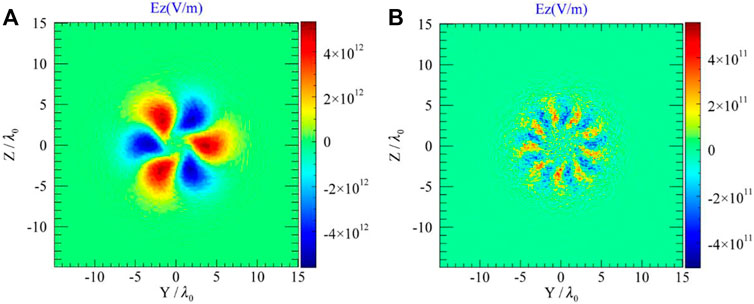
FIGURE 6. The electric field distribution of the (A) fourth, (B) thirteenth harmonics in the Z-Y plane if
Finally, the tunability of HHG efficiency (which acts as the key parameter of HHG process) through adjusting the intensity ratio of the two driving field components are also discussed, as displayed in Figure 7. Here the total intensity of the two driving pulses is kept constant (
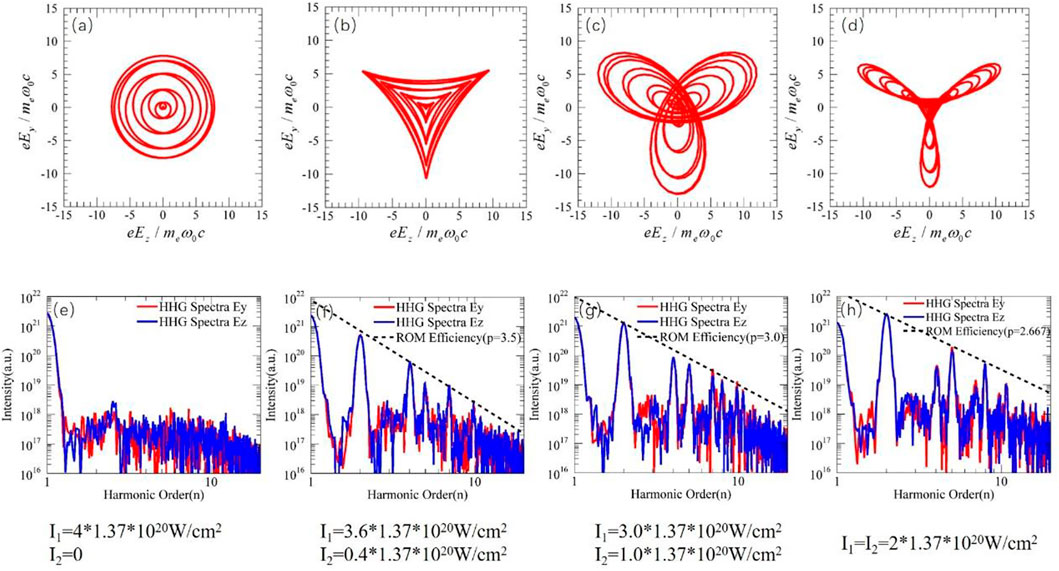
FIGURE 7. Polarization plane projections of the laser electric fields generated with intensity ratios (A)
Conclusion
With three-dimensional PIC simulations, we have demonstrated a tunable, table-top, intense harmonic radiation source with designable SAM and OAM driven by bi-circular LG lasers. The HHG efficiency can be adjusted through changing the intensity ratio of the two driving laser components, which is easy to implement in experiments. The underlying mechanism can be understood by the VOM model and related conservation laws. Such bright, circularly polarized vortex beams in XUV or soft X-ray region may open a wide range of applications including spatially resolved circular dichroism spectroscopies and the SAM and OAM dichroism X-ray absorption measurements, etc.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary material, further inquiries can be directed to the corresponding author.
Author contributions
DX and HZ conducted the simulations and drafted the manuscript. YY and TY supervised the work. All authors discussed the results and reviewed the manuscript.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2018YFA0404802), Scientific Research Foundation of Hunan Provincial Education Department (No. 20A042), National Natural Science Foundation of China (Grant Nos.. 12135009, 11774430 and 11875319) and Science and Technology Innovation Program of Hunan Province (Grant No. 2020RC4020).
Acknowledgments
We would like to thank the National Supercomputing Center in Guangzhou (NSCC-GZ) for providing their computing facilities.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
1. Allen L, Beijersbergen MW, Spreeuw RJC, Woerdman JP. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys Rev A (Coll Park) (1992) 45:8185–9. doi:10.1103/physreva.45.8185
2. Zhang X-M, Shen B-F, Shi Y, Wang X-F, Zhang L-G, Wang W-P, et al. Generation of intense high-order vortex harmonics. Phys Rev Lett (2015) 114:173901. doi:10.1103/physrevlett.114.173901
3. Ju LB, Huang TW, Li R, Jiang K, Wu CN, Zhang H, et al. Topological control of laser-driven acceleration structure for producing extremely bright ion beams. Nucl Fusion (2021) 61:066006. doi:10.1088/1741-4326/abeed6
4. Gauthier D, Rebernik P, Adhikary G, Camper A, Chappuis C, Cucini R, et al. Tunable orbital angular momentum in high-harmonic generation. Nat Commun (2017) 8:14971. doi:10.1038/ncomms14971
5. Hernandez-Garcia C, Picon A, San Roman J, Plaja L. Attosecond extreme ultraviolet vortices from high-order harmonic generation. Phys Rev Lett (2013) 111:083602. doi:10.1103/physrevlett.111.083602
6. Quere F, Thaury C, Monot P, Dobosz S, Marin P, Geindre JP, et al. Coherent wake emission of high-order harmonics from overdense plasmas. Phys Rev Lett (2006) 96:125004. doi:10.1103/physrevlett.96.125004
7. Nomura Y, Horlein R, Tzallas P, Dromey B, Rykovanov S, Major Z, et al. Attosecond phase locking of harmonics emitted from laser-produced plasmas. Nat Phys (2009) 5:124–8. doi:10.1038/nphys1155
8. Bulanov SV, Naumova NM, Pegoraro F. Interaction of an ultrashort, relativistically strong laser pulse with an overdense plasma. Phys Plasmas (1994) 1:745–57. doi:10.1063/1.870766
9. Lichters R, Meyer-ter-Vehn J, Pukhov A. Short-pulse laser harmonics from oscillating plasma surfaces driven at relativistic intensity. Phys Plasmas (1996) 3:3425–37. doi:10.1063/1.871619
10. von der Linde D, Rzazewski K. High-order optical harmonic generation from solid surfaces. Appl Phys B (1996) 63:499–506. doi:10.1007/bf01828947
11. Baeva T, Gordienko S, Pukhov A. Theory of high-order harmonic generation in relativistic laser interaction with overdense plasma. Phys Rev E (2006) 74:046404. doi:10.1103/physreve.74.046404
12. Thaury C, Quéré F, Geindre J-P, Levy A, Ceccotti T, Monot P, et al. Plasma mirrors for ultrahigh-intensity optics. Nat Phys (2007) 3:424–9. doi:10.1038/nphys595
13. Dromey B, Kar S, Bellei C, Carroll DC, Clarke RJ, Green JS, et al. Bright multi-kev harmonic generation from relativistically oscillating plasma surfaces. Phys Rev Lett (2007) 99:085001. doi:10.1103/physrevlett.99.085001
14. Chen Z-Y, Pukhov A. Bright high-order harmonic generation with controllable polarization from a relativistic plasma mirror. Nat Commun (2016) 7:12515. doi:10.1038/ncomms12515
15. Chen Z-Y. Spectral control of high harmonics from relativistic plasmas using bicircular fields. Phys Rev E (2018) 97:043202. doi:10.1103/physreve.97.043202
16. Xie D, Zhuo* H-B, Jiao J-L, Zhang S-J, Zhao N, Zhou H-Y. 3D particle simulation of harmonic radiation excited by double circularly-polarized laser pulses irradiating over-dense plasma surface. Appl Phys B (2019) 7:148. doi:10.1007/s00340-019-7263-3
17. Xie D, Yin Y, Yu T-P, Zhou H-Y, Chen Z-Y, Zhuo H-B. High-harmonic generation driven by two-color relativistic circularly polarized laser pulses at various frequency ratios. Plasma Sci Technol (2021) 23:045502. doi:10.1088/2058-6272/abe848
18. Li Q-N, Xu X-R, Wu Y-B, Yin Y, Zou D-B, Yu T-P. Efficient high-order harmonics generation from overdense plasma irradiated by a two-color co-rotating circularly polarized laser pulse. Opt Express (2022) 30:15470–81. doi:10.1364/oe.459866
19. Chen Z-Y, Li X-Y, Li B-Y, Chen M, Liu F. Isolated elliptically polarized attosecond soft X-ray with high-brilliance using polarization gating of harmonics from relativistic plasmas at oblique incidence. Opt Express (2018) 26:4572–80. doi:10.1364/oe.26.004572
20. Pukhov A, an der Brugge D, Kostyukov I. Relativistic laser plasmas for electron acceleration and short wavelength radiation generation. Plasma Phys Control Fusion (2010) 52:124039–10. doi:10.1088/0741-3335/52/12/124039
21. an der Brugge D, Pukhov A. Enhanced relativistic harmonics by electron nanobunching. Phys Plasmas (2010) 17:033110. doi:10.1063/1.3353050
22. Dromey B, Rykovanov S, Yeung M, Horlein R, Jung D, Gautier DC, et al. Coherent synchrotron emission from electron nanobunches formed in relativistic laser-plasma interactions. Nat Phys (2012) 8:804–8. doi:10.1038/nphys2439
23. Dorney K-M, Rego L, Brooks N-J, Roman J-S, Liao C-T, Ellis J-L, et al. Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin-orbit momentum conservation. Nat Photon (2019) 13:123–30. doi:10.1038/s41566-018-0304-3
Keywords: vortex beams, Laguerre-Gaussian lasers, relativistic plasmas, orbital angular momentum, vortex mirror model, conservation laws
Citation: Xie D, Yin Y, Yu T, Zhang H and Zhou H (2022) High-order vortex harmonics generation by bi-circular Laguerre-Gaussian laser fields with relativistic plasmas. Front. Phys. 10:962956. doi: 10.3389/fphy.2022.962956
Received: 07 June 2022; Accepted: 01 August 2022;
Published: 30 August 2022.
Edited by:
Jinqing Yu, Hunan University, ChinaReviewed by:
Xiaofei Shen, Heinrich Heine University of Düsseldorf, GermanyWillem Boutu, CEA Saclay, France
Copyright © 2022 Xie, Yin, Yu, Zhang and Zhou. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Duan Xie, NjI3MDY1MzkxQHFxLmNvbQ==
 Duan Xie
Duan Xie Yan Yin2
Yan Yin2 Tongpu Yu
Tongpu Yu