Searches for long-lived particles at the future FCC-ee

The electron-positron stage of the Future Circular Collider, FCC-ee, is a frontier factory for Higgs, top, electroweak, and flavour physics. It is designed to operate in a 100 km circular tunnel built at CERN, and will serve as the first step towards ≥100 TeV proton-proton collisions. In addition to an essential and unique Higgs program, it offers powerful opportunities to discover direct or indirect evidence of physics beyond the Standard Model. Direct searches for long-lived particles at FCC-ee could be particularly fertile in the high-luminosity Z run, where 5 × 10¹² Z bosons are anticipated to be produced for the configuration with two interaction points. The high statistics of Higgs bosons, W bosons and top quarks in very clean experimental conditions could offer additional opportunities at other collision energies. Three physics cases producing long-lived signatures at FCC-ee are highlighted and studied in this paper: heavy neutral leptons (HNLs), axion-like particles (ALPs), and exotic decays of the Higgs boson. These searches motivate out-of-the-box optimization of experimental conditions and analysis techniques, which could lead to improvements in other physics searches.

1 Introduction

The Standard Model (SM) of particle physics is a mature and consistent theory that, after the observation of the Higgs boson, still fails to explain important experimental observations such as dark matter (DM), neutrino masses, or the baryon asymmetry of the Universe (BAU), among others. Theoretical aspects of the SM, including the origins of the electroweak scale, the spectrum of fermions masses, or flavor patterns also await explanation. These questions may be answered by the direct observation of new particles and phenomena, or by measuring deviations from SM predictions. This is a chief motivation for new colliders that can push both the energy and intensity frontiers.

Long-lived particles (LLPs) are new, beyond the SM (BSM) states that travel a substantial distance between creation and decay in collider systems, presenting distinct experimental signatures [1]. LLPs feature in many BSM models and could provide answers to central questions in particle physics and beyond. The lifetime of a particle depends mostly on its mass and couplings, and so feebly-interacting particles (FIPs), with couplings to the SM particles several orders of magnitude smaller than the SM couplings, are often glaring examples of LLPs.

The experimental signatures of LLPs are particularly interesting. In contrast to promptly decaying particles, LLPs can decay after flying some distance from the primary interaction point. This produces a displaced vertex, with decay products including charged and neutral SM particles (e.g., charged leptons, light neutrinos, and pions). This kind of displaced signature is most commonly associated with LLPs. Other models predict disappearing LLPs giving rise to “short” or “broken” tracks; some are “stopped” or delayed; or produce unusual jets, such as “dark showers.” Such a variety of experimental signatures is very different from the usual SM processes studied at colliders, and any of these signatures would, if observed, constitute a striking “smoking gun” of new physics. In hadron collider environments, standard trigger and reconstruction techniques are often unable to recognize LLP signatures and their study requires dedicated techniques and experiments.

The Future Circular Collider (FCC) program is a design study for a post-LHC particle accelerator at CERN following the priorities set by the 2020 Update of the European Strategy for Particle Physics [2]. The first stage of the FCC design study (FCC-ee) is a high-luminosity, high-precision lepton collider with the goal of better understanding the electroweak (EW) sector, especially the Higgs boson. In addition to a robust program in its own right, FCC-ee will also act as a possible precursor to a high-energy hadron collider (FCC-hh), located in the same tunnel and complementary to it [3].

Though FCC-ee will be a high precision exploration tool, it also opens the possibility of directly discovering new physics [4]. In particular, a future FCC-ee program has an exciting potential for exploring LLPs. The large integrated luminosity of the FCC-ee run around the Z pole, producing 5 × 10¹² Z bosons (Tera-Z run), will facilitate direct searches for LLPs that could be closely linked to neutrino masses, explain the BAU, be sound DM candidates, or all at the same time. In the following, three central physics cases are discussed: heavy neutral leptons (HNLs) [5] in the context of the Phenomenological Type I Seesaw model, axion-like particles (ALPs), and exotic Higgs boson decays. In Section 2, the theoretical landscapes of these three physics cases are outlined. Section 3 discusses the experimental outlook. In particular, the common simulation details (Section 3.1), the experimental aspects of HNLs (Section 3.2), ALPs (Section 3.3), and exotic Higgs boson decays (Section 3.4) at FCC-ee, and considerations for additional detectors for LLPs at FCC-ee (Section 3.5) are covered. Finally, the summary and conclusions are presented in Section 4.

2 Theoretical landscape

In this section, the theoretical frameworks considered are briefly summarized. These representative scenarios are: the Phenomenological Type I Seesaw model (Section 2.1), axion-like particles (Section 2.2), and scalar singlet extensions of the SM (Section 2.3).

2.1 Heavy neutral leptons

The oscillations between neutrino flavor eigenstates in long-baseline experiments [6, 7] is one of the most pressing theoretical puzzles in particle physics today. The neutrino masses that produce these oscillations are also interesting because they imply either the existence of new particles and interactions or substantial changes to the SM paradigm [8, 9].

It is simply not enough to write effective neutrino masses, given the SM’s limited particle content and the desire to understand the mechanism (or mechanisms) that render neutrinos so much lighter than charged leptons and quarks. It is also desirable to understand the flavor/mixing pattern among neutrinos and the possible connections to lepton and quark flavors themselves.

Among the most popular solutions to these mysteries are the Seesaw models. These tie the smallness of neutrino masses ($m_{{\nu }_k}$ with k = 1, 2, 3) to the scale of new physics (Λ). Depending on the complexity, the scale (or scales) introduced by these models can range from well below the EW scale to the Planck scale. In the most minimal scenarios [9], general arguments only require Λ to be below 10¹⁴ GeV. In high-scale Seesaws, light neutrino masses scale inversely with this new physics scale, $m_{{\nu }_k}\propto 1/\mathrm{\Lambda }$. In low-scale Seesaws, the behavior can be more complicated, and in some cases light neutrino masses scale proportionally with this new physics scale, $m_{{\nu }_k}\propto \mathrm{\Lambda }$. The manner in which either is implemented can vary widely, cf. Section 5 in [10], and the most minimal, tree-level constructions are known popularly as the Types I [11–17], II [16, 18–22], and III [23] Seesaw models. Notably, these minimal scenarios are often stepping stones to fuller, more ultraviolet-complete models, including extended gauge theories and grand unified theories. Importantly, neutrino mass models predict a plethora of phenomenology that are testable at a variety of low-energy and high-energy experiments [10, 24–27], including particle colliders.

A common feature of several popular solutions to the origin of neutrino masses is the hypothetical existence of heavy, sterile neutrinos N_i, or heavy neutral leptons (HNLs) as they are sometimes called. Depending on the precise scenario, they can be Dirac or Majorana fermions, and mediate processes that violate lepton flavor symmetries. In practice, fermions may be arranged in a way that they form a Majorana state with Dirac-like properties [28, 29]. This state is known as a pseudo-Dirac fermion and results from underlying symmetries that explain the smallness of neutrino masses [30–33]. This leads to a phenomenology that practically interpolates between these limiting cases in the sense that the ratio between the rates of the lepton number violating and conserving decays (R_ll) can smoothly interpolate between R_ll = 0 and R_ll = 1 [34]. Searches for heavy Dirac and Majorana neutrinos at e⁺e⁻ facilities have a long history [35–38], and if they are discovered at the LHC, FCC-ee would be a natural program to study their properties [26, 39–51].

If HNLs mix with the SM neutrinos, they can participate in the SM weak interaction via the couplings.

${\mathcal{L}}_{\text{Type\hspace{0.17em}I}}^{\text{Int}}={\mathcal{L}}^W+{\mathcal{L}}^Z+{\mathcal{L}}^H,\text{where}(\mathrm{1a})$

${\mathcal{L}}^W=-\frac{g_W}{\sqrt{2}}\sum _{\ell =e}^{\tau }\sum _{i=1}^{n_s}\overline{N_i}{V}_{\ell i}^{*}{W}_{\mu }^{+}{\gamma }^{\mu }{P}_L{\ell }^{-}+\mathrm{H}.\mathrm{c}.,(\mathrm{1b})$

${\mathcal{L}}^Z=-\frac{g_W}{2\cos {\theta }_W}\sum _{\ell =e}^{\tau }\sum _{i=1}^{n_s}\overline{N_i}{V}_{\ell i}^{\ast }{Z}_{\mu }{\gamma }^{\mu }{P}_L{\nu }_{\ell }+\mathrm{H}.\mathrm{c}.,(\mathrm{1c})$

${\mathcal{L}}^H=-\frac{g_W}{2M_W}h\sum _{\ell =e}^{\tau }\sum _{i=1}^{n_s}\overline{N_i}{V}_{\ell i}^{\ast }{m}_{N_i}{P}_L{\nu }_{\ell }+\mathrm{H}.\mathrm{c}.(\mathrm{1d})$

Here, $N_1,\dots N_{n_s}$ are the heavy mass eigenstates of the theory. This model (1) is a common HNL benchmark for the pure type I Seesaw we use in this study. In extended models, the HNLs may have extra interactions, such as new gauge interactions [52–60]. The number of right-handed neutrino chiral eigenstates n_s is not constrained by gauge anomaly considerations in the model (1) because the chiral states are gauge singlets. Here, the $V_{\ell N_i}$ are the complex-valued, active-sterile mixing matrix elements and describe the coupling between the heavy mass eigenstate i and lepton flavor state ℓ.

The Lagrangian (1) approximates interactions to first order in the parameter |V_ℓi|. In this phenomenological framework, the masses of $N_i(m_{N_i})$ and V_ℓi are taken to be independent. Hypothesizing connections to other physics, e.g., the relic abundance of DM or the matter-antimatter asymmetry of the observable Universe, can greatly constrain masses and mixing, cf. Section 2.1.2. For simplicity, the analysis of Section 3.2 considers only the lightest heavy mass eigenstate N₁, denoted by N, with mass and mixing m_N and V_ℓN. It is important to stress that considering only one HNL is for bench-marking and discovery purposes; realistic scenarios usually contain multiple mass eigenstates.

In analogy to the SM effective field theory (SMEFT) framework [61–63], the above Lagrangian can be systematically extended by higher dimensional operators in a framework known as νSMEFT [64–66], which can parameterize ultraviolet completions.

In the minimal Type I Seesaw model, where n_s = 2, the requirement to reproduce the observed pattern of light neutrino masses and mixing imposes testable constraints on the relative size of the HNL couplings |V_ℓi|² to individual SM flavors [67–70]. These will improve in the future with the Deep Underground Neutrino Experiment (DUNE) [71], cf. Figure 1, leading to a prediction that can be tested with FCC-ee. The position in the triangle in Figure 1 is entirely determined by the low energy phases in the Pontecorvo-Maki-Nakagawa-Sakata (PMNS) matrix. The number of events observed in displaced decays of HNLs produced during the Z pole run permits the determination of the relative mixing |V_ℓi|²/(∑_ℓ|V_ℓi|²) at the percent level [44], allowing for the Majorana phase in the light neutrino mixing matrix to be indirectly constrained [68, 72]. For n_s = 3, the model is less constrained, and making a testable prediction would require an independent determination of the lightest neutrino mass in the SM, cf. Figure 11 in [70]. Beyond minimal models, measuring the |V_ℓi|²/(∑_ℓ|V_ℓi|²) can give insight into flavor at charge-parity (CP) symmetries of the neutrino mixing matrix [73–75], providing a hint towards possible ultraviolet completions.

FIGURE 1

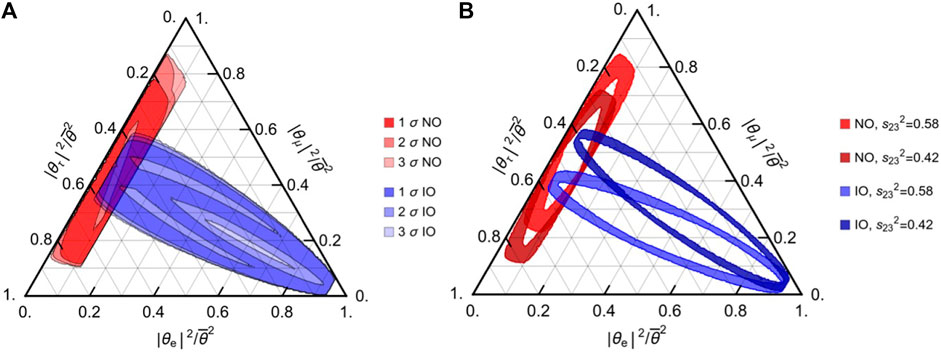
FIGURE 1. Allowed range for the relative magnitude of the HNL couplings to individual SM flavors in the model (27) with n_s =2, plot taken from [5]. (A): The range of relative flavor mixings (∑_i|V_ℓi|²)/(∑_i,ℓ|V_ℓi|²) consistent with the current neutrino oscillation data, cf. e.g., [68, 69, 76]. The contours correspond to the allowed Δχ² range taken from [77] for the case of normal (red) and inverted (blue) light neutrino mass ordering. (B): The projected 90% CL contours for the relative mixings after 14 years of data taking at DUNE [78], assuming maximal CP violation δ = −π/2 and two benchmark values of the PMNS angle θ₂₃, taken from the DUNE TDR [71], as indicated in the legend. FCC-ee can measure these ratios to the percent level in displaced HNL decays [44].

2.1.1 Phenomenology of Dirac and Majorana heavy neutral leptons

In the kinematically accessible regime, FCC-ee is an excellent machine to discover HNLs [39] and study their properties. An analysis was completed for prompt HNL signals [79] and reproduced in Ref. [3]. A comparison for various machines and setups was compiled for the European Strategy for Particle Physics Briefing Book [80] ¹. The sensitivity to active-sterile mixing, labeled here by Θ, is shown in the summary figure, Figure 2. Figure 3 shows an updated estimation of different sensitivities for current and proposed detectors including an FCC-ee displaced vertex analysis.

FIGURE 2

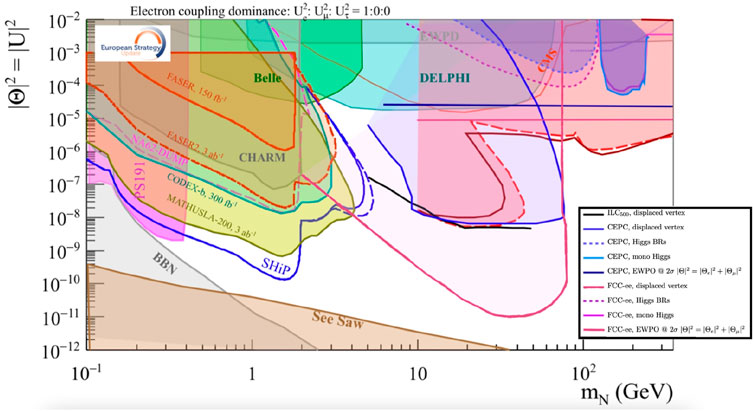
FIGURE 2. 90% CL exclusion limits for a Heavy Neutral Lepton mixed with the electron neutrino, as presented in the European Strategy for Particle Physics Briefing Book [80]. The FCC-ee curves are in (overlined) dark purple—for FCC-ee, this is equivalent to a plot as function of the sum of matrix elements squared |U_N|². The curve below the Z boson mass corresponds to the combined LLP and prompt analysis performed with 10¹²Z in Ref. [79]. The horizontal limit at high masses results from the effect of light-heavy neutrino mixing on the EW precision observables and remains valid up to O (1000 TeV).

FIGURE 3

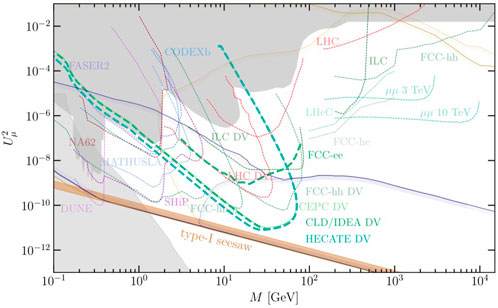
FIGURE 3. Bold green line: Sensitivity of displaced vertex searches at FCC-ee. The parameter region inside the curves corresponds to more than four observed HNL decays with $|V_{\ell N}{|}^2={\delta }_{\ell \mu }{U}_{\mu }^2$ from 5 × 10¹² Z bosons, assuming no background events and 95% reconstructed HNL decays (i.e., all decays except the invisible decay) inside the main detectors based on the IDEA or CLD design with a displacement of over 400 μm. Based on Tables 7.2 and 7.3 in [3] with 1 m of instrumentation required for detection, we assume a cylinder of length l = 8.6 m and radius r = 5 m (CLD) or l = 11 m and r = 4.5 m (IDEA) as fiducial volumes. The resulting curves for the CLD and IDEA detectors are visually indistinguishable. For comparison, we show what CEPC can achieve with 4.2 × 10¹² Z bosons [81] for an IDEA-type detector [82]. Bold turquoise line: Gain in sensitivity if the maximal observable displacement is increased with HECATE-like detectors [83] with l = 60 m, r = 15 m at two IPs. Medium gray: Constraints on the mixing of HNLs from past experiments [84–94]. Colorful lines: Estimated sensitivities of the main HL-LHC detectors [95–97] and NA62 [69], compared to the sensitivities of selected planned or proposed experiments (DUNE [98], FASER2 [99], SHiP [100, 101], MATHUSLA [102], CODEX-b [103], cf [10]. for a more complete list), prompt searches at FCC-ee or CEPC [50, 104], and searches at selected other proposed future colliders (FCC-hh [79, 97, 105, 106], ILC [43, 107] LHeC and FCC-he [108], and muon colliders [109], with DV indicating displaced vertex searches). The curves from [50, 95, 104] were re-scaled for a consistent integrated luminosity with [96, 97]. The sensitivity of FCC-ee and other future colliders can be further improved with dedicated long-lived particle detectors [83, 106, 110, 111]. Brown band: Indicative lower bound on the total HNL mixing $U_e^2+U_{\mu }^2+U_{\tau }^2$ from the requirement to explain the light neutrino oscillation data [77]. The band width corresponds to varying the light neutrino mass ordering and the lightest neutrino mass. The matter-antimatter asymmetry of the universe [112] can be explained by low scale leptogenesis [113–115] together with the light neutrino properties inside the mustard (violet) hashed contours with three [116] (two [117]) HNL flavours; solid and dashed contours indicate vanishing and thermal initial conditions in the early universe, respectively. Light gray: Lower bound on $U_{\mu }^2$ from BBN [118, 119]. Plot adapted from [5].

Figure 4 shows the four and one event contours. The four event contour corresponds to the 95% confidence level (CL) exclusion in the absence of signal events. The one event contour shows that for the analysis of the LLP signatures, there still is a 63% probability to observe one event, which, in the absence of background events, could be sufficient for discovery, all the way down to the see-saw limit around 20–40 GeV.

FIGURE 4

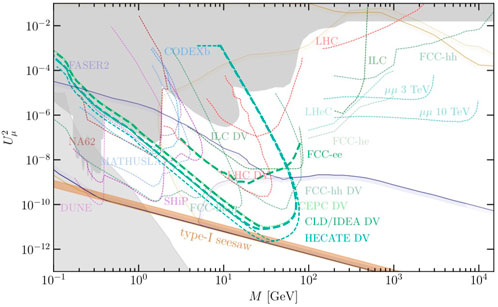
FIGURE 4. Comparison of the parameter regions in which four events (bold lines) and one event (non-bold lines) are expected in the IDEA/CLD detector or HECATE, with the same conventions and assumptions as in Figure 3.

If N is a Majorana fermion, then it can mediate processes that conserve lepton number as well as those that violate lepton number. Likewise, if lepton number is violated, then neutrinos must in principle possess Majorana properties [120, 121], though the amount of lepton number violation (LNV) in practice depends on the underlying model [121, 122]. Dirac neutrinos can only participate in processes that conserve lepton number. Therefore, differences between Dirac and Majorana N are closely related to differences between lepton number conservation (LNC) and LNV. The availability of LNV decay modes, for instance, leads to a Majorana N having a width (Γ_N) that is twice as large as a Dirac N. This implies that a Majorana N has a mean lifetime (τ_N), or mean displacement (d_N), that is half as long as that of a Dirac N.

Section 3.2.3 assumes a simple phenomenological model (1) with n_s = 1, i.e., only one mass eigenstate N that is either a Dirac or a Majorana fermion. Though this phenomenological model cannot completely reproduce the light neutrino oscillation data, it is sufficient to capture the collider phenomenology of the pure Dirac and Majorana HNLs benchmarks experimentally. Nature may be somewhere in the middle of these two cases. Therefore, observables that quantify differences between LNV and LNC processes, such as R_ll as defined in [34] or $\mathcal{A}$ as defined in [123, 124], can be used to interpolate between the benchmarks.

There is a rich phenomenology that connects R_ll, $\mathcal{A}$, and the decay rates of HNLs into different SM flavors to the mechanism that generates light neutrino masses. This connection can be accurately probed by studying the HNL properties at FCC [37, 48, 125] or other colliders [34, 123, 124, 126].

2.1.2 Probing cosmological questions

In addition to generating light neutrino masses, HNLs can, depending on their mass, affect the history of the Universe in different ways [114, 127, 128]. From a cosmological viewpoint, the most important motivation for HNL searches may be their potential connection to the origins of baryonic matter and DM.

Leptogenesis: Leptogenesis [129] provides an explanation for the matter-antimatter asymmetry in the observable Universe [112] and relates it to the properties of neutrinos. In the most popular scenario (based on the Type I Seesaw), HNLs generate the BAU via their CP-violating interactions with the thermal plasma. While it was originally believed that this mechanism only operates for HNL masses far above the EW scale [130], it is now established that sub-TeV HNLs can produce the observed BAU during their production [113, 114, 127] or freeze-out and decay [115, 131]. This implies that direct experimental searches have the potential to probe the origin of matter [132]. If any HNLs with masses at or below the EW scale are discovered in the near future, FCC-ee would provide a powerful tool to study their properties and test their connection to the BAU. A simple construction that supports low-scale leptogenesis is the Neutrino Minimal Standard Model (νMSM) [127]. Here, two HNLs simultaneously explain the neutrino masses and the BAU [114] for a wide range of experimentally accessible masses, cf. Figure 3. Due to its minimality, the model is highly testable [67, 68]. In particular, leptogenesis constrains the flavor mixing pattern beyond the experimental fits shown in Figure 1, which can be tested by comparing flavored branching ratios in displaced decays. Finally, if accessible, HNL oscillations in the detectors are sensitive to the HNL mass splitting [44], which is a crucial parameter for leptogenesis.

Dark matter: HNLs with sufficiently small masses and mixing angles could be viable DM candidates [133]. Constraints on the HNL lifetime and from indirect searches restrict the range of masses and mixings to values that are inaccessible to direct searches at colliders, cf [134, 135]. for reviews. However, FCC-ee can indirectly probe sterile neutrino SM scenarios by searching for signatures of other particles that were involved in the DM production.

HNLs can be resonantly produced in the early Universe through their mixing-suppressed weak interactions if the lepton asymmetry at temperatures around the quantum chromodynamics (QCD) crossover greatly exceeded the BAU [136–139]. In the νMSM, this large lepton asymmetry can be generated by heavier HNLs that are also responsible for the BAU and neutrino masses [140]. The first parameter space studies [141–143] suggest that this is possible only for comparably small mixing angles, possibly making FCC-ee or a similar machine the only facility at which these HNLs could be discovered. If the HNLs have additional gauge interactions (cf. e.g., [144–149]), the extended gauge sector can be probed directly or indirectly at FCC-ee. If the DM is produced via the decay of a singlet [150–152] or charged [153, 154] scalar during freeze-out or freeze-in [155, 156], precision studies of the SM Higgs and of the portal can shed light on the mechanism. Most of these possibilities have not been studied in detail to date.

2.2 Axion-like particles

Many models that address open, fundamental problems of the SM are governed by global symmetries. If an approximate global symmetry is spontaneously broken, a pseudo Nambu-Goldstone boson appears in the theory that is light compared to the symmetry breaking scale. If this pseudo Nambu-Goldstone boson is a pseudoscalar, it is often referred to as an axion-like particle or ALP. The ALP’s lightness singles it out as a uniquely promising experimental target that could open a first window onto high-scale new physics beyond the SM.

ALPs appear in many models that address open, fundamental problems in the SM. The most prominent example is the QCD axion, which was introduced in the 1980s to solve the strong CP problem [157–160] and found to simultaneously account for the observed DM relic abundance [161, 162]. QCD axions are typically very light, and these models are plagued by the “axion quality” problem, in which quantum gravity corrections destabilize the minimum of the axion potential, thereby reintroducing the strong CP problem [163–166]. Heavy-axion solutions to the strong CP problem circumvent this issue and so motivate ALPs with MeV-to-TeV scale masses [167–175]. ALPs in this mass range could also result from the breaking of global symmetries in low scale supersymmetric [176–178] or composite Higgs models [179–182]. Phenomenologically, they can also lead to successful EW baryogenesis [183].

An ALP dominantly couples to SM particles via dimension-5 operators,

$\begin{array}{ll}\hfill {\mathcal{L}}_{\text{eff}}& =\frac{1}{2}\left({\partial }_{\mu }a\right)\left({\partial }^{\mu }a\right)-\frac{m_{a,0}^2}{2}{a}^2+\sum _{\psi }\frac{c_{ff}}{2}\frac{{\partial }^{\mu }a}{f}\bar{\psi }{\gamma }_{\mu }{\gamma }_5\psi \hfill \\ \hfill & +c_{GG}\frac{{\alpha }_s}{4\pi }\frac{a}{f}{G}_{\mu \nu }^a{\tilde{G}}^{\mu \nu ,a}+c_{\gamma \gamma }\frac{\alpha }{4\pi }\frac{a}{f}{F}_{\mu \nu }{\tilde{F}}^{\mu \nu }\hfill \\ \hfill & +c_{\gamma Z}\frac{\alpha }{2\pi s_w{c}_w}\frac{a}{f}{F}_{\mu \nu }{\tilde{Z}}^{\mu \nu }+c_{ZZ}\frac{\alpha }{4\pi s_w^2{c}_w^2}\frac{a}{f}{Z}_{\mu \nu }{\tilde{Z}}^{\mu \nu }\hfill \\ \hfill & +c_{WW}\frac{\alpha }{2\pi s_w^2}\frac{a}{f}{W}_{\mu \nu }^{+}{\tilde{W}}^{-\mu \nu },\hfill \end{array}(2)$

where $G_{\mu \nu }^a$ is the field-strength tensor of SU(3)_c, while F_μν, Z_μν and $W_{\mu \nu }^{+}$ describe the photon, Z, and W boson in the broken phase of EW symmetry. The dual field-strength tensors are denoted by ${\tilde{F}}^{\mu \nu }=\frac{1}{2}{ϵ}^{\mu \nu \alpha \beta }{F}_{\alpha \beta }$, etc., (with ϵ⁰¹²³ = 1); α_s and α are the QCD coupling and fine-structure constants, respectively; s_w and c_w denote the sine and cosine of the weak mixing angle; and the sum runs over all fermion mass eigenstates ψ. The suppression scale f is related to the new physics scale Λ via Λ = 4πf, and to the axion decay constant f_a by f_a = −f/(2c_GG). The ALP dominantly interacts with the Higgs boson via dimension-6 and -7 operators,

${\mathcal{L}}_{\text{eff}}^H=\frac{c_{ah}}{f^2}\left({\partial }_{\mu }a\right)\left({\partial }^{\mu }a\right)H^{†}H+\frac{c_{Zh}}{f^3}\left({\partial }^{\mu }a\right)\left(H^{†}i{D}_{\mu }H+\text{h.c.}\right)H^{†}H.(3)$

At FCC-ee, ALPs are predominantly produced in association with a photon, Z boson, or Higgs boson, as shown in the Feynman diagrams in Figure 5, or via exotic Z and Higgs decays. Resonant production of an ALP, e.g., e⁺e⁻ → a, is possible but suppressed by $m_e^2/{(4\pi f)}^2$. ALP production in vector boson fusion has been considered in Ref. [184] and detection prospects in light-by-light scattering in Refs. [185, 186].

FIGURE 5

FIGURE 5. ALP production processes in electron-positron collisions.

The differential cross sections for associated γa/Za/ha production are given by [187, 188].

$\frac{d\sigma \left(e^{+}{e}^{-}\to \gamma a\right)}{d\mathrm{\Omega }}=\frac{\alpha {\alpha }^2\left(s\right)}{128{\pi }^3}\frac{s^2}{f^2}{\left(1-\frac{m_a^2}{s}\right)}^3\left(1+{\cos }^2\theta \right)\left(|V_{\gamma }\left(s\right){|}^2+|A_{\gamma }\left(s\right){|}^2\right),(4)$

$\frac{d\sigma \left(e^{+}{e}^{-}\to Za\right)}{d\mathrm{\Omega }}=\frac{\alpha {\alpha }^2\left(s\right)}{128{\pi }^3}\frac{s^2}{f^2}{\lambda }^{\frac{3}{2}}\left(x_a,x_Z\right)\left(1+{\cos }^2\theta \right)\left(|V_Z\left(s\right){|}^2+|A_Z\left(s\right){|}^2\right),(5)$

$\frac{d\sigma \left(e^{+}{e}^{-}\to ha\right)}{d\mathrm{\Omega }}=\frac{2{\pi }^3\alpha }{c_w^2{s}_w^2}\frac{|c_{Zh}{|}^2}{f^2}\frac{s{m}_Z^2}{{\left(s-m_Z^2\right)}^2}{\lambda }^{\frac{3}{2}}\left(x_a,x_h\right){\sin }^2\theta \left(g_V^2+g_A^2\right),(6)$

where λ(x, y) = (1 − x − y)² − 4xy, $x_i=(m_i^2/s)$, $\sqrt{s}$ is the center-of-mass energy, and θ describes the scattering angle of the photon, Z, or Higgs boson relative to the beam axis. The vector and axial-vector form factors are given by.

$V_{\gamma }\left(s\right)=\frac{c_{\gamma \gamma }}{s}+\frac{g_V}{2c_w^2{s}_w^2}\frac{c_{\gamma Z}}{s-m_Z^2+i{m}_Z{\mathrm{\Gamma }}_Z},A_{\gamma }\left(s\right)=\frac{g_A}{2c_w^2{s}_w^2}\frac{c_{\gamma Z}}{s-m_Z^2+i{m}_Z{\mathrm{\Gamma }}_Z},(7)$

$V_Z\left(s\right)=\frac{1}{c_w{s}_w}\frac{c_{\gamma Z}}{s}+\frac{g_V}{2c_w^3{s}_w^3}\frac{c_{ZZ}}{s-m_Z^2+i{m}_Z{\mathrm{\Gamma }}_Z},A_Z\left(s\right)=\frac{g_A}{2c_w^3{s}_w^3}\frac{c_{ZZ}}{s-m_Z^2+i{m}_Z{\mathrm{\Gamma }}_Z},(8)$

with $g_V=2s_w^2-1/2$, g_A = −1/2, and Γ_Z is the total width of the Z boson. The process where an ALP is radiated off an initial-state electron exhibits an additional suppression of $(m_e^2/s)$.

The integrated cross section of e⁺e⁻ → γa below the Z pole is dominated by the photon contribution, which is proportional to c_γγ, while above the Z pole the process proportional to c_γZ also contributes. Combining these measurements at low and high energies therefore enables us to access these couplings separately. At the Z pole, the cross section becomes

$\sigma \left(e^{+}{e}^{-}\to \gamma a\right)\approx \frac{\alpha }{24{\pi }^2}{\alpha }^2\left(m_Z^2\right){\left(1-\frac{m_a^2}{m_Z^2}\right)}^3\left[\frac{|c_{\gamma \gamma }{|}^2}{f^2}+\frac{m_Z^2}{{\mathrm{\Gamma }}_Z^2}\frac{|c_{\gamma Z}{|}^2}{16s_w^4{c}_w^4{f}^2}\right].(9)$

The contribution from the Z boson propagator is enhanced by $(m_Z^2/{\mathrm{\Gamma }}_Z^2)\sim 1336$, which allows one to directly access the coupling c_γZ (as long as c_γγ is not much bigger than c_γZ). ALPs can also be produced in exotic decays of Z and Higgs bosons [187–189]. The exotic decay rates are given by.

$\mathrm{\Gamma }\left(Z\to \gamma a\right)=\frac{\alpha \alpha \left(m_Z\right)m_Z^3}{96{\pi }^3{s}_w^2{c}_w^2{f}^2}{\left|c_{\gamma Z}\right|}^2{\left(1-\frac{m_a^2}{m_Z^2}\right)}^3,(10)$

$\mathrm{\Gamma }\left(h\to Za\right)=\frac{m_h^3{v}^2}{64\pi f^6}|c_{Zh}{|}^2{\lambda }^{3/2}\left(\frac{m_Z^2}{m_h^2},\frac{m_a^2}{m_h^2}\right),(11)$

$\mathrm{\Gamma }\left(h\to aa\right)=\frac{m_h^3{v}^2}{32\pi f^4}|c_{ah}{|}^2{\left(1-\frac{2m_a^2}{m_h^2}\right)}^2\sqrt{1-\frac{4m_a^2}{m_h^2}}.(12)$

Once produced, ALPs lead to a variety of signatures inside the detector. Very long-lived ALPs, for example, escape the detector and lead to a signature with missing momentum. ALPs with somewhat shorter lifetimes may decay into gauge bosons, leptons, and quarks inside the detector. The photon and lepton decay channels are shown in Figure 6. Their corresponding decay widths are given by.

$\mathrm{\Gamma }\left(a\to \gamma \gamma \right)=\frac{{\alpha }^2{m}_a^3}{64{\pi }^3{f}^2}{c}_{\gamma \gamma }^2,(13)$

$\mathrm{\Gamma }\left(a\to {\ell }^{+}{\ell }^{-}\right)=\frac{m_a{m}_{\ell }^2}{8\pi f^2}{c}_{\ell \ell }^2\sqrt{1-\frac{4m_{\ell }^2}{m_a^2}}.(14)$

An ALP decay into hadrons can be computed perturbatively for relatively large ALP masses, i.e., m_a ≫Λ_QCD. The decay width into bottom quarks specifically is given by

$\mathrm{\Gamma }\left(a\to b\bar{b}\right)=\frac{3m_a{m}_b^2\left(m_a\right)}{8\pi f^2}{c}_{bb}^2\sqrt{1-\frac{4m_b^2}{m_a^2}},(15)$

and similarly for $\mathrm{\Gamma }(a\to c\bar{c})$. The decay rate into light quarks (u, d, s) can be computed using quark-hadron duality and is given by [187, 190].

$\mathrm{\Gamma }\left(a\to \text{light\hspace{0.17em}hadrons}\right)=\frac{{\alpha }_s^2\left(m_a\right)m_a^3}{8{\pi }^3{f}^2}\left[1+\frac{83}{4}\frac{{\alpha }_s\left(m_a\right)}{\pi }\right]{\left|C_{GG}^{\text{eff}}\left(m_a\right)\right|}^2,(16)$

where the ALP couplings to both gluons and quarks contribute via

$C_{GG}^{\text{eff}}\left(m_a\right)=c_{GG}+\frac{1}{2}\sum _{q\ne t}{c}_{qq}{B}_1\left(\frac{4m_q^2}{m_a^2}\right).(17)$

The function B₁ behaves as $B_1(4m_q^2/m_a^2)\approx 1$ for m_q ≪ m_a and $B_1(4m_q^2/m_a^2)\approx -m_a^2/(12m_q^2)$ for m_q ≫ m_a. The explicit form of B₁ is given in e.g., [187]. For light ALPs, m_a ≪Λ_QCD, the decay into three pions may be kinematically accessible, with a decay rate which is given in [187, 191]. However, it is worth noting that the FCC-ee program as currently envisioned will not be able to produce significant numbers of ALPs that are heavy enough to decay in two top quarks, due to the high center of mass energy that would be required. Depending on their lifetime, ALPs can decay promptly at the interaction point or they may decay after having travelled a certain distance inside the detector.

FIGURE 6

FIGURE 6. ALP decay processes at FCC-ee.

At FCC-ee, all combinations of ALP production modes with visible and invisible decay modes can be investigated [188, 192]. While many processes, in particular exotic Higgs decays, depend on two independent couplings, under certain assumptions a few processes only depend on a single coupling parameter. For example, the e⁺e⁻ → γa → 3γ and e⁺e⁻ → Za → Zγγ processes only depend on the ALP-photon coupling c_γγ when it is assumed that both the ALP-photon and the ALP-photon-Z couplings originate from the ALP coupling to either SU(2)_L or U(1) gauge bosons before EW symmetry breaking. If the ALP only couples to U(1) gauge bosons, then $c_{\gamma Z}=-s_w^2{c}_{\gamma \gamma }$. In this case, Figure 7A shows the projected sensitivity of FCC-ee to c_γγ using the e⁺e⁻ → γa → 3γ channel [188]. This analysis assumes at least four signal events and combines the Z-pole run with runs at $\sqrt{s}=2m_W$ and $\sqrt{s}=250$ GeV. Further details are provided in [188]. Another process that depends only on a single coupling is e⁺e⁻ → γa → γℓ⁺ℓ⁻ when the ALP-photon and the ALP-photon-Z couplings are induced via a loop of leptons. In this case,

$c_{\gamma \gamma }=\sum _{\ell =e,\mu ,\tau }{c}_{\ell \ell }{B}_1\left(4m_{\ell }^2/m_a^2\right)\text{and}{c}_{\gamma Z}=\left(s_w^2-1/4\right)c_{\gamma \gamma }.(18)$

Figure 7B shows the projected sensitivity of FCC-ee to c_ℓℓ using the process e⁺e⁻ → γa → γℓ⁺ℓ⁻ [188].

FIGURE 7

FIGURE 7. Projected sensitivity of FCC-ee in (A) e⁺e⁻ → γa →3γ and (B) e⁺e⁻ → γa → γℓ⁺ℓ⁻ in purple. Figure adapted from Figure [188].

The e⁺e⁻ → γa → 3γ and e⁺e⁻ → γa → γℓ⁺ℓ⁻ searches are sensitive to ALP decay lengths of up to 1.5 m and 2 cm, respectively. The search for long-lived ALPs may be significantly improved with the installation of a dedicated far detector that could probe decay lengths of up to 100 m [193, 194]. For FCC-ee reach on the relaxion, see Ref. [195]. In addition to direct measurements, FCC-ee will be able to significantly constrain the ALP contribution to the oblique parameters [187, 188], whose determination is expected to improve by an order of magnitude [196].

2.3 Exotic Higgs boson decays

The Higgs boson has a unique role within the SM. It is the only apparently elementary scalar particle that has been discovered. In particular, whatever new physics is responsible for the cosmological DM, the apparent asymmetry between matter and antimatter, or small neutrino masses may well have some coupling to the Higgs boson. In short, the Higgs boson is a likely gateway to what lies beyond the SM.

The two-body decays of the Higgs boson to SM particles are controlled by small Yukawa couplings or loop suppression making its decay width much smaller than its mass. Consequently, current bounds on the Higgs width leave plenty of room for “exotic” decays, that is, decays not predicted by the SM. However, future colliders, like FCC-ee, will be able to measure the Higgs width much more precisely than at the LHC [197]. The products of these exotic Higgs boson decays can decay promptly themselves or be completely stable, each of which present their own experimental challenges and advantages. However, searches for particles whose lifetimes are more intermediate, i.e., that decay within the experimental detector but at a measurable distance from the interaction point, can have very low backgrounds in comparison to prompt searches. This gives Higgs boson decays to LLPs remarkable power to probe particles and sectors whose couplings to the Higgs are small but nonzero. The e⁺e⁻ to Zh processes shown in Figure 8 illustrate the utility of the FCC-ee collider. Because the initial state and the Z decays are well understood, invisible, partially invisible, and displaced decays of the Higgs boson can be probed with confidence. For a review, see Ref. [102] and the recent work in Ref. [198].

FIGURE 8

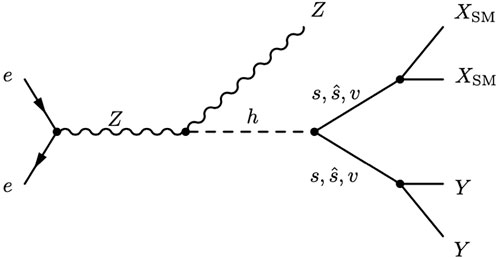
FIGURE 8. Example production of LLPs through exotic decays of the Higgs boson h. The Higgs decays to a pair of scalars s, pseudoscalars $\widehat{s}$, or vectors v. At least one of these decays within the detector volume to SM particles. The other may or may not decay within the detector and may decay to visible or invisible states.

The characteristics of LLPs vary considerably. Exotic Higgs decays to spin-zero particles are considered first. Such decays at future lepton colliders were considered in Ref. [199]. Long-lived scalars may result from simple constructions, such as adding a single scalar field to the SM:

$V_{\text{scalar}}=V_H+V_S+c_{1}S|H{|}^2+c_2{S}^2|H{|}^2.(19)$

They may also arise in rich, hidden sectors such as Hidden Valley models [200–202]. Of particular interest are hidden sectors motivated by Neutral Naturalness [203–206]. These models address the little hierarchy problem through new symmetries, but the symmetry partners of the SM quarks do not carry SM color. Instead they are charged under a hidden, QCD-like confining force.

In many models with the long-lived scalar s or pseudoscalar $\widehat{s}$, the Higgs boson decay products inherit much of the Higgs’ coupling structure. While the actual size of the couplings are reduced by a common small mixing angle θ, the branching fractions are those of a SM Higgs boson with the mass of the LLP. In the scalar case, one often finds

$\mathrm{\Gamma }\left(s\to X_{\text{SM}}{X}_{\text{SM}}\right)={\sin }^2\theta \mathrm{\Gamma }\left(h\left(m_s\right)\to X_{\text{SM}}{X}_{\text{SM}}\right).(20)$

The pseudoscalar case is slightly modified [207–209] and can also include the $h\to \widehat{s}Z$ decay channel, see for instance the ALP results given in Eqs 11, 12. Since the masses of the LLPs must be less than half the Higgs boson mass, the dominant decays modes are into the heaviest kinetically accessible SM quarks. Thus, for Higgs boson decays into spin-zero LLPs, hadronic final states, and b-jets especially, are particularly motivated.

Rather than scalars, the LLPs may be spin-half fermions. These can be related to the BAU [210] or to Seesaw explanations of the neutrino masses [11–17]. The heavy neutrinos N in these models have been shown to have a wide range of possible decay lengths, including within the volume of an FCC-ee detector [211–213]. The N mainly decay into a SM lepton and an off-shell weak gauge boson. This leads to three-body final states which may be composed of both quarks (jets) and leptons.

The Higgs boson can also decay to long-lived vectors v. A simple framework is the Hidden Abelian Higgs model [214]. In this case, a new U(1)′ gauge symmetry is broken by a hidden Higgs field h_D that generates a vacuum expectation value (VEV). The hidden photon $A_{\mu }^{\prime }$ of the new gauge symmetry gets a mass proportional to the hidden Higgs VEV and can also have kinetic mixing with the SM through

$-\frac{ϵ}{2\cos {\theta }_W}{F}_{\mu \nu }^{\prime }{F}_Y^{\mu \nu },(21)$

where θ_W is the weak mixing angle and $F_Y^{\mu \nu }$ is the field strength for SM hypercharge. The parameter ϵ can vary over a huge range, and controls the degree to which SM fermions couple to $A_{\mu }^{\prime }$. For sufficiently small ϵ, the massive hidden photon is a LLP.

The hidden photon’s coupling to SM fields is proportional to their hypercharge. This means that, when and if they are kinematically accessible, quark final states make up most of its branching fraction, though decay rates to leptons are non-negligible. A small ϵ also means that the direct coupling of the hidden photon to the SM Higgs boson is small. However, the mixing between SM Higgs and the hidden Higgs can be larger than ϵ. This allows the Higgs boson to decay to two hidden photons at a larger rate.

In summary, the Higgs boson may have appreciable decay widths into LLPs of various spin. The decay modes of the LLPs can vary, but it has been shown that hadronic final states play a significant role in all the decay types outlined above. Decays to long-lived fermions stand out as different, in that their leading decays are three-body. Pseudoscalars may also lead to $h\to \widehat{s}Z$ decays, but in general, the h → XX process captures most of the interesting possibilities. Assuming the X particle has significant branching into SM quarks (and possibly into b quarks in particular) appears to be the most motivated benchmark. Of course, the variety of other decays can be leveraged in more model-specific analyses.

Figure 9 displays an illustration, taken from Ref. [199], of how sensitive FCC-ee can be to Higgs boson decays to long-lived X particles. The 95% limit on the exotic branching fraction to these particles is plotted as a function of the X’s decay length. Two mass benchmarks, m_X = 10 (blue) and 50 (tan) GeV, are shown (additional benchmarks are considered in Ref. [199]) for two search strategies. The solid line corresponds to using an invariant mass cut to retain sensitivity to shorter decay lengths. In contrast, the dashed line depends on longer decay lengths to reduce SM backgrounds.

FIGURE 9

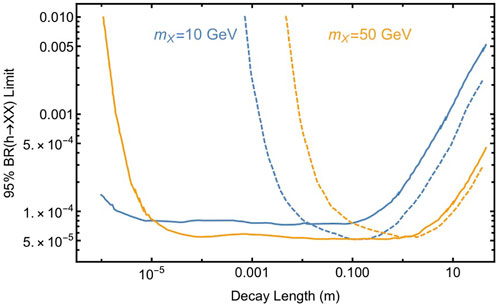
FIGURE 9. Plot of data recorded in [199] to illustrate the potential sensitivity of FCC-ee to exotic Higgs boson decays to LLPs, denoted X. Two LLP mass benchmarks are shown: 10 GeV (blue) and 50 GeV (tan). For each benchmark two search strategies are presented. The solid line employs an invariant mass cut to improve sensitivity at shorter decay lengths, the dashed line relies on longer decay lengths to reduce SM backgrounds.

3 Experimental outlook

This section presents new studies produced for this paper that follow up on the theoretical landscape presented in Section 2.

3.1 Simulation details

For all signal and background processes, the event generator MadGraph5_aMC@NLO v3.2.0 [215, 216] is used to simulate at leading order unpolarized, parton-level e⁺e⁻ collisions at $\sqrt{s}=91$ GeV. For all processes, parton-level events are passed to Pythia [217] v8.303 to simulate parton showering and hadronization. For each signal benchmark point, 50 × 10³ unscaled events were generated, and for each background process, 10⁷–10⁹ unscaled events were generated, depending on the process.

The detector response is simulated with Delphes v3.4.2 [218], using the latest Innovative Detector for Electron–positron Accelerators (IDEA) FCC-ee detector concept [219] card. The IDEA detector comprises of a silicon pixel vertex detector; a large-volume, light short-drift wire chamber surrounded by a layer of silicon micro-strip detectors; a thin, low-mass superconducting solenoid coil; a pre-shower detector; a dual-readout calorimeter; and muon chambers within the magnet return yoke.

The k4SimDelphes project [220] converts Delphes objects to the EDM4HEP format [221], which is the common data format used for the simulation of future colliders. A sophisticated analysis framework has been developed for all FCC analyses using the EDM4hep format. It is based on RDataFrames [222], where C++ code is compiled in a ROOT [223] dictionary as “analysers.” These are subsequently called in Python. Several external packages, such as ACTS [224], FastJet [225], and awkward [226], are included.

3.1.1 Heavy neutral leptons

To study Dirac and Majorana HNLs at FCC-ee, the processes.

$\mathbf{M}\mathbf{a}\mathbf{j}\mathbf{o}\mathbf{r}\mathbf{a}\mathbf{n}\mathbf{a}N:e^{+}{e}^{-}\to Z\to N{\nu }_e+N\overline{{\nu }_e},\text{with}N\to e^{+}{e}^{-}{\nu }_e+e^{+}{e}^{-}\overline{{\nu }_e},(\mathrm{22a})$

$\mathbf{D}\mathbf{i}\mathbf{r}\mathbf{a}\mathbf{c}N:e^{+}{e}^{-}\to Z\to N\overline{{\nu }_e}+\bar{N}{\nu }_e,\text{with}N\left(\bar{N}\right)\to e^{+}{e}^{-}{\nu }_e\left(\overline{{\nu }_e}\right),(\mathrm{22b})$

are simulated using the HeavyN [227, 228] and HeavyN_Dirac [97, 228] universal FeynRules Object [229–231] libraries in conjunction with MadGraph5_aMC@NLO. These libraries implement the interaction Lagrangian described in Section 2.1 for Majorana and Dirac N, respectively. A representative subset of Feynman diagrams common to both the Dirac and Majorana case is shown in Figure 11. For the Majorana case, both LNC and LNV channels are included. The Dirac case only permits LNC channels. The preservation of spin correlation in the production and decay of N with this setup was checked in Ref. [124]. When unspecified, the results consider the Majorana case. As a further benchmark, the assumption that N couples only to the electron-flavor sector is made, i.e., |V_eN| is kept nonzero and set |V_μN|, |V_τN| = 0. Only one heavy neutrino mass eigenstate is considered. SM inputs are fixed according to the values in Ref. [228].

3.1.2 Axion-like particles

To study the production ALPs a from Z decays at FCC-ee, the process

$\mathbf{A}\mathbf{L}\mathbf{P}:e^{+}{e}^{-}\to Z\to a\gamma ,\text{with}a\to \gamma \gamma ,(23)$

is simulated using the model libraries of Ref. [188] in conjunction with MadGraph5_aMC@NLO. These libraries implement the Lagrangian described in Section 2.2.

3.1.3 Exotic Higgs boson decays

A simulation study of exotic Higgs decays into LLPs is left for a future paper, as well as additional detector concepts, namely the CLIC-like detector (CLD) design [232].

3.2 Heavy neutral leptons

Although the most promising Seesaw models feature two or three HNL states in the same mass range, and possibly almost degenerate, a reasonable experimental approach is to begin by considering the production and decay of a single HNL particle.

The branching fraction of a Z boson decay into any light neutrino or antineutrino and a heavy neutrino N, which mixes with the three families of neutrinos is given by [97, 233]:

$\mathrm{B}\mathrm{R}\left(Z\to \nu N\right)=\frac{2}{3}|U_N{|}^2\mathrm{B}\mathrm{R}\left(Z\to \mathrm{i}\mathrm{n}\mathrm{v}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e}\right)\left(1+\frac{{m_N}^2}{{2m_Z}^2}\right)\left(1-\frac{{m_N}^2}{{m_Z}^2}\right),(24)$

where |U_N|² ≡∑_ℓ=e,μ,τ|U_ℓN|² is the sum of the mixing matrix elements of the HNL N with the three active neutrinos ν_ℓ. As the HNL masses considered here are much heavier than the tau lepton, the total charged current decay rate of the HNL N → ℓ_λW∗ is also proportional to the same combination of mixing angles.

${\mathrm{\Gamma }}_N=\frac{1}{c{\tau }_N}\simeq C_0{C}_{MD}|U_N{|}^2{\left(\frac{m_N}{\mathrm{50}\mathrm{G}\mathrm{e}\mathrm{V}}\right)}^5\times \left(\frac{3.10^9}{\mathrm{1}\mathrm{c}\mathrm{m}}\right)(25)$

Here, C₀ is a numerical coefficient of $\mathcal{O}(1)$ that takes into account the open charged- and neutral-current decays of the heavy neutrino, and C_MD is a coefficient that depends on the Dirac (C_MD = 1) or Majorana (C_MD = 2) nature of the particle, since twice as many decay channels are open for the Majorana particle decay. Potentially, with sufficient statistics, the direct comparison of the event rate with the lifetime for an HNL of a known mass would allow a discrimination between a Dirac and a Majorana particle.

The corresponding decay length is then of the order of a meter for a 50 GeV HNL. In those conditions, a HNL would decay in the volume of an FCC-ee detector, leading to the observable signature of a displaced vertex, with a significant time delay (several nanoseconds) with respect to ultra relativistic particles. This leads to a particularly clean signature, for which a first analysis [39] argued that it could be a background-free search, at least for the dominant charged current decay N → ℓW* → ℓ+ hadrons. Figure 10 shows what such a possible decay of the N at a future FCC-ee experiment would look like, in this case for a semileptonic final state.

FIGURE 10

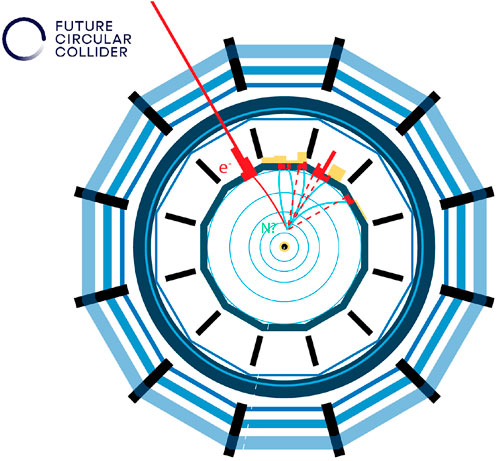
FIGURE 10. Representation of an event display at an FCC-ee detector of a HNL decay into an electron and a virtual W decaying hadronically. Courtesy of the FCC collaboration.

Furthermore, for Z → Nν_ℓ decays, the two-body Z decay kinematics results in a mono-chromatic HNL.

Therefore, even in cases where a full, final-state reconstruction is not possible, a simultaneous measurement of the decay path and of the time-of-flight provides a determination of both the mass and proper decay time on an event-by-event basis. A detailed simulation of the process is thus of great interest to understanding how much statistics are required, first to establish the existence of the new particle, and then to establish the possible existence of a lepton number violating process (Majorana vs. Dirac nature). This also leads to the identification of specific detector requirements to optimize the discovery potential.

3.2.1 Production and kinematics of electroweak-scale HNLs

As a first step to exploring the sensitivity of FCC-ee to EW-scale HNLs, Table 1 shows the cross section (center column) and the expected number of events (right column) for an HNL with a mass of m_N = 50 GeV when produced and decayed through the process described in Eq. 22 and shown in Figure 11.

TABLE 1

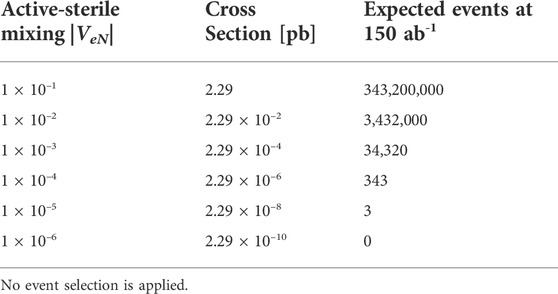
TABLE 1. The cross section and expected number of events at 150 ab⁻¹, for an HNL with a mass of 50 GeV and for several choices of |V_eN|.

FIGURE 11

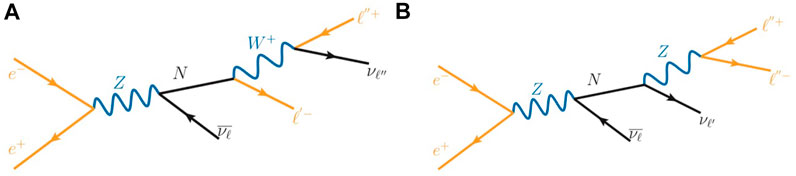
FIGURE 11. Representative diagrams depicting the e⁺e⁻→ Z → Nν_ℓ process at leading order, with N decaying via (A) charged current and (B) neutral current channels to the two-neutrino, two-charged lepton final state.

Results are shown for several choices of active-sterile mixing |V_eN|, and assume that an integrated luminosity of 150 ab⁻¹ is collected during the Tera-Z run of FCC-ee [3]. No event selection is applied at this stage.

The kinematics of HNLs in the m_N = 20–90 GeV mass range at FCC-ee can also be studied. Figure 12 shows the baseline kinematics distributions of N when no event selection is applied at this stage. Here and below, active-sterile mixing of |V_eN| = 1.41 × 10^–6 for representative masses of m_N = 30 (50) [70] {90} GeV is assumed.

FIGURE 12

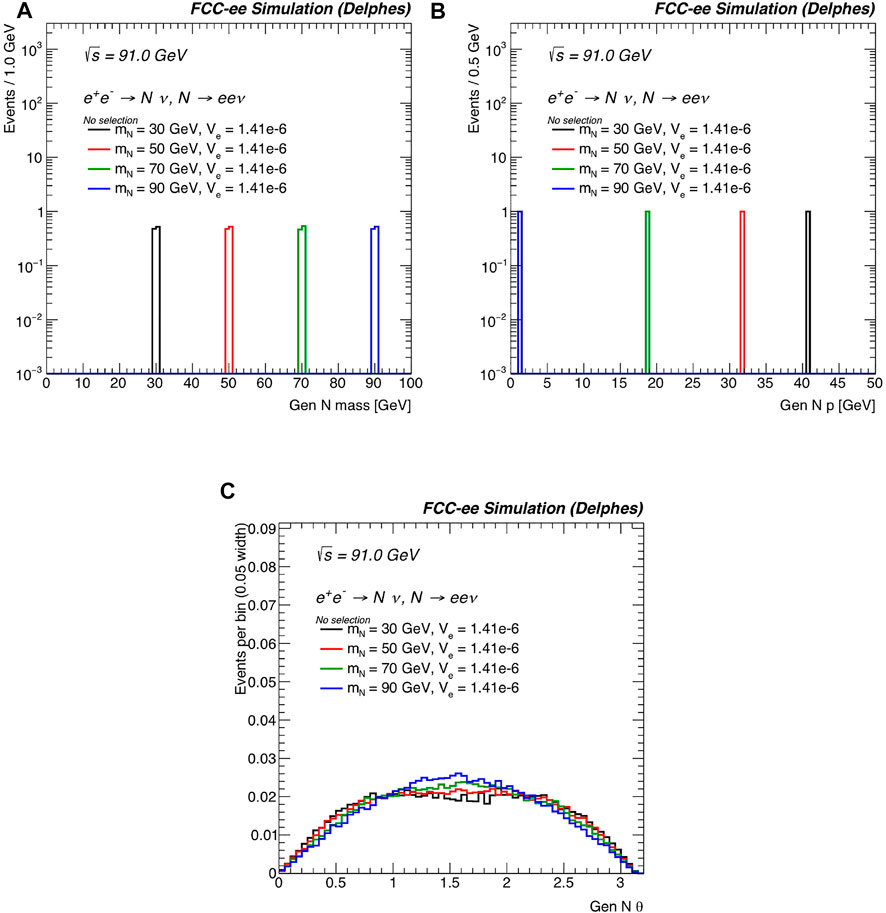
FIGURE 12. For the processes $e^{+}{e}^{-}\to N{\nu }_e+N\overline{{\nu }_e}$ with $N\to e^{+}{e}^{-}{\nu }_e+e^{+}{e}^{-}\overline{{\nu }_e}$ at $\sqrt{s}=91$ GeV, the generator-level distributions of (A) the invariant mass of N, (B) the magnitude of N’s three-momentum in the lab frame, and (C) the polar angle of N with respect to the beam axis in the lab frame are shown, for representative HNL masses and representative active-sterile mixing |V_eN| = 1.41 × 10^–6. The distributions are normalized to unit area.

Figure 12A shows the generator-level invariant mass of the HNL, which aligns with the pole mass of N. In Figure 12B, the magnitude of the normalized, generator-level three-momentum $|{\vec{p}}_N|$ in the lab frame is presented. From elementary kinematics, $|{\vec{p}}_N|$ is given analytically for a massless electron by the formula

$|{\vec{p}}_N|=\frac{M_Z}{2}\left(1-\frac{m_N^2}{M_Z^2}\right).(26)$

This corresponds to $|{\vec{p}}_N|\approx 40.7(31.9)[18.7]\{1.2\}$ GeV for the representative m_N under consideration and is in good agreement with the values $|{\vec{p}}_N|\approx 41(32)[19]\{1.2\}$ GeV shown in Figure 12B. Finally, the generator-level polar angle θ of N with respect to the beam axis in the lab frame is presented in Figure 12C. The distribution shows that a bulk of events feature central (0.5 < θ < 2.5) HNLs, as one would expect from a high-p_T process.

To explore the potential impact of finite detector resolution, limited geometric coverage, and detector mismeasurements, Figure 13 shows the distributions with respect to the invariant mass of the (e⁺e⁻) system, which is given for massless electrons by the formula

$m_{ee}=\sqrt{{\left(p_{e^{+}}+p_{e^{-}}\right)}^2}\approx \sqrt{2p_{e^{+}}\cdot p_{e^{-}}}=\sqrt{2E_{e^{+}}{E}_{e^{-}}\left(1-\cos {\theta }_{ee}\right)},(27)$

at (a) the generator level (Gen) and (b) the reconstruction level (Reco). In both cases, no selection criteria have been applied and the same representative inputs as above are assumed.

FIGURE 13

FIGURE 13. For the same processes and benchmark mass and |V_eN| choices as in Figure 12, the differential distributions with respect to the invariant mass of the (e⁺e⁻) system m_ee at (A) the generator level and (B) after reconstruction. No selection criteria have been applied. The distributions are normalized to unit area.

Consider first the generator-level case in Figure 13A. As both charged leptons in the final state originate from the N → e⁺e⁺X decay, the distribution of m_ee is dictated by the properties of N itself. For instance: for each of the mass benchmarks, the value of the observable m_ee does not exceed m_N itself, i.e., max(m_ee) < m_N. This can be understood from momentum conservation:

$m_N^2={\left(p_{e^{+}}+p_{e^{-}}+p_{\nu }\right)}^2=p_{\nu }^2+2\left(p_{\nu }\cdot p_{e^{+}}\right)+2\left(p_{\nu }\cdot p_{e^{-}}\right)+m_{ee}^2\gtrsim m_{ee}^2.(28)$

When m_ee is close to m_N, one can infer that the final-state neutrino carries little-to-no energy. For m_N = 90 GeV, kinematic peculiarities arise due to threshold effects. More specifically, since $\sqrt{s}=91$ GeV, one can consider N to be essentially at rest when m_N = 90 GeV. For such masses, the two-body decay N → e^±W^∓ becomes kinematically favored. The energy of this first electron and W are given approximately by formulae similar to Eq. 26, and come out to be E₁ ≈ 9.4 GeV and E_W ≈ 80.6 GeV.

Assuming that the decay products of the W boson are configured in the lab frame such that the second electron carries away all the energy of W, i.e., E₂ ≈ E_W, then the formula for m_ee shows that the maximum invariant mass for m_N = 90 GeV is about $\max (m_{ee})\approx \sqrt{4(9.4\mathrm{G}\mathrm{e}\mathrm{V})(80.6\mathrm{G}\mathrm{e}\mathrm{V})}\approx 55$ GeV. This is in agreement with Figure 13A.

Comparing Figures 13A,B demonstrates some impact of the event reconstruction. Importantly, many of the kinematic features found at the generator level survive at the reconstruction level. In particular, the endpoints of m_ee are preserved. Likewise, the means of each distribution, which span about $m_{ee}^{\text{mean}}\approx 14-28$ GeV, remain unaltered at the reconstruction level. The relatively small impact of reconstruction effects can be tied to the high requirements of the FCC sub-detector systems.

In the absence of additional new physics, HNLs with masses below the EW scale and active-sterile mixing much smaller than unity are generically long-lived. To explore this at FCC-ee, Figure 14 shows (a) the generator-level lifetime (s) of N, given by τ = γ_Nτ_N, where γ_N = E_N/m_N is the Lorentz boost of N in the lab frame, and τ_N is the proper lifetime; (b) the reconstructed three-dimensional decay length (mm) of the HNL (L_xyz); and (c) the χ² of the reconstructed displaced vertex.

FIGURE 14

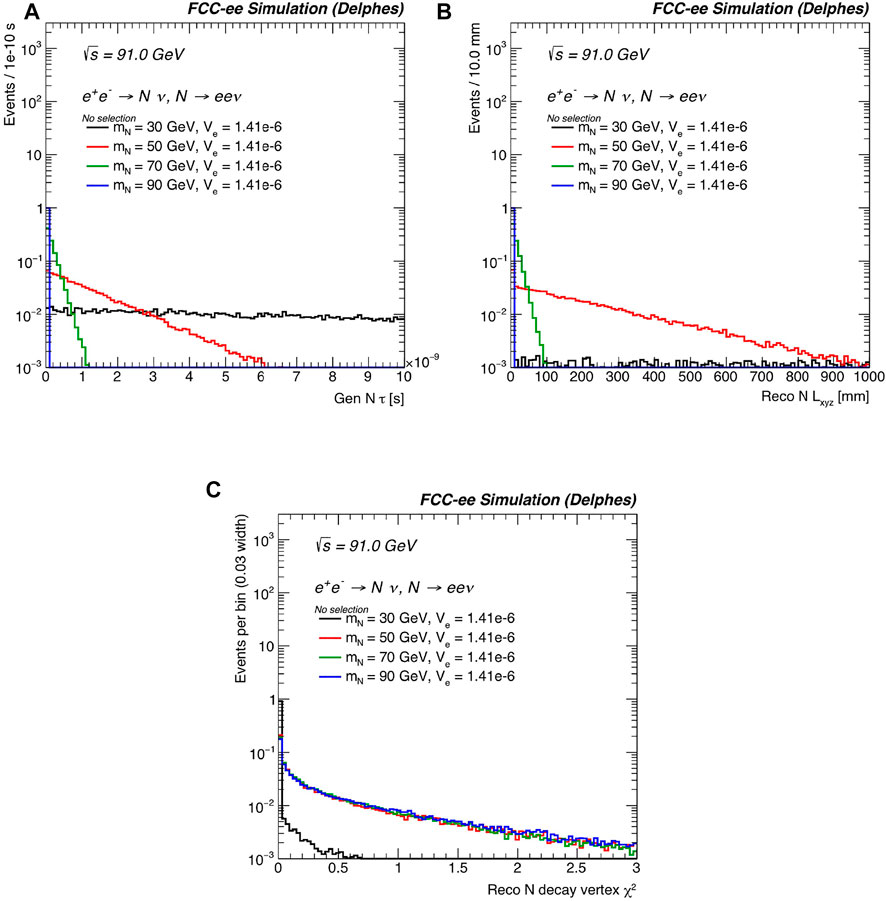
FIGURE 14. For the same processes and benchmark mass and |V_eN| choices as in Figure 12, the differential distributions with respect to (A) the generator-level lifetime of N in the lab frame; (B) the reconstruction-level three-dimensional decay length of the N; and (C) the χ² of the reconstructed decay vertex of the HNL are shown. No selection criteria have been applied. The distributions are normalized to unit area.

For a fixed width of |V_eN| = 1.41 × 10^–6, different qualitative features can be observed for the representative m_N. For instance, at m_N = 30 GeV, characteristic generator-level lifetimes readily exceed several seconds. This implies displaced vertices can be well beyond one or more meters, and therefore outside the fiducial coverage of the IDEA detector. In these instances, a large region of the event’s phase space corresponds to long-lived HNLs that ostensibly appear as missing momentum.

For heavier N, lifetimes are drastically smaller, with most HNL events exhibiting a lifetime of less than 1–2 s for m_N ≳ 50 GeV. For m_N = 50 (70) GeV, such lifetimes correspond to reconstructed displacements that are mostly within L_xyz = 50 (100) mm. Finally, in Figure 14C, the χ² curves indicate that the displaced vertices are well-reconstructed, with small χ² values.

3.2.2 Backgrounds and event selection

Several backgrounds to the HNL processes described in Eq. 22a, Eq. 22bare considered, namely, Z bosons that decay to electron-positron pairs, to tau pairs, to light quarks, to charm quark pairs, and to b quark pairs. These background processes were simulated with the conditions described above.

Figures 15, 16 show distributions of variables that distinguish the HNL signal from these background processes. Figure 15 shows the total missing momentum p̸ in each event. Unlike in a hadron collider, where only the missing momentum in the transverse direction can be considered, the three-dimensional missing momentum can be used at FCC-ee. As can be seen from this figure, requiring p̸ > 10 GeV significantly reduces the background contributions while maintaining a high efficiency for the HNL signal.

FIGURE 15

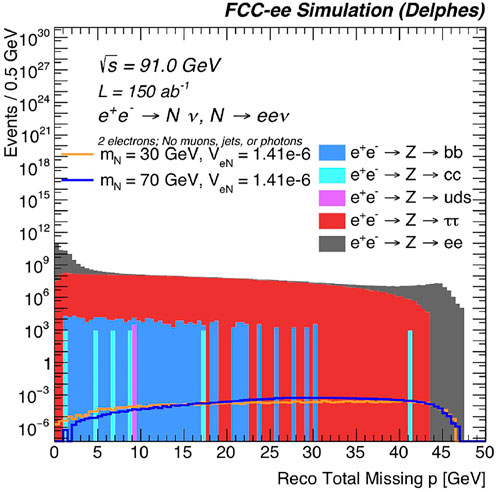
FIGURE 15. The normalized, reconstructed-level total missing momentum, for representative HNL signal benchmark mass and |V_eN| choices, as well as background processes. Exactly two reconstructed electrons are required, as well as that there are no reconstructed muons, jets or photons in each event.

FIGURE 16

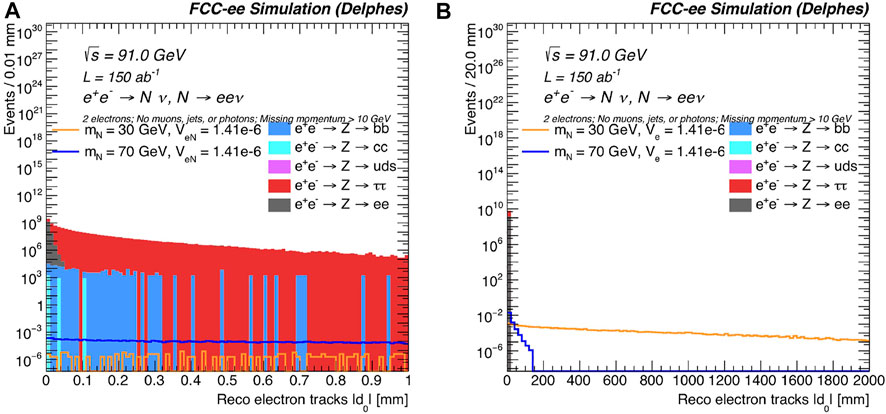
FIGURE 16. The normalized, reconstructed-level absolute value of the transverse impact parameter |d₀|, for representative HNL signal benchmark mass and |V_eN| choices, as well as background processes, for (A) 0–1 mm in |d₀| and (B) 0–2000 mm in |d₀|. Exactly two reconstructed electrons are required, as well as that there are no reconstructed muons, jets or photons in each event. The total missing momentum must be greater than 10 GeV.

Figure 16 shows the electron-track transverse impact parameter |d₀| for each event. The transverse impact parameter is the distance of closest approach in the transverse plane of the helical trajectory of the track with respect to the beam axis; it is a measurement of the reconstructed electron’s displacement. Requiring that both electron tracks have |d₀| > 0.5 mm removes the vast majority of the background.

Taking these and other distributions into account, a simple event selection is developed, using reconstructed-level variables. Events must have exactly two electrons, and no photons, jets, or muons. These requirements substantially reduce the background from light and heavy quarks. We next require p̸ > 10 GeV, which is particularly effective at reducing Z → ee events with spurious missing momentum associated with finite detector resolution. Finally, we require that both electrons are displaced with |d₀| > 0.5 mm to remove the vast majority of the remaining (prompt) backgrounds.

Table 2 shows the expected number of background events for each cumulative selection criterion, and Table 3 shows the same for representative HNL signal benchmark masses and |V_eN| choices, assuming an integrated luminosity of 150 ab⁻¹. Within these limitations, these tables show that after all the selection criteria are applied, the background can be substantially reduced while the majority of the signal events are retained. After all the selection criteria are applied, we can expect about 1 event for an HNL with a mass of 50 GeV and |V_eN| = 6 × 10^–6, with an integrated luminosity of 150 ab⁻¹. This benchmark point is illustrative of the maximum sensitivity to long-lived HNLs that can be achieved at FCC-ee, with the current study.

TABLE 2

TABLE 2. The expected number of events at an integrated luminosity of 150 ab⁻¹ is shown for the background processes, for each selection criterion.

TABLE 3

TABLE 3. The expected number of events at an integrated luminosity of 150 ab⁻¹ is shown for representative HNL signal benchmark masses and |V_eN| choices, for each selection criterion.

3.2.3 Majorana and Dirac nature of the HNL

If HNLs exist in nature, a chief goal is to ascertain whether they are Dirac or Majorana fermions. As discussed in Section 2.1 and elsewhere [33, 120–122], determining this is tantamount to observing processes that are mediated by N and exhibit LNV. However, at FCC-ee, the net lepton numbers of the processes $e^{+}{e}^{-}\to N{\nu }_{\ell }+N\overline{{\nu }_{\ell }}$ with N → (anything) are hidden because light neutrinos are not detected. This implies other metrics, such as angular distributions, are needed to disentangle the situation when lepton number violating states cannot be unambiguously identified.

To demonstrate the ability of FCC-ee to potentially disentangle the Dirac or Majorana nature of HNLs, the cleanest fully-leptonic decay channels are studied; the semileptonic decay channels have about twice as large a branching ratio and will be considered in future studies. Figure 17 shows the comparison of generator- and reconstruction-level observables for the two processes defined in Eq. 22. An important distinction to reiterate is that the Majorana HNL channel (solid line) includes final states that are both lepton number-conserving $(e^{+}{e}^{-}{\nu }_e\overline{{\nu }_e})$ as well as final states that are lepton number-violating $(e^{+}{e}^{-}{\nu }_e{\nu }_e,e^{+}{e}^{-}\overline{{\nu }_e}\overline{{\nu }_e})$. On the other hand, the Dirac HNL channel (dashed line) consists only of final states that are lepton number-conserving $(e^{+}{e}^{-}{\nu }_e\overline{{\nu }_e})$. Therefore, kinematical differences amount to differences between LNV and LNC.

FIGURE 17

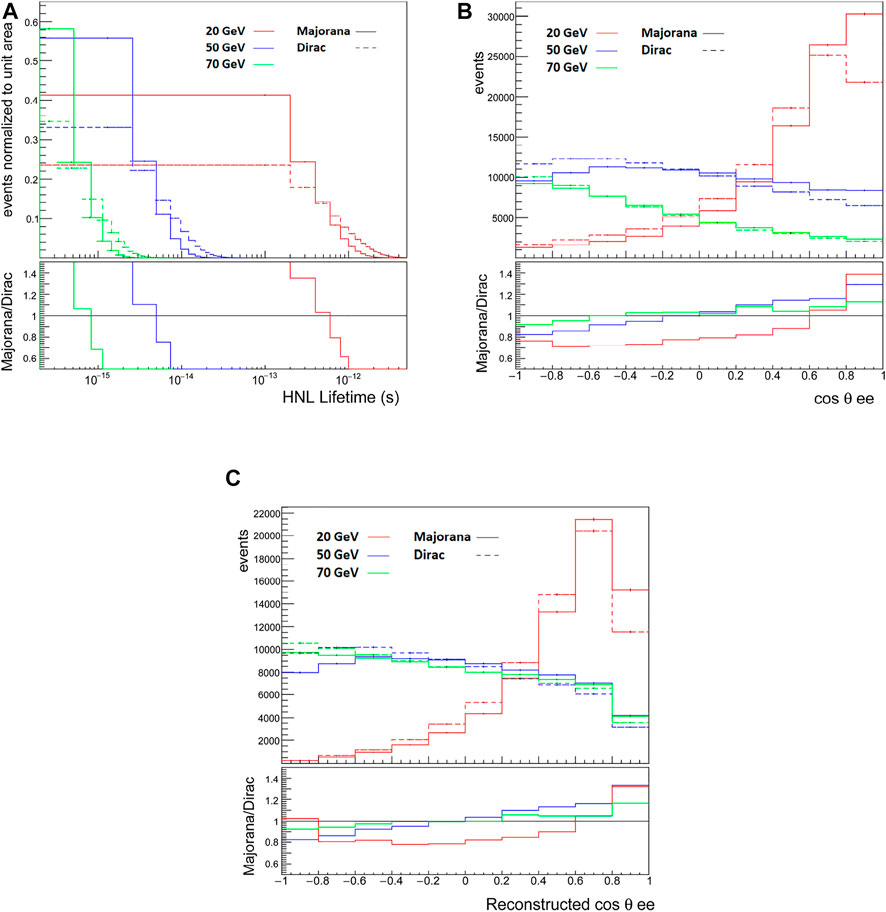
FIGURE 17. (A) The normalized distribution of lifetimes of Dirac (dashed) and Majorana (solid) HNLs in the processes defined in Eq. 22, for representative masses and assuming |V_eN| = 10^–3. (B) The generator-level angular separation cos θ_ee for Dirac and Majorana HNLs under the same scenario. (C) Same as (B) but at the reconstruction level.

Figure 17A shows the normalized distribution of lifetimes of Dirac and Majorana HNLs for representative masses and assuming |V_eN| = 10^–3. Systematically, the lifetimes for Dirac N are twice as large as for the Majorana case. For m_N = 20–70 GeV, the lifetimes are roughly $\tau \sim \mathcal{O}(10^{-11})-\mathcal{O}(10^{-15})$ s. As shown in Eqs 24, 25, the lifetime measurement can be used together with the total cross section to distinguish between the Dirac or Majorana nature of the observed HNL, because the combination of mixing angles that appears in both quantities is the same. For this to be done correctly, two more conditions must be met. First, the mass of the HNL must be known; this can be done by direct reconstruction, possibly combined with a kinematic fit if the HNL decays within the good quality tracker and calorimeter volumes. For longer lifetimes, a combination of decay length and laboratory decay time should be sufficient. Second, the event selection must have similar and well understood efficiencies for the three lepton flavors e, μ, τ, so that the differences can be corrected.

For the same scenario, Figure 17B shows the angular separation cos θ_ee of the e⁺e⁻ pair at the generator level. Here, several features can be observed. First, for small (large) m_N, the e⁺e⁻ pair are largely collimated (back-to-back). This behavior can be understood from the kinematics: a heavier N is produced with less three-momentum, leading to three-body decays that are more isotropically distributed, whereas a lighter N is produced with more energy, which leads to more collimated decay products. The second feature that can be observed is that differences between the Majorana channel (LNC + LNV) and the Dirac channel (LNC) can reach $\mathcal{O}(\pm 30\%)$. Differences are largest when the e⁺e⁻ pair are collimated (cos θ_ee ≈ 1) or back-to-back (cos θ_ee ≈ − 1), and are smallest when they are orthogonal (cos θ_ee ≈ 0).

Finally, Figure 17C shows the same angular separation at the reconstruction level. Again, several features can be observed. First is that reconstruction requirements markedly impact the cos θ_ee. In particular, isolation requirements significantly reduce cases where the e⁺e⁻ pair are collimated (cos θ_ee ≈ 1). Overall, the distribution for m_N = 50 GeV and m_N = 70 GeV become essentially indistinguishable. Moreover, differences between the Majorana channel (LNC + LNV) and the Dirac channel (LNC) can reduce to the $\mathcal{O}(\pm 20\%)$ level.

3.3 Axion-like particles

Figure 18 shows the generated ALP kinematics for m_ALP = 1 GeV and several benchmark choices of the hypercharge coupling c_YY. Figure 19 shows the generated ALP mass (m_ALP) and the invariant mass of the two-photon system (m_γγ), and Figure 20 shows the generated three-dimensional lifetime τ_xyz and decay length L_xyz for the ALP signal. These variables are useful in distinguishing the ALP signal from background, and also for different values of the ALP mass and couplings. In addition, calorimeter and precision timing variables will be extremely helpful to include in this study of ALPs that decay to photons. We leave these studies to a later date.

FIGURE 18

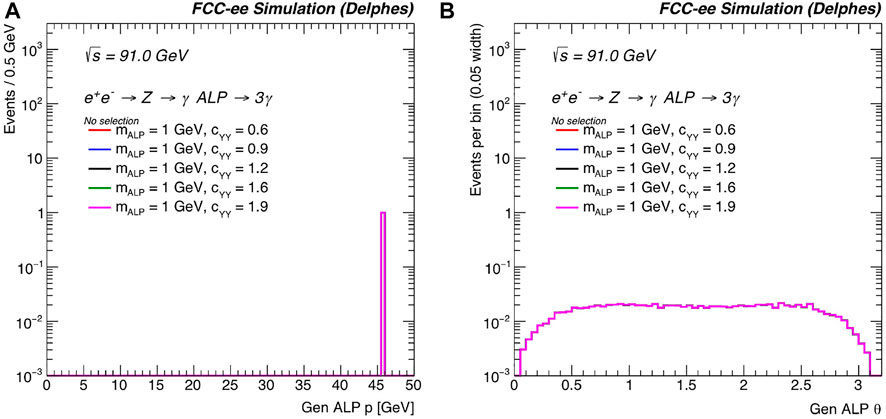
FIGURE 18. (A) Generated ALP momentum and (B) θ for m_ALP = 1 GeV and several benchmark choices of c_YY. The distributions are normalized to unit area.

FIGURE 19

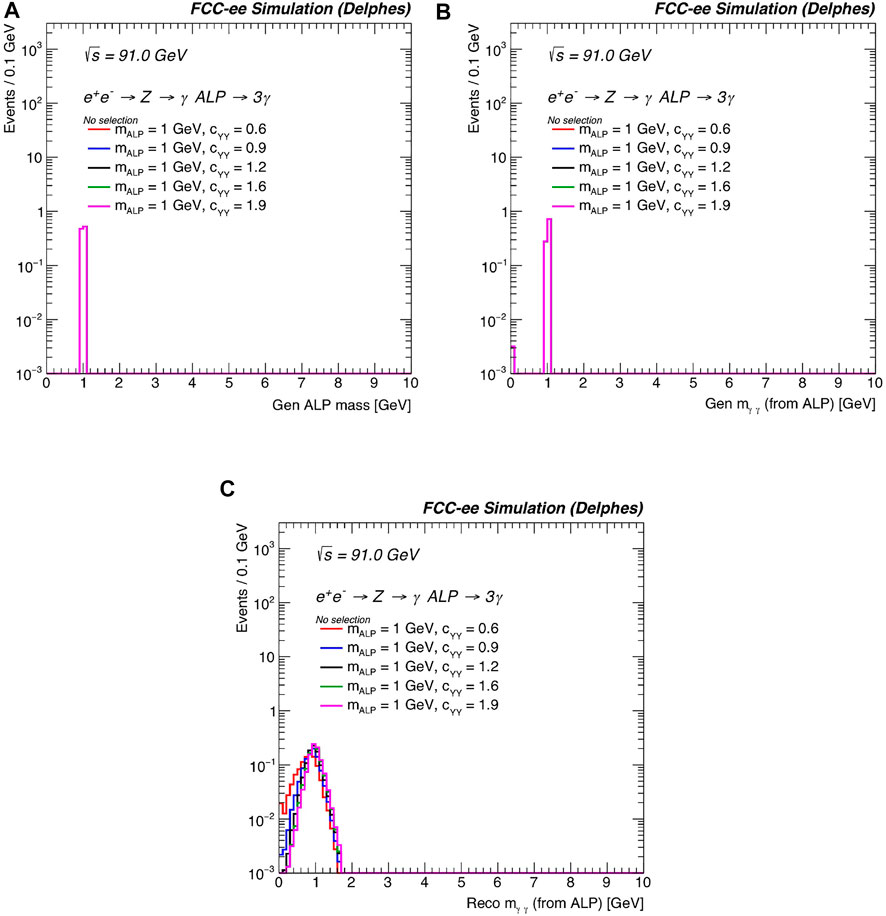
FIGURE 19. (A) Generated m_ALP, (B) generated m_γγ, and (C) reconstructed m_γγ for m_ALP = 1 GeV and several benchmark choices of c_YY. The distributions are normalized to unit area.

FIGURE 20

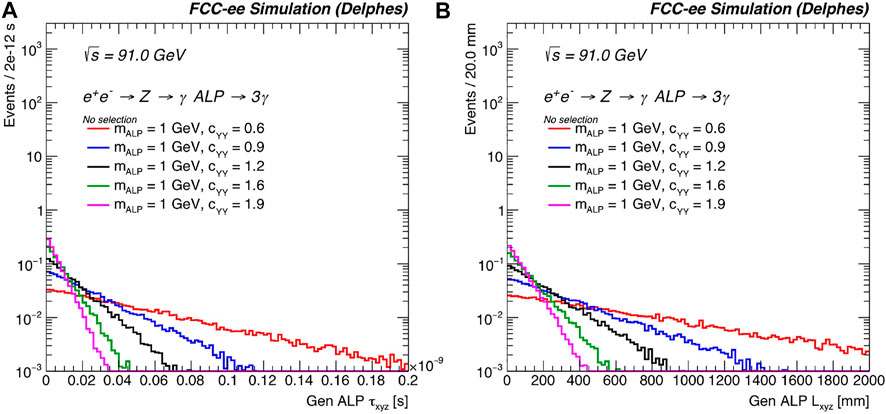
FIGURE 20. (A) Generated ALP τ_xyz and (B) L_xyz for m_ALP =1 GeV and several benchmark choices of c_YY. The distributions are normalized to unit area.

3.4 Exotic Higgs boson decays

Exotic decays of Higgs bosons to LLPs are also an interesting experimental case study at FCC-ee. As was pointed out in Section 2.3, hadronic final states play a significant role, and so we plan to simulate this physics benchmark in a future paper.

3.5 Additional detectors for long-lived particles

It is possible to envisage up to four FCC-ee detectors, two of which sitting in the very large caverns foreseen from the start for the subsequent hadron collider detectors. The caverns are foreseen to be deep (200–300 m) underground, considerably reducing the cosmic ray backgrounds. A detector fully optimized for this important discovery possibility can thus be considered [83, 110, 194].

4 Summary and conclusion

In this paper, we discuss three key BSM cases at the future FCC-ee that experimentally can display long-lived signatures: heavy neutral leptons, axion-like particles, and exotic Higgs boson decays. While FCC-ee is primarily envisioned as a precision collider, the discussed scenarios are examples of direct searches that could be performed and could answer central questions of particle physics.

The three cases are carefully discussed from a theoretical perspective, representing the state-of-the-art and current best expected limits. Simulation studies are then presented for HNLs and ALPs. These two BSM cases can present displaced signatures: a displaced vertex for the former, and a displaced photon pair in the latter.

Different HNL signals—as well as a limited collection of background processes—are generated, kinematic variables are explored, and a first possible set of requirements is presented to isolate the signal from the SM backgrounds. Possible kinematic variables that could characterize an HNL as Dirac or Majorana are also explored experimentally.

For ALPs, signals are generated and validated and some key distributions are presented.

The work presented here can be expanded into more detailed studies, such as also including exotic Higgs boson decays, additional HNL decay channels, larger simulated samples, the use of timing information, and alternative detector designs. The simulation work presented here represents the first step towards a comprehensive evaluation of the experimental potential of FCC-ee in direct searches for BSM. Possible limitations could be solved by innovative experimental solutions that could boost the reach of FCC-ee for other non-standard signals.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

Some of the contributions are stated in the paper itself. Others involve collaboration and cross-checks. Work produced for the master theses of LR and TS is included in the paper.

Funding

RS is supported by the Swedish Research Council (VR 2017-05092). SK is supported by the Austrian Science Fund Elise-Richter grant project number V592-N27. RR acknowledges the support of the Polska Akademia Nauk (grant agreement PAN.BFD.S.BDN. 613. 022. 2021—PASIFIC 1, POPSICLE). This work has received funding from the European Union’s Horizon 2020 research and innovation program under the Skłodowska-Curie grant agreement No. 847639 and from the Polish Ministry of Education and Science. AT was supported by the Australian Research Council through the ARC Discovery Project, DP210101900.

Acknowledgments

The authors would like to thank S. Petcov (SISSA/INFN) for the discussions during the writing of the paper and for providing comments to the draft.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Figure 8.19.

References

1. Alimena J, Beacham J, Borsato M, Cheng Y, Vidal X. C., Cottin G et al. Searching for long-lived particles beyond the standard model at the Large Hadron Collider. J Phys G (2020) 47:090501. 1903.04497.

Google Scholar

2. Group ES. Update of the European Strategy for particle physics (brochure). Tech Rep Cern-esu-015 (2020). CERN, Geneva. doi:10.17181/CERN.JSC6.W89E

CrossRef Full Text | Google Scholar

3. Benedikt M, Blondel A, Brunner O, Capeans Garrido M, Cerutti F, Gutleber J et al. FCC-ee: The lepton collider: Future circular collider conceptual design report volume 2. Future Circular Collider, Tech. Rep. CERN-ACC-2018-0057. 2, CERN, Geneva, 2018. doi:10.1140/epjst/e2019-900045-4

CrossRef Full Text | Google Scholar

4. Chrzaszcz M, Gonzalez Suarez R, Monteil S. Hunt for rare processes and long-lived particles at FCC-ee. Eur Phys J Plus (2021) 136(1056). [2106.15459]. doi:10.1140/epjp/s13360-021-01961-4

CrossRef Full Text | Google Scholar

5. Abdullahi AM, Alzas PB, Batell B, Boyarsky A, Carbajal S, Chatterjee A et al. The present and future status of heavy neutral leptons. Snowmass Summer Study (2022) 3:08039. 2203.,

Google Scholar

6.Super-Kamiokande collaboration, Fukuda Y, Havakawa T, Ichihara I, Inoue K, Ishihara K, Ishino H et al. Evidence for oscillation of atmospheric neutrinos. Phys Rev Lett (1998) 81:1562–7. [hep-ex/9807003].

Google Scholar

7.SNO collaboration, Ahmad QR, Allen RC, Andersen TC, D Anglin J, Barton JC, Beier EW et al. Direct evidence for neutrino flavor transformation from neutral current interactions in the Sudbury Neutrino Observatory. Phys Rev Lett (2002) 89:011301. [nucl-ex/0204008]. doi:10.1103/PhysRevLett.89.011301

PubMed Abstract | CrossRef Full Text | Google Scholar

8. Feruglio F. Pieces of the flavour puzzle. Eur Phys J C (2015) 75373. [1503.04071]. doi:10.1140/epjc/s10052-015-3576-5

CrossRef Full Text | Google Scholar

9. Ma E. Pathways to naturally small neutrino masses. Phys Rev Lett (1998) 81:1171–4. [hep-ph/9805219]. doi:10.1103/physrevlett.81.1171

CrossRef Full Text | Google Scholar

10. Agrawal P, Bauer M, Beacham J, Berlin A, Boyarsky A, Cebrian S et al. Feebly-interacting particles: FIPs 2020 workshop report. Eur Phys J C (2021) 81:1015. [2102.12143]. doi:10.1140/epjc/s10052-021-09703-7

CrossRef Full Text | Google Scholar

11. Minkowski P. μ → eγ at a Rate of one Out of 10⁹muon decays? Phys Lett B (1977) 67:421–8. doi:10.1016/0370-2693(77)90435-x

CrossRef Full Text | Google Scholar

12. Glashow SL. The future of elementary particle physics. NATO Sci Ser B (1980) 61:687.

CrossRef Full Text | Google Scholar

13. Gell-Mann M, Ramond P, Slansky R. Complex spinors and unified theories. Conf Proc C (1979) 790927:315–21. [1306.4669].

Google Scholar

14. Mohapatra RN, Senjanovic G. Neutrino mass and spontaneous parity nonconservation. Phys Rev Lett (1980) 44:912–5. doi:10.1103/physrevlett.44.912

CrossRef Full Text | Google Scholar

15. Yanagida T. Horizontal symmetry and masses of neutrinos. Prog Theor Phys (1980) 64:1103–5. doi:10.1143/ptp.64.1103

CrossRef Full Text | Google Scholar

16. Schechter J, Valle JWF. Neutrino masses in SU(2) ⊗ U(1) theories. Phys Rev D (1980) 22:2227–35. doi:10.1103/physrevd.22.2227

CrossRef Full Text | Google Scholar

17. Shrock RE. General theory of weak processes involving neutrinos. I. Leptonic pseudoscalar-meson decays, with associated tests for, and bounds on, neutrino masses and lepton mixing. Phys Rev D (1981) 24:1232–74. doi:10.1103/physrevd.24.1232

CrossRef Full Text | Google Scholar

18. Konetschny W, Kummer W. Nonconservation of total lepton number with scalar bosons. Phys Lett B (1977) 70:433–5. doi:10.1016/0370-2693(77)90407-5

CrossRef Full Text | Google Scholar

19. Magg M, Wetterich C. Neutrino mass problem and gauge hierarchy. Phys Lett B (1980) 94:61–4. doi:10.1016/0370-2693(80)90825-4

CrossRef Full Text | Google Scholar

20. Cheng TP, Li L-F. Neutrino masses, mixings, and oscillations in SU(2)×U(1) models of electroweak interactions. Phys Rev D (1980) 22:2860–8. doi:10.1103/physrevd.22.2860

CrossRef Full Text | Google Scholar

21. Lazarides G, Shafi Q, Wetterich C. Proton lifetime and fermion masses in an SO(10) model. Nucl Phys B (1981) 181:287–300. doi:10.1016/0550-3213(81)90354-0

CrossRef Full Text | Google Scholar

22. Mohapatra RN, Senjanovic G. Neutrino masses and mixings in gauge models with spontaneous parity violation. Phys Rev D (1981) 23:165–80. doi:10.1103/physrevd.23.165

CrossRef Full Text | Google Scholar

23. Foot R, Lew H, He XG, Joshi GC. Seesaw neutrino masses induced by a triplet of leptons. Z Phys C - Particles Fields (1989) 44:441–4. doi:10.1007/bf01415558

CrossRef Full Text | Google Scholar

24. Atre A, Han T, Pascoli S, Zhang B. The search for heavy Majorana neutrinos. JHEP (2009) 05030. 0901.3589.

CrossRef Full Text | Google Scholar

25. Deppisch FF, Bhupal Dev PS, Pilaftsis A. Neutrinos and collider physics. New J Phys (2015) 17:075019. [1502.06541]. doi:10.1088/1367-2630/17/7/075019

CrossRef Full Text | Google Scholar

26. Cai Y, Han T, Li T, Ruiz R. Lepton number violation: Seesaw models and their collider tests. Front Phys (2018) 6:40. [1711.02180]. doi:10.3389/fphy.2018.00040

CrossRef Full Text | Google Scholar

27. Bolton PD, Deppisch FF, Bhupal Dev PS. Neutrinoless double beta decay versus other probes of heavy sterile neutrinos. JHEP (2020) 03170. 1912.03058.

CrossRef Full Text | Google Scholar

28. Wolfenstein L. Different varieties of massive Dirac neutrinos. Nucl Phys B (1981) B186:147–52. doi:10.1016/0550-3213(81)90096-1

CrossRef Full Text | Google Scholar

29. Petcov ST. On pseudo-Dirac neutrinos, neutrino Oscillations and neutrinoless double β-decay. Phys Lett B (1982) 110B:245–9. doi:10.1016/0370-2693(82)91246-1

CrossRef Full Text | Google Scholar

30. Shaposhnikov M. A possible symmetry of the. Nucl Phys B (2007) 763:49–59. [hep-ph/0605047]. doi:10.1016/j.nuclphysb.2006.11.003

CrossRef Full Text | Google Scholar

31. Kersten J, Smirnov AY. Right-handed neutrinos at CERN LHC and the mechanism of neutrino mass generation. Phys Rev D (2007) 76:073005. [0705.3221]. doi:10.1103/physrevd.76.073005

CrossRef Full Text | Google Scholar

32. Ibarra A, Molinaro E, Petcov ST. TeV scale see-saw Mechanisms of neutrino mass generation, the Majorana Nature of the heavy singlet Neutrinos and (ββ)_0ν-Decay. JHEP (2010) 09108. [1007.2378].

CrossRef Full Text | Google Scholar

33. Moffat K, Pascoli S, Weiland C, (2017) Equivalence between massless neutrinos and lepton number conservation in fermionic singlet extensions of the Standard Model, 1712.07611.

Google Scholar

34. Anamiati G, Hirsch M, Nardi E. Quasi-Dirac neutrinos at the LHC. JHEP (2016) 10010. [1607.05641].

CrossRef Full Text | Google Scholar

35. Tsai Y-S. Decay Correlations of Heavy Leptons in e+ e- —> Lepton+ Lepton-. Phys Rev D (1971) 4:2821.

Google Scholar

36. Gronau M, Leung CN, Rosner JL. Extending limits on neutral heavy leptons. Phys Rev D (1984) 29:2539–58. doi:10.1103/physrevd.29.2539

CrossRef Full Text | Google Scholar

37. Petcov ST. Possible signature for production of Majorana particles in e⁺e⁻ and p-p¯collisions Collisions. Phys Lett B (1984) B 139:421–6. doi:10.1016/0370-2693(84)91844-6

CrossRef Full Text | Google Scholar

38. Dittmar M, Santamaria A, Gonzalez-Garcia MC, Valle JWF. Production Mechanisms and Signatures of isosinglet neutral heavy Leptons in Z⁰decays. Nucl Phys B (1990) 332:1–19. doi:10.1016/0550-3213(90)90028-c

CrossRef Full Text | Google Scholar

39.FCC-ee study Team collaboration, Blondel A, Graverini E, Serra N, Shaposhnikov M. Search for heavy right handed neutrinos at the FCC-ee. Nucl Part Phys Proc (2016) 1883–90. [1411.5230]. doi:10.1016/j.nuclphysbps.2015.09.304

CrossRef Full Text | Google Scholar

40. Duarte L, Peressutti J, Sampayo OA. Majorana neutrino decay in an effective approach. Phys Rev D (2015) 92:093002. [1508.01588]. doi:10.1103/physrevd.92.093002

CrossRef Full Text | Google Scholar

41. Banerjee S, Dev PSB, Ibarra A, Mandal T, Mitra M. Prospects of heavy neutrino searches at future lepton colliders. Phys Rev D (2015) 92:075002. doi:10.1103/physrevd.92.075002

CrossRef Full Text | Google Scholar

42. Duarte L, Romero I, Peressutti J, Sampayo OA. Effective Majorana neutrino decay. Eur Phys J C (2016) 76453. [1603.08052]. doi:10.1140/epjc/s10052-016-4301-8

CrossRef Full Text | Google Scholar

43. Antusch S, Cazzato E, Fischer O. Displaced vertex searches for sterile neutrinos at future lepton colliders. JHEP (2016) 12:007. [1604.02420].

CrossRef Full Text | Google Scholar

44. Antusch S, Cazzato E, Drewes M, Fischer O, Garbrecht B, Gueter D et al. Probing leptogenesis at future colliders. JHEP (2018) 09:124. [1710.03744].

CrossRef Full Text | Google Scholar

45. Duarte L, Zapata G, Sampayo OA. Final taus and initial state polarization signatures from effective interactions of Majorana neutrinos at future e⁺e⁻colliders. Eur Phys J C (2019) 79240. [1812.01154].

Google Scholar

46. Ding J-N, Qin Q, Yu F-S. Heavy neutrino searches at future Z-factories. Eur Phys J C (2019) 79:766. 1903.766. doi:10.1140/epjc/s10052-019-7277-3

CrossRef Full Text | Google Scholar

47. Barducci D, Bertuzzo E, Caputo A, Hernandez P, Mele B. The see-saw portal at future Higgs Factories. JHEP (2021) 03:117. 2011.04725.

CrossRef Full Text | Google Scholar

48. Blondel A, de Gouvêa A, Kayser B. Z-boson decays into Majorana or Dirac heavy neutrinos. Phys Rev D (2021) 104:055027. [2105.06576]. doi:10.1103/physrevd.104.055027

CrossRef Full Text | Google Scholar

49. Zapata G, Urruzola T, Sampayo OA, Duarte L. Lepton collider probes for Majorana neutrino effective interactions. Eur Phys J C (2022) 82(544). [2201.02480]. doi:10.1140/epjc/s10052-022-10448-0

CrossRef Full Text | Google Scholar

50. Shen Y-F, Ding J-N, Qin Q. Monojet search for heavy neutrinos at future Z-factories. Eur Phys J C (2022) 82:398. [2201.05831]. doi:10.1140/epjc/s10052-022-10301-4

CrossRef Full Text | Google Scholar

51. Barducci D, Bertuzzo E. The see-saw portal at future Higgs factories: The role of dimension six operators. JHEP (2022) 06:077. [2201.11754].

CrossRef Full Text | Google Scholar

52. Pati JC, Salam A. Lepton number as the fourth color. Phys Rev D (1974) 10:275–89. doi:10.1103/physrevd.10.275

CrossRef Full Text | Google Scholar

53. Mohapatra RN, Pati JC. Left-right gauge symmetry and an isoconjugate model ofCPviolation. Phys Rev D (1975) 11:566–71. doi:10.1103/physrevd.11.566

CrossRef Full Text | Google Scholar

54. Mohapatra RN, Pati JC. Natural left-right symmetry. Phys Rev D (1975) 11:2558–61. doi:10.1103/physrevd.11.2558

CrossRef Full Text | Google Scholar

55. Senjanovic G, Mohapatra RN. Exact left-right symmetry and spontaneous violation of parity. Phys Rev D (1975) 12:1502–5. doi:10.1103/physrevd.12.1502

CrossRef Full Text | Google Scholar

56. Senjanovic G. Spontaneous breakdown of parity in a class of gauge theories. Nucl Phys B (1979) 153:334–64. doi:10.1016/0550-3213(79)90604-7

CrossRef Full Text | Google Scholar

57. Langacker P. Grand unified theories and proton decay. Phys Rep (1981) 72:185–385. doi:10.1016/0370-1573(81)90059-4

CrossRef Full Text | Google Scholar

58. Hewett JL, Rizzo TG. Low-energy phenomenology of superstring inspired E(6) models. Phys Rep (1989) 183:193–381. doi:10.1016/0370-1573(89)90071-9

CrossRef Full Text | Google Scholar

59. Faraggi AE, Nanopoulos DV. A SUPERSTRING Z′ AT O (1-TeV) ? Mod Phys Lett A (1991) 6:61–8. doi:10.1142/s0217732391002621

CrossRef Full Text | Google Scholar

60. Buchmuller W, Greub C, Minkowski P. Neutrino masses, neutral vector bosons and the scale of B-L breaking. Phys Lett B (1991) 267:395–9. doi:10.1016/0370-2693(91)90952-m

CrossRef Full Text | Google Scholar

61. Grzadkowski B, Iskrzynski M, Misiak M, Rosiek J. Dimension-Six terms in the standard model Lagrangian. JHEP (2010) 10:085. [1008.4884.

CrossRef Full Text | Google Scholar

62. Brivio I, Trott M. The standard model as an effective field theory. Phys Rep (2019) 793:1–98. [1706.08945]. doi:10.1016/j.physrep.2018.11.002

CrossRef Full Text | Google Scholar

63. Gauld R, Pecjak BD, Scott DJ. One-loop corrections to h\to b\bar{b} and h\to \tau\bar \tau decays in the standard model dimension-6 EFT: Four-fermion operators and the large-m_tlimit. J High Energ Phys (2016) 05:080. [1512.02508]. doi:10.1007/jhep05(2016)080

CrossRef Full Text | Google Scholar

64. del Aguila F, Bar-Shalom S, Soni A, Wudka J. Heavy Majorana neutrinos in the effective Lagrangian description: Application to hadron colliders. Phys Lett B (2009) 670:399–402. [0806.0876]. doi:10.1016/j.physletb.2008.11.031

CrossRef Full Text | Google Scholar

65. Aparici A, Kim K, Santamaria A, Wudka J. Right-handed neutrino magnetic moments. Phys Rev D (2009) 80:013010. [0904.3244]. doi:10.1103/physrevd.80.013010

CrossRef Full Text | Google Scholar

66. Elgaard-Clausen G, Trott M. On expansions in neutrino effective field theory. JHEP (2017) 11(088). [1703.04415.

CrossRef Full Text | Google Scholar

67. Hernández P, Kekic M, López-Pavón J, Racker J, Salvado J. Testable baryogenesis in seesaw models. JHEP (2016) 08157. [1606.06719].

Google Scholar

68. Drewes M, Garbrecht B, Gueter D, Klaric J. Testing the low scale seesaw and leptogenesis. JHEP (2017) 08:018. 1609.09069.

CrossRef Full Text | Google Scholar

69. Drewes M, Hajer J, Klaric J, Lanfranchi G. NA62 sensitivity to heavy neutral leptons in the low scale seesaw model. JHEP (2018) 07(105). 1801.04207.

CrossRef Full Text | Google Scholar

70. Chrzaszcz M, Drewes M, Gonzalo TE, Harz J, Krishnamurthy S, Weniger C. A frequentist analysis of three right-handed neutrinos with GAMBIT. Eur Phys J C (2020) 80(569). 1908.569. doi:10.1140/epjc/s10052-020-8073-9

PubMed Abstract | CrossRef Full Text | Google Scholar

71.DUNE collaboration, Abi B, Acciarri R, Acero MA, Adamov G, Adams D, Adinolfi M et al. Deep underground neutrino experiment (DUNE), far detector technical design report, volume II: DUNE physics, 2002.03005.

Google Scholar

72. Caputo A, Hernandez P, Kekic M, López-Pavón J, Salvado J. The seesaw path to leptonic CP violation. Eur Phys J C (2017) 77(258). [1611.05000]. doi:10.1140/epjc/s10052-017-4823-8

CrossRef Full Text | Google Scholar

73. King SF, Luhn C. Neutrino mass and mixing with discrete symmetry. Rep Prog Phys (2013) 76:056201. [1301.1340]. doi:10.1088/0034-4885/76/5/056201

PubMed Abstract | CrossRef Full Text | Google Scholar

74. Feruglio F, Romanino A. Lepton flavor symmetries. Rev Mod Phys (2021) 93:015007. 1912.06028. doi:10.1103/revmodphys.93.015007

CrossRef Full Text | Google Scholar

75. Xing Z-z. Flavor structures of charged fermions and massive neutrinos. Phys Rep (2020) 854:1–147. 1909. doi:10.1016/j.physrep.2020.02.001

CrossRef Full Text | Google Scholar

76. Caputo A, Hernandez P, Lopez-Pavon J, Salvado J. The seesaw portal in testable models of neutrino masses. JHEP (2017) 06112. 1704.08721.

CrossRef Full Text | Google Scholar

77. Esteban I, Gonzalez-Garcia M, Maltoni M, Schwetz T, Zhou A, et al. The fate of hints: Updated global analysis of three-flavor neutrino oscillations. JHEP (2020) 09:178. 2007.14792.

CrossRef Full Text | Google Scholar

78.DUNE collaboration, Abi B, Acciarri R, Acero MA, Adamov G, Adams D, Adinolfi M et al. Long-baseline neutrino oscillation physics potential of the DUNE experiment. Eur Phys J C (2020) 80(978). 2006.16043.

PubMed Abstract | Google Scholar

79. Antusch S, Cazzato E, Fischer O. Sterile neutrino searches at future e⁻e⁺, pp, and e⁻p colliders. Int J Mod Phys A (2017) 32:1750078. [1612.02728]. doi:10.1142/s0217751x17500786

CrossRef Full Text | Google Scholar

80. Ellis RK, Physics briefing Book: Input for the European Strategy for particle physics update 2020, 1910.11775.

Google Scholar

81. Lou XL, Circular electron-positron collider status and progress (presented at the hkust-ias conference on high energy physics 2022), 2022.

Google Scholar

82.CEPC Study Group collaboration, Dong M. CEPC conceptual design report: Volume 2. Phys Detector (2018) 1811:10545.

Google Scholar

83. Chrząszcz M, Drewes M, Hajer J. Hecate: A long-lived particle detector concept for the FCC-ee or CEPC. Eur Phys J C (2021) 81:546. 2011.01005. doi:10.1140/epjc/s10052-021-09253-y

CrossRef Full Text | Google Scholar

84.CHARM collaboration, Dorenbosch J, Allaby JV, Amaldi U, Barbiellini G, Berger C, Bergsma F et al., A search for decays of heavy neutrinos in the mass range 0.5-GeV to 2.8-GeV. Phys Lett B (1986) 166:473–8.

Google Scholar

85. Abela R, Daum M, Eaton GH, Frosch R, Jost B, Kettle PR et al. Search for an admixture of heavy neutrino states in pion decay. Phys Lett B (1981) 105:263–6. doi:10.1016/0370-2693(81)90884-4

CrossRef Full Text | Google Scholar

86. Yamazaki T. Search for heavy neutrinos in kaon decay. Conf Proc C (1984) 840719:262.

Google Scholar

87.E949 collaboration, Artamonov AV. Search for heavy neutrinos in K⁺ → μ⁺ν_Hdecays. Phys Rev D (2015) 91:052001. [1411.3963].

CrossRef Full Text | Google Scholar

88. Bernardi G, Carugno G, Chauveau J, Dicarlo F, Dris M, Dumarchez J et al. Further limits on heavy neutrino couplings. Phys Lett B (1988) 203:332–4. doi:10.1016/0370-2693(88)90563-1

CrossRef Full Text | Google Scholar

89.NuTeV, E815 collaboration, Vaitaitis A, Drucker RB, Formaggio J, Koutsoliotas S, Adams T, Alton A et al. Search for neutral heavy leptons in a high-energy neutrino beam. Phys Rev Lett (1999) 83:4943–6. [hep-ex/9908011]. doi:10.1103/physrevlett.83.4943

CrossRef Full Text | Google Scholar

90. Vaitaitis AG. Search for neutral heavy leptons in a high-energy neutrino beam. PhD thesis. New York, NY: Columbia University (2000). doi:10.2172/1421441

CrossRef Full Text | Google Scholar

91.CMS collaboration, Sirunyan AM. Search for heavy neutral leptons in events with three charged leptons in proton-proton collisions at $\sqrt{s}=13$ TeV. Phys Rev Lett (2018) 120:221801. 1802.02965.

PubMed Abstract | Google Scholar

92.DELPHI collaboration, Abreu P. Search for neutral heavy leptons produced in Z decays. Z. Phys. C. (1997) 74:57–71. doi:10.1007/s002880050370

CrossRef Full Text | Google Scholar

93.ATLAS collaboration, Aad G. Search for heavy neutral leptons in decays of W bosons produced in 13 TeV pp collisions using prompt and displaced signatures with the ATLAS detector. JHEP (2019) 10:265. 1905.09787.

Google Scholar

94.CMS collaboration, Tumasyan A. Search for long-lived heavy neutral leptons with displaced vertices in proton-proton collisions at $\sqrt{s}=13$. TeV (2022) 2201:05578.

Google Scholar

95. Izaguirre E, Shuve B. Multilepton and lepton jet probes of sub-weak-scale right-handed neutrinos. Phys Rev D (2015) 91:093010. [1504.02470]. doi:10.1103/physrevd.91.093010

CrossRef Full Text | Google Scholar

96. Drewes M, Hajer J. Heavy Neutrinos in displaced vertex searches at the LHC and HL-LHC. JHEP (2020) 02:070. 1903.06100.

CrossRef Full Text | Google Scholar

97. Pascoli S, Ruiz R, Weiland C. Heavy neutrinos with dynamic jet vetoes: Multilepton searches at $\sqrt{s}=14$, 27, and 100 TeV. JHEP (2019) 06:049. 1812.08750.

Google Scholar

98. Ballett P, Boschi T, Pascoli S. Heavy neutral leptons from low-scale seesaws at the DUNE near detector. JHEP (2020) 03:111. 1905.00284.

CrossRef Full Text | Google Scholar

99.FASER collaboration, Ariga A, Ariga T, Boyd J, Cadoux F, Casper DW, Favre Y et al. FASER’s physics reach for long-lived particles. Phys Rev D (2019) 99:095011. [1811.12522]. doi:10.1103/physrevd.99.095011

CrossRef Full Text | Google Scholar

100.SHiP collaboration, Ahdida C, Albanese R, Alexandrov A, Anokhina A, Aoki S, Arduini G et al. Sensitivity of the SHiP experiment to heavy neutral leptons. JHEP (2019) 04:077. [1811.00930].

Google Scholar

101. Gorbunov D, Krasnov I, Kudenko Y, Suvorov S. Heavy Neutral Leptons from kaon decays in the SHiP experiment. Phys Lett B (2020) 810:135817. 2004.07974. doi:10.1016/j.physletb.2020.135817

CrossRef Full Text | Google Scholar

102. Curtin D, Drewes M, McCullough M, Meade P, Mohapatra RN, Shelton J et al. Long-lived particles at the energy frontier: The MATHUSLA physics case. Rep Prog Phys (2019) 82:116201. 1806.07396. doi:10.1088/1361-6633/ab28d6

PubMed Abstract | CrossRef Full Text | Google Scholar

103. Aielli G, Ben-Haim E, Cardarelli R, Charles MJ, Cid Vidal X, Coco V et al. Expression of interest for the CODEX-b detector. Eur Phys J C (2020) 801177. [1911.00481]. doi:10.1140/epjc/s10052-020-08711-3

CrossRef Full Text | Google Scholar

104. Bay Nielsen S. Prospects of sterile neutrino search with the FCC-ee. Master’s thesis. Copenhagen U. (2017).

Google Scholar

105. Antusch S, Cazzato E, Fischer O, Hammad A, Wang K. Lepton flavor violating dilepton dijet signatures from sterile neutrinos at proton colliders. JHEP (2018) 10067. 1805.11400.

CrossRef Full Text | Google Scholar

106. Boyarsky A, Mikulenko O, Ovchynnikov M, Shchutska L, Exploring the potential of FCC-hh to search for particles from B mesons, 2022, 2204.01622.

Google Scholar

107. Mękała K, Reuter J, Żarnecki AF. Heavy neutrinos at future linear e⁺e⁻colliders. JHEP (2022) 06:010. 2202.06703.

Google Scholar

108. Antusch S, Fischer O, Hammad A. Lepton-trijet and displaced vertex searches for heavy neutrinos at future electron-proton colliders. JHEP (2020) 03110. 1908.02852.

CrossRef Full Text | Google Scholar

109. Li P, Liu Z, Lyu F-F. progress.Heavy neutral leptons at muon colliders.

Google Scholar

110. Wang ZS, Wang K. Physics with far detectors at future lepton colliders. Phys Rev D (2020) 101:075046. [1911.06576]. doi:10.1103/physrevd.101.075046

CrossRef Full Text | Google Scholar

111. Giffin P, Gori S, Tsai Y-D, Tuckler D, Heavy neutral leptons at beam dump experiments of future lepton colliders, 2022, 2206.13745.

Google Scholar

112. Canetti L, Drewes M, Shaposhnikov M. Matter and antimatter in the universe. New J Phys (2012) 14:095012. [1204.4186]. doi:10.1088/1367-2630/14/9/095012

CrossRef Full Text | Google Scholar

113. Akhmedov EK, Rubakov VA, Smirnov AY. Baryogenesis via neutrino oscillations. Phys Rev Lett (1998) 81:1359–62. [hep-ph/9803255]. doi:10.1103/physrevlett.81.1359

CrossRef Full Text | Google Scholar

114. Asaka T, Shaposhnikov M. The νMSM, dark matter and baryon asymmetry of the universe. Phys Lett B (2005) 620:17–26. [hep-ph/0505013]. doi:10.1016/j.physletb.2005.06.020

CrossRef Full Text | Google Scholar

115. Pilaftsis A, Underwood TEJ. Resonant leptogenesis. Nucl Phys B (2004) 692:303–45. [hep-ph/0309342]. doi:10.1016/j.nuclphysb.2004.05.029

CrossRef Full Text | Google Scholar

116. Drewes M, Georis Y, Klarić J. Mapping the viable parameter space for testable leptogenesis. Phys Rev Lett (2022) 128:051801. [2106.16226]. doi:10.1103/physrevlett.128.051801

PubMed Abstract | CrossRef Full Text | Google Scholar

117. Klarić J, Shaposhnikov M, Timiryasov I. Reconciling resonant leptogenesis and baryogenesis via neutrino oscillations. Phys Rev D (2021) 104:055010. [2103.16545]. doi:10.1103/physrevd.104.055010

CrossRef Full Text | Google Scholar

118. Sabti N, Magalich A, Filimonova A. An extended analysis of heavy neutral leptons during big bang nucleosynthesis. JCAP (2020) 11(056). 2006.07387.

CrossRef Full Text | Google Scholar

119. Boyarsky A, Ovchynnikov M, Ruchayskiy O, Syvolap V. Improved big bang nucleosynthesis constraints on heavy neutral leptons. Phys Rev D (2021) 104:023517. 2008.00749. doi:10.1103/physrevd.104.023517

CrossRef Full Text | Google Scholar

120. Schechter J, Valle JWF. Neutrinoless double-βdecay in SU(2)×U(1) theories. Phys Rev D (1982) 25:2951–4. doi:10.1103/physrevd.25.2951

CrossRef Full Text | Google Scholar

121. Hirsch M, Kovalenko S, Schmidt I. Extended black box theorem for lepton number and flavor violating processes. Phys Lett B (2006) 642:106–10. [hep-ph/0608207]. doi:10.1016/j.physletb.2006.09.012

CrossRef Full Text | Google Scholar

122. Duerr M, Lindner M, Merle A. On the quantitative impact of the schechter-valle theorem. JHEP (2011) 06091. [1105.0901].

CrossRef Full Text | Google Scholar

123. Bray S, Lee JS, Pilaftsis A. Resonant CP violation due to heavy neutrinos at the LHC. Nucl Phys B (2007) 786:95–118. [hep-ph/0702294]. doi:10.1016/j.nuclphysb.2007.07.002

CrossRef Full Text | Google Scholar

124. Ruiz R. Quantitative study on helicity inversion in Majorana neutrino decays at the LHC. Phys Rev D (2021) 103:015022. 2008.01092. doi:10.1103/physrevd.103.015022

CrossRef Full Text | Google Scholar

125. de Gouvêa A, Fox PJ, Kayser BJ, Kelly KJ. Three-body decays of heavy Dirac and Majorana fermions. Phys Rev D (2021) 104:015038. [2104.05719]. doi:10.1103/physrevd.104.015038

CrossRef Full Text | Google Scholar

126. Hernández P, Jones-Pérez J, Suarez-Navarro O. Majorana vs pseudo-Dirac neutrinos at the ILC. Eur Phys J C (2019) 79220. [1810.07210]. doi:10.1140/epjc/s10052-019-6728-1

CrossRef Full Text | Google Scholar

127. Asaka T, Blanchet S, Shaposhnikov M. The νMSM, dark matter and neutrino masses. Phys Lett B (2005) 631:151–6. [hep-ph/0503065]. doi:10.1016/j.physletb.2005.09.070

CrossRef Full Text | Google Scholar

128. Drewes M. The phenomenology of right handed neutrinos. Int J Mod Phys E (2013) 22:1330019. [1303.6912]. doi:10.1142/s0218301313300191

CrossRef Full Text | Google Scholar

129. Fukugita M, Yanagida T. Barygenesis without grand unification. Phys Lett B (1986) 174:45–7. doi:10.1016/0370-2693(86)91126-3

CrossRef Full Text | Google Scholar

130. Davidson S, Ibarra A. A Lower bound on the right-handed neutrino mass from leptogenesis. Phys Lett B (2002) 535(25–32):25–32. [hep-ph/0202239]. doi:10.1016/s0370-2693(02)01735-5

CrossRef Full Text | Google Scholar

131. Pilaftsis A, Underwood TEJ. Electroweak-scale resonant leptogenesis. Phys Rev D (2005) 72:113001. [hep-ph/0506107]. doi:10.1103/physrevd.72.113001

CrossRef Full Text | Google Scholar

132. Chun EJ, Cvetic G, Dev PSB, Drewes M, Fong CS, Garbrecht B et al. Probing leptogenesis. Int J Mod Phys A (2018) 33(1842005). [1711.02865]. doi:10.1142/s0217751x18420058

CrossRef Full Text | Google Scholar

133. Dodelson S, Widrow LM. Sterile-neutrinos as dark matter. Phys Rev Lett (1994) 72:17–20. [hep-ph/9303287]. doi:10.1103/physrevlett.72.17

PubMed Abstract | CrossRef Full Text | Google Scholar

134. Drewes M, Adhikari R, Agostini M, Anh Ky N, Araki T, Archidiacono M et al. A white paper on keV sterile neutrino dark matter. JCAP (2017) 01:025. 1602.04816.

Google Scholar

135. Boyarsky A, Drewes M, Lasserre T, Mertens S, Ruchayskiy O. Sterile neutrino dark matter. Prog Part Nucl Phys (2019) 104:1–45. [1807.07938. doi:10.1016/j.ppnp.2018.07.004

CrossRef Full Text | Google Scholar

136. Shi X-D, Fuller GM. New dark matter candidate: Nonthermal sterile neutrinos. Phys Rev Lett (1999) 82:2832–5. [astro-ph/9810076]. doi:10.1103/physrevlett.82.2832

CrossRef Full Text | Google Scholar

137. Laine M, Shaposhnikov M. Sterile neutrino dark matter as a consequence of nuMSM-induced lepton asymmetry. JCAP (2008) 06(031). 0804.4543.

Google Scholar

138. Ghiglieri J, Laine M. Improved determination of sterile neutrino dark matter spectrum. JHEP (2015) 11171. [1506.06752].

CrossRef Full Text | Google Scholar

139. Venumadhav T, Cyr-Racine F-Y, Abazajian KN, Hirata CM. Sterile neutrino dark matter: Weak interactions in the strong coupling epoch. Phys Rev D (2016) 94:043515. [1507.06655]. doi:10.1103/physrevd.94.043515

CrossRef Full Text | Google Scholar

140. Shaposhnikov M. The nuMSM, leptonic asymmetries, and properties of singlet fermions. JHEP (2008) 08008. 0804.4542.

Google Scholar

141. Canetti L, Drewes M, Shaposhnikov M. Sterile neutrinos as the origin of dark and baryonic matter. Phys Rev Lett (2013) 110:061801. [1204.3902]. doi:10.1103/physrevlett.110.061801

PubMed Abstract | CrossRef Full Text | Google Scholar

142. Canetti L, Drewes M, Frossard T, Shaposhnikov M. Dark matter, baryogenesis and neutrino oscillations from right handed neutrinos. Phys Rev D (2013) 87:093006. [1208.4607]. doi:10.1103/physrevd.87.093006

CrossRef Full Text | Google Scholar

143. Ghiglieri J, Laine M. Sterile neutrino dark matter via coinciding resonances. JCAP (2020) 07(012). 2004.10766.

CrossRef Full Text | Google Scholar

144. Kusenko A, Takahashi F, Yanagida TT. Dark matter from split seesaw. Phys Lett B (2010) 693:144–8. [1006.1731]. doi:10.1016/j.physletb.2010.08.031

CrossRef Full Text | Google Scholar

145. Li T, Chao W. Neutrino masses, dark matter and symmetry at the LHC. Nucl Phys B (2011) 843:396–412. [1004.0296]. doi:10.1016/j.nuclphysb.2010.10.004

CrossRef Full Text | Google Scholar

146. Escudero M, Rius N, Sanz V. Sterile neutrino portal to Dark Matter I: The U(1)_B−Lcase. JHEP (2017) 02:045. 1606.01258.

Google Scholar

147. Bezrukov F, Hettmansperger H, Lindner M. keV sterile neutrino Dark Matter in gauge extensions of the Standard Model. Phys Rev D (2010) 81:085032. [0912.4415]. doi:10.1103/physrevd.81.085032

CrossRef Full Text | Google Scholar

148. Bezrukov F, Kartavtsev A, Lindner M. Leptogenesis in models with keV sterile neutrino dark matter. J Phys G: Nucl Part Phys (2013) 40:095202. [1204.5477]. doi:10.1088/0954-3899/40/9/095202

CrossRef Full Text | Google Scholar

149. Nemevsek M, Senjanovic G, Zhang Y. Warm dark matter in low scale left-right theory. JCAP (2012) 07:006. 1205.0844.

Google Scholar

150. Shaposhnikov M, Tkachev I. The νMSM, inflation, and dark matter. Phys Lett B (2006) 639:414–7. [hep-ph/0604236]. doi:10.1016/j.physletb.2006.06.063

CrossRef Full Text | Google Scholar

151. Petraki K, Kusenko A. Dark-matter sterile neutrinos in models with a gauge singlet in the Higgs sector. Phys Rev D (2008) 77:065014. [0711.4646]. doi:10.1103/physrevd.77.065014

CrossRef Full Text | Google Scholar

152. Boyanovsky D. Clustering properties of a sterile neutrino dark matter candidate. Phys Rev D (2008) 78:103505. [0807.0646]. doi:10.1103/physrevd.78.103505

CrossRef Full Text | Google Scholar

153. Frigerio M, Yaguna CE. Sterile neutrino dark matter and low scale leptogenesis from a charged scalar. Eur Phys J C (2015) 75(31). [1409.0659]. doi:10.1140/epjc/s10052-014-3252-1

PubMed Abstract | CrossRef Full Text | Google Scholar

154. Drewes M, Kang JU. Sterile neutrino Dark Matter production from scalar decay in a thermal bath. JHEP (2016) 05(051). [1510.05646].

CrossRef Full Text | Google Scholar

155. Merle A, Niro V, Schmidt D. New production mechanism for keV sterile neutrino dark matter by decays of frozen-in scalars. JCAP (2014) 03028. 1306.3996.

CrossRef Full Text | Google Scholar

156. König J, Merle A, Totzauer M. keV sterile neutrino dark matter from singlet scalar decays: The most general case. JCAP (2016) 11:038. [1609.01289.

Google Scholar

157. Peccei RD, Quinn HR. CPConservation in the presence of pseudoparticles. Phys Rev Lett (1977) 38:1440–3. doi:10.1103/physrevlett.38.1440

CrossRef Full Text | Google Scholar

158. Peccei RD, Quinn HR. Constraints imposed byCPconservation in the presence of pseudoparticles. Phys Rev D (1977) 16:1791–7. doi:10.1103/physrevd.16.1791

CrossRef Full Text | Google Scholar

159. Weinberg S. A new light boson? Phys Rev Lett (1978) 40:223–6. doi:10.1103/physrevlett.40.223

CrossRef Full Text | Google Scholar

160. Wilczek F. Problem of StrongPandTInvariance in the presence of instantons. Phys Rev Lett (1978) 40:279–82. doi:10.1103/physrevlett.40.279

CrossRef Full Text | Google Scholar

161. Preskill J, Wise MB, Wilczek F. Cosmology of the invisible axion. Phys Lett B (1983) 120:127–32. doi:10.1016/0370-2693(83)90637-8

CrossRef Full Text | Google Scholar

162. Dine M, Fischler W. The not so harmless axion. Phys Lett B (1983) 120:137–41. doi:10.1016/0370-2693(83)90639-1

CrossRef Full Text | Google Scholar

163. Kamionkowski M, March-Russell J. Planck scale physics and the Peccei-Quinn mechanism. Phys Lett B (1992) 282:137–41. [hep-th/9202003]. doi:10.1016/0370-2693(92)90492-m

CrossRef Full Text | Google Scholar

164. Barr SM, Seckel D. Planck scale corrections to axion models. Phys Rev D (1992) 46:539–49. doi:10.1103/physrevd.46.539

PubMed Abstract | CrossRef Full Text | Google Scholar

165. Holman R, Hsu SDH, Kephart TW, Kolb EW, Watkins R, Widrow LM. Solutions to the strong CP problem in a world with gravity. Phys Lett B (1992) 282:132–6. [hep-ph/9203206]. doi:10.1016/0370-2693(92)90491-l

CrossRef Full Text | Google Scholar

166. Ghigna S, Lusignoli M, Roncadelli M. Instability of the invisible axion. Phys Lett B (1992) 283:278–81. doi:10.1016/0370-2693(92)90019-z

CrossRef Full Text | Google Scholar

167. Rubakov VA. Grand unification and heavy axion. JETP Lett (1997) 65:621–4. [hep-ph/9703409]. doi:10.1134/1.567390

CrossRef Full Text | Google Scholar

168. Holdom B, Peskin ME. Raising the axion mass. Nucl Phys B (1982) 208:397–412. doi:10.1016/0550-3213(82)90228-0

CrossRef Full Text | Google Scholar

169. Berezhiani Z, Gianfagna L, Giannotti M. Strong CP problem and mirror world: The Weinberg-Wilczek axion revisited. Phys Lett B (2001) 500:286–96. [hep-ph/0009290]. doi:10.1016/s0370-2693(00)01392-7

CrossRef Full Text | Google Scholar

170. Hook A. Anomalous solutions to the StrongCPProblem. Phys Rev Lett (2015) 114:141801. [1411.3325]. doi:10.1103/physrevlett.114.141801

PubMed Abstract | CrossRef Full Text | Google Scholar

171. Fukuda H, Harigaya K, Ibe M, Yanagida TT. Model of visible QCD axion. Phys Rev D (2015) 92:015021. [1504.06084]. doi:10.1103/physrevd.92.015021

CrossRef Full Text | Google Scholar

172. Gherghetta T, Nagata N, Shifman M. A visible QCD axion from an enlarged color group. Phys Rev D (2016) 93(115010). [1604.01127]. doi:10.1103/physrevd.93.115010

CrossRef Full Text | Google Scholar

173. Dimopoulos S, Hook A, Huang J, Marques-Tavares G. A collider observable QCD axion. JHEP (2016) 11(052). [1606.03097].

CrossRef Full Text | Google Scholar

174. Agrawal P, Howe K. Factoring the strong CP problem. JHEP (2018) 12(029). [1710.04213].

CrossRef Full Text | Google Scholar

175. Gaillard MK, Gavela MB, Houtz R, Quilez P, Del Rey R. Color unified dynamical axion. Eur Phys J C (2018) 78(972). [1805.06465]. doi:10.1140/epjc/s10052-018-6396-6

CrossRef Full Text | Google Scholar

176. Nelson AE, Seiberg N. R symmetry breaking versus supersymmetry breaking. Nucl Phys B (1994) 416:46–62. [hep-ph/9309299]. doi:10.1016/0550-3213(94)90577-0

CrossRef Full Text | Google Scholar

177. Goh H-S, Ibe M. R-axion detection at LHC. JHEP (2009) 03:049. 0810.5773.

CrossRef Full Text | Google Scholar

178. Bellazzini B, Mariotti A, Redigolo D, Sala F, Serra J. R-axion at colliders. Phys Rev Lett (2017) 119:141804. [1702.02152]. doi:10.1103/physrevlett.119.141804

PubMed Abstract | CrossRef Full Text | Google Scholar

179. Gripaios B, Pomarol A, Riva F, Serra J. Beyond the minimal composite Higgs model. JHEP (2009) 04:070. 0902.1483.

CrossRef Full Text | Google Scholar

180. Ferretti G, Karateev D. Fermionic UV completions of Composite Higgs models. JHEP (2014) 03077. [1312.5330].

CrossRef Full Text | Google Scholar

181. Belyaev A, Cacciapaglia G, Cai H, Flacke T, Parolini A, Serôdio H. Singlets in composite Higgs models in light of the LHC 750 GeV diphoton excess. Phys Rev D (2016) 015004. [1512.07242].

CrossRef Full Text | Google Scholar

182. Ferretti G. Gauge theories of partial compositeness: Scenarios for run-II of the LHC. JHEP (2016) 06:107. 1604.06467.

CrossRef Full Text | Google Scholar

183. Jeong KS, Jung TH, Shin CS. Axionic electroweak baryogenesis. Phys Lett B (2019) 790:326–31. [1806.02591]. doi:10.1016/j.physletb.2019.01.036

CrossRef Full Text | Google Scholar

184. Yue C-X, Zhang H-Y, Wang H. Production of axion-like particles via vector boson fusion at future electron-positron colliders. Eur Phys J C (2022) 82(88). [2112.11604]. doi:10.1140/epjc/s10052-022-10007-7

CrossRef Full Text | Google Scholar

185. Zhang H-Y, Yue C-X, Guo Y-C, Yang S. Searching for axionlike particles at future electron-positron colliders. Phys Rev D (2021) 104:096008. [2103.05218]. doi:10.1103/physrevd.104.096008

CrossRef Full Text | Google Scholar

186. Coelho RO, Goncalves VP, Martins DE, Rangel MS. Production of axionlike particles in PbPb collisions at the LHC, HE–LHC and FCC: A phenomenological analysis. Phys Lett B (2020) 806:135512. 2002.135512. doi:10.1016/j.physletb.2020.135512

CrossRef Full Text | Google Scholar

187. Bauer M, Neubert M, Thamm A. Collider probes of axion-like particles. JHEP (2017) 12:044. 1708.00443.

CrossRef Full Text | Google Scholar

188. Bauer M, Heiles M, Neubert M, Thamm A. Axion-like particles at future colliders. Eur Phys J C (2019) 79:74. 1808.74. doi:10.1140/epjc/s10052-019-6587-9

CrossRef Full Text | Google Scholar

189. Cacciapaglia G, Deandrea A, Iyer AM, Sridhar K. Tera-Z stage at future colliders and light composite axionlike particles. Phys Rev D (2022) 105:015020. [2104.11064]. doi:10.1103/physrevd.105.015020

CrossRef Full Text | Google Scholar

190. Spira M, Djouadi A, Graudenz D, Zerwas PM. Higgs boson production at the LHC. Nucl Phys B (1995) 453:17–82. [hep-ph/9504378]. doi:10.1016/0550-3213(95)00379-7

CrossRef Full Text | Google Scholar

191. Bauer M, Neubert M, Renner S, Schnubel M, Thamm A. The low-energy effective theory of axions and ALPs. JHEP (2021) 04:063. 2012.12272.

CrossRef Full Text | Google Scholar

192. Knapen S, Thamm A. Direct discovery of new light states at the FCCee. Eur Phys J Plus (2021) 136:936. 2108.08949. doi:10.1140/epjp/s13360-021-01874-2

CrossRef Full Text | Google Scholar

193. Schäfer R, Tillinger F, Westhoff S, Near or far detectors? Optimizing long-lived particle searches at electron-positron colliders, 2202.11714.

Google Scholar

194. Tian M, Wang K, Wang ZS, Search for long-lived axions with far detectors at future lepton colliders, 2201.08960.

Google Scholar

195. Frugiuele C, Fuchs E, Perez G, Schlaffer M. Relaxion and light (pseudo)scalars at the HL-LHC and lepton colliders. JHEP (2018) 10:151. 1807.10842.

CrossRef Full Text | Google Scholar

196. de Blas J, Ciuchini M, Franco E, Mishima S, Pierini M, Reina L et al. Electroweak precision observables and Higgs-boson signal strengths in the standard model and beyond: Present and future. JHEP (2016) 12(135). [1608.01509].

CrossRef Full Text | Google Scholar

197. de Blas J, Cepeda M, D’Hondt J, Ellis RK, Grojean C, Heinemann B et al. Higgs Boson Studies at Future Particle Colliders, 01139 (2020). 1905.03764.JHEP.

198. Cepeda M, Gori S, Outschoorn VM, Shelton J Exotic Higgs Decays, 2111. p. 12751.

199. Alipour-Fard S, Craig N, Jiang M, Koren S. Long live the Higgs factory: Higgs decays to long-lived particles at future lepton colliders. Chin Phys C (2019) 43:053101. [1812.05588]. doi:10.1088/1674-1137/43/5/053101

CrossRef Full Text | Google Scholar

200. Strassler MJ, Zurek KM. Echoes of a hidden valley at hadron colliders. Phys Lett B (2007) 651:374–9. [hep-ph/0604261]. doi:10.1016/j.physletb.2007.06.055

CrossRef Full Text | Google Scholar

201. Strassler MJ, Zurek KM. Discovering the Higgs through highly-displaced vertices. Phys Lett B (2008) 661:263–7. [hep-ph/0605193]. doi:10.1016/j.physletb.2008.02.008

CrossRef Full Text | Google Scholar

202. Han T, Si Z, Zurek KM, Strassler MJ. Phenomenology of hidden valleys at hadron colliders. JHEP (2008) 07:008. [0712.2041.

CrossRef Full Text | Google Scholar

203. Chacko Z, Goh H-S, Harnik R. The Twin Higgs: Natural electroweak breaking from mirror symmetry. Phys Rev Lett (2006) 96:231802. [hep-ph/0506256]. doi:10.1103/physrevlett.96.231802

PubMed Abstract | CrossRef Full Text | Google Scholar

204. Burdman G, Chacko Z, Goh H-S, Harnik R. Folded supersymmetry and the LEP paradox. JHEP (2007) 02:009. [hep-ph/0609152].

CrossRef Full Text | Google Scholar

205. Cai H, Cheng H-C, Terning J. A quirky little Higgs model. JHEP (2009) 05:045. 0812.0843.

CrossRef Full Text | Google Scholar

206. Craig N, Katz A, Strassler M, Sundrum R. Naturalness in the dark at the LHC. JHEP (2015) 07:105. [1501.05310].

CrossRef Full Text | Google Scholar

207. Curtin D, Essig R, Gori S, Jaiswal P, Katz A, Liu T et al. Exotic decays of the 125 GeV Higgs boson. Phys Rev D (2014) 90:075004. [1312.4992]. doi:10.1103/physrevd.90.075004

CrossRef Full Text | Google Scholar

208. Haisch U, Kamenik JF, Malinauskas A, Spira M. Collider constraints on light pseudoscalars. JHEP (2018) 03:178. 1802.02156.

CrossRef Full Text | Google Scholar

209. Fuchs E, Matsedonskyi O, Savoray I, Schlaffer M. Collider searches for scalar singlets across lifetimes. JHEP (2021) 04:019. 2008.12773.

CrossRef Full Text | Google Scholar

210. Cui Y, Shuve B. Probing baryogenesis with displaced vertices at the LHC. JHEP (2015) 02:049. 1409.6729.

CrossRef Full Text | Google Scholar

211. Batell B, Pospelov M, Shuve B. Shedding light on neutrino masses with dark forces. JHEP (2016) 08:052. 1604.06099.

CrossRef Full Text | Google Scholar

212. Accomando E, Delle Rose L, Moretti S, Olaiya E, Shepherd-Themistocleous CH. Novel SM-like Higgs decay into displaced heavy neutrino pairs in U(1)’ models. JHEP (2017) 04:081. 1612.05977.

Google Scholar

213. Accomando E, Delle Rose L, Moretti S, Olaiya E, Shepherd-Themistocleous CH. Extra Higgs boson and Z’ as portals to signatures of heavy neutrinos at the LHC. JHEP (2018) 02:109. 1708.03650.

CrossRef Full Text | Google Scholar

214. Curtin D, Essig R, Gori S, Shelton J. Illuminating dark photons with high-energy colliders. JHEP (2015) 02157. [1412.0018].

CrossRef Full Text | Google Scholar

215. Stelzer T, Long WF. Automatic generation of tree level helicity amplitudes. Comput Phys Commun (1994) 81:357–71. [hep-ph/9401258]. doi:10.1016/0010-4655(94)90084-1

CrossRef Full Text | Google Scholar

216. Alwall J, Frederix R, Frixione S, Hirschi V, Maltoni F, Mattelaer O et al. The automated computation of tree-level and next-to-leading order differential cross sections, and their matching to parton shower simulations. JHEP (2014) 07(079). [1405.0301].

CrossRef Full Text | Google Scholar

217. Sjöstrand T, Ask S, Christiansen JR, Corke R, Desai N, Ilten P et al. An introduction to PYTHIA 8.2. Comput Phys Commun (2015) 191(159)–77. [1410.3012]. doi:10.1016/j.cpc.2015.01.024

CrossRef Full Text | Google Scholar

218.DELPHES 3 collaboration, de Favereau J, Delaere C, Demin P, Giammanco A, Lemaître V, Mertens A et al. DELPHES 3, A modular framework for fast simulation of a generic collider experiment. JHEP (2014) 02:057. 1307.6346.

CrossRef Full Text | Google Scholar

219.collaboration, Antonello M. Idea: A detector concept for future leptonic colliders. Nuovo Cim C (2020) 43:27.

Google Scholar

220. Volkl V, Madlener T, Helsens C, key4hep/k4simdelphes: v00-01-07, 2021. doi:10.5281/zenodo.5585287

CrossRef Full Text | Google Scholar

221. Volkl V, Madlener T, Gaede F, Sailer A, Helsens C, Declara PF et al. key4hep/edm4hep: v00-04, 2021. doi:10.5281/zenodo.5585967

CrossRef Full Text | Google Scholar

222. Guiraud E, Naumann A, Piparo D. Tdataframe: Functional chains for root data analyses (2017). doi:10.5281/zenodo.260230

CrossRef Full Text | Google Scholar

223. Brun R, root-project/root: v6.18/02, 2019. doi:10.5281/zenodo.3895860

CrossRef Full Text | Google Scholar

224. Ai X, Allaire C, Calace N, Gessinger P, Grasland H, Gray H et al. Acts project: v8.3.0, 2021. doi:10.5281/zenodo.4818137

CrossRef Full Text | Google Scholar

225. Cacciari M, Salam GP, Soyez G. FastJet user manual. Eur Phys J C (2012) 72:1896. [1111.6097]. doi:10.1140/epjc/s10052-012-1896-2

CrossRef Full Text | Google Scholar

226. Pivarski J, Osborne I, Das P, Hollands A, Schreiner H, Biswas A et al. scikit-hep/awkward-1.0: 1.8.0rc3, 2022. doi:10.5281/zenodo.5885291

CrossRef Full Text | Google Scholar

227. Alva D, Han T, Ruiz R. Heavy Majorana neutrinos from Wγ fusion at hadron colliders. JHEP (2015) 02:072. [1411.7305].

CrossRef Full Text | Google Scholar

228. Degrande C, Mattelaer O, Ruiz R, Turner J. Fully-Automated precision predictions for heavy neutrino production mechanisms at hadron colliders. Phys Rev D (2016) 94:053002. [1602.06957]. doi:10.1103/physrevd.94.053002

CrossRef Full Text | Google Scholar

229. Christensen ND, Duhr C. FeynRules - Feynman rules made easy. Comput Phys Commun (2009) 180:1614–41. [0806.4194]. doi:10.1016/j.cpc.2009.02.018

CrossRef Full Text | Google Scholar

230. Degrande C, Duhr C, Fuks B, Grellscheid D, Mattelaer O, Reiter T. UFO - the universal FeynRules output. Comput Phys Commun (2012) 183:1201–14. [1108.2040]. doi:10.1016/j.cpc.2012.01.022

CrossRef Full Text | Google Scholar

231. Alloul A, Christensen ND, Degrande C, Duhr C, Fuks B. FeynRules 2.0 -a complete toolbox for tree-level phenomenology. Comput Phys Commun (2014) 185:2250–300. [1310.1921]. doi:10.1016/j.cpc.2014.04.012

CrossRef Full Text | Google Scholar

232. Bacchetta N, Cld – a detector concept for the FCC-ee, (2019) 1911.12230.

Google Scholar

233. Ruiz RE. PhD thesis, 1509. Pittsburgh U. (2015). p. 06375.Hadron Collider Tests of Neutrino Mass-Generating Mechanisms.